【推荐】六年级下册数学试题-小升初专题练习:平面几何(一) 全国通用
六年级下册数学试题-小升初专项练习题:数论(1)(解析版)全国通用

小升初专项练习题数论1.【★】连续7个偶数的和是196.这7个数中最大的一个偶数是多少?【分析】 2468101242+++++=(19642)722-÷=这七个数分别是22,24,26,28,30,32,34最大是342.【★★】一个三位数除以43,商是a ,余数是b (a 、b 都是正数).求a +b 的最大值.【分析】 999432310÷= 那么一个三位数÷43=2242为余数最大.这个数432242988=⨯+= 最大值224264=+=.3.【★★】(1)把17分成两个自然数的和,使它们的乘积最大,应该怎样分?(2)把17分成若干个自然数的和,要是这几个数的乘积最大,应该怎样分?【分析】 (1)8和9(2)3,3,3,3,3,24.【★★】有四个不同的自然数,它们的和是1111,则它们的最大公约数最大是( ).【分析】 111111101=⨯, 111235=+++∴四个数分别1011101,⨯= 1012202,⨯=1013303,⨯= 1015505⨯=最大公约数为101.5.【★★】(2003年一零一培训学校期末考试题(2003年12月)第7题)一个整数m (m ≠1),除219,270,338得到的余数相同,则这个整数m =__________。
【分析】 219,270,338除以m 得到的余数相同,那么他们两两的差就能被m 整除。
270-219=51,33827068-=,338219119-=,m =[51,68,119]=17。
6.【★★】(北京市一零一中学计算机培训班六年级04~05学年一学期第三次随堂测试第10题)① 222(101)(1011)(11011)⨯-=___________② 852567(((=== ) ) );③ 2222(11000111(10101(11(-÷=))) );④ 473021605+=()() ( )10;⑤若(1030)140n =,则n =____________。
全国通用六年级下册数学试题-小升初强化:平面几何综合(下)(解析版)

如图,在四边形 ABCD 中,对角线 AC、BD 交于 E,且 AF=CE,BG=DE,如果四边形 ABCD 面积是 1,求△ EFG 的面积?
F
D
F
D
A E
A E
B
C
B
C
G
G
【解析】连结 AG、CG,如右图所示, AF EC ,有 SAGF SCGE ,又因为 BG=DE,有 SAED SABG ,且 SCDE SBCG 由此可见:△EFG 的三个部分中 SABG 补到了 SEAD , SAFG 补到了 SBCD ,而 SAEB 的位置不变, 由此一来相当于将△EFG 等积变形到了四边形 ABCD,两者面积相同,即: SEFG 1。
在四边形 ABCD 中,已知 SAOB 2 平方厘米, SAOD 3 平方厘米, SDOC 60 平方厘米,求三角形 BCO 的 面积是多少?
D
A3 O6
2
B
C
【解析】根据蝴蝶定理, SBOC 2 6 3 4 (平方厘米)。
如图,在平行四边形 ABCD 中,E、F 分别是 AC、BC 的三等分点,且 SABCD 54 平方厘米,求 SBEF 。
即 SPMN =42÷21×3=6(平方厘米)。
有红、黄、绿三块大小一样的正方形纸片,放在一个正方形盒内,它们之间相互叠合(如左下图),已知 露在外面的部分中,红色面积是 20,黄色面积是 12,绿色面积是 8,那么正方形盒的底面积是多少?
红 红红
【解析】黄色纸片露出部分与绿色纸片露出部分面积不同,由于三块纸片的大小一样,把黄色纸片向左 移动,在这个移动过程中,黄色纸片露出部分减少的面积等于绿色纸片纸片露出部分增加的面积,它们 露出部分的面积和不变,为 8+12=20。当黄色纸片移动到正方形盒的最左边时,如右上图所示,可知此 时黄色纸片露出部分与绿色纸片露出部分的面积相等,所以黄色纸片露出部分面积为 20÷2=10,绿色纸 片露出面积也为 10。右上图中,由于红色部分面积是绿色部分面积的 20÷10=2 倍,所以黄色部分面积 是空白部分面积的 2 倍。所以空白部分的面积为 10÷2=5,正方形盒的底面积为 20+10+10+5=45。 解答此题的关键是让黄色纸片移动,使复杂的图形变为基本图形。
【小升初】六年级下册数学总复习试题-应用题 专项练(含答案)

【小升初】六年级下册数学总复习试题-应用题专项练(含答案)一、列方程解应用题【基础概念】:列方程解决问题就是根据题目中的等量关系先列出方程,再求得问题中的未知量的一种解决问题的方法。
把所求问题用一个字母表示,并让其参与分析与列式,很快理清题中的数量关系,可以使一些整数、分数、百分数的应用题化难为易,既可以节省时间,又可以提高解题能力。
【典型例题1】:贵诚超市推销一种积压商品,减价25%出售,每件售价42元,原定价是多少元?【思路分析】:本题中的等量关系是:原价-减少的钱数=现价,减少的钱数=原价×25%,所以原价-原价×25%=现价,即可解决。
【解答】:解:设原定价是x元x-x×25%=4275%x=42x=56答:原定价是56元。
【小结】:解决这类问题首先要找到等量关系——原价-减少的钱数=现价,再根据等量关系列出方程,从而解决问题。
【巩固练习】1.列方程解答。
2.列方程解答。
【典型例题2】:甲乙两地相距480千米,客货两车同时从甲乙两地相向而行,客车平均每小时行65千米,货车平均每小时行60千米,行驶了3小时,这时两车还相距多少千米?【思路分析】:本题中的等量关系是:行驶的路程+剩下的路程=甲乙两地的距离,由于客车每小时行65千米,货车每小时行60千米,行驶了3小时,根据速度和×行驶的时间=行驶的路程,(65+60)×3就是行驶的路程,再设剩下的路程为x千米,列出方程:(65+60)×3+x=480,解出方程即可。
【解答】:解; 设剩下的路程为x千米,(65+60)×3+x=480125×3+x=480x=105答:这时两车还相距105千米。
【小结】:解决这类问题的关键是要明确“行驶的路程、剩下的路程、甲乙两地的距离”之间的关系,即行驶的路程+剩下的路程=甲乙两地的距离,列出方程解答即可。
【巩固练习】3. 甲乙两地相距480千米.客车和货车同时从两地相对开出,相向而行,4小时后,两车还相距80千米.已知货车每小时行53千米,问客车每小时行多少千米?4.一辆客车和一辆货车从甲乙两地同时出发相向而行,经过45 小时两车相遇,这时货车行了全程的40%,已知货车每小时行60千米,求甲乙两地的距离。
六年级下册数学试题-小升初能力训练:几何综合——立体几何(解析版)全国通用
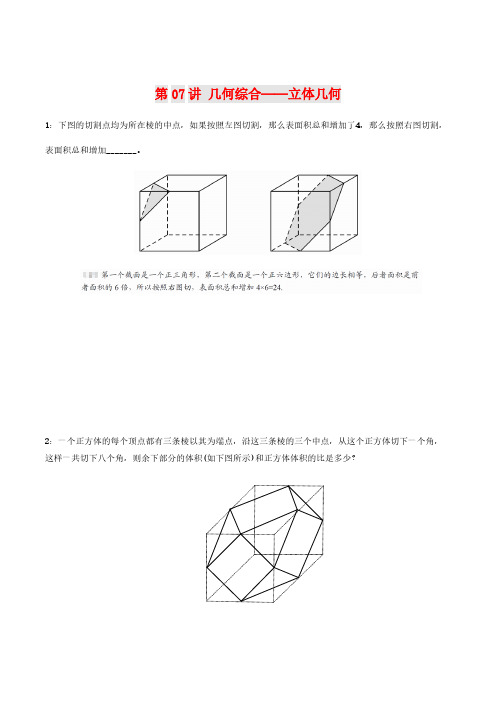
第07讲几何综合——立体几何1:下图的切割点均为所在棱的中点,如果按照左图切割,那么表面积总和增加了4,那么按照右图切割,表面积总和增加_______。
2:一个正方体的每个顶点都有三条棱以其为端点,沿这三条棱的三个中点,从这个正方体切下一个角,这样一共切下八个角,则余下部分的体积(如下图所示)和正方体体积的比是多少?假设正方体的边长为1,那么每个切去的角(三棱锥)的体积为,211111322248⎛⎫⨯⨯⨯= ⎪⎝⎭所以八个角一共切去的体积,所以余下的体积是正方体体积的,118486⨯=15166-=即余下部分的体积与正方体体积的比为.5:63:如图,原正方体的棱长为12厘米,沿图中的线将正方体切掉正面的部分,求剩下不规则立体图形的体积.倾斜于上下底面的切面,把正方体一分为二.被切掉的部分的图形和剩下的部分图形关于正方形的中心是对称的.33122864(cm )÷=4:如图,正方体的棱长为,连接正方体其中六条棱的中点形成一个正六边形,而连接其中三个顶点6cm 形成一个正三角形.正方体夹在六边形与三角形之间的立体图形有 个面,它的体积是.3cm乙9乙从图中可以看出,夹在六边形与三角形之间的立体图形有2个底面和6个侧面(六边形的每一条边对应一个侧面),所以共有个面,8由于正方体是关于它的中心成中心对称的,而根据正六边形和正三角形的连法,如果从正方体中去掉以这个正三角形为底面的三棱锥以及与它相对的三棱锥后,剩下的部分正好被六边形分成2个同样的立体图形,这就是所要求的立体图形.所以所要求的立体图形的体积是:.3111666266672(cm )232⎡⎤⎛⎫⨯⨯⨯-⨯⨯⨯⨯⨯= ⎪⎢⎥⎝⎭⎣⎦5:如图,有一个棱长为2厘米的正方体。
从正方体的上面正中间下挖一个棱长为1厘米的正方体小洞;接着在小洞的底面正中间再向下挖一个棱长为厘米的小洞;第三个小洞的挖法与前面两个相同,棱长为12厘米,最后得到的额例题图形的表面积是多少平方厘米?146:如图,把正方体用两个与它的底面平行的平面切开,分成三个长方体,这三个长方体的表面积比是3:4:5时,用最简单的整数比表示这三个长方体的体积比:::。
六年级下册数学试题-小升初专项练习:长方体与正方体(无答案)全国通用

长方体与正方体一、填空题1、一个正方体的底面积是25平方分米,它的表面积是()平方分米,它的体积是()立方分米。
2、有一个长方体木料长3厘米、宽3厘米、高2厘米。
把它切成1立方厘米的小方块可以切成()块。
3、有一个正方体,棱长3厘米。
若将每条棱长扩大到2倍,这个正方体的体积应是(),表面积应是()。
4、两个正方体组成一个长方体后,长方体的棱长总和是32厘米,那么它的表面积(),体积()。
5、一个7分米高的长方体,横截成两个长方体,表面积增加11平方分米,原来这个长方体的体积是( )。
二、判断题6、长方体和正方体的表面积相等,他们的体积也相等。
()7、长方体长扩大两倍,表面积好体积都扩大2倍。
()8、正方体的底面周长是20厘米,它的体积是125厘米。
( )9、两个长方体体积相等,它们的表面积也一定相等。
()10、正方体棱长扩大5倍,体积扩大15倍。
()三、解决问题11、东山乡要挖一条长是1.2千米,上口宽3米,下底宽1.2米,深1.5米的灌溉渠,计划15天挖完,平均每天挖多少立方米?12、个长方体玻璃缸,底面积是200平方厘米,高8厘米,里面盛有4厘米深的水,现在将一块石头放入水中,水面升高2厘米。
这块石头的体积是多少立方厘米?13、把一个体积为80立方厘米的铁块浸在底面积为20平方厘米的长方体容器中,水面高度为10厘米,如果把铁块捞出后,水面高多少14、一个长方体形状的儿童游泳池,长40米、宽14米,深1.2米。
现在要在四壁和池底贴上面积为16平方分米的正方形瓷砖,需要多少块?15、把一个长方体的宽增加2厘米,就变成一个棱长为10厘米的正方体,原来长方体的体积是多少立方厘米?【想一想】:求下列物体的体积。
(单位:厘米)(1) (2)。
六年级下册数学试题-小升初:8-用到的几何三大模型(无答案)全国通用
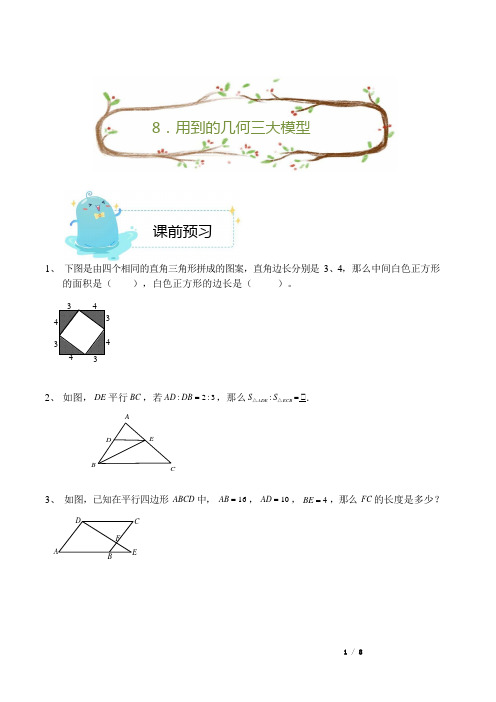
FA E 8.用到的几何三大模型课前预习1、下图是由四个相同的直角三角形拼成的图案,直角边长分别是3、4,那么中间白色正方形的面积是(),白色正方形的边长是()。
3 434434 32、如图,DE 平行BC ,若AD : DB = 2 : 3 ,那么S△ADE : S△E CB = .AEDBC3、如图,已知在平行四边形ABCD 中,AB = 16 ,AD = 10 ,BE = 4 ,那么FC 的长度是多少?D C模块一 勾股定理要点复习在直角三角形当中,两直角边长为 a 、b ,斜边长为 c 。
a b则a 2 + b 2 = c 2 ,在我国被称为勾股定理,而西方则称其为毕达哥拉斯定理。
常见勾股(整)数: 例11、 下面的折线 A-B-C-D-E ,相邻线段都是垂直的,并且 AB=7,BC=11,CD=13,DE=4,求A 、E 两点的距离。
DEB A2、 求下列梯形的周长和面积.1020 22Ca b c 3k 4k 5k 5k 12k 13k 7k 24k 25k 9k 40k 41k 8k 15k 17kc例21、下列两个图形都是以直角三角形ABC 的三边为边长向外作三个正方形,正方形内的数代表正方形的面积,求未知正方形的面积.A ?C2、如图在美丽的毕达哥拉斯树中,三角形都是直角三角形,四边形都是正方形,已知所有的正方形面积总共是80,那么最大的正方形面积是多少?例3如图,长方形ABCD 的长是5,宽是1。
现将长方形的右下角折到左上角,三角形ABM 的面积是多少?N DA1B C5M?3B14例4如图,已知ABFG 和BEDC 是两个正方形,其中AB 垂直于BC,GO//AC,AC=14,则四边形BEDO 的面积为()模块二金字塔模型要点复习金字塔模型AD F EB CG①AD =AE =DE =AF;AB AC BC AG=AF 2 : AG2 .②S△ADE:S△ABC例5如图,测量小玻璃管口径的量具ABC ,AB 的长为15 厘米,AC 被分为60 等份.如果小玻璃管口DE 正好对着量具上20 等份处( DE 平行AB ),那么小玻璃管口径DE 是多大?BEA0 10 20 30 40 50 60例6如图,△ABC 中,DE ,FG ,BC互相平行,AD =DF =FB ,则S△ADE : S四边形DEGF : S四边形FGCB=(A)。
全国通用六年级下册数学试题-小升初强化:平面几何综合(下)(解析版)
A
D
E
B
F
C
【解析】 S ABC
1 2 S ABCD
1 54 2
27
(平方厘米), SBCE
2 3 S ABC
2 27 3
18 (平方厘米),
S BEF
1 3 SBCE
1 18 3
6 (平方厘米)。
将同学们编为两组,做脑筋急转弯的游戏,一组出题,另一组回答,轮流进行。同学们有很多这样的题 目,仅举两例,抛砖引玉。
如图,平行四边形 BDEF 的底 BD=15 厘米,三角形 AFE 的高 AG=15 厘米,三角形 ABC 的底 BC=25 厘米, 则阴影部分的面积为多少平方厘米?
A
A
H
I
F B
E G
D
C
F B
E
G
J
D
C
【解析】因为 SABC SCAI , SAEF SEAH , SEDC SCEJ ; 所以 SABC SAEF SEDC SCAI SEAH SCEJ ,即 SBDEF SEHIJ ;
A
D
O
G
E
B
F
C
【解析】设△DEO 的面积为 x,那么 SDFG 4 x ,在梯形 ADFB 中根据蝴蝶定理, SABG SDFG 4 x ,
因为 SODC
1 4
S矩形ABCD
1 4
85
10 (平方厘米), SDEC
10
x ,所以
SABG SDEC 4 x 10 x 14 (平方厘米)。
即 SPMN =42÷21×3=6(平方厘米)。
有红、黄、绿三块大小一样的正方形纸片,放在一个正方形盒内,它们之间相互叠合(如左下图),已知 露在外面的部分中,红色面积是 20,黄色面积是 12,绿色面积是 8,那么正方形盒的底面积是多少?
小升初六年级奥数——几何(平面图形)
⼩升初六年级奥数——⼏何(平⾯图形)⼀、分数百分数问题,⽐和⽐例这是六年级的重点内容,在历年各个学校测试中所占⽐例⾮常⾼,重点应该掌握好以下内容:对单位1的正确理解,知道甲⽐⼄多百分之⼏和⼄⽐甲少百分之⼏的区别;求单位1的正确⽅法,⽤具体的量去除以对应的分率,找到对应关系是重点;分数⽐和整数⽐的转化,了解正⽐和反⽐关系;通过对“份数”的理解结合⽐例解决和倍(按⽐例分配)和差倍问题;⼆、⾏程问题应⽤题⾥最重要的内容,因为综合考察了学⽣⽐例,⽅程的运⽤以及分析复杂问题的能⼒,所以常常作为压轴题出现,重点应该掌握以下内容:路程速度时间三个量之间的⽐例关系,即当路程⼀定时,速度与时间成反⽐;速度⼀定时,路程与时间成正⽐;时间⼀定时,速度与路程成正⽐。
特别需要强调的是在很多题⽬中⼀定要先去找到这个“⼀定”的量;当三个量均不相等时,学会通过其中两个量的⽐例关系求第三个量的⽐;学会⽤⽐例的⽅法分析解决⼀般的⾏程问题;有了以上基础,进⼀步加强多次相遇追及问题及⽕车过桥流⽔⾏船等特殊⾏程问题的理解,重点是学会如何去分析⼀个复杂的题⽬,⽽不是⼀味的做题;三、⼏何问题⼏何问题是各个学校考察的重点内容,分为平⾯⼏何和⽴体⼏何两⼤块,具体的平⾯⼏何⾥分为直线形问题和圆与扇形;⽴体⼏何⾥分为表⾯积和体积两⼤部分内容。
学⽣应重点掌握以下内容:等积变换及⾯积中⽐例的应⽤;与圆和扇形的周长⾯积相关的⼏何问题,处理不规则图形问题的相关⽅法;⽴体图形⾯积:染⾊问题、切⾯问题、投影法、切挖问题;⽴体图形体积:简单体积求解、体积变换、浸泡问题;四、数论问题常考内容,⽽且可以应⽤于策略问题,数字谜问题,计算问题等其他专题中,相当重要,应重点掌握以下内容:掌握被特殊整数整除的性质,如数字和能被9整除的整数⼀定是9的倍数等;最好了解其中的道理,因为这个⽅法可以⽤在许多题⽬中,包括⼀些数字谜问题;掌握约数倍数的性质,会⽤分解质因数法,短除法,辗转相除法求两个数的最⼤公因数和最⼩公倍数;学会求约数个数的⽅法,为了提⾼灵活运⽤的能⼒,需了解这个⽅法的原理;了解同余的概念,学会把余数问题转化成整除问题,下⾯的这个性质是⾮常有⽤的:两个数被第三个数去除,如果所得的余数相同,那么这两个数的差就能被这个数整除;能够解决求⼀个多位数除以⼀个较⼩的⾃然数所得的余数问题,例如求1011121314 (9)899除以11的余数,以及求20082008除以13的余数这类问题;五、计算问题计算问题通常在前⼏个题⽬中出现概率较⾼,主要考察两个⽅⾯,⼀个是基本的四则运算能⼒,同时,⼀些速算巧算及裂项换元等技巧也经常成为考察的重点。
六年级下册数学试题-小升初强化:图形面积I(下)(解析版)全国通用
第一讲图形面积I(下)1、巩固并熟练应用三角形面积公式求解各类题型,复习前一讲内容;2、根据题目的特点运用非常规方法进一步巧妙解题;3、让学员在操作、观察、讨论、归纳等数学活动过程中,培养学员学习数学的兴趣。
在实际问题的研究中,我们还会常常用到以下结论:(1)等底等高的两个三角形面积相等。
(2)若两个三角形的高相等,其中一个三角形的底是另一个三角形的几倍,那么这个三角形的面积也是另一个三角形面积的几倍。
若两个三角形的底相等,其中一个三角形的高是另一个三角形的几倍,那么这个三角形的面积也是另一个三角形面积的几倍。
(3)夹在一组平行线之间的等积变形,如下图,△ACD和△BCD夹在一组平行线之间,且有公共底边CD, 那么ACD BCDS S∆∆=;反之,如果ACD BCDS S∆∆=,则可知直线AB平行于CD。
讲演者:得分:如图,平行四边形ABCD中,AD为20厘米,高CH为9厘米;E是底边BC上的一点,且BE为6厘米,那么两个阴影三角形的面积之和是多少平方厘米?【解析】观察图形,可得阴影部分的面积是整个平行四边形的一半。
平行四边形的面积=20×9=180平方厘米;180÷2=90平方厘米。
解答:两个阴影三角形的面积之和是90平方厘米。
讲演者:得分:如图,已知三角形ABC面积为1,延长AB至D,使BD=AB;延长BC至E,使CE=2BC;延长CA至F,使AF=3AC,求三角形DEF的面积。
ABCDEF【解析】本题是性质的反复使用;连接AE 、CD 、BF ,1111ABC ABC DBC DBC S S S S ∆∆∆∆==∴=,;同理可得其它,最后三角形DEF 的面积=18如图,长方形ABCD 的长为18厘米,宽为10厘米,P 是BC 上一点,且CP 为4厘米。
又已知E 、F 、G 分别是AB 、AD 、CD 边上的中点,那么阴影部分的总面积是多少平方厘米?【解析】观察图形,△AEP和△CGP的底相同,高的和为BC的长。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
平面几何(一)
1.一张长为10厘米,宽为8厘米的长方形纸片,把它剪开成两张同样的长方形纸片,每个
小长方形纸片的周长为多少厘米?
2.一个正方形相邻两条边的长度,如果分别增加它的12和它的14,那么所得的新长方形的
周长比原正方形的周长增加了百分之几?
3.有一块长方形草地,长20米,宽15米。在它的四周向外筑一条宽2米的小路,求小路
的面积。
4.如图,把正方形的土地分成如下四个长方形(它们的面积分别为10平方米、20平方米、
30平方米、40平方米),阴影部分是正方形且它包含在40平方米的长方形之内。求阴影部
分的面积。
5.如图中阴影部分的面积是多少?(单位:cm)
6.如图,求阴影部分的面积。(单位:厘米)
7.等腰三角形的面积为8平方厘米,求图中阴影部分的面积。
8.图中的两个正方形的边长分别是10厘米和6厘米,求阴影部分的面积。
9.如图所示的7个圆相切于一点,若圆的半径分别是(单位:分米)1、2、3、4、5、6、7,
则图中阴影部分的面是多少平方米?(π取3)
10.如图所示,BE长5厘米,长方形AEFD面积是38平方厘米。求CD的长度。
1.求阴影部分的周长。
2.把一个长8厘米 宽4厘米的长方形,如图所示折一折,得到右面图形,则阴影部分四个
三角形的周长之和是多少厘米?
课后练习
3.一个长方形花坛面积是6平方米,如果长增加13,宽增加14,现在的面积比原来增加多
少平方米?
4.用两块长方形纸片和一块正方形纸片围成一个新的大正方形纸片,两块长方形纸片的面
积分别是44平方厘米和28平方厘米。那么正方形纸片的面积是多少平方厘米?
5.小方桌的边长是1米,把它的四边撑开就成了一张圆桌(如图)求圆桌的面积。
6.在半径为10cm的圆内,C为AO的中点,则阴影的面积为多少?
7.图中阴影部分的面积是57平方厘米,求这个正方形的面积。
8.如图:阴影三角形的面积是多少?
9.下图是两个完全一样的直角三角形重叠在一起,按照图中的已知条件求阴影部分的面积
(单位:厘米)。
10.如图,直角△ABC的斜边AB=10,BC=5,∠ABC=60°,以点B为中心,将△ABC顺
时针旋转120°,点 A、C分别到达点E、D,则 AC边扫过的面积(即图中阴影部分的面积)
是多少? ( 取 3)
