考点6
高中历史一轮复习考点规范练6 辽宋夏金元的经济、社会与文化(含答案)

考点规范练辽宋夏金元的经济、社会与文化一、选择题1.(2021湖南卷,5)宋孝宗时绍兴府赈灾,有人户状告“检放秋苗不尽不实”。
朱熹受命调查后发现确实存在不实,但是当时田土大多已经种麦,没有稻根可据以核查受灾面积。
这反映了()A.绍兴府行政效率低下B.理学强调实事求是的精神C.宋代赈灾方式不合理D.绍兴农业精耕细作的特点2.宋代土地买卖盛行,出现“千年田换八百主”“田宅无定主”的现象,政府出台了较为严格的法律,对土地买卖实行规范化管理,要求买卖双方在政府机构办理登记备案手续,作为土地产权转移的证明。
这一做法()A.促进了土地私有制发展B.反映了宋代商业立法的完备C.有效保护了自耕农经济D.说明政府立法抑制土地兼并3.下面是北宋熙宁十年(1077)的商税统计情况表。
据此可以得出的结论是当时南方()A.已成为全国经济重心B.商业环境较北方优越C.农业生产较北方发达D.人口增长率高于北方4.下面是元朝各地的粮食岁收情况表(单位:石)。
据此可知元朝()A.继续维持重农抑商政策B.政治经济核心优势明显C.苏湖地区成为农业中心D.边远地区经济快速发展5.(2022福建厦门四模)宋元时期,市舶司对进出港船舶所载货物实行抽分(收取商税),元朝时期颁布的至元《市舶则法》规定“番货双抽,土货单抽”,这()A.体现了厚往薄来的理念B.突破了闭关自守的桎梏C.维护了自然经济的稳定D.推动了出口贸易的发展6.宋朝政府对土地买卖、典当基本不加干预,经营者仅办理法律手续,缴纳交易税即可。
对于百姓迁移住所、更换职业以及日常生活标准,官府也不再严格限制。
这主要说明宋朝()A.土地兼并日益严重B.对社会的控制有所放松C.社会矛盾趋向缓和D.政府行政能力显著降低7.(2021全国乙卷,26)宋代,官府强调“民生性命在农,国家根本在农,天下事莫重于农”,“毋舍本逐末”。
苏辙说:“凡今农工商贾之家,未有不舍其旧而为士者也。
”郑至道说,士农工商“皆百姓之本业,自生民以来未有能易之者也”。
高考地理微考点强化6:航天基地选择的区位条件

高考地理微考点强化6:航天基地选择的区位条件【考点规律】了解卫星发射基地的选址与各地理要素(纬度、气象、交通等)之间的关系,并结合材料判断某发射基地的区位优势。
【必背要点】1、航天发射基地选址的条件2、航天返回基地选择的条件①地势平坦开阔;②人烟稀少,有利于安全;③无大河、湖泊,少森林地区;④地质条件好;⑤气候干旱,多晴朗天气,能见度高。
【强化训练1】我国预计在2018年前后发射空间站的核心舱,逐步建立自己的空间站。
在此之前,“天宫二号”已经在酒泉卫星发射中心发射升空。
据此回答(1)~(2)题。
(1)相对于海南文昌卫星发射中心,酒泉卫星发射中心的优势主要在于( )A.纬度低,地球自转线速度大,可节省燃料B.降水少,晴天多,发射窗口期长(发射窗口期:适合卫星发射的时间段)C.空中及海上交通都很方便,便于运输D.无人区面积广,发射后残骸不危及人民安全(2)下列有关太阳活动对空间站影响的叙述,正确的是( )A.太阳活动对空间站的影响可以忽略B.空间站在地面实验过程中不会受到太阳活动的影响C.太阳黑子比耀斑对空间站的影响大D.太阳活动会影响空间站的安全及地—空联系(通信)【强化训练2】下图是世界某区域略图。
读图,回答问题。
简述①地建设航天发射基地的有利条件和不利因素。
【答案解析】【强化训练1】(1)海南文昌发射中心纬度低,地球自转线速度大,海上交通更方便,也更安全;而酒泉卫星发射中心位于我国西北,降水少,晴天多,发射窗口期长。
故B项正确。
(2)太阳活动严重影响空间站,也会影响地面;耀斑爆发,其高能带电粒子会影响无线电短波通信;太阳黑子是光球层温度的变化造成的,对空间站影响较小。
故D项正确。
【强化训练2】答案:有利条件:纬度低、海运便利、地形平坦开阔、人口稀少等。
不利因素:天气多变。
解析:分析该题有利条件注意从①地的纬度位置、海陆位置、地形、人口分布等角度分析。
①地为热带雨林气候,阴雨天气较多,对航天发射不利。
注安技术:低压电器设备必考点与6个记忆口诀全考点

注安技术:低压电器设备必考点与6个记忆口诀全考点一、电气设备外壳防护等级第一种防护:防固体异物进入或人体接触的等级防护等级简称防护性能O无防护没有专门的防护1防护大于50mm的固体能防止直径大于50mm的固体异物进入壳内;能防止人体的某一大面积部分(如手)偶然或意外触及壳内带电或运动部分,但不能防止有意识地接近这些部分2防护大于12mm的固体能防止直径大于12mm的固体异物进入壳内;能防止手指触及壳内带电或运动部分3防护大于2.5mm的固体能防止直径大于2.5mm的固体异物进人壳内;能防止厚度(或直径)大于2.5mm的工具、金属线等触及壳内带电或运动部分4防护大于1mm的固体能防止直径大于Imnm的固体异物进入壳内;能防止厚度(或直轻)大于Imm的工具、金属线等触及壳内带电或运动部分5防尘能防止灰尘进人达到影响产品正常运行的程度;能完全防止触及壳内带电或运动部分6尘密能完全防止灰尘进人壳内;能完全防止触及壳内带电运动部分记忆口诀:0123456,无5012251尘密第二种防护:防水进入的等级简称防护性能防护等级0无防护没有专门的防护1防滴垂直的滴水不能直接进入产品内部215。
防滴与垂线成15。
角范围内的滴水不能直接进人产品内部3防淋水与垂线成60。
角范围内的淋水不能直接进人产品内部4防溅任何方向的溅水对产品应无有害的影响5防喷水任何方向的喷水对产品应无有害的影响6强烈的海浪或强力喷水对产品应无有害的影响防海浪或强力喷水7浸水产品在规定的压力和时间下浸在水中,进水量应无有害影响8潜水产品在规定的压力下长时间浸在水中,进水量应无有害影响二、电动机危险因素(1)电动机漏电。
(2)电动机接线错误,导致外壳带电;电动机未连接保护线,导致外壳带故障电压。
(3)直流电动机和绕线型异步电动机滑环处的火花,各种绝缘击穿时产生的电火花,各种异常状态下产生的危险温度构成点火源。
(4)电动机故障停车,影响系统正常运行,排放有毒气体、可燃气体、烟尘的风机电动机故障停车将带来严重的次生灾难。
考点区域地理核心考点(6-10)
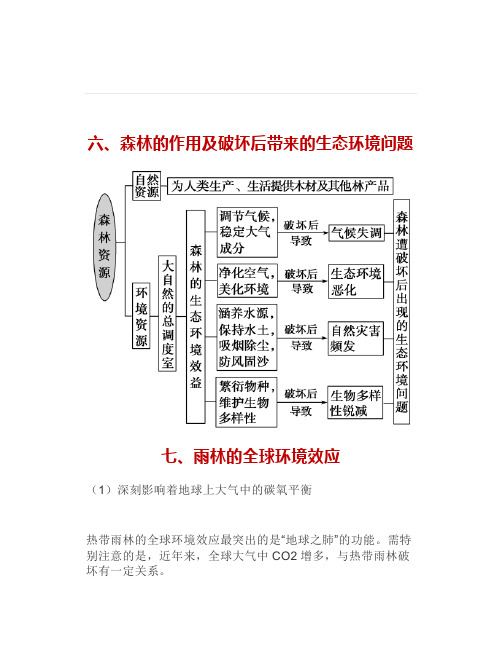
六、森林的作用及破坏后带来的生态环境问题七、雨林的全球环境效应(1)深刻影响着地球上大气中的碳氧平衡热带雨林的全球环境效应最突出的是“地球之肺”的功能。
需特别注意的是,近年来,全球大气中CO2增多,与热带雨林破坏有一定关系。
(2)具有促进全球水循环、调节全球水平衡的作用(3)热带雨林是世界生物基因宝库雨林是全球最古老的植物群落。
在生物进化史中,雨林成为地球上繁衍物种最多、保护时间最长的场所,因此被誉为“世界生物基因宝库”。
八、不同区域森林生态功能差异九、湿地的功能及保护1.湿地的主要功能2.湿地面积减少的原因(1)自然原因:湿地减少本身是一个自然过程,即沉积物自然充满湖泊,失去其充水洼地的形态与功能,但这一自然过程十分漫长。
所以从地球历史以百万年为单位的时间尺度看,一切湖泊和沼泽的存在都是一种过渡性现象。
(2)人为原因:近代人类活动的干预,极大地加速了湖沼消亡的过程,在几代人乃至一代人的时间内实现了湖沼的消亡。
湿地消失的人为因素见下表:3.不同湿地开发保护的主要目的十、区域能源、矿产资源开发条件评价1.区域能源、矿产资源开发条件评价的内容2.案例分析(以山西煤炭资源开发为例)(1)山西煤炭资源开发的优势条件资源开发的优势条件可从基础好(资源和开采条件)、拉动强(区位和市场条件)、有保证(交通条件)三大方面、五小方面分析,具体如下:(2)山西省煤炭资源开发限制条件交通运输能力不足我国能源生产地区和消费地区分布不平衡,致使出现了西煤东运、北煤南运的现象,使铁路运输的压力进一步加重水资源短缺一方面,山西省水资源总量贫乏,且水资源地区分布不平衡;另一方面,随着大型能源基地的建设,工业耗水量加大,特别是火电工业和有色金属工业水土流失严重山西省是我国水土流失较严重的地区,如果大面积地露天开采煤矿,会加剧水土流失,因此土地恢复和保护任务十分艰巨。
中考复习生命科学6人体的消化和呼吸系统

完成的,包括 和 两个过程,
(1)吸气:肋间肌 收缩 ,肋骨 向上向外 运动,膈肌 收缩 ,膈顶部 下降 ,胸廓容积 扩大 , 肺 扩张 ,肺内气压 下降,气体进入肺。 (2)呼气:肋间肌 舒张 ,肋骨 向下向内 运动,膈肌 舒张 ,膈顶部 回升 ,胸廓容积 缩小 , 肺 回缩 ,肺内气压 升高 ,气体出肺。
2.关键点
①吸气和呼气结束瞬间,肺内气压=外界气压。 ②先有胸廓扩大和缩小,后有气体的吸入和排出。 ③由于肺泡壁和毛细血管壁都只有一层上皮细胞,氧气从肺泡进入血液只穿过两层细胞(四层 细胞膜)。 ④呼出的气体和空气的差别:吸入的空气,CO2含量较 少 ,O2含量较 多 ;呼出的气体, CO2含量 增加 ,O2含量 减少 。
27
6.(2018·遂宁)人体细胞获得氧气的全过程,必须经过如图所示的①②③等过程来完成。下列有关 说法错误的是( D ) A.图中a代表氧气,组织细胞获得氧气进行呼吸作用,为生命活动提供动力 B.图中b代表组织细胞产生的二氧化碳,至少经过心脏一次,才能排出体外 C.过程②③都是通过气体扩散来完成的 D.经过过程③后,血液由静脉血变成动脉血
温度对酶活性的影响:
pH对酶活性的影响:
3.人体中有很多种酶,不同的酶催化体内不同的化学反应。 4.人体细胞若缺乏某种酶或酶不足时,就会发生代谢紊乱,并可能出现疾病。如白化病等。
1.如图表示过氧化氢在不同条件下被分解的速率,由图可以得出( C ) A.温度越高,酶催化效率越高 B.pH值越高,酶催化效率越高 C.酶 气体。扩散
(4)在探究实验中,哪一装置用于吸气并作为对照组?
实验结果是
甲瓶中的石灰水。变浑浊
实验结论是
人体呼出的气体中含有较多。的二氧化碳
乙。
记叙文暑期自我补习6考点四—六(学生)

考点四理解、赏析重点语句题型:1. 如何理解文中画线句(某一个句子)?2. 从文章画线句中任选一句,分析其表达效果。
3. 品读文章指定段落,从某一角度(如词语运用、修辞方法、人物描写等)结合相关语句进行赏析。
方法点拨对重点语句的考查主要是要求理解特定语句的含义,分析特定语句的表达效果,或从特定角度(或选择角度)赏析特定段落语句。
解答理解语句含义类的题,要从表层含义和深层含义两方面进行分析,还要注意联系文章中心思想。
赏析语句的表达效果可从以下角度着手:1.修辞方法的角度:要先点出句子所运用的修辞方法,再结合句子分析其表达效果(对句子本身的效果和对表现文章中心、人物情感等的作用等)。
2.描写方法的角度:要先点出句子所运用的描写方法,再结合句子分析其描写效果,如让人物形象栩栩如生,让故事情节更丰满,等等。
3.表达方式的角度:①议论:重点分析其蕴含的哲理,点明其对表达文章中心思想的作用。
②抒情:重点剖析其抒发的感情,分析其对表现文章中心、主题等的作用。
③描写:重点分析其运用的描写方法及其创设的意境,再分析其对表现文章内容、中心思想、人物形象或情感等的作用等。
4.(特殊)句式的角度:要先点明句子运用的句式,再联系文章主要内容及中心,分析其表达效果(作用)。
如:设问句(提醒注意,引发思考)、疑问句(吸引读者,制造悬念,引出内容)、反问句(加强语气,增强情感表达及感染力)、感叹句(抒情强烈,增强感召力)等。
5.用词的角度:抓住句中富有表现力的关键性词语,理解句子所表现的作者的情感,如好恶、褒贬等。
6.其他:如中心句或点睛句(点明中心,揭示主旨,画龙点睛;句子含义深刻,耐人寻味,读后给人以启迪)、矛盾句(从字面上看自相矛盾,却寄寓了作者深刻的用意;揭示深刻内涵,表达深刻见解)、引用句(增加文章的诗情画意以及表达的深刻性)等。
考点专练1. (2015舟山,6)其实很简单“抓强盗——抓强盗啊!,,”女人歇斯底里地叫喊着。
高考数学总复习考点知识讲解与提升练习6 函数的概念及其表示
高考数学总复习考点知识讲解与提升练习专题6 函数的概念及其表示考点知识1.了解函数的含义.2.在实际情境中,会根据不同的需要选择恰当的方法(如图象法、列表法、解析法)表示函数.3.了解简单的分段函数,并会简单的应用.知识梳理1.函数的概念一般地,设A,B是非空的实数集,如果对于集合A中的任意一个数x,按照某种确定的对应关系f,在集合B中都有唯一确定的数y和它对应,那么就称f:A→B为从集合A 到集合B的一个函数,记作y=f(x),x∈A.2.函数的三要素(1)函数的三要素:定义域、对应关系、值域.(2)如果两个函数的定义域相同,并且对应关系完全一致,则这两个函数为同一个函数.3.函数的表示法表示函数的常用方法有解析法、图象法和列表法.4.分段函数若函数在其定义域的不同子集上,因对应关系不同而分别用几个不同的式子来表示,这种函数称为分段函数.常用结论1.直线x =a 与函数y =f (x )的图象至多有1个交点.2.在函数的定义中,非空数集A ,B ,A 即为函数的定义域,值域为B 的子集.3.分段函数虽由几个部分组成,但它表示的是一个函数.分段函数的定义域等于各段函数的定义域的并集,值域等于各段函数的值域的并集. 思考辨析判断下列结论是否正确(请在括号中打“√”或“×”)(1)若两个函数的定义域和值域相同,则这两个函数是同一个函数.(×)(2)函数y =f (x )的图象可以是一条封闭曲线.(×)(3)y =x 0与y =1是同一个函数.(×)(4)函数f (x )=⎩⎨⎧ x -1,x ≥0,x 2,x <0的定义域为R .(√) 教材改编题1.(多选)下列所给图象是函数图象的是()答案CD解析A 中,当x >0时,每一个x 的值对应两个不同的y 值,因此不是函数图象;B 中,当x =x 0时,y 的值有两个,因此不是函数图象;CD 中,每一个x 的值对应唯一的y 值,因此是函数图象.2.下列各组函数表示同一个函数的是()A .y =x -1与y =x 2-1x +1B .y =x -1与y =-1xC .y =2x 2与y =2xD .y =2x -1与v =2t -1答案D解析y =x -1的定义域为R ,y =x 2-1x +1的定义域为{x |x ≠-1},定义域不同,不是同一个函数,故选项A 不正确;y =x -1=1x 与y =-1x的对应关系不同,不是同一个函数,故选项B 不正确; y =2x 2=2|x |与y =2x 的对应关系不同,不是同一个函数,故选项C 不正确;y =2x -1与v =2t -1的定义域都是(-∞,1)∪(1,+∞),对应关系也相同,所以是同一个函数,故选项D 正确.3.已知函数f (x )=⎩⎨⎧ ln x ,x >0,e x ,x ≤0,则函数f ⎝ ⎛⎭⎪⎫f ⎝ ⎛⎭⎪⎫13等于() A .3B .-3C.13D .-13答案C解析由题意可知,f ⎝ ⎛⎭⎪⎫13=ln 13=-ln3,所以f ⎝ ⎛⎭⎪⎫f ⎝ ⎛⎭⎪⎫13=f (-ln3)=e -ln3=13.题型一函数的定义域例1(1)函数y =ln (x +1)-x 2-3x +4的定义域为()A .(-4,-1)B .(-4,1)C .(-1,1)D .(-1,1]答案C解析由题意得⎩⎨⎧ x +1>0,-x 2-3x +4>0,解得-1<x <1,故定义域为(-1,1).(2)已知函数f (x )的定义域为(-4,-2),则函数g (x )=f (x -1)+x +2的定义域为________.答案[-2,-1)解析∵f (x )的定义域为(-4,-2),要使g (x )=f (x -1)+x +2有意义,则⎩⎨⎧ -4<x -1<-2,x +2≥0,解得-2≤x <-1,∴函数g (x )的定义域为[-2,-1).思维升华(1)无论抽象函数的形式如何,已知定义域还是求定义域,均是指其中的x 的取值集合;(2)若已知函数f (x )的定义域为[a ,b ],则复合函数f (g (x ))的定义域由不等式a ≤g (x )≤b 求出;(3)若复合函数f (g (x ))的定义域为[a ,b ],则函数f (x )的定义域为g (x )在[a ,b ]上的值域.跟踪训练1(1)函数f (x )=1ln (x -1)+3-x 的定义域为() A .(1,3] B .(1,2)∪(2,3]C .(1,3)∪(3,+∞) D.(-∞,3)答案B解析由题意知⎩⎨⎧ x -1>0,x -1≠1,3-x ≥0,所以1<x <2或2<x ≤3, 所以函数的定义域为(1,2)∪(2,3].(2)(2023·南阳检测)已知函数f (x )=lg1-x 1+x ,则函数g (x )=f (x -1)+2x -1的定义域是()A .{x |x >2或x <0}B.⎩⎨⎧⎭⎬⎫x ⎪⎪⎪ 12≤x <2 C .{x |x >2}D.⎩⎨⎧⎭⎬⎫x ⎪⎪⎪ x ≥12答案B解析要使f (x )=lg1-x 1+x 有意义, 则1-x 1+x >0, 即(1-x )(1+x )>0,解得-1<x <1,所以函数f (x )的定义域为(-1,1).要使g (x )=f (x -1)+2x -1有意义,则⎩⎨⎧ -1<x -1<1,2x -1≥0,解得12≤x <2, 所以函数g (x )的定义域为⎩⎨⎧⎭⎬⎫x ⎪⎪⎪ 12≤x <2.题型二函数的解析式例2(1)已知f (1-sin x )=cos 2x ,求f (x )的解析式;(2)已知f ⎝⎛⎭⎪⎫x +1x =x 2+1x 2,求f (x )的解析式; (3)已知f (x )是一次函数且3f (x +1)-2f (x -1)=2x +17,求f (x )的解析式.(4)已知f (x )满足2f (x )+f (-x )=3x ,求f (x )的解析式.解(1)(换元法)设1-sin x =t ,t ∈[0,2],则sin x =1-t ,∵f (1-sin x )=cos 2x =1-sin 2x ,∴f (t )=1-(1-t )2=2t -t 2,t ∈[0,2].即f (x )=2x -x 2,x ∈[0,2].(2)(配凑法)∵f ⎝⎛⎭⎪⎫x +1x =x 2+1x 2=⎝ ⎛⎭⎪⎫x +1x 2-2, ∴f (x )=x 2-2,x ∈(-∞,-2]∪[2,+∞).(3)(待定系数法)∵f (x )是一次函数,可设f (x )=ax +b (a ≠0),∴3[a (x +1)+b ]-2[a (x -1)+b ]=2x +17.即ax +(5a +b )=2x +17,∴⎩⎨⎧ a =2,5a +b =17,解得⎩⎨⎧ a =2,b =7.∴f (x )的解析式是f (x )=2x +7.(4)(解方程组法)∵2f (x )+f (-x )=3x ,①∴将x 用-x 替换,得2f (-x )+f (x )=-3x ,②由①②解得f (x )=3x .思维升华函数解析式的求法(1)配凑法;(2)待定系数法;(3)换元法;(4)解方程组法.跟踪训练2(1)已知f (x -1)=x 2+4x -5,则f (x )的解析式是()A .f (x )=x 2+6xB .f (x )=x 2+8x +7C .f (x )=x 2+2x -3D .f (x )=x 2+6x -10答案A解析f (x -1)=x 2+4x -5,设x -1=t ,x =t +1,则f (t )=(t +1)2+4(t +1)-5=t 2+6t ,故f (x )=x 2+6x . (2)若f ⎝ ⎛⎭⎪⎫1x =x 1-x,则f (x )=________. 答案1x -1(x ≠0且x ≠1) 解析f (x )=1x 1-1x=1x -1(x ≠0且x ≠1). (3)已知函数f (x )满足f (x )+2f ⎝ ⎛⎭⎪⎫-1x =3x ,则f (2)等于() A .-3B .3C .-1D .1答案A解析f (x )+2f ⎝ ⎛⎭⎪⎫-1x =3x ,① 则f ⎝ ⎛⎭⎪⎫-1x +2f (x )=-3x ,② 联立①②解得f (x )=-2x -x ,则f (2)=-22-2=-3. 题型三分段函数例3(1)已知函数f (x )=⎩⎨⎧ f (x -1),x >0,-ln (x +e )+2,x ≤0,则f (2024)的值为() A .-1B .0C .1D .2答案C解析因为f (x )=⎩⎨⎧ f (x -1),x >0,-ln (x +e )+2,x ≤0,所以f (2024)=f (2023)=f (2022)=…=f (1),又f (1)=f (1-1)=f (0)=-ln(0+e)+2=-1+2=1,所以f (2024)=1.(2)已知函数f (x )=⎩⎨⎧ -x 2-3x +2,x <-1,2x -3,x ≥-1,若f (a )=4,则实数a 的值是________;若f (a )≥2,则实数a 的取值范围是________.答案-2或5[-3,-1)∪[4,+∞)解析若f (a )=4,则⎩⎨⎧a <-1,-a 2-3a +2=4或⎩⎨⎧ a ≥-1,2a -3=4, 解得a =-2或a =5. 若f (a )≥2,则⎩⎨⎧ a <-1,-a 2-3a +2≥2或⎩⎨⎧ a ≥-1,2a -3≥2,解得-3≤a <-1或a ≥4,∴a 的取值范围是[-3,-1)∪[4,+∞).思维升华分段函数求值问题的解题思路(1)求函数值:当出现f (f (a ))的形式时,应从内到外依次求值.(2)求自变量的值:先假设所求的值在分段函数定义区间的各段上,然后求出相应自变量的值,切记要代入检验.跟踪训练3(1)已知函数f (x )=⎩⎨⎧ x +2,x ≤0,x +1x ,x >0,若f (f (a ))=2,则a 等于() A .0或1B .-1或1C .0或-2D .-2或-1答案D解析令f (a )=t ,则f (t )=2,可得t =0或t =1,当t =0时,即f (a )=0,显然a ≤0,因此a +2=0⇒a =-2,当t =1时,即f (a )=1,显然a ≤0,因此a +2=1⇒a =-1,综上所述,a =-2或-1.(2)(2023·重庆质检)已知函数f (x )=⎩⎨⎧log 2x ,x >1,x 2-1,x ≤1,则f (x )<f (x +1)的解集为________.答案⎝ ⎛⎭⎪⎫-12,+∞解析当x ≤0时,x +1≤1,f (x )<f (x +1)等价于x 2-1<(x +1)2-1,解得-12<x ≤0;当0<x ≤1时,x +1>1,此时f (x )=x 2-1≤0,f (x +1)=log 2(x +1)>0,∴当0<x ≤1时,恒有f (x )<f (x +1);当x >1时,x +1>2,f (x )<f (x +1)等价于log 2x <log 2(x +1),此时也恒成立.综上,不等式f (x )<f (x +1)的解集为⎝ ⎛⎭⎪⎫-12,+∞. 课时精练1.函数f (x )=lg(x -2)+1x -3的定义域是() A .(2,+∞) B.(2,3)C .(3,+∞) D.(2,3)∪(3,+∞)答案D解析∵f (x )=lg(x -2)+1x -3, ∴⎩⎨⎧ x -2>0,x -3≠0,解得x >2,且x ≠3,∴函数f (x )的定义域为(2,3)∪(3,+∞).2.(2023·三明模拟)已知集合A ={x |-2<x ≤1},B ={x |0<x ≤4},则下列对应关系中是从集合A 到集合B 的函数是()A .f :x →y =x +1B .f :x →y =e xC .f :x →y =x 2D .f :x →y =|x |答案B解析对于A ,当x =-1时,由f :x →y =x +1得y =0,但0∉B ,故A 错误;对于B,因为从A={x|-2<x≤1}中任取一个元素,通过f:x→y=e x在B={x|0<x≤4}中都有唯一的元素与之对应,故B正确;对于C,当x=0时,由f:x→y=x2得y=0,但0∉B,故C错误;对于D,当x=0时,由f:x→y=|x|得y=0,但0∉B,故D错误.3.已知f(x3)=lg x,则f(10)的值为()A.1B.310C.13D.1310答案C解析令x3=10,则x=13 10,∴f(10)=lg1310=13.4.图中的文物叫做“垂鳞纹圆壶”,是甘肃礼县出土的先秦时期的青铜器皿,其身流线自若、纹理分明,展现了古代中国精湛的制造技术.科研人员为了测量其容积,以恒定的流速向其内注水,恰好用时30秒注满,设注水过程中,壶中水面高度为h,注水时间为t,则下面选项中最符合h关于t的函数图象的是()答案A解析水壶的结构:底端与上端细、中间粗,所以在注水恒定的情况下,开始水的高度增加的快,中间增加的慢,最后又变快, 由图可知选项A 符合.5.函数y =1+x -1-2x 的值域为()A.⎝ ⎛⎭⎪⎫-∞,32B.⎝ ⎛⎦⎥⎤-∞,32 C.⎝ ⎛⎭⎪⎫32,+∞D.⎣⎢⎡⎭⎪⎫32,+∞ 答案B 解析设1-2x =t ,则t ≥0,x =1-t 22,所以y =1+1-t 22-t =12(-t 2-2t +3)=-12(t +1)2+2,因为t ≥0,所以y ≤32.所以函数y =1+x -1-2x 的值域为⎝ ⎛⎦⎥⎤-∞,32. 6.已知函数f (x )=⎩⎨⎧ -x 2+2x +3,x ≤2,6+log a x ,x >2(a >0且a ≠1),若函数f (x )的值域是(-∞,4],则实数a 的取值范围是()A.⎝ ⎛⎭⎪⎫22,1B.⎣⎢⎡⎭⎪⎫22,1 C .(1,2] D .(1,2)答案B解析当x ≤2时,f (x )=-x 2+2x +3=-(x -1)2+4,当x =1时,f (x )=-x 2+2x +3取得最大值4,所以当x ≤2时,函数f (x )的值域是(-∞,4],所以当x >2时,函数f (x )=6+log a x 的值域为(-∞,4]的子集,当a >1时,f (x )=6+log a x 在(2,+∞)上单调递增,此时f (x )>f (2)=6+log a 2>6,不符合题意,当0<a <1时,f (x )=6+log a x 在(2,+∞)上单调递减,此时f (x )<f (2)=6+log a 2≤4,即log a 2≤-2,所以a 2≥12,可得22≤a <1,所以实数a 的取值范围是⎣⎢⎡⎭⎪⎫22,1.7.(多选)下列四个函数,定义域和值域相同的是() A .y =-x +1B .133,0,1,0x x y x x ⎧≤⎪=⎨⎪>⎩C .y =ln|x |D .y =2x -1x -2答案ABD解析对A ,函数的定义域和值域都是R ;对B ,根据分段函数和幂函数的性质,可知函数的定义域和值域都是R ;对C ,函数的定义域为(-∞,0)∪(0,+∞),值域为R ;对D ,因为函数y =2x -1x -2=2+3x -2,所以函数的定义域为(-∞,2)∪(2,+∞),值域为(-∞,2)∪(2,+∞).所以ABD 是定义域和值域相同的函数.8.(多选)函数概念最早是在17世纪由德国数学家莱布尼茨提出的,后又经历了贝努利、欧拉等人的改译.1821年法国数学家柯西给出了这样的定义:在某些变数存在着一定的关系,当一经给定其中某一变数的值,其他变数的值可随着确定时,则称最初的变数叫自变量,其他的变数叫做函数.德国数学家康托尔创立的集合论使得函数的概念更严谨.后人在此基础上构建了高中教材中的函数定义:“一般地,设A ,B 是两个非空的数集,如果按某种对应法则f ,对于集合A 中的每一个元素x ,在集合B 中都有唯一的元素y 和它对应,那么这样的对应叫做从A 到B 的一个函数”,则下列对应法则f 满足函数定义的有()A .f (x 2)=|x |B .f (x 2)=xC .f (cos x )=xD .f (e x )=x答案AD解析令t =x 2(t ≥0),f (t )=|±t |=t ,故A 符合函数定义;令t =x 2(t ≥0),f (t )=±t ,设t =4,f (t )=±2,一个自变量对应两个函数值,故B 不符合函数定义;设t =cos x ,当t =12时,x 可以取±π3等无数多个值,故C 不符合函数定义; 令t =e x (t >0),f (t )=ln t ,故D 符合函数定义.9.已知函数f (x )=⎩⎨⎧ cos x ,x <0,f (x -π),x >0,则f ⎝ ⎛⎭⎪⎫11π3=________. 答案12解析由已知得f ⎝ ⎛⎭⎪⎫11π3=f ⎝ ⎛⎭⎪⎫8π3=f ⎝ ⎛⎭⎪⎫5π3=f ⎝ ⎛⎭⎪⎫2π3=f ⎝ ⎛⎭⎪⎫-π3=cos ⎝ ⎛⎭⎪⎫-π3=12.10.已知f (x )=x -1,则f (x )=________.答案x 2-1(x ≥0)解析令t =x ,则t ≥0,x =t 2,所以f (t )=t 2-1(t ≥0),即f (x )=x 2-1(x ≥0).11.已知函数f (x )的定义域为[-2,2],则函数g (x )=f (2x )+1-2x 的定义域为__________.答案[-1,0]解析由条件可知,函数的定义域需满足⎩⎨⎧ -2≤2x ≤2,1-2x ≥0,解得-1≤x ≤0,所以函数g (x )的定义域是[-1,0].12.已知f (x )=⎩⎨⎧ 2x +3,x >0,x 2-4,x ≤0,若f (a )=5,则实数a 的值是__________;若f (f (a ))≤5,则实数a 的取值范围是__________.答案1或-3[-5,-1]解析①当a >0时,2a +3=5,解得a =1;当a ≤0时,a 2-4=5,解得a =-3或a =3(舍).综上,a =1或-3.②设t =f (a ),由f (t )≤5得-3≤t ≤1.由-3≤f (a )≤1,解得-5≤a ≤-1.13.(2022·广州模拟)已知定义在R 上的函数f (x )满足,f (1-x )+2f (x )=x 2+1,则f (1)等于()A .-1B .1C .-13D.13答案B解析∵定义在R 上的函数f (x )满足,f (1-x )+2f (x )=x 2+1,∴当x =0时,f (1)+2f (0)=1,①当x =1时,f (0)+2f (1)=2,②②×2-①,得3f (1)=3,解得f (1)=1.14.(2023·南昌模拟)已知函数f (x )=⎩⎨⎧x +3,x ≤0,x ,x >0,若f (a -3)=f (a +2),则f (a )等于()A .2B.2C .1D .0答案B解析作出函数f (x )的图象,如图所示.因为f (a -3)=f (a +2),且a -3<a +2,所以⎩⎨⎧ a -3≤0,a +2>0,即-2<a ≤3,此时f (a -3)=a -3+3=a ,f (a +2)=a +2,所以a =a +2,即a 2=a +2,解得a =2或a =-1(不满足a =a +2,舍去),则f (a )= 2.15.∀x ∈R ,用M (x )表示f (x ),g (x )中最大者,M (x )={|x |-1,1-x 2},若M (n )<1,则实数n 的取值范围是()A .(-2,2)B .(-2,0)∪(0,2)C .[-2,2]D .(-2,2)答案B解析当x ≥0时,若x -1≥1-x 2,则x ≥1,当x <0时,若-x -1≥1-x 2,则x ≤-1,所以M (x )=⎩⎨⎧ |x |-1,x ≥1或x ≤-1,1-x 2,-1<x <1,若M (n )<1,则当-1<n <1时,1-n 2<1⇒-n 2<0⇒n ≠0,即-1<n <0或0<n <1, 当n ≥1或n ≤-1时,|n |-1<1,解得-2<n ≤-1或1≤n <2,综上,-2<n <0或0<n <2.16.(多选)德国数学家狄利克雷在数学领域成就显著,以其名字命名的函数F (x )=⎩⎨⎧ 1,x 为有理数,0,x 为无理数被称为狄利克雷函数.关于狄利克雷函数,下列说法正确的是()A .F (F (x ))=0B .对任意x ∈R ,恒有F (x )=F (-x )成立C .任取一个不为0的实数T ,F (x +T )=F (x )对任意实数x 均成立D .存在三个点A (x 1,F (x 1)),B (x 2,F (x 2)),C (x 3,F (x 3)),使得△ABC 为等边三角形答案BD解析∵当x为有理数时,F(x)=1,当x为无理数时,F(x)=0,当x为有理数时,F(F(x))=F(1)=1,当x为无理数时,F(F(x))=F(0)=1,所以F(F(x))=1恒成立,故A错误;因为有理数的相反数是有理数,无理数的相反数是无理数,所以对任意x∈R,恒有F(x)=F(-x)成立,故B正确;若x是有理数,T是有理数,则x+T是有理数;若x是有理数,T是无理数,则x+T是无理数;若x是无理数,则x+T是无理数或有理数,所以任取一个不为0的实数T,F(x+T)=F(x)不恒成立,故C错误;取x1=-33,x2=0,x 3=33,可得F(x1)=0,F(x2)=1,F(x3)=0,所以A⎝⎛⎭⎪⎫-33,0,B(0,1),C⎝⎛⎭⎪⎫33,0,恰好△ABC为等边三角形,故D正确.。
(完整word)HSK6考点
新HSK六级汉语水平语法知识点归纳一。
词类(一)。
名词1。
一般名词:妈妈教室词典自行车水平精神2. 方位名词:里外上下前后中左右东西南北复合方位名词:里边外边上边下边前边后边旁边中间东边西边南边北边3。
时间名词:年月日星期小时今天去年4. 名词重叠:年年月月天天人人家家(二)。
代词:1.人称代词:你(您)你们我我们他(她) 他们(她们) 咱咱们2.疑问代词:谁哪哪里(哪儿)什么怎么怎么样几多少3.指示代词:这这些那那些这里(这儿) 那里(那儿) 这么那么这样那样4.其他代词:各每有的有些别人别的它它们(三) 动词:1. 一般动词:看写打参观爱想喜欢希望像姓在进行2. 动词重叠:想想看看学习学习研究研究说(一)说试(一)试听了听走了走3。
助动词:能会要想可能可以愿意应该得(dei)(四)形容词:1. 一般形容词:大红多错全安静漂亮男女老少2. 形容词重叠:高高长长好好整整齐齐干干净净高高兴兴(五)数词:1。
基数:零 0 一十百千万二两半2。
序数:二年级 331路 14楼6门15号 2月5号第一3.概数:三四个十几个几十年四十多人两年多两个多小时4.分数、百分数:三分之二(2/3) 百分之四十(40%)5.倍数、小数:五倍七点八(7.8)三点一四一六(3.1416)(六) 量词:1。
名量词:个位本件种斤公斤克间棵课张把只条口米公尺2. 名量词重叠:个个(都不错) 张张(笑脸) 条条(大路)种种(事情)3。
动量词:次遍回下口(七)副词:1. 否定副词:不没(有) 别2. 时间副词: 正刚常常常已经正在总(是) 才(1) 就(1)3。
范围副词:都(1) 只一共4. 程度副词: 很太更最十分非常多(么)5. 频度副词: 又再还也(八)介词:1. 引出时间、处所、起点:当在从离2。
引出方向:向往朝3. 引出对象:对跟和比为给4. 引出目的、原因:为为了5。
引出施事:把被叫让6。
表示排除和加合:除了……除了……以外(九)连词:1。
考点狂练6:加速度
考点狂练6:加速度【考点剖析】:加速度等于物体的速度变化量与发生变化所用时间的比值,与两个因素相关,速度变化很大,加速度可能很小.速度变化很小,加速度可能很大.加速度与速度没有直接关系,加速度大小不断变小,速度不一定变小,相反,加速度变大,速度也不一定变大.物体速度的增减取决于加速度和速度的方向关系,不决定于加速度的正负,加速度的大小就是速度的变化率.1.(多选)以下对加速度的理解正确的是()A.加速度是增加的速度 B.加速度是描述速度变化快慢的物理量C.-8m/s2比5m/s2小 D.加速度方向可与初速度方向相同,也可相反2.关于加速度,下列说法中正确的是()A.加速度越大表示物体速度变化越快 B.物体速度增大,则加速度增大C.加速度方向总是与物体初速度方向一致 D.物体某时刻速度为零,则该时刻加速度一定为零3. (多选)下列运动情况可能出现的是()A.物体运动的加速度等于0,而速度却不等于0 B.物体的速度变化比较快,而加速度却比较小C.物体具有向东的加速度,而速度的方向却向西 D.物体的加速度在减小,但速度却在增大4.足球以8m/s的速度飞来,运动员把足球以12m/s的速度反向踢出,踢球时间为0.2s,设足球飞来的方向为正方向,则这段时间内足球的加速度是() A.- 20m/s2 B.20m/s2 C.- 100m/s2 D.100m/s25.为测定气垫导轨上滑块的加速度,滑块上安装了宽度为3.0cm的遮光板。
滑块在牵引力作用下先后通过两个光电门,配套的数字毫秒计记录了遮光板通过第一个光电门的时间为Δt1=0.30s, 通过第二个光电门的时间为Δt2=0.10s,遮光板从开始遮住第一个光电门到开始遮住第二个光电门的时间为Δt=4.00s,则滑块的加速度为 m/s26.关于加速度与速度的关系,下列说法正确的是()A.加速度越大,速度一定越大 B.速度改变量越大,加速度一定越大C.速度不变,加速度一定为零 D.速度为零,加速度一定为零7.下列关于速度、速度变化量和加速度的关系中,可能存在的是()A.速度变化量很大,加速度却很小 B.速度变化量方向为正,加速度方向为负C.速度越来越大,加速度越来越小 D.速度方向为正,加速度方向为负8.关于速度、速度的变化和加速度的关系,下列情景不可能发生的是( )A.物体加速度增大,速度反而越来越小 B.速度变化的方向为正,加速度的方向为负C.速度越来越大,加速度反而越来越小 D.加速度既不与速度同向,也不与速度反向9.近两年,在国家宏观政策调控下,我国房价上涨出现减缓趋势。
幼儿教育知识常考的个必备知识考点
幼儿教育知识常考的26个必备知识考点考点 1 婴幼儿发展的影响因素1. 客观因素(1)生物因素①遗传因素:遗传素质是人的身心发展的前提,为个体的身心发展提供了可能性;遗传奠定儿童身心发展个体差异的最初基础。
遗传素质是人发展的物质前提,但对人的发展不起决定作用。
②生理成熟:生理成熟的程序制约着儿童心理发展的顺序。
生理成熟儿童心理发展提供物质前提。
生理成熟的个体差异是儿童心理发展个体差异的生理基。
(2)社会因素①社会环境使遗传所供的心理发展的可能性变为现实。
②社会生活件和教育条件从根本上制约着幼儿心理发的水平和方向。
2. 主观因素(1儿童心理本身内部的因素是儿童心理发展的内部原因(2)儿童心理的内部矛盾是推动儿童心理发展的根本原因考点 2 成熟势力说成熟势力说简称成熟论,主要代表人物是美国心理学家格赛尔。
格赛尔认为支配儿童心理发展的是成熟和学习两个因素。
成熟是由内部因素控制的过程,它的基本方面不可能受到像教育这样一些外部因素的影响。
成熟是发展的重要条件,决定机体发展的方向和模式,因此成熟是推动儿童发展的主要动力。
而学习与外环境有关,并不是发展的主要原因,因为引起变化的原因是成熟的顺序或机体的机制所固有的,学习只是给发展提供适当的时机而已。
格赛尔的这种观点主要来源于其著名的双生子爬梯实验。
考点 3 埃里克森的人格发展理论运里克森改进了弗洛伊德的个性发展理论,并特别地品儿的发展。
学前儿童所涉及的前三个阶段:1. 信任感对不信任感(零至一岁或一岁半)2. 自主感对羞耻感、怀疑感(一或一岁半至三或四岁)3. 主动感对内疚感(三四岁至五六岁)考点 4 认知发展理论1. 皮亚杰的认知发展观皮亚杰认为,儿童的行为是主体对客体的主动适应,适应是儿童心理发展的真正原因;他们经过同化、顺应和平衡等历程达成对周围环境的适应,从而获得经验,不断形成新的认知结构,使智力得到发展。
2. 儿童认知发展阶段皮亚杰将儿童认知的发展划分为四个阶段:第一阶段:感知运动阶段(0~2 岁)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
考点6 万有引力定律及应用
1.如图1所示,在火星与木星轨道之间有一小行星带.假设该带中的小行星只受到太阳的引
力,小行星与地球绕太阳运动都看做匀速圆周运动.下列说法正确的是( )
图1
A.太阳对各小行星的引力都相同
B.各小行星绕太阳运动的周期均小于一年
C.小行星带内侧小行星的向心加速度值大于外侧小行星的向心加速度值
D.小行星带内各小行星圆周运动的线速度值大于地球公转的线速度值
答案 C
解析 各小行星质量不一定相同,太阳对小行星的引力可能不同,A错误;由GM·mr2=mr(2πT)
2
知,T=2πr3GM,则小行星的运行周期大于一年,B错误;由GM·mr2=ma=mv2r知,a=GMr2,
v=
GM
r
,故C正确,D错误.
2.(2017·湖南怀化市模拟)火星探测器绕火星近地做圆周轨道飞行,其线速度和相应的轨道半
径为v0和R0,火星的一颗卫星在圆轨道上的线速度和相应的轨道半径为v和R,则下列关系
正确的是( )
A.lg(vv0)=12lg(RR0)
B.lg(vv0)=2lg(RR0)
C.lg(vv0)=12lg(R0R)
D.lg(vv0)=2lg(R0R)
答案 C
解析 做圆周运动所需的向心力由万有引力提供,故有:GMmR2=mv2R①
GMmR02=mv02R0②
由①②两式得:v2v02=R0R,由对数运算可得:lg(v2v02)=lg(R0R),所以lg(vv0)=12lg(R0R).故C正确.
3.(2017·福建福州市3月质检)2016年10月19日凌晨,我国神舟十一号飞船与天宫二号自
动交会对接成功,对接时轨道高度是3.93×102km,地球同步卫星的轨道高度是3.59×104km,
则( )
A.天宫二号的周期大于地球自转周期
B.对接后的它们的线速度介于近地卫星与同步卫星之间
C.为了完成对接,神舟飞船要在较高的轨道上减速飞行
D.漂浮在天宫二号内的水滴不受地球的吸引
答案 B
4.(2017·江西省六校3月联考)2016年10月23日早上,天宫二号空间实验室上搭载的一颗
伴飞小卫星(伴星)在太空中成功释放,并且对天宫二号和神舟十一号组合体进行了第一次拍
照.“伴星”经调整后,和“天宫二号”一样绕地球做匀速圆周运动.但比“天宫二号”离
地面稍高一些,那么( )
A.“伴星”的运行周期比“天宫二号”稍小一些
B.从地球上发射一颗到“伴星”轨道运动的卫星,发射速度要大于11.2km/s
C.在同一轨道上,若后面的卫星一旦加速,将与前面的卫星相碰撞
D.若伴星失去动力且受阻力作用,轨道半径将变小,则有可能与“天宫二号”相碰撞
答案 D
解析 根据万有引力提供向心力,有GMmr2=m4π2T2r,得T=4π2r3GM,“伴星”比“天宫二号”
的轨道半径高一些,所以“伴星”的运行周期比“天宫二号”稍大一些,故A错误;如果发
射速度大于11.2km/s将脱离地球引力的束缚,不可能成为“伴星”轨道的卫星,故B错误;
在同一轨道上,若后面的卫星一旦加速,将做离心运动到更高的轨道上,不会与前面的卫星
碰撞,故C错误;若“伴星”失去动力且受阻力作用,在原轨道上速度减小,万有引力大于
所需要的向心力,轨道半径将变小,则有可能与“天宫二号”相碰撞,故D正确.
5.(多选)(2017·河南省六市第一次联考)随着地球资源的枯竭和空气污染如雾霾的加重,星球
移民也许是最好的方案之一.美国NASA于2016年发现一颗迄今为止与地球最类似的太阳
系外的行星,与地球的相似度为0.98,并且可能拥有大气层和流动的水,这颗行星距离地球
约1400光年,公转周期约为37年,这颗名叫Kepler452b的行星,它的半径大约是地球的1.6
倍,重力加速度与地球相近.已知地球表面第一宇宙速度为7.9km/s,则下列说法正确的是
( )
A.飞船在Kepler452b表面附近运行的速度小于7.9km/s
B.该行星的质量约为地球质量的1.6倍
C.该行星的平均密度约是地球平均密度的58
D.在地球上发射航天器到达该星球,航天器的发射速度至少要达到第三宇宙速度
答案 CD
解析 忽略行星自转的影响,根据万有引力等于重力列出等式:GMmR2=mg,g=GMR2,这颗
行星的重力加速度与地球相近,它的半径大约是地球的1.6倍,所以它的质量是地球的2.56
倍.要在该行星表面发射人造卫星,发射的速度最小为第一宇宙速度.第一宇宙速度v=gR,
这颗行星的重力加速度与地球相近,它的半径大约是地球的1.6倍,所以这颗行星的第一宇
宙速度是地球的1.6倍,而地球的第一宇宙速度为7.9km/s,故A、B错误;该行星的半径大
约是地球的1.6倍,它的质量是地球的2.56倍,由:ρ=MV=gR2G43πR3=3g4πGR,这颗行星的重力
加速度与地球相近,则密度与半径成反比,它的半径大约是地球的1.6倍,则该行星的平均
密度约是地球平均密度的58,故C正确;由于这颗行星在太阳系外,所以航天器的发射速度
至少要达到第三宇宙速度,故D正确.
6.(多选)(2017·辽宁实验中学等五校联考)如图2所示,卫星由地面发射后,进入地月转移轨
道,经多次变轨最终进入距离月球表面100公里,周期为118分钟的工作轨道Ⅲ,开始对月
球进行探测( )
图2
A.卫星在轨道Ⅲ上的运行速度比月球的第一宇宙速度小
B.卫星在轨道Ⅲ上经过P点速度比在轨道1上经过P点大
C.卫星在轨道Ⅲ上的运行周期比在轨道Ⅰ上短
D.卫星在轨道Ⅰ上的机械能比在轨道Ⅱ上的大
答案 ACD
7.在轨运行26年的哈勃太空望远镜,曾拍摄到天狼星A和天狼星B组成的双星系统在轨运动
图象,如图3所示.它们在彼此间的万有引力作用下同时绕某点(公共圆心)做匀速圆周运动.已
知mA=bmB,且b>1.则下列结论正确的是( )
图3
A.天狼星A和天狼星B的绕行方向可能相反
B.天狼星A和天狼星B的公共圆心可以不在质心连线上
C.天狼星A和天狼星B的向心加速度大小之比为b∶1
D.天狼星A和天狼星B的线速度大小之比为1∶b
答案 D
解析 双星系统由彼此之间的万有引力提供各自做匀速圆周运动的向心力,二者角速度相同,
且绕行方向必相同,公共圆心必须在质心连线上,两星才能稳定运行,选项A、B错误;根
据a=Rω2,v=ωR,知v1v2=a1a2=1b,选项C错误,D正确.
8.(多选)(2017·湖北七市联合考试)“嫦娥三号”携带“玉兔号”月球车首次实现月球软着陆
和月面巡视勘察,并开展月表形貌与地质构造调查等科学探测.“玉兔号”在地球表面的重
力为G1,在月球表面的重力为G2;地球与月球均视为球体,其半径分别为R1、R2;地球表
面重力加速度为g.则( )
A.月球表面的重力加速度为G1gG2
B.月球与地球的质量之比为G2R22G1R12
C.月球与地球的第一宇宙速度之比为G1R1G2R2
D.“嫦娥三号”环绕月球表面做匀速圆周运动的周期为2πG1R2G2g
答案 BD
解析 “玉兔号”的质量m=G1g,月球表面的重力加速度g月=G2m=G2gG1,故A错误;根据
mg=GMmR2得M=gR2G,M月M地=g月R月2g地R地2=G2R22G1R12,故B正确;根据v=GMR=gR,v月v地=g月R月g地R地=
G2R2G1R1,故C错误;根据GM·mR2=mR(2πT)2得T=4π2R3GM,根据mg=GMm
R
2
得GM=gR2,所
以嫦娥三号绕月球表面做匀速圆周运动的周期T=4π2R月3g月R月2=2πR月g月=2πG1R2G2g,故D
正确.
