2019年高二数学 暑假作业(11)(无答案)(新版)新人教版
人教b版选修2-3高二数学(理)周末滚动测试题(.3.19)(无答案).docx

高中数学学习材料唐玲出品周末滚动测试题(理)(时间:120分钟 总分:150分) 第Ⅰ卷(共50分)一、选择题:本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的.1. 若复数22(34)(56)z m m m m i =--+--为纯虚数,则实数m 的值为( )A .5B .6C .-1D .4 2. 用反证法证明“三角形的内角至多有一个钝角”,正确的假设是( )A .三角形的内角至多有两个钝角B .三角形的内角至少有一个钝角C .三角形的内角至少有两个钝角D .三角形的内角都是钝角3. 若i 为虚数单位,图中复平面内点Z 表示复数z ,则表示复数1z i+的点是( ) A .EB .FC .GD .H 4. 将5名大学毕业生全部分配给3所不同的学校,不同的分配方案有( )编号:LKGD002A .8B .15C .125D .2435. 等比数列{}n a 中,12a =,84a =,函数128()()()...()f x x x a xa x a =---,则(0)f '=( )A .62B .92C .122D .152 6. 函数3()5f x x x =-的极大值为m ,极小值为n ,则m n +为( )A .0B .1C .2D .4 7. 用数学归纳法证明422123 (2)n n n +++++=,则当1n k =+时左端应在n k =的基础上加上( )A .21k +B .222(1)(2)...(1)k k k ++++++ C.42(1)(1)2k k +++D .2(1)k + 8. 已知函数()f x 的导函数2()()f x a x b c =-+的图象如图所示,则函数()f x 的图象可能是( )9. 直线2y x =与曲线23y x =-所围成的图形的面积等于( )A .23B .23- C.323 D.35310. 已知函数()f x 是定义在R 上的可导函数,其导函数记为()f x ',若对于任意实数x ,有()()f x f x '>,且()1y f x =-为奇函数,则不等式()xf x e <的解集为( )A .(,0)-∞B .(0,)+∞C .4(,)e -∞D .4(,)e +∞第II 卷(共100分)二、填空题:本大题共5小题,每小题5分,共25分. 11. 20(sin )x x dx π-=⎰ .12. 如图,函数()y f x =的图象在点P 处的切线方程是8y x =-+,则(5)(5)f f '+=_______.13. 设ABC ∆的三边长分别为,,a b c ,ABC ∆的面积为S ,内切圆半径为r ,则2S r a b c=++,类比这个结论可知:四面体S ABC -的四个面的面积分别为1S ,2S ,3S ,4S ,内切球半径为R ,四面体S ABC -的体积为V , 则R =14. 设椭圆221x y a b+=的焦点在y 轴上,其中{1,2,3,4}a ∈,{1,2,3,4,5,6}b ∈,求满足上述条件的椭圆的个数为15.正整数排成一个三角形数阵:根据以上排列规律,数阵中第n (4n ≥)左至右的第4数是________.三、解答题:本题共6个小题,满分75分.16.(本小题满分12分)已知函数2()xf x x e -=.(Ⅰ)求函数图象在点(1,(1))P f 处的切线方程;(Ⅱ)求函数()f x 的极值点及其极值.17. (本小题满分12分)已知可导函数()f x 的定义域为R ,且对x R ∀∈,()0f x '>恒成立,若,a b R ∈. (Ⅰ)求证:如果0a b +≥,那么()()()()f a f b f a f b +≥-+-;(Ⅱ)判断(Ⅰ)中的命题的逆命题是否成立?并证明你的结论.18. (本小题满分12分)(Ⅰ)已知,a b R +∈,且21a b +=,求证11322a b+≥+. (Ⅱ)已知0a >,求证:221122a a a a+-≥+-.19. (本小题满分12分) 已知正项等比数列{}n a 中,12a =,2312a a +=;数列{}n b 中,12n n b b -=+,且11b =. (Ⅰ)求数列{}n a 的通项n a 及其前n 项和n S ;(Ⅱ)求数列{}n b 的通项n b 及其前n 项和n T ;(Ⅲ)试比较n a 与n T 的大小,并证明你的结论.20. (本小题满分13分)网购越来越受到消费者的喜爱,假设某网店的商品每日的销售量y (单位:件)与销售价格x (单位:元/件)满足的关系式24(6)2m y x x =+--(其中26x <<,m 为常数)。
河北省武邑中学高二数学下学期暑假作业试题 文(5)
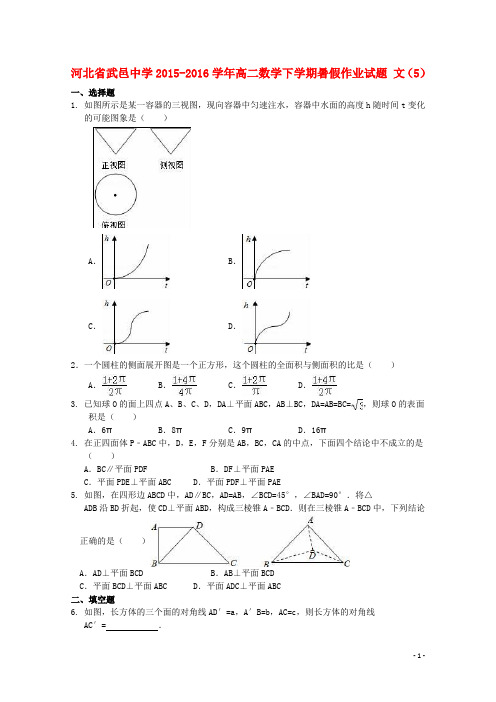
河北省武邑中学2015-2016学年高二数学下学期暑假作业试题文(5)一、选择题1. 如图所示是某一容器的三视图,现向容器中匀速注水,容器中水面的高度h随时间t变化的可能图象是()A.B.C.D.2.一个圆柱的侧面展开图是一个正方形,这个圆柱的全面积与侧面积的比是()A.B.C.D.3. 已知球O的面上四点A、B、C、D,DA⊥平面ABC,AB⊥BC,DA=AB=BC=,则球O的表面积是()A.6πB.8πC.9πD.16π4. 在正四面体P﹣ABC中,D,E,F分别是AB,BC,CA的中点,下面四个结论中不成立的是()A.BC∥平面PDF B.DF⊥平面PAEC.平面PDE⊥平面ABC D.平面PDF⊥平面PAE5. 如图,在四形边ABCD中,AD∥BC,AD=AB,∠BCD=45°,∠BAD=90°.将△ADB沿BD折起,使CD⊥平面ABD,构成三棱锥A﹣BCD.则在三棱锥A﹣BCD中,下列结论正确的是()A.AD⊥平面BCD B.AB⊥平面BCDC.平面BCD⊥平面ABC D.平面ADC⊥平面ABC二、填空题6. 如图,长方体的三个面的对角线AD′=a,A′B=b,AC=c,则长方体的对角线AC′=.7. 如图在三棱锥P ﹣ABC 中,PA⊥PB,PA⊥PC,PC⊥PB,PA=1,PB=2,PC=2,则该棱锥外接球的体积为 .三、解答题9. 如图,边长为2的正方形ABCD 中,(1)点E 是AB 的中点,点F 是BC 的中点,将△AED,△DCF 分别沿DE ,DF 折起,使A ,C 两点重合于点A′.求证:A′D⊥EF(2)当BE=BF=BC 时,求三棱锥A′﹣EFD 的体积.10 .如图,在正方体ABCD ﹣A 1B 1C 1D 1中,求证:(1)B 1D⊥平面A 1BC 1(2)记B 1D 与平面A 1BC 1的交点H ,求A 1B 1与平面A 1BC 1所成角的余弦值.答案1. B2. A3. C4. C5. D6.:.7.:.8. 证明:连结MN ,∵M 是AA 1的中点,N 是BB 1的中点,∴MN/CD,且MN=CD ,则四边形MNCD 为平行四边形,则DM∥CN,又AM∥B 1N ,AM=B 1N ,则四边形AMB 1N 为平行四边形,∴AN∥MB 1,∵DM∩MB 1=M ,∴面MDB 1∥面ANC .9. 解:(1)由正方形ABCD知,∠DCF=∠DAE=90°,∴A'D⊥A'F,A'D⊥A'E,∵A'E∩A'F=A',A'E、A'F⊆平面A'EF.∴A'D⊥平面A'EF.又∵EF⊂平面A'EF,∴A'D⊥EF.(2)由四边形ABCD为边长为2的正方形故折叠后A′D=2,A′E=A′F=,EF=则cos∠EA′F==则sin∠EA′F=故△EA′F的面积S△EA′F=•A′E•A′F•sin∠EA′F=由(1)中A′D⊥平面A′EF可得三棱锥A'﹣EFD的体积V=××2=.10 证明:(1)连结B1D1,∵正方体ABCD﹣A1B1C1D1中,A1B1C1D1是正方形,∴B1D1⊥A1C1,又DD1⊥面A1B1C1D1,∴DD1⊥A1C1,A1C1⊥面D1DB1,∴A1C1⊥B1D,同理可证B1D⊥A1B,又A1C1∩A1B=A1,∴B1D⊥平面A1BC1.(2)连结A1H、BH、C1H,由A1B1=BB1=C1B1,得A1H=BH=C1H,∴点H是△A1BC1的外心,又△A1BC1为正三角形,∴H是△A1BC1的中心,∴H为△A1BC1的重心,以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,设正方体ABCD﹣A1B1C1D1中棱长为1,A1(1,0,1),B1(1,1,1),B(1,1,0),C1(0,1,1),=(0,1,0),=(﹣1,1,0),=(0,1,﹣1),设平面A1BC1的法向量=(x,y,z),则,取x=1,得=(1,1,1),设A1B1与平面A1BC1所成角为θ,cosθ===,∴A1B1与平面A1BC1所成角的余弦值为.。
三年级下册数学暑假作业答案2021

三年级下册数学暑假作业答案2021同学们,这个暑假已经过去大半了,大家过了一个非常有意义的暑假呢?那我们知道高二数学暑假作业有哪些吗?下面是整理的三年级下册里边数学暑假作业答案2021,仅供参考,希望能够帮助帮助到大家。
三年级下册微积分暑假作业答案2021第1页一、直接写得数。
960 600720 6901500 100032 1610 7 (4)24 15二、在括号里填上合适萨德基的单位名称。
1. 2(米)2. 2(分米)3. 3(平方米)4. 20(米)5. 5(分米) 25(平方分米)6. (平方米)7. 18(平方分米)8. 18(厘米) 12(厘米) 216(平方厘米)三、走进生活。
1. 6×4=24(个)24个=24个答:6辆车准备24个轮子够了。
2. 1千米=1000米1000÷5=200(米)答:他平均每分钟跑200米。
第2页一、我会填。
1. (两)位数 (三)位数2. (十)位 (两)位数3. (0)二、夺金杯。
11 720240 22 180990 4200 80 640三、数学医院。
全错!改为:1 8 0 1 0 7 1 1 42)3 6 0 4)4 2 8 4)4 5 62 4 41 62 8 51 62 8 40 0 1 61 6第3页一、夺取金钥匙。
开始27→440→ 36→850→1000→107→ 130→※二、看谁投得准,用线连一连。
积小于600:42×11、29×11积大于600:32×21、38×29三、走进生活。
80×12÷6=960÷6=160(千克)答:平均每次运160千克。
第11页一、找朋友,用线连一连。
25×4=100 4×6-8=16480÷4=120 (70-20)×6=3000÷70=0 100-50÷2=75240÷4=60二、我来选。
七下数学暑假作业答案新人教版

七下数学暑假作业答案新人教版1.1 整式1.(1)c、d、f;(2)a、b、g、h;(3)a、b;(4)g;(5)e、i;2. ;3. ;4.四,四,- ab2c,- ,25 ;5.1,2;6. a3b2c;7.3x3-2x2-x;8. ;9.d;10.a;11.•b-;12.d ;13.c;14. ;15.a= ;16.n= ;四.-1.1.2 整式的加减1.-xy+2x2y2;2.2x2+2x2y;3.3;4.a2-a+6;5.99c-99a;6.6x2y+3x2y2-14y3;7. ;8. ;9.d; 10.d; 11.d; 12.b; 13.c;14.c; 15.b; 16.d; 17.c;18.解:原式= ,当a=-2,x=3时, 原式=1.19. 解:x=5,m=0,y=2,原式=5.20.(8a-5b)-[(3a-b)- ]= ,当a=10,b=8时,上车乘客是29人.21. 解:由 ,得xy=3(x+y),原式= .22. 解:(1)1,5,9,即后一个比前一个多4正方形.(2)17,37,1+4(n-1).四.解:3幅图中,需要的绳子分别为4a+4b+8c,4a+4b+4c,6a+6b+4c,所以(2)中的用绳最短,(3)中的用绳最长.1.3 同底数幂的乘法1. , ;2.2x5,(x+y)7 ;3.106;4.3;5.7,12,15,3 ;6.10;7.d ;8.•b-;9.d;10.d; 11.b;12.(1)-(x-y)10 ;(2)-(a-b-c)6;(3)2x5 ;(4)-xm13.解:9.6×106×1.3×108≈1.2×1015(kg).14.(1)① ,② .(2)①x+3=2x+1,x=2 ②x+6=2x,x=6.15.-8x7y8 ;16.15x=-9,x=- .四.105.毛1.4 幂的乘方与积的乘方1. , ;2. ;3.4 ;4. ;5. ;6.1,-1;7.6,108;8.37;9.a、d;10.a、c;11.b;12.d ;13.a ;14.;15.a;16.b.17.(1)0;(2) ;(3)0.18.(1)241 (2)540019. ,而 , 故 .20.-7;21.原式= ,另知的末位数与33的末位数字相同都是7,而的末位数字为5,∴原式的末位数字为15-7=8.四.400.毛1.5 同底数幂的除法1.-x3,x ;2.2.04×10-4kg;3.≠2;4.26;5.(m-n)6;6.100 ;7. ;8.2;9.3-,2,2; 10.2m=n;11.b;12.;13.c;14.b;15.c;16.a;17.(1)9;(2)9;(3)1;(4) ;18.x=0,y=5;19.0;20.(1) ;(2) .21. ;四.0、2、-2.1.6 整式的乘法1.18x4y3z2;2.30(a+b)10;3.-2x3y+3x2y2-4xy3;4.a3+3a;5.-36;•6.•a4--16;7.-3x3-x+17 ;8.2,39. ;10.c;11.c;12.c;13.d;14.d;15.d;16-.;17.a ; 18.(1)x= ;(2)0;19. ∵ ∴ ;20.∵x+3y=0 ∴x3+3x2y-2x-6y=x2(x+3y)-2(x+3y)=x20-20=0,21.由题意得35a+33b+3c-3=5,∴35a+33b+3c=8,∴(-3)5a+(-3)3b+(-3)c-3=-(35a+33b+3c)-3=-8-3=-11,22.原式=-9,原式的值与a的取值无关.23.∵ ,= ,= .∴能被13整除.四. ,有14位正整数.毛1.7 平方差公式(1)1.36-x2,x2- ;2.-2a2+5b;3.x+1;4.b+c,b+c;5.a-c,b+d,a-c,b+d ;6. ,159991;7.d; 8.c;9.d;10. -1;11.5050 ;12.(1) ,-39 ;(2)x=4;13.原式= ;14.原式= .15.这两个整数为65和63.四.略.1.7 平方差公式(2)1.b2-9a2;2.-a-1;3.n-m;4.a+,1;5.130+2 ,130-2 ,16896;6. 3x-y2;7.-24 ;8.-15;9.b; 10.d;11.c;12.a;13.c;14.b.15.解:原式= .16.解:原式=16y4-81x4;17.解:原式=10x2-10y2. 当x=-2,y=3时,原式=-50.18.解:6x=-9,∴x= .19.解:这块菜地的面积为:(2a+3)(2a-3)=(2a)2-9=4a2-9(cm2),20.解:游泳池的容积是:(4a2+9b2)(2a+3b)(2a-3b),=16a4-81b4(米3).21.解:原式=-6xy+18y2 ,当x=-3,y=-2时, 原式=36.一变:解:由题得:m=(-4x+3y)(-3y-4x)-(2x+3y)(8x-9y)=(-4x)2-(3y)2-(16x2-18xy+24xy-27y2)=16x2-9y2-16x2-6xy+27y2=18y2-6xy.四.2n+1.1.8 完全平方公式(1)1. x2+2xy+9y2, y-1 ;2.3a-4b,24ab,25,5 ;3.a2+b2+c2+2ab-2ac-2bc;4.4ab-,-2, ;5.±6;6.x2-y2+2yz-z2;7.2cm;8.d; 9.; 10.c;11.; 12.; 13.a;14.∵x+ =5 ∴(x+ )2=25,即x2+2+ =25∴x2+ =23 ∴(x2+ )2=232 即 +2+ =529,即 =527.15.[(a+1) (a+4)] [(a+2) (a+3)]=(a2+5a+4) (a2+5a+6)=(a2+5a)2+10(a2+5a)+24= .16.原式= a2b3-ab4+2b. 当a=2,b=-1时,原式=-10.17.∵a2+b2+c2-ab-bc-ca=0∴2(a2+b2+c2-ab-bc-ca)=0∴(a2-2ab+b2)+(b2-2bc+c2)+(a2-2ac+c2)=0即(a-b)2+(b-c)2+(a-c)2=0∴a-b=0,b-c=0,a-c=0∴a=b=c.1.8 完全平方公式(2)1.5y;2.500;2;250000+2000+4;252004.3.2;4.3a;6ab;b2;5.-6;6.4;7.2xy;2xy;8. ,4;9.d ; 10.d ; 11.; 12.b; 13.c; 14.b;15.解:原式 =2a4-18a2.16.解:原式 =8x3-2x4+32.当x=- 时,原式= .17.解:设m=1234568,则1234567=m-1,1234569=m+1,则a=(m-1)(m+1)=m2-1,b=m2.显然m2-118.解:-(x2-2)2>(2x)2-(x2)2+4x,-(x4-4x2+4)>4x2-x4+4x,-x4+4x2-4>4x2-x4+4x,-4>4x,∴x<-1.19.解:由①得:x2+6x+9+y2-4y+4=49-14y+y2+x2-16-12,6x-4y+14y=49-28-9-4,6x+10y=8,即3x+5y=4,③由③-②×③得:2y=7,∴y=3.5,把y=3.5代入②得:x=-3.5-1=-4.5,∴20.解:由b+c=8得c=8-b,代入bc=a2-12a+52得,b(8-b)=a2-12a+52,8b-b2=a2-12a+52,(a-b)2+(b-4)2=0,所以a-6=0且b-4=0,即a=6,b=4,把b=4代入c=8-b得c=8-4=4.∴c=b=4,所以△abc是等腰三角形.四.(1)20012+(2001×2002)2+20022=(2001×2002+1)2.(2) n2+[n(n+1)]2+(n+1)2=[n(n+1)]2.1.9 整式的除法1. ;2.4b;3. -2x+1;4. ;5.-10× ;6.-2yz,x(答案-不惟一);7. ; 8.3; 9.x2+2; 10.c; 11.b; 12.d; 13.a; 14.c; 15.d;16.(1)5xy2-2x2y-4x-4; (2)1 (3)2x2y2-4x2-6;17.由解得 ;∴ .18.a=-1,b=5,c=- ,∴原式= .19. ;20.设除数为p,余数为r,则依题意有:80=pa+r ①,94=pb+r②,136=pc+r ③,171=pd+r ④,其中p、a、b、c、•d-为正整数,r≠0②-①得14=p(b-a),④-③得35=p(d-c)而(35,14)=7故p=7或p=1,当p=7时,有80÷7=11…3 得r=3而当p=1时,80÷1=80余0,与余数不为0矛盾,故p≠1∴除数为7,余数为3.四.略.毛单元综合测试1. ,2.3,2;3.1.23× ,-1.49× ;4.6;4; ;5.-2 6-.单项式或五次幂等,字母a等; 7.25; 8.4002;9.-1;10.-1; 11.36;12.a=3,b=6-,c=4 ;13.; 14.a ; 15.a ;16.a ; 17.c ; 18.d;19.由a+b=0,cd=1,│m│=2 得x=a+b+cd- │m│=0原式= , 当x=0时,原式= .20.令 ,∴原式=(b-1)(a+1)-ab=ab-a+b-1-ab=b-a-1= .21.∵=∴∴ =35.22.= =123×3-12×3+1=334.毛第二章平行线与相交线2.1余角与补角(本文来源于:兔笨笨英语网 tooben )1.×、×、×、×、×、√;2.(1)对顶角(2)余角(3)补角;3.d;4.110°、70°、110°;5.150°;6.60°;7.∠aoe、∠boc,∠aoe、∠boc,1对;8.90°9.30°;10.4对、7对;11.c;12.195°;13.(1)90°;(2)∠mod=150°,∠aoc=60°;14.(1)∠aod=121°;(2)∠aob=31°,∠doc=31°;(3)∠aob=∠doc;(4)成立;四.405°.2.2探索直线平行的条件(1)1.d;2.d;3.a;4.a;5.d;6.64°;7.ad、bc,同位角相等,两直线平行;8、对顶角相等,等量代换,同位角相等,两直线平行;9.be∥df(答案不);10.ab∥cd∥ef;11.略;12.fb∥ac,证明略.四.a∥b,m∥n∥l.2.2探索直线平行的条件(2)1.ce、bd,同位角;bc、ac,同旁内角;ce、ac,内错角;2.bc∥de(答案不);3.平行,内错角相等,两直线平行;4.c;5.c;6.d;7.(1)∠bed,同位角相等,两直线平行;(2)∠dfc,内错角相等,两直线平行;(3)∠afd,同旁内角互补,两直线平行;(4)∠aed,同旁内角互补,两直线平行;8.b;9.c;10.b;11.c;12.平行,证明略;13.证明略;14.证明略;15.平行,证明略(提示:延长dc 到h);四.平行,提示:过e作ab的平行线.2.3平行线的特征1.110°;2.60°;3.55°;4.∠cgf,同位角相等,两直线平行,∠f,内错角相等,两直线平行,∠f,两直线平行,同旁内角互补;5.平行;6.①② ④(答案不);7.3个 ;8.d;9.c;10.d;11.d;12.c;13.证明略;14.证明略;四.平行,提示:过c作de的平行线,110°.2.4用尺规作线段和角(1)1.d;2.c;3.d;4.c;5.c;6.略;7.略;8.略;9.略;四.(1)略(2)略(3)①a② .4.4用尺规作线段和角(2)1.b;2.d;3.略;4.略;5.略;6.略;7.(1)略;(2)略;(3)相等;8.略;9.略;10.略;四.略.单元综合测试1.143°;2.对顶角相等;3.∠acd、∠b;∠bdc、∠acb;∠acd;4.50°;5.65°;6.180°;7.50°、50°、130°;8.α+β-γ=180°;9.45°;10.∠aod、∠aoc;11.c;12.a;13.c;14.d;15.a;16.d;17.d;18.c;19.d;20.c;21.证明略;22.平行,证明略;23.平行,证明略;24.证明略;第三章生活中的数据3.1 理解百万分之一1,1.73×10 ;2,0.000342 ; 3,4×10 ; 4,9×10 ; 5,c; 6,d;7,c ; 8,c; 9,c;10,(1)9.1×10 ;(2)7×10 ;(3)1.239×10 ;11, =10 ;10 个.3.2 近似数和有效数字1.(1)近似数;(2)近似数;(3)准确数;(4)近似数;(5)近似数;(6)近似数;(7)近似数;2.千分位;十分位;百分位;个位;百位;千位;3. 13.0,0.25 , 3.49×104 , 7.4*104;4.4个, 3个, 4个, 3个, 2个, 3个;5. a;6、c;7. ;8. d ;9. a ;10. b;11.有可能,因为近似数1.8×102cm是从范围大于等于1.75×102而小于1.85 ×102中得来的,有可能一个是1.75cm,而另一个是1.84cm,所以有可能相差9c12. ×3.14×0.252×6=0.3925mm3≈4.0×10-10m313.因为考古一般只能测出一个大概的年限,考古学家说的80万年,只不过是一个近似数而已,管理员却把它看成是一个精确的数字,真是大错特错了.四:1,小亮与小明的说法都不准确.3498精确到千位的近似数是3×1033.3 世界新生儿图1,(1)24% ;(2)200m以下 ;(3)8.2%;2,(1)59×2.0=118(万盒);(2)因为50×1.0=50(万盒),59×2.0=118(万盒),80×1.5=120 (万盒),所以该地区盒饭销量的年份是2000年,这个年的年销量是120万盒;(3) =96(万盒);答案:这三年中该地区每年平均销售盒饭96万盒.。
吉林省榆树市第一高级中学2019_2020学年高二数学上学期第一次月考试题(无答案)

榆树一中2019—2020学年度高二上学期第一次月考数学试题第I 卷(选择题,共60分)一、选择题(本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求)1、数列1,3,5,7,9, 的一个通项公式是 ( )A.()21n n N +-∈ B. ()1n n N +-∈ C. ()n n N +∈ D. ()33n n N +-∈2、在中,角A ,B ,C 所对的边分别为c b a ,,,如果12=a , 0030,45==C A ,那么c 等于 ( )A .B .C .212D .263、在数列{}n b 中,31-=n b n , 则13b b -的值为 ( ) A .34 B .32 C .31 D .1 4、已知实数c b a ,, 满足0>>>c b a ,则下列不等式正确的是 ( )A .b a 11>B .c a 11>C .c b b a +<+11D .ca cb +<+11 5、在等比数列{}n a 中,)(0*N n a n ∈>且 4,142==a a ,则数列{}n a 前3项的和是 ( )A .3B .27C .314 D . 6 6、在中,角A ,B ,C 所对的边分别为c b a ,,,其面积)(41222b a c S --=, 则角C 的大小是 ( )A .2πB .32πC .4π D . 43π7、等差数列{}n a 中,n S 是其前n 项和, 111-=a ,27979=-S S , 则=12S ( )A .-11B .0C .2D .-48、在中,角A ,B ,C 所对的边分别为c b a ,,,其中54sin ,9,10===B b a , 则 不同形状的个数有 ( )A .二个B .一个C . 0个D .以上都有可能 9、已知实数,,y x 若实数m 既是 23323与的等差中项,又是x 9与y 3的等比中项,则y x +2的值为 ( )A .3B .4C .1D .210、已知等差数列{}n b 中,n S 是它的前n 项和,若001312><S S 且 则当n S 最小时n 的值为 ( )A .8B .6C .13D .12 11、已知△ABC 的内角A ,B ,C 的对边分别为c b a ,,,若322cos =C ,23=a 33cos cos =+B a A b ,则边b 的值为 ( )A . 7B . 8C . 10D . 912、已知等差数列{}{},n n a b 的前n 项和分别为,n n S T ,若对于任意的自然数n , 都有131-+=n n T S n n ,则=++++82673115)(2b b a b b a a ( ) A .137 B .1315 C .715D .1516 第Ⅱ卷 (非选择题, 共90分)二、填空题(共4小题,每小题5分,共20分,将答案填在答题卡相应的位置上)13、已知在数列{}n a 中,若1a =1,123(1)n n a a n +=+≥,则=3a14、如图所示,已知两座灯塔A 和B 与海洋观察站C 的距离都等于km 2(千米),灯塔A 在观察站C 的北偏东020,灯塔B 在观察站C 的南偏东040,则灯塔A 与灯塔B 的距离为( 14题图) ( 15题图)15、如图,在ABC ∆中,030=B ,D 是边BC 上一点, 7,5,3,AC AD DC ===则AB 的长为16、已知数列{}n a 满足13)1(1+=--+n a a n n n ,则{}n a 的前40项和为 .三、解答题:(本大题共6小题,共70分. 解答应写出文字说明、证明过程或演算步骤).17、(本题满分10分)已知等差数列{}n a 中,7,141==a a .( Ⅰ )求数列{}n a 的通项公式; (本小题满分5分)( Ⅱ )若数列{}n a 的前k 项和100=kS ,求k 的值.(本小题满分5分) 18、(本小题满分12分)在ABC ∆中,角A ,B ,C 所对的边分别为c b a ,,,且2=a ,54cos =B . (Ⅰ)若3=b ,求A sin 的值; (本小题满分6分)(Ⅱ)若ABC ∆的面积3=∆ABC S ,求b 的值. (本小题满分6分)19、(本小题满分12分)若数列{}n a 满足11=a ,n a a n n +=+1()n N *∈ ,( Ⅰ ) 求42a a 与的值 (本小题满分6分)( Ⅱ )设111-=+n n a b ,且{}n b 前n 项和n S ,若使1019>n S 恒成立, 求n 的最小值 (本小题满分6分)20、(本小题满分12分)在ABC ∆中,角A ,B ,C 所对的边分别为c b a ,,,若,3π=B且边c b a ,,成等比数列,( Ⅰ ) 求角A 的大小; (本小题满分6分)( Ⅱ ) 若3=a ,求△ABC 外接圆面积. (本小题满分6分)21、(本小题满分12分)在ABC ∆中,角A ,B ,C 所对的边分别为c b a ,,,且bc a c b +=+222 ( Ⅰ ) 若A C B 2sin sin sin =⋅,判断ABC ∆的形状 (本小题满分6分)( Ⅱ ) 若c b ,是函数4013)(2+-=x x x f 的零点,求a 的值(本小题满分6分)22、(本题满分12分)若数列{}n a 的前n 项和n S 满足231(*)=-∈n n S a n N ,数列{}n b 满足112a b =.231+=+n n b b(Ⅰ)求数列{}n a ,{}n b 的通项公式; (本小题满分6分)(Ⅱ)设)1(3log+⋅=n b n n a c ,求数列{}n c 的前n 项和n T .(本小题满分6分。
上海市莘庄中学2019年第一学期高二数学第一次质量调查(无答案)

上海市莘庄中学2019学年第一学期高二数学第一次质量调查一、填空题(每题4分共48分)1.等差数列中,,则n= .2.,则向量在向量方向上的投影为.3.已知向量,则的单位向量坐标为.4.无穷数列中,,则= .5.若向量、满足,,则,则与的夹角为.6.已知两点-,点P在P1P2延长线上,且满足,则P点的坐标为.7.设数列、均为等差数列,则.8.已知,用数学归纳法证明时,.9.已知数列中,,点且满足y=2x-1,则=.10.设向量,若,设数列的前n项和为S n,则S n的最小值为.11.植树节某班20名同学在一段直线公路一侧植树,每人植一棵,相邻两棵树相距10米.开始时需将树苗集中放置在某一树坑旁边.现将树坑从1到20依次编号,为使各位同学从各自树坑前来领取树苗所走的路程总和最小,树苗可以放置的两个最佳坑位的编号为.12.已知数列满足,若是递减数列,则实数a的取值范围是.二、选择题(每题4分共16分)13.若四边形ABCD中,满足,则该四边形是()A.菱形 B.直角三角形 C.矩形 D.正方形14.已知数列的奇数项依次成等差数列,偶数项依次成等比数列,且,则()A. B.19 C.20 D.2315.已知等比数列的公比为q,前n项的和为S n,集合则P为()A. B. C. D.16.已知,点P在∠AOB内,且∠AOP=,设,则()A. B. C. D.2三、解答题(10+10+10+12+14)17.已知(1)当k为何值时,与平行?(2)当k为何值时,与垂直?18.设两个向量满足=2=1,与的夹角为60°,若向量+与向量的夹角为锐角,求实数t的取值范围.19.S n为数列的前n项的和.已知(1)求的通项公式;(2)设求数列所有项和.20.已知数列的前n项和(1)求数列的通项公式;(2)设求数列的2n项和;(3)对于(2)中的数列,求数列的前n项和T.21.已知数列的前n项和为S n,且(1)求数列的通项公式;(2)设,数列的前n项和为T n.求使不等式对一切都成立的最大的正整数k的值;(3)设是否存在,使得成立?若存在,求出m的值;若不存在,请说明理由。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
精 品 试 卷
推荐下载
2019年高二数学 暑假作业(11)
一、选择题:
1.△ABC中,a、b、c分别为∠A、∠B、∠C的对边.如果a、b、c成等差数列,
∠B=30°,△ABC的面积为23,那么b= ( )
A.231 B.31 C.232 D.32
2.在△ABC中,若a = 2 ,23b,030A , 则B等于 ( )
A.60 B.60或 120 C.30 D.30或150
3、对于任意实数a、b、c、d,命题①bcaccba则若,0,;②22,bcacba则若 ③babcac则若,22;
④baba11,则若;⑤bdacdcba则若,,0.其中真命题的个数是
( )
(A)1 (B)2 (C)3 (D)4
二、填空题:
4、在△ABC中,sinA=2cosBsinC,则三角形为 三角形
5、不等式21131xx的解集是 .
三、解答题:
6.△ABC中,D在边BC上,且BD=2,DC=1,∠B=60o,∠ADC=150o,求AC的长及△ABC的面积.
7. 在ABC△中,已知内角A,边23BC.设内角Bx,周长为y.(1)求函数()yfx的解析式和
定义域;(2)求y的最大值.
精 品 试 卷
推荐下载
一、选择题:
4.若实数a、b满足a+b=2,是3a+3b的最小值是 ( )
A.18 B.6 C.23 D.243
5.fxaxax()21在R上满足fx()0,则a的取值范围是 ( )
A.a0 B.a4 C.40a D.40a
6.若角α,β满足-2π<α<β<2π,则2α-β的取值范围是 ( )
A.(-π,0) B.(-π,π) C.(-23π,2π) D.(-23,23π)
二、填空题:
4.△ABC的面积为4222cba,则内角C等于_______________.
5.在三角形中,若三内角成等差数列,则最大内角与最小内角之和为______.
三、解答题:
6、某纺纱厂生产甲、乙两种棉纱,已知生产甲种棉纱1吨需耗一级子棉2吨、二级子棉1吨;生产乙种棉纱需耗
一级子棉1吨、二级子棉2吨,每1吨甲种棉纱的利润是600元,每1吨乙种棉纱的利润是900元,工厂在生
产这两种棉纱的计划中要求消耗一级子棉不超过300吨、二级子棉不超过250吨.甲、乙两种棉纱应各生产多
少(精确到吨),能使利润总额最大?
7.如图,海中有一小岛,周围3.8海里内有暗礁。一军舰从A地出发由西向东航行,望见小岛B在北偏东75°,航
行8海里到达C处,望见小岛B在北端东60°。若此舰不改变舰行的方向继续前进,问此舰有没有角礁的危险?
