结构动力学ch3-2
合集下载
结构动力学PPTppt课件

时间函数
§1-2 动荷载的定义和分类
荷载: 作用在结构上的主动力 荷载三要素: 大小、方向和作用点 荷载分类:
作用时间: 恒载 活载
作用位置: 固定荷载 移动荷载 对结构产生的动力效应: 静荷载 动荷载
静荷载: 动荷载:
大小、方向和作用点不随时间变 化或变化很缓慢的荷载。 大小、方向或作用点随时间变化 很快的荷载。
第二章
单自由度 体系模型
运动方程的建立
y( t) c m k Ft ( )
质量块m,用来表示结构的质量和惯性特性 自由度只有一个:水平位移y(t) 无重弹簧,刚度为 k,提供结构的弹性恢复力 无重阻尼器,阻尼系数c,表示结构的能量耗散,提供结 构的阻尼力 随时间变化的荷载F(t)
大型桥梁结构 的有限元模型
§1-5 运动方程的建立
定义
在结构动力分析中,描述体系质量运动规律的数学 方程,称为体系的运动微分方程,简称运动方程。 运动方程的解揭示了体系在各自由度方向的位移 随时间变化的规律。 建立运动方程是求解结构振动问题的重要基础。 常用方法:直接平衡法、虚功法、变分法。
确定性荷载:荷载的变化是时间的确定性函数。
FP
例如: 简谐荷载
t
FP
冲击荷载
t
FP
突加荷载
t
非确定性荷载: 荷载随时间的变化是不确定的或不确知的, 又称为随机荷载。 例如:
W ind speed (m/s) 25 20
脉动风 平均风
t(sec)
风荷载
15 10 5 0 0
50
100
150200Fra bibliotek250
3π x b3 si n l
n π x (x ) b ns in l n 1
有机化学-第8章:卤代烷

Zn + HCl
CH3(CH2)14CH2I
CH3(CH2)14CH3
RX HI RI HI
-HX
RH + I2
卤代烷的还原
2 中性还原剂
催化氢化
RX (or ArX) H2 / Pd*
RH (orArH) * PdC, Ni, Pt
O
OH
CH2CCH3
CH2CHCH3
O2N
C=N H2 / Pd C H2N
H Br H
CH2 = CHCH2CH3+ CH3CH=CHCH3
19%
81%
CH3 CH3CHCHCH2
H Br H
叔卤代烷
C2H5ONa, C2H5OH
CH3
CH3 CH= C(CH3)2+ CH3CH2C=CH2
71%
29%
消除反应 ( E )
Saytzeff(查依采夫)规律
(1875年俄国化学家Saytzeff总结了当时已知的大量实验事实, 得出以下经验结论.)
(3) ( 4S )-4-甲基-5-乙基-1-溴庚烷 CH3 H
CH3CH2CH C CH2CH2CH2Br C2H5
(2) ( 2S,3S )-2-氯-3-溴丁烷
H Br Cl H CH3 C C CH3
4. (1R,3R)-1,3-二溴环己烷
Br H
H Br
卤代烷的普通命名法
CH3CH2CH2CH2Cl
H2 H1
慢
Br
-
HO
C
-
Br
快
HO
H1 C H2
Br-
H3
定义:
H3ห้องสมุดไป่ตู้
结构动力学-2

设初始条件为 y(0) y0, y(0) v0
运动方程的特解
y(t)
y0
cost
v0
sin
t
令
y0 Asin , v0 / Acos
y(t) Asin( t )
y
其中
A
y02
v02
2
tan y0
v0
T 2 自振周期
1 2 自振频率
T
A t
A T
与外界无关,体系本身固有的特性
y02
( v0
y0 D
)2
y0D /(v0 y0 )
小阻尼情况
y(0) y0 , y(0) v0
1 (c 2m)
c1 (v0 y0 ) / D , c2 y0
令 D 1 2
方程的通解为
y(t) Aet sin( Dt D )
A
y02
( v0
y0 D
)2
y(t) et (c1 sin Dt c2 cosDt) tan D y0D /(v0 y0 )
设初始条件为 y(0) y0, y(0) v0
运动方程的特解
y(t)
y0
cost
v0
sin
t
令
y0 Asin , v0 / Acos
m
my(t)
y(t)
l EI
y(t) Asin( t )
y(t) 2 y(t) 0
km
二阶线性齐次常微分方程
运动方程的通解 y(t) c1 cost c2 sin t
令 c / 2m y 2y 2 y 0
设 y(t) Aet
2 2 2 0 特征方程
运动方程及其解
m y(t)
结构动力学
u
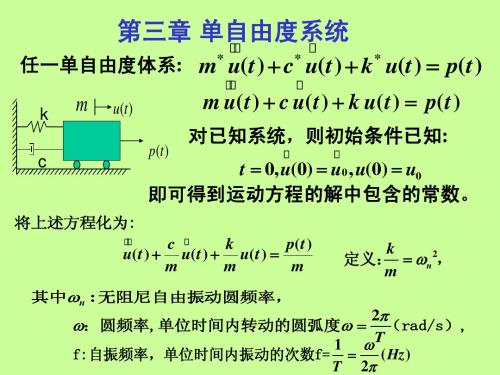
Td
2 2 2 ln wnTd wn wn 2 2 2 uQ wd wn 1 1
u 1 ln (求阻尼比的一种方法) 2 uQ
当 0
小结
3.1 无阻尼自由振动
u n2 u 0
u( t ) A1 cos n t A2 sin n t
m 2U kU p0
p0 U k
1
2 1 2 n
p0 w2 2 式中:令U 0 (静位移), 2 (频率比) k wn
1 则 : U U0 , 2 1
1 U 令:H ( ) 2 1 U0
( —频率响应函数, 其中:U —动响应;U 0 —静响应)
即可得到运动方程的解中包含的常数。
将上述方程化为:
c k p( t ) u( t ) u( t ) u( t ) m m m
其中n : 无阻尼自由振动圆频率,
k 定义: n 2, m
2 :圆频率,单位时间内转动的圆弧度 (rad/s), 1 T f:自振频率,单位时间内振动的次数f= ( Hz ) T 2
(1)c 0时,无阻尼,
c
p(t )
小车在临界位置左右摆动; (2)c , c ccr , 1时,
超过临界位置, 振荡起来; (4)c , c ccr , 1时,
不超过临界位置, 没振荡起来;
(3)c , c ccr , 1时, 处于临界状态, 可能振荡,也可能不振荡;
第三章 单自由度系统
任一单自由度体系: m* u(t ) c* u(t ) k * u(t ) p(t )
k c
Td
2 2 2 ln wnTd wn wn 2 2 2 uQ wd wn 1 1
u 1 ln (求阻尼比的一种方法) 2 uQ
当 0
小结
3.1 无阻尼自由振动
u n2 u 0
u( t ) A1 cos n t A2 sin n t
m 2U kU p0
p0 U k
1
2 1 2 n
p0 w2 2 式中:令U 0 (静位移), 2 (频率比) k wn
1 则 : U U0 , 2 1
1 U 令:H ( ) 2 1 U0
( —频率响应函数, 其中:U —动响应;U 0 —静响应)
即可得到运动方程的解中包含的常数。
将上述方程化为:
c k p( t ) u( t ) u( t ) u( t ) m m m
其中n : 无阻尼自由振动圆频率,
k 定义: n 2, m
2 :圆频率,单位时间内转动的圆弧度 (rad/s), 1 T f:自振频率,单位时间内振动的次数f= ( Hz ) T 2
(1)c 0时,无阻尼,
c
p(t )
小车在临界位置左右摆动; (2)c , c ccr , 1时,
超过临界位置, 振荡起来; (4)c , c ccr , 1时,
不超过临界位置, 没振荡起来;
(3)c , c ccr , 1时, 处于临界状态, 可能振荡,也可能不振荡;
第三章 单自由度系统
任一单自由度体系: m* u(t ) c* u(t ) k * u(t ) p(t )
k c
结构动力学3

2)当m1=nm2 , k1=nk2
[(n1)k
2
2
nm2
](k2
2m2
)k
2 2
0
k11=(1+n)k2,k12=-k2
求频率:
2 1 2
1 2
2
1 n
+
4 n
1 n2
k2 m2
求振型:Y2 k11 2m1 (n 1)k2 2nm2
k m
2 2
3 2
5
k m
2.61803 k m
2 1.61803
k m
求振型: ω1→第一主振型:
Y11 k12
Y21 k11 12m1
k
1
2k 0.38197k 1.618
ω2→第二主振型:
Y12 k12
Y22 k11 22m1
k
1
2k 2.61803k 0.618
质量集中在楼层上m1、m2 ,层间侧移刚度为k1、k2
m2
k21
1
k2 1 k11
m1
k1
k22 k12
解:求刚度系数:
k2
k1
k11=k1+k2 , k21=-k2 ,
k21
k2
k22
k11
k22=k2 ,
k12=-k2
k12
k
k1 k2
k2
k2
k2
例题:12,2质量m12集2 中kmk1112在楼km2层22 上+m1、12m2km,111层1间km2侧22 k移k12121刚度k1为1k2km211、mkk2122k121k12k22
结构动力学课件—dyanmics of structures-ch(2)
184 BEAM FLEXURE: ORTHOGONALITY OF VIBRATION MODE SHAPES
CHAPTER 18. ANALYSIS OF UNDAMPED FREE VIBRATION
The second orthogonality condition, For a nonuniform beam, the equation of motion in free vibrations
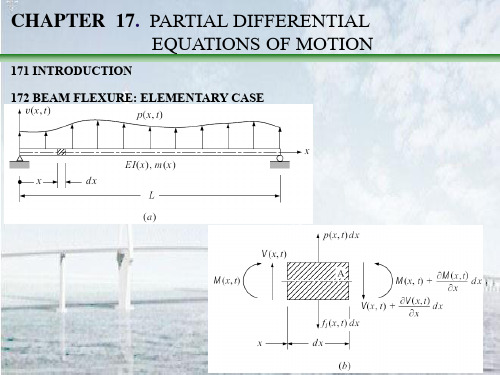
CHAPTER 17. PARTIAL DIFFERENTIAL EQUATIONS OF MOTION
173 BEAM FLEXURE: INCLUDING AXIALFORCE EFFECTS
momentequilibrium equation now becomes
Rotation of beam axis
Example E182. Cantilever Beam
CHAPTER 18. ANALYSIS OF UNDAMPED FREE VIBRATION
CHAPTER 18. ANALYSIS OF UNDAMPED FREE VIBRATION
CHAPTER 18. ANALYSIS OF UNDAMPED FREE VIBRATION
183 BEAM FLEXURE: WITH DISTRIBUTED ELASTIC SUPPORT Separating variables as before
giving two independent equations
CHAPTER 18. ANALYSIS OF UNDAMPED FREE VIBRATION
equilibrium relationship for vertical forces
CHAPTER 18. ANALYSIS OF UNDAMPED FREE VIBRATION
The second orthogonality condition, For a nonuniform beam, the equation of motion in free vibrations
CHAPTER 17. PARTIAL DIFFERENTIAL EQUATIONS OF MOTION
173 BEAM FLEXURE: INCLUDING AXIALFORCE EFFECTS
momentequilibrium equation now becomes
Rotation of beam axis
Example E182. Cantilever Beam
CHAPTER 18. ANALYSIS OF UNDAMPED FREE VIBRATION
CHAPTER 18. ANALYSIS OF UNDAMPED FREE VIBRATION
CHAPTER 18. ANALYSIS OF UNDAMPED FREE VIBRATION
183 BEAM FLEXURE: WITH DISTRIBUTED ELASTIC SUPPORT Separating variables as before
giving two independent equations
CHAPTER 18. ANALYSIS OF UNDAMPED FREE VIBRATION
equilibrium relationship for vertical forces
第12章结构动力学 ppt课件
§14-1 概 述
一、结构动力计算的特点 动力荷载作用下,结构将发生振动,各种量值均随时间而变化。
1、内容: (1)研究动力荷载作用下,结构的内力、位移等计算原理和计算方法。 求出它们的最大值并作为结构设计的依据。
(2)研究单自由度及多自由度的自由振动、强迫振动。 2、静荷载和动荷载 (1)静荷载:荷载的大小和方向不随时间变化(如梁板自重)。 (2)动荷载:荷载的大小和方向随时间变化,需要考虑惯性力。 3、特点 (1)必须考虑惯性力。 (2)内力与荷载不能构成静平衡。必须考据惯性力。依达朗伯原理, 加惯性力后,将动力问题转化为静力问题。
动力自由度的确定方法:加附加链杆约束质点位移,最少链杆数即为自 由度
图刚架上有四个集中质点,但只需要加三根链杆 便可限制全部质点的位置。如图e。
自由度=3 或
图示梁,其分布质量集度为m,可看作有无穷多 个mdx的集中质量,是无限自由度结构。
自由度的数目与结构是否静定或超静定无关
§14-2 结构振动的自由度
2、运动方程的解:
方程
y2y0
为一常系数线性齐次微分方程,其通解为
y (t) A 1 co t s A 2sitn
A1和A2为任意常数,可有初始条件来确定。
振动的初始条件为 t 0 时 y y , 0 , y y 0
式中y0—初位移, y0—初速度。则有Fra bibliotekA1y0,A2
y0
可得
yy0cots y0si nt
第十四章 结构动力学
§14-1 概 述 §14-2 结构振动的自由度 §14-3 单自由度结构的自由振动 §14-4 单自由度结构在简谐荷载作用下的强迫振动 §14-5 单自由度结构在任意荷载作用下的强迫振动 §14-6 多自由度结构的自由振动 §14-7 多自由度结构在简谐荷载作用下的强迫振动 §14-8 振型分解法 §14-9 无限自由度结构的振动 §14-10 计算频率的近似法
05 结构力学——结构动力学2
A0 1 ln (2)设经过na周,振幅将降到0.05厘米以下,由 2na Ana A0 1 . 5 0 1 ln na ln 10 . 32 11 2 An 2 0 . 0355 0 . 05
2
K kl
2
K J
k m
18
第三节
单自由体系自由振动
2、有阻尼的自由振动 ( 0 )
m y c y ky 0 2 y 2 y y 0
齐次线性微分方程的特征方程
2 2
k m c 2m
2
2 0 2 ( 1 ) 1 ,2
微分方程的解按特征根的性质不同,具有三种不同形式:
19
第三节
单自由体系自由振动
( 1)
2、有阻尼的自由振动 ( 0 ) 1 小阻尼的情况 两个特征根为复数
y ( t ) e( C cos t C sin t ) d 2 d
t 1
2
y y 0 0 y ( t ) e ( y cos t sin t ) d d
a
32
第四节
单自由体系受迫振动
1、单自由体系受迫振动的一般解
m y c y ky F ( t ) E F ( t) 2 E y 2 y y m y ( t ) y ( t ) y ( t ) 1 2
求特解的基本思路
将动荷载的作用看成是一系列在质点上暂短停留 的不变的力(脉冲)的集合,由叠加可得到任意 荷载作用的响应。
kg W
g W
g ys
1 m
自振频率和周期的特性:
2
K kl
2
K J
k m
18
第三节
单自由体系自由振动
2、有阻尼的自由振动 ( 0 )
m y c y ky 0 2 y 2 y y 0
齐次线性微分方程的特征方程
2 2
k m c 2m
2
2 0 2 ( 1 ) 1 ,2
微分方程的解按特征根的性质不同,具有三种不同形式:
19
第三节
单自由体系自由振动
( 1)
2、有阻尼的自由振动 ( 0 ) 1 小阻尼的情况 两个特征根为复数
y ( t ) e( C cos t C sin t ) d 2 d
t 1
2
y y 0 0 y ( t ) e ( y cos t sin t ) d d
a
32
第四节
单自由体系受迫振动
1、单自由体系受迫振动的一般解
m y c y ky F ( t ) E F ( t) 2 E y 2 y y m y ( t ) y ( t ) y ( t ) 1 2
求特解的基本思路
将动荷载的作用看成是一系列在质点上暂短停留 的不变的力(脉冲)的集合,由叠加可得到任意 荷载作用的响应。
kg W
g W
g ys
1 m
自振频率和周期的特性:
结构动力学
z
y
x
y
二维:薄板或薄壳的动力行为: 独立参数:x,y
x
一维:梁和杆系:
独立参数:x
x
梁的弯曲:基本情况
设梁为变截面直梁,主要物理性质如下:
抗弯刚度:EI(x) 横向荷载:p(x,t) 单位长度质量:m(x) 横向位移反应:v(x,t)
v( x, t )
p( x , t )
V
M
M M dx p( x , t ) x
设:
iv ( x ) m Y( t ) 4 ( x) EI Y ( t )
iv ( x ) 4 ( x ) 0 2 Y ( t ) Y ( t ) 0
故:
其中:
2
4 EI
m
无阻尼自由振动分析
iv ( x ) 4 ( x ) 0 Y ( t ) 2Y ( t ) 0
u ydA c s ydA t t x 2 2v 2 2v 2 cs y dA c s 2 y dA c s 2 y dA t x t x t x 3v cs I ( x ) 2 x t
对于具有连续分布特性的真实结构,原则上要取无限多个坐标才可以 收敛与精确解! 研究无限多个连接点的行为的正规数学方法是用微分方程,其中取位 置坐标为独立变量,因为在动力问题中时间也是一个独立变量,所以 按此途径形成运动方程时得到偏微分方程。
运动的偏微分方程
三维:研究三维固体的运动行为: 独立参数:x,y,z
v x
以上三式联立:
v 2v k' AG x p m t 2 x
y
x
y
二维:薄板或薄壳的动力行为: 独立参数:x,y
x
一维:梁和杆系:
独立参数:x
x
梁的弯曲:基本情况
设梁为变截面直梁,主要物理性质如下:
抗弯刚度:EI(x) 横向荷载:p(x,t) 单位长度质量:m(x) 横向位移反应:v(x,t)
v( x, t )
p( x , t )
V
M
M M dx p( x , t ) x
设:
iv ( x ) m Y( t ) 4 ( x) EI Y ( t )
iv ( x ) 4 ( x ) 0 2 Y ( t ) Y ( t ) 0
故:
其中:
2
4 EI
m
无阻尼自由振动分析
iv ( x ) 4 ( x ) 0 Y ( t ) 2Y ( t ) 0
u ydA c s ydA t t x 2 2v 2 2v 2 cs y dA c s 2 y dA c s 2 y dA t x t x t x 3v cs I ( x ) 2 x t
对于具有连续分布特性的真实结构,原则上要取无限多个坐标才可以 收敛与精确解! 研究无限多个连接点的行为的正规数学方法是用微分方程,其中取位 置坐标为独立变量,因为在动力问题中时间也是一个独立变量,所以 按此途径形成运动方程时得到偏微分方程。
运动的偏微分方程
三维:研究三维固体的运动行为: 独立参数:x,y,z
v x
以上三式联立:
v 2v k' AG x p m t 2 x
结构动力学-2(哈工大结构动力学)
m y(t)
cy(t)
my(t) k11 y(t )
运动方程 my cy k11y 0
令 c / 2m y 2y 2 y 0
设 y(t) Aet
2 2 2 0 特征方程
根为 i 1 2 由初始条件
小阻尼情况
y(0) y0 , y(0) v0
1 (c 2m)
c1 (v0 y0 ) / D , c2 y0
k
k
k
PROBLEMS:
3.A mass m is at rest,partially supported by a spring and partially by stops.In the position shown,the spring force is mg/2. At time t=0 the stops are rotated,suddenly releasing the mass.Determine the motion of the mass.
第二章单自由度体系的振动分析
§2.1 自由振动
一. 无阻尼体系 运动方程
y(t) 11[my(t)] k11y(t) my(t) 令 2 k11 1
m m11
y(t) 2 y(t) 0
二阶线性齐次常微分方程
m
my(t)
y(t)
l EI
km
运动方程的通解 y(t) c1 cost c2 sin t
令 D 1 2
方程的通解为
y(t) Aet sin( Dt D )
A
y02
( v0
y0 D
)2
y(t) et (c1 sin Dt c2 cosDt) tan D y0D /(v0 y0 )
