中考数学24题评分标准(一)
2024北京中考评分标准

2024北京中考评分标准北京市教育委员会发布的《北京市中等教育入学考试评卷标准(2024年版)》(以下简称《评分标准》)详细规定了2024年北京中考的评分要求和标准。
该标准旨在确保评卷工作的公正、公平和科学性,以便准确地评估学生的学业水平。
一、试卷结构2024年北京中考试卷由语文、数学、英语和其他科目组成。
每科试卷分为两部分:选择题和主观题。
选择题占总分的40%,主观题占60%。
具体分值和题型可以根据不同科目的要求有所调整。
二、选择题评分标准选择题的评分标准主要包括两个方面:答题卡填涂规范和答案正确性。
学生在填涂答题卡时必须使用2B铅笔进行填涂,并确保填涂完整、清晰、无误。
对于答案正确的选择题,按照评分标准给予相应的分数;对于答案错误的选择题,不给予分数。
三、主观题评分标准主观题的评分标准主要根据学生答案的准确性、完整性、逻辑性、表达能力和语言规范性等方面进行评判。
具体评分标准如下:1.语文评分标准(1)阅读理解:根据答案的准确性和完整性给予相应分数,对于答案错误或遗漏的部分不得分;(2)写作:根据作文的内容、结构、语言运用和表达能力等方面进行评价,评分标准分为A、B、C、D四档。
2.数学评分标准(1)计算题:根据答案的准确性给予相应分数,对于答案错误的部分不得分;(2)解答题:根据解题过程的正确性和逻辑性给予相应分数,对于解答过程错误或遗漏的部分不得分。
3.英语评分标准(1)听力理解:根据答案的准确性和完整性给予相应分数,对于答案错误或遗漏的部分不得分;(2)阅读理解和写作:根据答案的准确性、完整性和语言表达能力等方面进行评价,评分标准分为A、B、C、D四档。
4.其他科目评分标准其他科目的评分标准根据具体科目的要求进行评价,包括对学生实验操作、实验结果分析和综合应用等方面进行评分,具体标准由相应学科教研组确定。
四、评分流程和操作要求评卷工作由专门的评卷组组成,评卷组成员必须具备相应学科的专业知识和评卷经验,且必须经过培训合格后方可参与评卷工作。
中考数学评分标准 北京

中考数学评分标准北京中考数学评分标准是指在北京地区中考数学考试中,对学生答题进行评分的具体标准和要求。
中考数学评分标准的制定是为了保证评分的公平、公正,能够客观地反映学生的数学水平和能力。
下面将详细介绍北京地区中考数学评分标准的相关内容。
首先,北京地区中考数学评分标准对试题的命题要求非常严格,试题的设计需要符合中学数学教学大纲的要求,涉及的知识点和考查的能力应该全面、均衡。
试题的难度分布要合理,能够考察学生的基础知识和综合运用能力,不偏废某一方面。
同时,试题的表述要清晰准确,避免歧义,确保学生能够准确理解题意并给出正确的答案。
其次,中考数学评分标准要求评卷老师在评分过程中要严格按照评分标准进行,对学生的答题进行客观公正的评价。
评分标准应该明确具体,对于每一道题目都要有明确的分值和评分要点,避免主观性评分的出现。
同时,评分过程中要注重对学生答题过程的分析,对于有部分正确但未完全正确的答案也要给予适当的分数,鼓励学生表达自己的思路和方法。
另外,中考数学评分标准还要求评分标准的公布和解释工作要及时到位。
学校和教育部门应该在考试前向学生和家长公布评分标准,让他们了解到评分的依据和要求,以便学生在答题时能够有针对性地准备和发挥。
同时,评分标准的解释工作也要及时跟进,对于学生和家长提出的疑问和意见要进行认真解答,保证评分的公正性和透明度。
最后,中考数学评分标准的制定和执行需要各方的共同努力。
教育部门、学校、老师、学生和家长都应该共同关注和支持评分标准的制定和执行工作,共同维护考试的公平、公正,保障学生的权益和利益。
总之,中考数学评分标准的制定和执行是一个复杂而严谨的工作,需要各方的共同努力和配合。
只有通过科学合理的评分标准,才能够真正反映学生的数学水平和能力,为学生的学业发展和未来的发展打下坚实的基础。
希望各方能够共同关注和支持中考数学评分标准的工作,共同营造一个公平、公正的教育环境。
2023河北中考数学22题阅卷情况汇报及评卷标准

2023河北中考数学22题阅卷情况汇报及评卷标准一、本题亮点:题目从学生已有数学经验入手创设客户满意度调查的真实情境,借助统计图对问卷调查中的数据进行整理和分析,通过平均数,中位数,不等式计算做出决策和判断,第二问判断抽取的问卷所评分数为几分?问题设计开放性强,解决问题方法多样。
考查了数据观念及应用意识,体现了基础性、综合性、应用性和实践性,关注考生基础知识和学科核心素养的考查,注重理论知识与生活实际的紧密联系。
二、典型错误:从阅卷情况看,本题考生熟悉,贴近日常生活实际,绝大多数考生有信心参与答题,整体得分率较高。
但也有部分考生答题失分,主要集中在一下几点:1、(1)中位数:不排序计算;偶数个数中位数不会求,只列出3和4;(2)第二步求平均数分母忽略加1,仍用20;(3)不等式意义符合表示不准:小于写成“>”;(4)读不懂统计图2、计算失误:”“10243=+;”“55.32170>+x 结果为55.3>x ; 3、审题不认真,语言表达不规范,答非所问。
(1)列式不加括号3+4÷2=3.5;(2)不按问题作答:“不需要”写成“是”;“整改”写成“修改”;三、错误分析:1、审题不清,中位数概念、平均数公式掌握不牢,不会列不等式,基础知识薄弱;2、计算能力差,分析能力较弱;3、读题、识图、获取有效信息能力较差;四、评价建议:1、夯实基础知识,关注概念教学;2、培养良好的读题、审题、解题习惯;规范解题格式和过程,抓准答题要点,准确表达;3、加强统计图表的理解,注重运算能力培养,提高计算准确性;4、重视现实情景中提炼数学问题,加强数学的思维能力培养,培养现实世界的观察、表达、推理的能力。
五、评分标准:(1)中位数:3.5—————————— 2 分平均数:3.5————————————— 2 分不需整改(不是,否,意义相近均给1分)——— 1 分(2)所评分数为5分(列式正确给1分)——— 2 分中位数4分,发生变化(变小),——— 2 分(注;具备其一均得2分)。
2020年河南省普通高中招生考试 数学试题参考答案及评分标准
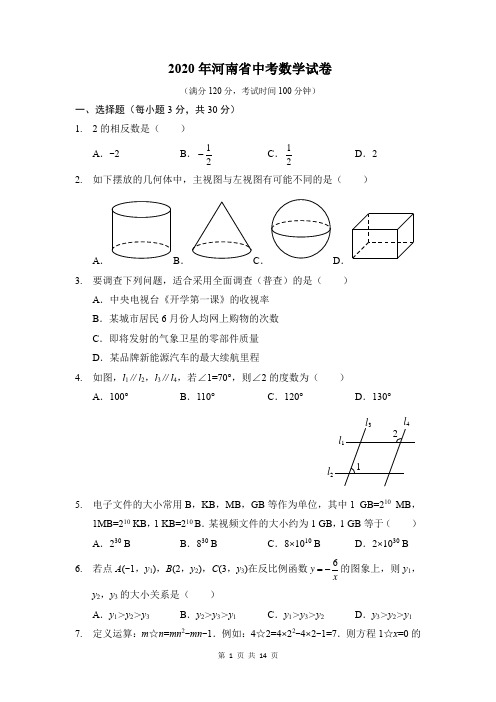
2020年河南省中考数学试卷(满分120分,考试时间100分钟)一、选择题(每小题3分,共30分) 1. 2的相反数是( )A .-2B .12-C .12D .22. 如下摆放的几何体中,主视图与左视图有可能不同的是( )AB .D .3. 要调查下列问题,适合采用全面调查(普查)的是( )A .中央电视台《开学第一课》的收视率B .某城市居民6月份人均网上购物的次数C .即将发射的气象卫星的零部件质量D .某品牌新能源汽车的最大续航里程4. 如图,l 1∥l 2,l 3∥l 4,若∠1=70°,则∠2的度数为( )A .100°B .110°C .120°D .130°5. 电子文件的大小常用B ,KB ,MB ,GB 等作为单位,其中1 GB=210 MB ,1MB=210 KB ,1 KB=210 B .某视频文件的大小约为1 GB ,1 GB 等于( ) A .230 BB .830 BC .8×1010 BD .2×1030 B6. 若点A (-1,y 1),B (2,y 2),C (3,y 3)在反比例函数6y x=-的图象上,则y 1,y 2,y 3的大小关系是( )A .y 1>y 2>y 3B .y 2>y 3>y 1C .y 1>y 3>y 2D .y 3>y 2>y 17. 定义运算:m ☆n =mn 2-mn -1.例如:4☆2=4×22-4×2-1=7.则方程1☆x =0的2l 1l 2l 3l 41根的情况为( )A .有两个不相等的实数根B .有两个相等的实数根C .无实数根D .只有一个实数根8. 国家统计局统计数据显示,我国快递业务收入逐年增加.2017年至2019年我国快递业务收入由5 000亿元增加到7 500亿元.设我国2017年至2019年快递业务收入的年平均增长率为x ,则可列方程为( ) A .5 000(1+2x )=7 500 B .5 000×2(1+x )=7 500C .5 000(1+x )2=7 500D .5 000+5 000(1+x )+5 000(1+x )2=7 5009. 如图,在△ABC 中,∠ACB =90°,边BC 在x 轴上,顶点A ,B 的坐标分别为(-2,6)和(7,0).将正方形OCDE 沿x 轴向右平移,当点E 落在AB 边上时,点D 的坐标为( ) A .(32,2) B .(2,2) C .(114,2) D .(4,2)10. 如图,在△ABC 中,AB =BCBAC =30°,分别以点A ,C 为圆心,AC的长为半径作弧,两弧交于点D ,连接DA ,DC ,则四边形ABCD 的面积为( ) A.B .9C .6D.二、填空题(每小题3分,共15分)A BCD11. 请写出一个大于1且小于2的无理数___________.12. 已知关于x 的不等式组x ax b>⎧⎨>⎩,其中a ,b 在数轴上的对应点如图所示,则这个不等式组的解集为___________.13. 如图所示的转盘,被分成面积相等的四个扇形,分别涂有红、黄、蓝、绿四种颜色.固定指针,自由转动转盘两次,每次停止后,记下指针所指区域(指针指向区域分界线时,忽略不计)的颜色,则两次颜色相同的概率是_____.14. 如图,在边长为ABCD 中,点E ,F 分别是边AB ,BC 的中点,连接EC ,FD ,点G ,H 分别是EC ,FD 的中点,连接GH ,则GH 的长度为____________.15. 如图,在扇形BOC 中,∠BOC =60°,OD 平分∠BOC 交BC ︵于点D ,点E 为半径OB 上一动点.若OB =2,则阴影部分周长的最小值为_________.三、解答题(本大题共8个小题,满分75分)aABCDEFGH16. (8分)先化简,再求值:21(1)11aa a -÷+-,其中1a =.17. (9分)为发展乡村经济,某村根据本地特色,创办了山药粉加工厂.该厂需购置一台分装机,计划从商家推荐试用的甲、乙两台不同品牌的分装机中选择.试用时,设定分装的标准质量为每袋500 g ,与之相差大于10 g 为不合格.为检验分装效果,工厂对这两台机器分装的成品进行了抽样和分析,过程如下:【收集数据】从甲、乙两台机器分装的成品中各随机抽取20袋,测得实际质量(单位:g )如下:甲:501 497 498 502 513 489 506 490 505 486 502 503 498 497 491 500 505 502 504 505 乙:505 499 502 491 487 506 493 505 499 498 502 503 501 490 501 502 511 499 499 501【整理数据】整理以上数据,得到每袋质量x (g )的频数分布表.根据以上信息,回答下列问题:(1)表格中的a =_________,b =_________;(2)综合上表中的统计量,判断工厂应选购哪一台分装机,并说明理由.18. (9分)位于河南省登封市境内的元代观星台,是中国现存最早的天文台,也是世界文化遗产之一.某校数学社团的同学们使用卷尺和自制的测角仪测量观星台的高度.如图所示,他们在地面一条水平步道MP 上架设测角仪,先在点M 处测得观星台最高点A 的仰角为22°,然后沿MP 方向前进16 m 到达点N 处,测得点A 的仰角为45°.测角仪的高度为1.6 m .(1)求观星台最高点A 距离地面的高度(结果精确到0.1 m .参考数据:sin22°≈0.37,cos22°≈0.93,tan22°≈0.40≈1.41);(2)“景点简介”显示,观星台的高度为12.6 m .请计算本次测量结果的误差,并提出一条减小误差的合理化建议.19. (9分)暑假将至,某健身俱乐部面向学生推出暑期优惠活动,活动方案如下:方案一:购买一张学生暑期专享卡,每次健身费用按六折优惠; 方案二:不购买学生暑假专享卡,每次健身费用按八折优惠.设某学生暑期健身x (次),按照方案一所需费用为y 1(元),且y 1=k 1x+b ;B C 22°45°按照方案二所需费用为y2(元),且y2=k2x.其函数图象如图所示.(1)求k1和b的值,并说明它们的实际意义;(2)求打折前的每次健身费用和k2的值;(3)八年级学生小华计划暑期前往该俱乐部健身8次,应选择哪种方案所需费用更少?说明理由.20.(9分)我们学习过利用尺规作图平分一个任意角,而“利用尺规作图三等分一个任意角”曾是数学史上一大难题,之后被数学家证明是不可能完成的.人们根据实际需要,发明了一种简易操作工具——三分角器.图1是它的示意图,其中AB与半圆O的直径BC在同一直线上,且AB的长度与半圆的半径相等;DB和AC垂直于点B,DB足够长.使用方法如图2所示,若要把∠MEN 三等分,只需适当放置三分角器,使DB 经过∠MEN 的顶点E ,点A 落在边EM 上,半圆O 与另一边EN 恰好相切,切点为F ,则EB ,EO 就把∠MEN 三等分了.为了说明这一方法的正确性,需要对其进行证明.如下给出了不完整的“已知”和“求证”,请补充完整,并写出“证明”过程.已知:如图2,点A ,B ,O ,C 在同一直线上,EB ⊥AC ,垂足为点B ,______. 求证:___________.21. (10分)如图,抛物线y =-x 2+2x +c 与x 轴正半轴,y 轴正半轴分别交于点A ,B ,且OA =OB ,点G 为抛物线的顶点. (1)求抛物线的解析式及点G 的坐标;(2)点M ,N 为抛物线上两点(点M 在点N 的左侧),且到对称轴的距离分别为3个单位长度和5个单位长度,点Q 为抛物线上点M ,N 之间(含点图1NMM ,N )的一个动点,求点Q 的纵坐标y Q 的取值范围.22. (10分)小亮在学习中遇到这样一个问题:小亮分析发现,此问题很难通过常规的推理计算彻底解决,于是尝试结合学习函数的经验研究此问题,请将下面的探究过程补充完整:(1) 根据点D 在BC ︵上的不同位置,画出相应的图形,测量线段BD ,CD ,FD 的长度,得到下表的几组对应值.操作中发现:①“当点D 为BC ︵的中点时,BD =5.0 cm ”,则上表中a 的值是_________;②“线段CF 的长度无需测量即可得到”,请简要说明理由.(2)将线段BD 的长度作为自变量x ,CD 和FD 的长度都是x 的函数,分别记为CD y 和FD y ,并在平面直角坐标系xOy 中画出了函数FD y 的图象,如图所示.请在同一坐标系中画出函数CD y 的图象;(3)继续在同一坐标系中画出所需的函数图象,并结合图象直接写出:当△DCF 为等腰三角形时,线段BD 长度的近似值(结果保留一位小数).23. (11分)将正方形ABCD 的边AB 绕点A 逆时针旋转至AB′,记旋转角为α,连接BB′,过点D 作DE 垂直于直线BB′,垂足为点E ,连接DB′,CE . (1)如图1,当α=60°时,△DEB′的形状为__________,连接BD ,可求出BB CE的值为________;(2)当0°<α<360°且α≠90°时,①(1)中的两个结论是否仍然成立?如果成立,请仅就图2的情形进行证明;如果不成立,请说明理由;②当以点B′,E ,C ,D 为顶点的四边形是平行四边形时,请直接写出BEB E的值.ABC DE B'图1ABCDEB'图2。
徐州市2020年中考数学试题及评分标准

(图1) 0102030A B C D选项 人数8%DCB A 16%20%56%O (图2)一、选择题(本大题共12小题,每小题2分,共24分.)1. 2-的绝对值是( )A . 2- B . 2 C . 12- D . 122. 徐州市2007年中考考生总数约为158 000人,这个数用科学记数法可以表示为( ) A .315810⨯ B .415.810⨯ C .51.5810⨯ D .60.15810⨯ 3. 函数1y x =+中自变量x 的取值范围是( )A .x ≥1-B .x ≤1-C .1x >-D .1x <- 4. 下列运算中错误的是( )A .235+=B .236⨯=C .632÷=D .22-=2()5. 方程322x x =-的解的情况是( ) A .2x = B .6x = C .6x =- D .无解6. 如图,水平放置的甲、乙两区域分别由若干大小完全相同的黑色、白色正三角形组成.小明随意向甲、乙两个区域各抛一个小球,P (甲)表示小球停在甲中黑色三角形上的概率,P (乙)表示小球停在乙中黑色三角形上的概率,下列说法中正确的是( ) A .P (甲)> P (乙) B .P (甲)= P (乙)C .P (甲)< P (乙)D .P (甲)与 P (乙)的大小关系无法确定7. 九年级某班在一次考试中对某道单选题的答题情况如下图所示.根据以上统计图,下列判断中错误的是( )A .选A 的有8人B .选B 的有4人C .选C 的有26人D .该班共有50人参加考试8. 图1是由6个大小相同的正方体组成的几何体,它的俯视图是( )A .B .C .D .9. 梯形的上底长为a ,下底长是上底长的3倍,则该梯形的中位线长为( )A .aB .1.5aC .2aD .4a 10A .3cm B .43cm C .2 cm D .23cm11.如图2,将两张完全相同的正方形透明纸片完全重合地叠放在一起, 中心是点O .按住下面的纸片不动,将上面的纸片绕点O 逆时针旋转15°, 所得重叠部分的图形( )A .既不是轴对称图形也不是中心对称图形B .是轴对称图形但不是中心对称图形C .是中心对称图形但不是轴对称图形D .既是轴对称图形又是中心对称图形甲 乙12.在图3的扇形中,90AOB ∠=︒,面积为4πcm 2 ,用这个扇形围成一个圆锥的侧面,这个圆锥的底面半径为( ) A . 1 cm B . 2 cm C D .4 cm二、填空题(本大题共4小题,每小题3分,共12分)13.若反比例函数的图象过点(2-,3),则其函数关系式为 .14.如图4,已知⊙O 是△ABC 的内切圆,且50ABC ∠=︒,80ACB ∠=则BOC ∠= °.15.一次考试中6名学生的成绩(单位:分)如下:24,72,68,45,86,92.16.如图现将17解:19证明:20解:...... 21.(A 类)已知2210a a ++=,求2243a a +-的值.(B 类)已知222450a b a b ++-+=,求2243a b +-的值. 解:我选做的是 类题.(图4)C(图9)G22.(A 类)如图7,已知AB是⊙O的直径,弦CD AB⊥于点E,16CD=cm,20AB=cm,求OE的长.(B 类)如图7,已知AB是⊙O的直径,弦CD AB⊥于点E,4BE=cm,16CD=cm,求⊙O的半径.解:我选做的是类题.23解:24..解:六、解答题(本大题共2小题,每小题8分,共16分)25.某隧道横断面由抛物线与矩形的三边组成,尺寸如图10所示.(1)以隧道横断面抛物线的顶点为原点,以抛物线的对称轴为y轴,建立直角坐标系.求该抛物线对应的函数关系式;(图10) (图12)AB CDE E'D'FO (2)某卡车空车时能通过此隧道,现装载一集装箱,箱宽3 m , 车与箱共高4.5 m .此车能否通过隧道?并说明理由. 解:26.如图11,一艘船以每小时30海里的速度向东北方向航行,在A 处观测灯塔S 在船的北偏东75°的方向.航行12分钟后到达B 处,这时灯塔S 恰好在船的正东方向.已知距离此灯塔8海里以外的海区为航行安全区域.这艘船可以继续沿东北方向航行吗?为什么?(精确到0.1) (参考数据:2 1.41≈,3 1.73≈) 解:七、解答题(本大题只有1小题,9分)27.如图12,△ABC 中,点D 在AC 上,点E 在BC 上,且DE ∥AB .将△CDE 绕点C 按顺时针方向旋转得到△CD E ''(使BCE '∠<180°),连结AD '、BE '.设直线BE '与AC 、AD '分别交于点O 、F .(1)若△ABC 为等边三角形,则AD BE ''的值为 ,AFB ∠的度数为 °;(2)若△ABC 满足60ACB ∠=︒,AC =3,BC =2,① 求AD BE''的值及∠AFB 的度数;② 若E 为BC 中点,求△OBC 面积的最大值.解:八、解答题(本大题只有1小题,10分)28.如图13,直线l1:1=分别交于M、N两点.设P为x轴上的一y x=-+与两直线l2:2=、l3:y xy x点,过点P的直线l:y x b=-+与直线l2、l3分别交于A、C两点,以线段AC为对角线作正方形ABCD.(1)写出正方形ABCD各顶点的坐标(用b表示);(2)当点P从原点O点出发,沿着x轴的正方向运动时,设正方形ABCD与△OMN重叠部分的面积为S,求S与b之间的函数关系式,并写出相应自变量b的取值范围.解:徐州市2007年初中毕业、升学考试数学试题参考答案及评分意见13.y x =-.14.115.15.70.16.8. 17.原式 = 1123-+-+ ------ 4分 18.解不等式①,得x ≤4-.-------2分= 1. -------- 5分 解不等式②,得5x >-. -----4分∴原不等式组的解集是:5x -<≤4-. ----5分19.法1:在△AOB 和△DOC 中,∵OA OD =,OB OC =,而AOB DOC ∠=∠,∴△AOB ≌△DOC , ----3分 A D ∠=∠, -----------4分 ∴AB ∥CD . ---------5分法2:连结AC 、BD . -----------1分∵OA OD =,OB OC =,∴四边形ACDB 是平行四边形, -----4分 ∴AB ∥CD . -----5分20.法1:设小王该月发送网内短信x 条、网际短信y 条. 根据题意,得1500.10.1519x y x y +=⎧⎨+=⎩,. ------- 2分解这个方程组,得7080x y =⎧⎨=⎩,. -------- 4分答:小王该月发送网内短信70条、网际短信80条.-------- 5分法2:设小王该月发送网内短信x 条,则发送网际短信(150)x -条.根据题意,得0.10.15(150)19x x +-=.-------- 2分 解这个方程,得70x =. ----- 3分所以15080x -=. ----- 4分 答:小王该月发送网内短信70条、网际短信80条.--- 5分 21.(A 类)法1:∵222432(21)5a a a a +-=++-, -----------3分而2210a a ++=,∴原式2055=⨯-=-.---------5分法2:∵2210a a ++=,∴221a a +=-,-------1分而222243(24)32(2)3a a a a a a +-=+-=+-,-------3分 ∴原式2(1)35=⨯--=-.--------5分法3:∵2210a a ++=,∴2(1)0a +=,---------2分 ∴1a =-,--------3分 ∴原式22(1)4(1)35=⨯-+⨯--=-.---------5分(B 类)因为222450a b a b ++-+=,∴22(21)(44)0a a b b +++-+=,------2分即22(1)(2)0a b ++-=, -----4分 ∴10a +=且20b -=,∴1a =-且2b =,------5分 ∴原式22(1)4237=⨯-+⨯-=. ---------7分22.(A 类)如图答1,连结OC .∵AB 是直径,CD AB ⊥,∴1116822CE CD ==⨯=.------------2分而11201022OC AB ==⨯=, ------3分 在Rt △OCE 中,∵222OE CE OC +=,--------4分∴6OE ==(cm ).-----------5分11232425将12y =-代入代入上式,得x =,----5分 ∴4.5 m (-=m .-----6分3,所以此车不能通过隧道.----------8分26.如图答2,过S 作SC ⊥直线AB 于C .设SC x =. -----------1分在R t △SBC 中,∵45CBS ∠=︒,∴tan 45SCBC x ==︒. ------2分在R t △SAC 中,∵754530CAS ∠=︒-︒=︒,∴tan30SCAC ==︒. --------3分∵1230660AB =⨯=,而AC BC AB -=,∴6AC BC -=, ------------4分 6x -=, ------5分 ∴1)x =. -------6分即1)8.28SC =≈>,∴这艘船可以继续沿东北方向航行.--------------------------------------8分27.(((最大.28.(可得B (3b ,2b ),D (2b ,3b ).---------4分(2)当点D 在直线l 1上时,67b =;-------5分当点B 在直线l 1上时,65b =;--------------6分① 当607b <<时,∵正方形ABCD 的边长为16b ,∴2136S b =;------------7分② 当67≤1b <时,如图答4,设DC 与直线l 1交于点E ,则E(12b,112b-),716DE b=-,∴2221174771(1)36267262S b b b b=--=-+-;--------8分③当1≤b≤65时,如图答5,设AB与直线l1交于点F,则F(13b,113b-),516BF b=-,∴22152551(1)267262S b b b=-=-+;--------------9分④当65b>时,0S=.--------------10分注:。
2020上海中考数学试卷评分标准

2020上海中考数学试卷评分标准一、考试性质上海市初中毕业统一学业考试(中考)是义务教育阶段数学课程的终结性考试。
其目的是全面、准确地评估初中毕业生在数学学科方面达到的水平,作为衡量初中学校教学质量的重要依据,并作为高中阶段学校录取的重要依据。
二、考试目标通过纸笔测试的形式,全面、准确地评估学生是否达到课程标准所规定的数学毕业水平,为高中阶段学校录取提供依据。
三、考试内容与要求数学试卷分为选择题、填空题和解答题三种题型。
选择题共8题,每题4分,合计32分;填空题共10题,每题4分,合计40分;解答题共8题,合计88分。
全卷难度值控制在0.70左右。
1. 选择题:侧重于对数学基础知识和基本技能的考查,如数的认识、数的运算、数的大小比较、平面图形的认识与性质、数据统计等。
每道选择题给出四个选项,要求考生从中选出符合题意的正确选项。
2. 填空题:侧重于对数学概念、原理和方法的深度理解和应用能力的考查,如代数式与方程、函数及其图像、三角形与四边形等。
每道填空题要求考生直接填写答案,无选项可选。
3. 解答题:侧重于对数学思想方法和问题解决能力的综合考查,如实际问题与一元二次方程、解直角三角形、相似三角形与锐角三角函数等。
每道解答题通常包括几个小问题或步骤,要求考生根据题目要求进行计算、推理或证明,并写出完整的解答过程。
四、评分标准1. 选择题评分标准:每道选择题正确答案只有一个,考生需从给出的四个选项中选择正确答案。
评分时采用标准答案与考生答案进行比对,完全符合则计分,若不完全符合则按一定比例扣分。
2. 填空题评分标准:每道填空题要求考生填写完整答案。
评分时采用标准答案与考生答案进行比对,完全符合则计分,若不完全符合则按一定比例扣分。
3. 解答题评分标准:每道解答题包括几个小问题或步骤,要求考生根据题目要求进行计算、推理或证明,并写出完整的解答过程。
评分时采用标准答案与考生答案进行比对,根据考生的解答步骤和思路进行给分,正确解答步骤和思路对应相应的分数,错误或未完成的解答步骤和思路则不给分。
中考数学压轴题评分标准

2010年全国各地中考数学压轴题 参考答案及评分标准(一)1.解:(1)∵抛物线y =-41 m x2+45m x +m2-3m +2经过原点 ∴m2-3m +2=0,解得m 1=1,m 2=2 由题意知m 1≠1,∴m =2 ∴抛物线的解析式为y =-41x2+25x ∵点B (2,n )在抛物线y =-41x2+25x 上,∴n =4 ∴点B 的坐标为(2,4)·····················································2分 (2)①设直线OB 的解析式为y =k 1x 求得直线OB 的解析式为y =2x∵A 点是抛物线与x 轴的一个交点,可求得A 点的坐标为(10,0) 设P 点的坐标为(a ,0),则E 点的坐标为(a ,2a ) 根据题意作等腰直角三角形PCD ,如图1 可求得点C 的坐标为(3a ,2a ) 由C 点在抛物线上,得2a =-41×(3a )2+25×3a即49a2-211a =0,解得a 1=922,a 2=0(舍去) ∴OP =922··············································································4分 ②依题意作等腰直角三角形QMN 设直线AB 的解析式为y =k 2x +b由点A (10,0),点B (2,4),求得直线AB 的解析式为y =-21x +5 当P 点运动到t 秒时,两个等腰直角三角形分别有一条边恰好落在同一条直线上, 有以下三种情况:第一种情况:CD 与NQ 在同一条直线上,如图2所示 可证△DPQ 为等腰直角三角形此时OP 、DP 、AQ 的长可依次表示为t 、4t 、2t 个单位 ∴PQ =DP =4t ,∴t +4t +2t =10∴t =710第二种情况:PC 与MN 在同一条直线上,如图3所示 可证△PQM 为等腰直角三角形此时OP 、AQ 的长可依次表示为t 、2t 个单位图1图2图3∴OQ =10-2t∵F 点在直线AB 上,∴FQ =t ,∴MQ =2t ∴PQ =MQ =CQ =2t ,∴t +2t +2t =10 ∴t =2第三种情况:点P 、Q 重合时,PD 与QM 在同一条直线上, 如图4所示此时OP 、AQ 的长可依次表示为t 、2t 个单位 ∴t +2t =10∴t =310综上,符合题意的t 值分别为710,2,310·······································································8分2.解:(Ⅰ)如图1,作点D 关于x 轴的对称点D ′,连接CD ′与x 轴交于点E ,连接DE若在边OA 上任取点E ′(与点E 不重合),连接CE ′、DE ′、D ′E ′ 由DE ′+CE ′=D ′E ′+CE ′>CD ′=D ′E +CE =DE +CE 可知△CDE 的周长最小∵在矩形OACB 中,OA =3,OB =4,D 为边OB 的中点 ∴BC =3,D ′O =DO =2,D ′B =6∵OE ∥BC ,∴Rt △D ′OE ∽Rt △D ′BC ,∴BC OE =B D OD '' ∴OE =BD OD ''·BC =62×3=1∴点E 的坐标为(1,0)··········································································6分(Ⅱ)如图2,作点D 关于x 轴的对称点D ′,在CB 边上截取CG =2,连接D ′G 与x 轴交于点E ,在EA 上截取EF =2,则四边形GEFC 为平行四边形,得GE =CF 又DC 、EF 的长为定值,∴此时得到的点E 、F 使四边形CDEF 的周长最小∵OE ∥BC ,∴Rt △D ′OE ∽Rt △D ′BG ,∴BG OE =B D OD '' ∴OE =BD OD ''·BG =BD OD ''·(BC -CG )=62×1=31∴OF =OE +EF =31+2=37∴点E 的坐标为(31,0),点F 的坐标为(37,0)··························10分3.解:(Ⅰ)当b =2,c =3时,抛物线的解析式为y =-x2+2x +3,即y =-(x -1)2+4∴抛物线顶点E 的坐标为(1,4)·················································································2分 (Ⅱ)将(Ⅰ)中的抛物线向下平移,则顶点E 在对称轴x =1上,又b =2 ∴抛物线的解析式为y =-x2+2x +c (a >0)图4∴此时抛物线与y 轴的交点为C (0,c ),顶点为E (1,1+c ) ∵方程-x2+2x +c =0的两个根为x 1=1-c +1,x 2=1+c +1∴此时抛物线与x 轴的交点为A (1-c +1,0),B (1+c +1,0) 如图,过点E 作EF ∥CB 与x 轴交于点F ,连接CF ,则S △BCE=S △BCF∵S △BCE=S △ABC,∴S △BCF=S △ABC∴BF =AB =2c +1设对称轴x =1与x 轴交于点D , 则DF =21AB +BF =3c +1 由EF ∥CB 得∠EFD =∠CBO∴Rt △EDF ∽Rt △COB ,∴DF ED =OBCO即c c ++131=cc ++11,结合题意,解得c =45 ∴点C (0,45),B (25,0)设直线BC 的解析式为y =mx +n ,则 ⎪⎪⎩⎪⎪⎨⎧n m n +== 25045 解得⎪⎪⎩⎪⎪⎨⎧-4521==n m ∴直线BC 的解析式为y =-21x +45··············································································6分 (Ⅲ)根据题意,设抛物线的顶点为E (h ,k ),(h >0,k >0) 则抛物线的解析式为y =-(x -h )2+k 此时抛物线与y 轴的交点为C (0,-h2+k ),与x 轴的交点为A (h -k ,0),B (h +k ,0).(k >h >0) 过点E 作EF ∥CB 与x 轴交于点F ,连接CF ,则S △BCE=S △BCF∵S △BCE=2S △AOC,∴S △BCF=2S △AOC∴BF =2AO =2(k -h )设该抛物线的对称轴与x 轴交于点D ,则DF =21AB +BF =3k -2h由Rt △EDF ∽Rt △COB ,得DF ED =OBCO即hk k 23-=kh k h ++-2,即2h2-5k h +2k =0结合题意,解得h =2k① ∵点E (h ,k )在直线y =-4x +3上,∴k =-4h +3 ② 由①②,并结合题意,解得k =1∴k =1,h =21∴抛物线的解析式为y =-x2+x +43············································································10分4.解:(1)∵∠B =30°,ACB ∠=90°,∴BAC ∠=60°∵AD =AE ,∴∠AED =60°=∠CEP∴∠EPC =30°····················································································································1分 ∴△BDP 为等腰三角形∵△AEP ∽△BDP ,∴∠EAP =∠EPA =∠DBP =∠DPB =30°··································2分 ∴AE =EP =1·······················································································································3分∴在RT △ECP 中,EC =21EP =21···················································································4分(2)如图2,过点D 作DQ ⊥AC 于点Q ,且设AQ =a ,BD =x ∵AE =1,EC =2,∴QC =3-a∵∠ACB =90°,∴△ADQ ∽△ABC ∴AB AD =AC AQ ,即1x 1+=3a ,∴a =1x 3+ ∵在RT △ADQ 中,DQ =22AQ AD-=21x 31)(+-=1x 8x 2x 2+-+∵BC DQ =ABAD,∴x 1x 8x 2x 2+-+=1x 1+·········································································5分 解得x =4,即BD =4··········································································································6分 过点C 作CF//DP ,则△ADE ∽△AFC∴AC AE =AF AD ,∴AF =AC ,即DF =EC =2 ∴BF =DF =2···························································7分∵△BFC ∽△BDP ,∴BD BF =BP BC =42=21即BC =CP =4··························································8分 ∴tan BPD ∠=CP EC =42=21···································9分(3)如图3,过D 点作DQ ⊥AC 于点Q ,则DQE △∽PCE △ 设AQ =a ,则QE =1-a∴EC QE =CP DQ 且tan BPD ∠=31,∴DQ =3(1-a ) 在Rt △ADQ 中,由勾股定理得:AD2=AQ2+DQ2即12=a2+[3(1-a )]2,解得a =1(舍去)或a =54,∴DQ =53·····························10分图3图2∵△ADQ ∽△ABC ,∴AB AD =BC DQ =AC AQ =x 154+=x554+ ∴AB =4x 55+,BC =4x33+··························································································12分 ∴三角形ABC 的周长y =AB +BC +AC =4x 55++4x33++1+x =3+3x 即y =3+3(x >0)··········································································································14分5.解:(1)如图①,过点C 作CD ⊥OA 于点D∵OC =AC ,∠ACO =120°,∴∠AOC =∠OAC =30° ∵OC =AC ,CD ⊥OA ,∴OD =DA =1 在Rt △ODC 中,OC =AOC OD ∠cos =30cos 1=332··············1分(ⅰ)当0<t<32时,OQ =t ,AP =3t ,OP =2-3t过点Q 作QE ⊥OA 于点E ,则EQ =21t∴S △OPQ=21OP ·EQ =21(2-3t )·21t =-43t2+21t即S=-43t2+21t ·····································································3分 (ⅱ)当32<t≤332时,如图②,OQ =t ,OP =3t -2 ∵∠BOA =60°,∠AOC =30°,∴∠POQ =90° ∴S △OPQ=21OQ ·OP =21t ·(3t -2)=23t2-t即S=23t 2-t 故当0<t<32时,S=-43t2+21t ,当32<t≤332时,S=23t2-t ····························5分 (2)D (33,1)或(332,0)或(32,0)或(34,332)·······························9分 (3)BMN 的周长不发生变化如图③,延长BA 至点F ,使AF =OM ,连结CF ∵∠MOC =∠F AC =90°,OC =AC ,∴△MOC ≌△F AC ∴MC =CF ,∠MCO =∠FCA ···············································10分 ∴FCN =∠FCA +∠NCA =∠MCO +∠NCA=∠OCA -∠MCN =60° ∴FCN =∠MCN又∵MC =CF ,CN =CN ,∴△MCN ≌△FCN∴MN =NF ··························································································································11分图①图②图③∴BM +MN +BN =BM +NF +BN =BO -OM +BA +AF =BA +BO =4∴BMN 的周长不变,其周长为4·····················································································12分6.解:(1)方法一:∵抛物线过C (0,-6),∴c =-6,即y =ax2+bx -6由⎪⎩⎪⎨⎧061214422 =+=--b a a b解得a =161,b =-41∴该抛物线的解析式为y =161x2-41x -6·········································································3分方法二:∵A 、B 关于x =2对称,∴A (-8,0) 设y =a (x +8)(x -12),∵C (0,-6)在抛物线上∴-6=a (0+8)(0-12),∴a =161∴该抛物线的解析式为y =161(x +8)(x -12) 即y =161x2-41x -6············································3分(2)存在,设直线CD 垂直平分PQ 在Rt △AOC 中,AC =2268+=10=AD∴点D 在对称轴上,连结DQ ,显然∠PDC =∠QDC ····················································4分 由已知∠PDC =∠ACD∴∠QDC =∠ACD ,∴DQ ∥AC ························································································5分 DB =AB -AD =20-10=10 ∴DQ 为△ABC 的中位线,∴DQ =21AC =5···································································6分 AP =AD -PD =AD -DQ =10-5=5,∴t =5÷1=5(秒)∴存在t =5秒时,线段PQ 被直线CD 垂直平分····························································7分 在Rt △BOC 中,BC =22612+=56,∴CQ =53∴点Q 的运动速度为每秒553单位长度·········································································8分(3)存在 过点Q 作QH ⊥x 轴于H ,则QH =3,PH =9在Rt △PQH 中,PQ =2239+=103··········································································9分①当MP =MQ ,即M 为顶点时设直线CD 的解析式为y =kx +m (k ≠0)则: ⎩⎨⎧m k m +==-206 解得⎩⎨⎧63- ==m k ∴y =3x -6 当x =1时,y =-3,∴M 1(1,-3)·············································································10分 ②当PQ 为等腰△MPQ 的腰且P 为顶点时 设直线x =1上存在点M (1,y ),由勾股定理得: 42+y2=(103)2,∴y =±74∴M 2(1,74),M 3(1,-74)················································································11分 ③当PQ 为等腰△MPQ 的腰且Q 为顶点时过点Q 作QE ⊥y 轴于E ,交直线x =1于F ,则F (1,-3) 设直线x =1上存在点M (1,y ),由勾股定理得: 52+( y +3)2=(103)2,∴y =-3±65∴M 4(1,-3+65),M 5(1,-3-65)·································································12分 综上所述,存在点M ,使△MPQ 为等腰三角形,点M 的坐标为:M 1(1,-3),M 2(1,74),M 3(1,-74),M 4(1,-3+65),M 5(1,-3-65)7.解:(1)把A (-1,0),B (1,0)代入y =ax2+bx +1得:⎩⎨⎧a -b +1=0a +b +1=0 解得⎩⎨⎧a =-1b =0 ∴抛物线的解析式为y =-x2+1··········································································3分(2)令x =0,得y =1,∴C (0,1)·········································································4分∴OA =OB =OC =1,∴∠BAC =∠ACO =∠BCO =∠ABC =45° ∵BD ∥CA ,∴∠ABD =∠BAC =45°如图1,过点D 作DE ⊥x 轴于E ,则△EDB 为等腰直角三角形 设EO =x ,则ED =x +1,∴D (-x ,-x -1) ∵点D 在抛物线y =-x2+1上,∴-x -1=-(-x)2+1解得x 1=2,x 2=-1(不合题意,舍去)∴ED =3··················································································································6分 (说明:先求出直线BD 的解析式,再用两个解析式联立求解得到点D 的坐标也可) ∴S 四边形ACBD =21AB ·OC +21AB ·ED =21×2×1+21×2×3 =4······································································································7分(说明:也可直接求直角梯形ACBD 的面积为4)(3)存在·························································································································8分∵∠ABC =∠ABD =45°,∴∠DBC =90° ∵MN ⊥x 轴,∴∠MNA =∠DBC =90°BC =22OC OB +=2,BD =22EB ED +=设M 点的横坐标为m ,则M (m ,-m2+1)①当点M 在y 轴左侧时,如图2,则m <-1ⅰ)若△NMA ∽△BCD ,则NA MN =BD BC即1 12---m m =232,整理得3m2+m -2=0 图1解得m 1=-1(舍去),m 2=32(舍去) ································································9分ⅱ)若△NAM ∽△BCD ,则NA MN =BC BD即1 12---m m =223,整理得m2+3m +2=0 解得m 1=-1(舍去),m 2=-2 ∴-m2+1=-(-2)2+1=-3∴M 1(-2,-3)·································································································10分 ②当点M 在y 轴右侧时,如图2,则m >1ⅰ)若△NMA ∽△BCD ,则AN MN =BD BC即1 1 2+-m m =232,整理得3m2-m -4=0 解得m 1=-1(舍去),m 2=34∴-m2+1=-(34)2+1=-97 ∴M 2(34,-97) (11)ⅱ)若NAM ∽△BCD ,则AN MN =BCBD即∴1 1 2+-m m =223,整理得m2-3m -4=0 解得m 1=-1(舍去),m 2=4 ∴-m2+1=-42+1=-15∴M 3(4,-15)∴存在点M ,使以A 、M 、N 为顶点的三角形与△BCD 相似,M 点的坐标分别为:M 1(-2,-3),M 2(34,-97),M 3(4,-15)············································12分8.解:(1)∵抛物线y =21x2+bx +c 经过点A (2,0),C (0,-1) ∴⎩⎨⎧1022- ==++c c b解得:b =-21,c =-1···································································································2分 ∴抛物线的解析式为y =21x2-21x -1··············································································3分 (2)设点D 的坐标为(m ,0)(0<m <2),则OD =m ,AD =2-m图2。
初三中考数学第24题题型及解析

初三中考数学第24题题型及解析第三讲中考数学第24题专练⼀1(14?长沙).如图,四边形ABCD是矩形,把矩形沿对⾓线AC折叠,点B落在点E处,CE 与AD相交于点O.(1)求证:△AOE≌△COD;(2)若∠OCD=30°,AB△AOC的⾯积.2.(2015?长沙)如图,在直⾓坐标系中,⊙M经过原点O(0,0),点A(,0)与点B(0,﹣),点D在劣弧上,连接BD 交x轴于点C,且∠COD=∠CBO.(1)求⊙M的半径;(2)求证:BD平分∠ABO;(3)在线段BD的延长线上找⼀点E,使得直线AE恰好为⊙M的切线,求此时点E的坐标.3(2016?长沙).如图,四边形ABCD 内接于⊙O ,对⾓线AC 为⊙O 的直径,过点C 作AC的垂线交AD 的延长线于点E ,点F 为CE 的中点,连接DB ,DC ,DF .(1)求CDE ∠的度数;(2)求证:DF 是⊙O 的切线;(3)若AC =,求tan ABD ∠的值.4(17年长沙).如图,AB 与⊙O 相切于C ,OB OA ,分别交⊙O 于点E D ,,CE CD =.(1)求证:OB OA =;(2)已知34=AB ,4=OA ,求阴影部分的⾯积.5(18*长沙)、如图,在ABC 中,AD 是边B C 上的中线,BAD CAD ,CE//AD ,CE 交B A 的延长线于点E,BC 8,A D 3。
(1)求C E 的长;(2)求证:ABC 为等腰三⾓形;(3)求ABC 的外接圆圆⼼P与内切圆圆⼼Q之间的距离。
6.(19*长沙)根据相似多边形的定义,我们把四个⾓分别相等,四条边成⽐例的两个凸四边形叫做相似四边形.相似四边形对应边的⽐叫做相似⽐.(1)某同学在探究相似四边形的判定时,得到如下三个命题,请判断它们是否正确(直接在横线上填写“真”或“假”).①条边成⽐例的两个凸四边形相似;(命题)②三个⾓分别相等的两个凸四边形相似;(命题)③两个⼤⼩不同的正⽅形相似.(命题)(2)如图1,在四边形ABCD 和四边形A 1B 1C 1D 1中,∠ABC =∠A 1B 1C 1,∠BCD =∠B 1C 1D 1,111111AB BC CDA B B C C D ==,求证:四边形ABCD 与四边形A 1B 1C 1D 1相似.(3)如图2,四边形ABCD 中,AB ∥CD ,AC 与BD 相交于点O ,过点O 作EF ∥AB 分别交AD ,BC 于点E ,F .记四边形ABFE 的⾯积为S 1,四边形EFDE 的⾯积为S 2,若四边形ABFE 与四边形EFCD 相似,求21S S 的值.第四讲专练⼆1.(18雅礼⼀模)如图,已知AB为⊙O的直径,AB⊥AC,BC交⊙O于D,E是AC的中点,ED与AB的延长线相交于点F.(1)求证:DE为⊙O的切线.(2)若BF=2,tan∠BDF=,求⊙O的半径.2.(19麓⼭三模)如图,在Rt△ABC中,∠ACB=90°,AO是△ABC的⾓平分线.以O为圆⼼,OC为半径作⊙O.(1)求证:AB是⊙O的切线.(2)已知AO交⊙O于点E,延长AO交⊙O于点D,tan D=,求的值.(3)在(2)的条件下,设⊙O的半径为3,求AB的长.3.(长沙第三次⽉考)如图,△ABC中,AB=AC,点D为BC上⼀点,且AD=DC,过A,B,D三点作⊙O,AE是⊙O的直径,连结DE.(1)求证:AC是⊙O的切线;(2)若sin C=,AC=6,求⊙O的直径.4.(长沙第三次⽉考)如图,在△ABC中,以AB为直径作⊙O交BC于点D,∠DAC=∠B.(1)求证:AC是⊙O的切线;(2)点E是AB上⼀点,若∠BCE=∠B,tan∠B=,⊙O的半径是4,求EC的长.1.(19⼴益三模)如图,?ABCD的两条对⾓线相交于O点,过O点作OE⊥AB,垂⾜为E,已知∠DBA=∠DBC,AB=5.(1)求证:四边形ABCD为菱形;(2)若sin∠ADB=,求线段OE的长.2.(19中、南雅⼀模)如图,在矩形ABCD中,P为边CD上⼀点,把△BCP沿直线BP折叠,顶点C的对应点为C′,连接BC′与AD交于点E,连接CE与BP交于点Q,若CE⊥BE.(1)若E为AD的中点,求证:△ABE≌△DEC;(2)连接C′Q,求证:四边形C′QCP是菱形;(3)若AB=12,AD=25,且DE<AE,求菱形的边长.第三讲答案1(14?长沙).如图,四边形ABCD是矩形,把矩形沿对⾓线AC折叠,点B落在点E处,CE与AD相交于点O.(1)求证:△AOE≌△COD;(2)若∠OCD=30°,AB,求△AOC的⾯积.解2.(2015?长沙)如图,在直⾓坐标系中,⊙M经过原点O(0,0),点A(,0)与点B(0,﹣),点D 在劣弧上,连接BD 交x轴于点C,且∠COD=∠CBO.(1)求⊙M的半径;(2)求证:BD平分∠ABO;(3)在线段BD的延长线上找⼀点E,使得直线AE恰好为⊙M的切线,求此时点E的坐标.解:(1)∵点A(,0)与点B(0,﹣),∴OA=,OB=,∴AB==2,∵∠AOB=90°,∴AB是直径∴⊙M的半径为:;(2)∵∠COD=∠CBO,∠COD=∠CBA,∴∠CBO=∠CBA,即BD平分∠ABO;(3)如图,过点A作AE⊥AB,垂⾜为A,交BD的延长线于点E,过点E作EF⊥OA于点F,即AE是切线,∵在Rt△AOB中,tan∠OAB===,∴∠OAB=30°,∴∠ABO=90°﹣∠OAB=60°,∴∠ABC=∠OBC=∠ABO=30°,∴OC=OB?tan30°=×=,∴AC=OA﹣OC=,∴∠ACE=∠ABC+∠OAB=60°,∴∠EAC=60°,∴△ACE是等边三⾓形,∴AE=AC=,∴AF=AE=,EF=AE=,∴OF=OA﹣AF=,∴点E的坐标为:(,).3(2016?长沙).如图,四边形ABCD内接于⊙O,对⾓线AC为⊙O的直径,过点C作AC的垂线交AD的延长线于点E,点F为CE的中点,连接DB,DC,DF.(1)求CDE∠的度数;(2)求证:DF是⊙O的切线;(3)若AC=,求tan ABD∠的值.解(1)对⾓线AC为⊙O的直径90ADC∴∠=?90CDE∴∠=?…………………(2分)(2)(⽅法⼀)连接,OF OD,在Rt CDE中,点F为斜边CE的中点DF FC∴=在DOF和COF中DF CFOF OFOD OC===∴DOF≌COF∴90ODF OCF∠=∠=?∴DF OD⊥∴DF是⊙O的切线……………(5分)(⽅法⼆)证明:连接OD,AC为⊙O的直径,CE AC⊥90ADC CDE O∴∠=∠=, 90ACF O∠=⼜在Rt CDE中,点F为斜边CE的中点,DF FC CDF DCF ∴=∠=∠⼜OD OC = ODC OCD ∴∠=∠90ODF ODC CDF OCD DCF ∴∠=∠+∠=∠+∠=? ∴DF 是⊙O 的切线 …………………(5分)(⽅法三)证明:连接OD ,CE AC ⊥,AC 为⊙O 的直径90ADC ADO ODC ∴∠=∠+∠=? 90DAO ACD ∠+∠=?90ACD DCF ∠+∠=?DAO DCF ∴∠=∠⼜OA OD = DAO ADO ∴∠=∠ ADO DCF ∴∠=∠⼜在Rt CDE ?中,点F 为斜边CE 的中点 ,DF FC CDF DCF ∴=∠=∠ADO CDF ∴∠=∠90ODF ODC CDF ODC ADO ∴∠=∠+∠=∠+∠=? ∴DF 是⊙O 的切线 …………………(5分)(3)(⽅法⼀)由圆周⾓定理可得 ABD ACD ∠=∠由题中条件可得 90,ADC CDE CAD ECD ∠=∠=?∠=∠,ADC ∴?∽CDE ? ∴AD DCCD DE= ∴2CD AD DE =? ………………(6分)由于AC = 所以可令 ,,DE a AD b ==则有,AC CD ==在Rt ACD ?中,由勾股定理可得 222)b += 上式两边同时除以2a 并整理后得到 2()200b b a a + -= 解之可得 4b a =或5ba=-(舍去) …………………(8分)tan tan 2AD ABD ACDDC ∴∠=∠==== …………………(9分)(⽅法⼆)设DE x =,AD y =,AC =易证ACD ?∽AED ? ∴2AC AD AE =?2)()y x y =?+(即2220x y yx =+2()200y y x x +-= 解得4y x=或5yx =-(舍去)∴2CD x = ∴4tan tan 22xABD ACD x ∠=∠==(⽅法三)设DE a =,tan ABD m ∠=,则AC =,AC m EC =,CDm DE=∴AC EC m ==,CD mDE ma == 在Rt CDE ?中222CD DE CE +=∴222()ma a += ∴22201m m+= ∴222()200m m +-= ∴22(5)(4)0m m +-= ∴24m =或25m =-(舍去)∴tan 2ABD ∠=4(17年长沙).如图,AB 与⊙O 相切于C ,OB OA ,分别交⊙O 于点E D ,,CE CD =.(1)求证:OB OA =;(2)已知34=AB ,4=OA ,求阴影部分的⾯积.5、如图,在 ABC 中,AD 是边 B C 上的中线,BAD CAD ,CE //AD ,CE 交 B A 的延长线于点 E ,BC 8,A D 3。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
中考数学24题评分标准(一)
中考数学24题评分标准
一、总体要求
•评分标准以解题思路、步骤、答案准确性为主要依据;
•评分应客观公正,遵循标准答案的要求;
•题目中未明确要求的内容,不计入评分。
二、具体评分细则
1. 解题思路(5分)
•解题思路清晰,合理性强:+5分;
•解题思路基本正确,稍有瑕疵:+3分;
•解题思路模糊,错误较多:+1分;
•解题思路混乱,错误严重:0分。
2. 步骤和计算过程(10分)
•步骤清晰,计算过程正确,无漏算、错算:+10分;
•步骤基本清晰,计算过程基本正确,个别错误可接受范围内:+6分;
•步骤不够清晰,计算过程中有较多错误,但答案基本正确:+3分;
•步骤混乱,计算过程错误较多,答案不正确或近似:+1分;•步骤混乱,计算过程严重错误,答案错误较多:0分。
3. 答案的准确性与合理性(9分)
•结果完全正确,解释合理:+9分;
•结果基本正确,解释基本合理:+6分;
•结果基本正确,解释不够清晰或有瑕疵:+3分;
•结果不完全正确,解释含糊不清或错误:+1分;
•结果完全错误,解释混乱或无解释:0分。
4. 符号使用(1分)
•符号使用正确,符合数学规范:+1分;
•符号使用基本正确,个别使用有瑕疵:分;
•符号使用错误较多,使计算过程混乱:0分。
5. 书写和排版(5分)
•书写规范,排版整洁,清晰可辨:+5分;
•书写基本规范,排版基本整洁,辨认困难:+2分;
•书写较差,排版混乱,辨认困难:+1分;
•书写极差,排版极混乱,几乎无法辨认:0分。
三、总结
•中考数学24题的评分标准主要根据解题思路、步骤、答案准确性、符号使用和书写排版五个方面进行评分。
•评分要求客观公正,遵循标准答案,将解题思路、步骤、答案准确性、符号使用和书写排版的优劣进行综合评定。
•解题思路和步骤的清晰性、答案的准确性和合理性、符号的正确使用、书写和排版的规范性都将对最终评分产生重要影响。
•学生在备考中应注重解题思路和步骤的训练,同时注意答案的准确性和合理性,符号的正确使用以及书写和排版的规范性。
这样才能在中考数学24题中获得较高的评分。
