cpk过程能力验证报告
CPK过程能力分析

CPK过程能力分析CPK(Process Capability Analysis)是一种统计工具,用于衡量一个过程的稳定性和能力,可帮助确定过程是否能够满足客户的需求。
CPK 过程能力分析将过程能力与设定的规范上下限进行比较,以评估过程的能力。
1.概念:-过程能力指数:CPK指数是衡量过程稳定性和能力的指标。
它是基于数据集的标准差和规范上下限之间的距离,用来表示过程的可控性和一致性。
CPK指数越大,说明过程能力越高。
-规格上下限:规格上下限是根据产品或服务的需求,确定的允许变动范围。
过程能力应当能够保持在规格上下限之内,以满足客户的要求。
2.计算方法:-过程能力指数CPK的计算需要使用数据集的平均值、标准差和规范上下限。
通常使用正态分布的近似方法计算CPK。
- CPK计算公式:CPK = min[(USL-μ)/(3σ),(μ-LSL)/(3σ)],其中USL表示规格上限,LSL表示规格下限,μ表示平均值,σ表示标准差。
3.CPK分析的应用:-制程改善:通过CPK分析,可以确定过程的稳定性和能力,并识别可能导致不良品的特殊原因。
通过改善这些原因,可以提高过程的能力和效率。
-过程控制:CPK过程能力分析可以帮助制定过程控制界限,确保过程稳定,符合规格要求。
通过及时监控过程变异性,并采取控制措施,可以提高过程品质。
-供应商评估:CPK过程能力分析可用于对供应商的能力进行评估。
通过比较供应商的CPK值,可以确定哪些供应商能够满足规格要求,并为采购决策提供依据。
4.CPK分析的局限性:-基于数据的稳定性:CPK分析需要基于大量的数据,来评估过程的稳定性和能力。
如果数据量不足或者不具有代表性,可能会导致CPK值的偏差。
-规格上下限的确定:规格上下限的确定需要考虑产品或服务的需求以及客户的期望。
如果规格上下限不准确或过于宽松,可能会导致对过程能力的误判。
综上所述,CPK过程能力分析是一种重要的统计工具,可以帮助组织评估和改进其过程的稳定性和能力。
过程能力分析CPK

过程能力分析CPKCPK(Capability Process Analysis)是一种用于衡量过程能力的指标。
它通过统计学方法来分析过程的稳定性和一致性,从而判断过程是否能够满足规定的要求。
在制造业中,CPK常用于评估产品的质量控制过程。
本文将介绍CPK的定义、计算方法,并探讨CPK的意义和应用。
首先,CPK是一个统计学指标,用于衡量过程的稳定性和一致性。
它是根据过程数据的均值、标准差和规格限制来计算的。
CPK的计算公式为:CPK = min((USL-μ)/(3σ),(μ-LSL)/(3σ)),其中USL为规格上限,LSL为规格下限,μ为过程的均值,σ为过程的标准差。
CPK的取值范围为[-1,1],其值越大表示过程能力越强,越接近于1表示过程能够满足规格要求的能力越高。
CPK的意义在于评估过程的质量控制能力。
一个具有良好过程能力的过程,可以稳定地产生符合规格要求的产品,减少次品品率和客户投诉的发生。
通过对过程能力的分析,企业可以及时发现并改进存在的问题,提高产品质量,降低生产成本。
此外,CPK还可以作为供应链管理中的一个指标,帮助企业评估供应商的能力和可靠性。
CPK的应用主要体现在以下几个方面。
首先,它可以用于制定质量控制标准。
通过分析过程能力,确定产品的规格上下限,有利于制定质量控制计划和控制界限,提高质量管理的科学性和有效性。
其次,CPK可用于评估和监控过程的改进效果。
对于已经进行过改进的过程,可以通过计算CPK的变化来衡量改进的效果,并及时进行调整和优化。
此外,CPK还可以用于制定持续改进的目标和策略,帮助企业实现品质管理的可持续发展。
在实际应用中,CPK的计算需要大量的数据支撑。
必须收集足够的过程数据,包括过程的样本数据和规格限制,才能准确计算CPK值。
此外,CPK的计算还要求过程数据服从正态分布。
如果过程数据不符合正态分布,可能会导致CPK值的计算误差。
因此,在使用CPK进行过程分析时,需要确保数据收集准确可靠,并对数据是否符合正态分布进行检验。
单边规格cpk报告模板

单边规格cpk报告模板1. 背景在制造业中,对产品的质量控制是非常重要的。
而其中一个常用的指标就是cpk值。
cpk值是一种统计学指标,用于衡量一个过程是否稳定,也就是指标是否符合一定的规格。
单边规格是指定了最小值或最大值的规格,而不是双边规格,在这种情况下,产生了单边规格cpk值的需要。
2. 报告模板2.1 概要•报告的目的•产品的基本信息•统计设备的参数2.2 测量结果•数据分析•偏离度分析•cpk的计算和分析2.3 结论•结果分析•后续计划•管理建议3. 概要3.1 报告的目的说明为什么要进行这项报告,可能是为了满足客户的需求,或是为了确保产品的质量符合规格。
3.2 产品的基本信息包括产品的型号、规格和描述等基本信息。
3.3 统计设备的参数包括统计设备的品牌、型号、精度、标准等信息。
4. 测量结果4.1 数据分析列出收集的数据并对其进行分析,可以采用直方图、散点图等方式展示数据。
4.2 偏离度分析通过计算偏离度,来判断测量数据是否符合要求。
可以计算出平均值、标准差等等。
4.3 cpk的计算和分析通过计算cpk值,来评估制程的稳定性和能力,以便确定产品质量是否达到要求。
5. 结论5.1 结果分析基于测量结果和cpk值,对产品的质量和生产过程进行综合评估,并提出首要的调整建议。
5.2 后续计划制定一些措施,对生产过程进行改进,以提高产品的质量水平。
5.3 管理建议提出一些相关的管理建议,以确保生产过程的质量和稳定性。
6. 结尾总结报告,感谢参与本次测试的所有人员。
如果有需要,可以对最终版本进行修改和修改,以便更好地满足需求。
CPK分析报告 案例

2.01
1.60
2.01
1.59
1.99
1.59
2.00
1.61
1.99
1.58
2.01
1.58
2.02
1.59
2.00
1.60
2.01
1.60
2.01
1.62
2.00
1.59
2.01
1.58
2.00
1.57
1.99
1.59
2.01
1.60
2.02
1.59
1.99
1.58
2.02
1.63
2.01
1.60
16.82
0.30
16.87
0.25
16.82
0.25
16.79
0.35
16.81
0.25
16.80
0.30
16.85
0.30
16.81
0.35
16.80
0.25
16.82
0.25
16.88
0.35
16.78
0.25
16.83
0.30
0.03
0.04
16.80
0.25
0.150.25Biblioteka 16.950.50
16.65
0.00
0.20
0.20
1.85
2.08
1.48
1.66
B
B
A
A
B
B
OK, 可再加 強
OK, 可再加強
> Group #REF! #REF! #REF!
0
0
> Group #REF! #REF! #REF! #REF!
制程能力参数CPK报告(CPK计算公式)
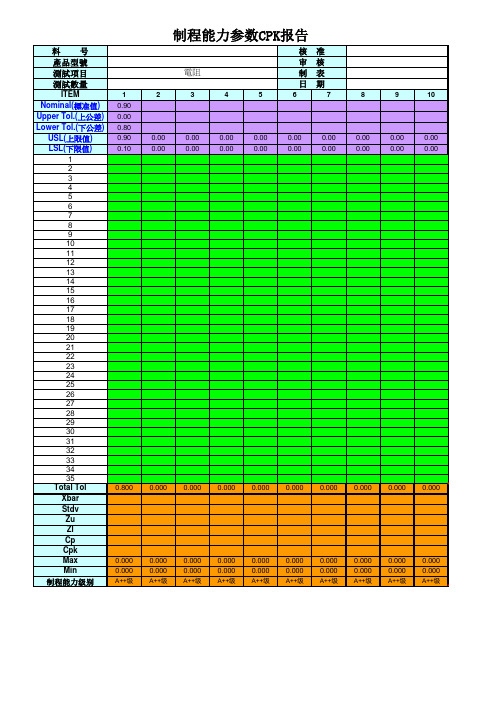
说明:
A++级 Cpk≥2.0 特优可考虑成本的降低
A+ 级 2.0 > Cpk ≥ 1.67 优应当保持之
A 级 1.67 > Cpk ≥ 1.33 良能力良好,状态稳定,但应尽力提升为A+级
B 级 1.33 > Cpk ≥ 1.0 一般状态一般,制程因素稍有变异即有产生不良的危险,应利用各种资源及方法将其提升为 A 级
C 级 1.0 > Cpk ≥ 0.67 差制程不良较多,必须提升其能力
D 级 0.67 > Cpk 不可接受其能力太差,应考虑重新整改设计制程。
Total Tol=USL-LSL(规格公差T=规格上限-规格下限)
Xbar=所测数据平均值
Stdev=估算样本的标准偏差。
标准偏差反映相对于平均值 (Xbar) 的离散程度。
Zu=(Usl-Xbar)/(3*Stdev)
Zi=(Xbar-Lsl)/(3*Stdev)
Cp=((Usl-Lsl)/(6*Stdev))
Cpk=min(Zu,Zi),取Zu,Zi的较小值。
CPK统计分析范文

CPK统计分析范文CPK是指过程能力指数(Process Capability Index),它反映了过程的稳定性和可控性。
计算CPK需要知道过程的规格范围和实际数据,通过分析数据的分布情况,确定过程在规格范围内的能力。
CPK分析通过计算过程的上限规格指数(Upper Specification Index,USL),下限规格指数(Lower Specification Index,LSL),过程均值(Process Mean,μ)和过程标准差(Process Standard Deviation,σ),来评估过程的能力。
CPK的计算公式为:CPK = min((USL-μ)/(3σ), (μ-LSL)/(3σ))CPK值是以1为中心点的一个指标,当CPK=1时,说明过程范围与规格范围基本一致;当CPK>1时,说明过程范围比规格范围更加宽松;当CPK<1时,说明过程范围比规格范围更加严格。
CPK分析通常分为两个步骤:数据收集和数据分析。
在数据收集阶段,需要收集关于过程的实际数据,并记录下来。
这些数据可以是过程中的样本数据或者连续数据。
在数据分析阶段,需要使用统计工具来分析数据的分布情况。
常用的统计工具包括直方图、正态概率图和盒须图等。
直方图可以帮助我们了解数据的分布情况,显示数据的频率分布。
通过直方图可以判断数据是否符合正态分布。
正态概率图则可以用来判断数据是否符合正态分布。
正态概率图展示了数据的累积分布情况,如果数据点大致沿着一条直线分布,那么可以认为数据符合正态分布。
盒须图可以展示数据的五个关键统计量:最小值、第一四分位数、中位数、第三四分位数和最大值。
通过盒须图可以判断数据的分布情况和离群值的存在情况。
除了这些统计工具之外,还可以计算数据的均值、标准差和过程能力指数等。
均值反映了数据的中心趋势,标准差反映了数据的分布范围。
CPK分析的结果可以帮助我们评估产品质量的合格程度,优化生产过程,并进行过程改进。
过程能力研究表(CPK)
ABC有限公司
部门
过程能力研究
(CPK分析报告)
工序
计算控制限日期
工程规范
最小值
~
最大值
机器编号
日期
特性
样本容量/频率
零件名称/编号
时间
8:00
10:00
12:00
14:00
16:00
8:00
10:00 12:00 14:00 16:00
8:00
10:00
12:00
14:00
16:00
8:00
10:00 12:00 14:00
4、 纠正计算或描点错误,采取正确的取样方法。
* 样本容量小于7时,没有极差的下控制线。
UCL
#DIV/0! #DIV/0! #DIV/0!
X
#DIV/0! #DIV/0! #DIV/0!
LCL
#DIV/0! #DIV/0! #DIV/0!
UCL
0
0
0
R
0.000
0.000
0.000
LCL
0
0
0
研究评定: 由以上计算结果可知CPK=
0.000
D4 3.27 2.57 2.28
0.000
0.000
0.000 0.000 0.000
对特殊原因采取的措施的说明:
* 任何超出控制限的点,证明在那点不稳定。
* 连续7点全在中心线之上或之下。
* 连续7点上升或下降。
* 任何其它明显非随机的图形。
0.000
0.000
0.000
UCLX=X+A2R= #DIV/0! USL= 最大值
#DIV/0! #DIV/0! #DIV/0!
CPK过程能力分析
50
60
70
80
%>US L E xp Obs
%<LS L E xp Obs
0 .0 0 0 .0 0 0 .0 0 0 .0 0
17
由 Cpk 的表达公式可以看出: 当均值与规范中心线重合M=μ,N=0时,Cp=Cpk; 当存在偏移N≠0时,Cp>Cpk
因此: 当Cp和Cpk都较小,且差别不大时,说明过程的主要问题是σ太大,改进过程应主要着眼于 降低过程波动; 当Cp较大,Cpk较小,且差别大时,说明过程的主要问题是偏移N太大,改进过程应主要着眼 于移动μ值; 当Cp本不够好,Cpk更小,,说明过程的σ和μ,改进过程应主要着眼于移动μ值和降低过程波 动;
which defects occur. ß LSL - Lower Specification Limit. The numerical value, below
which defects occur.
6
Terminology(3)
ß Common Cause - A natural type of
因此可得以下结论:当过程输出均值与规范中心线M,M=(USL+LSL)/2,重合时,Cp值越大 过程能力越好.
10
过程能力指数 Cp 值的评价参考(过程输出均值与规范中心线M重合)
Cp值的范围 级别 预计报废率
过程能力的评价参考
Cp>1.67
1 <0.6PPM
过程能力过高(视具体情况决定修正)
1.67>Cp>1.33 2 0.6PPM-60PPM 过程能力充分,技术管理能力很好,应当维持
过程固有波动,是仅由普通因素影响而产生的过程波动。
这部分波动可以通过控制图的R-bar/d2
cpk分析报告模板
cpk分析报告模板
1、CPK定义:制程能力指数,用一个数值来表达制程的水准。
其中Ca值代表制程的准确度,Cp值代表制程的精密度。
2、CPK取样方法与规定
(1)、T0阶段执行:Cpk尺寸在模具与注塑成型稳定后,成型机台连续稳定运行30分钟后才能取样。
(2)、研发试产阶段:Mini_Cpk与正式Cpk两类
Mini_Cpk取样规则:成型机台连续稳定运行30分钟后,开始取样,对于成型周期小于等于30S的,每间隔15分钟取样一次,每次每穴5PCS,样本数量:40PCS/穴,取样时间2小时,连续生产时间要大于2.5小时。
对于成型周期大于30S,每隔30模,取样一次,每次每穴5PCS,样本数量40PCS/穴。
通过条件为Cpk≥1.33,Ca≤50%,Cp≥1.0.
正式Cpk取样规则:成型机台连续稳定运行30分钟后,开始取样,对于成型周期小于等于30S的,每间隔30分钟取样一次,每次每穴2PCS,样本数量:40PCS/穴,取样时间10小时,连续生产时间要大于10.5小时。
对于成型周期大于30S,每隔60模,取样一次,每次每穴2PCS,样本数量40PCS/穴。
通过条件为Cpk≥1.33,Ca≤50%,Cp≥1.0.
Cpk样品须按照取样先后顺序进行标记,以便于尺寸测量是可以一一对应,测量后需要保留Cpk样品,便于复测与再次确认。
CPK分析报告(测试)
22
3.77 4.30 4.11 4.08 4.12 20.38 4.08 4.06 4.28 3.84 0.53 0.31 0.70 0.00
23
3.95 4.15 4.02 4.00 4.03 20.15 4.03 4.06 4.28 3.84 0.20 0.31 0.70 0.00
24
3.75 4.15 4.10 4.09 4.10 20.19 4.04 4.06 4.28 3.84 0.40 0.31 0.70 0.00
1.39
RANGES(R CHART )
样本序列 1
2
检1
查2
记
3 4
录5
4.10
3.98
4.05
3.95
4.11
4.13
4.09
4.07
4.10
4.11
TOTAL
20.45 20.24
AVERAGE(X) 4.09
4.05
CLX UCLX LCLX
4.06
4.06
4.28
4.28
3.84
3.84
MAX-MIN(R) 0.06
0.70
0.70
0.70
0.70
0.00
0.00
0.00
0.00
0.00
0.00
0.00
0.00
0.00
0.00
0.00
0.00
0.00
0.00
该过程目前能被接受,批准后即可开始生产,并按照控制计划进行。
肖林20160108
批准/ 日期:
黄静鹏20160108
21
3.78 4.01 4.23 3.88 3.98 19.88 3.98 4.06 4.28 3.84 0.45 0.31 0.70 0.00
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
过程能力验证报告
50'01 PSW'!A6'01 PSW'!A14'01 PSW'!D10'01 PSW'!A8
日期
加工场所工厂上海立杰汽车附件有限公司部门质量保证部过程信息描述性统计数值
零件号零件描述数据点的重要趋势X 图R 图样本个数100
图号工程变更链长度33下规范限 (LSL)226.900
设备设备号 链数42公称尺寸0.000
描述单位链长度56上规范限 (USL)227.100
工程规范227正偏差0.10负偏差0.10链数11总和22,701.440
下规范限226.90公称尺寸上规范限227.10超出控制限00平均值 (X)227.014
最大值227.080
最小值226.950
小于下规范限的样本数0
大于下规范限的样本数0
平均极差 (R)0.066
常数D2 (n=5)2.326
上单边容差能力指数(CPU)1.006
下单边容差能力指数 (CPL)1.344
能力指数 (Cp)1.175
过程能力(Cpk)1.01
能力比值 (CR)4.605
均方差 (n-1)0.030
均方差 (n)0.030
方差 (n-1)0.001
方差 (n)0.001
性能指数 (PP)1.121
性能比值 (PR)0.892
性能指数 (Ppk)
0.96
n1234567891011121314151617181920
1
226.99227.02227.06227.03226.98226.98226.98227.03227.06227.02226.98227.03227.06227.04226.98226.98227.02227.05227.06227.01
2
226.98227.02227.02227.02227.03226.98226.99227.02227.03227.01227.02227.08226.97226.96226.98226.98226.96227.02227.06227.01
3
227.02227.02227.01227.03226.98226.98227.02227.03227.01227.02227.01227.06227.05227.06227.02226.98226.98226.98226.97227.03
4
227.02227.06227.02226.98226.98227.01227.03227.03227.01227.05226.98227.02227.01227.02227.05227.06227.01227.05227.02227.06
5
227.06227.01227.03227.01227.01226.98227.01227.06227.02226.98226.96226.98227.02226.98227.01226.95227.01227.05227.02227.06
平均值227.014227.026227.028227.014226.996226.986227.006227.034227.026227.016226.990227.034227.022227.012227.008226.990226.996227.030227.026227.034
极差0.0800.0500.0500.0500.0500.0300.0500.0400.0500.0700.0600.1000.0900.1000.0700.1100.0600.0700.0900.050
NOTES8 consecutive data points above average X
8 consecutive data points below average X
上升
下降
尺寸
零件
2
2
7
.
0
5
2
2
.
0
0
0
3.0004.0005.0006.0007.0008.0009
.
0
0
0
10.00011.00012.00013.00014.00015.00016.00017.00018.00019.0002
0
.
0
0
0
2
2
7
.
0
1
4
2.0003.0004.0005.0006.0007.0008.0009.00010.00011.00012.00013.00014.00015.00016.00017.00018.00019.00020.000
2
2
6
.
9
7
6
2.0003.0004.0005.0006.0007.0008.0009
.
0
0
0
10.00011.00012.00013.00014.00015.00016.00017.00018.00019.0002
0
.
0
0
0
226.920
226.940
226.960
226.980
227.000
227.020
227.040
227.060
1234567891011121314151617181920
平
均
值
子组数
平均值(X图)
UCLxAveXLCLxData Values
0
.
1
4
0
2.0003.0004.0005.0006.0007.0008.0009.00010.00011.00012.00013.00014.00015.00016.00017.00018.00019.00020.000
0
.
0
6
6
234567891011121314151617181920
0.000
0.020
0.040
0.060
0.080
0.100
0.120
0.140
0.160
1234567891011121314151617181920
极
差
子组数
极差(R 图)
UCLrAveRLCLrData Values
042421633119010
0
5
10
15
20
25
30
35
频
数
直方图
矩形分布形状
双边容差下单边容差(MIN)上单边容差 (MAX)
