100所名校师范卷
全国100所名校最新高考模拟示范卷文科综合卷(一)(扫描版)
全国 100 所名校最新高考模拟示范卷文科综合卷(一)(扫描版)
全国 100 所名校最新高考模拟示范卷文科综合卷(一)(扫描版)
全国 100 所名校最新高考模拟示范卷文科综合卷(一)(扫描版)
全国 100 所名校最新高考模拟示范卷文科综合卷(一)(扫描版)
全国 100 所名校最新高考模拟示范卷文科综合卷(一)(扫描版)
全国 100 所名校最新高考模拟示范卷文科综合卷(一)(扫描版)
全国 100 所名校最新高考模拟示范卷文科综合卷(一)(扫描版)
全国 100 所名校最新高考模拟示范卷文科综合卷(一)(扫描版)
全国 100 所名校最新高考模拟示范卷文科综合卷(一)(扫描版)
全国 100 所名校最新高考模拟示范卷文科综合卷(一)(扫描版)
全国 100 所名校最新高考模拟示范卷文科综合卷(一)(扫描版)
全国 100 所名校最新高考模拟示范卷文科综合卷(一)(扫描版)
全国 100 所名校最新高考模拟示范卷文科综合卷(一)(扫描版)
全国 100 所名校最新高考模拟示范卷文科综合卷(一)(扫描版)
全国 100 所名校最新高考模拟示范卷文科综合卷(一)(扫描版)
全国 100 所名校最新高考模拟示范卷文科综合卷(一)(扫描版)
全版)
全国100所名校高三AB测试示范卷·数学

全国100所名校高三AB 测试示范卷·数学第十八套 数列综合(A 卷)一、选择题:本题共6小题.1.设S n 为等差数列{a n }的前n 项和,S 8=4a 6,a 5=-2,则a 9= A .-6 B .-4 C .-2 D .22.已知数列{a n }是等比数列,数列{b n }是等差数列,若2610a a a =-611π3b =,则21026tan 1b b a +-的值是AB. CD.3.数列{a n }为等比数列的充分不必要条件可以是A .24n n a =(n ∈N *)B .221n n n a a a ++=(n ∈N *)C .a m a n =2m +n (m ,n ∈N *) D .a n a n +3=a n +1a n +2(n ∈N *) 4.数列{a n }的前n 项和212n S n kn =+,且a 2=2,若a m =10k ,则m =A .1B .5C .10D .205.已知函数()f x =,若数列{a n }的各项使得0,f (a 1),f (a 2),…,f (a n ),2n +2成等差数列,则数列{a n }的前n 项和S n = A .3(31)2n - B1)n -C.31)2- D1)-6.(多选题)已知等差数列{a n }的公差为2,a 1=1,数列{b n }满足b 1=10,b n -b n-1=a n (n≥2),则A .b n =n 2+9B .b n =11-n 2C .3n n b a +的最大值为12D .3n n b a +的最小值为136二、填空题:本题共3小题,把答案填在题中的横线上.7.在等差数列{a n }中,a 1=6,S n 为{a n }的前n 项和,当且仅当n =7时,S n 取得最大值,则该等差数列的公差d 的取值范围为________.8.设数列{a n }满足a 1=5,14433n n n a a a +++=+(n ∈N *),则a 4=________,a 2020=________.9.已知定义在R 上的函数f (x )满足1()(2)2f x f x =-,当x ∈[0,2)时,f (x )=23||25,[0,1)41(),[1,2)2x x x x x -⎧-++∈⎪⎪⎨⎪∈⎪⎩,f (x )在[2n-2,2n]上的最大值记为a n (n ∈N *),则数列{a n }的前n 项和S n =________.三、解答题:本题共3小题,解答应写出文字说明、证明过程及演算步骤.10.在①S 11=a 6;②222272105a a a a +=+;③2425a a a =这三个条件中任选一个,补充在下面的问题中,然后解答补充完整的题目.记S n 为公差不为0的等差数列{a n }的前n 项和,已知________. (1)求a 6;(2)若a 2=6,求使得S n >0的n 的取值范围. 11.已知数列{a n }的前n 项和S n =2a n -2. (1)求数列{a n }的通项公式;(2)记11(22)(22)n n n n a b a a ++=--(n ∈N ),数列{b n }的前n 项和为T n ,若T n <a 对任意的n 恒成立,求实数a 的取值范围.12.已知数列{a n },{b n }满足a 1=2,b 1=1,3a n =2a n-1+b n-1+3,3b n =a n-1+2b n-1+3,(n≥2,n ∈N *).(1)证明:{a n -b n }是等比数列,{a n +b n }是等差数列.(2)设数列22n n n c a b =-,T n =c 1+c 2+c 3+…+c n ,求使得1484381n n n T -+=成立的正整数n 的值.【命题视角】本题考查等差数列的基础知识和基本运算,考查考生的运算求解能力.【解题分析】S 8=4(a 1+a 8)=4(a 3+a 6),所以a 3=0,53153a a d -==--,则a 9=a 5+4d =-6. 2.【答案】C【命题视觉】本题考查等差数列的性质及其应用,考查考生的运算求解能力.【解题分析】由题意得,325106a a a a ==-,解得6a =,又611π3b =,所以210626211ππtantan tan()tan 11333b b b a +==-==-- 3.【答案】C【命题视觉】本题考查等比数列的定义,考查考生的逻辑推理与判断能力.【解题分析】若a 1=-2,a 2=4,a 3=8,则满足24n n a =(n ∈N *),但{a n }不是等比数列,故A项错误;若a n =0,则满足221n n n a a a ++=(n ∈N *),但{a n }不是等比数列,故B 项错误;若a n =0,则满足a n a n +3=a n +1a n +2(n ∈N *),但{a n }不是等比数列,故D 项错误;若a m ·a n =2m +n(m ,n ∈N *),则有111222m n m n n m n m n n a a a a a a +++++⋅===⋅,则{a n }是等比数列,故选C 项.4.【答案】B【命题视角】本题考查数列的项与前n 项和的关系,考查学生的计算能力与推理能力. 【解题分析】2211(22)()22a S S k k =-=+-+=,解得12k =,从而有a n =S n -S n-1=n (n≥2),n =1也符合,故而a n =n ,由a m =10k =5,可得m =5. 5.【答案】A【命题视角】本题考查等差数列与等比数列的应用,等比数列求和,考查学生的运算求解能力.【解题分析】设等差数列的公差为d ,则由题意,得2n +2=0+(n +1)d ,解得d =2,于是12a =,24a =,36a =,…,从而13a ==,223a ==,333a ==,…,易知数列{a n }是等比数列,其公比213a q a ==,所以3(13)3(31)132n n n S --==-. 6.【答案】AD【命题视角】本题考查利用累加法求数列的通项公式,与对勾函数的结合求最值,考查学生的运算求解能力和抽象思维能力.【解题分析】等差数列{a n }的公差为2,a 1=1,从而可得a n =2n-1, 1122321112()()()()10n n n n n n n n n b b b b b b b b b b a a a ------=-+-+-++-+=++++23(21)(1)1092n n n +-=-+=+(n≥2),当n =1时,也符合,从而b n =n 2+9, 229(1)2(1)10110[(1)2]32132(1)21n n b n n n n a n n n ++-++===++-+-+++,令t =n +1, 则12y =10(2)t t +-,其中t≥2,且为整数,∵函数y在上递减,在)+∞上递增,函数y 无最大值,∴当t =3时,136y =;当t =4时,94y =,∴min 136y =.7.【答案】6(1,)7--【命题视角】本题考查等差数列的基本量的运算,等差数列性质的应用,考查学生的运算求解能力.【解题分析】当且仅当n =7时,S n 取得最大值,所以78000d a a <⎧⎪>⎨⎪<⎩,即1106070d a d a d <⎧⎪+>⎨⎪+<⎩,解得617d -<<-.8.【答案】-5 -5【命题视角】本题考查周期数列的判断及计算,考查学生的运算求解能力及逻辑思维能力.【解题分析】记b n =a n +3,则由14433n n n a a a +++=+(n ∈N *),得184n n b b +=-,b 1=a 1+3=8,b 2=3,343b =,b 4=-2,b 5=8,b 6=3,743b =,82b =-,知{b n }是以4为周期的周期数列,因此a 4=b 4-3=-5,b 2020=b 4,又b 2020=a 2020+3,从而a 2020=-5. 9.【答案】332n-【命题视角】本题考查数列与函数综合,等比数列的求和,考查学生的抽象思维能力和运算求解能力.【解题分析】当x ∈[0,2)时,23||25,[0,1)4()1(),[1,2)2x x x x f x x -⎧-++∈⎪⎪=⎨⎪∈⎪⎩,可得当0≤x <1时,22513()()422f x x x x =-++=--+,最大值为13()22f =;当1≤x <2时,3||0211()()()122x f x -=≤=,所以当x ∈[0,2)时,f (x )的最大值为32;当2≤x <4时,1()(2)2f x f x =-的最大值为34;当4≤x <6时,1()(2)2f x f x =-的最大值为38,从而数列{a n }是以32为首项,12为公比的等比数列,31(1())32231212n n n S -==--. 10.【命题视角】本题考查等差数列,考查学生的运算求解能力和逻辑思维能力. 【解题分析】(1)若选①,由S 11=a 6,即1111166()11112a a S a a +=⨯==,得a 6=0. 若选②,由222272105a a a a +=+,得222275102a a a a -=-,(a 7-a 5)(a 7+a 5)=(a 10-a 2)(a 10+a 2),2d×2a 6=8d×2a 6,从而可得a 5=0.若选③,2425a a a =,得(a 1+3d )2=(a 1+d )(a 1+4d ),解得a 6=a 1+5d =0.(2)由(1)知a 6=0,设等差数列{a n }的公差为d ,则有11650a d a d +=⎧⎨+=⎩,解得132152d a ⎧=-⎪⎪⎨⎪=⎪⎩,从而1533(1)()9222n a n n =+--=-,若S n >0,则1(1)2n n n S na -=+d >0,即1(1)2n a -+d >0, 又a 6=0,所以a 1+5d =0,115d a =-,11(1)1()025n a a -+->,解得n <11,所以n 的取值范围是{n|1≤n≤10,n ∈N *}. 11.【命题视角】本题考查等比数列和裂项相消法求和,考查学生的运算求解能力和抽象思维能力. 【解题分析】(1)当n =1时,S 1=2a 1-2,得a 1=2;当n≥2时,S n =2a n -2,S n-1=2a n-1-2,两式相减,得a n =2a n -2a n-1,即有a n =2a n-1(n≥2),从而数列{a n }是以2为首项,2为公比的等比数列,得a n =2n .(2)1112121211(22)(22)(22)(22)2222n n n n n n n n n a b a a +++++++===-------,从而123n n T b b b b =++++2334451211111111()()()()2222222222222222n n ++=-+-+-++--------- 21112222n +=-<-,因为T n <a 对任意的n 恒成立,所以a >T n ,又12n T <,从而12a ≥. 12.【命题视角】本题考查等差与等比数列定义的判断,错位相减法求和,考查学生的逻辑推理能力和运算求解能力. 【解题分析】(1)由3a n =2a n-1+b n-1+3,3b n =a n-1+2b n-1+3,两式相减,得3(a n -b n )=a n-1-b n-1,nn 111a b ()3n n a b ---=-(n≥2.n ∈N *),从而{a n -b n }是以a 1-b 1=1为首项,13为公比的等比数列,11()3n n n a b --=.同理,由3a n =2a n-1+b n-1+3,3b n =a n-1+2b n-1+3,两式相加得3(a n +b n )=3(a n-1+b n-1)+6,(a n +b n )=(a n-1+b n-1)+2(n≥2,N ∈N *),从而{a n +b n }是以a 1+b 1=3为首项,2为公差的等差数列,a n +b n =3+(n-1)×2=2n +1.(2)由(1)得2211()()(21)()3n n n n n n n n c a b a b a b n -=-=-+=+,从而22112311113157()(21)()(21)()3333n n n n T c c c c n n --=++++=⨯+⨯+⨯++-++,23111111135()7()(21)()(21)()333333n n n T n n -=⨯+⨯+⨯++-++,所以1212111124312()2()2()(21)()4333333n n n nn T n -+=⨯+⨯+⨯++-+=-, 3663n n n T +=-,又1363648466333381n n n n n n n n T -++=-+=-=,所以113243n=,解得n =5.。
全国100所名校单元测试示范卷(高三):地理人教版(21-24单元) 22

全国100所名校单元测试示范卷·高三·地理卷(二十二)中国地理总论(90分钟100分)第Ⅰ卷(选择题共44分)一、选择题(本大题共22小题,每小题2分,共44分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
)读我国沿北回归线地形剖面图,完成1~2题。
1.图中所示剖面线经过我国的省(区)有A.云、桂、粤、台B.黔、湘、闽、台C.粤、琼、闽、台D.云、桂、琼、台2.图示M地形区A.气候高寒,降水季节变化大B.地形崎岖,喀斯特地貌广布C.河湖众多,地表水十分丰富D.山麓自然带为温带落叶阔叶林带【解析】1.北回归线穿过我国的云、桂、粤、台四省区。
2.M地形区为云贵高原,属亚热带季风气候;由于地形坡度大且多喀斯特地貌,因此地表水不易储存,地表水缺乏。
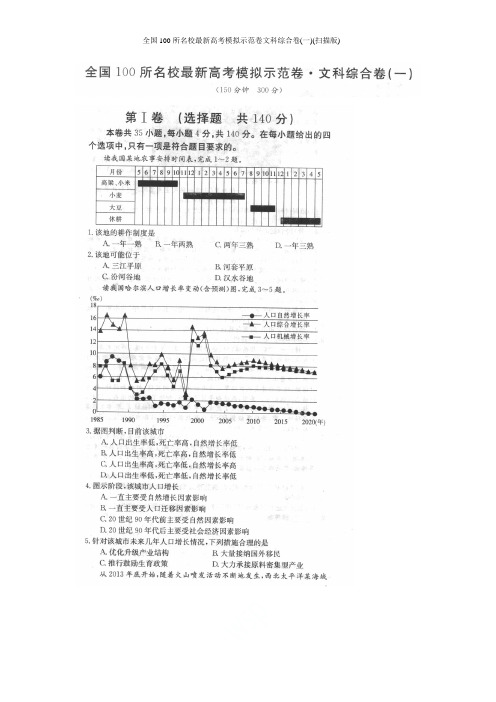
【答案】1.A 2.B未来30年间,我国将先后迎来劳动年龄人口、老龄人口和总人口三大高峰。
我国人口正面临人口素质总体不高、流动人口规模庞大、出生性别比攀升、艾滋病蔓延、贫困人口脱贫五大难题。
读我国人口总量增长图(单位:亿人口)和人口年龄构成表,完成3~5题。
A.人口增长速度不断加快B.人口抚养负担逐渐加重C.少年儿童人口数量逐渐减少D.劳动年龄人口数量不断增加4.下列人口问题与西部大开发关系最密切的是①人口素质总体不高②流动人口规模庞大③出生性别比持续攀升④贫困人口脱贫难度大A.①②B.②③C.③④D.①④5.下列应对我国老龄人口高峰的措施,较合理的是A.实施鼓励人口生育的政策B.将老龄人口向海外迁移C.建立完善的社会保障制度D.吸纳大量的青壮年移民【解析】3.1953年至2010年我国人口增长速度先加快、后减慢;后阶段人口抚养比(总体人口中非劳动年龄人口数与劳动年龄人口数之比)不断下降,抚养负担减轻;少年儿童人口数量先增加、后减少。
4.我国西部地区贫困人口多,人口素质总体偏低。
贫困人口脱贫会消耗大量的人力、物力和资金,给西部大开发带来困难;人口素质偏低可能导致西部大开发人才的短缺。
全国100所名校最新高考模拟示范卷22届新高考语文七

全国100所名校最新高考模拟示范卷22届新高考语文七1、下列词语中,加着重号字的注音正确的一项是()[单选题] *A、虹霓(ní)哂笑(xī)B、抽噎(yē)铿锵(kēng)(正确答案)C、茶峒(dòng)跬步(guǐ)D、残羹冷炙(zì)刮痧(shā)2、下列选项中加着重号字的读音完全相同的一项是()[单选题] *A、翩然偏执扁舟翩跹(正确答案)B、阡陌陷阱纤维纤夫C、缥缈剽窃漂白饿殍D、点缀辍学拾掇赘述3、下列对有关名著的说明,不正确的一项是( ) [单选题] *A.《红楼梦》秦可卿死后,贾珍因尤氏犯了旧疾,不能料理事务,请王熙凤帮助丧事。
王熙凤安排妥当,恩威并施,威重令行,将两府的事情安排得停停当当。
B.《红楼梦》展现了贾府这一富贵之家从繁盛到衰败的过程,描写了以贾宝玉和一群红楼女子为中心的人物的悲剧命运,反映了具有一定觉醒意识的青年男女在封建体制下的历史宿命。
C.《红楼梦》中宝玉挨打后,林黛玉“早听人一句话,也不至今日。
别说老太太,太太心疼,就是我们看着,心里也疼”的一席话,表达了对宝玉的无比爱怜与关心。
(正确答案)D.“玫瑰花又红又香,无人不爱的,只是刺戳手,也是一位神道,可惜不是太太养的,”“老鸹窝里出凤凰”。
这是《红楼梦》中兴儿所言,“玫瑰花”指的是探春。
4、《荷塘月色》的作者是()[单选题] *周作人郭达朱自清(正确答案)鲁迅5、“每当夏月塘荷盛开时,我每天至少有几次徘徊在塘边”中“徘徊”的读音是“pái huái”。
[判断题] *对(正确答案)错6、下列关于《红楼梦》的说法,正确的一项是( ) [单选题] *A.贾府的“四春”分别是:精明的贾元春、孤僻的贾迎春、孤独的贾探春、懦弱的贾惜春,取“原应叹息”之意。
B.《红楼梦》中贾宝玉的通灵宝玉上的字是“不离不弃,仙寿恒昌”。
薛宝钗金锁上錾刻的字是“莫失莫忘,芳龄永继”。
铭文相对应,这就是所谓的“金玉良缘”的依据。
全国100所名校最新高考模拟示范卷

全国100所名校最新高考模拟示范卷•数学卷(九)(120分钟 150分)一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 已知集合}0,2{-=M ,}13,1{+-=a N ,若}2{-=N M ,则实数a 的值为A.1B.31-C.1-或31- D.1-2. 复数i2i 2019-的共轭复数为A.i 5251+B.i 5251-C.i 5251+-D.i 5251-- 3.已知等差数列}{n a 的前n 项和为n S ,若53=a ,147=S ,则数列}{n a 的公差为A.3B.1-C.23- D.3-4.调查某人汽车使用年限x 和该年支出维修与保养费用y (万元),得到如下数据:可得回归方程a x b yˆˆˆ+=中的17.0ˆ=b ,预计使用年限为10年的维修与保养费用为 A.1.71万元 B.1.72万元 C.1.73万元 D.1.74万元5.已知y x ,满足不等式组⎩⎨⎧≥≤-+4062xy y x ,则x y z 2-=的最大值为A 6- B.8- C.2 D.2- 6.执行下边的程序框图,若输出的3=S ,则正整数m 的值为A.3B.4C.5D.87.与右边三视图对应的几何体的最大体积为A.34B.38C.32D.28. 古希腊数学家阿波罗尼奥斯在他的著作《圆锥曲线论》中记载了用平面 切割圆锥得到圆锥曲线的方法.如图,将两个完全相同的圆锥对顶放置 (两圆锥的轴重合),已知两个圆锥的底面半径均为1,母线长均为2, 记过圆锥轴的平面ABCD 为平面α(α与两个圆锥面的交线为AC ,BD ), 用平行于α的平面截圆锥,该平面与两个圆锥侧面的截线即为双曲线E 的 一部分,且双曲线E 的两条渐近线分别平行于AC ,BD ,则双曲线E 的离心率为 A.332 B. 2 C.3 D. 2A.x 2sin 2-B.x 3sin 2C.)62cos(2-xD.)63sin(2π-x10.积为A.34B.33C.32D.311. 正三棱锥111C B A ABC -的所有棱长均为4,E 为棱AB 的中点,过E 作此正三棱柱的外接球的截面,则该截面面积的最小值是A.π2B.π22 C.π4 D.π8。
全国100所名校单元测试示范卷(高三):数学 14数学全国教师5(理)

全国100所名校单元测试示范卷·高三·数学卷(五)第五单元函数的综合应用(120分钟150分)第Ⅰ卷一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.a、b为实数,集合M={,1},N={a,0},f:x→2x表示把集合M中的元素x,映射到集合N 中为2x,则a+b等于A.-2B.0C.2D.±2解析:由于M中元素1能对应a,能对应0,所以=0,a=2,所以b=0,a=2,因此a+b=2.答案:C2.已知函数f(x)=--则f[f(-1)]等于A.B.2 C.1 D.-1解析:f[f(-1)]=f(1)=2.答案:B3.函数y=(a>1)的图象大致形状是解析:当x>0时,y=a x,因为a>1,所以是增函数,排除C、D,当x<0时,y=-a x,是减函数,所以排除A.答案:B4.设函数f(x)为定义在R上的奇函数,当x≥0时,f(x)=2x-2x+m(m为常数),则f(-2)等于A.-B.-1C.1D.3解析:因为函数f(x)为定义在R上的奇函数,所以f(0)=0,即20+m=0,所以m=-1,所以当x≥0时,函数f(x)=2x-2x-1,所以f(-2)=-f(2)=-(4-4-1)=1.答案:C5.记min{a,b}为a,b两个数的较小者,max{a,b}为a,b两个数的较大者,f(x)=-则--·-的值为A.min{a,b}B.max{a,b}C.bD.a--=b.解析:(1)若a>b,则a-b>0,∴f(a-b)=1.∴原式=(2)若a<b,a-b<0,∴f(a-b)=-1.∴原式==a.--·-=min{a,b}.所以答案:A6.已知f(x+199)=4x2+4x+3(x∈R),那么函数f(x)的最小值为A.1B.2C.3D.5解析:求f(x)的解析式运算量较大,但这里我们注意到,y=f(x+199)与y=f(x),其图象仅是左右平移关系,它们取得的最大值和最小值是相同的,由y=4x2+4x+3=4(x+)2+2,所以f(x)的最小值即f(x+199)的最小值是2.答案:B7.函数f(x)是定义域为R的偶函数,又是以2为周期的周期函数.若f(x)在[-1,0]上是减函数,那么f(x)在[2,3]上是A.增函数B.减函数C.先增后减的函数D.先减后增的函数解析:∵f(x)为[-1,0]上的减函数,且f(x)为R上的偶函数,∴f(x)在[0,1]上是增函数,又f(x)是以2为周期的函数,∴f(x)在[2,3]上的单调性与[0,1]上相同,即递增.答案:A8.已知y=f(x)是偶函数,y=g(x)是奇函数,它们的定义域均为[-π,π],且它们在x∈[0,π]上的图象如图所示,则不等式<0的解集为A.(-,)B.(,π)C.(-,)∪(,π)D.(-,0)∪(,π)解析:<0⇒f(x)与g(x)在同一区间内符号相反,由图可知当x∈(0,π)时,两者异号的区间为(,π),又f(x)为偶函数,g(x)为奇函数,∴它们在[-π,0]上的图象大致为如图所示,可知其异号的区间为(-,0),∴<0的解集为(-,0)∪(,π).答案:D9.已知函数f(x)=mx3+nx2的图象在点(-1,2)处的切线恰好与直线3x+y=0平行,若f(x)在区间[t,t+1]上单调递减,则实数t的取值范围是A.[-2,-1]B.(-2,-1)C.(-2,0)D.(-1,1)解析:由题可知---即---得∴f'(x)=3x2+6x,令f'(x)≤0,得-2≤x≤0,∵f(x)在区间[t,t+1]上递减,∴-得-2≤t≤-1.答案:A10.已知函数f(x)满足:①定义域为R;②对任意x∈R,有f(x+2)=2f(x);③当x∈[-1,1]时,f(x)=-|x|+1.则方程f(x)=log4|x|在区间[-4,4]内的解的个数是A.9B.6C.5D.4解析:∵f(x+2)=2f(x),∴f(4)=2f(2)=4f(0)=4,又log44<2,∴当0≤x≤4时,作出草图可知f(x)=log4|x|有3个解,又f(-2)=f(0)==log4|-2|,∴作出草图可知当-4≤x<0时,f(x)=log4|x|有2个解,∴在[-4,4]内解的个数是5个.答案:C11.2011年3月发生在日本的9级大地震虽然过去多年了,但它对日本的核电站的破坏却是持续的,其中有一种放射性元素铯137在其衰变过程中,假设近似满足:其含量M(单位:太贝克)与时间t(单位:年)满足函数关系:M(t)=M0-,其中M0为t=0时铯137的含量.已知t=30时,铯137含量的变化率是-10ln2(太贝克/年),则M(60)等于A.5太贝克B.72ln2太贝克C.150ln2太贝克D.150太贝克解析:因为铯137含量的变化率为M'(t)=-M0-ln2,所以当t=30时,M'(30)=-M0-ln2=-ln2=-10ln2,所以M0=600,可解得M(60)=150.答案:D12.已知函数f(x)=ln x++ax,x∈(0,+∞)(a为实常数).若f(x)在[2,+∞)上是单调函数,则a的取值范围是A.(-∞,-]B.(-∞,-]∪[0,+∞)C.(-∞,0)∪[,+∞]D.(-∞,0)∪(,+∞)-,解析:f'(x)=-+a=当a≥0时,ax2+x-1在[2,+∞)上恒大于零,即f'(x)>0,符合要求.当a<0时,令g(x)=ax2+x-1,g(x)在[2,+∞)上只能恒小于零,解得a≤-,故Δ=1+4a≤0或-∴a的取值范围是(-∞,-]∪[0,+∞).答案:B第Ⅱ卷二、填空题:本大题共4小题,每小题5分,共20分.把答案填在题中的横线上.13.函数f(x)=log0.1|x-1|的定义域是.解析:∵|x-1|>0,∴x∈R且x≠1.答案:{x|x∈R且x≠1}14.已知f(x)是定义在R上的偶函数,f(2)=1且对任意x∈R都有f(x+3)=f(x),则f(2014)=.解析:由f(x+3)=f(x)知,f(x)是以周期为3的周期函数.所以f(2014)=f(671×3+1)=f(1)=f(3-2)=f(-2)=f(2)=1.答案:115.若lg x+lg y=0,则2x·2y的最小值是.解析:lg xy=0,xy=1,x+y≥2=2,2x·2y=2x+y≥22=4.答案:416.抛物线y2=3x与圆x2+y2=4围成的封闭图形的面积是.解析:得或-如图,则抛物线y2=3x与AB围成的图形面积是S=2dx=2×=因为A的坐标是A(1,),所以∠AOx=,劣弧AB与弦AB围成的面积是π·22-×2=π-,所以抛物线与圆围成的封闭图形面积是+π-=π+.答案:π+三、解答题:本大题共6小题,共70分.解答应写出必要的文字说明、证明过程及演算步骤.17.(本小题满分10分)(1)已知f(+1)=x+2,求f(x),f(x+1),f(x2);(2)已知2f(x)+f()=10x,求f(x).解析:(1)设t=+1≥1,则=t-1(t≥1),x=(t-1)2,∴f(t)=(t-1)2+2(t-1)=t2-1(t≥1),∴f(x)=x2-1(x≥1),∴f(x+1)=(x+1)2-1=x2+2x(x≥0),∴f(x2)=x4-1(x≤-1或x≥1).5分(2)由2f(x)+f()=10x,用代换x,则2f()+f(x)=1,两式联立消去f()得f(x)=×10x-×1.10分18.(本小题满分12分)某段高速公路全长240公里,两端收费站已建好,余下工程只需要在该段两端已建好的收费站之间修路面和等距离修建安全出口,经预算,修建一个安全出口的工程费用为400万元,铺设距离为x公里的相邻两安全出口之间道路费用为x2+x万元.设余下工程的总费用为y万元.(1)试将y表示成关于x的函数;(2)需要修建多少个安全出口才能使y最小,其最小值为多少万元?解析:(1)设需要修建k个安全出口,则(k+1)x=240,即k=-1.所以y=400k+(k+1)(x2+x)=400×(-1)+(x2+x)=+240x-160.因为x表示相邻两安全出口之间的距离,则0<x≤240.故y与x的函数关系是y=+240x-160(0<x≤240).6分(2)y=+240x-160≥2-160=9440.当且仅当=240x即x=20时取等号,此时k=-1=-1=11.故需要修建11个安全出口才能使y最小,最小值为9440万元.12分19.(本小题满分12分)设函数y=f(x)的定义域为R,并且满足f(x+y)=f(x)+f(y),f()=1,且当x>0时,f(x)>0.(1)求f(0)的值;(2)判断函数的奇偶性;(3)如果f(x)+f(2+x)<2,求x的取值范围.解析:(1)令x=y=0,则f(0)=f(0)+f(0),∴f(0)=0.3分(2)令y=-x,得f(0)=f(x)+f(-x)=0,∴f(-x)=-f(x),故函数是奇函数.6分(3)任取x1,x2∈R,x1<x2,则x2-x1>0,∴f(x2)-f(x1)=f(x2-x1+x1)-f(x1)=f(x2-x1)+f(x1)-f(x1)=f(x2-x1)>0f(x1)<f(x2).故f(x)是R上的增函数.∵f()=1,∴f()=f(+)=f()+f()=2,∴f(x)+f(2+x)=f[x+(2+x)]=f(2x+2)<f(),又由y=f(x)是定义在R上的增函数,得2x+2<,解之得x<-.故x∈(-∞,-).12分20.(本小题满分12分)函数f(x)的图象是[-2,2]上连续不断的曲线,且满足2014f(-x)=,且在[0,2]上是增函数,若f(log2m)<f[log4(m+2)]成立,求实数m的取值范围.解析:∵2014f(-x)=,即201-=2014-f(x),可得f(-x)=-f(x).又因为函数的定义域[-2,2]关于原点对称,所以函数f(x)为奇函数.由奇函数的性质可知,函数在关于原点对称的两个区间上的单调性是相同的,而已知函数f(x)在[0,2]上是单调递增的,所以函数f(x)在[-2,0]上也是单调递增的.故由f(log2m)<f[log4(m+2)],可得--6分由-2≤log2m≤2,解得≤m≤4.由-2≤log4(m+2)≤2,解得≤m+2≤16,即-≤m≤14.由log2m<log4(m+2),得log4m2<log4(m+2),故有解得0<m<2.综上所述,m的取值范围为[,2).12分21.(本小题满分12分)已知函数f(x)=(a+)ln x+-x(a>1).(1)试讨论f(x)在区间(0,1)上的单调性;(2)当a∈[3,+∞)时,曲线y=f(x)总存在相异两点P(x1,f(x1)),Q(x2,f(x2)),使得曲线y=f(x)在点P、Q处的切线互相平行,求证x1+x2>.解析:(1)由已知x>0,f'(x)=--1=--=---.由f'(x)=0,得x1=,x2=a.因为a>1,所以0<<1,且a>.所以在区间(0,)上,f'(x)<0;在区间(,1)上,f'(x)>0.故f(x)在(0,)上单调递减,在(,1)上单调递增.6分(2)由题意可得,当a∈[3,+∞)时,f'(x1)=f'(x2)(x1,x2>0且x1≠x2).即--1=--1,所以a+=+=,a∈[3,+∞).因为x1,x2>0且x1≠x2,所以x1x2<()2恒成立,所以>,又x1+x2>0,所以a+=>,整理得x1+x2>.令g(a)=,因为a∈[3,+∞),所以g(a)在[3,+∞)上单调递减,所以g(a)=在[3,+∞)上的最大值为g(3)=,所以x1+x2>.12分22.(本小题满分12分)已知函数f(x)=e x-ax(a∈R).(1)求f(x)的极值;(2)若f(x)≥x+b恒成立,求(a+1)b的最大值.解析:(1)f'(x)=e x-a,显然,当a≤0时,f'(x)>0恒成立,所以函数f(x)在R上单调递增,函数f(x)不存在极值.当a>0时,由f'(x)>0,得x>ln a,当x∈(ln a,+∞)时,f'(x)>0,函数f(x)单调递增,当x∈(-∞,ln a)时,f'(x)<0,函数f(x)单调递减,所以x=ln a时,函数f(x)取得极小值,f(ln a)=a-aln a.4分(2)f(x)≥x+b恒成立,即e x-ax≥x+b,得e x-(a+1)x≥b.(i)若a+1<0,对任意实数b,x<0时,因为e x<1,-,所以e x-(a+1)x<1-(a+1)x,令1-(a+1)x<b,得x<因此,a+1<0,f(x)≥x+b不恒成立.(ii)若a+1=0,则(a+1)b=0.(iii)若a+1>0,设g(x)=e x-(a+1)x,则g'(x)=e x-(a+1),当x∈(-∞,ln(a+1))时,g'(x)<0,当x∈(ln(a+1),+∞)时,g'(x)>0,从而g(x)在(-∞,ln(a+1))上单调递减,在(ln(a+1),+∞)上单调递增,故g(x)有最小值,g(ln(a+1))=a+1-(a+1)ln(a+1),所以f(x)≥x+b恒成立等价于b≤a+1-(a+1)ln(a+1),因此(a+1)b≤(a+1)2-(a+1)2ln(a+1),10分设h(a)=(a+1)2-(a+1)2ln(a+1),则h'(a)=(a+1)(1-2ln(a+1)),所以h(a)在(-1,-1)上单调递增,在(-1,+∞)上单调递减,故h(a)在a=-1处取得最大值h(-1)=,从而h(a)≤,即(a+1)b≤,所以(a+1)b的最大值是.12分。
全国100所名校高三单元测试示范卷地理
全国100所名校高三单元测试示范卷地理知识文章标题:深度解读全国100所名校高三单元测试示范卷地理一、引言在教育领域,全国100所名校高三单元测试示范卷地理一直备受关注。
地理作为一门重要的学科,对于学生的综合素质和社会适应能力具有重要作用。
在本文中,我们将就全国100所名校高三单元测试示范卷地理这一主题展开全面的探讨,以帮助读者更深入地了解这一领域。
二、对全国100所名校高三单元测试示范卷地理的深度评估我们需要从全国100所名校高三单元测试示范卷地理的考察范围和内容难度入手,来全面评估这份示范卷的深度和广度。
经过对多份示范卷的分析和比对,我们发现这些示范卷在地理知识的考察上涵盖了人文地理、自然地理、地理实践等多个领域,涉及的知识面广,相关案例和实例也非常丰富。
示范卷中的问题设计采用了多种形式,如选择题、判断题、简答题和论述题,考察了学生的地理基础知识和综合运用能力。
在具体考察内容上,全国100所名校高三单元测试示范卷地理更注重对地理理论和实际问题的结合,需要学生灵活运用所学知识解决实际问题。
而且,示范卷的题目涉及到现实生活中的地理问题,激发了学生对地理知识的兴趣,也培养了学生的地理思维和地理素养。
从示范卷的考察范围和内容难度来看,确实具有一定的深度和广度。
三、对全国100所名校高三单元测试示范卷地理的撰写在文章的撰写过程中,我们需要将重点放在对全国100所名校高三单元测试示范卷地理的解析和总结上。
我们可以对示范卷中的重要知识点和典型题型进行详细的解析,以帮助读者深入理解这些知识点,并掌握解题技巧。
我们还可以结合示范卷中的实际案例,进行案例分析和实例论证,从而帮助读者将地理理论与实际问题相结合,有助于拓展思维。
我们需要对示范卷进行总结和回顾,归纳出地理学习的要点和重点,帮助读者全面、深刻而灵活地掌握地理知识。
四、个人观点和理解对于全国100所名校高三单元测试示范卷地理,我个人认为这对学生的地理学习和发展起到了积极的作用。
全国100所名校高三AB测试示范卷.语文周测(10)
全国100所名校高三AB测试示范卷.语文周测(十)1.[答案]C[命题视角]本题考查考生文言文断句的能力。
[解题分析]原文标点:安世日:”圣朝不贵金玉,所以同于瓦砾:又皇上德通冲明,山不爱宝故无用无金无山无玉。
”费初将大市,得安世言,惭而罢。
2. [答案]A[命题视角]本题考查考生识记理解文化常识的能力,[解题分析]博土不能称从事。
从事不是学官.而是中央或地方长官自己任用的僚属,又称从事员。
3.[答案]C[命题视角]本题考查考生概括文意的能力。
[解题分析]后来他又上疏提出均田制"与文意不符,根据文意,均田制并不是李安世提出的4. [答案](1)李安世容貌俊美,举止优雅,刘绩等人相互交谈说:“如果没有他,国家还能成为国家吗?”(2)前任刺史亲自前往讨伐他们,被李波打得大败,于是李波族人家成为藏匿逃亡者的地方,李波宗族成了公家私室的祸患。
[命题视角]本题考查考生理解和翻译文言句子的能力。
[解题分析]第(1)题注意落实得分点:”善”“君子”国”。
第(2)题注意落实得分点:“-.-.”迪逃”“薮”。
[归因导学]错点错因1.错误理解"善”的含义不能结合语境选择同语的义项2.错误理解“国”的含义未发现“国"在句中是名河活用为动词3.未翻译出“大为波败”的特殊甸式未注意“大为波败”是个被动句4.将“遂为通逃之数”翻译成被动句不能准确把握句子的大意对应学法:1.结合上下文,把握句子大意+2.结合语境理解关键实词的含义:3.注意实词的词类活用现象:4.注意特殊句式的翻译参考译文:李安世,年幼时就聪明有悟性。
兴安二年,文成帝接见侍郎、博士的儿子,选取其中水出的,打算极为由书学生。
李安世当年十一岁,皇帝见他还小,召来询问他。
李安世陈说父亲、祖父时,很有条理,当即把他招为学生。
皇帝每次到国学,他总是单独被召去询问,天安初年,任中数,因为恭谨慎重,皇帝亲近宠爱他。
屡经升迁为主客令。
南齐使者刘增来朝贡,李安世奉诏今慰劳他。
全国100所名校最新高考模拟示范卷(一)(江西)[1]
全国100所名校最新高考模拟示范卷卷(一)数学(理科,江西专用)江西金太阳教育研究所数学研究室编一.选择题(本大题12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项符合要求)1.数列{}na是首项为2,公差为3的等差数列,数列{}nb是首项为2-,公差为4的等差数列.若n na b=,则n的值为( ).A.4B.5C.6D.72.函数221212cos()sin()1y x xππ=-++-的最小正周期为( ).A.4πB.2πC.πD.2π3.已知(10)xf x=,则(5)f=( ).A.510 B.105 C.lg5 D.5log104.两个集合A与B之差记为“/A B”,定义为/{|,}A B x x A x B=∈∉.如果集合2{|log1,}A x x x R=<∈,集合{||2|1,}B x x x R=-<∈,那么/A B=( ).A.{|1}x x≤ B.{|3}x x≥ C.{|12}x x≤≤ D.{|01}x x<≤5.设,a b R∈,132biia i-+-+=,则limn nn nna ba b→∞-+等于( ).A.1B.1- C. 1-或1 D.不存在6.已知球面上的四点P、A、B、C,PA、PB、P C的长分别为3、4、5,且这三条线段两两垂直,则这个球面的表面积为( ).A. B. C.50π D.200π7.正方体1111ABCD A B C D-中,若E为棱AB的中点,则直线1C E与平面11ACC A所成角的正切值为( ).A.6B.4C.17D.8.已知椭圆22281(0x ymm+=<<的两焦点分别为1F、2F,点P满足12||||PF PF+=,则m=( ).A.21 D.29.直线0Ax By C++=与圆224x y+=交于M、N两点,若满足222C A B=+,则OM ON⋅(O为坐标原点)等于( ).A.2- B.1- C.0 D.110.已知方程2(1)10x a x a b+++++=的两根为12,x x,且1201x x<<<,则ba的取值范围是( ).A.12(1,]-- B.12(1,)-- C.12(2,]-- D.12(2,)--11.五个人站在图中A、B、C、D、E五个位置上互相传球,规定每次只能传给相邻的人,如B不能直接传给D等.若开始时球在A手中,则经过四次传球后,球又回到A手中的传法种数是( ).A.16B.32C.64D.12812.设()f n为整数n(十进制)的各位数上的数字的平方之和,比如222(123)123=++f,记1()()=f n f n,1()[()](1,2,3,)+==k kf n f f n k,则2007(2006)f等于( ).A.20B.42C.37D.45第(Ⅱ)卷 (非选择题共90分)二.填空题(本大题4个小题,每小题4分,共16分,把答案填在题中横线上)13.已知(2,1)a=-,(1,2)b=,且||a tb+=则实数t=__________.14.已知232012(1)(1)(1)(1)++++++++=+n nnx x x x a a x a x a x,且01126+++=na a a,那么二项式1n的展开式中常数项为__________.15.过双曲线M:2221(0)ybx b-=>的左顶点A作斜率为1的直线l,若l与双曲线M的两条渐近线分别交于点B、C,且||||AB BC=,则双曲线M的离心率__________.16.在000,001,,999这1000个连号中抽奖,若抽出的号码中,出现仅出现两个偶数数字则中奖,那么抽取一个号码能中奖的概率是________.三.解答题(本大题6个小题,共74分,解答题应写出文字说明、证明过程或演算步骤)17.(本小题满分12分)在ABC∆中,角A、B、C的对边分别为a、b、c,已知513sin B=,且a、b、c成等比数列.(Ⅰ)求cot cotA C+的值;(Ⅱ)若12AB BC⋅=-,求a c+的值.18.(本小题满分12分)四个纪念币A、B、C、D,投掷时正面向上的概率如下表所示(01)<<a.纪念币A B C D概率1212a a这四个纪念币同时投掷一次,设ξ表示出现正面向上的个数.(Ⅰ)求ξ的分布列及数学期望;(Ⅱ)在概率()(0,1,2,3,4)ξ==P i i中,若(2)ξ=P的值最大,求a的取值范围;AB C19.(本小题满分12分)如图,在斜三棱柱111ABC A B C -中,侧面11AA B B ⊥底面A B C ,侧棱1AA 与底面A B C 成60︒的角,12AA =.底面A B C 是边长为2的正三角形, 其重心为G 点.E 是线段1BC 上的一点,且113BE BC =. (Ⅰ)求证://G E 侧面11AA B B ;(Ⅱ)求平面1B GE 与底面A B C 所成的锐二面角的大小.20.(本小题满分12分)设33()=xf x ,2323()()=-∈g x t x t t R .(Ⅰ)当8=t 时,求函数()()=-y f x g x 的单调区间; (Ⅱ)求证:当0>x 时,()()≥f x g x 对任意正实数t 成立.21.(本小题满分12分)已知为正实数,数列{}n a 由11=a ,11(1,2,3,)++== nn c a a n 确定.(Ⅰ)对于一切的*∈n N ,证明:111+≤≤n c a ;(Ⅱ)若a 是满足1+=c aa 的正实数,且12||||||=-+-++- n n S a a a a a a ,证明:1<n S .22.(本小题满分14分)已知常数列0>a ,点(,0)-A a 是直角∆ABC 的直角顶点,顶点B 在定直线l :2=a x 上移动,斜边B C 所在直线恒过定点(,0)D a .(Ⅰ)求顶点C 的轨迹T 的方程;(Ⅱ)设P 是轨迹T 上的任一点,l 是过点P 法线(即与过P 点的切线垂直的直线),且(2,0)-M a ,(2,0)N a ,证明:直线M P 、N P 与直线l 的夹角相等.A1ACBEG 1B1C全国100所名校最新高考模拟示范卷卷(一)数学(理科,江西专用) 参考答案江西金太阳教育研究所数学研究室 编一.选择题(本大题12个小题,每小题5分,共60分.) 题号 1 2 3 4 5 6 7 8 9 10 11 12 答案 B C C D B C C D A D B B二.填空题(本大题4个小题,每小题4分,共16分,) 13.0 14. 540-15.16.27200.三.解答题(本大题6个小题,共74分,解答题应写出文字说明、证明过程或演算步骤) 17.(本小题满分12分)在ABC ∆中,角A 、B 、C 的对边分别为a 、b 、c ,已知513sin B =,且a 、b 、c 成等比数列.(Ⅰ)求cot cot A C +的值; (Ⅱ)若12AB BC ⋅=-,求a c +的值. 解:(Ⅰ)依题意,2b ac =,由正弦定理及513sin B =,得225169sin sin sin A C B ==.cos cos sin()sin 516913sin sin sin sin sin sin 13255cot cot A C A C BACA CA CA C ++=+===⨯=.(Ⅱ)由12AB BC ⋅=- ,得cos()12ac B π-=-,即cos 12ac B =.由513sin B =,得1213cos B =±(舍负)∴213b ac ==,由余弦定理,得2121313()22a c ac ac =+--⨯,∴2()63a c +=,故a c += 18.(本小题满分12分)四个纪念币A 、B 、C 、D ,投掷时正面向上的概率如下表所示(01)<<a .纪念币 A B C D概率1212a a这四个纪念币同时投掷一次,设ξ表示出现正面向上的个数.(Ⅰ)求ξ的分布列及数学期望;(Ⅱ)在概率()(0,1,2,3,4)ξ==P i i 中,若(2)ξ=P 的值最大,求a 的取值范围;解:(Ⅰ)()P ξ是ξ个正面向上,4ξ-个背面向上的概率.其中ξ的可能取值为0,1,2,3,4. ∴02022221124(0)(1)(1)(1)P C C a a ξ==--=-,10201222211112222(1)(1)(1)(1)(1)(1)P C C a C C a a a ξ==⋅--+--=-,220211022222222221111122224(2)()(1)(1)(1)(1)(122)P C C a C C a a C C a a a ξ==⋅-+⋅--+-=+-,22112222221112222(3)()(1)(1)a P C C a a C C a ξ==-+⋅-=,22222221124(4)()P C C a a ξ===.∴ξ的分布列为ξ1 2 34P214(1)a -12(1)a -214(122)a a +-2a214aξ的数学期望为2221111424240(1)1(1)2(122)3421a E a a a a a a ξ=⨯-+⨯-+⨯+-+⨯+⨯=+.(Ⅱ)∵01a <<,∴(0)(1)P P ξξ=<=,(4)(3)P P ξξ=<=.则14(2)(1)(12P P a ξξ=-==+221242)(241)0a a a a --=--+≥,2211424(2)(3)(122)(21)0a P P a a a ξξ=-==+--=--≥,由222410210a a a ⎧-+≤⎪⎨-≤⎪⎩,得222a -≤≤,即a的取值范围是222[-.19.(本小题满分12分)如图,在斜三棱柱111ABC A B C -中,侧面11AA B B ⊥底面A B C ,侧棱1AA 与底面 A B C 成60︒的角,12AA =.底面A B C 是边长为2的正三角形, 其重心为G 点.E 是线段1BC 上的一点,且113BE BC =.(Ⅰ)求证://G E 侧面11AA B B ;(Ⅱ)求平面1B GE 与底面A B C 所成的锐二面角的大小. 解:(Ⅰ)延长1B E 交B C 于点F ,则111122BF B C BC ==,即F 为B C 的中点.∵G 为ABC ∆的重心,∴A 、G 、F 三点共线,且113FG FE FAFB ==,∴1//GE AB ,故//G E 侧面11AA B B .(Ⅱ)作1B H AB ⊥于H ,∴1B H ⊥面A B C .∵侧棱1AA 与底面A B C 成60︒的角,12AA =. ∴160B BH ∠=︒,1BH =,1B H =.作HT AF ⊥于T ,连1B T ,则1B T AF ⊥,∴1B TH ∠为所求二面角的平面角.又3AH AB BH =+=,30H AT ∠=︒,∴32sin 30H T AH =︒=,在1Rt B HT ∆中,113tan B H H TB T H ∠==,故所求锐二面角的大小为3arctan.20.(本小题满分12分)设33()=xf x ,2323()()=-∈g x t x t t R .(Ⅰ)当8=t 时,求函数()()=-y f x g x 的单调区间; (Ⅱ)求证:当0>x 时,()()≥f x g x 对任意正实数t 成立. (Ⅰ)解:当8=t 时,316334xy x =-+,由240y x '=-=,得2x =±.∵当(,2)(2,)x ∈-∞-+∞ 时,0y '>;当(2,2)x ∈-时,0y '<,∴y 的单调增区间是(,2)-∞-,(2,)+∞;单调增区间是(2,2)-.(Ⅱ)证明:令23233()()()(0)xh x f x g x t x t x =-=-+>,则232()h x x t '=-.当0t >时,由()0h x '=,13x t =;当13(,)x t ∈+∞时,()0h x '>;当13(0,)x t ∈时,()0h x '<,∴()h x 在(0,)+∞上的最小值是13()0h t =,故当0>x 时,()()≥f x g x 对任意正实数t 成立.A1A CBEG1B 1C21.(本小题满分12分)已知为正实数,数列{}n a 由11=a ,11(1,2,3,)++== nn c a a n 确定.(Ⅰ)对于一切的*∈n N ,证明:111+≤≤n c a ;(Ⅱ)若a 是满足1+=c aa 的正实数,且12||||||=-+-++- n n S a a a a a a ,证明:1<n S .解:(Ⅰ)用数学归纳法证明:当1n =时,11a =,0c >,1111c a +≤≤成立.假设n k=时结论成立,即111k c a +≤≤,则111k c c c a c ++≤+≤+,即2111111kc c a c c +++++≤≤<.∴1111k c a ++≤<,∴1n k =+时结论也成立,综上,对一切的*∈n N ,111+≤≤n c a 成立.(Ⅱ)11)()111(||||||||||nn n n n n n c a c ac a c a a a a a a a a a a a a ++++++-=-=-=-≤-,∴11||||n n a a a a a --≤-.当1a ≥时,111c +<,与1+=c aa 矛盾,故01a <<.∴112111||||||||||||n n n S a a a a a a a a a a a a a a -=-+-++-≤-+-++- 2111(1)(1)(1)1n aa a a a a --=-++++<-⨯= .22.(本小题满分14分)已知常数列0>a ,点(,0)-A a 是直角∆ABC 的直角顶点,顶点B 在定直线 l :2=a x 上移动,斜边B C 所在直线恒过定点(,0)D a .(Ⅰ)求顶点C 的轨迹T 的方程;(Ⅱ)设P 是轨迹T 上的任一点,l 是过点P 法线(即与过P 点的切线垂直的直线),且(2,0)-M a , (2,0)N a ,证明:直线M P 、N P 与直线l 的夹角相等.解:(Ⅰ)设2(,)a B t ,(,)C x y ,依题意0A B A C ⋅= ,∴32(,)(,)0a t x a y ⋅+=,即32()0ax a ty ++=①.又C D 与BD 共线,∴2()()0a a x t y --+⋅= ②. 由①②消去t ,得222231(0)x ya a y -=≠.(Ⅱ)由双曲线的对称性,不妨设00(,)P x y 是双曲线上位于x 轴上方的点,由222231x yaa-=,得y =∴3x y '=故过点P的切线的斜率3x k =切,而22002231x y aa-=,∴03y x k =切,∴03l x y k =-,002M P x ay k +=.设θ是M P 与直线l 的夹角,则0000000000222000000244232223636313tan ||||||x a x x x ay y x y ay y ay y y y x ax y aax ax θ+⋅+--+++-+-====. 设α是N P 与直线l 的夹角,02NP x ay k -=,则0000000000222000000244232223636313tan ||||||x a x x x ay y x y ay y ay y y y x ax y aax ax α-⋅----+----====.∴tan tan θα=,又090,090θα︒<<︒︒<<︒,∴θα=,故直线M P 、N P 与直线l 的夹角相等.。
《100所名校》湖南省师范大学附属中学2018
此卷只装订不密封班级 姓名 准考证号 考场号 座位号(1)此细胞处于有丝分裂的________期。
(2)该细胞在分裂中期时有_______条染色体。
(3)①和⑤两条染色体中的DNA是经过_______形成的(4)此时期继续发展,将在赤道板位置出现_______,逐渐扩展形成____,最终分裂为两个子细胞。
2018-2019学年湖南省师范大学附属中学高一上学期期末考试生物答案1.C【解析】【分析】细胞是生命活动的结构单位和功能单位,病毒没有细胞结构,不能独立生活,必须寄生在细胞中进行生活。
生命活动离不开细胞是指单细胞生物每个细胞能完成各种生命活动,多细胞生物通过各种分化细胞协调完成各种复杂的生命活动。
【详解】A、一切生物的生命活动都在细胞内或在细胞参与下完成,多细胞生物的生命活动需要多种细胞密切合作,正确;B、缩手反射的完成需要完整的反射弧,需要多种神经细胞密切合作,正确;C、病毒没有细胞结构,不能独立生活,必须寄生在细胞中进行生活,不能独立完成生命活动,错误;D、变形虫、草履虫等单细胞生物,只靠一个细胞就可以完成摄食、分裂等多种生命活动,正确。
故选C。
【点睛】生命活动离不开细胞,表现在:①病毒没有细胞结构,必须寄生在宿主细胞中才能进行生活;②单细胞生物依赖单个细胞就能完成各种生命活动;③不能依赖各种分化的细胞密切合作,共同完成一系列复杂的生命活动。
2.D【解析】细胞学说没有揭示动物细胞与植物细胞的区别,A错误;细胞学说表面新细胞可以从老细胞中产生,但没有揭示细胞为什么要产生新细胞,B错误;细胞学说没有揭示细胞之间的差异性,C错误;细胞学说的主要内容之一是“动植物都是由细胞构成的”,这说明生物体结构的统一性,D 正确。
【考点定位】细胞学说的建立、内容和发展【名师点睛】细胞学说是由德植物学家施莱登和动物学家施旺提出的,其内容为:(1)细胞是一个有机体,一切动植物都是由细胞发育而来,并由细胞和细胞的产物所构成;(2)细胞是一个相对独立的单位,既有它自己的生命,又对与其他细胞共同组成的整体的生命起作用;(3)新细胞可以从老细胞中产生。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
100所名校师范卷*错题集* 选择最佳答案; 1. The hours____the children spend in their one-way relationship with television people Undoubtedly affect their relationships with real-life people. A. that B. when C. in which D. when 2. __What do you think made Mary so unhappy ? __ ______ in the exam.. A. As she failed B. Failed C. Failing D. Because of failing 3. When I first met Mr. Cavor , he was about to finish building the machine _____he planned to travel to the moon A. in which B. with that C. in it D. by what 4. __You seem to have had that car for years. __ Yes ,I should sell it ____ it still runs. A. before B. during C. until D. while 5. __Was that the headmaster who walked by ? __ _____. A. It must be that B It must be him C. It must be it D. It must have been him 6. __I can’t manage this Sunday. Another time , but not Sunday. __Why_____ me earlier ? I’ve been looking forward to it. A. hadn’t you told B. don’t you tell C. not to tell D. didn’t you tell 7. __Oh, my God ! It’s just a sea of cars. How can you _____your car ? __That’s ease. Mine is colored differently from any other one. A. find out B. throw out C. pick out D. look out 8. On the long journey, Peter____ a most interesting guide. We all had a wonderful time. A. practiced B. behaved C. proved D. was proved 9. Cosmetics giant Avon Products Inc said last Friday it____ government permission to try direct sales in Beijing, Tianjin and Guangdong this month. A. got B. will get C. had got D. has got 10. I didn’t see your sister at the meeting. If she ____, she would have met my brother. A. has come B. did come C. came D. had come 11. He was beaten in the badminton match._____, he lost the game. A. In other word B. In a word C. In other words D. With words 12. Only in this way____ get over so many difficulties. A. we are sure to B. can we C. that we can D. that can we 13. The talk between the two leaders meant to end the long____of war between the two countries. A. sense B. case C. state D. condition 14. As early as 1647, Ohio made a decision that free tax supported schools must be established in every town______ 50 households to go to school. A. having B. to have C. to have had D. having had 15. For these college students, at the Fifth China International Air Show, the most important is___ willingness to devote themselves to making the show ____ success. A. a , / B. a , a C. the , a D. the , / 16. Learning another language is like stepping out of a door,____ I can look back and see more clearly in my own language. A. by which B. which C. on which D. though which 17. I guess you should hold on to the old map which is ____ in scientific research. A. great valuable B. of very valuable C. of great value D. much value 18. I had no chance ___ the famous singer, not to speak of taking photos of her. A. to approach B. approaching C. experience D. draw 19. A lot of attention, I think , should be ____ the pollution to our drinking water. A. made to control B. made to controlling B. paid to control . D paid to controlling 20. _____made the school proud was____ more than 95% of the students had been admitted to key universities. A, What ; because B. What ; that C. That ; what D. That ; because 21. ____a mobile phone can you ring _____you want to talk with anywhere. A. By ; whomever B. With ; whoever C. Only on ; whomever D. Using; whoever 22. Doctors should do what they can to ____their patients___ illness. A. cure ; of B. remind ; of C. keep ; out of D. separate ; from 23. __What do you think of the medicine ? __ To tell you the truth, _____according to the directions, it has side effect. A. when taken B. when taking C. when to take D. when to be take 24. ____the news, he couldn’t help crying. A. Being hearing B. Having been heard C. Listening D. Upon hearing 25. ____, Mother will wait for him to have dinner together. A. However late is he B. However late he is C. However he will be late D. However he is late 26. Nobody knows what the future may hold ______. A. in store B. in use C. in touch D. in order 27. __When can I use your computer ? __Never ! ______should you touch it. A. At no time B. In no time C. At any time D. At one time 28. Tom, you ___leave all your clothes on the floor like this ! A. wouldn’t B. mustn’t C. couldn’t D. may not 29. With the weather conditions ____, they flew to London immediately. A. taken account into B. taken into account C. taking account into D. taking into account 30. When I was young, I_____ education abroad. A. wish B. longed C. hoped D. hungered for 31. It was evening ____we reached the little town of Winchester. A. that B. until C. since D. before 32. If a man ___ succeed, he must work as hard as he can. A. will B. is to C. would D. should 33. The police arrived, after ____ the situation became more peaceful. A. that B. which C. whom D. them
