二次插补
数控车床编程实例 100
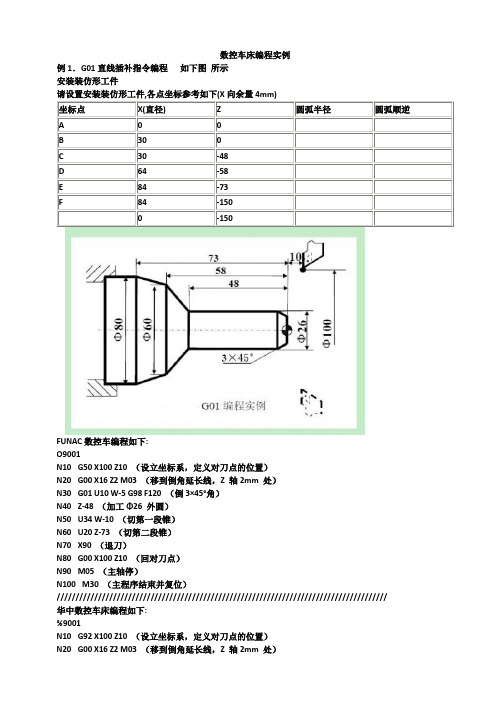
数控车床编程实例例1.G01直线插补指令编程如下图所示安装装仿形工件请设置安装装仿形工件,各点坐标参考如下(X向余量4mm)坐标点X(直径)Z圆弧半径圆弧顺逆A00B300C30-48D64-58E84-73F84-1500-150FUNAC数控车编程如下:O9001N10G50 X100 Z10 (设立坐标系,定义对刀点的位置)N20G00 X16 Z2 M03 (移到倒角延长线,Z 轴2mm 处)N30G01 U10 W-5 G98 F120 (倒3×45°角)N40Z-48 (加工Φ26 外圆)N50U34 W-10 (切第一段锥)N60U20 Z-73 (切第二段锥)N70X90 (退刀)N80G00 X100 Z10 (回对刀点)N90M05 (主轴停)N100M30 (主程序结束并复位)////////////////////////////////////////////////////////////////////////////////////////华中数控车床编程如下:%9001N10G92 X100 Z10 (设立坐标系,定义对刀点的位置)N20G00 X16 Z2 M03 (移到倒角延长线,Z 轴2mm 处)N30G01 U10 W-5 F300 (倒3×45°角)N40Z-48 (加工Φ26 外圆)N50U34 W-10 (切第一段锥)N60U20 Z-73 (切第二段锥)N70X90 (退刀)N80G00 X100 Z10 (回对刀点)N90M05 (主轴停)N100M30 (主程序结束并复位)===============================================================例2.G02/G03圆弧插补指令编程,如下图安装装仿形工件请设置安装装仿形工件,各点坐标参考如下(X向余量3mm)坐标点X(直径)Z圆弧半径圆弧顺逆A00B60C30-24183D32-3182E32-40F45-4045-1000-100FUNAC数控车编程如下:O9002N10 G50 X40 Z5(设立坐标系,定义对刀点的位置)N20 M03 S400 (主轴以400r/min旋转)N25 G50 S1000(主轴最大限速1000r/min旋转)N30 G96 S80 (恒线速度有效,线速度为80m/min)N40 G00 X0 (刀到中心,转速升高,直到主轴到最大限速)N50 G01 Z0 G98 F60 (工进接触工件)N60 G03 U24 W-24 R15 (加工R15 圆弧段)N70 G02 X26 Z-31 R5 (加工R5 圆弧段)N80 G01 Z-40 (加工Φ26 外圆)N90 X40 Z5 (回对刀点)N100 G97 S300 (取消恒线速度功能,设定主轴按300r/min 旋转)N110 M30 (主轴停、主程序结束并复位)///////////////////////////////////////////////////////////////////////////////////////////////////////// //////////////////华中数控车床编程如下:%9002N10 G92 X40 Z5(设立坐标系,定义对刀点的位置)N20 M03 S400 (主轴以400r/min旋转)N40 G00 X0 (刀到中心,转速升高,直到主轴到最大限速)N50 G01 Z0 F60 (工进接触工件)N60 G03 U24 W-24 R15 (加工R15 圆弧段)N70 G02 X26 Z-31 R5 (加工R5 圆弧段)N80 G01 Z-40 (加工Φ26 外圆)N90 X40 Z5 (回对刀点)N100 M30 (主轴停、主程序结束并复位)====================================================================例3G32螺纹切削指令编程如下图格式:G32 X(U)__Z(W)__F__说明:X、Z:为绝对编程时,有效螺纹终点在工件坐标系中的坐标;U、W:为增量编程时,有效螺纹终点相对于螺纹切削起点的位移量;F:螺纹导程,即主轴每转一圈,刀具相对于工件的进给值;使用G32指令能加工圆柱螺纹、锥螺纹和端面螺纹。
轨迹控制

Xe,Ye的最大允许值受系统字长的限制,假设系统 字长为m,则Xe、Ye的最大允许值为2ⁿ-1,若取 1
K= 2ⁿ ,则必然满足(I)式的条件。
方法2: 假设Xe>Ye,即X轴累加溢出脉冲总数多于Y轴,
累加最有效的情况是,每次累加,X轴都有脉冲溢 出,Y轴则不一定,于是选累加次数m=Xe,则
K= 1/Xe.将(3)式改写成:
Δx = K • Xe • Δt Δy = K • Ye • Δt
位移量为
(3)
x
t
0
KX e dt
KXet
i 1
n
y
t
0
Kye dt Kye t
i 1
n
取单位时间 Δ t=1,则公式化为
X KX e i 1 n y Kye i 1
这类插补方法有:数字积分法(DDA)、二阶近似插补法、双DDA插补 法、角度逼近插补法、时间分割法等。这些算法大多是针对圆弧插 补设计的。
这类插补算法主要用于交、直流伺服电机为伺服驱动系统的闭环, 半闭环数控系统,也可用于以步进电机为伺服驱动系统的开环数控 系统,而且,目前所使用的CNC系统中,大多数都采用这类插补方
一、概述
这类插补算法有:逐点比较法;最小偏差法;数字积
分法;目标点跟踪法;单步追综法等
它们主要用早期的采用步进电机驱动的数控系统。
由于此算法的速度指标和精度指标都难以满足现在零
件加工的要求,现在的数控系统已很少采用这类算法 了。
一、概述
数字增量插补(时间标量插补)
特点:
插补程序以一定的时间间隔定时(插补周期)运行,在每个周
数控车床编程实例 100

数控车床编程实例例1.G01直线插补指令编程????如下图所示?安装装仿形工件请设置安装装仿形工件,各点坐标参考如下(X向余量4mm)N50?U34W-10(切第一段锥)N60?U20Z-73(切第二段锥)N70?X90(退刀)N80?G00X100Z10(回对刀点)N90?M05(主轴停)N100?M30(主程序结束并复位)??===============================================================?例2.G02/G03圆弧插补指令编程,如下图安装装仿形工件请设置安装装仿形工件,各点坐标参考如下(X向余量3mm)O9002N40G00X0N90X40Z5N110M30//////////%9002N40G00X0N80G01Z-40(加工Φ26外圆)N90X40Z5(回对刀点)N100M30(主轴停、主程序结束并复位)====================================================================例3?G32螺纹切削指令编程?如下图格式:G32X(U)__Z(W)__F__说明:X、?Z:为绝对编程时,有效螺纹终点在工件坐标系中的坐标;U、W:为增量编程时,有效螺纹终点相对于螺纹切削起点的位移量;F:螺纹导程,即主轴每转一圈,刀具相对于工件的进给值;使用G32指令能加工圆柱螺纹、锥螺纹和端面螺纹。
安装装仿形工件请设置安装装仿形工件,各点坐标参考如下(X向余量3mm)N170G00X40(X轴方向快退)N180X50Z120(回对刀点)N190M05(主轴停)N200M30(主程序结束并复位)/////////////////////////////////////////////////////////////////////////////////////////////////////////华中数控车床格式:G32X(U)__Z(W)__R__E__P__F__说明:X、?Z:?为绝对编程时,有效螺纹终点在工件坐标系中的坐标;U、W:?为增量编程时,有效螺纹终点相对于螺纹切削起点的位移量;F:螺纹导程,即主轴每转一圈,刀具相对于工件的进给值;R、?E:螺纹切削的退尾量,R?表示Z?向退尾量;E?为X?向退尾量,R、E?在绝对或增量编程时都是以增量方式指定,其为正表示沿Z、X?正向回退,为负表示沿Z、X?负向回退。
SIEMENS系统中用参数编写二次曲线轮廓加工程序的方法与技巧

SIEMENS系统中用参数编写二次曲线轮廓加工程序的方法与技巧⑴二次曲线的编程方法所谓二次曲线是指具有二次方程作为数学模型的曲线轮廓,如抛物线、双曲线、椭圆等.关于二次曲线的编程,简单分为四个步骤: ①参数定义; ②计算点坐标;③插补; ④循环推断.⑵SIEMENS 802S 系统中,椭圆参数编程举例1) 标准椭圆参数方程X=a * cosAY=b * sinA其中,a 表示椭圆长半轴值.用自量值A 表示角度的变化,以计算每个角度值对应的椭圆上的X, Y 坐标值.2) 将等分点用直线段连接获得近似椭圆,其近似程度取决于自变量A的增值大小.举例: ( 以SIEMENS802S 为例,如图1-49所示)R1 =0; ①(R1 为方程变量,初值从0开始)MM : R5=12.5*SIN(R1); ②(R5 为椭圆轮廓上的X 坐标值)R6 =25*COS(R1) -25; (R6 为椭圆轮廓上的Z 坐标值,标准椭圆轮廓向–Z方向平移了25mm)G01 G64 X =2*R5 Z =R6; ③(直线插补进给,2*R5为X方向直径值)R1=R1+0.5 (0.5 为角度增量值)IF R1≤90 GOTOB MM; ④(推断椭圆进给是否到达终点,90°为终点角度,循环返回到MM处)①参数定义. 首先定义方程中各变量. 用机床给定用户定义参数代替,如SIEMENS802S系统,用户定义参数为R0~R299.②计算点坐标. 列出方程让数控系统根据所列方程自动计算坐标点. R5为X坐标,数控车床通常用直径编程,故插补进给中X值取2*R5. R6为Z坐标,编程原点在端面,而零件轮廓的数学模型原点在椭圆中心,椭圆中心向负Z方向移动25mm , 故由标准椭圆方程计算出坐标值应减去25.③插补. 坐标插补用G01完成. 加G64连续路径,机床连续进给,切削平稳,减小零件上的棱纹.④循环推断. 以上程序变量增加一个增量,插补一个点,当插补过程还没有完成时,要重复以上②、③过程,因此要使用循环推断来推断是否到达终点,“否”继续循环,“是”结束循环,向下执行.⑶编程技巧以上介绍了二次曲线的简单编程步骤,其他任何曲线都能够使用此方法.不一致曲线只需将第②步换成所要编的曲线方程即可.在FANUC系统中,把用户宏程序的内容放在G73固定循环里编写椭圆程序的技巧⑴用户宏程序编程特点用户宏程序编程的最大特点是使用变量,且变量之间能进行算术与逻辑运算. 因此,在数控机床加工一定批量的形状相同但尺寸不一致,或者由型腔、曲面、曲线等构成的工件时,使用用户宏程序功能进行编程能够减少程序重复编制,减少字符数,节约内存,使得编程更方便,更容易.FANUC系统中宏程序主体与SIEMENS系统的参数编程方法是一样的,只是变量符号与编程格式不一样. SIEMENS系统的变量号,用R参数表示. FANUC系统变量用“#”与数字合起来表示.根据变量号不一致,变量能够分成四种类型,见表1-3.在编程用户加工程序进行逻辑运算与函数运算时,通常能够用局部变量# 1~ # 33或者公共变量# 100 ~ # 199.而公共变量# 500 ~ # 999与# 1000以后的系统变量通常是提供给机床厂家进行二次开发,不能随便使用.若使用不当,便会导致整个数控系统的崩溃.下面举例介绍用户宏程序编写方法:⑵零件分析与编程技巧如图1-50 所示: 毛坯直径为 50mm,总长为102mm,材料为45钢棒料.该零件难点在椭圆编程上.根据已知条件可得椭圆方程: 即椭圆轮廓向Z轴负方向平移了18mm的距离,因此在计算Z坐标时,务必减去18mm的距离。
逐点比较法的性能和数字积分法

的速度分量为Vx,Vy,
则有
Y
V Vx Vy k OE X e Ye
Vy V E(Xe,Ye)
(k为常数) (3-16)
各坐标轴的位移量为
Vx
X Vxdt kXedt
O
X
Y Vydt kYedt (3-17)
图3-19 DDA直线插补
数字积分法是求式(3-17)从 O到E区间的定积分。此积分值等 于由O到E的坐标增量,因积分是 从原点开始的,所以坐标增量即是 终点坐标。
1. 数字积分法直线插补 例子:
若要产生直线OE,其起点为坐标原点O, 终点坐标为E(7,4)。设寄存器和累加 器容量为1,将Xe=7,Ye=4分别分成8
段,每一段分别为7/8,4/8,将其存入
X和Y函数寄存器中。
第一个时钟脉冲来到时,累加器里 的值分别为7/8,4/8,因不大于累加器 容量,没有溢出脉冲。
停止插补。
例题
设欲加工第一象限直线OE,起点在原点,终点坐标Xe=5, Ye=4,试写出插补计算过程并绘制插补轨迹。
步数 偏差判别 坐标进给
偏差计算
终点判别
1 F0=0 2 F1<0 3 F2>0 4 F3<0 5 F4>0 6 F5<0 7 F6>0 8 F7<0 9 F8>0
F0=0
+X
F1.= F0 - Ye =0-4=-4
Ⅱ Ⅲ
-X -X
+Y -Y
Fm1 Fm Ye Fபைடு நூலகம்1 Fm Xe
Ⅳ
+X
-Y
不同象限直线的逐点比较插补
二、圆弧插补 1.偏差计算公式
因为
Rm2
X
2 m
Ym2
取
利用插补法求解组距数列的中位数和众数

利用插补法求解组距数列的中位数和众数一、中位数(Median)中位数是一组数据按从小到大排序后,处在中间位置上的变量值,用Me 表示。
中位数将全部数据等分成两部分,使一部分数据比中位数大,另一部分数据则比中位数小。
中位数是一个位置代表值,它主要用于测定数据的集中趋势,且不受极端数值的影响。
此外,中位数还具有一个性质,就是各变量值与中位数的离差绝对值之和最小,即)m i n (1最小=-∑=ni ei Mx (1)根据未分组数据计算中位数时,要先对数据进行排序,然后确定中位数的位置,其公式为:中位数的位置=21+n ,式中的n 为数据的个数,凭此确定中位数的具体数值。
设有一组数据从小到大排序后为n x x x x ,,,,321⋅⋅⋅。
若n 为奇数,则中位数为21+n x ;若n 为偶数,则中位数是2nx 与12+nx 的平均数。
即⎪⎩⎪⎨⎧+=++为偶数时当为奇数时当n x x x Me n n n )(21n 12221 (2)根据分组数据计算中位数时,要先根据公式2∑f确定中位数的位置,并确定中位数所在的组。
如果是单项数列,则中位数就取中位数所在组的组值(即标志值);如果是组距数列,则采用下面的公式计算中位数的近似值:if S fL Me mm ⨯-+=-∑12(3)式(3)中,∑ƒ为数据的个数(总次数);L 为中位数所在组的下限值;1-m S 为中位数所在组以前各组的累积频数;m f 为中位数所在组的频数;i 为中位数所在组的组距。
式(3)中,假定中位数所在组的频数在该组内是均匀分布的。
图-1 组距数列中位数的分布图那么,我们接下来要讨论的是如何求证式(3),即组距数列中位数的计算公式。
假设上面图-1是某组距数列次数分布图。
利用插补法进行比例推算。
图-1中,A 点表示中位数所在组的下限,其值为L ;B 点表示中位数所在组的上限;C 点表示中位数所处的位置,其值为Me ;A 点到B 点所夹的距离,也就是中位数所在组的组距,其值为i ;A 点到C 点所夹的距离,就是中位数所在组的下限到中位数位置的距离,其值设为X 。
华中数控实例
数控车床编程实例例1.G01直线插补指令编程如下图所示安装装仿形工件FUNAC数控车编程如下:O9001N10 G50 X100 Z10 (设立坐标系,定义对刀点的位置)N20 G00 X16 Z2 M03 (移到倒角延长线,Z 轴2mm 处)N30 G01 U10 W-5 G98 F120 (倒3×45°角)N40 Z-48 (加工Φ26 外圆)N50 U34 W-10 (切第一段锥)N60 U20 Z-73 (切第二段锥)N70 X90 (退刀)N80 G00 X100 Z10 (回对刀点)N90 M05 (主轴停)N100 M30 (主程序结束并复位)////////////////////////////////////////////////////////////////////////////////////////华中数控车床编程如下:%9001N10 G92 X100 Z10 (设立坐标系,定义对刀点的位置)N20 G00 X16 Z2 M03 (移到倒角延长线,Z 轴2mm 处)N30 G01 U10 W-5 F300 (倒3×45°角)N40 Z-48 (加工Φ26 外圆)N50 U34 W-10 (切第一段锥)N60 U20 Z-73 (切第二段锥)N70 X90 (退刀)N80 G00 X100 Z10 (回对刀点)N90 M05 (主轴停)N100 M30 (主程序结束并复位)===============================================================例2.G02/G03圆弧插补指令编程,如下图安装装仿形工件请设置安装装仿形工件,各点坐标参考如下(X向余量3mm)FUNAC数控车编程如下:O9002N10 G50 X40 Z5(设立坐标系,定义对刀点的位置)N20 M03 S400 (主轴以400r/min旋转)N25 G50 S1000 (主轴最大限速1000r/min旋转)N30 G96 S80 (恒线速度有效,线速度为80m/min)N40 G00 X0 (刀到中心,转速升高,直到主轴到最大限速)N50 G01 Z0 G98 F60 (工进接触工件)N60 G03 U24 W-24 R15 (加工R15 圆弧段)N70 G02 X26 Z-31 R5 (加工R5 圆弧段)N80 G01 Z-40 (加工Φ26 外圆)N90 X40 Z5 (回对刀点)N100 G97 S300 (取消恒线速度功能,设定主轴按300r/min 旋转)N110 M30 (主轴停、主程序结束并复位)/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////// 华中数控车床编程如下:%9002N10 G92 X40 Z5(设立坐标系,定义对刀点的位置)N20 M03 S400 (主轴以400r/min旋转)N40 G00 X0 (刀到中心,转速升高,直到主轴到最大限速)N50 G01 Z0 F60 (工进接触工件)N60 G03 U24 W-24 R15 (加工R15 圆弧段)N70 G02 X26 Z-31 R5 (加工R5 圆弧段)N80 G01 Z-40 (加工Φ26 外圆)N90 X40 Z5 (回对刀点)N100 M30 (主轴停、主程序结束并复位)====================================================================例3 G32螺纹切削指令编程如下图格式:G32 X(U)__Z(W)__F__说明:X、Z:为绝对编程时,有效螺纹终点在工件坐标系中的坐标;U、W:为增量编程时,有效螺纹终点相对于螺纹切削起点的位移量;F:螺纹导程,即主轴每转一圈,刀具相对于工件的进给值;使用G32指令能加工圆柱螺纹、锥螺纹和端面螺纹。
细说视频中的场
细说视频中的“场”场指南Field Pointer场的概念原于电视,电视由于要克服信号频率带宽的限制,无法在制式规定的刷新时间内(PAL制式是25fps)同时将一帧图象显现在屏幕上,只能将图象分成两个半幅的图像,一先一后地显现,由于刷新速度快,肉眼是看不见地。
普通电视都是采用隔行扫描方式。
隔行扫描方式是将一帧电视画面分成奇数场和偶数场两次扫描。
第一次扫出由1、3、5、7…等所有奇数行组成的奇数场,第二次扫出由2、4、6、8…等所有偶数行组成的偶数场(premiere中称为顶部场Upper First和底部场Low Field,关系为偶数场Even field应对应顶部场upper field,奇数场odd field应对应底部场lower field)。
这样,每一幅图象经过两场扫描,所有的象素便全部扫完。
众所周知,电视荧光屏上的扫描频率(即帧频)有30Hz(美国、日本等,帧频为30fps的称为NTFS制式)和25Hz(西欧、中国等,帧频为25fps的称为PAL制式)两种,即电视每秒钟可传送30帧或25帧图像,30Hz和25Hz分别与相应国家电源的频率一致。
电影每秒钟放映24个画格,这意味着每秒传送24幅图像,与电视的帧频24Hz意义相同。
电影和电视确定帧频的共同原则是为了使人们在银幕上或荧屏上能看到动作连续的活动图像,这要求帧频在24Hz以上。
为了使人眼看不出银幕和荧屏上的亮度闪烁,电影放映时,每个画格停留期间遮光一次,换画格时遮光一次,于是在银幕上亮度每秒钟闪烁48次。
电视荧光屏的亮度闪烁频率必须高于48Hz才能使人眼觉察不出闪烁。
由于受信号带宽的限制,电视采用隔行扫描的方式满足这一要求。
每帧分两场扫描,每个场消隐期间荧光屏不发光,于是荧屏亮度每秒闪烁50次(25帧)和60次(30帧)。
这就是电影和电视帧频不同的历史原因。
但是电影的标准在世界上是统一的。
场是因隔行扫描系统而产生的,两场为一帧,目前所看到的普通电视的成像,实际上是由两条叠加的扫描折线组成的,比如你想把一张白纸涂黑,你就拿起铅笔,在纸上从上边开始,左右划折线,一笔不断的一直画到纸的底部,这就是一场,然而很不幸,这是你发现画的太稀,于是你又插缝重复补画一次,于是就是电视的一帧。
石学敏教授的中风疗法
1. 刺内关,操作1分钟。
双手同时操作。
2. 刺人中:要捻转360度,目的是要缠针,然后施用提插手法时不会拔出来。
以眼球湿润为度。
人中有三叉神经通过,痛感强,三叉神经兴奋后易出现流泪,故有时并非疼痛之故。
因人中较痛,故两三次后可改用印堂,手法一样,但疼痛明显减轻。
3. 刺风池、完骨、翳风,患者在床上坐起,要向结喉刺,深达2寸——2寸半。
小幅高频捻转补法(所谓小幅指<180度,高频指在140-160次/分)。
每对穴操作1分钟,双侧同时操作。
留针20分钟,留针时可嘱仰卧无妨。
翳风穴有点痛。
石提示皮质脑干引起的假球麻痹及缺血性延髓麻痹(真球麻痹)所致的吞咽困难,全球范围内无有效方法。
假球麻痹醒脑开窍法治疗后一般2周内可撤掉胃管,自己饮食,但真球麻痹难些。
4. 刺双人迎:解决缺血性延髓麻痹,手法同风池。
5. 刺三阴交:用2寸针,取穴与传统取法不同,胫骨后缘(而非传统的在胫骨和跟腱中间)向后斜刺45度,下方可达传统的三阴交穴处,抽动3次为度,抽动时针会弯,换一根再刺,用提插泻法。
6. 刺委中:仰卧位直腿抬高,提插泻法,下肢痿废和疼痛也要这么取穴和针刺,可收奇效。
7. 丘墟透照海:2-2.5寸针,在照海部皮下可见到针尖的蠕动,针后内翻立即改善。
留针时提出1-1.5寸,只留1寸,以免痉挛性上曲反射。
8. 极泉:取穴较传统取法下移1-2寸至肌肉丰满处,避开腋毛,操作时可见手的抽动,以抽动3次为度。
9. 尺泽:外展前伸120度。
直刺提插。
10. 合谷透三间:此处可用合谷刺。
对握固和功能减退均有效。
刺后患手即松开,如不拔针,患者手不会再握固。
对此患者的后续治疗,石的建议是:1、要解决吞咽困难的问题,2、要恢复上下肢功能。
在治疗过程中注意控制血糖。
石还提及中风病人的大关节保护十分重要,可以在肩部和腕部刺络拔罐,出血3-4cm。
也可配合推拿。
“醒脑开窍”针刺法理论内涵——石学敏院士学术思想浅析之一李军(300193中国天津中医学院第一附属医院针灸部部长)前言中风单元的综合治疗模式是国际上公认的最有效的方法,是一种住院病人的管理模式。
(完整)数控加工中心编程指令代码
常用地址符含义数控FANUC加工中心编程指令代码详解辅助功能M指令注:在一个程序段中只能有指令一个M指令,如果在一个程序中出现两个或两个以上的M指令时,则只有最后一个M指令有效,其余无效!其他指令(1)F—进给速度指令F及后面的若干数字表示,当指令为G94单位是mm/min,当指令为G95单位是mm/r。
(2)S—主轴转速指令S及后面的若干数字表示,单位是r/min.(3)T-刀具指令T及后面的三位数字表示,表示刀号。
(4)H和D—刀具长度补偿值和刀具半径补偿值H和D及其后面的三位数字表示,该三位数字为存放刀具补偿量地存储器地址(番号)。
G指令代码详解一、机床功能设定1、G53—选择机床坐标系格式:G53 X Y Z ;(X Y Z为机床坐标值)注:当指定G53指令时,就清除刀具的半径补偿、刀具长度补偿和刀具偏值,一般在换刀是指定Z轴.2、G54~G59—选择工件坐标系注:电源接通并返回参考点后,系统自动选择G54.3、G54。
1 P1~P48—选择附加工件坐标系4、G52-局部坐标系格式:G52X Y Z ;格式含义:为了编程的方便设定工件坐标系的子坐标系,G52中的X Y Z的值是工件坐标系G54~G59中的位置坐标。
取消局部坐标系——G52 X 0 Y 0 Z 0 ;注:当指令G52局部坐标系或取消局部坐标系时就取消了刀具长度补偿、刀具半径补偿等刀具偏值,在后续的程序中必须重新设置指定刀具长度补偿、刀具半径补偿等刀具偏值。
5、G90—绝对编程绝对编程是刀具移动到距离工件坐标系原点的某一位置.6、G91—增量编程增量编程刀具移动的距离是以前一点为基准计算,是前一点的增量。
7、G21-毫米输入 G20—英寸输入8、G16—启用极坐标指令 G15—取消极坐标指令二、插补功能指令1、G00—快速定位指令格式:G00 X Y Z ;格式含义:G00指令使刀具以点位控制方式从刀具当前点以最快速度运动到另一点。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二次插补算法及其目的和应用
插补:
数控车床的运动控制中,工作台(刀具)X、Y、Z轴的最小移动单位是一
个脉冲当量。因此,刀具的运动轨迹是具有极小台阶所组成的折线(数据点
密化)。例如,用数控车床加工直线OA、曲线OB,刀具是沿X轴移动一步或
几步(一个或几个脉冲当量Dx),再沿Y轴方向移动一步或几步(一个或几个
脉冲当量Dy),直至到达目标点。从而合成所需的运动轨迹(直线或曲线)。
数控系统根据给定的直线、圆弧(曲线)函数,在理想的轨迹上的已知点之
间,进行数据点密化,确定一些中间点的方法,称为插补。
二次插补法:
二次插补算法是指插补分粗插补和精插补两部份,粗插补由软件实现,
精插补由硬件完成。该方法可应用于步进开环数控系统和脉冲式全数字交流
伺服系统,大大提高了系统的性能指标,即实时性和可靠性。这种算法主要
应用于多轴联动、机械手、机器人等运动控制的设计。
插补运算的完成采用类似上、下位机的形式。粗插补部分由上位计算机
来完成,在每个插朴运算周期里输出的不是单个脉冲,而是一个直线段(位置
增量坐标值),粗插补采用完全离线进行;精插补部分由硬件智能运动控制器
来实时完成,主要完成各控制轴的轨迹规划和精确定位运动。这样,粗插补
完全离线进行,而精插补采用实时控制,一方面系统的实时性较好,另一方
面可把上位计算机解放出来去完成更重要的工作。
二次插补算法中的粗插补算法:
我们知道,物体运行的轨迹不管是空间的还是平面的,最终都可以离散成两种最
基本的单元:空间直线和空间圆弧,可用大量成熟的软件来完成这部分,从宏观
轨迹离散成微观两种最基本单元的工作,如Unigraph、Pro/ENGINEER、Cimatron、
Mastercam等等,在通常的控制系统中读入的轨迹代码就是这两种最基本的单元。
下面仅就这两种基本单元来设计它们的算法。
空间直线的粗插补算法:
空间直线离散成微直线段,得到微直线段实际上是要得到在某个数值范围内
的位置增量坐标值ΔX、ΔY、ΔZ。
设空间直线AB的起点为A(坐标为Xa、Ya、Za),终点为B(Xb、Yb、Zb),
此处各坐标值用步数来表示,参见图1所示。
空间直线的粗插补实际上是要得到空间直线
在各个坐标轴上的投影直线段ΔX、ΔY、ΔZ。这些投影值的绝对值代表运
动的步数,正负代表运动的方向。当然这些投影直线段还必须在一定的数值范围
内。这个数值实际就是下一阶段精插补所允许输入的最大步数,如超出了这个数
值范围,还必须将空间直线离散成更小的直线段。
图1 空间直线插补
则直线AB在三个坐标轴上的投影为:
ΔX=Xb-Xa;
ΔY=Yb-Ya;
ΔZ=Zb-Za;
设下一阶段精插补所允许的最大步数为S,则
a)如
[ΔX]
b)如(1)式不成立,则说明直线AB在各个坐标轴上的投影的绝对值超出了下
一阶段精插补所允许的数值范围。必须将直线AB离散成更小的直线段,下面是
其离散算法:
1)比较并求出[ΔX]、lΔY]、[ΔZ ]中的最大者。现假设[ΔX]最大。
2)完成如下的运算:
如ΔX>0,则ΔX1=S;
如ΔX<0,则ΔX=S;
X1:ΔY:ΔZ=ΔX:ΔY:ΔZ;
得出ΔX、ΔY、ΔZ的值。
3)输出一次ΔX、ΔY、ΔZ给下一阶段的精插补。并令
ΔX-ΔX1→ΔX;
ΔY-ΔY1→△y;
ΔZ-ΔZ1→△Z;
接着再重复a)的步骤,直到(1)式成立为止。
微直线段的轨迹参数规划:
对得到的一系列微直线段,即位置增量坐标值X、Y、Z,二次插朴算法中的
粗插补还要要完成对这些微直线段的轨迹参数规划,即使三个轴以一定比例关系
的速度运行相应的步数时,能按规定的轨迹运行,对相应的参数我们要预先进行
规划:各轴的运行方向、各轴的运行步数、各轴的运行速度。其算法如下:
a)各轴的运行方向
位置增量坐标值ΔX、ΔY、ΔZ的正负就代表运行的方向(如值为正就表示此
轴运动的方向为正,如其值为负就表示此轴运动的方向为负)。
b)各轴的运行步数
取位置增量坐标值ΔX、ΔY、ΔZ的绝对值就得到了各轴的运动步数X、Y、
Z。
c)各轴的运行速度
各轴的运行速度的设定实际上是根据各个轴的运行步数得到各个轴的速度
参数的设定。下面研究其算法:
设各个轴的运动步数为X、Y、Z,假设也得到了各个轴的速度参数的设定:
Xs、Ys、Zs,则下式一定成立:
Xs、Ys、Zs =X、Y、Z
且 Xs
从(2)可以看出,要得到Xs、Ys、Zs,只须X、Y、Z分别乘以某个常数M,
即 Xs=X×M;
Ys=y×M;
Zs=Z×M;
下面确定常数M:
从(2)可以看出,在某一微直线段各轴是匀速运行的,且M值为常量。但是
在下一微直线段内,由于各轴的运行步数的比例关系可能发生变化,各轴的运行
速度可能变了,但是在此微直线段内各轴仍是匀速运行。为了保证宏观上运行的
平稳
性,我们必须使各个微直线段内的最大运行速度相一致。由于各轴在每个微直线
段内运行步数的变化,那么M的值在不同的微直线段内是变化的。在我们设计的
这个系统中,各轴的轨迹控制由硬件(如智能运动控制器)完成,因此结合智能运
动控制器来确定求M的值的算法。
1)求出步数X、Y、Z中的最大值step[max]
2)M=F/step[max]×C
其中F代表此次运行各轴速度中最大的速度;
C是与智能运动控制器相关的一个常数。
从空间直线的轨迹参数规划可以看出,可把它推而广之到四轴、五轴甚至更
多轴的联动。
圆弧的粗插补算法:
圆弧粗插补的实质是在保证一定精度的前提下,用弦进给去代替弧进给,即用直
线来代替圆弧。粗插朴的结果是要得到一系列离散的直线段。本算法可实现圆弧
的直接跨象限插补,而且粗插补精度达到一个脉冲当量。其粗插补算法如下。
设有圆弧AC,其起点为A。起点坐标为Xa、Ya、Za,终点为C,终点坐标为Xc、
Yc、Zc,圆弧的半径为R。并假设圆弧粗插补为顺时针方向。如图2所示。
图2 圆弧粗插补示意图
a)确定圆弧AC相对于X轴正向的起始角a。
b)确定圆弧AC的离散角度Δa,可根据实际需要确定Δa的大小,Δa越大则
圆弧的轨迹精度就越低,Δa越小则圆弧的轨迹精度就越高。如是
顺时针方向插补则Δa取正值,反之如实逆时针方向,粗插补则Δa取负值。可以
输出一个直线段AB到上一节的空间直线的粗插补,这样就得到了圆弧粗插补的第
一个点。
c)假设从A点开始.沿圆弧顺时针方向粗插补的第一点为日点,OA和OB的夹
角为Δa,下面求其坐标Xb、Yb、Zb,其算法如下:
Xb=R*cos(a-k*Δa) (3)
Yb=R*sin(a-k*Δa) (4)
可以输出一个直线段AB到上一节的空间直线的粗插补,这样就得到了圆弧粗
插补的第一个点。
d)下面判断是否插补到圆弧终点C,实际就是求出BC直线段的长度L,并判断
其是否小于某一给定的插补逼近精度值P,其算法如下:
L=((Xc-Xb)^2+(Yb-Yc)^2)^0.5 (5)
假设P=1个脉冲当量(P的值可根据插补逼近精度来确定)
如L
束。
e)在d中判断是否插补到终点有一个例外的情况,那就是作整圆插补时。起
点和终点重合,那么只经过一次插补,(5)式就判断插补到终点了,实际插补才
刚开始。为了避免这一情况,我们可以让步骤3先进行10次后,再进行是否插
补到终点的判断,这是因为我们需要插朴的圆弧一般都不止20个脉冲当量长。
虽然上面的插补算法是沿顺时针方向插补,但是可以类推出,当沿圆弧逆时针方
向粗插朴时,只须把式(3)、(4)中括号内的减号(一)改为加号(+)
就可以达到要求了。从上面的粗插补算法还可以看出,按照此种插补算法,圆弧
插补可以直接过象限,即不论圆弧AC是在第一象限、第二象限、第三象限、第
四象限或是圆弧AC横跨几个象限都可直接实现圆弧的粗插补。
上面列举了XOY平面内的圆弧插补,可以很顺利地类推出在XOZ、YOZ等另
外两个平面内的圆弧插补。
二次插补算法中的精插补:
通过二次插补中的粗插补,得到一系列微直线段的轨迹规划,下面我们要完
成这一系列轨迹的运行,即二次插补算法中的精插补。精插补必须解决在相同的
时间片内,各个联动轴能同时以恰当的速率完成相应步数的运行,如此微段内,
x轴运行10步,y轴运行5步,z轴运行3步,那么此次时间片结束时,这三个
轴必须以相应的速率同时到达相应位置。这实际就是数字积分法中的直线插补法。
精插补在我们的这个设计中是由硬件来完成的。把通过离线粗插补得到的各
轴的运行参数(运行方向、运行步数、运行速度)写到运动控制器上相应的参数寄
存器,然后启动运动控制器开始作精插补工作,在完成一段微直线段的精插补后,
让智能运动控制器发出一个中断信号,通知主程序刷新参数寄存器的值(写入下
一个微直线段的运行参数),启动下一个微直线段的精插补。这样一直运行到所
有微直线段的精插补结束。
这种算法主要应用于多轴联动、机械手、机器人等运动控制的设计。
