12.2 三角形的性质(4)三角形的外角及分类(课时练习)-2016-2017学年八年级数学上册(解析版)
2016年秋八年级数学上册 11.2.2 三角形的外角练习题(无答案)(新版)新人教版

三角形的外角
1.下列说法中,正确的是 ( )
A .三角形的一个外角等于这个三角形的两个内角的和
B .三角形的一个外角小于它的一个内角
C .三角形的一个外角与它相邻的内角是邻补角
D .三角形的一个外角大于这个三角形的任何一个内角
2. 三角形的每一个顶点处取一个外角,则三角形的三个外角中,钝角的个数至少有( )
A .0个
B .2个
C .3个
D .4个
3. △ABC 中,∠ABC 的角平分线与∠ACB 的外角平分线交于点O ,且∠A=α,则∠BOC= ( )
A .12α
B .180°-12α
C .90°-12α
D .90°+1
2α
4. 在△ABC 中,∠A=15∠C=1
3∠B ,则△ABC 的三个外角的度数分别为 .
5. 如图所示,则α= °.
6. 如图,在△ABC 中,∠B=60°,∠C=52°,AD 是∠BAC 的平分线,DE 平分∠ADC 交AC 于点E ,
则∠BDE= °.
7. 如图,∠A=55°,∠B=30°,∠C=35°,求∠D 的度数.
8.如图,AC ⊥DE ,垂足为O ,∠A=27°,∠D=20°,
求∠B 与∠ACB 的度数.
D B A E
O C A
B D E
C (第6题) A C
D B 58° (第5题) 24° 32° α。
人教版_部编版八年级数学上册第十一章第二节三角形的外角作业练习题(含答案) (47)

人教版_部编版八年级数学上册第十一章第二节三角形的外角作业练习题(含答案)如图,在△ABC中,△B=40°,△BCD=100°,EC平分△ACB,求:△A与△ACE 的度数.【答案】60°,40°【解析】【分析】首先根据三角形的一个外角等于和它不相邻的两个内角的和即可求得∠A的度数;再根据平角的定义及角平分线的性质求出∠ACB的度数即可.【详解】∠∠B=40°,∠BCD=100°,∠∠A=∠BCD-∠B=60°,∠∠BCD=100°,∠∠ACB=180°-100°=80°,又∠EC平分∠ACB,∠∠ACE=1∠ACB=40°.262.如图,已知AB∥CD,分别探讨下面的四个图形中∠APC与∠PAB,∠PCD 的关系,请你从所得关系中任意选取一个加以说明.【答案】图()1结论360APC PAB PCD ∠+∠+∠=;图()2结论APC PAB PCD ∠=∠+∠;图()3结论PAB APC PCD ∠=∠+∠;图()4结论PCD PAB APC ∠=∠+∠.证明见解析.【解析】【分析】关键是过转折点作平行线,根据两直线平行,内错角相等,同位角相等,同旁内角互补或结合三角形的外角性质求证即可.【详解】解:图()1结论360.APC PAB PCD ∠+∠+∠=图()2结论.APC PAB PCD ∠=∠+∠图()3结论.PAB APC PCD ∠=∠+∠图()4结论.PCD PAB APC ∠=∠+∠如图1:过点P 做.PF AB,AB CD ∥.PF CD ∴180.APF A ∴∠+∠=180.CPM C ∠+∠=两式相加得360.A C APM CPM ∠+∠+∠+∠=即360.APC PAB PCD ∠+∠+∠=如图2:过点P 做.PE AB因为,PE AB CD所以,.BAP APE EPC PCD ∠=∠∠=∠,APE EPC BAP PCD ∠+∠=∠+∠即.APC PAB PCD ∠=∠+∠如图3: PAB APC PCD ∠=∠+∠.延长BA 与PC 交于点F .AB CD ,.PFA PCD ∴∠=∠(两直线平行,同位角相等),又,PAB APC PFA ∠=∠+∠(三角形的一个外角等于与它不相邻的两个内角的和).PAB APC PCD ∴∠=∠+∠.如图4:,AB CD ∥.PFB PCD ∴∠=∠(两直线平行,同位角相等),又PFB APC PAB ∠=∠+∠(三角形的一个外角等于与它不相邻的两个内角的和).PCD APC PAB ∴∠=∠+∠.【点睛】本题考查平行线的性质.熟练掌握平行线的性质并能灵活运用是解决此题的关键.63.将一副直角三角板如图放置,已知AE ∥BC ,求∠AFD 的度数.【答案】∠AFD=75°【解析】【详解】根据平行线的性质及三角形外角解答由直角三角板可知∠E=45°,∠C=30°.因为AE ∥BC ,所以∠EAC=∠C=30°,因为∠AFD 是△AEF 的外角,所以∠AFD=∠E+∠EAC所以∠AFD=45°+30°=75°.64.如图,在ABC ∆中,延长BC 至D ,60,45A B ∠=∠=︒︒.(1)过点C 作直线CE ∥AB (尺规作图,不写作法,保留作图痕迹);(2)求ACD ∠的度数【答案】(1)见解析; (2)105ACD ∠=︒【解析】【分析】(1)过点C 作ECD B ∠=∠,即可得到直线CE ∠AB(2)根据三角形的外角性质即可求出.【详解】(1)如图所示(2)由外角性质可得∠=∠+∠=+=︒ACD B A6045105三、填空题65.如图,已知直线AB△CD,△C=125°,△A=45°,则△E的度数为.【答案】80°.【解析】【分析】由直线AB∠CD,∠C=125°,根据两直线平行,同位角相等,即可求得∠1的度数,又由三角形外角的性质,即可求得∠E的度数.【详解】解:∠直线AB∠CD,∠C=125°,∠∠1=∠C=125°,∠∠1=∠A+∠E,∠A=45°,∠∠E=∠1﹣∠A=125°﹣45°=80°.故答案为:80°.考点:平行线的性质;三角形的外角性质66.如图,在△ABC中,∠A=60°,若剪去∠A得到四边形BCDE,则∠1+∠2=______.【答案】240.【解析】【详解】试题分析:∠1+∠2=180°+60°=240°.考点:1.三角形的外角性质;2.三角形内角和定理.67.三个等边三角形的位置如图所示,若△3=40°,则△1+△2= °.【答案】140.【解析】试题分析:∵图中是三个等边三角形,∵3=40°,∵∵ABC=180°﹣60°﹣40°=80°,∵ACB=180°﹣60°﹣∵2=120°﹣∵2,∵BAC=180°﹣60°﹣∵1=120°﹣∵1,∵∵ABC+∵ACB+∵BAC=180°,∵80°+(120°﹣∵2)+(120°﹣∵1)=180°,∵∵1+∵2=140°.故答案为140.考点:等边三角形的性质.68.如图,已知l1△l2,△A=40°,△1=60°,△2= .【答案】100°.【解析】试题分析:已知l1∵l2,∵1=60°,由平行线的性质可得∵B=∵1=60°,在∵ABC 中根据三角形外角的性质可得∵2=∵B+∵A=60°+40°=100°.考点:平行线的性质;三角形外角的性质.69.如图,直线l1∥l2,并且被直线l3,l4所截,则∠α=________.【答案】64°【解析】试题分析:如图1,∵∵1+56°=120°,∵∵1=120°﹣56°=64°,又∵直线l1∵l2,∵∵α=∵1=64°.故答案为64°.考点:平行线的性质.70.如图,AB△CD,AD与BC交于点E.若△B=35°,△D=45°,则△AEC= .【答案】80°.【解析】试题分析:∵AB∵CD,∵B=35°,∵∵C=35°,∵∵D=45°,∵∵AEC=∵C+∵D=35°+45°=80°,故答案为80°.考点:1.平行线的性质;2.三角形的外角性质.。
人教版数学八年级上册11.2.2 三角形的外角课件(共28张PPT)

外角
小试牛刀
下列各图中,∠1 是△ABC 的外角的是( D )
1 C
A
B
A
C
1 AB B
C 1
A
B
C
B
1
A
C
D
三角形的外角应具备的条件:
①角的顶点是三角形的顶点;②角的一边是三角形的一边;
③另一边是三角形中一边的延长线.
探究 要知道传球传给谁,就要知道外角∠ACD,内角∠B的度数
大小,你能比较外角∠ACD,内角∠B的度数大小吗?
解法二:延长BD交AC于点E.
A
(
在△ABE中,∠1=∠ABE+∠BAE,
51 °
F
E
在△ECD中,∠BDC=∠1+∠ECD.
所以∠BDC=∠BAC+∠ABD+∠ACD 方法总结
=51° +20°+30°=101°.
20 ° D B
30 ° C
解题的关键是正确地构造三角形,利用三角形 解法三:连接延长CD交AB于点F(解题过程同解法二).
课堂小结
定义
角一边必须是三角形的一边,另一边必须 是三角形另一边的延长线
三角形 的外角
性质
三角形的一个外角等于与它不相邻的两个 内角的和
三角形的 外角和
三角形的外角和等于360 °
下节课,再见!
∠2 +∠CBF = 180°,
E
∠3 +∠ACD = 180°,
A
得∠1 +∠2 +∠3 +∠BAE +∠CBF +∠ACD = 540°, 1
由∠1 +∠2 +∠3 = 180°,
数学人教版八年级上册11.2.2 三角形的外角课后作业.2.2三角形的外角
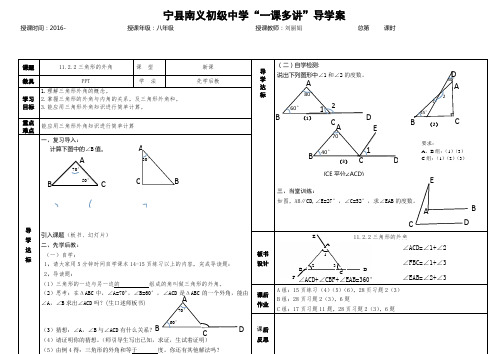
宁县南义初级中学“一课多讲”导学案 授课时间:2016- 授课年级:八年级 授课教师:刘丽娟 总第 课时
课题 11.2.2三角形的外角 课 型 新课 导
学 达 标 (二)自学检测: 说出下列图形中∠1和∠2的度数。 三、当堂训练: 如图,AB∥CD,∠E=27°,∠C=52°,求∠EAB的度数。 教具 PPT 学 法 先学后教 学习 目标 1.理解三角形外角的概念。 2.掌握三角形的外角与内角的关系,及三角形外角和。 3.能应用三角形外角知识进行简单计算。 重点 难点 能应用三角形外角知识进行简单计算 导 学 达 标 一、复习导入: 计算下图中的∠B值。 引入课题(板书、幻灯片) 二、先学后教: (一)自学: 1、请大家用5分钟时间自学课本14-15页练习以上的内容,完成导读题: 2、导读题: (1)三角形的一边与另一边的 组成的角叫做三角形的外角。 (2)思考:在ΔABC中,∠A=70º,∠B=60°,∠ACD是ΔABC的一个外角,能由∠A,∠B求出∠ACD吗?(生口述师板书) (3)猜想:∠A,∠B与∠ACD有什么关系? (4)请证明你的猜想。(师引导生写出已知,求证,生试着证明) (5)由例4得:三角形的外角和等于 度。你还有其他解法吗? 板书 设计 11.2.2三角形的外角 课后 作业 A组:15页练习(4)(5)(6),28页习题2(3) B组:28页习题2(3),6题 C组:17页习题11题,28页习题2(3),6题 课后 反思 A B C D ∠ACD=∠1+∠2 ∠FBC=∠1+∠3 ∠EAB=∠2+∠3 C B A D A B C C B A D 1 2 60° 80° A B C D 1 2 30°
45°
C B A
D E
40° 70°
1
C B
A 70° 50°
30°
70° 60°
(CE平分∠ACD) E F 1 2 3
∠ACD+∠CBF+∠EAB=360°
12.5.4 全等三角形的判定(课时测试)-2016-2017学年八年级数学上册(原卷版)

矿产资源开发利用方案编写内容要求及审查大纲
矿产资源开发利用方案编写内容要求及《矿产资源开发利用方案》审查大纲一、概述
㈠矿区位置、隶属关系和企业性质。
如为改扩建矿山, 应说明矿山现状、
特点及存在的主要问题。
㈡编制依据
(1简述项目前期工作进展情况及与有关方面对项目的意向性协议情况。
(2 列出开发利用方案编制所依据的主要基础性资料的名称。
如经储量管理部门认定的矿区地质勘探报告、选矿试验报告、加工利用试验报告、工程地质初评资料、矿区水文资料和供水资料等。
对改、扩建矿山应有生产实际资料, 如矿山总平面现状图、矿床开拓系统图、采场现状图和主要采选设备清单等。
二、矿产品需求现状和预测
㈠该矿产在国内需求情况和市场供应情况
1、矿产品现状及加工利用趋向。
2、国内近、远期的需求量及主要销向预测。
㈡产品价格分析
1、国内矿产品价格现状。
2、矿产品价格稳定性及变化趋势。
三、矿产资源概况
㈠矿区总体概况
1、矿区总体规划情况。
2、矿区矿产资源概况。
3、该设计与矿区总体开发的关系。
㈡该设计项目的资源概况
1、矿床地质及构造特征。
2、矿床开采技术条件及水文地质条件。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
12.2 三角形的性质(4)三角形的外角及分类 (练)
一.选择题
1. 如图,∠1是三角形的一个外角,则∠1的角度为( )
A.85° B.95° C.105° D.75°
【答案】D.
【解析】∠1=30°+45°=75°,故选:D.
考点:三角形的外角性质.
2.如图,图中∠1的大小等于( )
A.40° B.50° C.60° D.70°
答案:D.
【解析】由三角形的外角性质得,∠1=130°-60°=70°.故选D.
考点:三角形的外角性质.
3.如图,∠x的两条边被一直线所截,用含α和β的式子表示∠x为( )
A.α-β B.β-α C.180°-α+β D.180°-α-β
【答案】B.
【解析】∵β=x+α,整理得:x=β-α.故选B.
考点:三角形的外角性质.
4. 如图,平面上直线a、b分别过线段AB两端点(数据如图),则a、b相交所成的锐角是( )
A.20° B.30° C.80° D.100°
【答案】A.
【解析】a,b相交所成的锐角=100°-80°=20°.故选:A.
考点:三角形的外角性质.
5.下面给出的四个三角形都有一部分被遮挡,其中不能判断三角形类型的是( )
A. B. C. D.
答案:C.
【解析】A、知道两个角,可以计算出第三个角的度数,因此可以判断出三角形类型;
B、露出的角是钝角,因此是钝角三角形;
C、露出的角是锐角,其他两角都不知道,因此不能判断出三角形类型;
D、露出的角是钝角,因此是钝角三角形;
故选:C.
考点:三角形的分类.
6. 将一副三角尺按如图方式进行摆放,则∠1的度数为( )
A.60° B.90° C.120° D.135°
答案:C.
【解析】如图,∠1=∠2+∠3=90°+30°=120°,故选:C.
考点:三角形的外角性质.
二、填空题
7.如图,△ABC中,∠B=45°,∠C=72°,则∠1的度数为____________ °.
【答案】117.
【解析】∠1=∠B+∠C=45°+72°=117°,故答案为:117.
考点:三角形的外角性质.
8.在△ABC中,如果∠B=35°,∠C=62°,那么与∠A相邻的一个外角等于____________
度.
【答案】97.
【解析】∠A的外角=∠B+∠C=35°+62=97°.故答案为:97.
考点:三角形的外角性质.
9. 图中x的值为____________
.
【答案】60°.
【解析】根据三角形外角的性质可得:x+x+20°=x+80°,解得:x=60°,故答案为:60°.
考点:三角形的外角性质.
10.如图,∠A+∠B+∠C+∠D+∠E+∠F+∠G=__________
度.
【答案】540.
【解析】连接DG、AC.在四边形EFGD中,得∠E+∠F+∠EDG+∠DGF=360°,又∠1+∠2=∠3+∠4,∠5+∠6+
∠B=180°,∴∠A+∠B+∠C+∠D+∠E+∠F+∠G=540°.故答案为540.
考点:三角形的外角性质;三角形内角和定理.
三、解答题
11.一个零件的形状如图,按规定∠A应等于90°,∠B、∠C应分别是21°和32°,现测量得∠BDC=148°,
你认为这个零件合格吗?为什么?
【答案】这个零件不合格,理由见解析.
【解析】延长CD与AB相交于点F.∵∠DFB=∠C+∠A=32°+90°=122°,又∵∠BDC=∠DFB+∠B=122°+21°
=143°,∵实际量得的∠BDC=148°,143°≠148°,∴这个零件不合格.
考点:三角形的外角性质.
12. 如图,D是△ABC的BC边上一点,∠B=∠BAD,∠ADC=80°,∠BAC=70°
求:(1)∠B的度数;(2)∠C的度数.
【答案】(1)40°;(2)70°.
【解析】(1)∵∠ADC=∠B+∠BAD=80°(三角形的一个外角等于与它不相邻的两个内角的和)且∠B=∠BAD,
∴∠B=40°;
(2)∵∠BAC+∠B+∠C=180°(三角形内角和定理),∠BAC=70°,∠B=40°,∴∠C=70°.
考点:三角形的外角性质;三角形内角和定理.
