matlab小波去噪函数
小波阈值的函数介绍

1 阈值获取MATLAB 中实现信号阈值获取的函数有ddencmp 、thselect 、wbmpen 和wdcbm ,下面对它们的用法进行简单的说明。
函数Ddencmp 的调用格式(1)[THR ,SORH ,KEEPAPP ,CRIT]=ddencmp(IN1,IN2,X)(2)[THR ,SORH ,KEEPAPP ,CRIT]=ddencmp(IN1,'wp',X)(3)[THR ,SORH ,KEEPAPP]=ddencmp(IN1,'wv',X)函数ddencmp 用于获取在消噪或压缩过程中的默认阈值。
输入参数X 为一维或二维信号;IN1取值为'den'或'crop',den 表示进行去噪,crop 表示进行压缩;IN2取值为'wv'或'wp',wv 表示选择小波,wp 表示选择小波包。
返回值THR 是返回的阈值;SORH 是软阈值或硬阈值选择参数;KEEPAPP 表示保存低频信号;CRIT 是熵名(只在选择小波包时用)。
函数thselect 的调用格式THR=thselect(X ,TPTR)THR=thselect(X ,TPTR)根据字符串TPTR 定义的阈值选择规则来选择信号X 的自适应阈值。
自适应阈值选择规则包括下面四种:"(1)TPTR='rigrsure',自适应阈值选择使用Stein 的无偏风险估计原理。
(2)TPTR='heursure',使用启发式阈值选择。
(3)TPTR='sqtwolog',阈值等于sqrt(2*log(1ength(X)))。
(4)TPTR='minimaxi',用极大极小原理选择阈值。
阈值选择规则基于模型e t f y +=)(,e 是高斯A 噪声N(O ,1)。
函数wbmpen 的调用格式THR=wbmpen(C ,L ,SIGMA ,ALPHA)THR=wbmpen(C ,L ,SIGMA ,ALPHA)返回去噪的全局阈值THR 。
Mtalb小波去噪

数字图像阈值去噪算法研究与实现摘要图像在获取和传输的过程中经常要受到噪声的污染。
噪声对图像分析有着非常重要的影响,必须在分析前去除。
所以,图像去噪成为图像分析和处理的重要技术。
传统的去噪方法不仅滤出了图像的噪声,同时使图像细节变得模糊。
小波变换是继傅琨叶变换之后的又一时频分析工具。
小波变换由于在时域频域同时具有良好的局部化性质和多分辨率分析的特点,因此不仅能满足各种去噪要求,如低通、高通、随机噪声的去除,而且与传统的去噪方法相比较,有着无可比拟的优点,成为信号分析的一个强有力的工具,被誉为分析信号的数学显微镜。
其应用包括图像预处理、图像压缩与传输、图像分析、特征提取等图像处理的很多阶段。
首先,介绍了本课题的研究目的,并介绍了目前常用的去噪方法及这些方法之间的比较。
其次,在简述了小波变换的发展历史和小波变换的基本理论知识后,对以小波为工具在数字图像处理方面进行了有益的探索。
再次,给出了小波边缘检测理论,接下来针对小波去噪的理论和方法着重进行了介绍,包括小波去噪的原理、方法和阈值去噪处理等方面的内容。
最后,对本文的工作进行了总结。
小波变换由于具有“数学显微镜”的作用,在去噪的同时能保持图像细节,得到原图像的最佳恢复。
在众多的小波去噪方法中,运用最多的是Donoho小波阈值萎缩法,但Donoho给出的阈值有“过扼杀”小波系数的倾向,重建误差较大。
本文提出基于小波变换与中值滤波相结合的方法实现了图像去噪。
该方法在去噪之前,先通过小波边缘检测确定图像边缘特征的小波系数,保留这些位置的小波系数,其不受闽值去噪影响,对其它位置的小波系数进行自适应阈值去噪,去除高斯噪声。
然后对图像进行中值滤波,去除椒盐噪声。
该算法的实验结果表明不仅能滤出图像中高斯噪声和椒盐噪声的混合噪声,而且能较好的保留图像的边缘细节,其滤波效果优于传统的图像去噪方法。
关键词:小波变换,高斯噪声,椒盐噪声,边缘检测,图像去噪ABSTRACTThe image iS often corrupted by noise in its acquisition or transmission.The noise to be removed before analysis has an important effect on image analysiS.Image~denoising is an important technology in image analysis and processingdomain.Traditional denoising methods can filter noise。
Matlab中的小波变换与小波包分析方法详解

Matlab中的小波变换与小波包分析方法详解引言近年来,小波变换在信号处理领域中得到了广泛的应用。
小波变换是一种能够捕捉信号时频特性的有效工具,可以用来分析、压缩和去噪各种类型的信号。
本文将详细介绍Matlab中的小波变换和小波包分析方法,以帮助读者更好地理解和应用这一强大的信号处理技术。
一、小波变换(Wavelet Transform)小波变换是一种将信号分解成不同尺度的基函数的技术。
与传统的傅里叶变换相比,小波变换具有更好的时频局部化特性。
Matlab中提供了丰富的小波分析工具箱,可以方便地进行小波变换的计算。
1.1 小波基函数小波基函数是小波变换的基础。
不同类型的小波基函数适用于不同类型的信号。
在Matlab中,我们可以使用多种小波基函数,如Daubechies小波、Haar小波和Morlet小波等。
1.2 小波分解小波分解是指将信号分解成多个尺度的小波系数。
通过小波分解,我们可以获取信号在不同尺度上的时频特性。
Matlab中提供了方便的小波分解函数,例如'dwt'和'wavedec'。
1.3 小波重构小波重构是指根据小波系数重新构建原始信号。
通过小波重构,我们可以恢复原始信号的时域特性。
在Matlab中,可以使用'idwt'和'waverec'函数进行小波重构。
二、小波包分析(Wavelet Packet Analysis)小波包分析是对小波变换的进一步扩展,它允许对信号进行更精细的分解和重构。
小波包分析提供了一种更灵活的信号分析方法,能够获得更详细的时频特性。
2.1 小波包分解小波包分解是指将信号分解成具有不同频带的小波包系数。
与小波分解相比,小波包分解提供了更高的分辨率和更详细的频谱信息。
在Matlab中,可以使用'wavedec'函数进行小波包分解。
2.2 小波包重构小波包重构是根据小波包系数重新构建原始信号。
小波图像去噪及matlab分析
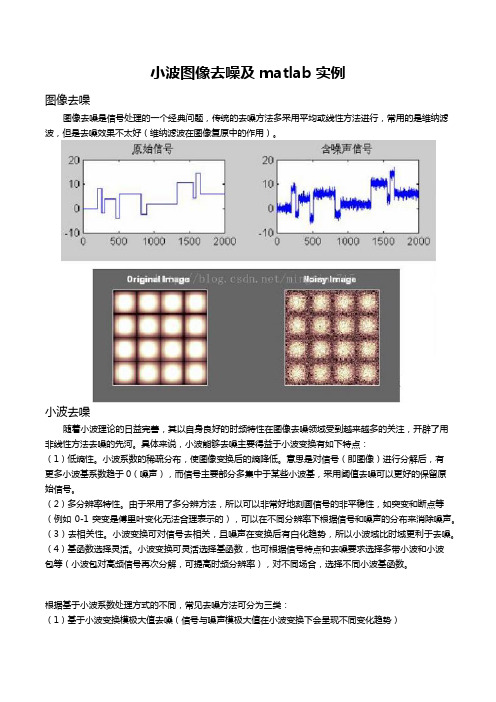
小波图像去噪及matlab实例图像去噪图像去噪是信号处理的一个经典问题,传统的去噪方法多采用平均或线性方法进行,常用的是维纳滤波,但是去噪效果不太好(维纳滤波在图像复原中的作用)。
小波去噪随着小波理论的日益完善,其以自身良好的时频特性在图像去噪领域受到越来越多的关注,开辟了用非线性方法去噪的先河。
具体来说,小波能够去噪主要得益于小波变换有如下特点:(1)低熵性。
小波系数的稀疏分布,使图像变换后的熵降低。
意思是对信号(即图像)进行分解后,有更多小波基系数趋于0(噪声),而信号主要部分多集中于某些小波基,采用阈值去噪可以更好的保留原始信号。
(2)多分辨率特性。
由于采用了多分辨方法,所以可以非常好地刻画信号的非平稳性,如突变和断点等(例如0-1突变是傅里叶变化无法合理表示的),可以在不同分辨率下根据信号和噪声的分布来消除噪声。
(3)去相关性。
小波变换可对信号去相关,且噪声在变换后有白化趋势,所以小波域比时域更利于去噪。
(4)基函数选择灵活。
小波变换可灵活选择基函数,也可根据信号特点和去噪要求选择多带小波和小波包等(小波包对高频信号再次分解,可提高时频分辨率),对不同场合,选择不同小波基函数。
根据基于小波系数处理方式的不同,常见去噪方法可分为三类:(1)基于小波变换模极大值去噪(信号与噪声模极大值在小波变换下会呈现不同变化趋势)(2)基于相邻尺度小波系数相关性去噪(噪声在小波变换的各尺度间无明显相关性,信号则相反)(3)基于小波变换阈值去噪小波阈值去噪是一种简单而实用的方法,应用广泛,因此重点介绍。
阈值函数选择阈值处理函数分为软阈值和硬阈值,设w是小波系数的大小,wλ是施加阈值后小波系数大小,λ为阈值。
(1)硬阈值当小波系数的绝对值小于给定阈值时,令其为0,而大于阈值时,保持其不变,即:(2)软阈值当小波系数的绝对值小于给定阈值时,令其为0,大于阈值时,令其都减去阈值,即:如下图,分别是原始信号,硬阈值处理结果,软阈值处理结果。
一维信号去噪方法及matlab方法

一维信号去噪方法及matlab方法
一维信号去噪方法及MATLAB实现步骤如下:
一维信号去噪方法:
1. 小波变换:利用小波变换对信号进行多尺度分析,保留有用信号的小波系数,去除噪声的小波系数,最后重构信号。
2. 滤波器:设计合适的滤波器,使噪声信号经过滤波器后被滤除,保留有用信号。
常用的滤波器有中值滤波器、低通滤波器、高通滤波器等。
3. 统计方法:利用统计方法对信号进行概率统计,根据信号和噪声的不同统计特性进行去噪。
常用的统计方法有均值滤波、加权均值滤波、中位数滤波等。
4. 频域变换:将信号从时域变换到频域,利用信号和噪声在频域的不同特性进行去噪。
常用的频域变换方法有傅里叶变换、小波变换等。
MATLAB实现步骤:
1. 导入信号:使用MATLAB中的函数读取一维信号数据。
2. 预处理:对信号进行必要的预处理,如平滑处理、去除异常值等。
3. 去噪处理:根据选择的方法对信号进行去噪处理,如小波变换去噪、滤波器去噪、统计方法去噪或频域变换去噪等。
4. 后处理:对去噪后的信号进行必要的后处理,如数据归一化、插值等。
5. 显示结果:使用MATLAB中的绘图函数将原始信号、噪声信号和去噪后的信号进行可视化比较。
6. 保存数据:将去噪后的数据保存到文件中,方便后续分析。
需要注意的是,不同的一维信号去噪方法适用于不同类型的噪声和信号,应根据实际情况选择合适的方法。
同时,MATLAB提供了丰富的函数和工具箱,可以方便地实现各种一维信号去噪处理。
matlab去噪声方法

matlab去噪声方法MATLAB中去噪声的方法有很多,以下列举了一些常用的方法:1. 均值滤波:均值滤波是一种简单且有效的去噪声方法,它通过计算邻域内像素的平均值来减小噪声。
具体操作是创建一个与输入图像大小相同的零矩阵,然后遍历图像的每个像素,将邻域内的像素值求和,最后除以邻域内像素的数量,得到滤波后的像素值。
2. 中值滤波:中值滤波主要用于去除图像中的脉冲噪声和椒盐噪声。
该方法的核心思想是将图像中相邻像素的灰度值进行排序,然后取中间值作为滤波后的像素值。
3. 高斯滤波:高斯滤波是一种广泛应用于图像去噪的方法,它通过在图像上滑动一个高斯核函数来降低噪声。
高斯核函数的宽度决定了滤波的效果,宽度越大,去噪效果越明显,但同时也会导致图像变得模糊。
4. 双边滤波:双边滤波是一种基于邻域的滤波方法,它同时考虑了像素的空间距离和灰度差异。
通过在图像上滑动一个双边核函数,可以有效地去除噪声并保留图像的细节。
5. 基于小波变换的方法:小波变换可以将图像分解为不同尺度、方向和频率的子带,通过对子带的处理,可以有效地去除图像中的噪声。
常用的有小波分解、小波合成和小波去噪等方法。
6. 基于深度学习的方法:深度学习方法,如卷积神经网络(CNN)和循环神经网络(RNN),在图像去噪领域也取得了很好的效果。
通过训练神经网络,可以学习到图像的复杂特征,从而在去噪的同时保留图像的细节。
在MATLAB中实现这些方法,可以利用内置的图像处理函数或自行编写代码。
例如,使用imfilter函数实现均值滤波,使用im2double函数将图像转换为双精度值等。
同时,可以借助图像处理工具箱中的各种滤波器和图像读取、显示函数,如sobel、roberts、prewitt算子等,来实现特定的去噪效果。
基于MATLAB环境下的小波图像去噪

ZHANG n u n, ANG n - u Lt a XI Fe g h a
【 bt c】 I g enin as rb ni a poes gT et dt n eo igue h vrg rier A s at mae -o igi a l ipol mis n rcsi . h a ioa dn in sdteaeae na r d s s c sc e gl n r il s ol
( )Xx3 f) ( (d )
’
1 小波变换
1 1 基本 原理 .
与 时域 函数 对应 , 在频 域上则 有 :
( )=√a 一 (Z ) e O O () 4
在数学上 , 小波定义卫 队给定函数局部化的新 领域 , 波可 由一个 定义 在 有 限 区域 的 函数 ( 小 ) 来构造 , ( 称为母小波( o e w vl ) ) m t r ae t 或者叫 h e 做基本 小波。 一组小波基 函数 , { ( } 可以通 ) , 过缩 放 和平移基 本小 波 ( 来 生成 : )
,
J
( )= 2 ( 一 — 2 )
() 2
其 中, 为平移参数 , i 为缩放 因子, 函数 厂 ( ) 以小 波 ( )为 基 的 连 续 小 波 变 换 定 义 为 函 数 厂 ) ( 和 ( )的内积 :
小波变换 函数 matlab

小波变换函数 matlab小波变换是一种信号处理方法,可以将信号分解成不同尺度的频谱成分。
它在许多领域中得到广泛的应用,如图像处理、音频处理、压缩编码等。
在Matlab中,我们可以使用小波变换函数来实现对信号的分析和处理。
我们需要了解小波变换的基本原理。
小波变换利用一组基函数,即小波函数,将信号分解成不同频率和不同时间的成分。
小波函数具有局部性和多尺度性的特点,可以更好地描述非平稳信号。
与傅里叶变换相比,小波变换能够提供更加详细的时间和频率信息。
在Matlab中,可以使用wavelet函数进行小波变换。
首先,我们需要选择合适的小波基函数和尺度。
常用的小波函数有Daubechies、Haar、Symlets等,每种小波函数都有不同的特性。
在选择小波基函数时,需要根据信号的特点和需求进行选择。
然后,我们可以使用wavedec函数对信号进行小波分解。
wavedec 函数将信号分解成不同尺度的频谱成分,并返回每个尺度的系数和小波基函数。
通过调整分解的尺度,可以得到不同精度的频谱信息。
接下来,我们可以使用waverec函数对分解后的信号进行重构。
waverec函数将小波系数和小波基函数作为输入,将信号重构回原始信号。
通过调整重构的尺度,可以得到不同精度的信号重构结果。
除了信号的分解和重构,小波变换还可以用于信号的去噪和压缩编码。
通过对小波系数的处理,可以去除信号中的噪声成分,提高信号的质量。
同时,由于小波变换具有多尺度分析的能力,可以对信号进行压缩编码,减小信号的存储空间。
在Matlab中,除了wavelet函数外,还提供了丰富的小波变换工具箱。
这些工具箱包含了各种小波函数和小波变换算法,可以方便地进行信号的分析和处理。
同时,Matlab还提供了图形界面工具,可以通过可视化界面来进行小波变换的操作和参数调整。
总结起来,小波变换是一种重要的信号处理方法,在Matlab中有着丰富的函数和工具箱支持。
通过小波变换,我们可以分析信号的频谱成分,并进行信号的分解、重构、去噪和压缩编码等操作。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
matlab小波去噪函数
小波去噪是一种通过使用小波变换来减少图像或信号中噪声的技术。
在处理信号时,小波变换可以将信号分解成多个频带。
这些频带可以在不同尺度上进行分析,并且可以通过移除某些频带来提高信号的清晰度。
Matlab是一种流行的用于数学计算和数据可视化的软件。
Matlab 中有很多小波去噪函数,可以用于处理不同类型的信号和图像。
这些函数可以帮助用户快速准确地完成小波去噪的任务。
在Matlab中,最常用的小波去噪函数是wdenoise和wden。
这些函数都可以用于去除信号或图像中的噪声,并且可以通过设置参数来调整去噪的效果。
wdenoise函数可以对一维和二维信号进行去噪。
该函数使用离散小波变换来分解信号,并使用软阈值技术来减少噪声。
软阈值技术可以通过将小于某个阈值的系数设置为零来减少噪声。
这可以帮助保留信号中的重要信息,并去除噪声。
wden函数可以对一维信号进行去噪。
该函数使用小波变换和硬阈值技术来减少噪声。
硬阈值技术将小于某个阈值的系数设置为零,从而减少噪声。
与软阈值技术不同的是,硬阈值技术可能会导致信号中出现一些不连续的点。
因此,该技术更适用于信号中的高频噪声。
除了上述函数之外,Matlab中还有许多其他小波去噪函数,例如wpdencmp和modwpt。
这些函数可以帮助用户根据不同的需求进行去噪,并且可以通过设置参数来调整去噪的效果。
在使用小波去噪函数进行处理之前,用户需要了解信号或图像的特征,例如信号的频率和振幅,以及图像的亮度和对比度。
这可以帮助用户选择合适的小波去噪函数,并设置合适的参数来最大程度地减少噪声,同时保留信号或图像中的重要信息。
Matlab提供了许多小波去噪函数,可以帮助用户快速准确地处理信号和图像中的噪声。
在使用这些函数进行处理之前,用户需要了解信号或图像的特征,并选择合适的函数和参数来实现最佳的去噪效果。
