二年级奥数 一笔画PPT
小学奥数之一笔画
小学奥数之一笔画
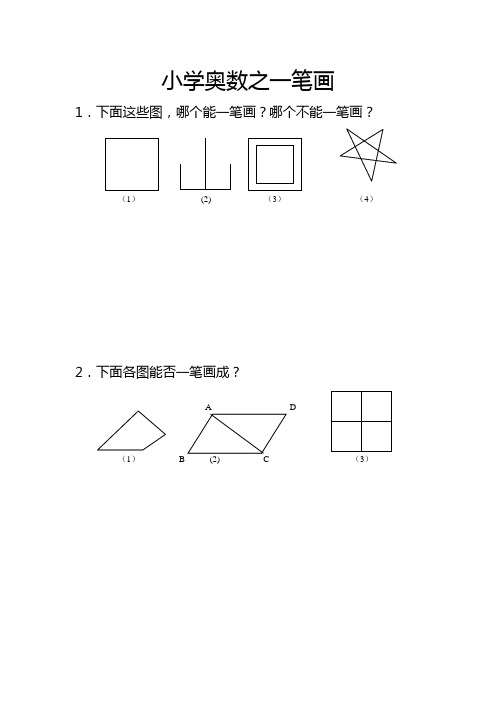
1.下面这些图,哪个能一笔画?哪个不能一笔画?
2.下面各图能否一笔画成?
(1) (2) (3)
(4)
(1) (2)
(
3) D
3.下面和图形,哪些能一笔画?哪些不能一笔画?
4.下页图(1),至少要画几笔才能画成?请你给出一种画法。
5.小丁是一名刚刚参加工作的邮递员,他将他所要走的街道画成地图(如下图),打算设计一种最好的方法,使得自
己每天不重复的走遍每一条街。
小丁动脑筋想了想,很快就
D A(
G
F D
6 科学家用小白鼠做实验,试图让它偿重复的穿过右图中每一个相邻的房间。
小白鼠由A出发。
小朋友你能很快就看出小白鼠所应走的路线吗?并请你绘出它走的路线。
7.一笔画出下列图形。
8.下列图形,至少几笔画出?
9.一只蜗牛由A 点出发,不重复的爬过每一个小格,评估你绘出一条路线。
10.一只蚂蚁由A 点出发,到达B 点,必须不重复的经过每
A A
B。
小学奥数知识讲解-一笔画问题

第一讲一笔画问题小朋友们,你们能把下面的图形一笔画出来吗?如果用笔在纸上连续不断又不重复,一笔画成某种图形,这种图形就叫一笔画。
那么是不是所有的图形都能一笔画成呢?这一讲我们就一起来学习一笔画的规律。
典型例题例【 1】下面这些图形,哪个能一笔画?哪个不能一笔画?( 1)(2)(3)(4)分析图(1)一笔画出,可以从图中任意一点开始画该图,画到同一点结束。
经过尝试后,可以发现图(2)不能一笔画出。
图(3)不是连通的,显然也不能一笔画出。
图(4)也可以一笔画出,且从任何一点出发都可以。
通过观察,我们可以发现一个几何图形中和一点相连通的线的条数不同。
由一点发出有偶数条线,那么这个点叫做偶点。
相应的,由一点出发有奇数条数,则这个点叫做奇点。
再看图( 1)、(4),其中每一点都是偶点,都可以一笔画,且可以从任意一点画起。
而图(2)有 4 个奇点, 2 个偶点,不能一笔画成。
这样我们发现,一个图形能否一笔画和这个图形奇点,偶点的个数有某种联系,到底存在什么样的关系呢,我们再看一个例题。
例【 2】下面各图能否一笔画成?(1)(2)(3)分析图(1)从任意一点出都可以一笔画成,因为它的每一个点都是与两条线相连的偶点。
关于图(2),经过反复试验,也可找到画法:由 A B C AD C。
图中 B、D 为偶点, A、C 为奇点,即图中有两个奇点,两个偶点。
要想一笔画,需从奇点出发,回到奇点。
经过尝试,图( 3)无法一笔画成,而图中有 4 个奇点, 5 个偶点。
解图( 1)、(2)可以一笔画。
这样我们可以发现能否一笔画和奇点、偶点的数目有着紧密的关系。
如果图形只有偶点,可以以任意一点为起点,一笔画出。
如果只有两个奇点,也可以一笔画出,但必须从奇点出发,由另一点结束。
如果图形的奇点个数超过两个,则图形不能一笔画出。
例【 3】下面的图形,哪些能一笔画出?哪些不能一笔画出?分析图( 1)有两个奇点,两个偶点,可以一笔画,须由 A 开始或由 B 开始到 B 结束或到 A 结束。
小学数学一笔画课件2021推选

以下哪些图形能一笔画出来,哪些不能?
根据今天学习知识,先判断以下图
形能不能一笔画成?再想一想该从 根据今天学习知识,先判断以下图形能不能一笔画成?再想一想该从哪里开始画?最后再动手画画看。 哪里开始画?最后再动手画画看。 画时必须从一个单数点为起点,以另一单数点为终点。
以下哪些图形能一笔画出来,哪些不能? 一个图形能否一笔画成,关键在于图 中单数点的多少。 以下哪些图形能一笔画出来,哪些不能? 一个图形能否一笔画成,关键在于图 中单数点的多少。 画时必须从一个单数点为起点,以另一单数点为终点。 根据今天学习知识,先判断以下图形能不能一笔画成?再想一想该从哪里开始画?最后再动手画画看。 两条相交的线处都有一个交点。 “一笔画〞是指笔不离开纸,而且每条线都只画一次不准重复而画成的图形。 〔1〕但凡图形中没有单数点的一定可以一笔画成。 一个图形能否一笔画成,关键在于图 中单数点的多少。 〔1〕从这点出发的线的数目是双数的,叫双数点〔偶点〕。 数一数以下图形各有几个交点? 数一数以下图形各有几个交点?
甲乙两个邮递员去送信,两人以同样的速 度走遍所有的街道,甲从A点出发,乙从 B点出发,最后都回到邮局〔C〕。如果 要选择最短的线路,谁先回到邮局?
邮局
乙 甲
谢谢观看
〔2〕但凡图形中只有一个或者两个单数点,一定可以一笔画成。 根据今天学习知识,先判断以下图形能不能一笔画成?再想一想该从哪里开始画?最后再动手画画看。 根据今天学习知识,先判断以下图形能不能一笔画成?再想一想该从哪里开始画?最后再动手画画看。
〔 2 〕 从 这 点 出 发 的 线 的 数 目 数一数以下图形各有几个交点?
小学数学一笔画课件
“一笔画〞是指笔不 离开纸,而且每条线 都只画一次不准重复 而画成的图形。
二年级春季数学奥数班第1讲 一笔画

一笔画月日姓名【知识要点】1.概念:一笔画是指笔不离开纸,而且每条线都只画一次不准重复而画成的图形。
2.分类:图中的点可分两大类:(1)双数点:从这点出发的线的数目是双数的,叫双数点。
(2)单数点:从这点出发的线的数目是单数的,叫单数点。
3.规律:一个图形能否一笔画成,关键在于图中单数点的多少。
(1)凡是图形中没有单数点的一定可以一笔画成。
(2)凡是图形中只有两个单数点,一定可以一笔画成,画时必须从一个单数点为起点,最后以另一单数点为终点。
(3)凡是图形中单数点的个数多于两个时,此图肯定是不能一笔画成。
【典型例题】例1.判断下面图形中哪些点是单数点,哪些点是双数点。
例2.下列图形中各有几个单数点?能一笔画成吗?(1)(2)(3)(4)例3.如图,能不能一笔画成?如果能,应该怎样画?例4.将下图去掉最少的线改成一笔画图形。
随堂小测姓名成绩1.判断下面图形哪些是单数点,哪些是双数点。
2. 下列图形中各有几个单数点?能一笔画成吗?3. 一个邮递员投递信件要走的街道如下左图,为节约时间,他想自己设计一条线路,可以不重复的走遍每一条街道,你能帮帮他吗?4. 一只蚂蚁要想不重复的爬遍每一条线路,应从哪里出发,到哪里结束?(3)AC E(1)(2)(3)(4)5. 将下图加上最少的线改成一笔画的图形。
【知识拓展】1.为迎接2008年奥运会在北京召开,你能一笔画出奥运会的五环图案吗?2.你能用一笔画成4条线段把下图的9朵小花都连起来吗?课后作业姓名成绩1.判断下面图形中哪些点是单数点哪些点是双数点。
2.判断下面图形能不能一笔画成。
(1)(2)B3.下图能否一笔画成?如果能,应怎样画?4.如图,是一个公园的平面图,请你设计好入口、出口,并给出一种游玩路线,要求走遍每一条路且不重复。
5.如图,是一个名画展厅的平面图,要使参观者不重复地走遍每一条画廊,问:出口、入口应设在哪里?家长签名:【课外知识链接】七桥问题著名古典数学问题之一。
奇妙一笔画精品PPT课件

例1 下图中,哪些是奇点,哪些是偶点?
一笔画
D、H、J、O
A、B、C、E F、G、I、
一笔画
E、K
A、B、C、D F、G、I、H
答:能。
答:不能。 一笔画
答:能。
答:能。
答:不能。 一笔画
答:不能。
例4 能否从入口进入不重复地穿过所有门。如果可 以,画出路线。如果不行,关闭哪扇门就可以?
You Know, The More Powerful You Will Be
结束语
当你尽了自己的最大努力时,失败也是伟大的, 所以不要放弃,坚持就是正确的。
When You Do Your Best, Failure Is Great, So Don'T Give Up, Stick To The End 演讲人:XXXXXX 时 间:XX年XX月XX日
一笔
一笔画
一笔画
连通
一笔画
一笔画
聪明的 发现:
能不能一笔画只要观察图形的
就能知道!
奇点
连线
… 1, 3, 5 , …
偶点
连线
… 2, 4, 6 , …
奇点 偶点
不能成双成对 能成双成对
能
奇点
不能
奇点
一笔画
奇点
奇点 0 2
没有奇点
从任何地方开始都可以一笔画
2个奇点
从一个奇点开始,另一个奇点结束,
例4 能否从入口进入不重复地穿过所有门。如果可 以,画出路线。如果不行,关闭哪扇门就可以?
例5 “七桥问题”:游人要一次不重复地走过所 有的桥,应该怎么走?
练习5 “七桥问题”:游人要一次不重复地走过 所有的桥,应该怎么走?
《一笔画》课件

图5
图2
图4
图6
下图是一个公园的平面图,要使游 人走遍每一条路不重复,出口和入 口应设在哪儿?
甲乙两个邮递员去送信,两人以同样的速 度走遍所有的街道,甲从A点出发,乙从 B点出发,最后都回到邮局(C)。如果 要选择最短的线路,谁先回到邮局?
乙
邮局
甲
主页
一笔画问题
小岛A
小岛B
主页
(Leonhard Euler 公元1707-1783年) 欧拉
判断下列图形能否一笔画
不连通的图形不能一笔画
图1 图2 图3
连通的图形有可能一笔画
图4 图5
观察下列图形,完成统计表
可以一笔画的图形
图形序号 奇点个数 偶点个数
不能一笔画的图形
图形序号 奇点个数 偶点个数
图1
图2
图3
图4
图5
图6
图7
图8
不连通的图形不能一笔画 奇点个数超过两个的连通图 连通的图 形不能一笔画 形有可能 一笔画 全都是偶点的连 画时以任一点为起点, 通图可以一笔画 最后仍回到该点 有两个奇点的连 画时以一个奇点为起点, 通图可以一笔画 另一个奇点为终点
你能笔尖不离纸,一笔画出图中 的每个图形吗?
小学二年级奥数下学期一笔画问题教
第五讲一笔画问题一天,小明做完作业正在休息,收音机中播放着轻松、悦耳的音乐.他拿了支笔,信手在纸上写了“中”、“日”、“田”几个字.突然,他脑子里闪出一个念头,这几个字都能一笔写出来吗?他试着写了写,“中”和“日”可以一笔写成(没有重复的笔划),但写到“田”字,试来试去也没有成功.下面是他写的字样.(见下图)这可真有意思!由此他又联想到一些简单的图形,哪个能一笔画成,哪个不能一笔画成呢?下面是他试着画的图样.(见下图)经过反复试画,小明得到了初步结论:图中的(1)、(3)、(5)能一笔画成;(2)、(4)、(6)不能一笔画成.真奇怪!小明发现,简单的笔画少的图不一定能一笔画得出来.而复杂的笔画多的图有时反倒能够一笔画出来,这其中隐藏着什么奥秘呢?小明进一步又提出了如下问题:如果说一个图形是否能一笔画出不决定于图的复杂程度,那么这事又决定于什么呢?能不能找到一条判定法则,依据这条法则,对于一个图形,不论复杂与否,也不用试画,就能知道是不是能一笔画成?先从最简单的图形进行考察.一些平面图形是由点和线构成的.这里所说的“线”,可以是直线段,也可以是一段曲线.而且为了明显起见,图中所有线的端点或是几条线的交点都用较大的黑点“●”表示出来了.首先不难发现,每个图中的每一个点都有线与它相连;有的点与一条线相连,有的点与两条线相连,有的点与3条线相连等等.其次从前面的试画过程中已经发现,一个图能否一笔画成不在于图形是否复杂,也就是说不在于这个图包含多少个点和多少条线,而在于点和线的连接情况如何——一个点在图中究竟和几条线相连.看来,这是需要仔细考察的.第一组(见下图)(1)两个点,一条线.每个点都只与一条线相连.(2)三个点.两个端点都只与一条线相连,中间点与两条线连.第一组的两个图都能一笔画出来.(但注意第(2)个图必须从一个端点画起)第二组(见下图)(1)五个点,五条线.A点与一条线相连,B点与三条线相连,其他的点都各与两条线相连.(2)六个点,七条线.(“日”字图)A点与B点各与三条线相连,其他点都各与两条线相连.第二组的两个图也都能一笔画出来,如箭头所示那样画.即起点必需是A点(或B点),而终点则定是B点(或A点).第三组(见下图)(1)四个点,三条线.三个端点各与一条线相连,中间点与三条线相连.(2)四个点,六条线.每个点都与三条线相连.(3)五个点,八条线.点O与四条线相连,其他四个顶点各与三条线相连.第三组的三个图形都不能一笔画出来.第四组(见下图)(1)这个图通常叫五角星.五个角的顶点各与两条线相连,其他各点都各与四条线相连.(2)由一个圆及一个内接三角形构成.三个交点,每个点都与四条线相连(这四条线是两条线段和两条弧线).(3)一个正方形和一个内切圆构成.正方形的四个顶点各与两条线相连,四个交点各与四条线相连.(四条线是两条线段和两条弧线).第四组的三个图虽然比较复杂,但每一个图都可以一笔画成,而且画的时候从任何一点开始画都可以.第五组(见下图)(1)这是“品”字图形,它由三个正方形构成,它们之间没有线相连.(2)这是古代的钱币图形,它是由一个圆形和中间的正方形方孔组成.圆和正方形之间没有线相连.第五组的两个图形叫不连通图,显然不能一笔把这样的不连通图画出来.进行总结、归纳,看能否找出可以一笔画成的图形的共同特点,为方便起见,把点分为两种,并分别定名:把和一条、三条、五条等奇数条线相连的点叫做奇点;把和两条、四条、六条等偶数条线相连的点叫偶点,这样图中的要么是奇点,要么是偶点.提出猜想:一个图能不能一笔画成可能与它包含的奇点个数有关,对此列表详查:从此表来看,猜想是对的.下面试提出几点初步结论:①不连通的图形必定不能一笔画;能够一笔画成的图形必定是连通图形.②有0个奇点(即全部是偶点)的连通图能够一笔画成.(画时可以任一点为起点,最后又将回到该点).③只有两个奇点的连通图也能一笔画成(画时必须以一个奇点为起点,而另一个奇点为终点);④奇点个数超过两个的连通图形不能一笔画成.最后,综合成一条判定法则:有0个或2个奇点的连通图能够一笔画成,否则不能一笔画成.能够一笔画成的图形,叫做“一笔画”.用这条判定法则看一个图形是不是一笔画时,只要找出这个图形的奇点的个数来就能行了,根本不必用笔试着画来画去.看看下面的图可能会加深你对这条法则的理解.从画图的过程来看:笔总是先从起点出发,然后进入下一个点,再出去,然后再进出另外一些点,一直到最后进入终点不再出来为止.由此可见:①笔经过的中间各点是有进有出的,若经过一次,该点就与两条线相连,若经过两次则就与四条线相连等等,所以中间点必为偶点.②再看起点和终点,可分为两种情况:如果笔无重复地画完整个图形时最后回到起点,终点和起点就重合了,那么这个重合点必成为偶点,这样一来整个图形的所有点必将都是偶点,或者说有0个奇点;如果笔画完整个图形时最后回不到起点,就是终点和起点不重合,那么起点和终点必定都是奇点,因而该图必有2个奇点,可见有0个或2个奇点的连通图能够一笔画成.。
一笔画(二年级)打印版
二年级暑期奥数班第一讲:一笔画【专题简析】1.概念:一笔画是指笔不离开纸,而且每条线都只画一次不准重复而画成的图形。
2.图中的点可分两大类:(1)双数点:从这点出发的线的数目是双数的,叫双数点。
(2)单数点:从这点出发的线的数目是单数的,叫单数点。
3.规律---- 一个图形能否一笔画成,关键在于图中单数点的多少。
(1)凡是图形中没有单数点的一定可以一笔画成。
(2)凡是图形中只有两个单数点,一定可以一笔画成,画时必须从一个单数点为起点,最后以另一单数点为终点。
(3)凡是图形中单数点的个数多于两个时,此图肯定是不能一笔画成。
【题目】1 判断下面图形中哪些点是单数点哪些点是双数点。
单数点()()()()()()()双数点()()()()()()()A D AA DEBC BCCB 单数点()()()双数点()()()2 下列图形中各有几个单数点?能一笔画成吗?1双数点()()()单数点()()()()双数点()()()()2 判断下面图形能不能一笔画成?如果能,应该怎样画?AB C单数点()()()双数点()()()A F AAB DEBC DCB C单数点()()()双数点()()()单数点()()()()双数点()()()()2单数点()()()()双数点()()()()单数点()()()双数点()()()单数点()()()双数点()()()单数点()()()双数点()()()【例1】我们把一个图形上与偶数条线相连的点叫做偶点,与奇数条线相连的点叫做奇点.下图中,哪些点是偶点?哪些点是奇点?【例2】下面图形能不能一笔画成?若果能,应该怎样画?【例3】下面的图形,哪些能一笔画出?哪些不能一笔画出?【例4】下图中不能一笔画成,请你在下图中添加最少的线段,将其改成一笔画的图形,并画出路线图.【例5】下图中的线段表示小路,请你仔细观察,认真思考,能够不重复的爬遍小路的是甲蚂蚁还是乙蚂蚁?该怎样爬?【例6】下图是儿童乐园的道路平面图,要使游客走遍每条路并且不重复,那么出、入口应设在哪里?【例7】邮递员叔叔向11个地点送信一次信,不走重复路,怎样走最合适?【例8】观察下面的图,看各至少用几笔画成?【例9】判断下列图形能否一笔画.若能,请给出一种画法;若不能,请加一条线或去一条线,将其改成可一笔画的图形.A H GG H A BIB J FFIAE F G HBK L ECC E CD图a 图b DD图c【例10】18世纪的哥尼斯堡城是一座美丽的城市,在这座城市中有一条布勒格尔河横贯城区,这条河有两条支流在城市中心汇合,汇合处有一座小岛 A 和一座半岛D,人们在这里建了一座公园,公园中有七座桥把河两岸和两个小岛连接起来( 如图a) .如果游人要一次走过这七座桥,而且对每座桥只许走一次,问如何走才能成功?5。
一笔画和七桥问题ppt课件
就转化成了 “一笔画问题”
• 所谓图的一笔画,指的就是:从图的一
点出发,笔不离纸,遍历每条边恰好一 次,即每条边都只画一次,不准重复.
B
BA
A
C
A→B→C→A
A→头部→翅膀→
尾部→翅膀→嘴B
5
1.起点;2、终点 ;3、过路点;
4.奇点:和某个点连接的线的条数是奇数;
5.偶点:B和某个点连接的线的条数是偶数;
其中的一个奇点,终点一定是另一 个奇点。
8
D
C
A→B→C→D→A→C
A
B
起点→过路点→…→过路点→终点
过路点都是偶点
1、起点和终点重合时,这一点 也为偶点,故奇点个数为0;
2、起点和终点不重合时,这两 点都为奇点,故奇点个数为2。
9
A
1.“七桥问题”如图所示,此图
D
能一笔画出来吗?为什么?
C
答:因为此图奇点的个数是4,
实验与探究
七桥问题与一笔画
1
能不能既不 重复又不遗 漏地一次相 继走遍这七 七 哥 座桥? 桥尼 问斯 题堡
2
能不能既不 重复又不遗 漏地一次相 继走遍这七
座桥?
①
⑥
②
⑤
⑦
③ ④
3
• 把河的两岸、两个小岛看成四个点 • 把七座桥看成是七条线 • 转化成数学模型后如图所示 A
D C
B 4
• 数学模型建立好之后,那么“七桥问题” 也
所以不能一笔画出来。
2.下列图形能不能用一笔画出来? B
为什么?
E
A
A
D
F
D B FC
ABC C D E
B
因奇点的个数是0 因奇点的个数是0 因奇点的个数是2
小学二年级奥数 第14讲:有趣的一笔画
一、基本概念
1.一笔画要求
⑴笔不离纸
⑵每条线只画一次,不重复有趣的一笔画
【例1】(★★)
你能试着用一笔把下列图形画出来吗?如果可以,说说你是怎样画的?
【拓展】(★★)
【例2】(★★) 【例3】(★★★)
下列图形能一笔画成吗?为什么?并试着画一画。
判断下列各图能否一笔画出?
【拓展】(★★★)
1
【例4】(★★★) 【例5】(★★★★)一笔画的实际应用下面的图形都不能一笔画成,你能否在图中添上一条线段,使它能一
笔画成。
1.我们的奥运五环能否一笔画呢?
2.著名的“七桥问题”
【拓展】(★★★★)
请你判断下图能否一笔画?若不能,你能用什么方法把它改成一笔画?
【例6】(★★★★) 【本讲总结】
下图是我们公园的平面图。
要使游客走遍每条路而不重复,出入口应设在哪里?可以怎样走?一、基本概念三、一笔画的实际应用
1.一笔画要求转化成:点线图
⑴笔不离纸四、多笔画转化为一笔画
⑵每条线只画一次,不重复宗旨:减少奇点的个数
2.奇点、偶点方法:添线、去线
二、一笔画判断(在两个奇点之间哦!)
1.必须是连通图
2.奇点=0
哪儿进,哪儿出
奇点=2
起点:一个奇点
终点:另一个奇点
2。
