2018届中考数学复习第17讲几何初步及平行线相交线导学18
中考数学几何初步及平行线、相交线复习.docx
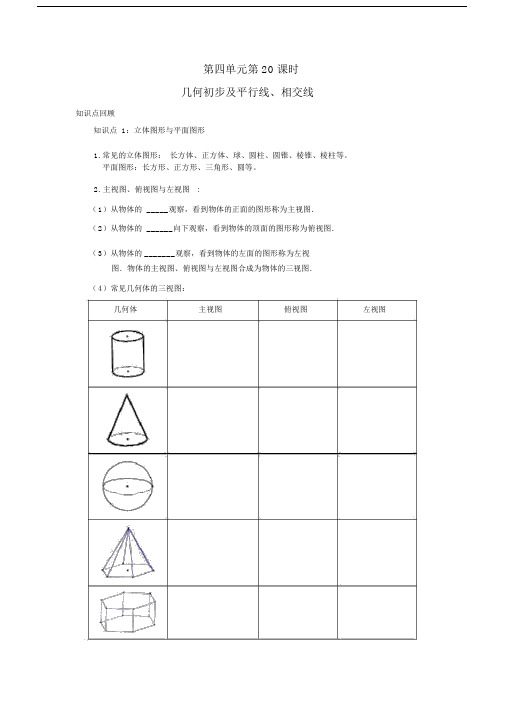
第四单元第 20 课时几何初步及平行线、相交线知识点回顾知识点 1:立体图形与平面图形1.常见的立体图形:长方体、正方体、球、圆柱、圆锥、棱锥、棱柱等。
平面图形:长方形、正方形、三角形、圆等。
2.主视图、俯视图与左视图 :(1)从物体的 _____观察,看到物体的正面的图形称为主视图.(2)从物体的 ______向下观察,看到物体的顶面的图形称为俯视图.(3)从物体的 _______观察,看到物体的左面的图形称为左视图.物体的主视图、俯视图与左视图合成为物体的三视图.(4)常见几何体的三视图:几何体主视图俯视图左视图3.几种常见几何体的展开图:1.圆柱展开图:上、下底面为________,侧面是 ________ ,长方形的长是圆柱的底面周长,宽是圆柱的高。
2.圆锥展开图:底面是_______,侧面是 ________,扇形的弧长是底面圆的周长。
3.棱柱展开图:上、下底面是_____________ ,侧面都是 _________。
4.棱锥展开图:底面是__________,侧面都是 ________,这些三角形的公共顶点就是棱锥的顶点。
4.正方体的表面展开图 :把正方体的表面展开成平面图形后,有很多种形状,如果将经过平移、旋转等变化后可以重合的两个图形看成是同一图形,那么正方体的表面展开图共有11 种不同的情况。
我们可以将则11 种图形分类:( 1)“一·四·一”型,中间一行 4 个作侧面,两边各 1 个分别作上下底面,?共有 6种.如图( 1)——( 6).( 2)“二·三·一” (或一·三·二)型,中间 3 个作侧面,上(或下)边2?个那行,相连的正方形作底面,不相连的再下折作另一个侧面,共 3 种.如图( 7)——( 9).( 3)“二·二·二”型,成阶梯状.如图(10).( 4)“三·三”型,两行只能有 1 个正方形相连.如图(11).(1)( 2)( 3)( 5)( 4)( 6)(7)(8)(9)(10)(11)例 1、( 2009 年内蒙古包头)将一个正方体沿某些棱展开后,能够得到的平面图形是()A.B.C.D.【解析】本题考查图形的展开与折叠中,正方体的常见的十余种展开图有关内容,可将这四个图折叠后,看能否组成正方形,显然只有 C 符合要求。
2018年安徽中考数学复习课件5.1 几何初步及相交线、平行线(安徽)

【解析】此题考查了邻补角的定义. 【答案】D
【例2】已知:岛P位于岛Q的正西方,由岛P,Q分别测得船R位于 南偏东30°和南偏西45°方向上,符合条件的示意图是 ( )
【解析】选项A中船R位于岛P的南偏东60°方向上;选项B中船R 位于岛P的北偏东60°方向上,位于岛Q的北偏西45°方向上;选 项C中船R位于岛P的南偏东45°方向上,位于岛Q的南偏西30°方 向上;选项D中船R位于岛P的南偏东30°方向上,位于岛Q的南偏 西方向上. 【答案】D
线段、角、相 交线与平行线
角
度量单位:度、分、秒
大小比较 角平分线的概念 平行
对顶角 邻补角 性质:垂线段最短 点到直线的距离:垂线段长度
角 相交 垂线
5.1.1 三种基本图形——直线、射线、线段
(1)直线公理:经过两点有且只有一条直线. (2)射线性质:射线只能向一方无限延伸,无法度量长度. (3)线段公理:两点之间,线段最短. 点拨:两个点之间连线有很多条,但只有线段最短,这条线段的长 度,就叫做这两点之间的距离.
【例3】(2017年桂林)如图,直线a,b被直线所截,下列条件能 判断a∥b的是 ( )
A.∠1=∠2 C.∠3+∠4=180°
B.∠1=∠4 D.∠2=30°,∠4=35°
【解析】此题考查了平行线的判定,∵∠1=∠4 ,∴a∥b(同位角 相等两直线平行).
【例4】如图,AB∥CD,DA⊥AC,垂足为A,若∠ADC=35°,则 ∠1的度数为 ( ) A.65° B.55° C.45° D.35°
5.1.4 对顶角
(1)邻补角:有一条公共边,它们的另一边互为反向延长线,具 有这种关系的两个角互为邻补角. (2)一个角的两边分别是另一个角的两边的反向延长线,这两个 角则叫做对顶角. (3)对顶角的性质:对顶角相等.
北京2018年中考数学复习考题训练(17)几何初步及平行线、相交线

考题训练(十七)几何初步及平行线、相交线A组·真题演练1.[2017·北京]如图J17-1所示,点P到直线l的距离是()A.线段PA的长度B.线段PB的长度C.线段PC的长度D.线段PD的长度图J17-1图J17-22.[2015·北京]如图J17-2,直线l1,l2,l3交于一点,直线l4∥l1.若∠1=124°,∠2=88°,则∠3的度数为() A.26°B.36°C.46°D.56°B组·模拟训练1.[2017·通州一模]如图J17-3所示,用直尺度量线段AB,可以读出AB的长度为()图J17-3A.6 cm B.7 cm C.9 cm D.10 cm2.[2016·东城一模]如图J17-4,直线AB∥CD,BE平分∠ABC,交CD于点D,∠CDB=30°,那么∠C的度数为()A.150°B.130°C.120°D.100°图J17-4图J17-53.[2016·东城一模]如图J17-5,将一块三角尺的直角顶点放在直尺的一边上,当∠2=38°时,∠1=() A.52°B.38°C.42°D.62°4.[2017·门头沟一模]一个三角板(含30°、60°角)和一把直尺摆放位置如图J17-6所示,直尺与三角板的一角相交于点A,一边与三角板的两条直角边分别相交于点D、点E,且CD=CE,点F在直尺的另一边上,那么∠BAF 的大小为()图J17-6A.10°B.15°C.20°D.30°C组·自测训练一、选择题1.把一条弯曲的公路改成直道,可以缩短路程.用几何知识解释其道理正确的是()A.两点确定一条直线B.垂线段最短C.两点之间线段最短D.三角形两边之和大于第三边2.[2017·顺义二模]能与60°的角互余的角是()图J17-73.[2017·石景山一模]如图J17-8,直线a∥b,直线l与a,b分别交于A,B两点,过点B作BC⊥AB交直线a于点C,若∠1=65°,则∠2的度数为()A.25°B.35°C.65°D.115°图J17-84.[2017·顺义一模]如图J17-9,AB∥CD,E是BC延长线上一点,若∠B=50°,∠D=20°,则∠E的度数为()A.20°B.30°C.40°D.50°5.[2017·西城二模]如图J17-10是由射线AB,BC,CD,DE,EA组成的平面图形,若∠1+∠2+∠3+∠4=225°,ED∥AB,则∠1的度数为()图J17-10A.55°B.45°C.35°D.25°6.如图J17-11,已知∠MON=60°,OP是∠MON的平分线,点A是OP上一点,过点A作ON的平行线交OM于点B,AB=4.则直线AB与ON之间的距离是()图J17-11A. 3 B.2 C.2 3 D.47.[2016·东城一模]如图J17-12,在△ABC中,AC<BC,如果用尺规作图的方法在BC上确定一点P,使PA +PC=BC,那么符合要求的作图痕迹是()图J17-12二、填空题8.[2017·西城二模]如图J17-13,在长方体中,所有与棱AB平行的棱是________.图J17-13图J17-149.如图J17-14,已知AB∥CD,∠1=130°,则∠2=________.10.如图J17-15,直线l1∥l2,∠α=∠β,∠1=40°,则∠2=________°.图J17-1511.两个角的两边分别平行,若其中一个角为50°,则另一个角为________.三、解答题12.[2017·顺义二模]如图J17-16,△ABC中,点D在AB的延长线上,BE平分∠CBD,BE∥AC.求证:AB =BC.图J17-1613.如图J17-17,直线AC∥BD,连接AB,直线AC,BD及线段AB把平面分成①,②,③,④四个部分,规定:线上各点不属于任何部分.当动点P落在某个部分时,连接PA,PB,构成∠PAC,∠APB,∠PBD三个角.(提示:有公共端点的两条重合的射线所组成的角是0°角)(1)当动点P落在第①部分时,求证:∠APB=∠PAC+∠PBD.(2)当动点P落在第②部分时,∠APB=∠PAC+∠PBD是否成立?(直接回答成立或不成立)图J17-17参考答案|真题演练|1.B2.B|模拟训练|1.B2.C3.A4.B|自测训练|1.C2.A3.A4.B5.B6.C7.C8.DC,EF,HM9.50°10.140[解析] 如图,延长AB与直线l2相交于点C,∵直线l1∥l2,∴∠3=∠1=40°,∵∠α=∠β,∴AC∥DE,∴∠3+∠2=180°,∴∠2=140°,故填140.11.50°或130°[解析] 此题考查了平行线的性质与邻补角的定义.解此题的关键是掌握两直线平行,同旁内角互补定理的应用与数形结合思想的应用.具体过程如下:如图,∠2与∠3的两边与∠1的两边分别平行,即AB∥CD,AD∥BC,∠1=50°,∴∠1+∠A=180°,∠3+∠A=180°,∴∠3=∠1=50°.∵∠2+∠3=180°,∴∠2=130°.故另一个角是50°或130°.12.证明:∵BE平分∠CBD,∴∠1=∠2.∵BE∥AC,∴∠1=∠A,∠2=∠C.∴∠A=∠C.∴AB=BC.13.解:(1)证明:如图,过点P作FP∥AC.∴∠PAC =∠APF.∵AC∥BD,∴FP∥BD,∴∠FPB=∠PBD,∴∠APB=∠APF+∠FPB=∠PAC+∠PBD.(2)不成立.。
中考基础复习查漏补缺第一轮第17讲几何初步及平行线相交线24[可修改版ppt]
![中考基础复习查漏补缺第一轮第17讲几何初步及平行线相交线24[可修改版ppt]](https://img.taocdn.com/s3/m/086d49a8b84ae45c3a358c47.png)
( C)
A.38° C.142°
图 17-1
B.104° D.144°
第17讲┃ 归类示例
[解析] 根据对顶角相等求出∠AOC 的度数,再根据角平 分线的定义求出∠AOM 的度数,然后根据平角等于 180°列 式计算.
∵∠BOD=76°, ∴∠AOC=∠BOD=76°. ∵射线 OM 平分∠AOC, ∴∠AOM=12∠AOC=12×76°=38°, ∴∠BOM=180°-∠AOM=180°-38°=142°.
中考基础复习查漏 补缺第一轮第17讲 几何初步及平行线
相交线24
第17讲┃ 考点聚焦
考点聚焦
考点1 三种基本图形——直线、射线、线段
直线公理 线段公理 两点间的
距离
经过两点有且只有____一____条直线 两点之间,__线__段____最短
连接两点间的线段的__长__度____,叫做这两点 间的距离
大90°
第17讲┃ 考点聚焦 考点5 邻补角、对顶角
邻补角 定义
若两角有一条公共边,它们的另一边互 为反向延长线,具有这种关系的两个角,
互为邻补角
对 顶
定义
两条直线相交所形成的角中,没有公共 边的两个角互为对顶角
角 性质
对顶角相等
第17讲┃ 考点聚焦
考点6
“三线八角”的概念
同位 角
如果两个角在截线l的同侧,且在被截直 线a、b的同一方向叫做同位角(位置相 同).∠1和∠5,∠4和∠8,∠2和∠6,
► 类型之三 度、分、秒的计算 命题角度: 1.度、分、秒的换算; 2.度、分、秒的计算.
[2011·芜湖] 一个角的补角是36°35′,这个角的 度数是_1_4_3_°__2_5_′.
初三一轮复习系列---第18课时几何初步与相交线平行线

第18课时几何初步与相交线、平行线一、考点:生活中常见的几何体,直线、射线、线段, 角的有关概念及性质,相交线, 垂线的性质与判定,平行线的性质与判定。
二、教学目标:1.点、线、面、角(1)通过实物和具体模型,了解从物体抽象出来的几何体、平面、直线和点等。
(2)会比较线段的大小,理解线段的和、差,以及线段中点的意义。
(3)掌握基本事实:两点确定一条直线。
(4)掌握基本事实:两点间直线段最短。
(5)理解两点间距离的意义,能度量两点之间的距离。
(6)理解角的概念,能比较角的大小。
(7)认识度、分、秒,会对度、分、秒进行简单的换算,并计算角的和、差。
2.相交线与平行线(1)理解对顶角、余角、补角等概念,探索并掌握对顶角相等、同角(等角)的余角相等,同角(等角)的补角相等的性质。
(2)理解垂线、垂线段等概念,能用三角尺或量角器过一点画已知直线的垂线。
(3)理解点到直线的距离的意义,能度量点到直线的距离。
(4)掌握基本事实:过一点有且只有一条直线与这条直线垂直。
(5)理解平行线概念;掌握基本事实:两条直线被第三条直线所截,如果同位角相等,那么两直线平行。
(6)掌握基本事实:过直线外一点有且只有一条直线与这条直线平行。
(7)掌握平行线的性质定理:两条平行直线被第三条直线所截,同位角相等;了解该定理的证明。
(8)能用三角尺和直尺过已知直线外一点画这条直线的平行线。
(9)探索并证明平行线的判定定理:两条直线被第三条直线所截,如果内错角相等(或同旁内角互补),那么两直线平行;探索并证明平行线的性质定理:两条平行直线被第三条直线所截,内错角相等(或同旁内角互补)。
(10)了解平行于同一条直线的两条直线平行。
三、教学重难点:重点:线段与角的有关计算,平行线的性质与判定。
难点:点到直线的距离。
四、教学过程:(一)基础诊断:1.如图,OA⊥OB,若∠1=55°,则∠2的度数是()A.35°B.40°C.45°D.60°2. 如图,点C 是线段AB 上的点,点D 是线段BC 的中点,若AB=12,AC=8,则CD= .3.已知:如图,BD 平分∠ABC ,点E 在BC 上,EF//AB .若∠CEF=100,则∠ABD 的度数为( ) A.060 B.050 C.040 D.0304. 如图,△ABC 中,090=∠C ,AC=3,点P 是边BC 上的动点,则AP 长不可能是( ) A.2.5 B.3 C.4 D. 5建模一一、直线、射线、线段1.直线的基本性质(1)两条直线相交,只有________交点.(2)经过两点有且只有一条直线,即:两点确定一条________. 2.线段的性质所有连接两点的线中,线段最短,即:两点之间______最短. 3.线段的中点把一条线段分成两条________线段的点,叫做这条线段的中点. 4.直线、射线、线段的区别与联系有几个端点 向几个方 向延伸表示 图形直线 0 2 两个大写字母或 一个小写字母射线 1 1 两个大写字母线段 2 0 两个大写字母或一个小写字母1.角的有关概念角是由一条射线绕着它的端点旋转而成的图形.射线端点叫做角的顶点,两条射线是角的两边.从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线就叫做这个角的______________.2.角的单位与换算 1°=60′,1′=60″,1周角=2平角=4直角. 3.余角与补角如果两个角的和等于________,就说这两个角互为余角;如果两个角的和等于______,就说这两个角互为补角.同角(或等角)的余角________;同角(或等角)的补角______.4.对顶角与邻补角在两条相交直线形成的四个角中,如果两个角有公共顶点,一个角的两边分别是另一个角两边的反向延长线,这样的两个角称为对顶角.如果两个角有公共顶点,有一条公共边,它们的另一边互为反向延长线,这样的两个角为邻补角.对顶角________,邻补角________.三、垂线的性质与判定 1.垂线及其性质垂线:两条直线相交所构成的四个角中有一个角是_________,则这两条直线互相垂直,其中一条直线叫做另一条直线的垂线.性质:(1)过一点有且只有一条直线与已知直线垂直;(2)直线外一点与直线上各点连接的所有线段中,垂线段最短.(简说成:垂线段最短)2.点到直线的距离直线外一点到这条直线的________的长度,叫做点到直线的距离. 3.判定若两条直线相交且有一个角为直角,则这两条直线互相垂直. 四、平行线的性质与判定 1.概念在同一平面内,不相交的两条直线,叫做平行线. 2.平行公理经过直线外一点,有且只有一条直线与已知直线平行. 3.性质如果两条直线平行,那么同位角相等,内错角相等,同旁内角互补. 4.判定同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行;在同一平面内垂直于同一直线的两直线________,平行于同一直线的两直线______. (二)典例分析:例1 . 如图,ο90,=∠∆ACB ABC Rt 中,DE 过点C ,且DE//AB ,若ο50=∠ACD ,则∠A= ,∠B= .例2:如图,能判定EB ∥AC 的条件是( ) A .∠C =∠ABEB . ∠A =∠EBDC . ∠C =∠ABCD . ∠A =∠ABE例3.已知线段AB=8cm ,在直线AB 上画线段BC ,使BC=3cm ,则线段AC=________. 【点拨】由于在直线上画线段,所以要分类讨论,这条线段是画在线段的外部或线段两种情况.例4:如图,已知直线a ∥b ,0401=∠,0602=∠,则3∠等于( ) A .100° B .60° C .40° D .20° 建模二:学习反思 (三)济南市真题再现:1.(2011)济南)如图,直线l 与直线a 、b 分别交于点A 、B ,//a b ,若0170∠=,则∠2=______度.2. (2012济南)如图,直线a ∥b ,直线c 与a ,b 相交,∠1=65°,则∠2=( ) A .115°B .65°C .35°D .25°3.(2014济南)如图,点O在直线AB 上,若ο401=∠,则2∠的度数是( )A .ο50 B .ο60 C .ο140 D .ο1504.(2013济南)如图,直线a ,b 被直线c 所截,a b ∥,1130∠=°,则2∠的度数是 (A )130° (B )60° (C )50° (D )40°5.(2015•济南)如图,OA ⊥OB ,∠1=35°,则∠2的度数是( ) A . 35° B . 45° C . 55° D . 70°(四)反思建构(五)当堂检测:A —基础训练一、选择题(每小题有四个选项,只有一个选项是正确的.) 1.借助一副三角尺,你能画出下面哪个度数的角( ) A .65° B .75° C .85° D .95°2.如图,已知AB ∥CD , 则图中与∠1互补的角有( )A .2个B .3 个C .4 个D .5个3.如图,点A 、B 、C 是直线l 上的三个点,图中共有线段条数是 ( ) A .1条 B .2条 C .3条 D .4条4. 下列各图中,∠1大于∠2的是( )5.如图,BC ⊥AE 于点C ,CD ∥AB ,∠B =55°,则∠1等于( ) A . 35°B . 45°C . 55°D . 65°二、填空题6.计算:50°﹣15°30′= .7. 如图,直线AB 与CD 相交于点O ,∠AOD =50°,则∠BOC = .8.如图,直线l 1∥l 2,l 3⊥l 4,∠1=44°,那么∠2的度数( ) A . 46°B . 44°C . 36°D . 22°9.(2014•德州)如图,AD 是∠EAC 的平分线,AD ∥BC ,∠B =30°,则∠C 为( ) A . 30°B . 60°C . 80°D . 120°21(AB=AC )C B Aba21(a b )ba 21D21C BAABCD10.(2012泰州)如图,△ABC中,∠C=90°,∠BAC的平分线交BC于点D,若CD=4,则点D到AB的距离是.B组一、选择题(每小题有四个选项,只有一个选项是正确的.)1.如图,直线l∥m∥n,等边△ABC的顶点B、C分别在直线n和m上,边BC与直线n所夹的角为25°,则∠α的度数为()A.25°B.45°C.35°D.30°2.一辆汽车在公路上行驶,两次拐弯后,仍在原来的方向上平行行驶,那么两个拐弯的角度可能为()A. 先向左转130°,再向左转50°B. 先向左转50°,再向右转50°C. 先向左转50°,再向右转40°D. 先向左转50°,再向左转40°3.如图,在△ABC中,∠B=46°,∠C=54°,AD平分∠BAC,交BC于D,DE∥AB,交AC于E,则∠ADE 的大小是()A.45°B.54°C.40°D.50°4.如图,=∠=∠=∠3,1402,651,//00则b a ( ) A.0100 B.0105 C.0110 D.0115二、填空题5. 如图,直线AB 、CD 相交于点O ,OE 平分∠AOD ,若∠BOD =100°,则∠AOE =_____.6.如图,AE∥BD,C是BD上的点,且AB=BC,∠ACD=110°,则∠EAB=度.7.如图:AB∥CD,直线MN分别交AB、CD于点E、F,EG平分∠AEF.EG⊥FG于点G,若∠BEM=50°,则∠CFG= 度。
第18讲 几何初步及其平行线、相交线

第18讲 │ 考点随堂练 18讲
考点3 相交线
相等 直角
垂线段
内错角
同旁内角
只有
第18讲 │ 考点随堂练 18讲
10.下面四个图形中, 1 与∠2 是对顶角的图形的个数是 B 下面四个图形中, 是对顶角的图形的个数是( 下面四个图形中 ∠ )
A.0 . C.2 .
图 18-8 - B.1 . D.3 .
14325这个角为180新课标两个角是否互为余角或互为补角与位置无关只要看它们的和是否等于90或180新课标如图184abcd分别探讨下面四个图形中apcpabpcd的关系请你从所得到的关系中任选一个加以证明
几何初步及其平行线、 第18讲 │ 几何初步及其平行线、相交线 18讲
第18讲 18讲 几何初步及其平行线、 几何初步及其平行线、相交线
第18讲 │ 考点随堂练 18讲
6.∠A 与∠B 互为补角,且∠A>∠B,那么∠B 的余角等于 . 互为补角, ∠ ,那么∠ ( A ) 1 1 A. (∠A-∠B) ∠ - B. (∠A+∠B) ∠ + 2 2 1 1 D. ∠B C. ∠A 2 2
[解析 ∠A 与∠B 互为补角,则∠A+∠B=180°,所以 解析] 互为补角, 解析 + = , 的余角为= - ∠B=180°-∠A,则∠B 的余角为=90°-(180°-∠A)= = - , - = 1 1 ∠A-90°=∠A- (∠A+∠B)= (∠A-∠B). - = - ∠ + = ∠ - . 2 2
第18讲 │ 考点随堂练 18讲
12.如图 18-10,已知∠1=70°,∠2=70°,∠3=60°,则∠4= 如图 - ,已知∠ = , = , = , = 60° ______.
图 18-10 -
陕西省2018年中考数学复习课件:第一编第11课时几何初步与相交线、平行线.pptx
第11课时:几何初步与相交线、平行线
~
《中考内参(ห้องสมุดไป่ตู้学)2018》配套课件
第11课时:几何初步与相交线、平行线
《中考内参(数学)2018》配套课件
第11课时:几何初步与相交线、平行线
定义、 命题、 定理
1
直线、 射线、 线段
2
3
角
4
相交线
5
平行线
几何中 的三种 距离
6
《中考内参(数学)2018》配套课件
《中考内参(数学)2018》配套课件
第11课时:几何初步与相交线、平行线
【点评】本题主要考查平行线的性质及折叠图形的性质,掌握相关性质并 能灵活运用是解题的关键。
《中考内参(数学)2018》配套课件
第11课时:几何初步与相交线、平行线
请完成《中考内参(数学)》(听课手册) 本节【当堂目标检测】。
第11课时:几何初步与相交线、平行线
布置作业:
温馨提示: 请完成本课时《课后达标作业》.
《中考内参(数学)2018》配套课件
《中考内参(数学)2018》配套课件
第11课时:几何初步与相交线、平行线
B
【点评】本题考查了角平分线定义和平行线性质的应用,注意:平行线的性质有: ①两条平行线被第三条直线所截,同位角相等,②两条平行线被第三条直线所截, 内错角相等,③两条平行线被第三条直线所截,同旁内角互补.
《中考内参(数学)2018》配套课件
第11课时:几何初步与相交线、平行线
《中考内参(数学)2018》配套课件
第11课时:几何初步与相交线、平行线
D
解:∵用剪刀沿直线将一片平整的树叶剪掉一部分,发现剩下树叶的周长比 原树叶的周长要小,∴线段AB的长小于点A绕点C到B的长度, ∴能正确解释这一现象的数学知识是“两点之间,线段最短”,故选D. 【点评】本题考查学生应用数学原理解释生活现象的能力,能够正 确理解题意,并找到对应的数学原理是解答本题的关键。
中考数学一轮复习第17讲几何初步及平行线相交线专题精练
中考数学一轮复习第17讲几何初步及平行线相交线专题精练一、夯实基础1.如图1,已知a∥b,∠1=50°,则∠2=______度.(1)(2)(3)2.已知∠α与∠β互余,且∠α=40°,且∠β的补角为______度.3.时钟在4点整时,时针与分针的夹角为_______度.4.如图2,点A、B、C在直线L上,则图中共有______条线段.5.如图3,若AB∥CD,EF与AB、CD分别相交于点E、F,EP⊥EF,∠EFD 的平分线与EP相交于点P,且∠BEP=40°,则∠EPF=_______度.6.如图4,•将一副三角板的直角顶点重合,•摆放在桌面上,•若∠AOD=145°,则∠BOC=_______度.7.如图5,AB∥CD,若∠ABE=120 °, ∠DCE= 35 °,•则有∠BEC=_______度.(4)(5)(6)二、能力提升8.如图6,是共产主义青年团团旗上的图案,点A、B、C、D、E五等分圆,则∠A+∠B+∠C+∠D+∠E的度数是()A.180° B.150° C.135° D.120°9.已知:如图7,∠AOB的两边OA、OB均为平面反光镜,∠AOB=40°,在OB•上有一点P,从P点射出一束光线经OA上的Q点反射后,反射光线QR恰好与OB平行,则∠QPB 的度数是()A.60° B.80° C.100° D.120°10.如图8,B是线段AC的中点,过点C的直线L与AC成60°的角,•在直线L上取一点P,使∠APB=30°,则满足条件的点P共有()A.1个 B.2个 C.3个 D.无数个三、课外拓展11.如图9,AB∥CD,直线EF分别交AB,CD于E,F两点,∠BEF 的平分线交CD于点G,若∠EFG=72°,则∠EGF等于()A.36° B.54° C.72° D.108°(7)(8)(9)12.小颖在做下面的数学作业时,因钢笔漏墨水,•不小心将部分字迹污损了,作业过程如下(涂黑部分即污损部分);已知:如图所示,OP平分∠AOB,MN∥OB.求证:OM=NM.证明:因为OP平分∠AOB所以▅▅▅▅又因为MN∥OB所以▅▅▅▅故∠1=∠3所以OM=NM.小颖思考:污损部分应分别是以下四项中的两项:①∠1=∠2 ②∠2=∠3 ③∠3=∠4 ④∠1=∠4那么她补出来的结果应是()A.①④ B.②③ C.①② D.③④四、中考链接13.已知图中小方格的边长为1,求点C到线段AB的距离.14.如图,已知在△ABC中,AB=AC,∠BAC=120°,AC的垂直平分线EF交AC于点E,交BC于点F.求证:BF=2CF.15.如图,已知AB⊥BC,DC⊥BC,BE∥CF,求证:∠1=∠2.参考答案一、夯实基础1.130°2.130°3.120°4.35.65°6.35°7.95°二、能力提升8.A9.B10.B三、课外拓展11.B12.C四、中考链接13.414.连结AF,则AF=FC,AF=BF,∴BF=2C F 1215.利用平行线内错角相等及等角的余角相等即可证明。
教育最新K122018届中考数学 几何初步及平行线、相交线复习学案(无答案)
几何初步及平行线、相交线复习案【复习目标】1. 明确平行线的3个性质和3个判定;会用其进行简单的推理。
2.通过平行线的性质和判定的综合,体会数形结合和转化的思想。
3.体会几何语言的严密性,形成“用数学”的意识。
【重点】平行线的性质和判定的综合 【难点】平行线的性质和判定的综合。
【使用说明与学法指导】先用5分钟左右的时间复习,然后35分钟独立完成复习案,有疑惑的做好标记。
【考点链接】1. 两点确定一条直线,两点之间线段最短._____ _ _____叫两点间距离.2. 1周角=__________平角=_____________直角=____________.3. 如果两个角的和等于90度,就说这两个角互余,同角或等角的余角相等;如果_____________________互为补角,__________________的补角相等.4. ___________________________________叫对顶角,对顶角___________.5. 过直线外一点心___________条直线与这条直线平行.6. 平行线的性质:两直线平行,_________相等,________相等,________互补.7. 平行线的判定:________相等,或______相等,或______互补,两直线平行.8. 平面内,过一点有且只有_____条直线与已知直线垂直. 【课前热身】1. 如图,延长线段AB 到C ,使4BC =, 若8AB =,则线段AC 是BC 的 倍.2.如图,已知直线a b ∥,135=∠,则2∠3.如图,在不等边ABC △中,DE BC ∥,60ADE =∠,图中等于60的角还有______________.4.经过任意三点中的两点共可以画出的直线条数是( )A .一条或三条B .三条C .两条D .一条ADB CE(第3题)a(第5题)ABD a b70° 31°5.如图,直线a b ∥,则A ∠的度数是( )A .28B .31C .39D .42 【典例精析】例1 如图:AB∥CD,直线EF 分别交AB 、CD 于E 、F ,EG 平分∠BEF,若∠1=720,则∠2等于多少度?例2 如图,ABC △中,B C ∠∠,的平分线相交于点O ,过O 作DE BC ∥,若5BD EC +=,则DE 等于多少?【中考演练】1.如图,直线a 、b 被直线c 所截,若要a∥ b ,需增加条件______.(填一个即可) 2.如图直线l 1//l 2,AB ⊥CD ,∠1=34°,那么∠2的度数是 .3.如图, 已知直线25,115,//=∠=∠A C CD AB , 则=∠E ( )A. 70B. 80C. 90D.100DBAB C21DCBAl 2l1( 第1题) ( 第2题) (第3题)4.如图,在△ABC 中,AB =BC =12cm ,∠ABC =80°,BD 是∠ABC 的平分线,DE ∥BC . (1) 求∠EDB 的度数;(2) 求DE 的长.5. 如图,AB∥CD, AC⊥BC,∠BAC=65°,求∠BCD 度数.【拓展提升】ABCDE。
2018年中考数学复习第4单元图形的初步认识与三角形第17课时图形的认识及平行线相交线检测湘教版
课时训练(十七)图形的认识及平行线、相交线 |夯 实 基 础| 一、选择题 1.[2016·永州]对下列生活现象的解释其数学原理运用错误的是( ) A.把一条弯曲的道路改成直道可以缩短路程是运用了“两点之间线段最短”的原理 B.木匠师傅在刨平的木板上任选两个点就能画出一条笔直的墨线是运用了“直线外一点与直线上各点连接的所有线段中,垂线段最短”的原理 C.将自行车的车架设计为三角形形状是运用了“三角形的稳定性”的原理 D.将车轮设计为圆形是运用了“圆的旋转对称性”的原理 2.如图K17-1,∠AOC为直角,OC是∠BOD的平分线,且∠AOB=57.65°,则∠AOD的度数是( )
图K17-1 A.122°20′ B.122°21′ C.122°22′ D.122°23′ 3.已知∠A与∠B互余,∠B与∠C互补,若∠A=60°,则∠C的度数是( ) A.30° B.60° C.120° D.150° 4.[2016·福州]如图K17-2,直线a,b被直线c所截,∠1与∠2的位置关系是( ) A.同位角 B.内错角 C.同旁内角 D.对顶角
图K17-2 图K17-3 5.[2017·宿迁]如图K17-3,直线a,b被直线c,d所截,若∠1=80°,∠2=100°,∠3=85°,则∠4的度数是( ) A.80° B.85° C.95° D.100°
6.[2017·邵阳]如图K17-4,要在一条公路的两侧铺设平行管道,已知一侧铺设的角度为120°,为使管道对接,另一侧铺设的角度大小应为( )
图K17-4 A.120° B.100° C.80° D.60° 7.[2016·张家界]如图K17-5,将一块直角三角板的直角顶点放在直尺的一边上.如果∠1=50°,那么∠2的度数是( ) A.30° B.40° C.50° D.60° 图K17-5 图K17-6 8.[2016·深圳]如图K17-6,已知a∥b,直角三角板的直角顶点在直线b上,若∠1=60°,则下列结论错误的是( ) A.∠2=60° B.∠3=60° C.∠4=120° D.∠5=40°
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第17讲几何初步与平行线、相交线
一、知识梳理
三种基本图形——直线、射线、线段
直线公理 经过两点有且只有________条直线
线段公理 两点之间,________最短
两点间的
距离
连接两点间的线段的________,叫做这两点间的距离
角
角
的概念
定义1 有公共端点的两条____组成的图形叫做角.这个公共
端点叫做角的____,这两条射线叫做角的____
定义2 一条射线绕着它的____从一个位置旋转到另一个位置
所成的图形叫做角
角的分类 角按照大小可以分为平角、周角、____、____、钝角
角的大小比较 (1)叠合法 (2)度量法
角
平分线
定义 从一个角的顶点引出的一条射线,把这个角分成两个
相等的角,这条射线叫做这个角的平分线
性
质
角平分线上的点到这个角两边的距离相等
几何计数
1
数直线的 条数 过任意三个不在同一直线上的n个点中的
两个点可以画________条
2
数线段的 条数 线段上共有n个点(包括两个端点)时,共有
线段________条
3 数角的 个数 从一点出发的n条直线可组成______个角
4 数交点的 个数 n条直线最多有________个交点
5
数直线分 平面的份数 平面内有n条直线,最多可以把平面分成
________个部分
互为余角、互为补角
互为
余角
定义 如果两个角的和等于90°,则这两个角互余
性质 同角(或等角)的余角________
互为
补角
定义 如果两个角的和等于180°,则这两个角互补
性质 同角(或等角)的补角________
拓展 一个角的补角比这个角的余角大90°
邻补角、对顶角
邻补角定义
若两角有一条公共边,它们的另一边互为反向延长
线,具有这种关系的两个角,互为邻补角
对顶
角
定义
若两角有一个公共顶点,且两角的两边互为反向延
长线,具有这种位置关系的两个角,互为对顶角
性质 对顶角相等
“三线八角“的概念
同
位角
如果两个角在截线l的同侧,且在被截直线a、
b的同一方向叫做同位角(位置相同).∠1和∠5,∠4
和∠8,∠2和∠6,∠3和∠7是同位角
内
错角
如果两个角在截线l的两旁(交错),在被截线a、
b之间(内)叫做内错角(位置在内且交错).∠2和∠8,
∠3和∠5是内错角
同
旁
内
角
如果两个角在截线l的同侧,在被截直线a、b
之间(内)叫做同旁内角.∠5和∠2,∠3和∠8是同旁
内角
平行
平行线的定义 在同一平面内,________的两条直线叫做平行线
平行公理 经过直线外一点,有且只有____条直线与这条直线______
平行公理的推论 如果两条直线都与第三条直线平行,那么这两条直线也互
相________
平行线的判定 同位角相等,两直线平行
