2018年秋九年级数学上册 第三章 3.4 简单几何体的表面展开图(第2课时)同步测试 (新版)浙教版
浙教版初中数学九年级下册 3.4 简单几何体的表面展开图学案2练习题

浙教版初中数学重点知识精选掌握知识点,多做练习题,基础知识很重要!浙教版初中数学和你一起共同进步学业有成!3.4简单几何体的表面展开图【教师寄语】知识就是力量【学习目标】1.了解圆柱的概念和性质,认识圆柱的底面和侧面; 2.了解圆柱的侧面展开图,会根据展开图想象实际物体;3.会计算圆柱的侧面积和全面积。
【学习重点】圆柱的侧面展开图、明晰展开图与原几何体的关系、以及掌握侧面积和全面积的计算。
【学习过程】一.观察与思考设矩形的边长分别为r 和h ,将矩形绕其边长为h 的一边旋转360°,可以得到一个圆柱体,请思考圆柱体的底面和侧面分别为什么图形?并用r 、h 表达圆柱体的侧面积和全面积公式。
二.典例分析一个圆柱形水池的底面半径为4米,池深1.2米.在池的内壁与底面抹上水泥,抹水泥部分的面积是多少平方米?三.牛刀小试1.圆柱的底面半径为2cm ,高为3cm ,则它的侧面积是 cm 22.已知圆柱的高是5cm ,侧面展开图的面积为20лcm 2,则这个圆柱的底面半径为 cm .3.圆柱铁桶的侧面展开图是边长为12лcm 的正方形,则该铁桶的底面直径是( ).(A )12лcm (B)6лcm (C)12cm (D)6c m四.收获与反思圆柱体的侧面展开图为矩形,当圆柱体的底面半径为r 、高为h 时,圆柱体的侧面积为2rh p ,全面积为22r rh p p +;五.巩固提高1.用一张边长为20cm 的正方形纸片围成一个圆柱的侧面,则这个圆柱的底面直径是( ).(A) cm (B ) cm (C )cm (D ) cm 20л10л2лл202. 甲乙两人分别利用一张长20厘米,宽15厘米的纸用两种不同的方法围成一个圆柱体(接头处不重叠),那么围成的圆柱( )A .高一定相等B .侧面积一定相等C .侧面积和高都相等D .侧面积和高都不相等 答案:B相信自己,就能走向成功的第一步教师不光要传授知识,还要告诉学生学会生活。
九年级数学下册第3章投影与三视图3.4简单几何体的表面展开图第3课时圆锥的表面展开图同步练习 112145
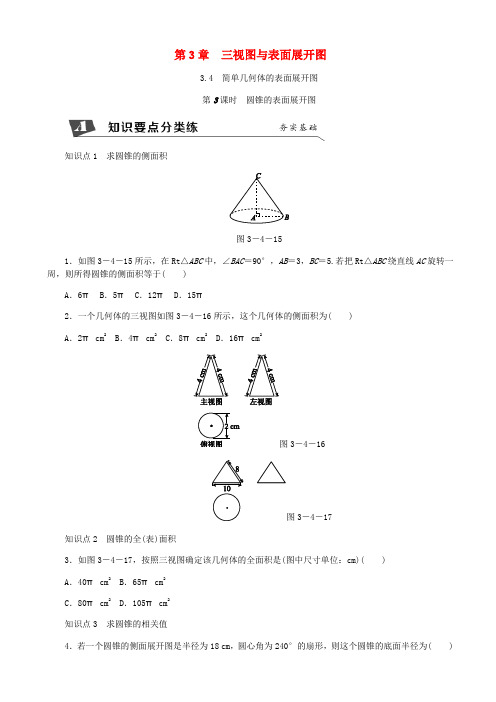
第3章三视图与表面展开图3.4 简单几何体的表面展开图第3课时圆锥的表面展开图知识点1 求圆锥的侧面积图3-4-151.如图3-4-15所示,在Rt△ABC中,∠BAC=90°,AB=3,BC=5.若把Rt△ABC绕直线AC旋转一周,则所得圆锥的侧面积等于( )A.6π B.5π C.12π D.15π2.一个几何体的三视图如图3-4-16所示,这个几何体的侧面积为( )A.2π cm2 B.4π cm2 C.8π cm2 D.16π cm2图3-4-16图3-4-17知识点2 圆锥的全(表)面积3.如图3-4-17,按照三视图确定该几何体的全面积是(图中尺寸单位:cm)( )A.40π cm2 B.65π cm2C.80π cm2 D.105π cm2知识点3 求圆锥的相关值4.若一个圆锥的侧面展开图是半径为18 cm,圆心角为240°的扇形,则这个圆锥的底面半径为( )A.6 cm B.9 cm C.12 cm D.18 cm图3-4-185.如图3-4-18是一圆锥的左视图,根据图中所标数据,圆锥侧面展开图的扇形圆心角的大小为( ) A.90° B.120°C.135° D.150°6.用一个圆心角为120°,半径为6的扇形作一个圆锥的侧面,这个圆锥的底面圆的半径是________.7.图3-4-19是某几何体的三视图,根据图中数据,求得该几何体的表面积为________.图3-4-198.如图3-4-20,一个圆锥的高为3 3 cm,侧面展开图是半圆.求:(1)圆锥的母线长与底面半径之比;(2)∠BAC的度数;(3)圆锥的侧面积(结果保留π).图3-4-209.如图3-4-21,这是一个由圆柱体材料加工而成的零件.它是以圆柱体的上底面为底面,在其内部“掏去”一个与圆柱体等高的圆锥而得到的.其底面直径AB=12 cm,高BC=8 cm.求这个零件的表面积.(结果保留π)图3-4-21。
【K12教育学习资料】2018年秋九年级数学下册 第3章 三视图与表面展开图 3.2 简单几何体的三
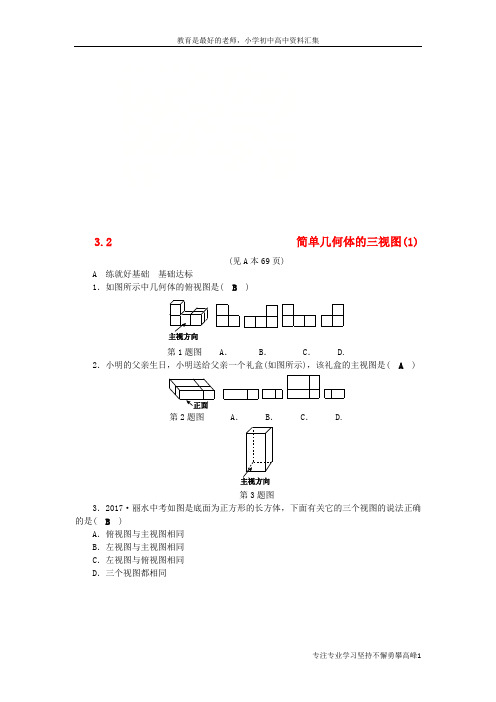
3.2简单几何体的三视图(1)(见A本69页)A 练就好基础基础达标1.如图所示中几何体的俯视图是( B)第1题图A.B. C. D.2.小明的父亲生日,小明送给父亲一个礼盒(如图所示),该礼盒的主视图是( A)第2题图A. B.C. D.第3题图3.2017·丽水中考如图是底面为正方形的长方体,下面有关它的三个视图的说法正确的是( B)A.俯视图与主视图相同B.左视图与主视图相同C.左视图与俯视图相同D.三个视图都相同第4题图4.由6个大小相同的立方体搭成的几何体如图所示,则关于它的视图说法正确的是( C)A.主视图的面积最大B.左视图的面积最大C.俯视图的面积最大D.三个视图的面积一样大5.潍坊中考如图所示的几何体的左视图是( C)5题图A.B.C. D.6.一个几何体的三视图如图所示,则几何体是__圆柱体__.第6题图第7题图7.如图所示是由六个棱长为1的立方体组成的几何体,其俯视图的面积是__5__.8.画出图中由几个立方体组成的几何体的三视图.第8题图解:三视图如图:第8题答图第9题图9.如图所示是由相同的5个小立方体组成的几何体,请画出它的三种视图(比例为1∶1);若每个小立方体的棱长为a,试求出该几何体的表面积.解:主视图如图所示.表面积:4a2×2+3a2×4=20a2.第9题答图B 更上一层楼能力提升10.如图所示,该几何体的左视图是( C)第10题图A.B.C. D.第11题图11.菏泽中考如图所示是由6个同样大小的立方体摆成的几何体.将立方体①移走后,所得几何体( D)A.主视图改变,左视图改变B.俯视图不变,左视图不变C.俯视图改变,左视图改变D.主视图改变,左视图不变12.一个几何体是由一些大小相同的小立方体摆成的,其主视图与左视图如图所示,则组成这个几何体的小立方体最少有__5__个.第12题图13.有一个几何体的形状为直三棱柱,如图是它的主视图和左视图.(1)请补画出它的俯视图,并标出相关数据;(2)根据图中所标的尺寸(单位: cm),计算这个几何体的表面积.第13题图解:(1)如图:第13题答图(2)由勾股定理,得斜边长为10 cm , S 底=12×8×6=24(cm 2),S 侧=(8+6+10)×3=72(cm 2),S 表=72+24×2=120(cm 2). 14.如图所示是由几个小立方体叠成的几何体的主视图和左视图,求组成几何体的小立方体个数的最大值与最小值.第14题图解:12个,7个C 开拓新思路 拓展创新15.一个长方体主视图是边长为1 cm 的正方形.沿这个正方形的对角线向垂直于正方形的方向将长方体切开,截面是一个正方形,那么这个长方体的俯视图是( D )A .B .C . D.16.有一个立方体,在它的各个面上分别标有数字1,2,3,4,5,6.小明、小刚、小红三人从不同的角度去观察此立方体,观察结果如图所示.问这个正方体各个面上的数字对面各是什么数字?第16题图解:从前两个小立方体上的数字可知,与写有数字1的面相邻的面上的数字是2,3,4,6,所以数字1的对面是数字5,从后两个小立方体上的数字可知:数字3的对面数字是6,数字2的对面数字是4.。
【浙教版】2018年秋九年级数学下册第3章投影与三视图3.4简单几何体的表面展开图第1课时同步测试新版浙教版
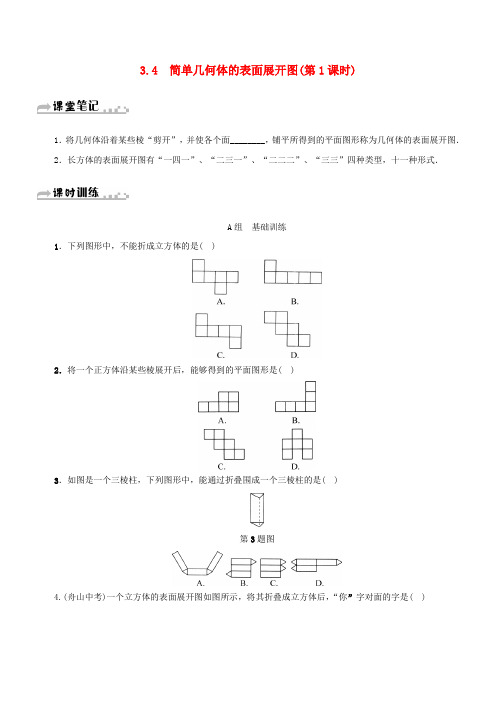
3.4 简单几何体的表面展开图(第1课时)1.将几何体沿着某些棱“剪开”,并使各个面________,铺平所得到的平面图形称为几何体的表面展开图.2.长方体的表面展开图有“一四一”、“二三一”、“二二二”、“三三”四种类型,十一种形式.A组基础训练1.下列图形中,不能折成立方体的是( )2.将一个正方体沿某些棱展开后,能够得到的平面图形是( )3.如图是一个三棱柱,下列图形中,能通过折叠围成一个三棱柱的是( )第3题图4.(舟山中考)一个立方体的表面展开图如图所示,将其折叠成立方体后,“你”字对面的字是( )第4题图A.中 B.考C.顺 D.利5.如图是一个直三棱柱的表面展开图,其中AD=10,CD=2,则下列可作为AB长的是( )第5题图A.5 B.4 C.3 D.26.下列四张正方形硬纸片,剪去阴影部分后,如果沿虚线折叠,可以围成一个封闭的长方体包装盒的是( )7.骰子是一种特别的数字立方体(如图),它符合规则:相对两面的点数之和总是7.下列四幅图中可以折成符合规则的骰子是( )第7题图8.马小虎准备制作一个封闭的正方体盒子,他先用5个大小一样的正方形制成如图所示的拼接图形(实线部分),经折叠后发现还少一个面,请你在如图的拼接图形上再接一个正方形,使新拼接成的图形经过折叠后能成为一个封闭的正方体盒子(添加所有符合要求的正方形,添加的正方形用阴影表示).第8题图9.一个包装盒的表面展开图如图.描述这个包装盒的形状,并求这个包装盒的表面积和容积(纸板厚度忽略不计).第9题图10.画出如图所示的底面为直角三角形的直棱柱的表面展开图,并计算它的侧面积和表面积.第10题图B组自主提高11.如图,将一张边长为3的正方形纸片按虚线裁剪后恰好围成一个底面是正三角形的棱柱,这个棱柱的侧面积为( )第11题图A .9-3 3B .9C .9-52 3D .9-32312.如图是飞行棋的一颗骰子,每个面上分别有代表数1,2,3,4,5,6的点,根据A ,B ,C 三种状态所显示的数字推出“?”处的数字是________.第12题图13.如图是一个多面体的展开图,每个面上都标注了字母,请你根据要求回答问题: (1)这个多面体是一个什么物体?(2)如果D 是多面体的底部,那么哪一面会在上面? (3)如果B 在前面,C 在左面,那么哪一面在上面? (4)如果E 在右面,F 在后面,那么哪一面会在上面?第13题图C 组 综合运用14.已知直四棱柱的尺寸如图,一只蚂蚁从点A 处沿直四棱柱的表面爬到点C 处,试求它爬行的最短距离.(单位:cm )第14题图3.4 简单几何体的表面展开图(第1课时)【课堂笔记】 1.连在一起 【课时训练】 1-5.BCBCB 6-8.第8题图如上图,可以拼在①②③④中的其中一个位置.9. 长方体:S 表=25×15+35×5=550cm 2,V =5×5×25=625cm 3. 10. 展开图如图:第10题图侧面积=3×2.5+3×2+3×1.5=18平方厘米 表面积=18+2×12×2×1.5=21平方厘米11. A 12. 613. (1)这个多面体是一个长方体; (2)面“B”与面“D”相对,如果D 是多面体的底部,那么B 在上面; (3)由图可知,如果B 在前面,C 在左面,那么A 在下面,∵面“A”与面“E”相对,∴E 面会在上面; (4)由图可知,如果E 在右面,F 在后面,那么分两种情况:①如果EF 向前折,D 在下,B 在上;②如果EF 向后折,B 在下,D 在上.14. 分别把正面与右面,正面与上面,左面与上面在同一平面内展开如下图.第14题图正面与右面:AC=122+52=13cm.正面与上面:AC=102+72=149cm.左面与上面:AC=122+52=13cm.答:蚂蚁爬行的最短距离为149cm.。
九年级数学下册 第3章 投影与三视图 3.4 简单几何体的表面展开图 第1课时 棱柱的表面展开图同步练习 (新版

第3章三视图与表面展开图3.4 简单几何体的表面展开图第1课时直棱柱的表面展开图知识点1 立方体、长方体的表面展开图1.2016·绍兴如图3-4-1是一个正方体,则它的表面展开图可以是( )图3-4-1图3-4-22.如图3-4-3是一个长方体包装盒,则它的表面展开图是( )图3-4-3 图3-4-4知识点2 其他直棱柱的展开图图3-4-53.图3-4-5是某个几何体的表面展开图,该几何体是( )A.三棱柱B.圆锥C.四棱柱D.圆柱4.下列图形经过折叠不能围成一个棱柱的是( )图3-4-65.2017·包头将一个无盖正方体形状盒子的表面沿某些棱剪开,展开后不能得到的平面图形是( )图3-4-76.2017·舟山一个立方体的表面展开图如图3-4-8所示,将其折叠成立方体后,“你”字对面的字是( )图3-4-8A.中 B.考 C.顺 D.利7.图3-4-9①②为同一长方体房间的示意图,图③为该长方体的表面展开图.(1)蜘蛛在顶点A′处.①苍蝇在顶点B处时,试在图①中画出蜘蛛为捉住苍蝇,沿墙面爬行的最近路线;②苍蝇在顶点C处时,图②中画出了蜘蛛捉住苍蝇的两条路线,往天花板ABCD爬行的最近路线A′GC和往墙面BB′C′C爬行的最近路线A′HC,试通过计算判断哪条路线更近.(2)在图③中,半径为10 dm的圆M与D′C′相切,圆心M到边CC′的距离为15 dm.蜘蛛P在线段AB上,苍蝇Q在圆M的圆周上,线段PQ为蜘蛛的爬行路线.若PQ与圆M相切,试求PQ长度的取值范围.图3-4-9综上所述,PQ长度的取值范围是20 6 dm≤PQ≤55 dm.图(c) 图(d)。
浙教版2018-2019学年九年级数学下册第3章3.4简单几何体的表面展开图第1课时棱柱的表面展开图同步练习
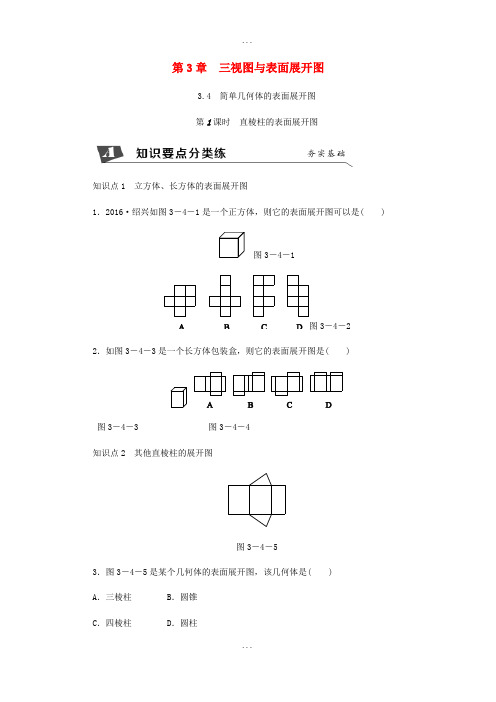
第3章三视图与表面展开图3.4 简单几何体的表面展开图第1课时直棱柱的表面展开图知识点1 立方体、长方体的表面展开图1.2016·绍兴如图3-4-1是一个正方体,则它的表面展开图可以是( )图3-4-1图3-4-22.如图3-4-3是一个长方体包装盒,则它的表面展开图是( )图3-4-3 图3-4-4知识点2 其他直棱柱的展开图图3-4-53.图3-4-5是某个几何体的表面展开图,该几何体是( )A.三棱柱B.圆锥C.四棱柱D.圆柱4.下列图形经过折叠不能围成一个棱柱的是( )图3-4-65.2017·包头将一个无盖正方体形状盒子的表面沿某些棱剪开,展开后不能得到的平面图形是( )图3-4-76.2017·舟山一个立方体的表面展开图如图3-4-8所示,将其折叠成立方体后,“你”字对面的字是( )图3-4-8A.中 B.考 C.顺 D.利7.图3-4-9①②为同一长方体房间的示意图,图③为该长方体的表面展开图.(1)蜘蛛在顶点A′处.①苍蝇在顶点B处时,试在图①中画出蜘蛛为捉住苍蝇,沿墙面爬行的最近路线;②苍蝇在顶点C处时,图②中画出了蜘蛛捉住苍蝇的两条路线,往天花板ABCD爬行的最近路线A′GC和往墙面BB′C′C爬行的最近路线A′HC,试通过计算判断哪条路线更近.(2)在图③中,半径为10 dm的圆M与D′C′相切,圆心M到边CC′的距离为15 dm.蜘蛛P在线段AB上,苍蝇Q在圆M的圆周上,线段PQ为蜘蛛的爬行路线.若PQ与圆M相切,试求PQ长度的取值范围.图3-4-9综上所述,PQ长度的取值范围是20 6 dm≤PQ≤55 dm.图(c) 图(d)。
最新新版浙教版2018年秋九年级数学下册第3章投影与三视图3.4简单几何体的表面展开图第3课时同步测试-附答案
3.4 简单几何体的表面展开图(第3课时)若圆锥的底面半径为r,母线为l,圆锥的侧面展开图扇形的圆心角为θ,则:(1)S锥侧=________,S锥全=________;(2)θ=____________.A组基础训练1.下列图形中,是圆锥侧面展开图的是( )第1题图2.若圆锥的侧面积为12πcm2,它的底面半径为3cm,则圆锥的母线长为( )A.4πcm B.4cm C.2πcm D.2cm3.如图,小丽要制作一个圆锥模型,要求圆锥的母线长为9cm,底面圆的直径为10cm,那么制作的这个圆锥的侧面展开图的扇形纸片的圆心角度数是( )A.240° B.200° C.180° D.150°第3题图2.(随州中考)如图是某工件的三视图,则此工件的表面积为( )第4题图A .15πcm 2B .51πcm 2C .66πcm 2D .24πcm 25.如图,在Rt △ABC 中,∠BAC =90°,AB =3,BC =5,若把Rt △ABC 绕直线AC 旋转一周,则所得圆锥的侧面积等于( )A .6πB .9πC .12πD .15π第5题图3.如图,扇形DOE 的半径为3,边长为3的菱形OABC 的顶点A ,C ,B 分别在OD ,OE ,弧DE 上,若把扇形DOE 围成一个圆锥,则此圆锥的高为( )第6题图 A.12 B .2 2 C.372 D.3527.如图,圆锥的底面半径为6cm ,高为8cm ,那么这个圆锥的侧面积是________cm 2.第7题图4.将半径为3cm 的圆形纸片沿AB 折叠后,圆弧恰好能经过圆心O ,用图中阴影部分的扇形围成一个圆锥的侧面,则这个圆锥的高为________.第8题图9.(齐齐哈尔中考)一个侧面积为162πcm 2的圆锥,其主视图为等腰直角三角形,则这个圆锥的高为________cm.10.已知一个圆锥沿轴剖开是一个等腰三角形.若这个三角形的底为8cm ,腰为10cm.(1)求圆锥侧面展开图的扇形弧长;(2)求圆锥的表面积.B组自主提高11.若一个圆锥的侧面积是10,圆锥母线l与底面半径r之间的函数关系图象大致是(D)12.已知圆锥的轴截面是等边三角形,则它的侧面展开图的扇形圆心角为________.13.“神舟五号”太空仓的示意图如图所示.太空仓的外表面须做特别处理,以承受重返地球大气层时因空气摩擦而产生的高热.求该太空仓要接受防高热处理的面积(结果精确到0.1m2).第13题图C组综合运用14.如图,在Rt△ABC中,∠C=90°,AC=6,BC=8.(1)分别以直线AC,BC为轴,把△ABC旋转一周,得到两个不同的圆锥,求这两个圆锥的侧面积;(2)以直线AB为轴,把△ABC旋转一周,求所得几何体的表面积.第14题图3.4 简单几何体的表面展开图(第3课时)【课堂笔记】(1)πrl πrl +πr 2 (2)r l×360° 【课时训练】1-5.BBBDD6.D7.60π8.22cm9.410. (1)l 弧=πd =8πcm ; (2)S 表=πrl +πr 2=40π+16π=56πcm 2.11. D12. 180°13. 圆锥母线l = 2.12+22=8.41=2.9m ,S 表=πrl +2πrh +πr 2=17.8π≈55.9m 2.14.(1)∵∠C=90°,AC =6,BC =8,∴AB =AC 2+BC 2=10,所以以直线AC 为轴,把△ABC 旋转一周,得到的圆锥的侧面积=π×8×10=80π;以直线BC 为轴,把△ABC 旋转一周,得到的圆锥的侧面积=π×6×10=60π;(2)作CD⊥AB 于点D ,∵12CD ·AB =12AC ·BC ,∴CD =6×810=245,以直线AB 为轴,把△ABC 旋转一周,所得几何体是以CD 为底面半径的两个圆锥,则它的表面积=π×245×8+π×245×6=3365π.。
九年级数学下册第3章投影与三视图3.4简单几何体的表面展开图第3课时圆锥的表面展开图同步练习新版浙教版
第3章三视图与表面展开图3.4 简单几何体的表面展开图第3课时圆锥的表面展开图知识点1 求圆锥的侧面积图3-4-151.如图3-4-15所示,在Rt△ABC中,∠BAC=90°,AB=3,BC=5.若把Rt△ABC 绕直线AC旋转一周,则所得圆锥的侧面积等于( )A.6π B.5π C.12π D.15π2.一个几何体的三视图如图3-4-16所示,这个几何体的侧面积为( )A.2π cm2 B.4π cm2 C.8π cm2 D.16π cm2图3-4-16图3-4-17知识点2 圆锥的全(表)面积3.如图3-4-17,按照三视图确定该几何体的全面积是(图中尺寸单位:cm)( )A.40π cm2 B.65π cm2C.80π cm2 D.105π cm2知识点3 求圆锥的相关值4.若一个圆锥的侧面展开图是半径为18 cm,圆心角为240°的扇形,则这个圆锥的底面半径为( )A.6 cm B.9 cm C.12 cm D.18 cm图3-4-185.如图3-4-18是一圆锥的左视图,根据图中所标数据,圆锥侧面展开图的扇形圆心角的大小为( )A.90° B.120°C.135° D.150°6.用一个圆心角为120°,半径为6的扇形作一个圆锥的侧面,这个圆锥的底面圆的半径是________.7.图3-4-19是某几何体的三视图,根据图中数据,求得该几何体的表面积为________.图3-4-198.如图3-4-20,一个圆锥的高为3 3 cm,侧面展开图是半圆.求:(1)圆锥的母线长与底面半径之比;(2)∠BAC的度数;(3)圆锥的侧面积(结果保留π).图3-4-209.如图3-4-21,这是一个由圆柱体材料加工而成的零件.它是以圆柱体的上底面为底面,在其内部“掏去”一个与圆柱体等高的圆锥而得到的.其底面直径AB=12 cm,高BC =8 cm.求这个零件的表面积.(结果保留π)图3-4-21。
九年级下3.4简单几何体的表面展开图(3)课时练习含答案
3.4 简单几何体的外表展开图(3)1. 假设圆锥的侧面积为12π cm 2,它的底面半径为3 cm ,那么圆锥的母线长为(B ) A. 4π cm B. 4 cm C. 2π cm D. 2 cm2.假设一个圆锥的底面周长是4πcm ,母线长是6cm ,那么该圆锥的侧面展开图的圆心角的度数是(C ) A .40° B .80° C .120° D .150°(第3题)3.小军将一个直角三角尺(如图)绕它的一条直角边所在的直线旋转一周形成一个几何体,将这个几何体的侧面展开得到的大致图形是(D )4.圆锥的侧面积是50π cm 2,圆锥的底面半径为r (cm),母线长为l (cm),那么l 关于r 的函数的图象大致是(B )5. 一个圆锥的底面直径为8 cm ,母线长为5 cm ,它的外表积为__36π__cm 2.6.圆锥的轴截面是直角三角形,母线长为4cm ,那么圆锥的高线长为__2_2__cm. 7.母线长为2的圆锥的侧面展开图是一个圆心角为90°的扇形,那么此圆锥的底面半径为__12__.(第8题)8. 小明制作的一个圆锥形纸帽的示意图如图,围成这个纸帽的纸的面积为多少(单位:cm ,π取3.14)?【解】∵d=20,∴r=10.∴S侧=πrl=3.14×10×30=942 (cm2).9. 将直径为60cm的圆形铁皮,做成三个相同的圆锥容器的侧面(不计接缝处的材料损耗),那个每个圆锥容器的底面半径为(A)A.10cm B.30cmC.40cm D.300cm【解】∵要做成三个相同的圆锥容器的侧面,∴每个侧面展开图扇形的圆心角为120°.∵l=30,·360,∴120=r30∴r=10.(第10题)10.如图,圆锥形烛台的侧面积是底面积的2倍,那么两条母线所夹的∠AOB为__60°__.(第10题解)【解】如解图,设圆锥的母线长为l,底面半径为r.∵2πr2=πrl,∴2r=l,∴r=l2.∴∠POB=30°,∴∠AOB=60°.11. 如图①,在等腰梯形ABCD中,AB∥CD,CD=50 cm,AB=90 cm,高h=DE=30 cm.以直线AB为轴旋转一周,得到一个上、下是圆锥,中间是圆柱的组合体(如图②),求这个组合体的全面积.(第11题)【解】在等腰梯形ABCD中,∵CD=50,AB=90,且DE⊥AB,∴AE=12×(90-50)=20.∴AD=202+302=10 13 ,∴S锥侧=πrl=π×30×10 13=300 13π,S柱侧=2πrh=2π×30×50=3000π.∴S全=2S锥侧+S柱侧=600 13π+3000π=600(13+5)π (cm2).12. 工人师傅要在如图的一边长为40 cm的正方形铁皮上裁剪下一块完整的圆形和一块完整的扇形铁皮,使之可以做成一个圆锥模型.请你帮助工人师傅设计三种不同的裁剪方案(画出示意图).(第12题)【解】设计方案示意图如解图所示.(第12题解)13.如图是一个几何体的三视图.(1)写出这个几何体的名称;(2)根据图中标注的数据,请计算这个几何体的外表积;(3)假设一只蚂蚁要从这个几何体的点B 出发,沿外表爬到AC 的中点D ,请你求出这条路线的最短距离.(第13题)【解】 (1)圆锥.(2)S 外表积=S 底+S 侧=π×⎝⎛⎭⎫422+π×42×6=16π(cm 2).(第13题解)(3)如解图,把圆锥侧面展开,得到扇形ABB′,圆心角为∠BAB′=360°×26=120°,AC 平分∠BAB ′.蚂蚁爬行的最短距离相当于BD 的长. ∵∠BAC =12∠BAB ′=60°,AC =AB =6,∴△ABC 是正三角形. ∵D 是AC 的中点, ∴BD 为正△ABC 的高. ∴BD =3 3.。
新浙教版九年级数学下册第三章《3.4简单几何体的表面展开图》优课件(共12张PPT)
一起探究
—— 40 —— —— 40 —— —— 40 —— —20—
—20—
—20—
主 视 图
俯 视 图
—20—
—20—
左 视 图
主 视 图
—20—
俯 视 图
—20—
左 视 图
—— 40 ——
(1) (3)
(2) (4)
练习
下列各图是几何体的平面展开图,猜想下列展开图可折成 什么立体图形,并指出围成的几何体的形状.
一起探究
图3-4和图3-5分别是某几何体的三视图.(单位: mm)
(1)请分别说出他们所对应的几何体的名称. (2)分别计算这两个几何体的表面积. (3)小明认为,图3-5所示三视图所对应的几何体
一起探究
一个外形为长方体的纸箱的大小如图3-6所示(单位: cm),一只昆虫要从纸箱的顶点A沿表面爬到另一个顶点B, 它沿那条路线爬行的距离最短?请说明理由,并求出这个 最短距离.
G E
A
B D
F C
观察与思考
观察下面小亮的回答问题的过程,想一想它的解法是否
确.为什么? 小亮是这样解答的:
将纸箱看成长方体,它的平面展开图3-7所示.连结AB, 根据两点之间线段最短,可知线段AB就是昆虫爬行距离 最短的路线. 在RT△ACB中,根据勾股定理,有AB≈42.42(cm)
浙教版九年级下
3.4 简单几何体的表面展开图
几何体的展开图在生产时间中有着广泛的应用.通过 几何体的展开图可以确定和制作立体模型,也可以计算 相关集合体的侧面积和表面积.
观察与思考
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
最新中小学教案、试题、试卷
教案、试题、试卷中小学
1
3.4 简单几何体的表面展开图(第2课时)
若圆柱的底面半径为r,母线为l,则S柱侧=________,S柱全=____________.
A组 基础训练
1.已知圆柱的底面半径为1,母线长为2,则圆柱的侧面积为( )
A.2 B.4 C.2π D.4π
2.(湖州中考)如图是按1∶10的比例画出的一个几何体的三视图,则该几何体的侧面积是( )
第2题图
A.200cm2 B.600cm2 C.100πcm2 D.200πcm2
1.如图是某几何体的三视图,其侧面积是( )
第3题图
A.6
B.4π
C.6π
D.12π
4.把长和宽分别为6cm和4cm的矩形纸片卷成一个圆柱状,则这个圆柱的底面半径为( )
A.2πcm B.3πcm C.π3cm D.2πcm或3πcm
5.圆柱的底面直径为2,侧面积为8π,则圆柱的高为( )
A.2 B.4 C.6 D.1
6.已知一个几何体的三视图如图,根据主视图中的有关数据(单位:cm),这个几何体的表面积为(A)
最新中小学教案、试题、试卷
教案、试题、试卷中小学
2
第6题图
A.340πcm2 B.276πcm2 C.349πcm2 D.320πcm2
2.如图,茶杯中部是一条装饰带,这条装饰带的面积是________cm2.
第7题图
8.已知矩形ABCD的一边AB=2cm,另一边AD=4cm,则以直线AD为轴旋转一周所得到的图形是
________,其侧面积是________cm2.
9.如图是一个几何体的三视图(含有数据),则这个几何体的全面积等于________.
第9题图
2.农村常需要搭建截面为半圆形的全封闭蔬菜塑料暖房(如图所示),则需塑料布y(m2)与半径R(m)
的函数关系式是(不考虑塑料埋在土里的部分)________________.
第10题图
11.如图,透明的圆柱形容器(容器厚度忽略不计)的高为12cm,底面周长为10cm,在容器内壁离容
器底部3cm的点B处有一饭粒,此时一只蚂蚁正好在容器外壁,且离容器上沿3cm的点A处,则蚂蚁吃到
饭粒需爬行的最短路径是多少?
最新中小学教案、试题、试卷
教案、试题、试卷中小学
3
第11题图
B组 自主提高
12.一个圆柱的侧面展开图是一个正方形,它的底面半径为10cm,则这个圆柱的高为( )
A.10πcm B.20πcm C.10cm D.20cm
13.如图所示,一只封闭的圆柱形水桶内盛了半桶水(桶的厚度忽略不计),圆柱形水桶的底面直径与
母线长相等,现将该水桶水平放置后如图所示,设图中水所形成的几何体的表面积分别为S1,S2,则S1与
S2的大小关系是( )
第13题图
A.S1=S2
B.S1>S2
C.S1
14.已知一个圆柱的侧面展开图为如图所示的矩形,则其底面圆的面积为____________.
第14题图
C组 综合运用
