弹性力学问题的求解方法
弹性力学公式

2°斜截面上的正应力:全应力矢量p N 在外法线方向n 上的投影即为斜截面上的正应力σN :=r r m n ⋅r r r r r r nσ=n p n ⋅()()x y z p ip j p k li j k ++++(){}{}x T x y z y n p p l p m p n lmn p n p ⎧⎫⎪⎪=++==⎨⎬l zx yxx ττσ⎫⎧⎟⎞⎜⎛z p ⎪⎪⎩⎭}){(}{)(n n n m n ml ij Tzyzxzzy y xyσστττστ=⎪⎭⎪⎬⎪⎩⎪⎨⎟⎟⎠⎜⎜⎝=即}){(}{n n ij T N σσ=(2-15)j 3°斜截面上的切应力:全应力矢量p N 在斜截面内的投影即斜截面上的切应力分量为:||n n n p τ=×r r ++216或2222222()()n n n x y z x y z p p p p p l p m p n τσ=−=++−(2-16)τxσz4-4、弹塑性力学中常用的简化力学模型44、弹塑性力学中常用的简化力学模型σA B分析计算有困难与实际符合较好1、理想弹塑性模型:o εεsσ⎨⎧>=≤=ss sE E εεεσεεεσ当当s理想弹塑性力学模型⎩Bσ1tg −2、线性强化弹塑性力学模型As σ1E 计算复杂⎨⎧>−+=≤=ss s s E E εεεεσσεεεσ当当)(1εoEtg 1−sε⎩型线性强化弹塑性力学模3、幂强化力学模型:σ1=n 参数少想弹性模型n A n<<=εσ100=n 便于分析理想塑性模型当理想弹性模型当A n A n ====σεσ01ε1幂强化力学模型4、刚塑性力学模型(理想塑性模型)在应力到达屈服极限之前应变为零。
AσB分析计算容易oε刚塑性力学模型5σ(刚塑性力学模型)5.理想塑性力学模型σssσσ=ε6.σ6.理想弹性力学模型εσE =ε4-6、常用屈服条件:对屈服条件的研究已有两个世纪。
6-1弹性力学平面问题(基本理论)

v 0 x x l
x ( sin ) xy cos 0 y cos yx ( sin ) 0
例6-3
图示薄板,在y方向受均匀拉力作用, 证明在板中间突出部分(1 2 )的尖 点A处无应力存在。
(a) (b)
(2) x C ( x 2 y 2 ), y Cy 2, xy 2Cxy;
解:(1) 将式(a)代入平衡方程:
x xy Fbx 0 x y yx y Fby 0 x y
3xy 2 3xy 2 0
y y 0
y
xy
x y y 0 p( x) p0 l (2) BC段(x l): l1 1, l2 0
u |x l 0, v |x l 0
u y 0,
x l
y 0
0
(3) AC段(y x tan):
l1 cos( N , x) cos(90 ) sin
( x ) s l1 ( yx ) s l2 px ( xy ) s l1 ( y ) s l2 p y
px p y 0
x x h 0
xy x h
0
右侧面: x h l1 1, l2 0 px y, p y 0 代入应力边界条件公式,有
l O x a b
z p
y
l a , l b ——近似认为无限长
2. 受力特征
外力(体力、面力)平行于横截面作用,且沿长度 z 方 向不变化。
如水坝、滚柱、厚壁圆筒等。
水坝 3. 简化分析
(1)位移分量
《弹性力学》第五章平面问题的复变函数法

在非线性弹性力学中的应用
解决几何非线性问题
01
通过引入复变函数法,可以更精确地描述和分析材料
的几何非线性行为,如大变形、弯曲和扭转等。
分析材料非线性特性
02 复变函数法可用于研究材料的非线性本构关系,包括
弹性模量、泊松比和屈服强度等随应变变化的规律。
求解非线性弹性力学方程
03
利用复变函数法的数学工具,可以更有效地求解非线
03
典型应力集中问题的 复变函数解法
通过实例详细讲解复变函数法在求解 典型应力集中问题中的应用,如圆孔 、椭圆孔、矩形孔等孔边应力集中的 求解。
裂纹问题的复变函数解法
裂纹问题的定义和 分类
介绍裂纹的概念、分类以及裂 纹对材料和结构的影响,如疲 劳裂纹、脆性裂纹等。
复变函数法在裂纹 问题中的应用
阐述如何利用复变函数法求解 裂纹问题,包括裂纹尖端应力 场的求解、裂纹扩展的判据等 。
在迭代计算过程中,要判断 计算结果的收敛性。如果结 果不收敛,应调整计算参数 或改进算法。误差Fra bibliotek析程序实现
分析计算结果的误差来源, 如模型误差、离散化误差、 舍入误差等。尽量减小误差, 提高计算精度。
编写稳定、可靠的程序,实 现复变函数法的数值计算。 程序应具有良好的可读性和 可维护性。
06 复变函数法在弹性力学中 的拓展应用
04 复变函数法在平面问题中 的应用
应力集中问题的复变函数解法
01
应力集中问题的定义 和分类
阐述应力集中的概念,如孔边应力集 中、缺口应力集中等,以及不同类型 的应力集中对材料和结构的影响。
02
复变函数法在应力集 中问题中的应用
介绍如何利用复变函数法求解应力集 中问题,包括应力函数的构造、边界 条件的处理等。
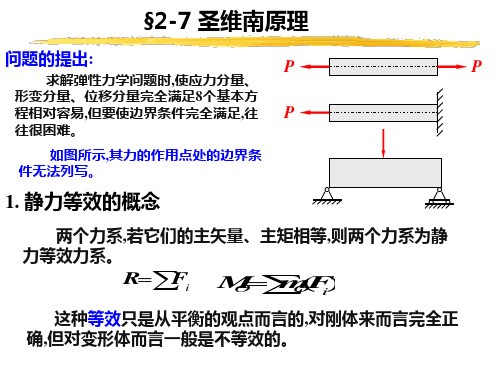
圣维南原理
2 x
y 2
2C
2 y x 2
0
2 xy 2C
xy
式(b)满足相容方程,∴(b)为可能的应变分量。
2y2x2x2y 2 xxyy2C2C0
例 图示矩形截面悬臂梁,在自由端受集中力P作用,不计体力。试根据材料
力 =0学,然公后式说,写明y出这弯些曲表应达力式是否和代剪表x应正力确解。 的表 xy达式,并取挤压应力
x
1 E
( x
y
1 E
( y
xy
xy
G
y
)
x
)
应变协调方程
数学意义:
几何方程——3个应变分量通过2个位移分量描述
力学意义——变形连续
弹性体任意一点的变形必须受到其相邻单元体变形 的约束
•应变协调方程是变形连续的必要和充分条件。
• 例 设 x 3x, y 2y, xy xy, z xz yz 0,求
例 下面给出平面应力问题(单连通域)的应力场和应变场,试分别判断它们
是否为可能的应力场与应变场(不计体力)。
(1) x2 3x2y2, y1 4y4, xy x3;y
(a)
(2) xC (x2y2),yC2,yxy 2 C;xy(b)
解 (1) 将式(a)代入平衡方程:
x xy X 0
研究大坝的应力分布常常用石膏材料或光学 性能好的环氧树脂,而不用混凝土材料
(2)应力函数物理意义 分析:量纲为[N],在平面问题中,边界面力[NL-2], 集中力[NL-1] ,弯矩[N],
应力函数是对平面内某一点的矩。
(3). 应力函数 (x,求y解) 方法
逆解法 半ቤተ መጻሕፍቲ ባይዱ解法
§2-9 按位移求解平面问题
5第三章弹性力学平面问题的解析解法讲解

2 X Y 2 x y y 2 x 2 ( x y ) (1 )
(平面应力情形)
(3)边界条件:
l ( x ) s m( xy ) s X m( y ) s l ( xy ) s Y
x 2 y
2
y 2 x
2
xy
2 xy
(2-28)
(无体力情形)
(3) 再让 x , y , xy满足应力边界条件和位移单值条件 (多连体问题)。
第三章 弹性力学平面问题的 解析解法
第四节 第五节 逆解法与半逆解法—多项式解答 矩形梁的纯弯曲
(2)边界条件: 位移边界条件: 应力边界条件:
(1 )
u s u , vs v
(2)
E u v 1 u v l m X 2 y s 2 y x s 1 x (3 ) v u 1 v u E m l Y 2 1 y x s 2 x y s
4.
按应力求解平面问题的基本方程 说明:
(1)对位移边界问题,不易按应力 求解。
(1)平衡方程
x xy X 0 x y yx y Y 0 x y
(2)相容方程(形变协调方程)
(2)对应力边界问题,且为单连通 问题,满足上述方程的解是唯 一正确解。
(3)对多连通问题,满足上述方程 外,还需满足位移单值条件, 才是唯一正确解。
按应力求解平面问题(X = 常量、Y = 常量)的归结为: (1) 先由方程(2-27)求出应力函数: ( x ,7) 0 4 2 2 4 x x y y x , y , xy (2) 然后将 ( x , y ) 代入式(2-26)求出应力分量:
弹性力学平面问题

§3.1 弹性力学基本概念
4)完全弹性假设 ❖ 假设物体在外加因素去除后能完全恢复原来形状,没有剩余变形。
同时认为应力与应变呈线性关系,即服从虎克定律。
5)微小变形假设 ❖ 假设物体在载荷作用下产生的位移远远小于物体的特征尺寸, 应变分量和转角均远小于1。 •上述5项假设中,前四个属于物理假设,符合前四个基本假设的称 为理想弹性体。第五个假设属于几何假设,符合该假设的理想弹性 体的问题称为线性弹性力学。
第三章 弹性力学平面问题有限元法
§3.1 弹性力学基本概念
• 弹性力学研究方法概述 1)研究弹性体内微分单元体的平衡,写出一组平衡微分方程; 2)由于平衡方程数少于未知应力数,必须考虑几何方面的关系:应 变分量和位移分量之间的微分方程。 3)再引入应力和应变之间的物理关系——广义虎克定律。 4)边界上单元体的内部应力和外部载荷之间的平衡,得到应力边界 条件;考虑边界位移约束得到位移边界条件。 上述基本方程和边界条件组成一个复杂的偏微分方程边值问题,
§3.1 弹性力学基本概念
四、弹性力学中的基本量
• 弹性力学中用以描述研究对象状态的基本力学量包括:外力、应 力、应变、位移。
❖ 外力 1) 体积力(体力):物体内部单位体积上所受外力称为体力 (矢量)。如:重力、惯性力等。 2) 表面力(面力):物体表面单位面积上所受外力称为面力 (矢量)。如:静水压力、接触力等。
❖ 通过前面的基本方程求解弹性力学 问题时,必须考虑上述边界上位移 的协调和力的平衡——边界条件。
❖ 边界条件描述如下:
1)位移边界条件
u = u,v = v 在 Su 上
2)应力边界条件
l x + m xy = t x m y + l xy = t y
弹性力学平面问题极坐标解法
sin θ cosθ ∂ 2 − r2 ∂θ 2
极坐标下的应力函数和相容方程( 极坐标下的应力函数和相容方程(3)
∂2 ∂2 ∂2 1 ∂ 1 ∂2 + 2 = 2 + + 2 2 r ∂r r ∂θ 2 ∂x ∂y ∂r
应力函数的相容方程
∂2 ∂2 2 ∂2 1 ∂ 1 ∂2 2 ∇ 2ϕ = ( 2 + 2 ) ϕ = ( 2 + + 2 ) ϕ =0 2 ∂x ∂y ∂r r ∂r r ∂θ
极坐标系是正交曲线坐标系 极坐标系是正交曲线坐标系 正交
r坐标曲线:坐标θ为常数的曲线(过原点和空间点的直线) 坐标曲线:坐标 为常数的曲线 过原点和空间点的直线) 为常数的曲线( 坐标曲线 θ坐标曲线:坐标 为常数的曲线(过空间点的圆弧) 坐标曲线: 为常数的曲线( 坐标曲线 坐标r为常数的曲线 过空间点的圆弧) 由坐标确定的空间点, 由坐标确定的空间点,既是两条坐标曲线的交点 过一个空间点的两条坐标曲线都是唯一的,且相互正交。 过一个空间点的两条坐标曲线都是唯一的,且相互正交。其 切线构成局部正交坐标标架
极坐标和直角坐标的坐标变换
∂r 2 x = = cos θ ∂x 2r ∂r 2 y = = sin θ ∂y 2r ∂θ 1 −y y sin θ = ⋅ 2 =− 2 =− 2 y x ∂x r r 1+ 2 x 1 1 x cos θ ∂θ = ⋅ 2 = 2 = 2 y x ∂y r r 1+ 2 x
ε
(1) r
P′A′ − PA AA′ − PP′ = = PA PA ∂u (u r + r d r ) − u r ∂ur ∂r = = dr dr ∂r
ε θ(1) =
弹性力学
22211sin sin 22411cos sin 2241sin cos sin 2d d d ϕϕϕϕϕϕϕϕϕϕϕϕ=-=+=⎰⎰⎰⒈ 何谓理想弹性体?微小位移和形变的假定在推导弹性力学基本方程时起什么作用?⒉ 应力分量除了满足平衡微分方程之外,还需满足什么才是正确的解答?⒊ 如果某一应力边界问题中有m 个主要边界和n 个次要边界,试问在主要边界、次要边界上各应满足什么类型的应力边界条件?各有几个条件?二、取满足相容方程的应力函数Φ=Axy 2,其中A >0为常数,试求出应力分量(不计体力),并画出该应力函数在图示弹性体(厚度为1)边界上的面力分布,在次要边界上表示出面力的主矢量和主矩。
(10分)用应力函数Φ=Axy +Bxy 3+Cy 3+Dy 2求其应力分量(不计体力),并确定常数A 、B 、C 、D 。
(20分)四、半平面体在边界上的O 点作用有水平方向集中力F ,如图所示。
试用应力函数(cos sin )A B Φ=+ρϕϕϕ求其应力分量,并确定常数A 、B 。
(20分)提示:《弹性力学》试题参考答案(答题时间:100分钟)一、填空题(每小题4分)1.最小势能原理等价于弹性力学基本方程中: 平衡微分方程 , 应力边界条件 。
2.一组可能的应力分量应满足: 平衡微分方程 ,相容方程(变形协调条件) 。
3.等截面直杆扭转问题中, M dxdy D=⎰⎰2ϕ的物理意义是 杆端截面上剪应力对转)h轴的矩等于杆截面内的扭矩M 。
4.平面问题的应力函数解法中,Airy 应力函数ϕ在边界上值的物理意义为 边界上某一点(基准点)到任一点外力的矩 。
5.弹性力学平衡微分方程、几何方程的张量表示为:0,=+i j ij X σ ,)(21,,i j j i ij u u +=ε。
二、简述题(每小题6分)1.试简述力学中的圣维南原理,并说明它在弹性力学分析中的作用。
圣维南原理:如果物体的一小部分边界上的面力变换为分布不同但静力等效的面力(主矢与主矩相同),则近处的应力分布将有显著的改变,但远处的应力所受影响可以忽略不计。
弹性力学极坐标求解
的位移分别为
u
u
d
和
u
u
d ,
见图4-2(b)。同样考虑
PA
的转角α
是微小的,我们可以得出:
PA 的线应变: 0
转角:
AAPP u PA
14.05.2021
9
第四章 平面问题的极坐标求解
PB 的线应变:
BBPB PP 1u
转角:
u
需要说明的是: u 是由于环向位移而引起的环向线段的
而ρ,φ又是x,y的函数,如式(b)所示。因此 x, y
可以认为是通过中间变量(ρ,φ)的关于(x,y)的复 合函数。按照复合函数的求导公式,有:
x x x y y y
14.05.2021
17
第四章 平面问题的极坐标求解
其中ρ,φ对x,y的导数,可以由式(b)得出:
弹性力学极坐标求解
第四章 平面问题的极坐标求解
2.正负符号的规定
(1)在极坐标中,ρ从原点出发,以向外为正; 而φ以 x轴正向到 y轴正向的转向为正; (2)应力的表示和符号规定与直角坐标相同,仍 以正面正向,负面负向的应力为正,反之为负; (3)微分体上的体力为 f ρ 和 f φ ,表示于微分体的 中心,分别沿径向和环向,以沿正坐标方向为正 ,反之为负。
14.05.2021
25
第四章 平面问题的极坐标求解
4.5 轴对称应力和相应的位移
1.概念
轴对称,即绕一轴对称,是指通过此轴的任何面均为 对称面。
2.轴对称物理量的特点
(1)方向必须对称,因此,方向不对称的物理量不应 存在。因此:
0
(2)数值必须相同,因此,它只能是ρ的函数,沿φ 向不变 。由此可见,凡是轴对称问题,总是使自变量 减少一维,即:
弹性力学有限元法详解
x
4
i1 4
Ni ( ,)xi
y
i1
Ni ( ,) yi
总体坐标系适用于整体结构,局部坐标系只适用于具体某个 单元。
常用的对于平面问题还有八节点等参元,空间问题有八节 点空间等参元,二十节点等参元等 。
第18页,共40页。
3.2 连续体离散化
5.轴对称单元
对于回转结构,如果约束条件和载荷都对称于回转轴,其 应力、应变和位移也都对称于回转轴线,这类应力应变问题称 为轴对称问题 ,通常用柱坐标来描述应力、应变和位移,单元 为实心圆环体,仅截面不同
1
2
ai
(1
0
)
ai (1 0 ) ai (1 0 )
1
2
ai
(1
0
)
(i, j,l,m)
对于平面应变问题:
E
E 1 2
1
第29页,共40页。
3.3 单元分析
2. 单元分析
由虚功原理得:
Fe
K e BT DBdxdyt A
BT DBdxdyt δe
A
Fe Keδe
单元刚度矩阵可分块表示为:
第10页,共40页。
3.2 连续体离散化
3. 薄板弯曲单元和薄板单元
A. 薄板弯曲单元
l
θxi
i
θyi
wi
m
j
四边形弯 曲单元
四边形单元有四个节点,每个节点有三个自由度,主要承 受横向载荷和绕水平轴的弯矩。
第11页,共40页。
3.2 连续体离散化
3.薄板弯曲单元和薄板单元
A. 薄板弯曲单元
m
θxi
对于平面应变问题:
E
E 1 2
