高考数学二轮复习疯狂专练9立体几何理
备战2023年新高考数学二轮专题复习课件立体几何

第三讲立体几何——大题备考【命题规律】立体几何大题一般为两问:第一问通常是线、面关系的证明;第二问通常跟角有关,一般是求线面角或二面角,有时与距离、几何体的体积有关.微专题1线面角保分题[2022·辽宁沈阳二模]如图,在四棱锥P-ABCD中,底面ABCD是正方形,P A⊥平面ABCD,P A=2AB=4,点M是P A的中点.(1)求证:BD⊥CM;(2)求直线PC与平面MCD所成角的正弦值.提分题例1 [2022·全国乙卷]如图,四面体ABCD中,AD⊥CD,AD=CD,∠ADB=∠BDC,E 为AC的中点.(1)证明:平面BED⊥平面ACD;(2)设AB=BD=2,∠ACB=60°,点F在BD上,当△AFC的面积最小时,求CF与平面ABD所成的角的正弦值.听课笔记:【技法领悟】利用空间向量求线面角的答题模板巩固训练1[2022·山东泰安一模]如图,在四棱锥P-ABCD中,底面ABCD是矩形,AB=2AD=2,P A⊥平面ABCD,E为PD中点.(1)若P A=1,求证:AE⊥平面PCD;(2)当直线PC与平面ACE所成角最大时,求三棱锥E-ABC的体积.微专题2二面角保分题[2022·山东临沂二模]如图,AB是圆柱底面圆O的直径,AA1、CC1为圆柱的母线,四边形ABCD是底面圆O的内接等腰梯形,且AB=AA1=2BC=2CD,E、F分别为A1D、C1C的中点.(1)证明:EF∥平面ABCD;(2)求平面OEF与平面BCC1夹角的余弦值.提分题例2 [2022·湖南岳阳三模]如图,在四棱锥P-ABCD中,底面ABCD是菱形,F是PD 的中点.(1)证明:PB∥平面AFC;(2)若直线P A⊥平面ABCD,AC=AP=2,且P A与平面AFC所成的角正弦值为√21,求7锐二面角F-AC-D的余弦值.听课笔记:AD,现例3 [2022·山东日照二模]如图,等腰梯形ABCD中,AD∥BC,AB=BC=CD=12以AC为折痕把△ABC折起,使点B到达点P的位置,且P A⊥CD.(1)证明:平面APC⊥平面ADC;(2)若M为PD上一点,且三棱锥D-ACM的体积是三棱锥P-ACM体积的2倍,求二面角P-AC-M的余弦值.听课笔记:【技法领悟】利用空间向量求二面角的答题模板巩固训练21.[2022·广东韶关二模]如图,在四棱锥P-ABCD中,底面ABCD为矩形,点S是边AB 的中点.AB=2,AD=4,P A=PD=2√2.(1)若O是侧棱PC的中点,求证:SO∥平面P AD;(2)若二面角P-AD-B的大小为2π,求直线PD与平面PBC所成角的正弦值.32.[2022·河北保定一模]如图,在等腰梯形ABCD中,AD∥BC,AD=AB=CD=1,∠BCD =60°,现将DAC沿AC折起至P AC,使得PB=√2.(1)证明:AB⊥PC;(2)求二面角A-PC-B的余弦值.微专题3探索性问题提分题例4 [2022·山东聊城三模]已知四边形ABCD为平行四边形,E为CD的中点,AB=4,△ADE为等边三角形,将三角形ADE沿AE折起,使点D到达点P的位置,且平面APE⊥平面ABCE.(1)求证:AP⊥BE;(2)试判断在线段PB上是否存在点F,使得平面AEF与平面AEP的夹角为45°.若存在,试确定点F的位置;若不存在,请说明理由.听课笔记:【技法领悟】1.通常假设问题中的数学对象存在或结论成立,再在这个前提下进行推理,如果能推出与条件吻合的数据或事实,说明假设成立,并可进一步证明;否则假设不成立.2.探索线段上是否存在满足条件的点时,一定注意三点共线的条件的应用.巩固训练3[2022·湖南岳阳一模]如图,在三棱锥S-ABC中,SA=SB=SC,BC⊥AC.(1)证明:平面SAB⊥平面ABC;(2)若BC=SC,SC⊥SA,试问在线段SC上是否存在点D,使直线BD与平面SAB所成的角为60°,若存在,请求出D点的位置;若不存在,请说明理由.第三讲立体几何微专题1线面角保分题解析:(1)证明:如图,连接AC,∵四边形ABCD是正方形,∴AC⊥BD.又P A ⊥平面ABCD ,BD ⊂平面ABCD ,∴P A ⊥BD , ∵P A ,AC ⊂平面P AC ,P A∩AC =A , ∴BD ⊥平面P AC , 又CM ⊂平面P AC , ∴BD ⊥CM .(2)易知AB ,AD ,AP 两两垂直,以点A 为原点,建立如图所示的空间直角坐标系A - xyz . ∵P A =2AB =4,∴A (0,0,0),P (0,0,4),M (0,0,2),C (2,2,0),D (0,2,0), ∴MC⃗⃗⃗⃗⃗⃗ =(2,2,-2),MD ⃗⃗⃗⃗⃗⃗ =(0,2,-2),PC ⃗⃗⃗⃗ =(2,2,-4). 设平面MCD 的法向量为n =(x ,y ,z ),则{n ·MC⃗⃗⃗⃗⃗⃗ =2x +2y −2z =0n ·MD ⃗⃗⃗⃗⃗⃗ =2y −2z =0,令y =1,得n =(0,1,1).设直线PC 与平面MCD 所成角为θ,由图可知0<θ<π2,则sinθ=|cos 〈n ,PC ⃗⃗⃗⃗ 〉|=|n·PC ⃗⃗⃗⃗⃗||n ||PC ⃗⃗⃗⃗⃗|=√12+12×√22+22+(−4)2=√36.即直线PC 与平面MCD 所成角的正弦值为√36.提分题[例1] 解析:(1)证明:∵AD =CD ,∠ADB = ∠BDC ,BD =BD , ∴△ABD ≌△CBD ,∴AB =CB .∵E 为AC 的中点,∴DE ⊥AC ,BE ⊥AC . ∵DE∩BE =E ,DE ,BE ⊂平面BED , ∴AC ⊥平面BED .∵AC ⊂平面ACD ,∴平面BED ⊥平面ACD .(2)如图,连接EF .由(1)知AC ⊥平面BED . 又∵EF ⊂平面BED , ∴EF ⊥AC . ∴S △AFC =12AC ·EF .当EF ⊥BD 时,EF 的长最小,此时△AFC 的面积最小. 由(1)知AB =CB =2. 又∵∠ACB =60°,∴△ABC 是边长为2的正三角形,∴BE =√3. ∵AD ⊥CD ,∴DE =1,∴DE 2+BE 2=BD 2,∴DE ⊥BE .以点E 为坐标原点,直线EA ,EB ,ED 分别为x 轴、y 轴、z 轴建立空间直角坐标系,则E (0,0,0),A (1,0,0),B (0,√3,0),C (-1,0,0),D (0,0,1),∴AB ⃗⃗⃗⃗⃗ =(-1,√3,0),AD ⃗⃗⃗⃗⃗ =(-1,0,1),DB ⃗⃗⃗⃗⃗ =(0,√3,-1),ED⃗⃗⃗⃗⃗ =(0,0,1),EC ⃗⃗⃗⃗ =(-1,0,0).设DF ⃗⃗⃗⃗⃗ =λDB ⃗⃗⃗⃗⃗ (0≤λ≤1), 则EF ⃗⃗⃗⃗ =ED ⃗⃗⃗⃗⃗ +DF ⃗⃗⃗⃗⃗ =ED ⃗⃗⃗⃗⃗ +λDB ⃗⃗⃗⃗⃗ =(0,0,1)+λ(0,√3,-1)=(0,√3λ,1-λ). ∵EF ⊥DB , ∴EF⃗⃗⃗⃗ ·DB ⃗⃗⃗⃗⃗ =(0,√3λ,1-λ)·(0,√3,-1)=4λ-1=0, ∴λ=14,∴EF ⃗⃗⃗⃗ =(0,√34,34),∴CF ⃗⃗⃗⃗ =EF ⃗⃗⃗⃗ −EC ⃗⃗⃗⃗ =(0,√34,34)-(-1,0,0)=(1,√34,34).设平面ABD 的法向量为n =(x ,y ,z ), 则{n ·AB ⃗⃗⃗⃗⃗ =0,n ·AD⃗⃗⃗⃗⃗ =0,即{−x +√3y =0,−x +z =0.取y =1,则x =√3,z =√3,∴n =(√3,1,√3).设当△AFC 的面积最小时,CF 与平面ABD 所成的角为θ,则sin θ=|cos 〈n ,CF ⃗⃗⃗⃗ 〉|=|n·CF ⃗⃗⃗⃗⃗||n ||CF ⃗⃗⃗⃗⃗ |=|√3×1+1×√34+√3×34|√3+1+3× √1+316+916=4√37. 故当△AFC 的面积最小时,CF 与平面ABD 所成的角的正弦值为4√37. [巩固训练1]解析:(1)证明:∵P A ⊥平面ABCD ,CD ⊂平面ABCD ,∴P A ⊥CD , ∵四边形ABCD 为矩形,∴AD ⊥CD ,又AD∩P A =A ,AD 、P A ⊂平面P AD ,∴CD ⊥平面P AD , ∵AE ⊂平面P AD ,∴AE ⊥CD ,在△P AD 中,P A =AD ,E 为PD 的中点,∴AE ⊥PD , 而PD∩CD =D ,PD 、CD ⊂平面PCD , ∴AE ⊥平面PCD .(2)以A 为坐标原点,分别以AB 、AD 、AP 所在直线为x 、y 、z 轴建立空间直角坐标系, 设AP =a (a >0),则C (2,1,0),P (0,0,a ),E (0,12,a2),∴AC ⃗⃗⃗⃗⃗ =(2,1,0),AE ⃗⃗⃗⃗⃗ =(0,12,a 2),PC ⃗⃗⃗⃗ =(2,1,-a ), 设平面ACE 的一个法向量为n =(x ,y ,z ), 则{n ·AC ⃗⃗⃗⃗⃗ =2x +y =0n ·AE⃗⃗⃗⃗⃗ =12y +a 2z =0,取y =-a ,可得n =(a2,-a ,-1).设直线PC 与平面ACE 所成角为θ,则sin θ=|cos 〈n ,PC ⃗⃗⃗⃗ 〉|=|n·FC⃗⃗⃗⃗⃗ ||n ||FC⃗⃗⃗⃗⃗ |=√54a 2+1·√5+a 2=√29+20a2+5a ≤27,当且仅当a =√2时等号成立.即当AP =√2时,直线PC 与平面ACE 所成角最大, 此时三棱锥E - ABC 的体积V =13×12×2×1×√22=√26.微专题2 二面角保分题解析:(1)证明:取AD 的中点M ,连接EM 、MC ,∵E 为A 1D 的中点,F 为CC 1的中点,∴EM ∥AA 1,EM =12AA 1,又CF ∥AA 1,CF =12AA 1, ∴EM ∥CF ,EM =CF ,∴四边形EMCF 为平行四边形,∴EF ∥CM , 又EF ⊄平面ABCD ,CM ⊂平面ABCD , ∴EF ∥平面ABCD .(2)设AB =AA 1=2BC =2CD =4,∵AC ⊥BC ,∴AC =2√3.由题意知CA 、CB 、CC 1两两垂直,故以C 为坐标原点,分别以CA 、CB 、CC 1所在直线为x 、y 、z 轴建立空间直角坐标系.则A 1(2√3,0,4)、O (√3,1,0)、F (0,0,2)、C (0,0,0)、D (√3,-1,0), ∴A 1D 的中点E 的坐标为(3√32,-12,2), ∴OF⃗⃗⃗⃗⃗ =(-√3,-1,2),EF ⃗⃗⃗⃗ =(-3√32,12,0),设平面OEF 的一个法向量为n =(x ,y ,z ),则{n ·OF ⃗⃗⃗⃗⃗ =0n ·EF ⃗⃗⃗⃗ =0,即{−√3x −y +2z =0−3√32x +12y =0,即{√3x +y −2z =03√3x −y =0, 令x =√3,得n =(√3,9,6),∵AC ⊥BC ,AC ⊥CC 1,BC ∩CC 1=C , ∴AC ⊥平面BCC 1,∴平面BCC 1的一个法向量为CA ⃗⃗⃗⃗⃗ =(2√3,0,0),cos 〈n ,CA ⃗⃗⃗⃗⃗ 〉=n·CA ⃗⃗⃗⃗⃗|n |·|CA ⃗⃗⃗⃗⃗|=√3+81+36·2√3=√1020, ∴平面OEF 与平面BCC 1夹角的余弦值为√1020. 提分题[例2] 解析:(1)证明:连接BD 交AC 于O , 易证O 为BD 中点,又F 是PD 的中点, 所以OF ∥PB ,又OF ⊂平面AFC ,且PB 不在平面AFC 内, 故PB ∥平面AFC .(2)取PC 中点为Q ,以O 为坐标原点,OB 为x 轴,OC 为y 轴,OQ 为z 轴建立空间直角坐标系,设OB =m ,则A (0,-1,0),B (m ,0,0),C (0,1,0),P (0,-1,2),D (-m ,0,0)⇒F (-m2,-12,1),AP ⃗⃗⃗⃗⃗ =(0,0,2),OF ⃗⃗⃗⃗⃗ =(-m 2,-12,1),OC⃗⃗⃗⃗⃗ =(0,1,0), 设平面AFC 的法向量为n =(x ,y ,z ),由{n ⊥OF ⃗⃗⃗⃗⃗ n ⊥OC ⃗⃗⃗⃗⃗ ⇒{−m2x −12y +z =0y =0,令x =2,有n =(2,0,m ),由P A 与平面AFC 所成的角正弦值为√217⇒√217=|AP ⃗⃗⃗⃗⃗ ·n||AP⃗⃗⃗⃗⃗ |·|n|=2√4+m 2⇒m =√3, 平面ACD 的法向量为m =(0,0,1),则锐二面角F - AC - D 的余弦值为 |m·n ||m |·|n |=√3√7=√217.[例3] 解析:(1)证明:在梯形ABCD 中取AD 中点N ,连接CN , 则由BC 平行且等于AN 知ABCN 为平行四边形,所以CN =AB , 由CN =12AD 知C 点在以AD 为直径的圆上,所以AC ⊥CD .又AP ⊥CD ,AP∩AC =A, AP ,AC ⊂平面P AC , ∴CD ⊥平面P AC , 又CD ⊂平面ADC , ∴平面APC ⊥平面ADC .(2)取AC 中点O ,连接PO ,由AP =PC ,可知PO ⊥AC ,再由平面P AC ⊥平面ACD ,AC 为两面交线,所以PO ⊥平面ACD ,以O 为原点,OA 为x 轴,过O 且与OA 垂直的直线为y 轴,OP 为z 轴建立空间直角坐标系,令AB =2,则A (√3,0,0),C (-√3,0,0),P (0,0,1),D (-√3,2,0), 由V P - ACM ∶V D - ACM =1∶2,得PM⃗⃗⃗⃗⃗⃗ =13PD ⃗⃗⃗⃗⃗ , 所以OM ⃗⃗⃗⃗⃗⃗ =OP ⃗⃗⃗⃗⃗ +PM ⃗⃗⃗⃗⃗⃗ =OP ⃗⃗⃗⃗⃗ +13PD ⃗⃗⃗⃗⃗ =(-√33,23,23), 设平面ACM 的法向量为n =(x ,y ,z ), 则由{n ·OM ⃗⃗⃗⃗⃗⃗ =0n ·OA ⃗⃗⃗⃗⃗ =0得{−√33x +23y +23z =0√3x =0,取z =-1得x =0,y =1,所以n =(0,1,-1),而平面P AC 的法向量m =(0,1,0),所以cos 〈n ,m 〉=m·n |m ||n |=√22. 又因为二面角P - AC - M 为锐二面角,所以其余弦值为√22.[巩固训练2]1.解析:(1)证明:取线段PD 的中点H ,连接SO 、OH 、HA ,如图,在△PCD 中,O 、H 分别是PC 、PD 的中点,所以OH ∥CD 且OH =12CD ,所以OH ∥AS 且OH =AS ,所以四边形ASOH 是平行四边形,所以SO ∥AH ,又AH ⊂平面P AD ,SO ⊄平面P AD ,所以SO ∥平面P AD .(2)取线段AD 、BC 的中点E 、F ,连结PE 、EF .由点E 是线段AD 的中点,P A =PD 可得PE ⊥AD ,又EF ⊥AD ,所以∠PEF 是二面角P - AD - B 的平面角,即∠PEF =23π,以E 为原点,EA⃗⃗⃗⃗⃗ 、EF ⃗⃗⃗⃗ 方向分别为x 轴、y 轴正方向,建立如图所示坐标系,在△P AD 中,AD =4,P A =PD =2√2知:PE =2,所以P (0,-1,√3),D (-2,0,0),B (2,2,0),C (-2,2,0),所以PD⃗⃗⃗⃗⃗ =(-2,1,-√3),PB ⃗⃗⃗⃗⃗ =(2,3,-√3),PC ⃗⃗⃗⃗ =(-2,3,-√3), 设平面PBC 的法向量n =(x ,y ,z ),则{n ·PB ⃗⃗⃗⃗⃗=0n ·PC⃗⃗⃗⃗ =0,即{2x +3y −√3z =0−2x +3y −√3z =0,可取n =(0,1,√3),设直线PD 与平面PBC 所成角为θ, 则sin θ=|cos 〈PD⃗⃗⃗⃗⃗ ,n 〉|=2·2√2=√24,所以直线PD 与平面PBC 所成角的正弦值为√24.2.解析:(1)证明:在等腰梯形ABCD 中,过A 作AE ⊥BC 于E ,过D 作DF ⊥BC 于F ,因为在等腰梯形ABCD 中,AD ∥BC ,AD =AB =CD =1,∠BCD =60°,所以BE =CF =12CD =12,AE =DF =√12−(12)2=√32, 所以AC =BD =√(32)2+(√32)2=√3, BC =2,所以BD 2+CD 2=BC 2,所以BD ⊥CD ,同理AB ⊥AC , 又因为AP =AB =1,PB =√2, ∴AP 2+AB 2=PB 2,∴AB ⊥AP又AC∩AP =A ,AC ,AP ⊂平面ACP , 所以AB ⊥平面ACP , 因为PC ⊂平面ACP , 所以AB ⊥PC .(2)取AC 的中点为M ,BC 的中点为N ,则MN ∥AB , 因为AB ⊥平面ACP ,所以MN ⊥平面ACP ,因为AC ,PM ⊂平面ACP ,所以MN ⊥AC ,MN ⊥PM , 因为P A =PC ,AC 的中点为M ,所以PM ⊥AC , 所以MN ,MC ,MP 两两垂直,所以以M 为原点,以MN 所在直线为x 轴,以MC 所在直线为y 轴,以MP 所在直线为z 轴建立空间直角坐标系,则A (0,-√32,0),B (1,-√32,0),C (0,√32,0),P (0,0,12),PC ⃗⃗⃗⃗ =(0,√32,-12),PB ⃗⃗⃗⃗⃗ =(1,-√32,-12), 平面APC 的一个法向量为m =AB⃗⃗⃗⃗⃗ =(1,0,0), 设平面PBC 的一个法向量为n =(x ,y ,z ),则 {n ·PC⃗⃗⃗⃗ =√32y −12z =0n ·PB ⃗⃗⃗⃗⃗ =x −√32y −12z =0,令y =1,则n =(√3,1,√3),所以cos 〈m ,n 〉=m·n |m ||n |=√31×√7=√217, 因为二面角A - PC - B 为锐角, 所以二面角A - PC - B 的余弦值为√217.微专题3 探索性问题提分题[例4] 解析:(1)证明:因为四边形ABCD 为平行四边形,且△ADE 为等边三角形, 所以∠BCE =120°,又E 为CD 的中点,所以CE =ED =DA =CB ,即△BCE 为等腰三角形, 所以∠CEB =30°.所以∠AEB =180°-∠AED -∠BEC =90°, 即BE ⊥AE .又因为平面AEP ⊥平面ABCE ,平面APE ∩平面ABCE =AE ,BE ⊂平面ABCE , 所以BE ⊥平面APE ,又AP ⊂平面APE ,所以BE ⊥AP .(2)取AE 的中点O ,连接PO ,由于△APE 为正三角形,则PO ⊥AE , 又平面APE ⊥平面ABCE ,平面APE ∩平面ABCE =AE ,PO ⊂平面EAP , 所以PO ⊥平面ABCE ,PO =√3,BE =2√3, 取AB 的中点G ,则OG ∥BE ,由(1)得BE ⊥AE ,所以OG ⊥AE ,以点O 为原点,分别以OA ,OG ,OP 所在的直线为x 轴,y 轴,z 轴,建立如图所示的空间直角坐标系O - xyz ,则O (0,0,0),A (1,0,0),B (-1,2√3,0),P (0,0,√3),E (-1,0,0), 则EA ⃗⃗⃗⃗⃗ =(2,0,0),EB ⃗⃗⃗⃗⃗ =(0,2√3,0),PB ⃗⃗⃗⃗⃗ =(-1,2√3,-√3),EP ⃗⃗⃗⃗ =(1,0,√3), 假设存在点F ,使平面AEF 与平面AEP 的夹角为45°, 设PF⃗⃗⃗⃗ =λPB ⃗⃗⃗⃗⃗ =(-λ,2√3λ,-√3λ),λ∈[0,1], 则EF ⃗⃗⃗⃗ =EP ⃗⃗⃗⃗ +PF ⃗⃗⃗⃗ =(1,0,√3)+(-λ,2√3λ,-√3λ)=(1-λ,2√3λ,√3−√3λ), 设平面AEF 的法向量为m =(x ,y ,z ),由{EF ⃗⃗⃗⃗·m =0EA ⃗⃗⃗⃗⃗ ·m =0得{(1−λ)x +2√3λy +(√3,-√3λ)z =02x =0, 取z =2λ,得m =(0,λ-1,2λ);由(1)知EB⃗⃗⃗⃗⃗ 为平面AEP 的一个法向量, 于是,cos 45°=|cos 〈m ,EB ⃗⃗⃗⃗⃗ 〉|=|m·EB ⃗⃗⃗⃗⃗||m |·|EB ⃗⃗⃗⃗⃗|=2√3|λ−1|2√3·√5λ2−2λ+1=√22,解得λ=13或λ=-1(舍去),所以存在点F ,且当点F 为线段PB 的靠近点P 的三等分点时,平面AEF 与平面AEP 的夹角为45°.[巩固训练3]解析:(1)证明:取AB 的中点E ,连接SE ,CE ,∵SA =SB ,∴SE ⊥AB , ∵BC ⊥AC ,∴三角形ACB 为直角三角形,∴BE =EC , 又BS =SC ,∴△SEC ≌△SEB ,∴∠SEB =∠SEC =90°, ∴SE ⊥EC ,又SE ⊥AB ,AB∩CE =E ,∴SE ⊥平面ABC . 又SE ⊂平面SAB ,∴平面SAB ⊥平面ABC .(2)以E 为坐标原点,平行AC 的直线为x 轴,平行BC 的直线为y 轴,ES 为z 轴建立空间直角坐标系,如图,不妨设SA =SB =SC =2,SC ⊥SA ,则AC =2√2,BC =SC =2知EC =2√3,SE =1,则A (-√2,1,0),B (√2,-1,0),C (√2,1,0),E (0,0,0),S (0,0,1), ∴AB⃗⃗⃗⃗⃗ =(2√2,-2,0),SA ⃗⃗⃗⃗ =(-√2,1,-1), 设D (x ,y ,z ),CD ⃗⃗⃗⃗⃗ =λCS⃗⃗⃗⃗ (0≤λ≤1),则(x -√2,y -1,z )=λ(-√2,-1,1), ∴D (√2−√2λ,1-λ,λ),BD⃗⃗⃗⃗⃗ =(-√2λ,2-λ,λ). 设平面SAB 的一个法向量为n =(x 1,y 1,z 1),则{n ·AB⃗⃗⃗⃗⃗ =2√2x 1−2y 1=0n ·SA ⃗⃗⃗⃗ =−√2x 1+y 1−z 1=0,取x 1=1,得n =(1,√2,0),sin 60°=|n·BD ⃗⃗⃗⃗⃗⃗ ||n ||BD ⃗⃗⃗⃗⃗⃗ |,则√2−2√2λ|√3√2λ2+(2−λ)2+λ2=√32, 得λ2+7λ+1=0,又∵0≤λ≤1,方程无解,∴不存在点D ,使直线BD 与平面SAB 所成的角为60°.。
2020届高考数学二轮复习疯狂专练8三视图(理)
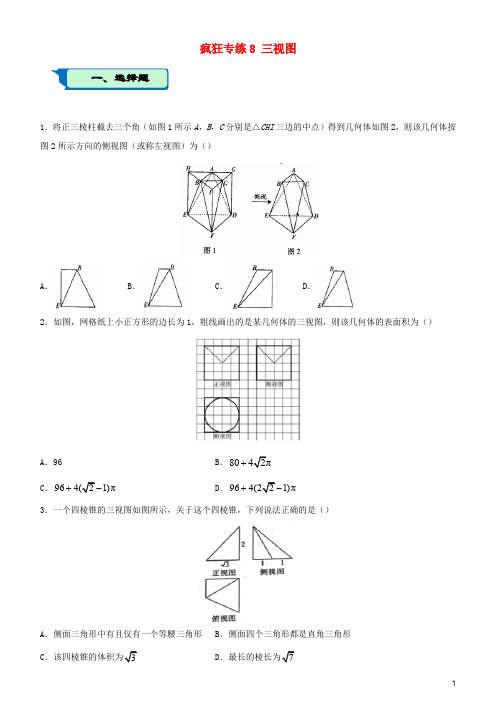
疯狂专练8 三视图1.将正三棱柱截去三个角(如图1所示A ,B ,C 分别是△CHI 三边的中点)得到几何体如图2,则该几何体按图2所示方向的侧视图(或称左视图)为()A .B .C .D .2.如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则该几何体的表面积为()A .96B .80+C .961)π+D .961)π+-3.一个四棱锥的三视图如图所示,关于这个四棱锥,下列说法正确的是()A .侧面三角形中有且仅有一个等腰三角形B .侧面四个三角形都是直角三角形C D一、选择题4.如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的表面积为()A.18+B.54+C.90 D.815.如下图所示,空心圆柱体的主视图是()A.B.C.D.6.一个几何体三视图如图:(每个小正方形边长为1),则该几何体体积为()A.372B.352C.332D.3127.若某几何体的三视图如图所示,则该几何体的表面积为()A.264 B.270 C.274 D.2828.某几何体的三视图如图所示,其中正视图中的曲线为圆弧,则该几何体的体积为()A .322π-B .644π-C .164π-D .16π-9.某柱体的正视图与侧视图是全等的正方形,俯视图是圆,记该柱体的表面积为1S ,其内切球的表面积 为2S ,且12S S λ=,则λ=() A .1B .23C .43D .3210.如图,网格纸上小正方形的边长为1,粗实线及粗虚线画出的是某四棱锥的三视图,则该四棱锥各个 侧面中,最大的侧面面积为()A .2B C .3 D .411.如图,网格纸的小正方形的边长是1,在其上用粗实线和粗虚线画出了某几何体的三视图,则该几何体的体积是()A .7πB .9πC .11πD .13π12.如图,网格纸上小正方形的边长为1,粗实线及粗虚线画出的是某多面体的三视图,则该多面体的 表面积为()A.7+B.7+C.112+D.112+13.在《九章算术》中有称为“羡除”的五面体体积的求法.现有一个类似于“羡除”的有三条棱互相平行的五面体,其三视图如图所示,财该五面体的体积为______.14.某三棱锥的三视图如下图所示,则这个三棱锥中最长的棱与最短的棱的长度分别为___________,__________.15角形,若该几何体的外接球的体积为36π,则该几何体的体积为__________.二、填空题16.如下图,在一个几何体的三视图中,主视图和俯视图都是边长为2的等边三角形,左视图是等腰直角三角形,那么这个几何体外接球的表面积为__________.1.【答案】A【解析】解题时在图2的右边放扇墙(心中有墙),图2所示方向的侧视图, 由于平面AED 仍在平面HEDG 上,故侧视图中仍然看到左侧的一条垂直下边线段的线段,可得答案A . 2.【答案】C【解析】由几何体的三视图可知,几何体为边长为四的正方体,挖去一个底面半径为2,高为2的圆锥所得的组合体,其表面积是正方体的表面面积减去圆锥底面积,加上圆锥侧面积,2264π2π2964π⨯-⨯+⨯⨯=-+,故选C .3.【答案】C 【解析】如图所示:根据三视图知:PD ⊥平面ABCD ,AB AD ⊥,CD AD ⊥,2PD =,AD =1AB =,2CD =,则2DB =,PB PC ==PBC △,PDC △均为等腰三角形,A 错误;PBC △中,PB PC ==2BC =,不满足勾股定理,不是直角三角形,B 错误; 11(12)232P ABCD V -=⨯+⨯=,C 正确;根据以上计算知,最长棱为PB PC ==,D 错误, 故答案选C . 4.【答案】B【解析】由已知中的三视图可得:该几何体是一个以俯视图为底面的斜四棱柱,答 案 与解析一、选择题其底面面积为:3618⨯=, 前后侧面的面积为:36236⨯⨯=,左右侧面的面积为:32=故棱柱的表面积为:183654++=+B . 5.【答案】C【解析】圆柱体的主视图是矩形,因为是空心圆柱,所以要用虚线体现出中间的轮廓线, 故选C . 6.【答案】C【解析】如图所示,根据三视图还原立体图形:将体积分为左右两部分四棱锥和三棱柱体积相加121133334331322V V V =+=⨯⨯⨯+⨯⨯⨯=, 故答案选C . 7.【答案】A【解析】由三视图可得,该几何体的直观图如图所示,延长BE 交DF 于A 点,其中16AB AD DD ===,3AE =,4AF =, 所以表面积()3436536246302642S ⨯=⨯+⨯+⨯+⨯+=,故选A . 8.【答案】D【解析】由三视图可知,几何体为一个长方体切掉14个圆柱, 长方体体积122416V =⨯⨯=;14个圆柱的体积221π14π4V =⨯⨯=,∴几何体体积1216πV V V =-=-,本题正确选项D .9.【答案】D【解析】由已知可得:此柱体为底面直径与高相等的圆柱,设底面圆的半径为r ,则高为2r ,则2212π2π(2)6πS r r r r =+⋅=,又此柱体内切球的半径为r ,则224πS r =,则21226π34π2S r S r λ===,故选D . 10.【答案】B【解析】根据三视图可知,给几何体可以有棱长为2的正方体切割而来即四棱锥O −ABCD ,A 、D为棱的中点,所以最大的侧面面积为OAD S =△B .11.【答案】A【解析】根据空间结构体的三视图,得原空间结构体如下图所示:该几何体是由下面半球的34和上面四棱锥的34组成, 由三视图的棱长及半径关系,可得几何体的体积为32324131341313ππ3π2π237π3243432434V R R =⨯⨯+⨯⨯⨯=⨯⨯⨯+⨯⨯⨯⨯=,所以选A . 12.【答案】A【解析】根据三视图可知,该几何体为四棱锥O ABCD -,由棱长为2的正方体切割而成, 底面ABCD为矩形,2ABCD S ==2112222OCD OBC S S S ===⨯=△△正方形,12OAD ABCD S S ==△易得AB =3OA =,OB =由余弦定理cos OAB ∠==π4OAB ∠=.1332OAB S ∴=⨯⨯=△,四棱锥的表面积2237S =⨯+=+.13.【答案】24【解析】由三视图可得,该几何体为如下图所示的五面体ABCEFD ,其中,底面ABC 为直角三角形,且90BAC ∠=︒,4AB =,3AC =,侧棱DB ,EC ,FA 与底面垂直,且2DB =,5EC FA ==.过点D 作DH BC ∥,DG BA ∥,交EC ,FA 分别于H ,G ,则棱柱ABC DHG -为直棱柱,四棱锥D EFGH -的底面为矩形EFGH ,高为BA . 所以211(43)2342423ABC DHG D EFGH ABCEFD V V V --=+=⨯⨯⨯+⨯⨯=五面体. 故答案为24. 14.【答案】2二、填空题【解析】把三视图还原,可得几何体,如图:易知AC 为最长的棱,长为CD 为最短的棱,长为2.15. 【解析】根据几何体的三视图,得出该几何体如图所示,由该几何体的外接球的体积为36π,即34π36π3R =,3R ∴=,则球心O 到底面等边ABC △的中心O '的距离OO ==',故三棱锥的高32h OO '==,故三棱锥的体积21344V =⨯⨯=. 16.【答案】25π3【解析】2正三角形,因此外接球的半径等于OA ===表面积为225254π4ππ123R =⨯=.11。
2021届全国高考理科数学二轮复习专题强化双基训练 专题九立体几何 A卷含答案

2021届全国高考理科数学二轮复习专题强化双击训练 专题九立体几何 A 卷1.在边长为30米的正六边形广场正上空悬挂一个照明光源,已知这个光源发出的光线过旋转轴的截面是一个等腰直角三角形,要使整个广场都照明,光源悬挂的高度至少为( )A.30米B.20米C.D.15米2.某几何体的三视图如图所示(单位:cm),则该几何体的表面积(单位:2cm )是( )A.16+ B. 16+ C. 18+ D. 18+3.已知四棱锥P ABCD -的体积是,底面ABCD 是正方形,PAB 是等边三角形,平面PAB ⊥平面ABCD ,则四棱锥P ABCD -的外接球的体积为( )A.D.4.设,m n 是两条不同的直线,,αβ是两个不同的平面,则下列命题正确的是( ) A.若//,//m n αα,则//m n B.若//,,m n αβαβ⊂⊂,则//m n C.若,,m n n m αβα⋂=⊂⊥,则n β⊥ D.若,//,m m n n αβ⊥⊂,则αβ⊥5.如图,在长方体1111ABCD A B C D -中,若,,,E F G H 分别是棱 111111,,,A B BB CC C D 的中点,则必有( )A .1BD GH ∥B .BD EF ∥C .平面EFGH ∥平面ABCD D .平面EFGH ∥平面11A BCD6.已知ABC O 的球面上.若球O 的表面积为16π,则O 到平面ABC 的距离为( )B.32C.17.如图,在长方体1111ABCD A B C D -中,1,AB BC ==,点M 在棱1CC 上,且1MD MA ⊥,则当1MAD △的面积最小时,棱1CC 的长为( )A.2C.2 8.如图所示,为了制作一个圆柱形灯笼,先要制作4个全等的矩形骨架,总计耗用9.6米铁丝,骨架把圆柱底面8等分,当灯笼的底面半径为0.3米时,则异面直线82A B 与26A A 所成角的余弦值为( )9.如图,正方体1111ABCD A B C D -的棱长为,线段11B D 上有两个动点,E F ,且12EF =,则下列结论中错误的是( )A. AC BE ⊥B. //EF 平面ABCDC.三棱锥A BEF -的体积为定值D. AEF △的面积与BEF △的面积相等10..若圆柱的一个底面的圆周经过四棱锥四条侧棱的中点,另一个底面的圆心为四棱锥底面的中心,则该圆柱的体积为_____________.11.某空间几何体的三视图如图所示,且该几何体的体积为1,则该几何体的所有面中最大面的面积为____________.12.如图,已知圆柱的轴截面11ABB A 是正方形,C 是圆柱下底面半圆AB 的中点,1C 是圆柱上底面半圆11A B 的中点,那么异面直线1AC 与BC 所成角的正切值为________________.13.如图,在底面是直角梯形的四棱锥P ABCD -中,侧棱PA ⊥底面ABCD ,BC AD ,90ABC ∠=︒,2PA AB BC ===,1AD =,则AD 到平面PBC 的距离为_______.14.如图,AE ⊥平面,,,,1,2ABCD CFAE ADBC AD AB AB AD AE BC ⊥====.(1)求证:BF平面ADE;(2)求直线CE与平面BDE所成角的正弦值;(3)若二面角E BD F--的余弦值为13,求线段CF的长.15.如图,四边形ABCD为正方形,,E F分别为,AD BC的中点,以DF为折痕把DFC折起,使点C到达点P的位置,且PF BF⊥.(1)证明:平面PEF⊥平面ABFD;(2)求DP与平面ABFD所成角的正弦值.答案以及解析1.答案:A解析:设正六边形广场为ABCDEF ,光源悬挂的最低点为P ,则正六棱锥P ABCDEF -的底面边长为30米,高即所求,由题意可知APD 为等腰直角三角形,90,60APD AD ∠=︒=米,所以正六棱锥的高为斜边AD 的一半,即30米,故选A. 2.答案:C解析:几何体的三视图转换为直观图为:该几何体为由棱长为2的正方体切去一个正三棱锥体A BCD -构成的不规则几何体.如图,所以113463222222182322S =⨯-⨯⨯⨯+⨯⨯⨯=+表.故选C .3.答案:A解析:由已知可得13AB AB AB =⨯⨯,则6AB =,设球心为,O O 到平面ABCD 的距离为x ,球O 的半径为R ,则由OP OA =,得22222333)x x ++=+,解得x =所以R 34π3V R ==球,选A.4.答案:D解析:A 错误,同时和一个平面平行的两直线不一定平行,可能相交,可能异面; B 错误,两平面平行,两平面内的直线不一定平行,可能异面;C 错误,一个平面内垂直于两平面交线的直线,不一定和另一平面垂直,可能斜交;D 正确,由,//m m n α⊥便得n α⊥,又n β⊂, βα⊥∴,即αβ⊥.故选D .5.答案:D解析:对于A ,由图形知1BD 与GH 是异面直线,∴A 错误;对于B ,由题意知BD 与EF 也是异面直线,∴B 错误; 对于C ,平面EFGH 与平面ABCD 是相交的,∴C 错误;对于D ,平面//EFGH 平面11A BCD ,理由是:由,,,E F G H 分别是棱111111,,,A B BB CC C D 的中点,得出111//,//EF A B EH A D ,所以//EF 平面11A BCD ,//EF 平面11A BCD ,又EFEH E =,所以平面//EFGH 平面11A BCD .故选D.6.答案:C解析:由等边三角形ABC 2AB =3AB =,则ABC 的外接圆半径23r AB AB ==设球的半径为R ,则由球的表面积为16π,得24π16πR =,得2R =,则球心O 到平面ABC 的距离1d ==,故选C.7.答案:A解析:当Q 为1CC 的中点时,平面1//D BQ 平面PAO ,证明如下:连接11,,D B D Q BQ ,以D 为坐标原点,建立如图所示的空间直角坐标系Dxyz ,则A ,设1(0,1,),(0,0,)(0)M t D z z t ≥≥,则1(0,1,),(3,1,)MD z t AM t =--=-,1,0MD MA t ⊥∴≠,11()0MD AM t z t ⋅=-+-=,即1z t t -=,1111||||22MAD S AM MD ∴==△12==32,当且仅当2t z=时取等号,1CC z ∴==,故选A.8.答案:B解析:设圆柱的高为h ,则20.3889.6h ⨯⨯+=,解得0.6h =,以底面中心O 为原点,2OA 为x 轴,4OA 为y 轴建立如图所示的空间直角坐标系,则8226(0,0.3,0),(0.3,0,0.6),(0.3,0,0),(0.3,0,0)A B A A --,8226(0.3,0.3,0.6),(0.6,0,0)A B A A ∴==-.设直线82A B 与26A A 所成的角为θ,则82268226cos 0.3A B A A A B A A θ⋅====.故选B.9.答案:D解析:对于A ,由题意及图形知,AC ⊥面11DD B B ,故可得出AC BE ⊥,故A 正确;对于B ,由正方体1111ABCD A B C D -的两个底面平行, EF 在其一面上,故EF 与平面ABCD 无公共点,故有//EF 平面ABCD ,故B 正确;对于C ,由几何体的性质及图形知,三角形BEF 的面积是定值, EF 点到面11DD B B ,故可得三棱锥A BEF -的体积为定值,故C 正确;对于D ,由图形可以看出,B 到线段EF 的距离与EF 到EF 的距离不相等,故AEF △的面积与BEF △的面积相等不正确,故D 错误.∴错误命题是D.故选D. 10.答案:π4解析:由题可得,四棱锥底面对角线的长为2,则圆柱底面的半径为12,易知四棱锥的高为2=,故圆柱的高为1,所以圆柱的体积为21ππ124⎛⎫⨯⨯= ⎪⎝⎭.11.答案:3解析:由三视图可知,该几何体为如图所示的四棱锥,记为P ABCD -,其中PA ⊥平面,22,ABCD AB AD BC PA x ====,由该几何体的体积为1,得1(12)2132x +⨯⨯⨯=,解得1x =,故PB CD PD PC ====1,1212PCD PAB PAD S S S >=⨯⨯=△△△,112PBC S =⨯△,1(12)232ABCD S =⨯+⨯=四边形,12PCD S =△,故该几何体中最大面的面积为3 .12.解析:如图,在圆柱下底面圆的圆周上取点D ,其中C 与D 的连线垂直于AB ,连接1,C D AD ,因为C 是圆柱下底面半圆AB 的中点,所以ADBC ,所以直线1AC 与AD 所成的角等于异面直线1AC 与BC 所成的角.易知1C D ⊥圆柱下底面,所以1C D AD ⊥.因为圆柱的轴截面11ABB A 是正方形,所以1C D =,所以直线1AC 与AD .所以异面直线1AC 与BC13.解析:分析知,,AB AD AP 两两垂直,∴可建立以A 为坐标原点,,,AB AD AP 所在的直线分别为x 轴、y 轴、z 轴的空间直角坐标系(如图所示),则()()()()()()0,0,0,2,0,0,2,2,0,0,0,2,2,0,2,0,2,0A B C P PB BC =-=,设平面PBC 的法向量为(),,a b c =n ,则00PB BC ⎧⋅=⎪⎨⋅=⎪⎩n n ,即22020a c b -=⎧⎨=⎩,取1a =,则0,1b c ==,则()1,0,1=n 是平面PBC 的一个法向量.又(2,0,0),AB AD =平面,PBC ∴所求距离为||||AB ⋅=n n 14.答案:(1)依题意,可以建立以A 为原点,分别以,,AB AD AE 的方向为x 轴,y 轴,z 轴正方向的空间直角坐标系(如图),可得()()()()()0,0,01,0,0,1,2,0,0,1,0,,,,002A B C D E .设()0CF h h =>,则()1,2,F h.依题意,()1,0,0AB =是平面ADE 的法向量,又(0,2,)BF h =,可得0BF AB ⋅=,又直线BF ⊄平面ADE ,所以BF 平面ADE .(2)依题意,(1,1,0),(1,0,2),(1,2,2)BD BE CE =-=-=--.设(),,x y z =n 为平面BDE 的法向量,则0,0,BD BE ⎧⋅=⎪⎨⋅=⎪⎩n n 即0,20,x y x z -+=⎧⎨-+=⎩不妨令1z =,可得()2,2,1=n .因此有4cos ,9||||CE CE CE ⋅〈〉==-nn n . 所以,直线CE 与平面BDE 所成角的正弦值为49. (3)设(),,x y z =m 为平面BDF 的法向量,则0,0,BD BF ⎧⋅=⎪⎨⋅=⎪⎩m m 即0,20,x y y hz -+=⎧⎨+=⎩不妨令1y =,可得21,1,h ⎛⎫=- ⎪⎝⎭m . 由题意,有||1|cos ,|||||3⋅〈〉===m n m n m n ,解得87h =.经检验,符合题意. 所以,线段CF 的长为87. 15.答案:(1)由已知可得,,BF PF BF EF ⊥⊥,所以BF ⊥平面PEF . 又BF ⊂平面ABFD ,所以平面PEF ⊥平面ABFD .(2)作PH EF ⊥,垂足为H .由(1)得,PH ⊥平面ABFD . 以H 为坐标原点,HF 的方向为y 轴正方向,||BF 为单位长,建立如图所示的空间直角坐标系H xyz -.由(1)可得,DE PE ⊥.又2,1DP DE ==,所以PE =. 又1,2PF EF ==,故PE PF ⊥.可得32PH EH ==.则333(0,0,0),,1,,0,1,,,22H P D DP HP ⎛⎛⎫⎛⎛⎫--== ⎪ ⎪ ⎪ ⎝⎭⎝⎭⎝⎭⎝⎭为平面ABFD 的法向量.设DP 与平面ABFD 所成角为θ,则34sin 3||||HP DP HP DP θ⋅===.所以DP 与平面ABFD .。
高考数学二轮复习第2部分专题篇素养提升文理专题3立体几何文科第1讲空间几何体三视图表面积与体积文理

表面两两垂直的平面共有
(C )
A.3对
B.4对
C.5对
D.6对
23
【解析】 根据几何体的三视图转换为直观图为:该几何体为四 棱锥体.如图所示:平面与平面的位置关系:平面ABCD⊥平面PBC、 平面ABCD⊥平面PCD、平面PBC⊥平面PCD、平面PAB⊥平面PBC、 平面PAD⊥平面PCD.故选C.
Ⅲ卷
题号 3、12 11、 20(2)
9
考查角度
分值
与棱锥有关的计算;求球的表面积 10
在求点到面的距离时涉及球的表面积;
求四棱锥的体积
11
由三视图求几何体的表面积
5
9
年份 2019
2018
卷别 Ⅰ卷 Ⅱ卷 Ⅲ卷 Ⅰ卷 Ⅱ卷
Ⅲ卷
题号 16 16 16 9 16
3、12
考查角度 点到平面的距离 多面体的棱长与面的个数
21
(3)已知图形中平行于x轴的线段,在直观图中长度保持不变,平 行于y轴的线段,长度变为原来的一半.
(4)在已知图形中过O点作z轴垂直于xOy平面,在直观图中对应的 z′轴也垂直于x′O′y′平面,已知图形中平行于z轴的线段,在直 观图中仍平行于z′轴且长度不变.
22
1.(2020·浙江模拟)一个几何体的三视图如图所示,则该几何体
38
考向2 空间几何体的体积
典例3 (1)(2020·葫芦岛模拟)正方体ABCD-A1B1C1D1的棱
长为2,在A,B,C,D,C1,D1这六个顶点中,选择两个点与A1,B1构
成正三棱锥P,在剩下的四个顶点中选择两个点与A1,B1构成正三棱锥
Q,M表示P与Q的公共部分,则M的体积为
( A)
A.13
2020届高考数学二轮复习疯狂专练3框图(理)
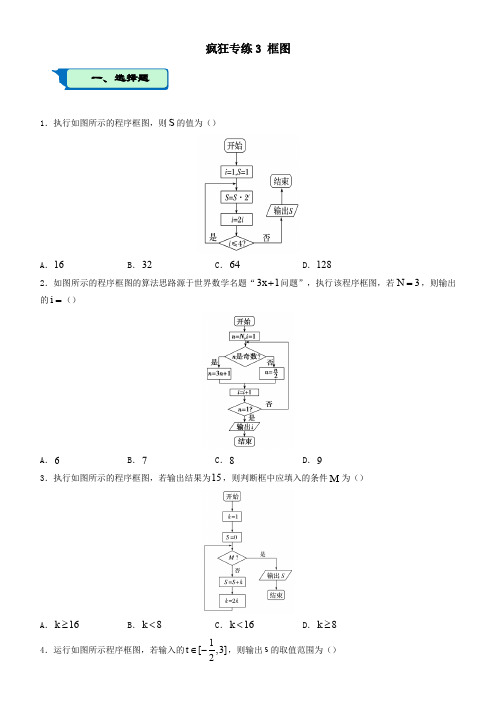
疯狂专练3 框图1.执行如图所示的程序框图,则S的值为()A.16B.32C.64D.1282.如图所示的程序框图的算法思路源于世界数学名题“31x+问题”,执行该程序框图,若3N=,则输出的i=()A.6B.7C.8D.93.执行如图所示的程序框图,若输出结果为15,则判断框中应填入的条件M为()A.16k≥B.8k<C.16k<D.8k≥4.运行如图所示程序框图,若输入的1[,3]2t∈-,则输出s的取值范围为()一、选择题A .[1B .1[,8]2C .[1D .[0,8]5.中国南宋数学家秦九韶(公元1208126)在《数书九章》中给出了求n 次多项式1110n n n n a x a x a x a --++++在x t =处的值的简捷算法,例如多项式323210a x a x a x a +++可改写为3210(())a x a x a x a +++后,再进行求值.如图是实现该算法的一个程序框图,该程序框图可计算的多项式为()A .432234x x x x ++++B .4322345x x x x ++++C .54322345x x x x x +++++D .543223456x x x x x +++++6.元代数学家朱世杰的数学名著《算术启蒙》是中国古代数学的通论,其中关于“松竹并生”的问题:松长五尺,竹长两尺,松日自半,竹日自倍,松竹何日而长等.如图是源于其思想的一个程序框图,若32a =,12b =,则输出的n 等于()A .3B .4C .5D .67.阅读如图的程序框图,如果输出5k =,那么空白的判断框中应填入的条件是()A .24S <-B .25S <-C .26S <-D .25S >-8.运行如图所示的程序框图,则输出的结果S 为()A .1-B .0C .12D .32-9.执行如图所示的程序框图,若输入的04a =,11a =-,23a =,32a =-,41a =,则输出的t 的值为()A .5B .10C .12D .1410.如图给出的是计算11124100+++的值的一个程序框图,则图中判断框内(1)处和执行框中的(2)处应填的语句是()A .100i >,1n n =+B .100i >,2n n =+C .50i >,2n n =+D .50i ≤,2n n =+11.执行如图所示的程序框图,输出的S 值是()A .B .0C D 12.执行如图所示的程序框图,当输出的2S =时,则输入的S 的值为()A .2-B .1-C .12-D .1213.如图所示的茎叶图为某班54名学生的政治考试成绩,程序框图中输入的1a ,2a ,…,54a 为茎叶图中的学生成绩,则输出的S 和n 的值分别是.14.执行如图所示的程序框图,输出的s 值为.二、填空题15.执行如图所示的程序框图,输出S的值为.=在16.运行如图所示的程序框图,设输出的数据构成集合A,从集合A中任取一个元素α,则函数y xα(0,)+∞上是增函数的概率为.1.【答案】D【解析】模拟程序的运行,可得1i =,1S =, 执行循环体,2S =,2i =,满足条件4i ≤, 执行循环体,8S =,4i =,满足条件4i ≤,执行循环体,128S =,8i =,此时,不满足条件4i ≤,退出循环,输出S 的值为128. 2.【答案】C【解析】第一步:10n =,2i =;第二步:5n =,3i =; 第三步:16n =,4i =;第四步:8n =,5u =; 第五步:4n =,6i =;第六步:2n =,7i =; 第七步:1n =,8i =,结束循环,输出的8i =. 3.【答案】A【解析】根据题中所给的程序框图,可以确定该题要求的是1248S =++++,对应的正好是以1为首项,以2为公比的等比数列,该数列的前4项和正好是15. 4.【答案】C【解析】由程序框图可知,该程序表示分段函数222π12cos π,1221(),132t t t t t s t -⎧+-≤<⎪⎪=⎨⎪≤≤⎪⎩,当112t -≤<时,解析式化为π2sin(π)16s t =++,ππ7ππ[,)636t +∈-,[1s ∈,当13t ≤≤时,2321t t -≤-≤,1[,8]2s ∈, 综上所述,s 的取值范围是[1-. 5.【答案】C【解析】依次运行程序可得,①1i =,1P x =+,满足条件,继续运行.②2i =,2(1)22P x x x x =++=++,满足条件,继续运行.③3i =,232(2)323P x x x x x x =+++=+++,满足条件,继续运行.④4i =,32432(23)4234P x x x x x x x x =++++=++++,满足条件,继续运行. ⑤5i =,4325432(234)52345P x x x x x x x x x x =+++++=+++++,不满足条件,答 案 与解析一、选择题停止运行,输出54322345x x x x x +++++. 6.【答案】B【解析】记执行第n 次循环时,a 的值为n a ,则有332()2nn a =⨯,记执行第n 次循环时,b 的值为n b ,则有122nn b =⨯,令332()1222n n⨯≤⨯,则有33()48n≤,故4n ≥. 7.【答案】A【解析】第一次执行循环体后,1S =,1k =,不满足输出的条件,2k =,第二次执行循环体后,0S =,2k =,不满足输出的条件, 3k =,第三次执行循环体后,3S =-,3k =,不满足输出的条件, 4k =,第四次执行循环体后,10S =-,4k =,不满足输出的条件,5k =,第五次执行循环体后,25S =-,5k =,满足输出的条件.8.【答案】B【解析】由程序框图知,1n =,12S =;2n =,0S =;3n =,1S =-;4n =,32S =-;5n =,1S =-;6n =,0S =;7n =,12S =;8n =,0S =;9n =,1S =-, 故S 的值以6为周期循环,而20163366=⨯,所以0S =. 9.【答案】D【解析】初始值1i =,1t =,第一次循环,得2120t =⨯-=,2i =;第二次循环,得033t =+=,3i =; 第三次循环,得2315t =⨯-=,4i =;第四次循环得25414t =⨯+=,5i =,不满足循环条件,退出循环,输出的14t =. 10.【答案】C 【解析】因为12,14,…,1100共50个数,所以算法框图应运行50次,所以变量i 应满足50i >, 因为是求偶数的和,所以应使变量n 满足2n n =+. 11.【答案】D【解析】当1n =,0S =时,πsin3S ==2n =;22018n =<,执行第一次循环可得2πsin 23S =+=,3n =;32018n =<,执行第二次循环可得sin πS =+=,4n =;42018n =<,执行第三次循环可得4πsin3S ==,5n =;52018n =<,执行第四次循环可得5πsin 03S ==,6n =; 62018n =<,执行第五次循环可得6πsin03S ==,7n =; 72018n =<,执行第六次循环可得S =; …,归纳可知,其周期为6,所以20182S S ==S =12.【答案】B【解析】若输入2S =-,则执行循环得13S =,2k =;32S =,3k =;2S =-,4k =;13S =,5k =;32S =,6k =;2S =-,7k =;13S =,8k =;32S =,9k =,结束循环,输出32S =,与题意输出的2S =矛盾; 若输入1S =-,则执行循环得12S =,2k =;2S =,3k =;1S =-,4k =; 12S =,5k =;2S =,6k =;1S =-,7k =;12S =,8k =;2S =,9k =, 结束循环,输出2S =,符合题意; 若输入12S =-,则执行循环得23S =,2k =;3S =,3k =;12S =-,4k =; 23S =,5k =;3S =,6k =;12S =-,7k =;23S =,8k =;3S =,9k =, 结束循环,输出3S =,与题意输出的2S =矛盾; 若输入12S =,则执行循环得2S =,2k =;1S =-,3k =;12S =,4k =; 2S =,5k =;1S =-,6k =;12S =,7k =;2S =,8k =;1S =-,9k =, 结束循环,输出1S =-,与题意输出的2S =矛盾.二、填空题13.【答案】86,13【解析】S 为大于等于80分的学生的平均成绩,计算得86S =,n 表示60分以下的学生人数, 由茎叶图可知13n =. 14.【答案】12-【解析】运行程序如下12018≤,3s =-,2n =,22018≤,12s =-;3n =,32018≤,13s =; 4n =,42018≤,2s =;5n =,所以s 的周期为4,因为2018除以4的余数为2,所以输出12s =-. 15.【答案】1009【解析】执行程序框图,π01sin012S =+⋅=+,3i =,32018≤; 3π013sin0132S =++⋅=+-,5i =,52018≤; 5π0135sin01352S =+-+⋅=+-+,7i =,72018≤; …,2017π0132017sin 01320172S =+-++⋅=+-++,2019i =,20192018>,输出0135720152017S =+-+--+(01)(35)(79)(20152017)=++-++-+++-+1222150421009=++++=+⨯=. 16.【答案】23【解析】执行如图所示的程序框图,可知,第一次循环,满足1i <,2(2)22(2)8y =--⨯-=,输出8y =,此时1i =-; 第二次循环,满足1i <,2(1)2(1)3y =--⨯-=,输出3y =,此时0i =; 第三次循环,满足1i <,20200y =-⨯=,输出0y =,此时1i =,此时终止循环,所以输出的集合{8,3,0}A =,所以从集合A 中任取一个元素α,则函数y x α=在(0,)+∞上是增函数的概率为23P =.。
2022高考数学二轮复习 立体几何经典题型精练(原卷版)

微专题16 立体几何经典题型精练典型例题例1.(2022·全国·高三专题练习)如图所示,三棱柱111ABC A B C -中,所有棱长均为2,1160BAC BAA CAA ∠=∠=∠=︒,P ,Q 分别在AB ,11A C 上(不包括两端),1AP AQ =.(1)求证://PQ 平面11BCC B ;(2)设PQ 与平面ABC 所成角为θ,求sin θ的取值范围.例2.(2022·全国·高三专题练习)如图,在直三棱柱111ABC A B C -中,AC BC ⊥,1AC BC AA ==,D 为11A B 的中点,G 为1AA 的中点,E 为1C D 的中点,3BF AF =,点P 为线段1BC 上的动点(不包括线段1BC 的端点).(1)若//EP 平面CFG ,请确定点P 的位置;(2)求直线CP 与平面CFG 所成角的正弦值的最大值.例3.(2022·辽宁·大连市一0三中学高三开学考试)如图,在四棱锥P ABCD -中,2BC =,//AD BC ,E 为棱P A 的中点,//BE 平面PCD .(1)求AD 的长;(2)若PB AB BC ===,平面PAB ⊥平面PBC ,求二面角B PC D --的大小的取值范围.例4.(2022·全国·高三专题练习)如图,三棱柱111ABC A B C -的底面是边长为4的正三角形,侧面11ACC A ⊥底面ABC ,且侧面11ACC A 为菱形,160A AC ∠=.(1)求二面角1A AB C 所成角θ的正弦值.(2),M N 分别是棱11A C ,11B C 的中点,又2AP BP =.求经过,,M N P 三点的平面截三棱柱111ABC A B C -的截面的周长.过关测试1.(2022·全国·高三专题练习)已知正方体1111ABCD A B C D -.(1)若正方体的棱长为1,求点A 到平面1A BD 的距离;(2)在一个棱长为10的密封正方体盒子中,放一个半径为1的小球,任意摇动盒子,求小球在盒子中不能达到的空间的体积;(3)在空间里,是否存在一个正方体,它的定点1111A B C D A B C D 、、、、、、、到某个平面的距离恰好为0、1、2、3、4、5、6、7,若存在,求出正方体的棱长,若不存在,说明理由. 2.(2022·山东烟台·一模)如图,在四棱锥V -ABCD 中,底面ABCD 为矩形,24AB BC ==,E 为CD 的中点,且△VBC 为等边三角形.(1)若VB ⊥AE ,求证:AE ⊥VE ;(2)若二面角A -BC -V 的大小为30,求直线AV 与平面VCD 所成角的正弦值. 3.(2022·陕西·一模(理))如图,已知直三棱柱111ABC A B C -,O ,M ,N 分别为线段BC ,1AA ,1BB 的中点,P 为线段1AC 上的动点,116AA =,8AC =.(1)若12AO BC =,试证1C N CM ⊥; (2)在(1)的条件下,当6AB =时,试确定动点P 的位置,使线段MP 与平面11BB C C 所成角的正弦值最大.4.(2022·安徽·芜湖一中一模(理))如图所示,已知矩形ABCD 和矩形ADEF 所在的平面互相垂直,222AD AF AB ===,M ,N 分别是对角线BD ,AE 上异于端点的动点,且BM AN =.(1)求证:直线//MN 平面CDE ;(2)当MN 的长最小时,求二面角A MN D --的余弦值.5.(2022·天津·一模)如图,在四棱锥P ABCD -中,底面ABCD 为直角梯形,其中AD BC ∥,3AD =,2AB BC ==,PA ⊥平面ABCD ,且3PA =,点M 在棱PD 上,点N 为BC 中点.(1)证明:若2DM MP =,直线//MN 平面PAB ;(2)求二面角C PD N --的正弦值;(3)是否存在点M ,使NM 与平面PCD PM PD 值;若不存在,说明理由.6.(2022·全国·高三专题练习)如图,四棱锥P —ABCD 的底面ABCD 是边长为2的正方形,P A =PB =3.(1)证明:∠P AD =∠PBC ;(2)当直线P A 与平面PCD 所成角的正弦值最大时,求此时二面角P —AB —C 的大小. 7.(2022·贵州贵阳·高三期末(理))如图,在四棱锥P ABCD -中,底面ABCD 是矩形,PA ⊥平面,ABCD AF PB ⊥,F 为垂足.(1)当点E 在线段BC 上移动时,判断AEF 是否为直角三角形,并说明理由;(2)若2,PA AB EF ==∥PC ,且PB 与平面PAE 所成角为30,求二面角C PE D --的大小.8.(2022·全国·高三专题练习)如图,四边形ABCD 中,π2ADC ∠=,24AD CD ==,AE EC =,沿对角线AC 将△ACD 翻折成△ACD ',使得BE CD '⊥.(1)证明:BD BC '=;(2)若ABD '△为等边三角形,求二面角D AB C '--的余弦值.9.(2022·江苏泰州·高三期末)如图,在三棱锥P ABC -中,2,4,AB PB BC PA PC AC ======(1)平面PAC ⊥平面ABC ;(2)点D 是棱BC 上一点,BD BC λ=,且二面角B PA D --与二面角C PA D --的大小相等,求实数λ的值.10.(2022·江苏扬州·高三期末)如图,在三棱台ABC -A 1B 1C 1中,底面△ABC 是等腰三角形,且BC =8,AB =AC =5,O 为BC 的中点.侧面BCC 1B 1为等腰梯形,且B 1C 1=CC 1=4,M 为B 1C 1中点.(1)证明:平面ABC ⊥平面AOM ;(2)记二面角A -BC -B 1的大小为θ,当θ∈[6π,2π]时,求直线BB 1平面AA 1C 1C 所成角的正弦的最大值.11.(2022·辽宁营口·高三期末)在三棱柱111ABC A B C -中,侧面11AAC C 和侧面11AA B B 是都是边长为2的菱形,D 是1AA 中点,BC =1160CAA BAA ∠=∠=︒(1)求证:1AA ⊥平面BCD ;(2)求二面角1B AC A --的余弦值.12.(2022·全国·高三专题练习(理))如图,四棱锥S ABCD -的底面是正方形,每条侧棱的P 为侧棱SD 上的点.(1)求证:AC SD ⊥;(2)若SD ⊥平面PAC ,求二面角P AC S --的大小;(3)在(2)的条件下,侧棱SC 上是否存在一点E ,使得//BE 平面PAC ?若存在,求:SC SE 的值;若不存在,试说明理由.13.(2022·浙江·高三专题练习)如图,AE ⊥平面,//,//ABCD CF AE AD BC ,,1,2AD AB AB AD AE BC ⊥====.(1)求证://DE 平面BCF ;(2)若二面角E BD F --的余弦值为13,求直线FB 与平面ABCD 所成角的正切值. 14.(2022·全国·高三专题练习(理))如图,在正四棱锥P ABCD -中,PA AB ==E F 、分别为PB PD 、的中点,平面AEF 与棱PC 的交点为G .(1)求异面直线AE 与PF 所成角的大小;(2)求平面AEGF 与平面ABCD 所成锐二面角的大小;(3)求点G 的位置.15.(2022·山西运城·高三期末(理))在①2AE =,②AC BD ⊥,③EAB EBA ∠=∠,这三个条件中选择一个,补充在下面问题中,并给出解答如图,在五面体ABCDE 中,已知___________,AC BC ⊥,//ED AC ,且22AC BC ED ===,DC DB ==(1)求证:平面ABE ⊥与平面ABC ;(2)线段BC 上是否存在一点F ,使得平面AEF 与平面ABE ,若存在,求BF BC 的值;若不存在,说明理由. 16.(2022·全国·高三专题练习)如图,四棱锥P ABCD -中,PAB △是等边三角形,底面ABCD 是直角梯形,AB ∥CD ,,AB AD ⊥2,AB BC ==3ABC π∠=,F ,G 分别是,PC AD 的中点.(1)求证:FG ∥平面PAB ;(2)若3PC =,求直线FG 与平面PBC 所成角的正弦值.17.(2022·全国·高三专题练习)如图,P 为圆锥的顶点,O 是圆锥底面的圆心,AC 为底面直径,ABD △为底面圆O E 在母线PC 上,且1,AE CE EC BD ==⊥.(1)求证:平面BED ⊥平面ABD ;(2)设线段PO 上动点为M ,求直线DM 与平面ABE 所成角的正弦值的最大值. 18.(2022·全国·高三专题练习)如图,在四棱锥P ABCD -中,底面ABCD 是正方形,侧面PAD ⊥底面ABCD ,E ,F 分别为,PA BD 中点,2PA PD AD ===.(1)求证://EF 平面PBC ;(2)求二面角E DF A --的余弦值;(3)在棱PC 上是否存在一点G ,使GF ⊥平面EDF ?若存在,指出点G 的位置;若不存在,说明理由.。
2019届高考数学二轮复习 专题五 立 体 几 何 (讲义训练):第3讲 立体几何中的计算 课时讲义(含答案)
第3讲 立体几何中的计算 课时讲义1. 高考对立体几何的计算,主要是能利用公式求常见几何体(柱体、锥体、台体和球)的表面积与体积.有时还需能解决距离、翻折、存在性等比较综合性的问题.2. 高考中常见的题型为:(1) 常见几何体的表面积与体积的计算;(2) 利用等积变换求距离问题;(3) 通过计算证明平行与垂直等问题;(4) 几何体的内切和外接.1. 棱长都是2的三棱锥的表面积为________. 答案:43解析: 因为四个面是全等的正三角形,则S 表面积=4×34×4=43.2. 如图,正方体ABCDA 1B 1C 1D 1的棱长为1,点P 是棱BB 1的中点,则四棱锥PAA 1C 1C的体积为________.答案:13解析:四棱锥PAA 1C 1C 的体积为13×22×2×1=13.3. (2018·南京学情调研)将一个正方形绕着它的一边所在的直线旋转一周,所得圆柱的体积为27π cm 3,则该圆柱的侧面积为________cm 2.答案:18π解析:设正方形的边长为a cm ,则πa 2·a =27π,解得a =3,所以侧面积2π×3×3=18π.4. (2018·海安质量测试)已知正三棱锥的体积为36 3 cm 3,高为4 cm ,则底面边长为________cm.答案:63解析: 设正三棱锥的底面边长为a ,则其面积为S =34a 2.由题意13·34a 2×4=363,解得a =63., 一) 表面积与体积, 1) 如图,在以A ,B ,C ,D ,E 为顶点的六面体中,△ABC 和△ABD 均为等边三角形,且平面ABC ⊥平面ABD ,EC ⊥平面ABC ,EC =3,AB =2.(1) 求证:DE ∥平面ABC ; (2) 求此六面体的体积.(1) 证明:作DF ⊥AB ,交AB 于点F ,连结CF. 因为平面ABC ⊥平面ABD , 且平面ABC ∩平面ABD =AB , 所以DF ⊥平面ABC.因为EC ⊥平面ABC ,所以DF ∥EC. 因为△ABD 是边长为2的等边三角形, 所以DF =3,因此DF =EC ,所以四边形DECF 为平行四边形,所以DE ∥CF.因为DE ⊄平面ABC ,CF ⊂平面ABC , 所以DE ∥平面ABC.(2) 解:因为△ABD 是等边三角形,所以点F 是AB 的中点. 又△ABC 是等边三角形,所以CF ⊥AB. 由DF ⊥平面ABC 知,DF ⊥CF , 所以CF ⊥平面ABD.因为DE ∥CF ,所以DE ⊥平面ABD , 因此四面体ABDE 的体积为13S △ABD ·DE =1;四面体ABCE 的体积为13S △ABC ·CE =1,而六面体ABCED 的体积=四面体ABDE 的体积+四面体ABCE 的体积, 故所求六面体的体积为2.(2018·苏州暑假测试)如图,正四棱锥P ABCD 的底面一边AB 的长为2 3 cm ,侧面积为83 cm 2,则它的体积为________cm 3.答案:4解析:记正四棱锥P ABCD 的底面中心为点O ,棱AB 的中点为H, 连结PO ,HO ,PH ,则PO ⊥平面ABCD .因为正四棱锥的侧面积为83 cm 2,所以83=4×12×23×PH ,解得PH =2.在直角△PHO 中,PH =2,HO =3,所以PO =1,所以V PABCD =13×S 四边形ABCD ×PO =13×23×23×1=4(cm 3)., 二) 翻折与切割问题, 2) 如图,在菱形ABCD 中,AB =2,∠ABC =60°,BD ∩AC =O ,现将其沿菱形对角线BD 折起得到空间四边形EBCD ,使EC =2.(1) 求证:EO ⊥CD ;(2) 求点O 到平面EDC 的距离.(1) 证明:∵ 四边形ABCD 为菱形,∴ AC ⊥BD . ∵ BD ∩AC =O ,∴ AO ⊥BD ,即EO ⊥BD .∵ 在菱形ABCD 中,AB =2,∠ABC =60°,∴ AD =CD =BC =2,AO =OC =1. ∵ EC =2,CO =EO =1,∴ EO 2+OC 2=EC 2,∴ EO ⊥OC . 又BD ∩OC =O ,∴ EO ⊥平面BCD ,∴ EO ⊥CD .(2) 解:设点O 到平面ECD 的距离为h ,由(1)知EO ⊥平面OCD .V 三棱锥O CDE =V 三棱锥E OCD ,即13S △OCD ·EO =13S △ECD ·h . 在Rt △OCD 中,OC =1,OD =3,∠DOC =90°,∴ S △OCD =12OC ·OD =32.在△CDE 中,ED =DC =2,EC =2,∴ S △CDE =12×2×22-(22)2=72, ∴ h =S △OCD ·EO S △ECD =217,即点O 到平面EDC 的距离为217.如图①,在直角梯形ABCD 中,AD ∥BC ,∠BAD =π2,AB =BC =12AD =a ,点E 是AD的中点,O 是AC 与BE 的交点.将△ABE 沿BE 折起到如图②中△A 1BE 的位置,得到四棱锥A 1BCDE .(1) 求证:CD ⊥平面A 1OC ;(2) 当平面A 1BE ⊥平面BCDE 时,四棱锥A 1BCDE 的体积为362,求a 的值.,①) ,②)(1) 证明:在图①中,因为AB =BC =12AD =a ,点E 是AD 的中点,∠BAD =π2,所以BE ⊥AC ,即在图②中,BE ⊥A 1O ,BE ⊥OC . 又A 1O ∩OC =O ,所以BE ⊥平面A 1OC . 在图①中,BC ∥ED ,且BC =ED ,所以四边形BCDE 是平行四边形,所以BE ∥CD , 所以CD ⊥平面A 1OC .(2) 解:因为平面A 1BE ⊥平面BCDE ,所以A 1O 是四棱锥A 1BCDE 的高. 根据图①可得A 1O =22AB =22a ,平行四边形BCDE 的面积S =BC ·AB =a 2, 所以VA 1BCDE =13×S ×A 1O =13×a 2×22a =26a 3.由26a 3=362,解得a =6., 三) 立体几何中的以算代证问题, 3) (2018·泰州中学学情调研)在直三棱柱ABCA 1B 1C 1中,AB =AC =AA 1=3a ,BC =2a ,D 是BC 的中点,E ,F 分别是AA 1,CC 1上一点,且AE =CF =2a.(1) 求证:B 1F ⊥平面ADF ; (2) 求三棱锥B 1ADF 的体积.(1) 证明:∵ AB =AC ,D 为BC 中点,∴ AD ⊥BC.在直三棱柱ABC -A 1B 1C 1中,B 1B ⊥底面ABC ,AD ⊂底面ABC ,∴ AD ⊥B 1B.∵ BC ∩B 1B =B ,∴ AD ⊥平面B 1BCC 1. ∵ B 1F ⊂平面B 1BCC 1,∴ AD ⊥B 1F.在矩形B 1BCC 1中,C 1F =CD =a ,B 1C 1=CF =2a , ∴ Rt △DCF ≌Rt △FC 1B 1,∴ ∠CFD =∠C 1B 1F , ∴ ∠B 1FD =90°,∴ B 1F ⊥FD . ∵ AD ∩FD =D ,∴ B 1F ⊥平面AFD . (2) 解: ∵ B 1F ⊥平面AFD ,∴ VB 1-ADF =13·S △ADF ·B 1F =13×12×AD ×DF ×B 1F =52a 33.如图①,在直角梯形ABCD 中,∠ADC =90°,CD ∥AB ,AB =4,AD =CD =2.将△ADC 沿AC 折起,使平面ADC ⊥平面ABC ,得到几何体DABC ,如图②.(1) 求证:BC ⊥平面ACD ; (2) 求几何体DABC 的体积.(1) 证明:(证法1)在图①中,由题意知,AC =BC =22,∴ AC 2+BC 2=AB 2,∴ AC ⊥BC .取AC 的中点O ,连结DO ,由AD =CD ,得DO ⊥AC .又平面ADC ⊥平面ABC ,且平面ADC ∩平面ABC =AC ,DO ⊂平面ACD , ∴ OD ⊥平面ABC ,∴ OD ⊥BC . 又AC ⊥BC ,AC ∩OD =O , ∴ BC ⊥平面ACD .(证法2)在图①中,由题意得AC =BC =22,∴ AC 2+BC 2=AB 2, ∴ AC ⊥BC .∵ 平面ADC ⊥平面ABC ,平面ADC ∩平面ABC =AC ,BC ⊂平面ABC , ∴ BC ⊥平面ACD .(2) 解:由(1)知,BC 为三棱锥BACD 的高, 且BC =22,S △ACD =12×2×2=2,∴ 三棱锥BACD 的体积V BACD =13S △ACD ·BC =13×2×22=423,即几何体DABC 的体积为423.1. (2018·天津卷)如图,已知正方体ABCDA 1B 1C 1D 1的棱长为1,则四棱锥A 1BB 1D 1D 的体积为________.答案:13解析:如图,连结A 1C 1,交B 1D 1于点O ,很明显A 1C 1⊥平面BDD 1B 1,则A 1O 是四棱锥的高,且A 1O =12A 1C 1=12×12+12=22,S 四边形BDD 1B 1=BD ×DD 1=2×1=2,结合四棱锥体积公式可得其体积为V =13Sh =13×2×22=13.2. (2018·江苏卷)如图,正方体的棱长为2,以其所有面的中心为顶点的多面体的体积为________.答案:43解析:由图可知,该多面体为两个全等正四棱锥的组合体,正四棱锥的高为1,底面正方形的边长等于2,所以该多面体的体积为2×13×1×(2)2=43.3. (2017·北京卷)如图,在三棱锥PABC 中,PA ⊥AB ,PA ⊥BC ,AB ⊥BC ,PA =AB =BC =2,点D 为线段AC 的中点,E 为线段PC 上一点.(1) 求证:PA ⊥BD ;(2) 求证:平面BDE ⊥平面PAC ;(3) 当PA ∥平面BDE 时,求三棱锥EBCD 的体积.(1) 证明:因为PA ⊥AB ,PA ⊥BC ,AB ∩BC =B ,所以PA ⊥平面ABC. 因为BD ⊂平面ABC ,所以PA ⊥BD.(2) 证明:因为AB =BC ,点D 为AC 的中点,所以BD ⊥AC. 由(1)知,PA ⊥BD ,PA ∩AC =A ,所以BD ⊥平面PAC. 又BD ⊂平面BDE , 所以平面BDE ⊥平面PAC.(3) 解:因为PA ∥平面BDE ,平面PAC ∩平面BDE =DE ,所以PA ∥DE. 因为点D 为AC 的中点,所以DE =12PA =1,BD =DC =2.由(1)知,PA ⊥平面ABC ,所以DE ⊥平面ABC , 所以三棱锥EBCD 的体积为V =13×12×BD ×DC ×DE =13.4. (2017·全国卷Ⅰ)如图,在四棱锥PABCD 中,AB ∥CD ,且∠BAP =∠CDP =90°. (1) 求证:平面PAB ⊥平面PAD ;(2) 若PA =PD =AB =DC ,∠APD =90°,且四棱锥PABCD 的体积为83,求该四棱锥的侧面积.(1) 证明:由已知∠BAP =∠CDP =90°,得AB ⊥AP ,CD ⊥PD .由于AB ∥CD ,故AB ⊥PD .又PA ∩PD =P ,所以AB ⊥平面PAD . 又AB ⊂平面PAB ,所以平面PAB ⊥平面PAD .(2) 解:如图,在平面PAD 内作PE ⊥AD ,垂足为点E .由(1)知,AB ⊥平面PAD ,故AB ⊥PE ,由AB ∩AD =A ,可得PE ⊥平面ABCD .设AB =x ,则由已知可得AD =2x ,PE =22x ,故四棱锥PABCD 的体积V PABCD =13AB ·AD ·PE =13x 3.由题设得13x 3=83,解得x =2. 从而PA =PD =2,AD =BC =22,PB =PC =22,所以△PBC 为等边三角形,可得四棱锥PABCD 的侧面积为 12PA ·PD +12PA ·AB +12PD ·DC +12BC 2sin 60°=6+2 3.5. (2017·全国卷Ⅲ)如图,在四面体ABCD 中,△ABC 是正三角形,AD =CD .(1) 求证:AC ⊥BD ;(2) 已知△ACD 是直角三角形,AB =BD ,若E 为棱BD 上与D 不重合的点,且AE ⊥EC ,求四面体ABCE 与四面体ACDE 的体积比.(1) 证明:如图,取AC 的中点O ,连结DO ,BO .因为AD =CD ,所以AC ⊥DO .又由于△ABC 是正三角形,所以AC ⊥BO . 又DO ∩BO =O ,所以AC ⊥平面DOB . 因为BD ⊂平面DOB ,所以AC ⊥BD . (2) 解:连结EO .由(1)及题设知∠ADC =90°,所以DO =AO . 在Rt △AOB 中,BO 2+AO 2=AB 2. 又AB =BD ,所以BO 2+DO 2=BO 2+AO 2=AB 2=BD 2, 故∠DOB =90°.由题设知△AEC 为直角三角形,所以EO =12AC .又△ABC 是正三角形,且AB =BD ,所以EO =12BD ,故点E 为BD 的中点.所以点E 到平面ABC 的距离为点D 到平面ABC 的距离的12,四面体ABCE 的体积为四面体ABCD 的体积的12,即四面体ABCE 与四面体ACDE 的体积之比为1∶1.(本题模拟高考评分标准,满分14分) (2018·长春模拟)如图,四边形ABCD 为菱形,G 为AC 与BD 的交点,BE ⊥平面ABCD .(1) 求证:平面AEC ⊥平面BED ;(2) 若∠ABC =120°,AE ⊥EC ,三棱锥EACD 的体积为63,求该三棱锥的侧面积.(1) 证明:因为四边形ABCD 为菱形,所以AC ⊥BD . 因为BE ⊥平面ABCD ,AC ⊂平面ABCD ,所以AC ⊥BE .(2分) 因为BD ∩BE =B ,故AC ⊥平面BED .又AC ⊂平面AEC ,所以平面AEC ⊥平面BED .(6分)(2) 解:设AB =x ,在菱形ABCD 中,由∠ABC =120°,得AG =GC =32x ,GB =GD=x2. 因为AE ⊥EC ,所以在Rt △AEC 中,可得EG =32x .(8分)由BE ⊥平面ABCD ,知△EBG 为直角三角形,可得BE =22x .由已知得三棱锥EACD 的体积为63,即13×12·AC ·GD ·BE =624x 3=63,解得x =2.(9分)从而可得AE =EC =ED =6.所以△EAC 的面积为3,△EAD 的面积与△ECD 的面积均为 5.故三棱锥EACD 的侧面积为3+25.(14分)1. 若一个圆柱的侧面展开图是边长为2的正方形,则此圆柱的体积为________. 答案:2π解析: 设圆柱的底面半径为r ,高为h ,则有2πr =2,即r =1π,故圆柱的体积为V =πr 2h =π⎝ ⎛⎭⎪⎫1π2×2=2π.2. 如图,已知AF ⊥平面ABCD ,四边形ABEF 为矩形,四边形ABCD 为直角梯形,∠DAB =90°,AB ∥CD ,AD =AF =CD =2,AB =4.(1) 求证:AF ∥平面BCE ; (2) 求证:AC ⊥平面BCE ; (3) 求三棱锥EBCF 的体积.(1) 证明:∵ 四边形ABEF 为矩形,∴ AF ∥BE .又BE ⊂平面BCE ,AF ⊄平面BCE , ∴ AF ∥平面BCE .(2) 证明:如图,过点C 作CM ⊥AB ,垂足为点M . ∵ AD ⊥DC ,∴ 四边形ADCM 为矩形, ∴ AM =DC =MB =AD =2.∴ AC =22,CM =2,BC =22,∴ AC 2+BC 2=AB 2,∴ AC ⊥BC . ∵ AF ⊥平面ABCD ,AF ∥BE , ∴ BE ⊥平面ABCD ,∴ BE ⊥AC .∵ BE ⊂平面BCE ,BC ⊂平面BCE ,BC ∩BE =B , ∴ AC ⊥平面BCE .(3) 解:∵ AF ⊥平面ABCD ,∴ AF ⊥CM .∵ CM ⊥AB ,AF ⊂平面ABEF ,AB ⊂平面ABEF ,AF ∩AB =A ,∴ CM ⊥平面ABEF ,∴ V 三棱锥EBCF =V 三棱锥CBEF =13×12×BE ×EF ×CM =16×2×4×2=83.3. (2016·江苏卷)现需要设计一个仓库,它由上、下两部分组成,上部分的形状是正四棱锥P A 1B 1C 1D 1,下部分的形状是正四棱柱ABCD A 1B 1C 1D 1(如图),并要求正四棱柱的高O 1O 是正四棱锥的高PO 1的4倍.(1) 若AB =6 m ,PO 1=2 m ,则仓库的容积是多少?(2) 若正四棱锥的侧棱长为6 m ,则当PO 1为多少时,仓库的容积最大?解:(1) ∵ PO 1=2 m ,正四棱柱的高O 1O 是正四棱锥的高PO 1的4倍,∴ O 1O =8 m ,∴ 仓库的容积V =13×62×2+62×8=312(m 3). (2) 若正四棱锥的侧棱长为6 m ,设PO 1=x m ,则O 1O =4x m ,A 1O 1=36-x 2 m ,A 1B 1=2·36-x 2 m , 则仓库的容积V (x )=13×(2·36-x 2)2·x +(2·36-x 2)2·4x =-263x 3+312x (0<x<6), V ′(x )=-26x 2+312(0<x <6).当0<x <23时,V ′(x )>0,V (x )单调递增; 当23<x <6时,V ′(x )<0,V (x )单调递减. 故当x =23时,V (x )取最大值. 即当PO 1=23 m 时,仓库的容积最大.请使用“课后训练·第19讲”活页练习,及时查漏补缺!。
20届高考数学(理)二轮复习 第2部分 专题3 第2讲 立体几何(1)
第2讲 立体几何(大题)热点一 平行、垂直关系的证明用向量知识证明立体几何问题,仍然离不开立体几何中的定理.如要证明线面平行,只需要证明平面外的一条直线和平面内的一条直线平行,即化归为证明线线平行,用向量方法证明直线a ∥b ,只需证明向量a =λb (λ∈R )即可.若用直线的方向向量与平面的法向量垂直来证明线面平行,仍需强调直线在平面外.例1 如图,在直三棱柱ADE -BCF 中,平面ABFE 和平面ABCD 都是正方形且互相垂直,点M 为AB 的中点,点O 为DF 的中点.运用向量方法证明:(1)OM ∥平面BCF ; (2)平面MDF ⊥平面EFCD .证明 方法一 (1)由题意,得AB ,AD ,AE 两两垂直,以点A 为原点建立如图所示的空间直角坐标系A -xyz .设正方形边长为1,则A (0,0,0),B (1,0,0),C (1,1,0),D (0,1,0),F (1,0,1),M ⎝⎛⎭⎫12,0,0,O ⎝⎛⎭⎫12,12,12. OM →=⎝⎛⎭⎫0,-12,-12,BA →=(-1,0,0), ∴OM →·BA →=0,∴OM →⊥BA →. ∵棱柱ADE -BCF 是直三棱柱,∴AB ⊥平面BCF ,∴BA →是平面BCF 的一个法向量, 且OM ⊄平面BCF ,∴OM ∥平面BCF . (2)设平面MDF 与平面EFCD 的法向量分别为 n 1=(x 1,y 1,z 1),n 2=(x 2,y 2,z 2).∵DF →=(1,-1,1),DM →=⎝⎛⎭⎫12,-1,0,DC →=(1,0,0),CF →=(0,-1,1), 由⎩⎪⎨⎪⎧ n 1·DF →=0,n 1·DM →=0,得⎩⎪⎨⎪⎧x 1-y 1+z 1=0,12x 1-y 1=0,令x 1=1,则n 1=⎝⎛⎭⎫1,12,-12. 同理可得n 2=(0,1,1).∵n 1·n 2=0,∴平面MDF ⊥平面EFCD . 方法二 (1)OM →=OF →+FB →+BM →=12DF →-BF →+12BA →=12(DB →+BF →)-BF →+12BA → =-12BD →-12BF →+12BA →=-12(BC →+BA →)-12BF →+12BA →=-12BC →-12BF →.∴向量OM →与向量BF →,BC →共面, 又BF ,BC ⊂平面BCF ,OM ⊄平面BCF , ∴OM ∥平面BCF .(2)由题意及(1)知,BF ,BC ,BA 两两垂直, ∵CD →=BA →,FC →=BC →-BF →, ∴OM →·CD →=⎝⎛⎭⎫-12BC →-12BF →·BA →=0, OM →·FC →=⎝⎛⎭⎫-12BC →-12BF →·(BC →-BF →) =-12BC →2+12BF →2=0,∴OM →⊥CD →,OM →⊥FC →, 即OM ⊥CD ,OM ⊥FC ,又CD ∩FC =C ,CD ,FC ⊂平面EFCD , ∴OM ⊥平面EFCD .又OM ⊂平面MDF ,∴平面MDF ⊥平面EFCD .跟踪演练1 如图,在四棱锥P -ABCD 中,P A ⊥底面ABCD ,AD ∥BC ,AD ⊥CD ,BC =2,AD =CD =1,M 是PB 的中点.(1)求证:AM ∥平面PCD ; (2)求证:平面ACM ⊥平面P AB .证明 (1)如图,以C 为坐标原点建立空间直角坐标系C -xyz ,则A (1,1,0),B (0,2,0),C (0,0,0),D (1,0,0),P (1,1,a )(a >0),M ⎝⎛⎭⎫12,32,a 2,CP →=(1,1,a ),CD →=(1,0,0),AM →=⎝⎛⎭⎫-12,12,a 2, 设平面PCD 的法向量为n 1=(x 0,y 0,z 0),则⎩⎪⎨⎪⎧x 0+y 0+az 0=0,x 0=0,令y 0=a ,则n 1=(0,a ,-1), 所以AM →·n 1=a 2-a 2=0,又AM ⊄平面PCD , 所以AM ∥平面PCD .(2)由(1)得,CA →=(1,1,0),CM →=⎝⎛⎭⎫12,32,a 2, 设平面ACM 的法向量为n 2=(x 1,y 1,z 1), 则⎩⎪⎨⎪⎧x 1+y 1=0,12x 1+32y 1+a2z 1=0, 令x 1=1,则n 2=⎝⎛⎭⎫1,-1,2a , AP →=(0,0,a ),AB →=(-1,1,0),设平面P AB 的法向量为n 3=(x 2,y 2,z 2),则⎩⎪⎨⎪⎧-x 2+y 2=0,az 2=0,令x 2=1,则n 3=(1,1,0), 所以n 2·n 3=1-1=0. 所以平面ACM ⊥平面P AB .热点二 利用空间向量求空间角设直线l ,m 的方向向量分别为a =(a 1,b 1,c 1),b =(a 2,b 2,c 2).平面α,β的法向量分别为μ=(a 3,b 3,c 3),v =(a 4,b 4,c 4)(以下相同). (1)线线夹角设l ,m 的夹角为θ⎝⎛⎭⎫0≤θ≤π2, 则cos θ=|a ·b ||a ||b |=|a 1a 2+b 1b 2+c 1c 2|a 21+b 21+c 21 a 22+b 22+c 22. (2)线面夹角设直线l 与平面α的夹角为θ⎝⎛⎭⎫0≤θ≤π2, 则sin θ=|a ·μ||a ||μ|=|cos 〈a ,μ〉|. (3)二面角设α-a -β的平面角为θ(0≤θ≤π), 则|cos θ|=|μ·v ||μ||v |=|cos 〈μ,v 〉|. 例2 (2019·南昌模拟)如图,四棱台ABCD -A 1B 1C 1D 1中,底面ABCD 是菱形,CC 1⊥底面ABCD ,且∠BAD =60°,CD =CC 1=2C 1D 1=4,E 是棱BB 1的中点.(1)求证:AA 1⊥BD ;(2)求二面角E -A 1C 1-C 的余弦值.(1)证明 因为C 1C ⊥底面ABCD ,所以C 1C ⊥BD . 因为底面ABCD 是菱形,所以BD ⊥AC . 又AC ∩CC 1=C ,AC ,CC 1⊂平面ACC 1A 1, 所以BD ⊥平面ACC 1A 1. 又AA 1⊂平面ACC 1A 1, 所以BD ⊥AA 1.(2)解 如图,设AC 交BD 于点O ,依题意,A 1C 1∥OC 且A 1C 1=OC , 所以四边形A 1OCC 1为平行四边形, 所以A 1O ∥CC 1,且A 1O =CC 1. 所以A 1O ⊥底面ABCD .以O 为原点,OA ,OB ,OA 1所在直线分别为x 轴,y 轴,z 轴建立空间直角坐标系. 则A (23,0,0),A 1(0,0,4),C 1(-23,0,4),B (0,2,0), AB →=(-23,2,0).由A 1B 1----→=12AB →,得B 1(-3,1,4).因为E 是棱BB 1的中点, 所以E ⎝⎛⎭⎫-32,32,2, 所以EA 1→=⎝⎛⎭⎫32,-32,2,A 1C 1----→=(-23,0,0).设n =(x ,y ,z )为平面EA 1C 1的法向量,则⎩⎨⎧n ·A 1C 1----→=-23x =0,n ·EA 1→=32x -32y +2z =0,取z =3,得n =(0,4,3),平面A 1C 1C 的法向量m =(0,1,0),又由图可知,二面角E -A 1C 1-C 为锐二面角, 设二面角E -A 1C 1-C 的平面角为θ, 则cos θ=|m ·n ||m ||n |=45,所以二面角E -A 1C 1-C 的余弦值为45.跟踪演练2 (2019·河南名校联盟联考)如图,在四棱锥P -ABCD 中,∠P AB =90°,AB ∥CD ,且PB =BC =BD =6,CD =2AB =22,∠P AD =120°.E 和F 分别是棱CD 和PC 的中点.(1)求证:CD ⊥BF ;(2)求直线PB 与平面PCD 所成的角的正弦值. (1)证明 ∵E 为CD 中点,CD =2AB , ∴AB =DE .又AB∥CD,∴四边形ABED为平行四边形.∵BC=BD,E为CD中点,∴BE⊥CD,∴四边形ABED为矩形,∴AB⊥AD.由∠P AB=90°,得P A⊥AB,又P A∩AD=A,P A,AD⊂平面P AD,∴AB⊥平面P AD.∵AB∥CD,∴CD⊥平面P AD.又PD⊂平面P AD,∴CD⊥PD.∵EF∥PD,∴CD⊥EF.又CD⊥BE,BE∩EF=E,BE,EF⊂平面BEF,∴CD⊥平面BEF.又∵BF⊂平面BEF,∴CD⊥BF.(2)解由(1)知AB⊥平面P AD.以A为原点,AB所在直线为x轴,AD所在直线为y轴,平面P AD内过点A且与AD垂直的线为z轴建立空间直角坐标系A-xyz,如图所示.∵∠P AD=120°,∴∠P Az=30°.又PB=6,AB=2,AB⊥P A,∴P A=2.∴点P到z轴的距离为1.∴P(0,-1,3),同时知A(0,0,0),B(2,0,0).又BC=BD=6,CD=22,∴BE=2.∴C (22,2,0),D (0,2,0).设平面PCD 的一个法向量为n =(x ,y ,z ), 由⎩⎪⎨⎪⎧n ·PD →=(x ,y ,z )·(0,3,-3)=0,n ·CD →=(x ,y ,z )·(-22,0,0)=0,得⎩⎨⎧3y -3z =0,-22x =0.令y =1,则n =(0,1,3). 又PB →=(2,1,-3),设直线PB 与平面PCD 所成的角为θ. 则sin θ=|cos 〈n ,PB →〉|=|n ·PB →||n |·|PB →|=22+1+3×1+3=66.即直线PB 与平面PCD 所成的角的正弦值为66. 热点三 利用空间向量解决探索性问题与空间向量有关的探究性问题主要有两类:一类是探究线面的位置关系;另一类是探究线面角或二面角满足特定要求时的存在性问题.处理原则是:先建立空间直角坐标系,引入参数(有些是题中已给出),设出关键点的坐标,然后探究这样的点是否存在,或参数是否满足要求,从而作出判断.例3 (2019·临沂模拟)如图,平面ABCD ⊥平面ABE ,四边形ABCD 是边长为2的正方形,AE =1,F 为CE 上的点,且BF ⊥平面ACE .(1)求证:AE ⊥平面BCE ;(2)线段AD 上是否存在一点M ,使平面ABE 与平面MCE 所成二面角的余弦值为34?若存在,试确定点M 的位置;若不存在,请说明理由. (1)证明 ∵BF ⊥平面ACE ,AE ⊂平面ACE , ∴BF ⊥AE ,∵四边形ABCD 是正方形,∴BC ⊥AB ,又平面ABCD ⊥平面ABE ,平面ABCD ∩平面ABE =AB , ∴CB ⊥平面ABE , ∵AE ⊂平面ABE , ∴CB ⊥AE ,∵BF ∩BC =B ,BF ,BC ⊂平面BCE , ∴AE ⊥平面BCE .(2)解 线段AD 上存在一点M ,当AM =3时,使平面ABE 与平面MCE 所成二面角的余弦值为34. ∵AE ⊥平面BCE ,BE ⊂平面BCE , ∴AE ⊥BE ,在Rt △AEB 中,AB =2,AE =1, ∴∠ABE =30°,∠BAE =60°,以A 为原点,建立空间直角坐标系A -xyz , 设AM =h ,则0≤h ≤2, ∵AE =1,∠BAE =60°, ∴M (0,0,h ),E ⎝⎛⎭⎫32,12,0,B (0,2,0),C (0,2,2),所以ME →=⎝⎛⎭⎫32,12,-h ,CE →=⎝⎛⎭⎫32,-32,-2,设平面MCE 的一个法向量n =(x ,y ,z ), 则⎩⎨⎧n ·ME →=3x 2+12y -hz =0,n ·CE →=3x 2-32y -2z =0,令z =2,解得n =⎝⎛⎭⎫33(2+3h ),h -2,2,平面ABE 的一个法向量m =(0,0,1),由题意可知cos 〈m ,n 〉=m ·n|m ||n |=213(2+3h )2+(h -2)2+4=34, 解得h =3,所以当AM =3时,使平面ABE 与平面MCE 所成二面角的余弦值为34. 跟踪演练3 如图,在直三棱柱ABC -A 1B 1C 1中,AC ⊥BC ,AC =BC =AA 1=2,点P 为棱B 1C 1的中点,点Q 为线段A 1B 上一动点.(1)求证:当点Q 为线段A 1B 的中点时,PQ ⊥平面A 1BC ;(2)设BQ →=λBA 1→,试问:是否存在实数λ,使得平面A 1PQ 与平面B 1PQ 所成锐二面角的余弦值为3010?若存在,求出这个实数λ;若不存在,请说明理由. (1)证明 连接AB 1,AC 1,∵点Q 为线段A 1B 的中点, ∴A ,Q ,B 1三点共线, 且Q 为AB 1的中点, ∵点P 为B 1C 1的中点, ∴PQ ∥AC 1.在直三棱柱ABC -A 1B 1C 1中, AC ⊥BC ,∴BC ⊥平面ACC 1A 1, 又AC 1⊂平面ACC 1A 1, ∴BC ⊥AC 1.∵AC =AA 1,∴四边形ACC 1A 1为正方形, ∴AC 1⊥A 1C ,又A 1C ,BC ⊂平面A 1BC ,A 1C ∩BC =C , ∴AC 1⊥平面A 1BC , 而PQ ∥AC 1, ∴PQ ⊥平面A 1BC .(2)解 由题意可知,CA ,CB ,CC 1两两垂直,以C 为原点,分别以CA ,CB ,CC 1所在直线为x 轴、y 轴、z 轴建立空间直角坐标系C -xyz , 连接B 1Q ,PB ,设Q (x ,y ,z ), B (0,2,0),A 1(2,0,2), P (0,1,2),B 1(0,2,2), ∵BQ →=λBA 1→,∴(x ,y -2,z )=λ(2,-2,2), ∴⎩⎪⎨⎪⎧x =2λ,y =2-2λ,z =2λ,∴Q (2λ,2-2λ,2λ). ∵点Q 在线段A 1B 上运动,∴平面A 1PQ 的法向量即为平面A 1PB 的法向量, 设平面A 1PB 的法向量为n 1=(x ,y ,z ), BP →=(0,-1,2),P A 1→=(2,-1,0), 由⎩⎪⎨⎪⎧n 1·BP →=0,n 1·P A 1→=0,得⎩⎪⎨⎪⎧-y +2z =0,2x -y =0,令y =2,得n 1=(1,2,1),设平面B 1PQ 的法向量为n 2=(x ,y ,z ), PB 1→=(0,1,0),B 1Q →=(2λ,-2λ,2λ-2).由⎩⎪⎨⎪⎧n 2·PB 1→=0,n 2·B 1Q →=0,得⎩⎪⎨⎪⎧y =0,2λx -2λy +(2λ-2)z =0,令z =1得n 2=⎝⎛⎭⎫1-λλ,0,1=1λ(1-λ,0,λ), 取n 2=(1-λ,0,λ),由题意得|cos 〈n 1,n 2〉|=|()1,2,1·()1-λ,0,λ|6·(1-λ)2+λ2=16×2λ2-2λ+1=3010,∴9λ2-9λ+2=0, 解得λ=13或λ=23,∴当λ=13或λ=23时,平面A 1PQ 与平面B 1PQ 所成锐二面角的余弦值为3010.真题体验(2019·全国Ⅰ,理,18)如图,直四棱柱ABCD -A 1B 1C 1D 1的底面是菱形,AA 1=4,AB =2,∠BAD =60°,E ,M ,N 分别是BC ,BB 1,A 1D 的中点.(1)证明:MN ∥平面C 1DE ; (2)求二面角A -MA 1-N 的正弦值.(1)证明 连接B 1C ,ME .因为M ,E 分别为BB 1,BC 的中点,所以ME ∥B 1C ,且ME =12B 1C .又因为N 为A 1D 的中点,所以ND =12A 1D .由题设知A 1B 1∥DC 且A 1B 1=DC ,可得B 1C ∥A 1D 且B 1C =A 1D ,故ME ∥ND 且ME =ND ,因此四边形MNDE 为平行四边形,MN ∥ED .又MN ⊄平面C 1DE ,ED ⊂平面C 1DE ,所以MN ∥平面C 1DE .(2)解 由已知可得DE ⊥DA ,以D 为坐标原点,DA →的方向为x 轴正方向,建立如图所示的空间直角坐标系D -xyz ,则A (2,0,0),A 1(2,0,4),M (1,3,2),N (1,0,2),A 1A →=(0,0,-4),A 1M →=(-1,3,-2),A 1N →=(-1,0,-2),MN →=(0,-3,0).设m =(x ,y ,z )为平面A 1MA 的一个法向量,则 ⎩⎪⎨⎪⎧m ·A 1M →=0,m ·A 1A →=0,所以⎩⎨⎧-x +3y -2z =0,-4z =0,可得m =(3,1,0).设n =(p ,q ,r )为平面A 1MN 的一个法向量,则 ⎩⎪⎨⎪⎧n ·MN →=0,n ·A 1N →=0,所以⎩⎨⎧-3q =0,-p -2r =0,可取n =(2,0,-1).于是cos 〈m ,n 〉=m ·n |m ||n |=232×5=155,所以二面角A -MA 1-N 的正弦值为105.押题预测如图1,在梯形ABCD 中,AB ∥CD ,过A ,B 分别作AE ⊥CD ,BF ⊥CD ,垂足分别E ,F ,AB =AE =2,CD =5,已知DE =1,将梯形ABCD 沿AE ,BF 同侧折起,得空间几何体ADE -BCF ,如图2.(1)若AF ⊥BD ,证明:DE ⊥平面ABFE ;(2)若DE ∥CF ,CD =3,线段AB 上存在一点P ,满足CP 与平面ACD 所成角的正弦值为520,求AP 的长.(1)证明 由已知得四边形ABFE 是正方形,且边长为2,在图2中,AF ⊥BE , 由已知得AF ⊥BD ,BE ∩BD =B ,BE ,BD ⊂平面BDE , ∴AF ⊥平面BDE ,又DE ⊂平面BDE ,∴AF ⊥DE ,又AE ⊥DE ,AE ∩AF =A ,AE ,AF ⊂平面ABFE , ∴DE ⊥平面ABFE .(2)解 在图2中,AE ⊥DE ,AE ⊥EF ,DE ∩EF =E ,DE ,EF ⊂平面DEFC ,即AE ⊥平面DEFC ,在梯形DEFC 中,过点D 作DM ∥EF 交CF 于点M ,连接CE , 由题意得DM =2,CM =1, 由勾股定理可得DC ⊥CF , 则∠CDM =π6,CE =2,过E 作EG ⊥EF 交DC 于点G , 可知GE ,EA ,EF 两两垂直,以E 为坐标原点,以EA →,EF →,EG →分别为x 轴,y 轴,z 轴的正方向建立空间直角坐标系, 则A (2,0,0),B (2,2,0),C (0,1,3),D ⎝⎛⎭⎫0,-12,32,AC →=(-2,1,3),AD →=⎝⎛⎭⎫-2,-12,32.设平面ACD 的一个法向量为n =(x ,y ,z ), 由⎩⎪⎨⎪⎧n ·AC →=0,n ·AD →=0,得⎩⎪⎨⎪⎧-2x +y +3z =0,-2x -12y +32z =0, 取x =1,得n =(1,-1,3), 设AP =m ,则P (2,m ,0),0≤m ≤2, 得CP →=(2,m -1,-3), 设CP 与平面ACD 所成的角为θ, sin θ=|cos 〈CP →,n 〉|=|m |5×7+(m -1)2=520⇒m =23(舍负). 所以AP =23.A 组 专题通关1.(2019·全国Ⅱ)如图,长方体ABCD -A 1B 1C 1D 1的底面ABCD 是正方形,点E 在棱AA 1上,BE ⊥EC 1.(1)证明:BE ⊥平面EB 1C 1;(2)若AE =A 1E ,求二面角B -EC -C 1的正弦值.(1)证明 由已知得,B 1C 1⊥平面ABB 1A 1,因为BE ⊂平面ABB 1A 1,故B 1C 1⊥BE . 又BE ⊥EC 1,EC 1∩B 1C 1=C 1, 所以BE ⊥平面EB 1C 1. (2)解 由(1)知∠BEB 1=90°.由题设知Rt △ABE ≌Rt △A 1B 1E ,所以∠AEB =45°,故AE =AB ,AA 1=2AB .以D 为坐标原点,DA →的方向为x 轴正方向,|DA →|为单位长,建立如图所示的空间直角坐标系D -xyz ,则C (0,1,0),B (1,1,0),C 1(0,1,2),E (1,0,1),CB →=(1,0,0),CE →=(1,-1,1),CC 1→=(0,0,2). 设平面EBC 的法向量为n =(x ,y ,z ),则⎩⎪⎨⎪⎧CB →·n =0,CE →·n =0,即⎩⎪⎨⎪⎧x =0,x -y +z =0,所以可取n =(0,-1,-1).设平面ECC 1的法向量为m =(x 1,y 1,z 1),则 ⎩⎪⎨⎪⎧CC 1→·m =0,CE →·m =0,即⎩⎪⎨⎪⎧2z 1=0,x 1-y 1+z 1=0,所以可取m =(1,1,0).于是cos 〈n ,m 〉=n ·m |n ||m |=-12,sin 〈n ,m 〉=1-⎝⎛⎭⎫-122=32, 所以二面角B -EC -C 1的正弦值为32. 2.(2019·全国Ⅲ)图1是由矩形ADEB ,Rt △ABC 和菱形BFGC 组成的一个平面图形,其中AB =1,BE =BF =2,∠FBC =60°.将其沿AB ,BC 折起使得BE 与BF 重合,连接DG ,如图2. (1)证明:图2中的A ,C ,G ,D 四点共面,且平面ABC ⊥平面BCGE ; (2)求图2中的二面角B —CG —A 的大小.(1)证明 由已知得AD ∥BE ,CG ∥BE ,所以AD ∥CG , 故AD ,CG 确定一个平面,从而A ,C ,G ,D 四点共面.由已知得AB ⊥BE ,AB ⊥BC ,BE ∩BC =B , BE ,BC ⊂平面BCGE ,故AB ⊥平面BCGE . 又因为AB ⊂平面ABC ,所以平面ABC ⊥平面BCGE .(2)解 作EH ⊥BC ,垂足为H .因为EH ⊂平面BCGE ,平面BCGE ⊥平面ABC ,平面BCGE ∩平面ABC =BC ,所以EH ⊥平面ABC .由已知,菱形BCGE 的边长为2,∠EBC =60°, 可求得BH =1,EH = 3.以H 为坐标原点,HC →的方向为x 轴的正方向, 建立如图所示的空间直角坐标系H -xyz ,则A (-1,1,0),C (1,0,0),G (2,0,3),CG →=(1,0,3),AC →=(2,-1,0). 设平面ACGD 的法向量为n =(x ,y ,z ), 则⎩⎪⎨⎪⎧CG →·n =0,AC →·n =0,即⎩⎨⎧x +3z =0,2x -y =0.所以可取n =(3,6,-3).又平面BCGE 的法向量可取为m =(0,1,0), 所以cos 〈n ,m 〉=n ·m |n ||m |=32.因此二面角B -CG -A 的大小为30°.3.(2019·马鞍山模拟)如图,在三棱柱ABC -A 1B 1C 1中,∠ACB =90°,A 1B ⊥AC 1,AC =AA 1=4,BC =2.(1)求证:平面A 1ACC 1⊥平面ABC ;(2)若∠A 1AC =60°,在线段AC 上是否存在一点P ,使二面角B -A 1P -C 的平面角的余弦值为34?若存在,确定点P 的位置;若不存在,请说明理由. (1)证明 如图,∵AC =AA 1, ∴四边形AA 1C 1C 为菱形,连接A 1C ,则A 1C ⊥AC 1,又A 1B ⊥AC 1,且A 1C ∩A 1B =A 1, A 1C ,A 1B ⊂平面A 1CB ,∴AC 1⊥平面A 1CB ,则AC 1⊥BC , 又∠ACB =90°,即BC ⊥AC ,又AC 1∩AC =A ,AC 1,AC ⊂平面A 1ACC 1, ∴BC ⊥平面A 1ACC 1,而BC ⊂平面ABC ,∴平面A 1ACC 1⊥平面ABC .(2)解 在平面ACC 1A 1中,过点C 作CE ⊥AC 交A 1C 1于E , 由(1)知,CE ⊥平面ABC ,以C 为坐标原点,分别以CA ,CB 所在直线为x 轴,y 轴建立如图所示的空间直角坐标系C -xyz ,∵AC =AA 1=4,BC =2,∠A 1AC =60°, ∴C (0,0,0),B (0,2,0),A (4,0,0),A 1(2,0,23).设在线段AC 上存在一点P ,满足AP →=λAC →(0≤λ<1),使得二面角B -A 1P -C 的平面角的余弦值为34. 则AP →=(-4λ,0,0).BP →=BA →+AP →=(4,-2,0)+(-4λ,0,0) =(4-4λ,-2,0),A 1P →=A 1A →+AP →=(2-4λ,0,-23), CA 1→=(2,0,23).设平面BA 1P 的一个法向量为m =(x 1,y 1,z 1), 由⎩⎪⎨⎪⎧m ·BP →=(4-4λ)x 1-2y 1=0,m ·A 1P →=(2-4λ)x 1-23z 1=0,取x 1=1,得m =⎝⎛⎭⎪⎫1,2-2λ,1-2λ3;平面A 1PC 的一个法向量为n =(0,1,0). 由|cos 〈m ,n 〉|=|m ·n ||m ||n |=|2-2λ|1+(2-2λ)2+(1-2λ)23×1=34, 解得λ=43或λ=34,因为0≤λ<1,所以λ=34.故在线段AC 上存在一点P ,满足AP →=34AC →,使二面角B -A 1P -C 的平面角的余弦值为34.B 组 能力提高4.如图所示,在四棱锥P -ABCD 中,P A =PD =AD =2CD =2BC =2,且∠ADC =∠BCD =90°.(1)当PB =2时,证明:平面P AD ⊥平面ABCD ;(2)当四棱锥P -ABCD 的体积为34,且二面角P -AD -B 为钝角时,求直线P A 与平面PCD所成角的正弦值.(1)证明 如图所示,取AD 的中点O ,连接PO ,OB .∵P A =PD ,∴PO ⊥AD . ∵∠ADC =∠BCD =90°, ∴BC ∥AD ,又BC =12AD =1,∴BC =OD ,∴四边形BCDO 为矩形, ∴OB =CD =1.在△POB 中,PO =3,OB =1,PB =2, ∴∠POB =90°,则PO ⊥OB .∵AD ∩OB =O ,∴PO ⊥平面ABCD , 又PO ⊂平面P AD , ∴平面P AD ⊥平面ABCD .(2)解 由(1)知AD ⊥PO ,AD ⊥BO , ∵PO ∩OB =O ,∴AD ⊥平面POB , 又AD ⊂平面ABCD , ∴平面POB ⊥平面ABCD . 过点P 作PE ⊥平面ABCD ,则垂足E 一定落在平面POB 与平面ABCD 的交线OB 上. ∵四棱锥P -ABCD 的体积为34,∴13×PE ×12×(AD +BC )×CD =13×PE ×12×(2+1)×1 =12PE =34, ∴PE =32.∵PO =3,∴OE =PO 2-PE 2=32. 以O 为坐标原点,OA ,OB 所在直线分别为x 轴,y 轴, 在平面POB 内过点O 作垂直于平面AOB 的直线为z 轴, 建立如图所示的空间直角坐标系O -xyz . 由题意可知A (1,0,0),P ⎝⎛⎭⎫0,-32,32,D (-1,0,0),C (-1,1,0), 则DP →=⎝⎛⎭⎫1,-32,32,DC →=(0,1,0),P A →=⎝⎛⎭⎫1,32,-32.设平面PCD 的法向量为n =(x ,y ,z ), 则⎩⎪⎨⎪⎧ n ·DP →=0,n ·DC →=0,即⎩⎪⎨⎪⎧x -32y +32z =0,y =0,令x =1,则y =0,z =-23,∴n =⎝⎛⎭⎫1,0,-23. 设直线P A 与平面PCD 所成的角为θ,则sin θ=|P A →·n ||P A →||n |=22×133=31313,故直线P A 与平面PCD 所成角的正弦值为31313.5.如图,已知圆锥OO 1和圆柱O 1O 2的组合体(它们的底面重合),圆锥的底面圆O 1的半径为r =5,OA 为圆锥的母线,AB 为圆柱O 1O 2的母线,D ,E 为下底面圆O 2上的两点,且DE =6,AB =6.4,AO =52,AO ⊥AD .(1)求证:平面ABD ⊥平面ODE; (2)求二面角B -AD -O 的正弦值.(1)证明 依题意知,圆锥的高为h =(52)2-52=5,又圆柱的高为AB =6.4,AO ⊥AD ,所以OD 2=OA 2+AD 2, 因为AB ⊥BD , 所以AD 2=AB 2+BD 2,连接OO 1,O 1O 2,DO 2,易知O ,O 1,O 2三点共线,OO 2⊥DO 2,所以OD 2=OO 22+O 2D 2, 所以BD 2=OO 22+O 2D 2-AO 2-AB 2=(6.4+5)2+52-(52)2-6.42=64,解得BD =8,又因为DE =6,圆O 2的直径为10,圆心O 2在∠BDE 内, 所以∠BDE =90°,所以DE ⊥BD .因为AB ⊥平面BDE ,DE ⊂平面BDE ,所以DE ⊥AB , 因为AB ∩BD =B ,AB ,BD ⊂平面ABD , 所以DE ⊥平面ABD . 又因为DE ⊂平面ODE , 所以平面ABD ⊥平面ODE .(2)解 如图,以D 为原点,DB ,DE 所在直线为x ,y 轴,建立空间直角坐标系.则D (0,0,0),A (8,0,6.4),B (8,0,0),O (4,3,11.4).所以DA →=(8,0,6.4),DB →=(8,0,0),DO →=(4,3,11.4), 设平面DAO 的法向量为u =(x ,y ,z ),所以DA →·u =8x +6.4z =0,DO →·u =4x +3y +11.4z =0,令x =12,则u =(12,41,-15).可取平面BDA 的一个法向量为v =(0,1,0),所以cos 〈u ,v 〉=u·v |u||v |=41582=8210, 所以二面角B -AD -O 的正弦值为3210.。
人教版高考数学(理)二轮复习微专题:微专题7 立体几何中的计算问题
微专题7 立体几何中的计算问题真 题 感 悟(2019·江苏卷)如图,长方体ABCD -A 1B 1C 1D 1的体积是120,E 为CC 1的中点,则三棱锥E -BCD 的体积是________.解析 设长方体中BC =a,CD =b,CC 1=c,则abc =120, ∴V E -BCD =13×12ab×12c =112abc =10.答案 10考 点 整 合空间几何体的两组常用公式(1)直棱柱、正棱锥、正棱台的侧面积及球的表面积公式: ①S 直棱柱侧=ch(c 为底面周长,h 为高); ②S 正棱锥侧=12ch′(c 为底面周长,h′为斜高);③S 正棱台侧=12(c +c′)h′(c′,c 分别为上、下底面的周长,h′为斜高);④S 球表=4πR 2(R 为球的半径). (2)柱体、锥体和球的体积公式: ①V 柱体=Sh(S 为底面面积,h 为高); ②V 锥体=13Sh(S 为底面面积,h 为高);③V 球=43πR 3.热点一 表面积(侧面积)的计算【例1】 (2019·全国Ⅲ卷)图①是由矩形ADEB,Rt△ABC和菱形BFGC组成的一个平面图形,其中AB=1,BE =BF=2,∠FBC=60°.将其沿AB,BC折起使得BE与BF重合,连接DG,如图②.(1)证明:图②中的A,C,G,D四点共面,且平面ABC⊥平面BCGE;(2)求图②中的四边形ACGD的面积.(1)证明由已知得AD∥BE,CG∥BE,所以AD∥CG,故AD,CG确定一个平面,从而A,C,G,D四点共面.由已知得AB⊥BE,AB⊥BC,且BE∩BC=B,BE,BC⊂平面BCGE,故AB⊥平面BCGE.又因为AB⊂平面ABC,所以平面ABC⊥平面BCGE.(2)解取CG的中点M,连接EM,DM.因为AB∥DE,AB⊥平面BCGE,所以DE⊥平面BCGE,又EM,CG⊂平面BCGE,故DE⊥EM,DE⊥CG.由已知,四边形BCGE是菱形,且∠EBC=60°,得EM⊥CG,又DE∩EM=E,DE,EM⊂平面DEM,故CG⊥平面DEM.又DM⊂平面DEM,因此DM⊥CG.在Rt△DEM中,DE=1,EM=3,故DM=2.又CG=BF=2,所以四边形ACGD的面积S=CG·DM=2×2=4.探究提高(1)解决与折叠有关的问题的关键是找出折叠前后的变化量和不变量,一般情况下,折线同一侧的线段的长度是不变量,而位置关系往往会发生变化,抓住不变量是解决问题的突破口.(2)在解决问题时,要综合考虑折叠前后的图形,既要分析折叠后的图形,也要分析折叠前的图形.【训练1】(2019·南京、盐城高三二模)已知正四棱锥P-ABCD的所有棱长都相等,高为2,则该正四棱锥的表面积为________.解析设正四棱锥的棱长为2a,由题得(3a)2=a2+(2)2,所以a=1.所以四棱锥的棱长为2.所以正四棱锥的表面积=2×2+34×22×4=4+4 3.答案4+4 3热点二体积的计算【例2】(1)(2017·江苏卷)如图,在圆柱O1O2内有一个球O,该球与圆柱的上、下底面及母线均相切.记圆柱O 1O 2的体积为V 1,球O 的体积为V 2,则V 1V 2的值是________.(2)(2018·徐州、连云港、宿迁三检)在三棱柱ABC -A 1B 1C 1中,侧棱AA 1⊥平面AB 1C 1,AA 1=1,底面三角形ABC 是边长为2的正三角形,则此三棱柱的体积为________.(3)(2019·南通模拟)设一个正方体与底面边长为23,侧棱长为10的正四棱锥的体积相等,则该正方体的棱长为________.解析 (1)设球半径为R,则圆柱底面圆半径为R,母线长为2R.又V 1=πR 2·2R=2πR 3,V 2=43πR 3,所以V 1V 2=2πR 343πR 3=32.(2)因为AA 1⊥平面AB 1C 1,AB 1⊂平面AB 1C 1,所以AA 1⊥AB 1,又知AA 1=1,A 1B 1=2,所以AB 1=22-12=3,同理可得AC 1=3,又知在△AB 1C 1中,B 1C 1=2,所以△AB 1C 1的边B 1C 1上的高为h =3-1=2,其面积S △AB1C1=12×2×2=2,于是三棱锥A -A 1B 1C 1的体积V三棱锥A -A1B1C1=V三棱锥A1-AB1C1=13×S △AB1C1×AA 1=23,进而可得此三棱柱ABC -A 1B 1C 1的体积V =3V 三棱锥A -A1B1C1=3×23= 2. (3)由题意可得正四棱锥的高为2,体积为13×(23)2×2=8,则正方体的体积为8,所以棱长为2.答案 (1)32(2) 2 (3)2探究提高 (1)涉及柱体、锥体及其简单组合体的计算问题,要在正确理解概念的基础上,画出符合题意的图形或辅助线(面),再分析几何体的结构特征,从而进行解题.(2)求三棱锥的体积,等体积转化是常用的方法,转换原则是其高易求,底面放在已知几何体的某一面上. (3)若所给的几何体的体积不能直接利用公式得出,则常用转换法、分割法、补形法等方法求解. 【训练2】 (2019·苏北四市高三期末)将一个半径为2的圆分成圆心角之比为1∶2的两个扇形,且将这两个扇形分别围成圆锥的侧面,则所得体积较小的圆锥与较大圆锥的体积之比为________.解析 设圆的半径为R,卷成的两个圆锥的底面半径分别为r 1,r 2,高分别为h 1,h 2,由题意圆心角之比为1∶2,可知两个扇形的圆心角分别为120°,240°,∴⎩⎪⎨⎪⎧2πR3=2πr 1,4πR 3=2πr 2,∴r 1=R 3,r 2=2R 3,∴h 1=R 2-r 21=22R 3,h 2=R 2-r 22=5R 3,∴这两个圆锥的体积之比为:13πr 21h 113πr 22h 2=22R 32745R327=1010=110. 答案 1∶10热点三 点到平面距离的计算【例3】 (2019·全国Ⅰ卷)如图,直四棱柱ABCD -A 1B 1C 1D 1的底面是菱形,AA 1=4,AB =2,∠BAD=60°,E,M,N 分别是BC,BB 1,A 1D 的中点. (1)证明:MN∥平面C 1DE ; (2)求点C 到平面C 1DE 的距离. (1)证明 连接B 1C,ME.因为M,E 分别为BB 1,BC 的中点,所以ME∥B 1C,且ME =12B 1C.又因为N 为A 1D 的中点,所以ND =12A 1D.由题设知A 1B 1綊DC,可得B 1C 綊A 1D,故ME 綊ND,因此四边形MNDE 为平行四边形,所以MN∥ED. 又MN ⊄平面C 1DE,ED ⊂平面C 1DE,所以MN∥平面C 1DE.(2)解 在菱形ABCD 中,∠BAD=60°,E 为BC 中点,所以DE⊥BC. 因为棱柱为直棱柱,所以有DE⊥平面BCC 1B 1, 又EC 1⊂平面BCC 1B 1,所以DE⊥EC 1, 又由题意有DE =3,C 1E =17, 所以S △DEC1=12×3×17,设点C 到平面C 1DE 的距离为d,则由V C -C1DE =V C1-CDE ,得13×12×3×17×d=13×12×1×3×4,解得d =417=41717,所以点C 到平面C 1DE 的距离为41717.探究提高 有关立体几何中点到平面的距离的求解,一般利用等积法;求点到平面的距离也可以先作出点到平面的垂线段(要证明所作的线段为垂线段),再求出垂线段的长即为点到平面的距离.【训练3】 (2019·全国Ⅰ卷)已知∠ACB=90°,P 为平面ABC 外一点,PC =2,点P 到∠ACB 两边AC,BC 的距离均为3,那么P 到平面ABC 的距离为________.解析 如图,过点P 作PO⊥平面ABC 于O,则PO 为P 到平面ABC 的距离. 再过O 作OE⊥AC 于E,OF⊥BC 于F, 连接OC,PE,PF,则PE⊥AC ,PF⊥BC. 所以PE =PF =3,所以OE =OF,所以CO为∠ACB的平分线,即∠ACO=45°.在Rt△PEC中,PC=2,PE=3,所以CE=1,所以OE=1,所以PO=PE2-OE2=(3)2-12= 2.答案 2【新题感悟】(2019·全国Ⅱ卷)中国有悠久的金石文化,印信是金石文化的代表之一.印信的形状多为长方体、正方体或圆柱体,但南北朝时期的官员独孤信的印信形状是“半正多面体”(图1).半正多面体是由两种或两种以上的正多边形围成的多面体.半正多面体体现了数学的对称美.图2是一个棱数为48的半正多面体,它的所有顶点都在同一个正方体的表面上,且此正方体的棱长为 1.则该半正多面体共有________个面,其棱长为________.解析先求面数有如下两种方法,法一由“半正多面体”的结构特征及棱数为48可知,其上部分有9个面,中间部分有8个面,下部分有9个面,共有2×9+8=26(个)面.法二一般地,对于凸多面体顶点数(V)+面数(F)-棱数(E)=2.(欧拉公式)由题图知,棱数为48的半正多面体的顶点数为24.故由V+F-E=2,得面数F=2+E-V=2+48-24=26.再求棱长.作中间部分的横截面,由题意知该截面为各顶点都在边长为1的正方形上的正八边形ABCDEFGH,如图,设其边长为x,则正八边形的边长即为棱长.连接AF,过H,G分别作HM⊥AF,GN⊥AF,垂足分别为M,N,则AM=MH=NG=NF=22x.又AM+MN+NF=1,∴22x+x+22x=1.∴x=2-1,即半正多面体的棱长为2-1. 答案26 2-1一、填空题1.(2018·江苏卷)如图所示,正方体的棱长为2,以其所有面的中心为顶点的多面体的体积为________.解析 正方体的棱长为2,以其所有面的中心为顶点的多面体是正八面体,其中正八面体的所有棱长都是2,则该正八面体的体积为13×(2)2×1×2=43.答案 432.(2019·苏北四市调研)已知圆锥的母线长为10 cm,侧面积为60π cm 2,则此圆锥的体积为________cm 3. 解析 设圆锥底面圆的半径为r cm,则侧面积为10πr=60π,解得r =6,则高h =102-r 2=8, 故此圆锥的体积为13πr 2h =13π×36×8=96π(cm 3).答案 96π3.(2019·南京市高三模拟)已知正四棱锥底面边长为42,体积为32,则此正四棱锥的侧棱长为________. 解析 设正四棱锥的高为h,则V =13×(42)2h =32,解得h =3,所以此正四棱锥的侧棱长为h 2+⎝ ⎛⎭⎪⎫22×422=5.答案 54.(2019·徐州市高三模拟)已知一个圆锥的母线长为2,侧面展开图是半圆,则该圆锥的体积为________. 解析 设圆锥的底面半径是r,则由题意得2πr=12×2π×2,所以r =1,所以圆锥的高为h =22-12=3,所以圆锥的体积为V =13πr 2h =33π.答案33π 5.(2019·如皋市高三模拟)如图,直三棱柱ABC -A 1B 1C 1中,∠CAB=90°,AC =AB =2,CC 1=2,P 是BC 1的中点,则三棱锥C -A 1C 1P 的体积为________.解析 连接A 1B,则V C -A1C1P =12V C -A1C1B=12(V ABC -A1B1C1-V A1-ABC -V B -A1B1C1) =12⎝ ⎛⎭⎪⎫12×2×2×2-13×12×2×2×2-13×12×2×2×2 =23. 答案 236.如图,在圆锥VO 中,O 为底面圆心,半径OA⊥OB ,且OA =VO =1,则O 到平面VAB 的距离为________.解析 由题意可得三棱锥V -AOB 的体积为V 三棱锥V -AOB =13S △AOB ·VO=16.△VAB 是边长为2的等边三角形,其面积为34×(2)2=32,设点O 到平面VAB 的距离为h,则由V 三棱锥O -VAB =V 三棱锥V -AOB ,得13S △VAB ·h=16,即13×32h =16,解得h =33,即点O 到平面VAB 的距离是33.答案337.(2019·苏州调研)将半径为5的圆分割成面积之比为1∶2∶3的三个扇形作为三个圆锥的侧面,设这三个圆锥的底面半径依次为r 1,r 2,r 3,则r 1+r 2+r 3=________. 解析 由题意可得三个扇形的弧长分别为5π3,10π3,5π,分别等于三个圆锥底面圆的周长,即2πr 1=5π3,2πr 2=10π3,2πr 3=5π,则r 1=56,r 2=53,r 3=52,所以r 1+r 2+r 3=56+53+52=5. 答案 58.(2019·南京高三模拟)已知棱长为1的正方体ABCD -A 1B 1C 1D 1中,F 是棱BC 的中点,M 是线段A 1F 上的动点,则△MD D 1与△MCC 1的面积和的最小值是________.解析 由题意,就是求M 到DD 1与CC 1距离和的最小值,由于A 1F 在平面ABCD 上的射影为AF,故问题转化为正方形ABCD 中AF 上的点到D,C 距离和的最小值.设D 关于AF 的对称点为D′,则DD′的长即为M 到DD 1与CC 1距离和的最小值,易求得DD′=455,cos∠CDD′=55.在△CDD′中,由余弦定理得CD′=1+165-2×1×455×55=655,所以△MDD 1与△MCC 1的面积和的最小值是12×655×1=6510.答案6510二、解答题9.如图,在四棱锥P -ABCD 中,AB∥CD ,且∠BAP=∠CDP=90°. (1)证明:平面PAB⊥平面PAD ;(2)若PA =PD =AB =DC,∠APD=90°,且四棱锥P -ABCD 的体积为83,求该四棱锥的侧面积.(1)证明 由已知∠BAP=∠CDP=90°,得AB⊥AP ,CD⊥PD.由于AB∥CD ,故AB⊥PD ,又AP∩PD=P,AP,PD ⊂平面PAD,从而AB⊥平面PAD. 又AB ⊂平面PAB,所以平面PAB⊥平面PAD. (2)解 在平面PAD 内作PE⊥AD ,垂足为E.由(1)知,AB⊥平面PAD,又PE ⊂平面PAD,故AB⊥PE ,又AD∩AB =A,AD,AB ⊂平面ABCD,所以PE⊥平面ABCD.设AB =x,则由已知可得AD =2x,PE =22x. 故四棱锥P -ABCD 的体积V P -ABCD =13AB·AD·PE=13x 3.由题设得13x 3=83,故x =2.从而PA =PD =AB =DC =2,AD =BC =2 2. 由(1)易知AB⊥PA ,CD⊥PD ,故PB =PC =2 2.可得四棱锥P -ABCD 的侧面积为12PA·PD+12PA·AB+12PD·DC+34BC 2=6+2 3.10.(2019·全国卷Ⅱ)如图,长方体ABCD -A 1B 1C 1D 1的底面ABCD 是正方形,点E 在棱AA 1上,BE⊥EC 1.(1)证明:BE⊥平面EB 1C 1;(2)若AE =A 1E,AB =3,求四棱锥E -BB 1C 1C 的体积.(1)证明 由已知得B 1C 1⊥平面ABB 1A 1,BE ⊂平面ABB 1A 1,故B 1C 1⊥BE.又BE⊥EC 1,B 1C 1∩EC 1=C 1,B 1C 1,EC 1⊂平面EB 1C 1,所以BE⊥平面EB 1C 1. (2)解 由(1)知∠BEB 1=90°. 由题设知Rt△ABE≌Rt△A 1B 1E, 所以∠AEB=∠A 1EB 1=45°, 故AE =AB =3,AA 1=2AE =6.如图,作EF⊥BB 1,垂足为F,则EF⊥平面BB 1C 1C,且EF =AB =3. 所以四棱锥E -BB 1C 1C 的体积 V =13×3×6×3=18. 11.(2018·全国Ⅰ卷)如图,在平行四边形ABCM 中,AB =AC =3,∠ACM=90°.以AC 为折痕将△ACM 折起,使点M 到达点D 的位置,且AB⊥DA.(1)证明:平面ACD⊥平面ABC ;(2)Q 为线段AD 上一点,P 为线段BC 上一点,且BP =DQ =23DA,求三棱锥Q -ABP 的体积.(1)证明 由已知可得,∠BAC=90°,即BA⊥AC.又BA⊥AD ,AC∩AD=A,AC,AD ⊂平面ACD,所以AB⊥平面ACD. 又AB ⊂平面ABC, 所以平面ACD⊥平面ABC.(2)解 由已知可得,DC =CM =AB =3,DA =AM =3 2. 又BP =DQ =23DA,所以BP =2 2.作QE⊥AC ,垂足为E,则QE∥DC 且QE =13DC =1.由已知及(1)可得DC⊥平面ABC,所以QE⊥平面ABC. 因此,三棱锥Q -ABP 的体积为1 3×QE×S△ABP=13×1×12×3×22sin 45°=1.V Q-ABP=。
高考数学二轮复习 疯狂时刻 空间向量与立体几何
2014数学高考疯狂时刻引领状元之路:空间向量与立体几何1.已知矩形ABCD和矩形ADEF所在平面互相垂直,点M,N分别在对角线BD,AE上,且BM=13BD,AN=13AE.求证:MN∥平面CDE.2.已知正方体ABCD A1B1C1D1中,E,F分别为BB1,CD 的中点,求证:D1F⊥平面ADE.3.在正方体ABCD A1B1C1D1中,求二面角A1BD C1的平面角的余弦值.结合空间向量判断或证明线面位置关系例1 如图,在直三棱柱ABC A1B1C1中,AC=3,BC=4,AB=5,AA1=4,(1) 求证: AC⊥BC1;(2) 在AB上是否存在点D,使得AC1⊥CD(例1)练习如图,正三棱柱ABC-A1B1C1的所有棱长都为4,点D为CC1的中点,求证:AB1⊥平面A1BD.(练习)结合空间向量求角度或三角函数值例2 如图,在直三棱柱A1B1C1-ABC中,AB⊥AC,AB=AC=2,A1A=4,点D是BC的中点.(1) 求异面直线A1B与C1D所成角的余弦值;(2) 求平面ADC1与平面ABA1所成二面角的平面角的正弦值.(例2)练习如图,在直三棱柱ABC-A1B1C1中,∠BAC=π2,AB=AC=AA1=1,延长A1C1 至点P,使C1P=A1C1,连接AP交棱CC1于点D.求:(1) 直线PB1与A1B所成角的余弦值;(2) 二面角A A1D B的平面角的正弦值.(练习)例3 在四棱锥P ABCD中,侧面PCD⊥底面ABCD,PD⊥CD,底面ABCD是直角梯形,AB∥CD,∠ADC=π2,AB=AD=PD=1,CD=2.设Q为侧棱PC上一点,PQu u u r=λPCu u u r,试确定λ的值,使得二面角Q BD P的平面角为45°.(例3)练习如图,在直三棱柱ABC A1B1C1中,AC=3,BC=4,AB=5,AA1=4.(1) 设ADu u u r=λABu u u r,异面直线AC1与CD所成角的余弦值为925,求λ的值;(2) 若点D是AB的中点,求二面角D CB1B的平面角的余弦值.(练习)结合空间向量求长度或距离例 4 如图所示的多面体是由底面为ABCD的长方体被截面AEC1F所截而得到的,其中AB=4,BC=2,CC1=3,BE=1.(1) 求BF的长;(2) 求点C到平面AEC1F的距离.(例4)练习如图,在四棱锥P-ABCD中,PA⊥底面ABCD,BC=CD=2,AC=4,∠ACB=∠ACD=π3,点F为PC的中点,AF⊥PB,求PA的长.(练习)1. 已知棱长为a的正方体ABCD A1B1C1D1中,在棱DD1上是否存在点P,使得B1D⊥平面PAC?2. 如图,已知三棱柱ABC A1B1C1中,AB⊥AC,AB=2,AC=4,AA1=3,点D是BC的中点.(1) 求直线DB1与平面A1C1D所成角的正弦值;(2) 求二面角B1A1D C1的平面角的正弦值.(第2题)3. 如图,在三棱柱ABC A1B1C1中,四边形AA1C1C是边长为4的正方形,平面ABC⊥平面AA1C1C,AB=3,BC=5.(1) 求证:AA1⊥平面ABC;(2) 求二面角A1BC1B1的平面角的余弦值;(3) 求证:在线段BC1存在点D,使得AD⊥A1B;并求1BDBC的值.(第3题)1. 证明略2. 证明略3. 1 3[分类解析]例1 (1)证明略(2) 存在点D 练习证明略例23105练习105例3 λ2-1练习(1) λ=12234例4 (1) BF的长为6433练习31. 存在33534551625(3) 9 253. (1) 证明略(2)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
立体几何
1.[2017·铜梁一中]右图为一正方体的平面展开图,在这个正方体中,有下列四个命题:
①//; ②与成角;
③与成异面直线且; ④与面所成角为.
其中正确的个数是( )
A. B. C. D.
【答案】A
【解析】将正方体纸盒展开图还原成正方体,如图知与不平行,故①错误;连接、
,将平移到,则与成角,故②正确;同理与成角,
故③错误;与面所成角不为,故④错误,综上可得只有②正确,故选A.
2.[2017·天水一中]设是两条不同的直线,是三个不同的平面,给出下列
四个命题,其中正确命题的序号是( )
①若,则; ②若,则
;
③若,则; ④若,则.
A.①② B.②③ C.③④ D.①④
【答案】A
一、选择题(5分/题)
【解析】①可以作为线面垂直的性质定理,①正确;②在时,有,又
,得,②正确;③在时,可能相交,可能异面,也可能平
行,③错误;④把门绕轴旋转,它在每一个位置都与地面垂直,但门所在的各个位置并不垂
直,④错误,故选A.
3.[2017·福建联考]已知矩形,,,将沿矩形的对角线
所在的直线进行翻折,在翻折过程中( )
A.存在某个位置,使得直线与直线垂直
B.存在某个位置,使得直线与直线垂直
C.存在某个位置,使得直线与直线垂直
D.对任意位置,三对直线“与”,“与”,“与”均不垂直
【答案】C
【解析】如图,,,依题意,,,,
.
A,若存在某个位置,使得直线与直线垂直,则∵,∴平面,
从而,这与已知矛盾,排除A;
B,若存在某个位置,使得直线与直线垂直,则平面,从而平面
平面,即在底面上的射影应位于线段上,这是不可能的,排除B;
C,若存在某个位置,使得直线与直线垂直,则平面,平面平
面,取中点,连接,则,∴就是二面角的
平面角,此角显然存在,即当在底面上的射影位于的中点时,直线与直线垂
直,故C正确;
D,由上所述,可排除D;故选C.
4.[2017·河西南师大附中]已知三棱锥中,,,
