20150611信号与系统第一章答案
信号与系统习题解答 (1)

第一章作业参考答案: 1.18求下列积分值: (a )解:26242)2()2(2)()0()2()(2)()()]2(2)([)()]2(2)()[23(44444444442=+=-+=-+=-+=-+++⎰⎰⎰⎰⎰-----dtt x dt t x dtt t x dt t t x dtt t t x dt t t t t δδδδδδδδ(b) 解:6510)2()2()()0()5()5()2()()()()5()()]2()()5([)()]2()()5()[1(4444444444442=++=-+++-=-+++=-+++=-++++⎰⎰⎰⎰⎰⎰------dtt x dt t x dt t x dtt t x dt t t x dt t t x dtt t t t x dt t t t t δδδδδδδδδδδδ(C )解:1)2()cos 1()2()cos 1(2=--=--⎰⎰--ππππππδπδdt t dt t t(d )解:42312121231)(cos )23()(cos )2()(cos )2()(cos )23()(cos )1(200222=++++-+-=++-+-=+⎰⎰⎰⎰⎰-----ππππδπδπδπδπδππππππππdtt x dt t x dt t x dt t x dt t t 1.19解:1.21 判断下列每个信号是否周期的?如果是周期的,是求它的基波周期。
(a )解:32,/23)cos(2)43cos(200ππωϕωπ===+=+T T t t 基波周期为:是周期信号(b)解:e eeT e e et j T t j Tj T j t j T t j )1()1)(()1()1)((12--±±±--±====ππππππ,时,当 是周期信号,基波周期是 T 0=2(c)解:互质与是有理数,且74,742782)2cos()278cos(==Ω+Ω=+ππππn n 所以原式是周期信号,基波周期N 0=7.(d)解:不是有理数,,812412cos 4cos πππ==ΩΩ=nn所以原式不是周期信号(e )解:。
第一章 信号与系统分析导论 答案

第一章信号与系统分析导论答案&评讲
注意:连续和离散的区别;连续是找一个实数T,而离散是找一个整数N;
注意:连续和离散的区别;连续是找一个实数T,而离散是找一个整数N;
注意:能量信号与功率信号的定义;
信号的时间取值范围;
连续和离散的区别;
注意:步骤详细一点;
●在判断可分解性时,应考察系统的完全响应y(t)是否可以表示为两部分之和,其中一部
分只与系统的初始状态有关,而另一部分只与系统的输入激励有关。
●在判断系统的零输入响应yx(t)是否具有线性时,应以系统的初始状态为自变量(如上
述例题中y(0)),而不能以其它的变量(如t等)作为自变量。
●在判断系统的零状态响应yf(t)是否具有线性时,应以系统的输入激励为自变量(如上述
例题中f(t)),而不能以其它的变量(如t等)作为自变量。
注意:步骤详细一点;
线性?时不变?都要判断
说法:线性――非线性;时不变-时变
注意:步骤详细一点;
因果系统:当且仅当输入信号激励系统时才产生系统输出响应的系统。
信号与系统第一章习题
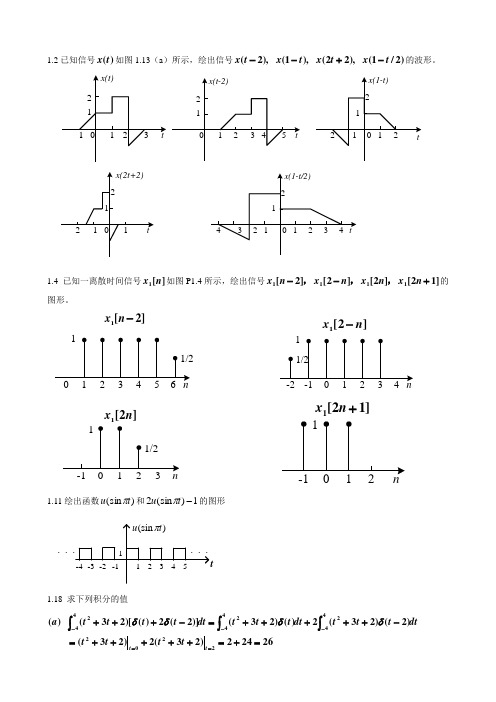
1.2已知信号)(t x 如图1.13(a )所示,绘出信号)2/1(),22(),1(),2(t x t x t x t x -+--的波形。
1.4 已知一离散时间信号][1n x 如图P1.4所示,绘出信号]12[]2[]2[]2[1111+--n x n x n x n x ,,,的图形。
1.11绘出函数)(sin t u π和1)(sin 2-t u π的图形t)(sin t u π1-1123. . .. . .54-2-3-41.18 求下列积分的值26242)23(2)23()2()23(2)()23()]2(2)()[23()(222442442442=+=+++++=-+++++=-+++==---⎰⎰⎰t t t t t t dtt t t dt t tt dt t t t t a δδδδ]2[1-n x]2[1n x-]2[1nx ]12[1+n x651)1()1(0)2()1()()1()5()1()]2()()2()[1()(2202442442442442=+=++++=-++++++=-++++==----⎰⎰⎰⎰t t t t dtt t dt t t dt t t dt t t t t b δδδδδδ12cos1)cos 1()2()cos 1()(2=-=-=--=-⎰ππδπππt t dt t t c4)231()21()21()231()1()1()1()1()23()1()2()1()2()1()23()1()(cos )1(1,23,2,2,23420cos )(23222322222222224321=++++-+-=+++++++=-++-+++++++=+==-=-=====-=-=-----⎰⎰⎰⎰⎰πππππδπδπδπδδπππππππππππππππππππt t t t t t t t dt t t dtt t t dt t t dt t t dt t t t t t t n n t t d 冲击强度均为公式可得它们对应项的由冲击函数的复合函数个根,仅包含取奇数,在积分限内,令:1.21 判断下列每个信号是否是周期的?如果是周期的,试求出它的基波周期。
《信号与系统》第一章知识要点+典型例题

y() 表示系统的输出。
1、线性系统与非线性系统 若系统满足下列线性性质: (1)可分解性 全响应 y () 可分解为零输入响应 y zi () 与零状态响应 y zs () 之和,即
y() y zi () y zs ()
(2)齐次性 零输入响应 y zi () 满足齐次性,零状态响应 y zs () 满足齐次性,即
( t ) 、 ( t ) 的重要性质
1
( t )dt 1 ,
t
( t )dt 0 , ( t )dt ( t ) ( k ) (k )
f ( k ) ( k ) f (0) ( k ) f ( k ) ( k k 0 ) f ( k 0 ) ( k k 0 )
f ( t ) ( t a )dt f (a )
k
f ( k ) ( k ) f (0)
(at )
5
1 (t ) a
1 b (at b) ( t ) a a f ( t ) ( t ) f (0) ( t ) f (0) ( t ) f ( t ) ( t ) f (0) ( t ) f (0) ( t )
2
。
而对离散的正弦(或余弦)序列 sin( k ) [或 cos( k ) ]( 称为数字角频率,单位为 rad ), 只有当
2
为有理数时才是周期序列,其周期 N M
2
, M 取使 N 为整数的最小整数。
如对信号 cos(6 k ) ,由于
2
2 1 为有理数,因此它是周期序列,其周期 N 1 。 6 3
信号与系统课后习题参考答案.pdf

-5
-4 -3 -2
-1
2 1
2
3
-1
x(-t+4)
t
45
6
2 1
4
6
-1
x(-t/2+4)
t 8 10 12
(e)[x(t)+x(-t)]u(t)
-2
-1
2
x(-t)
1
t
01
2
-1
(f)
x(t)[δ(t +
3) − δ(t - 3)]
2
2
3
[x(t)+x(-t)]u(t)
1 t
01
2
-1
-3/2 (-1/2)
x(t)[δ(t + 3) − δ(t - 3)]
2
2
3/2
t
0 (-1/2)
6
1.22
(a)x[n-4]
x[n-4]
11 1 1
1/2 1/2
1/2 n
0 1 23 4 5 6 7 8
-1/2
-1
(b)x[3-n]
x[n+3]
11 1 1
1/2 1/2
1/2 n
-7 -6 -5 -4 -3 -2 -1 0 1
=
2π 4
=π 2
则:整个信号的周期为:T = LCM{T1,T2} = π
1.11
j 4πn
解: e 7
→
ω1
=
4πn 7
,则:
2π ω1
=
2π 4π
=7= 2
N1 k
,⇒
N1
=
7
7
j 2πn
e5
→ ω2
《信号与系统》习题一讲解

抹灰清包合同范本合同编号:_______甲方(发包方):_______乙方(承包方):_______根据《中华人民共和国合同法》、《中华人民共和国建筑法》及其他有关法律、法规的规定,遵循平等、自愿、公平、诚信的原则,甲、乙双方就抹灰清包工程事项协商一致,签订本合同。
一、工程概况1.1 工程名称:_______1.2 工程地点:_______1.3 工程范围:_______1.4 工程内容:_______1.5 工程面积:_______二、合同价款2.1 工程合同价款:人民币(大写):_______元整(小写):_______元。
2.2 合同价款支付方式:_______三、施工期限3.1 工程施工期限:_______天,自_______年_______月_______日起至_______年_______月_______日止。
3.2 乙方应按照约定的施工期限完成工程,如因乙方原因导致工程延期,乙方应承担违约责任。
四、质量标准4.1 工程质量标准:_______4.2 乙方应按照约定的质量标准进行施工,如因乙方原因导致工程质量不符合约定,乙方应无条件返工,直至达到约定的质量标准。
五、材料供应5.1 工程所需材料由_______方负责供应。
5.2 材料供应时间:_______5.3 材料质量:_______六、安全生产6.1 乙方应严格遵守安全生产法律法规,确保施工安全。
6.2 乙方应制定安全生产措施,加强施工人员的安全教育,预防安全事故的发生。
6.3 如因乙方原因导致安全事故,乙方应承担全部责任。
七、验收与保修7.1 工程竣工后,乙方应通知甲方进行验收。
甲方应在接到乙方通知后_______日内组织验收。
7.2 验收合格后,双方签署工程验收报告。
验收不合格的,乙方应无条件返工,直至达到约定的质量标准。
7.3 工程保修期为_______年,自工程验收合格之日起计算。
保修期内,如因乙方原因导致工程出现问题,乙方应无偿修复。
信号与系统 人民邮电出版社 第二版第一章 课后答案
w
w
.k hd
第一章 信号与系统的基本概念 习题
南京邮电大学 信号分析与信息处理教学中心
aw
信号与系统
2006.1
.c
SIGNALS AND SYSTEMS
om
.c
∫
1 2 0
1-1 下列信号中哪些是周期信号,哪些是脉冲信号?哪 些是能量信号?哪些是功率信号它们的平均功率各为多 少? ω 0t ω 0t j (ω 0t +θ )
om
∫
q
w
画系统 x (t ) q ∑ 模拟图:
∫
15
∑
y (t )
w
5
11
15
w
aw
) 1-23 已知某系统的数学模型为 y " ( t ) + a y ' ( t ) + a y ( t ) = b ' x ( t ) + b x ( t, 其模拟图如下,试导出微分方程中的系数 a1, a0 , b1, b0 与模拟图 与模拟 中的系数 α1,α0 , β1, β0的关系。 解:设辅助函数 q" x(t ) β0 β1 如图所示,则 q" = β 0 x + α 0 y + α1q' y (t ) q' q"
w
w
1 y ( t ) = {[[ x1( t ) + x2 ( t )]2 [[ x1( t ) x2 (t )]2 } 4 = x1(t ) x2 ( t )
.k hd
对所假设系统,有:
q(3) (t ) = x (t ) 5q" (t ) 11q' (t ) 15q(t )
信号与系统 陈后金版 第一章习题(部分)
21e
4 t
,t 0
(2)
y (0 ) 1 时
y zi ( t )
1 2
y zi1 ( t ) 3 e
4 t
,t 0
4 t 1
输 入 3 x ( t 1) 时
y zs ( t ) 3 5 e
4 t
t 1
21e
,t 1
1-1: (a)
x(t )
3 2 1 0
A
A
12 3 4 5
确定 连续
t 非周期
功率信号
1-4: (1)
x(t ) sin( t ), t 0
周期信号定义是区间 t 上满足x(t ) x(t T ) 所以,该信号是非周期信号。
(4)
x(t ) e
yzs (t ) 2
d [ x1 (t ) x2 (t )] dt
2
dx1 (t ) dt
2
dx2 (t ) dt
yzs1 (t ) yzs 2 (t )
故系统为线性系统。
5
(5)
y[k ] 2 y[0] 6 x [k ]
2
1)具有可分解性,yzi [k ] 2 y[0];yzs [k ] 6 x [k ]
k k
1
1
1
k 1
2( ) 3
1
k 1
,k 1
9
y ( t ) y zi ( t ) y zs ( t ) 3e
5 e t 1 21e 4 t 1 , t 1 3
8
1-10:
线性非时变系统 y zi [ k ] 2 y zi1 [ k ] 3 y zi 2 [ k ] 8( ) 9( ) , k 0 2 3
信号与系统课后习题参考答案
信号与系统课后习题参考答案1试分别指出以下波形就是属于哪种信号?题图1-11-2试写出题1-1图中信号得函数表达式。
1-3已知信号与波形如题图1-3中所⽰,试作出下列各信号得波形图,并加以标注。
题图1-3⑴⑵⑶⑷⑸⑹⑺⑻⑼1-4已知信号与波形如题图1-4中所⽰,试作出下列各信号得波形图,并加以标注。
题图1-4⑴⑵⑶⑷⑸⑹⑺⑻⑼1-5已知信号得波形如题图1-5所⽰,试作出信号得波形图,并加以标注。
题图1-51-6试画出下列信号得波形图:⑴⑵⑶⑷1-7试画出下列信号得波形图:⑴⑵⑶⑷⑸⑹1-8试求出以下复变函数得模与幅⾓,并画出模与幅⾓得波形图。
⑴⑵⑶⑷1-9已知信号,求出下列信号,并画出它们得波形图。
1-10试作出下列波形得奇分量、偶分量与⾮零区间上得平均分量与交流分量。
题图1-101-11试求下列积分:⑴⑵⑶⑷⑸⑹1-12试求下列积分:⑴⑵⑴(均为常数)⑵⑶⑷⑸⑹⑺⑻1-14如题图1-14中已知⼀线性时不变系统当输⼊为时,响应为。
试做出当输⼊为时,响应得波形图。
题图1-14 1-15已知系统得信号流图如下,试写出各⾃系统得输⼊输出⽅程。
题图1-151-16已知系统⽅程如下,试分别画出她们得系统模拟框图。
⑴⑵⑶1-17已知⼀线性时不变系统⽆起始储能,当输⼊信号时,响应,试求出输⼊分别为与时得系统响应。
第⼆章习题2-1试计算下列各对信号得卷积积分:。
⑴(对与两种情况)⑵⑶⑷⑸⑹2-2试计算下列各对信号得卷积与:。
⑴(对与两种情况)⑵⑶⑷⑸⑹2-3试计算下图中各对信号得卷积积分:,并作出结果得图形。
题图2-32-4试计算下图中各对信号得卷积与:,并作出结果得图形。
题图2-42-5已知,试求:⑴⑵⑶2-7系统如题图2-7所⽰,试求系统得单位冲激响应。
已知其中各⼦系统得单位冲激响应分别为:题图2-72-8设已知LTI 系统得单位冲激响应,试求在激励作⽤下得零状态响应。
2-9⼀LTI 系统如题图2-9所⽰,由三个因果LTI ⼦系统级联⽽成,且已知系统得单位样值响应如图中。
信号与系统自测题(第1章 参考答案)
《信号与系统》自测题第1章 信号与系统的概念一、填空题1、描述信号的基本方法有 数学表达式 、 波形 。
2、()Sa t 信号又称为 抽样信号或取样信号 。
3、()du t dt=()t δ。
4、()t δ-=()t δ(用单位冲激函数表示)。
5、对于一个自变量无穷但能量有限的信号,其平均功率为0。
6、对于下图示波形可用单位阶跃函数表示为()(1)(2)3(3)u t u t u t u t +-+---。
7、2(321)(1)t t t dt δ∞-∞++-=⎰6 。
8、525(32)(1)t t t dt δ--+-=⎰ 0 。
9、00()(2)t t u t t dt δ∞-∞--=⎰ 0 (已知00t >)。
10、0()(2)3t d τδττ--=⎰ -6 。
11、0sin()[(1)(1)]2t t t dt πδδ-∞-++=⎰ 1 。
12、0sin()(1)2t t dt πδ∞-=⎰ 1 。
13、系统的数学描述方法有 输入输出描述法 和 状态变量描述法 。
14、满足 齐次性 和 可加性或叠加性 条件的系统称为线性系统。
15、若某系统是时不变的,则当()()f f t y t −−−→系统,应有()d f t t -−−−→系统()d y t t -。
16、系统对()f t 的响应为()y t ,若系统对0()f t t -的响应为0()y t t -,则该系统为 时不变 系统。
17、连续系统模拟中常用的理想运算器有 加法器 、 数乘器 、 乘法器 、 延时器 和 积分器 。
18、离散系统模拟中常用的理想运算器有 加法器 、 数乘器 、 乘法器 和 延时器 。
二、单项选择题1、连续时间信号2()[5sin(8)]f t t =的周期是( C )。
A 、π B 、4πC 、8πD 、2π注:sin(8)t 的周期为4π,而2()[5sin(8)]f t t =的周期为8π。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1
习题1
1.1 (1) )3π/sin()(ttx为周期信号,基波周期为2πT。
(2) )110sin()14cos(2)(tttx为周期信号,基波周期为πT。
(3) ttx2cos)(为周期信号,基波周期为πT。
(4) )π3sin(2)cos(π)(tttx不是周期信号。
1.2 (1) )4/j(πe][nnx为周期信号,基波周期为8N。
(2) )5/π2j()3/π4j(ee1][
nn
nx为周期信号,基波周期为15N。
(3) )8/(πcos][
2
nnx为周期信号,基波周期为8N。
(4) )4/cos(π)2/cos(][nnnx不是周期信号。
1.3 (1) 0,e)(
2
ttxt:14E, 0P,所以()xt为能量信号。
(2) (t)10,0xtt:
E
,P
, 所以()xt既非能量信号也非功率信号。
(3)
(t)10cos(5)cos(10t)xt
:
25P
,E
,所以()xt为功率信号。
(4) 33,2][nnx
n
:218564E,0P,所以[]xn为能量信号。
(5)
n
nx)2/1(][:E,P,所以[]xn既非能量信号也非功率信号。
(6) )4/cos(π][nnx:
1/2P
,E
,所以[]xn为功率信号。
1.4 (1) 错误,如指数信号。
(2) 错误,一个能量信号与一个功率信号之和为功率信号。
(3) 正确,由能量定义可证明,具体过程略。
(4) 错误,如0,e)(
2
ttx
t
(5) 错误,可能既非能量信号也非功率信号,如(t)10,0xtt。
(6) 正确。222121212lim|()()|lim|()|lim|()|TTTTTTTTTExtxtdtxtdtxtdtEE
1.5 nmktkkAtxje)(,由于ki时ki,则j()1limed02ikTtTTtT,因此,信号功率
jjjjj
2**
j()22,111lim|e|dlim(e)(e)dlim(e)(e)d22211lim(||e)d||lim1d22kkkkkiknnnnnTTTtttttxkkkkkTTTTTTkmkmkmkmkmnnTTtkikkTTTTkmikmikPAtAAtAAtTTTAAAtAtTTj()
,
22
1
limed
2
||0||
ik
nn
T
tikTTkmikmiknnkkkmkmAAtTAA
