3三因素完全随机区组试验的方差分析 实例2
方差分析

二期矽肺 100.67 93.47 74.97 88.06 113.52 101.14 95.10 118.98
三期矽肺 97.58 83.58 103.81 107.10 108.42 82.58 89.01 77.11
方差分析的基本思想
总变异:从例中看出,32个观察值大小参差不 齐,这种个体值与总均数之间的差异称为总变 异。
多个样本均数间的多重比较
多个样本均数间的多重比较:也称为两两 比较,主要用于探索与证实多组均数中, 哪两个总体均数间有差别,哪两个均数间 没有差别。 如果多组均数的比较采用两样本均数比较 的t检验,会加大I型错误。
多个样本均数间的多重比较
LSD-t检验:最小显著差法
容易获得P<0.05,但是假阳性率较高;
完全随机设计资料的方差分析
方差分析结果表 变异来源 总 组间 组内 SS 86.740 45.091 41.649 ν 39 3 36 MS F P <0.05
15.030 12.990 1.157
3.确定P值和作出推断结论:以ν组间=3,ν组内=36, 查F界值表得P<0.05, 按α=0.05水准拒绝H0 ,接受 H1,故可以认为给予不同剂量的三菱莪术液,小鼠瘤 重间差别有统计学意义。
方差分析
主要内容
方差分析的基本思想 完全随机设计、随机区组设计、拉丁方设 计、交叉设计和析因设计资料方差分析的 基本过程
多个样本均数的比较
两个样本均数的比较:
1次t-test,α=0.05;
三个样本均数的比较:
3次t-test,α=1-(1-0.05)3=0.14;
四个样本均数的比较:
6次t-test,α=1-(1-0.05)6=0.26;
Excel数据处理之三 方差分析

统计学中的几个基本概念1、同质(homogeneity)与变异(variation)严格地讲,同质是指被研究指标的影响因素完全相同。
但在医学研究中,有些影响因素往往是难以控制的(如遗传、营养等),甚至是未知的。
所以,在统计学中常把同质理解为对研究指标影响较大的、可以控制的主要因素尽可能相同。
例如研究儿童的身高时,要求性别、年龄、民族、地区等影响身高较大的、易控制的因素要相同,而不易控制的遗传、营养等影响因素可以忽略。
同质基础上的个体差异称为变异。
如同性别、同年龄、同民族、同地区的健康儿童的身高、体重不尽相同。
事实上,客观世界充满了变异,生物医学领域更是如此。
哪里有变异,哪里就需要统计学。
若所研究的同质群体中所有个体一模一样,只需观察任一个体即可,无须进行统计研究。
2、总体(population)与样本(sample)任何统计研究都必须首先确定观察单位(observed unit),亦称个体(individual)。
观察单位是统计研究中最基本的单位,可以是一个人、一个家庭、一个地区、一个样品、一个采样点等。
总体是根据研究目的确定的同质观察单位的全体,或者说,是同质的所有观察单位某种观察值(变量值)的集合。
例如欲研究山东省2002年7岁健康男孩的身高,那么,观察对象是山东省2002年的7岁健康男孩,观察单位是每个7岁健康男孩,变量是身高,变量值(观察值)是身高测量值,则山东省2002年全体7岁健康男孩的身高值构成一个总体。
它的同质基础是同地区、同年份、同性别、同为健康儿童。
总体又分为有限总体(finite population)和无限总体(infinite population)。
有限总体是指在某特定的时间与空间范围内,同质研究对象的所有观察单位的某变量值的个数为有限个,如上例;无限总体是抽象的,无时间和空间的限制,观察单位数是无限的,如研究碘盐对缺碘性甲状腺病的防治效果,该总体的同质基础是缺碘性甲状腺病患者,同用碘盐防治;该总体应包括已使用和设想使用碘盐防治的所有缺碘性甲状腺病患者的防治效果,没有时间和空间范围的限制,因而观察单位数无限,该总体为无限总体。
三水平试验方差分析

344.84 458.39 460.10 478.30
976.56 360.62 461.39 527.62
(1)计算
计算各列各水平的yjk值
计算各列各水平对应数据之和yj1、yj2、yj3及其平方yj12、 yj22、yj32。
计算各列偏差平方和及自由度 Sj bakb1y2jk1a(in1yi)2
L27(313)交互列表
解:(选用正交表L27(313)
P 1 ( 100 . 64 ) 2 375 . 13 , 27
根据前面的公式作如下计算:Q A
1 9
( 36
. 73
2
30
. 70
2
33
. 21
2)
377
. 17 ,
QB
1 9
( 33
. 46
2
31
. 30
2
35
. 88
2)
376
. 29 ,
QC
1 ( 6 . 27 9
2 35
. 21
2 59
. 16
2)
531
. 00 ,
Q ( A B )1
1 9
( 35
. 63
2
32
. 08
2
32
. 93
2)
375
. 89 ,
Q ( A B )2
1 ( 34 9
. 30
2
31
. 73
2 34
. 61
2)
375
. 68 ,
Q ( A C ) 1
方差分析(2): 由于这里的试验指标是产品的产量,越大越好,所以最优方案应取 各因素中yjk的最大值所对应的水平。因素A应取第1水平,因素B应 取第3水平,因素C应取第3水平。交互作用A×B也是显著的,但由 于A×B占两列,直观分析法有些困难,因此把A和B的各种组合的试 验结果对照起来分析。
第九章方差分析

2 2 X
2 R
F
nk 2 R nk
nk
SS E SSW SS R
dfT nk 1
MS B df B SS E MS E df E
SS B
dfT df B df R df E df B k 1
Fmax
2 S max 2 S mix
查Fmax临界值表(附表5),当算出的小Fmax
于表中相应的临界值,就可认为几个要比较的
样本方差两两之间无显著性差异.
第二节 完全随机设计方差分析
为了检验某一个因素多种不同水平间差 异的显著性,将从同一个总体中随机抽取的 被试,再随机的分入各实验组,施以各种不 同的实验处理之后,用方差分析法对这多个 独立样本平均数差异的显著性进行检验,称 为 完全随机设计的方差分析(单因素、组间 或单向方差分析)。
• 检验两个方差之间的差异要用F检验:
MS B F MSW
• 如果组间与组内方差相等,即F值等于或接近1, 表明各组平均数无显著性差异,如果F值很大, 超过F抽样分布上某种显著性水平的临界值, 则应拒绝H0,接受H1.(决定采用单侧检验) • 若P < 0.05 时,说明不同的实验处理之间存 在着显著差异;若P > 0.05 时,说明不同的实 验处理之间差异不大.
86 84 85 3 255 85 21677 21675
83 82 87 3 252 84 21182 21168
73 74 78 3 255 75 16889 16875
• 解:(1)提出假设: • H0: μ1=μ2= μ3=μ4= μ5 • H1 :五个总体的平均数不全相等 • (2)选择检验统计量并计算其值 • 五组测验分数假定是从五个相应的正态总体随 机抽出的独立样本。故可用组间与组内方差的 F比值来检验五个总体的平均数差异的显著性
方差分析几个案例

方差分析方法之迟辟智美创作方差分析是统计分析方法中,最重要、最经常使用的方法之一.本文应用多个实例来说明方差分析的应用.在实际把持中,可采纳相应的统计分析软件来进行计算.1. 方差分析的意义、用途及适用条件1.1 方差分析的意义方差分析又称为变异数分析或F检验,其基本思想是把全部观察值之间的变异(总变异),按设计和需要分为二个或多个组成部份,再作分析.即把全部资料的总的离均差平方和(SS)分为二个或多个组成部份,其自由度也分为相应的部份,每部份暗示一定的意义,其中至少有一个部份暗示各组均数之间的变异情况,称为组间变异(MS组间);另一部份暗示同一组内个体之间的变异,称为组内变异(MS组内),也叫误差.SS除以相应的自由度(υ),得均方(MS).如MS组间>MS组内若干倍(此倍数即F 值)以上,则暗示各组的均数之间有显著性不同.方差分析在环境科学研究中,经常使用于分析试验数据和监测数据.在环境科学研究中,各种因素的改变都可能对试验和监测结果发生分歧水平的影响,因此,可以通过方差分析来弄清与研究对象有关的各个因素对该对象是否存在影响及影响的水平和性质.1.2 方差分析的用途1.2.1 两个或多个样本均数的比力.1.2.2 分离各有关因素,分别估计其对变异的影响.1.2.3 分析两因素或多因素的交叉作用.1.2.4 方差齐性检验.1.3 方差分析的适用条件1.3.1 各组数据均应服从正态分布,即均为来自正态总体的随机样本(小样本).1.3.2 各抽样总体的方差齐.1.3.3 影响数据的各个因素的效应是可以相加的.1.3.4 对不符合上述条件的资料,可用秩和检验法、近似F值检验法,也可以经过变量变换,使之基本符合后再按其变换值进行方差分析.一般属Poisson分布的计数资料经常使用平方根变换法;属于二项分布的百分数可用反正弦函数变换法;当标准差与均数之间呈正比关系,用平方根变换法又不容易校正时,也可用对数变换法.2. 单因素方差分析(单因素多个样本均数的比力)根据某一试验因素,将试验对象按完全随机设计分为若干个处置组(各组的样本含量可相等或不等),分别求出各组试验结果的均数,即为单因素多个样本均数.用方差分析比力多个样本均数的目的是推断各种处置的效果有无显著性不同,如各组方差齐,则用F检验;如方差不齐,用近似F值检验,或经变量变换后到达方差齐,再用变换值作F检验.如经F检验或近似F值检验,结论为各总体均数不等,则只能认为各总体均数之间总的来说有不同,但不能认为任何两总体均数之间都有不同,或某两总体均数之间有不同.需要时应作均数之间的两两比力,以判断究竟是哪几对总体均数之间存在不同.在环境科学研究中,经常要分析比力分歧季节对江、河、湖水中某种污染物的含量有无显著性影响;各种气象条件如风向、风速、温度对年夜气中某种污染物含量的影响等问题.我们把季节、风向、风速、温度等称为因素.仅按分歧季节,或分歧的风向,或分歧的温度来分组,称为单因素.例1 某年度某湖分歧季节湖水中氯化物含量(mg/L)测定结果如表—6.1所示.试比力分歧季节湖水中氯化物含量有无显著性不同.从表—1的测定结果可见有三种变异:1. 组内变异:每个季节内部的各次测定结果不尽相同,但显然不是季节的影响,而只是由于误差(如个体不同、随机丈量误差等)所致.2. 组间变异:各个季节的均数也不相同,说明季节对湖水中氯化物的含量可能有一定的影响,也包括误差的作用.3.总变异:32次测定结果都不尽相同,既可能受季节的影响,也包括误差的作用.分歧季节湖水中氯化物含量的均数之间的变异究竟是由于误差所致,还是由于分歧季节的影响,可以用方差分析来解决此问题.方差分析可暗示:⑴从总变异中分出组间变异和组内变异,并用数量暗示变异的水平.⑵将组间变异和组内变异进行比力,如二者相差甚微,说明季节影响不年夜;如二者相差较年夜,组间变异比组内变异年夜很多,说明季节影响不容忽视.以下是三种变异的计算方法:3.1 多个方差的齐性检验已知多个样本(理论上均来自正态总体)方差,可以据此推断它们所分别代表的总体方差是否相等,即多个方差的齐性检验.其经常使用于:⑴说明多组变量值的变异度有无不同.⑵方差齐性检验.以例1为例(各组样本含量相等),如表—4所示.3.确定P值:根据υ=4—1=3,查附表—12得P<0.005.4.判断结果:由于P<0.005,因此,四组方差不齐.3.2 近似F值检验(F'检验)以例2为例,如表—6所示.公式26最经常使用,公式27适用于原数据中有小值和零时.K为常数,可以根据需要选用合适的数值.⑵对数变换的用途:①当几个样本均数作比力时,如样本方差不齐,尤其是当标准差与均数之比的比值接近时,必需经对数变换以缩小各方差之间的分歧,到达方差齐后才华进行t检验或方差分析.②适用于呈对数正态分布的资料.③在曲线拟合中,对数变换经常是直线化的重要手段,如指数曲线、双曲线、logistic曲线的直线化等.例3 欲用t检验比力某河丰水期和枯水期的河水BOD5(mg/L)含量均数,资料如表—7所示.此数据能否直接用t 检验方法?如不能,试作变量变换.二者比力接近,可以试用对数变换.⑶将X作“lgX +1”变换后,再作方差齐性检验,得F=1.72,P>0.05,两组方差齐,可以用变换值作两样本均数比力的t检验.以原数据的平方根作为统计分析的变量值,称为平方根变换.⑴平方根变换的形式:⑶百分数的概率单元变换:主要用于S形或反S形曲线的直线化、正态性检验,尤其适用于剂量反应曲线的直线化.⑷百分数的logit变换:主要用于S形或反S形曲线的直线化.⑸反双曲正切变换:用于两直线相关系数的比力与合并.4. 两因素方差分析(双因素多个样本均数的比力)将试验对象按性质相同或相近者组成配伍组,每个配伍组有三个或三个以上试验对象,然后随机分配到各个处置组.这样,分析数据时将同时考虑两个因素的影响,试验效率较高.例5 某市为了研究一日中分歧时点以及分歧区域年夜气中氮氧化物含量的变动情况,该市环保所于某年1月15~19日,在市区选择了7个采样点,对年夜气中氮氧化物的含量进行测定.表—9为各个采样点每个时点五天的平均含量,试分析分歧时点、分歧区域氮氧化物含量之间有无显著性不同.5. 多因素方差分析(多因素多个样本均数的比力)在环境科学研究中,所研究的事物或现象往往是比力复杂的多因素问题,而各种因素自己尚有水平的分歧,其间往往又存在交互作用.当研究的因素在三个或三个以上时,可以用正交试验法.正交试验是一种高效、快速的多因素试验方法.正交试验的设计与分析见另外章节.“多因素多个样本均数的比力”不单可以用于正交试验,也可以用于拉丁方试验分析与析因试验分析等.6.多个样本均数间的两两比力(多重比力)经方差分析后,如果各总体均数有显著性不同时,常需进一步确定哪两个总体均数间有显著性不同,哪两个之间无显著性不同.因此,可以利用方差分析提供的信息作样本均数间的两两比力.以例5为例:(每组样本含量相等)经方差分析后,认为分歧时点以及分歧区域的氮氧化物含量之间均有高度显著性不同.现在需要进一步检验分歧时点的氮氧化物含量均数两两之间有无显著性不同.检验步伐如下:1.检验假设:各时点的氮氧化物含量均数之间两两相等.⑷q值的计算方法与上例相同.3.确定P值与判断结果如表—13所示.。
2三因素完全随机区组试验的方差分析 实例1
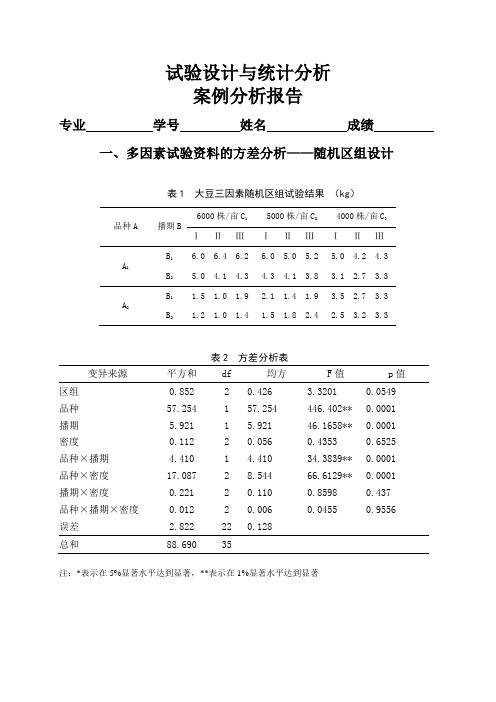
试验设计与统计分析案例分析报告专业学号姓名成绩一、多因素试验资料的方差分析——随机区组设计表1 大豆三因素随机区组试验结果(kg)品种A 播期B6000株/亩C1 5000株/亩C2 4000株/亩C3ⅠⅡⅢⅠⅡⅢⅠⅡⅢA1B1B2 6.0 6.4 6.25.0 4.1 4.36.0 5.0 5.24.3 4.1 3.85.0 4.2 4.33.1 2.7 3.3A2B1B2 1.5 1.0 1.91.2 1.0 1.42.1 1.4 1.91.5 1.82.43.5 2.7 3.32.53.2 3.3表2 方差分析表变异来源平方和df 均方F值p值区组0.852 2 0.426 3.3201 0.0549 品种57.254 1 57.254 446.402** 0.0001 播期 5.921 1 5.921 46.1658** 0.0001 密度0.112 2 0.056 0.4353 0.6525 品种×播期 4.410 1 4.410 34.3839** 0.0001 品种×密度17.087 2 8.544 66.6129** 0.0001 播期×密度0.221 2 0.110 0.8598 0.437 品种×播期×密度0.012 2 0.006 0.0455 0.9556 误差 2.822 22 0.128总和88.690 35注:*表示在5%显著水平达到显著,**表示在1%显著水平达到显著表3 不同密度下产量的多重比较密度/株/亩大豆产量4000 3.42±0.74 a A6000 3.33±2.20 a A5000 3.29±1.62 a A注:小写字母代表5%显著水平,大写字母代表1%显著水平。
【解释说明】方差分析结果表明,品种、播期、品种和播期的互作、品种和密度的互作效应均达到了极显著水平,而密度因素对大豆产量的影响不显著。
随机区组试验设计与分析
第一节 完全随机实验设计及分析
本试验中,水平数m=3,重复r=5,共进行35=15次试验。 此15次试验先做哪一个呢? 试验的先后顺序必须随机确定。随机化方法可采用抽签的方 法,也可用随机数字表确定试验顺序。 现在采用查随机数字表确定试验顺序 (1)对所有试验编号 (2)确定读取随机数字的起始点,并读取相应数目的随机数字。 (3)根据随机数字的大小确定试验的先后顺序。
然后分别在各区组内,用随机的方法将各个处理逐个安排于各供试 单元中。
第二节 随机区组试验设计方法
由于同一区组内的各处理单元的排列顺序是随机而定的,故这 样的区组叫做随机区组。 随机区组设计是一种适用性较广泛的设计方法。既可用于单因素试 验,也适用于多因素试验。
第二节 随机区组试验设计方法
随机区组试验设计方法安排单因素试验
除杂方法(Ai) 平均值 xt
差异显著性
a=0.05
a=0.01
A4
28.4
a
A
A2
27.5
ab
A
A3
27.0
b
A
A1
25.2
c
B
A5
21.3
d
C
第二节 随机区组试验设计方法
2.1 设计方法
实验设计五原则中,其中的一条就是区组的原则。 随机区组试验设计是一种随机排列的完全区组的试验设计。 其方法是: 根据局部控制的原理,将试验的所有供试单元先按重复划分成非处 理条件相对一致的若干单元组,每一组的供试单元数与试验的处理数 相等。
雌鼠编号 1 2 3 4 5 6 7 8 … 39 40
随机数字 09 47 27 96 54 49 17 46 … 03 10
余数
1 3 3 4 2 1 1 2 …3 2
方差分析实例详解
方差分析计算实例一、单因素方差分析二、双因素方差分析一、单因素方差分析(一)完全随机试验设计1、重复数相同(1)实例:不同浇水量对某蔬菜产量的影响试验,设置5个浇水量A、B、C、D、E;每个浇水量设置四个小区,小区采用完全随机试验设计;各小区产量见下表(单位:kg)(2)基本参数计算处理数k=5,重复数n=4220.0250.9750.485,11.143χχ==(3)方差同质性检验2220.0250.975,c χχχ≤≤五个处理的方差无显著差异平方和计算:(4)方差分析自由度计算:方差分析表:22222222/()/()(45.2869.5288.55108.48130.12)/4441.95/(45)1089.89t i ij SS T n x nk =−=++++−⨯=∑∑1107.051089.8917.16e T t SS SS SS =−=−=222222()/()16.6115.9531.11441.95/(45)1107.05T ijij SS x x nk =−=+++−⨯=∑∑1514t df k =−=−=(1)5(41)15e df k n =−=−=145119T df nk =−=⨯−=变异来源平方和自由度均方F 值F 0.05处理间1089.894272.47238.213.056误差17.1615 1.14总变异1107.0519F 值大于F 0.05,五个处理蔬菜产量平均值差异显著。
将五个处理小区产量平均值从大到小排列,采用字母标记法表示各均值间差异是否显著,均值间的差值大于LSD ,差异显著,标记不同的字母;均值间的差值小于LSD ,差异不显著,标记相同的字母。
标记字母时,第一个值标a ,用最大值减第二个值,差值若大于LSD 则标b ,差值若小于LSD 则标a ,再以最大值减第三个值,直到出现大于LSD 值,标记b ,再以该值为标准向上比较,若差值大于LSD 就停止比较,若小于LSD 值则在a 后面加上b ,直至出现差值大于LSD 就停止比较;再以最上面标记b 的均值为标准在向下比较;直到所有的平均值都标记字母。
第6章 方差分析
2.Dunnett-t检验
它适用于k-1个试验组与一个对照组均数差 别的多重比较。 公式为:
t
Xi X0
1 1 MS 误差 ( ) ni n0
照组的均数,MS误差为方差分析中所计算的误差均 方,ni和n0分别为第i个试验组和对照组的例数。 v=v误差
X 为第i个(i=1,2,…k-1)试验组的均数, 0 为对 X i
两两比较计算表
对比组 两均数 之差
XA XB
A与B (1) (2)
q值
(3) (2) 0.3899
组 数
a (4)
q界值
P
(3)
α=0.05 (5)
α=0.01 (6)
(7)
1与2 1与3 2与3
1.0323 2.7543 1.7220
2.65 7.06 4.42
2 3 2
2.83 3.40 2.83
方差分析
Analysis of Variance
本章内容
方差分析的基本思想 完全随机设计的单因素方差分析 随机区组设计的两因素方差分析 多个样本均数间的多重比较 变量变换
例1.某研究者为研究核黄素缺乏对尿中氨基氮的 影响,将60只Wistar大白鼠随机分为核黄素缺乏、 限食量、不限食量三组不同饲料组。每组20只 大白鼠。一周后测尿中氨基氮的三天排出量, 结果如表1。
一、方差分析的基本思想
4. 方差分析的基本思想: 根据变异的不同来源将全部观察值总的 离均差平方和与自由度分解为两个或多 个部分,除随机误差外,其余每个部分 的变异可由某个因素的作用(或某几个 因素的交互作用)加以解释,通过比较 不同变异来源的均方,借助F分布作出 统计推断,从而了解该因素对观测指标 有无影响。
随机区组设计方差分析
但双因素方差分析的设计对选择受试对象及试验条件 等方面要求较为严格,应用该设计方法时要十分注意。 该设计方法中,总变异可以分出三个部分:
具体做法:将受试对象按性质(如性别、年龄、病 情等,这些性质是非处理因素,可能影响试验结果)
相同或相近者组成b个区组(配伍组),每个区组 中有k个受试对象,分别随机地分配到k个处理组。
这样,各个处理组不仅样本含量相同,生物学 特点也较均衡。比完全随机设计更容易察觉处理间 的差别 。
双因素方差分析的特点: 按照随机区组设计的原则来分析两个因素对试验结果
end
按随机区组设计方案,以窝别作为区组标志,给断 奶后小鼠喂以三种不同营养素A、B、C,问营养素对 小鼠所增体重有无差别。
表 8个区组小鼠按随机区组设计的分配结果
区组
1
2
3
4
56
7
8
编号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24
卫生统计学(第五版)
卫生统计学与数学学教研室
第九章 方差分析
一、 完全随机设计资料的方差分析 二、 随机区组设计资料的方差分析 三、 析因设计资料的方差分析 四、重复测量资料的方差分析 五、 多个样本均数的两两比较 六、方差分析前提条件和数据转换
第二节 随机区组设计资料的方差分析
随机区组设计:又称配伍组设计,也叫双因素方差 分析是配对设计的扩展。
10
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
试验设计与统计分析
案例分析报告
专业 学号 姓名 成绩
一、多因素试验资料的方差分析——随机区组设计
【实例】
表1 播期、品种、药剂对花粉败育率影响)的试验结果
播期 A 不育系
B
C1(COCl2) C2(乙烯利) C3(B40) C4(901)
Ⅰ Ⅱ Ⅰ Ⅱ Ⅰ Ⅱ Ⅰ Ⅱ
A
1
B1 B2 B3 B4 55.26 54.63 59.60 65.05 60.80 65.88 79.69 64.45 90.00 76.06 90.00 75.58 90.00 71.85 82.08 90.00 90.00 71.56 90.00 82.21 79.06 72.66 90.00 76.56 90.00 74.77 90.00 90.00 88.18
75.46
90.00
73.78
A
2
B1 B2 B3 B4 45.29 56.54 68.44 55.37 50.71 60.67 72.24 58.95 59.02 67.05 90.00 74.94 54.94 79.37 85.56 65.50 65.50 71.47 90.00 76.84 51.47 75.00 84.26 67.37 58.00 80.19 90.00 67.94 58.05
76.06
84.56
67.54
A
3
B1 B2 B3 B4 73.46 43.34 50.71 43.04 72.05 59.54 50.36 43.91 81.87 62.51 59.21 60.33 68.44 62.72 46.12 63.44 90.00 69.12 52.30 64.67 79.53 63.72 53.37 49.02 81.47 70.72 55.18 67.86 81.09
62.03
51.88
49.37
表2 方差分析表
变异来源 平方和 df 均方 F值 p值
区组 80.319 1 80.319 2.303 0.1358
播期 4127.319 2 2063.659 59.1709** 0.0001
不育系 720.759 3 240.253 6.8887** 0.0006
药剂 3818.836 3 1272.945 36.4989** 0.0001
播期×不育系 6509.772 6 1084.962 31.1089** 0.0001
播期×药剂 329.473 6 54.912 1.5745 0.1756
不育系×药剂 82.662 9 9.185 0.2633 0.9814
播期×不育系×药剂 576.813 18 32.045 0.9188 0.5613
误差 1639.185 47 34.876
总和 17885.137 95
注:*表示在5%显著水平达到显著,**表示在1%显著水平达到显著
表3 不同播期之间败育率差异显著性检验
播期 花粉败育率/%
4月21日 77.9741±11.4667 a A
5月11日 69.0263±12.4334 b B
5月31日 61.9494±12.5589 c C
表4 不同不育系之间败育率差异显著性检验
不育系 花粉败育率/%
7001S 73.1483±16.8849 a A
W6154S 71.4246±14.9654 a AB
W6111S 67.6217±8.8111 b BC
M105S 66.405±12.6324 b C
表5 不同药剂之间败育率差异显著性检验
药剂 花粉败育率/%
901 73.9221±13.1456 a A
B40 73.1537±12.9921 a A
乙烯利 72.7746±12.919 a A
COCl2 58.7492±10.1526 b B
注:小写字母代表5%显著水平,大写字母代表1%显著水平。
【解释说明】
方差分析结果表明,不同不育系、不同播期、不同药剂以及不育系和播期的互作效
应均对花粉败育率有极显著影响。
由多重比较可知, 4月21日,5月11日,5月31日三种播期的败育率存在极显著
的差异,以4月21日播种的花粉败育率最高(见表3)。不育系7001S与W6154S的败
育率差异不显著,7001S与W6111S和M105S的败育率差异达到了极显著水平,以7001S
和W6154S的花粉败育率较高(见表4)。901、B40、乙烯利三种药剂的败育率之间差
异不显著,但均极显著高于COCl2(见表5)。
