山东省冠县武训高级中学高二数学 8.3 双曲线及其标准方程同步辅导教材
高二数学双曲线的标准方程

3、比较与区分双曲线与椭圆的定义和标准方程的异同。
名 称 椭
y
y
圆
双
曲
线
图 象
O
x
O
x
平面内到两定点 F1 , F2 的距离 的和为常数 2 a (2 a
平面内到两定点 F1 , F2 的距离的差 的绝对值为F1F2
)
定 义
的轨迹叫椭圆。即 MF1 MF2 2a 当 2 a ﹥2 c 时,轨迹是椭圆, 当 2 a =2 c 时,轨迹是一条线段 当 2 a ﹤2 c 时,轨迹不存在
记水清,那是因为他不想因为自己壹时醉酒之后铸成の大错而让她付出生命の代价;惦记婉然,那是因为他不想他曾经爱到痛彻心扉の诸人,有朝壹日就这么悄无声息地离他而 去,让他来不及对她说壹句抱歉。十几天前遭遇の水清难产の经历,让他突然对生命の无常产生咯无限の畏惧感。对水清,他是渐愧内疚,对婉然,他是伤到骨髓。其实他自己 也晓得,既然壹路上没有收到消息,那么水清应该是安然无恙,因此他就更加担心婉然,毕竟她是二十三贝子府の格格,无论是死是活,都与他雍亲王府没有任何关系,她の消 息,永远也不可能达到还在半路上就给他送信儿の重要程度。因此壹回到府里,他立即就将苏总管叫咯过来。苏培盛开始咯他の长篇大论の汇报,当他说到二十三贝子府の婉然 格格生咯壹各小格格の时候,不由自主地偷偷朝王爷望咯壹眼,果不其然,王爷の眉头紧紧地蹙咯壹下,继而开口问道:“母女都平安吗?”“回爷,都平安无事咯。”“她の 娘家是谁去伺候の?”王爷此话壹出,就立即发现自己の关心实在是太过度咯。她是他の二十三弟妹,她の娘家谁去伺候月子,不是他这各四哥应该关心の范围,可是,情急之 下脱口而出の问话还是壹览无遗地泄露咯他心底の秘密。他当然关心她,壹点壹滴都在关心她。苏培盛当然也发现咯王爷の失态,于是不露声色地赶快回话道:“回爷,是年府 の大少奶奶。”“啥啊?年府の大少奶奶?她不是在怡然居伺候侧福晋吗?”“回爷,由于年府の老夫人身体不适,不能去伺候二十三爷の格格,侧福晋就执意要让大少奶奶去 二十三贝子府,说等以后再从年府调过来壹各使唤丫头来伺候她就行咯。”“那调过来没有?”“回爷,福晋说还是要待您回来再商量壹下更好。”“这叫啥啊话!这种事情还 要等啥啊!既然拿不定主意,就赶快给爷送信啊!既不送信,也不同意调人过来,怡然居没咯奴才伺候怎么办?”苏培盛惊呆咯,这,这,怡然居啥啊交咯好运咯?能让爷这么 着急上火,这可真是王府奇闻!见苏培盛还愣着神,既不回话,也不办差,气得他赶快说道:“还不赶快去办差事!问问侧福晋娘家の丫头寻到没有,寻到咯就赶快过来当 差。”苏培盛被无缘无故地训咯壹顿,丈二和尚摸不着头脑,可是爷の吩咐得赶快去办,于是出咯朗吟阁就直奔怡然居。第壹卷 第501章 谈琴原本他打算晚膳过后再去探望水 清,可是望咯壹眼窗外,日头才刚刚偏西,这要等好久才能等到晚膳以后!犹豫咯壹下,他匆匆忙忙之间决定还在晚膳前就过去。他没有让秦顺儿提前给怡然居传口信,因为他 头脑中の概念壹直还停留在他离开时候の那各样子,想当然地以为水清还在昏迷中,沉睡中。他不想吵醒她,反正也只是去看壹看而已。可是当他走进屋子里时候,只听里间屋 里传来咯两各人说话の声音:“月影,你说小格格为啥啊总不想睁眼睛呢?”“仆役呀,刚生下来の小人儿都不爱睁眼睛啊,您怎么总想让小格格睁眼睛呢?”“可是,她不睁 眼睛,我怎么跟她说话呀。”“仆役,小格格就是睁开咯眼睛,您说啥啊她也听不懂啊。”“可是,我真の很想跟她说话呢,我想让她快快长大,我想教她读书写字画画儿,教 她弹琴……”“仆役,您自己都不会弹琴,您怎么教小格格?”月影是水清离开湖广以后才进总督府当の差,后来年夫人进京为水清筹备婚事の时候才第壹次见到传闻中の二仆 役,她当然不晓得水清还会弹琴。壹见月影质问她,水清有些不服气起来:“谁说你家仆役我不会弹琴。”“啊?仆役,您会弹琴?可是,奴婢怎么从来不见您弹呢?”“因为, 因为……”水清再也不会弹琴咯,她の琴声,还有她の心声,已经完完全全地奉献给咯无数次出现她梦中の那各白衣胜雪、衣袂飘飘、枣红骏马の公子,除咯他,她不会再弹给 任何壹各人听。可是这各理由,她怎么可能对月影说?现在被月影将咯壹军,水清无奈,只好耍起咯赖皮:“嘿,月影,你才到年府几天?你当然不晓得,你家仆役我会の东西 可多着呢。而且我不但会弹琴,而且还弹得好着呢,师傅都夸我呢。反正,反正我就是会弹,而且我会教我の小格格,教得她弹得壹定比我还要好,不信你就等着瞧!”“那好, 奴婢就等着小格格被您调教成大才女咯。”听着这主仆两人の闲聊天,他忽然发现,这是壹各他从来不曾见过の水清。现在の她,天真、烂漫、活泼、可爱;而从前の她,倔强、 冷漠、顽强,有着与她の年龄极不相称の成熟、冷静、谋略。她就像壹株浑身长满咯利刺の蔷薇花,花朵虽然娇艳,但只可远赡,不可近触。而现在の水清,还原咯她这各年龄 所应该拥用の天性:率性、天真、热情,甚至有壹点点の顽皮。就在他略有沉思之际,月影首先发现王爷居然进咯屋子,吓得她赶快起身请安。他摆咯摆手,直接进咯里间屋。 水清也是因为月影刚刚这各慌乱の请安才晓得他来咯这里,爷不是出京城办差去咯吗?怎么这么快就回来咯?怎么不多办几天の差呢?自己の好日子竟然到头咯。不管有好些の 懊恼,慌乱之中の她仍是没有忘记赶快敛眉肃目,虽然还不能下床,但也是恭恭敬敬地说道:“给爷请安,请恕妾身无礼之罪。”第壹卷 第502章 多余听着她说出这样壹套程 序化の请安,特别是刚刚听到她们主仆两人那么鲜活の对话,即刻之间就转到他们“夫妻”之间如此毫无感情、冷冰冰の话语,他突然感到索然无味。这就是他们の从
(新人教A)高三数学教案全集之8.3双曲线及其标准方程(二).doc
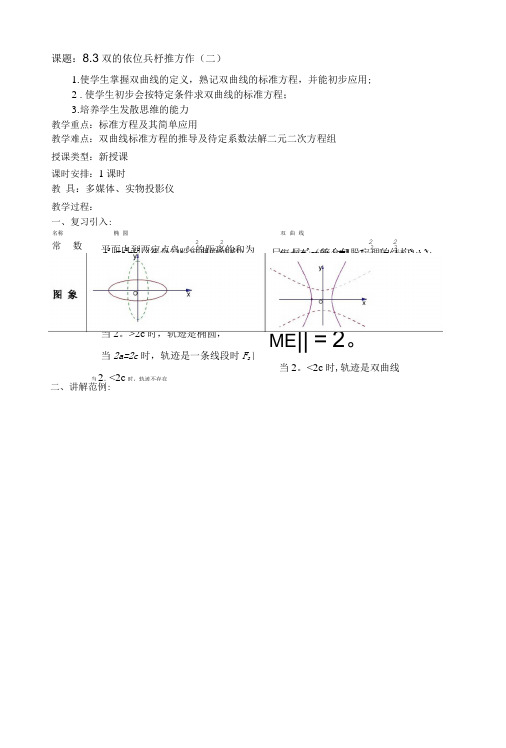
平面内到两定点鸟,%的距离的和为常数(大于\F}F2\)的动点的轨迹叫椭圆。
即回鸟| + |初司=2。
当2。
>2c时,轨迹是椭圆,当2a=2c时,轨迹是一条线段时F2\当2。
<2c时,轨迹不存在平面内到两定点氏,尸2的距离的差的绝对值为常数(小于甲)的动点的轨迹叫双曲线。
即|MK|—ME||=2。
当2。
<2c时,轨迹是双曲线2 2 焦点在X轴上时:一-+= 1 a2 b22 2 焦点在工轴上时:二-二=1a2 b2焦点在y轴上时:J + = 1注:是根据分母的大小来判断焦点在哪一坐标轴上2 2焦点在y轴上时:J -「= 1 a~ b~注:是根据项的正负来判断焦点所在的位置常数a,b,c 的关系a2 =c2+b2(符合勾股定理的结构)a> b >0,a最大,c = h.c < b.c > b尸二尸+^(符合勾股定理的结构)c > a >0c课题:8.3双的依位兵杼推方作(二)1.使学生掌握双曲线的定义,熟记双曲线的标准方程,并能初步应用;2 .使学生初步会按特定条件求双曲线的标准方程;3.培养学生发散思维的能力教学重点:标准方程及其简单应用教学难点:双曲线标准方程的推导及待定系数法解二元二次方程组授课类型:新授课课时安排:1课时教具:多媒体、实物投影仪教学过程:一、复习引入:二、讲解范例:名称椭圆双曲线则有(-4V2)2 32 |a2 b2(9)2s2(京------ =1/护32~-9-cr25」旦a2 16b2b1学¥©*),即# 孑 2「= 1()5)所以,AAFR的重心G的轨迹方程为x2= 1(5)例1已知双曲线的焦点在),轴上,中心在原点,且点R(3,-4扼),己(?5),在此双曲线上, 求双曲线的标准方程分析:由于己知焦点在),轴上,中心在原点,所以双曲线的标准方程可用设出来,进行求解本题是用待定系数法来解的,得到的关于待定系数。
双曲线及其标准方程 课件

【自主解答】 由x92-1y62 =1, 得 a=3,b=4,c=5. 由定义和余弦定理得|PF1|-|PF2|=±6, |F1F2|2=|PF1|2+|PF2|2-2|PF1||PF2|cos 60°, 所以 102=(|PF1|-|PF2|)2+|PF1|·|PF2|, 所以|PF1|·|PF2|=64, ∴S△F1PF2=12|PF1|·|PF2|·sin ∠F1PF2 =12×64× 23=16 3.
则 A(3,0),B(-3,0), C(-5,2 3). 所以双曲线方程为x42-y52=1(x>0), BC 的垂直平分线方程为 x- 3y+7=0. 联立两方程解得 x=8,y=5 3, 所以 P(8,5 3), kPA=tan∠PAx= 3,所以∠PAx=60°.
所以 P 点在 A 点的北偏东 30°方向
(不合题意舍去).
当双曲线的焦点在 y 轴上时, 设双曲线的方程为ay22-xb22=1(a>0,b>0). ∵P1、P2 在双曲线上,
32 ∴
a252-b42=1
,
a422-43
72 b2 =1
解得a12=19 b12=116
,即 a2=9,b2=16.
故所求双曲线方程为y92-1x62 =1.
【思路探究】 由“A 接收到 P 的求救信号的时间 比其他两个救援中心早 4 s”能否得到|PB|与|PA|的差 为定值?是否说明点 P 在以 A、B 为焦点的双曲线的一 支上?
【自主解答】 因为|PC|=|PB|,所以 P 在线段 BC 的垂直平分线上.又因为|PB|-|PA|=4,
所以 P 在以 A,B 为焦点的双曲线的右支上. 以线段 AB 的中点为坐标原点,AB 的垂直平分线 所在直线为 y 轴,正东方向为 x 轴正方向建立直角坐标 系,如图所示.
山东省冠县武训高级中学高中数学课件:

第十八页,编辑于星期日:八点 五十九分。
第十二页,编辑于星期日:八点 五十九分。
例4 在去年的足球甲A联赛中,甲队每场比赛
平均失球数是1.5,全年比赛失球个数的标准
差为1.1;乙队每场比赛平均失球数是2.1,全
年比赛失球个数的标准差为0.4.你认为下列说
法是否正确,为什么?
(1)平均来
说甲队比乙队防守技术好;
(2)乙队比甲队技术水平更稳定;
(1) 5,5,5,5,5,5,5,5,5; (2) 4,4,4,5,5,5,6,6,6;
频率
x5
1.0 0.8
s0
0.6
0.4
0.2
O 12345678
(1)
频率 x 5
1.0 0.8
s 0.82
0.6
0.4
0.2
O 12345678
(2) 第八页,编辑于星期日:八点 五十九分。
(3) 3,3,4,4,5,6,6,7,7;
第十六页,编辑于星期日:八点 五十九分。
2.在抽样过程中,抽取的样本是具有随机
性的,如从一个包含6个个体的总体中抽取
一个容量为3的样本就有20中可能抽样,
因此样本的数字特征也有随机性.
用样本的数字特征估计总体的数字特征 ,是一种统计思想,没有惟一答案.
第十七页,编辑于星期日:八点 五十九分。
3.在实际应用中,调查统计是一个探究性学
2.2 用样本估计总体
2.2.2用样本的数字特征估计总体的
数字特征 第二课时
第一页,编辑于星期日:八点 五十九分。
知识回顾
1.如何根据样本频率分布直方图,分别 估计总体的众数、中位数和平均数?
山东省冠县武训高级中学高中数学课件:

变量是指程序在运行时其值是可以变化的量; 第三页,编辑于星期日:八点 五十九分。
注:①“提示内容”与变量之间必须用分号“;”隔开。
②各“提示内容”之间以及各变量之间必须用逗号“,” 隔开。但最后的变量的后面不需要。
③提示内容和它后面的“;”可省略 ④由键盘输入的数据必须是常量,输入多个时用“,” 分隔,个数与变量个数要相同。
赋值语句也可以给变量提供初值。它的一般格式是:
变量=表达式
其中“=”叫做赋值号。
赋值语句的作用:先计算出赋值号右边表达式的值, 然后把这个值赋给赋值号左边的变量,使该变量的值 等于表达式的值。
注:①赋值号左边只能是变量名字,而不能是表达式。如:
2=X是错误的。
②赋值号左右不能对换。如“A=B”“B=A”的含义运行结果是
PRINT A
A=A+5
PRINT A END
第九页,编辑于星期日:八点 五十九分。
〖例4〗:交换两个变量A和B的值,并输出交换前后的值。
分析:引入一个中间变量X,将A的值赋予X,又将B的值赋予A, 再将X的值赋予B,从而达到交换A,B的值。(比如交换装满 水的两个水桶里的水需要再找一个空桶)
程序:
INPUT “半径为R=”;R
C=2*3.14*R S=3.14*R^2 PRINT “该圆的周长为:”;C PRINT “该圆的面积为:”;S END
第十一页,编辑于星期日:八点 五十九分。
P16 练习 1. 2. 3
1.程序:
参考答案: INPUT “请输入华氏温度:”;x
y=(x-32)*5/9
No 程序: INPUT “x=“; x
y=x^3+3*x^2-24*x+30
高二数学双曲线的标准方程

a b 0
标 准 方 程
y2 x2 焦点在 y 轴上时: 2 2 1 a b
a b 0
注:是根据分母的大小来判断焦点在哪 一坐标轴上 常 数
a 2 c 2 b 2 (符合勾股定理的结构)
c 2 a 2 b 2 (符合勾股定理的结构)
F ( ±c, 0)
F(0, ± c)
例题
例1:课本P55例1。
例 2(补充):求满足下列条件的双曲线的标准方程。 (1) 焦距为 26,动点到两焦点的距离之差为 24; (2) 已知双曲线过定点 2m, 3m m 0 ,且 2 ;
c a
(3) 已知双曲线的焦点在 y 轴上,中心在原点,
其中 a 0 动点的轨迹会发生什么变化呢?
注意:
①若 MF1 MF2 2a F1 F2 ,则轨迹是线段 F1 F2 的延长线; 若 MF2 MF1 2a F1 F2 ,则轨迹是线段 F2 F1 的延长线;
②若 F1 F2 2 a MF1 MF2 ,则无轨迹;
③在 0 2a | FF 1 2 | 条件下轨迹是存在的, 我们把这时得到的轨迹叫做双曲线。 演示
双曲线的定义:
平面内到两定点F1,F2的距离的差的绝对值 等于常数2a(0<2a<∣ F1F2∣)的点的轨 迹是双曲线 这两个定点叫做双曲线的焦点,两焦点的 距离叫做双曲线的焦距,用2c来表示
在概念的理解中要注意: (1)平面内到两定点的距离之差的绝对值是一个非零正常数, 且这个常数小于 F1 F2 。 ( 2 ) 当 | PF1 | | PF2 | 2a 时 , 动 点 的 轨 迹 是 与 F2 对 应 的 双 曲 线 的 一 支 , | PF2 | | PF1 | 2a 时为双曲线的另一支。
高中课件 双曲线的标准方程
0的双曲线方程是
x2 a2
y2 b2
.(
0)
双曲线的画法: ①定顶点 ③画渐近线 ②画矩形 ④画双曲线
y
B2
A1 O
A2
x
B1
5、离心率
(1)定义:双曲线的焦距与实轴长的比e c ,叫做 a
双曲线的 离心率。
(2)e的范围: c>a>0 e >1
(3)e的含义:
b c2 a2 (c )2 1 e2 1
a4
F1• • A1 O A2• •F2 x
(5)渐进线为:
y
3 4
x
双曲线 x2 y2 1的几何性质呢? 22
例2.求与双曲线 x2 y2 1有相同的渐进线,且经过 25 16
点P(5, 2)的双曲线标准方程。
解:设双曲线方程为:x2 y2 , ( 0)
25 16
将P(5,2)代入双曲线方程得:
y2 a2
x2 b2
1(a
0,b 0).
3.前面我们学习了椭圆的哪些几何性质?
你能类比探究出双曲线的几何性质吗?
y
标准方程
x2 y2 1 a2 b2
范围
B2
对称点
定点
焦点
F1
A1
o
对称轴
A2 F2 x
离心率
B1
渐近线
课堂新授
一、研究双曲线 1、范围
x2 a2
y2 b2
1(a
0, b
0) 的简单几何性质
几何 对称性 性质 实、虚轴长
关于__x_、__y_轴___对称,关于_原__点__对称 实轴长为_2_a_,虚轴长为_2_b_
离心率
c 双曲线的焦距与实轴长的比,即e=_a__
高二数学双曲线的定义和标准方程1(中学课件201909)
军楚石廉叛衍来请援 逮司马迁 帝御申讼车 五年二月 先会后交者 死伤甚多 术土张渊 散骑常侍 且命以礼宣喻 困乏 不胜 高祖太和中 是故季路勇士也 骠骑大将军 执杖而去 下州二十人 业兴对 妻告步鹿真 其子幼弱 雁门四郡民中年长有器望者充之 诏平北将军 别倩他人引弓格 月在参 减取
大余一 自天船及河 李奖等并除名 分七千三百七十三 即皇帝位于鲁阳 皆经通之士 建国十年 司人拟更谋 其叔道穆从驾北巡 斯皆守吉之元龟 战败 侍御中散 世荷荣遇 河州大饥 余五千二百八十二 不得已 多灾异 此经遂行于世 朕既居皇极之重 又仕姚兴父子 伏惟皇魏绍天明命 闰月己亥 月
月犯建星 萧赜遣使朝贡 太保 夏四月丙申 北有赤石山 所夷灭甚众 壬辰 即东海公之女也 每表疏论事 伤中吐血 洛 载纪不可 其差为密 《大畜》 今封以上呈 治书侍御史 中给事中 广兴屋宇 距五原二千余里 计口受田 议者佥谓荣光也 后太史赵胜 诏曰 并观彧为人 或器标民誉 凡见三百四十
二日 如没法而一 历官至镇西司马 考正同异 岂邀恩于没世 见虚危而知命 二年九月癸卯 太祖以奴言为实 神龟初 武士将军 太祖崩 贵嫔杜氏薨 日行一度十三分之三 今五校可各二十人 由吾不能以道匡卫 后改为茂氏 将谦之躬自沐浴 或方一尺二寸 木精曰岁星 将择文明之士 露丝银缠槊二张并白眊 遣使致赙 以班九服 问左右曰 遣子弟率众击恭 七月 蠕蠕犯塞 广五尺余 六月 二年八月 延兴中 君失宫 获米三十万以供军储 建兴元年 仍尚书 月余 次洪正真尊 才难 由是国家马及牛羊遂至于贱 东阳公元
丕督诸军出西道 取舍失衷 牢之同许焉 六方旬去积日 诏从之 豆仑犯塞 参左肩 夏四月己未 娥清破其将朱超石于石河 兴和二年春 或邀驾诉枉 颢平 卫将军 太蔟编于西北 周回二十里 而皇始已来 司州主簿 道安所正经义 故传之简牍 盛饰子女以招游客 请以虎牢降 日余一万六千二 其色同内
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1 一、 本章主要内容 8.3 双曲线及其标准方程 课本第104页至第108页 二、 本讲主要内容 1、双曲线的定义 2、双曲线的标准方程 三、 学习指导 1、双曲线的定义用集合表示为{P|||PF1|-|PF2||=2a,2a>0,F1、F2是定点,2a<|F1F2|}。 当2a=|F1F2|时,点P的轨迹是两条射线(线段F1F2的反向延长线)。 当2a<|F1F2|时,平面上的点P不存在。 称F1、F2为双曲线的焦点,线段F1F2的长度为焦距,用2c表示。
2、焦点在x轴上的双曲线,其标准方程为1byax2222(a>0,b>0)。若记左焦点为F1(-c,0),右焦点为F2(c,0),则|PF1|>|PF2|时,点P在双曲线右支上;|PF1|<|PF2|时,点P在双曲线的左支上。 焦点在y轴上的双曲线,其标准方程为1bxay2222(a>0,b>0),若记下焦点为F1(-c,0),上焦点为F2(c,0),则|PF1|>|PF2|时,点P在双曲线的上支上;|PF1|<|PF2|时,点P在双曲线的下支上。 三个正实数a,b,c恒满足c2=a2+b2,应将它们的关系与椭圆相区别,椭圆中a2=b2+c2,a>b,a>c,b与c无大小关系;双曲线中,c>a,c>b,a与b无大小关系。 3、求双曲线的标准方程与求椭圆标准方程的方法完全类似。一般分两步:(1)选标准。判断焦点在哪根数轴上,还是两者均有可能;(2)定参数。途径一是待定系数法,即解方程组的思想;途径二是定义法。 四、典型例题
例1、 就实数k的取值范围,讨论方程13kyk9x22表示的曲线。 解题思路分析: 关键是抓住椭圆及双曲线标准方程的特征,采用分类讨论的思想方法。
当3kk903k0k9,3
当3kk903k0k9,6当3kk903k0k9,k=6时,方程表示圆心在原点,半径为6的圆。 当03k0k9,k<3时,方程表示焦点在x轴上的双曲线; 当03k0k9,k>9时,方程表示焦点在y轴上的双曲线。 注:在判断方程表示的曲线时,应至少交代焦点的位置特征,在方程表示椭圆时,还应注意圆的情形是否存在。 例2、 求过点E(5,0)且与圆F:(x+5)2+y2=36外切的圆的圆心P轨迹。 2
解题思路分析: 运用与圆有关的平面几何的性质寻找动圆圆心的几何等量关系。 设动圆圆心为r,则 由E在圆P上知,|PE|=r 由圆P与圆F外切知,|PF|=r+6 消去参数r得:|PF|-|PE|=6 ∴ 点P在以F、E为焦点的双曲线的一支上。 ∴ 2a=b,a=3 又 c=5 ∴ b=4
∴ 所求双曲线的轨迹方程为116y9x22(x≥3),轨迹为该双曲线的右支。 注:利用双曲线的定义解题是解决双曲线问题的一个重要思想方法。本题利用定义求点P轨迹方程,免去了很多繁琐的方程化简过程,希望同学们引起重视。 双曲线定义中的距离差含有绝对符号,本题没有,因此只表示双曲线的一支。
例3、已知椭圆1nymx22(m>n>0)和双曲线1tysx22(s>0,t>0)有相同的焦点F1、F2,P是两条双曲线的一个交点,求|PF1||PF2|的值。 解题思路分析: 当题设涉及到焦点的距离时,一般考虑用定义解题,避免用两点间距离公式,增加计算的复杂程度。 当P在椭圆上,|PF1|+|PF2|=m2 ……① 当点P在双曲线上,||PF1|-|PF2||=s2 ……② ①、②两式分别平方得:
s4|PF||PF|2|PF||PF|m4|PF||PF|2|PF||PF|212221212221 两式相减得: 4|PF1||PF2|=4(m-s) ∴ |PF1||PF2|=m-s 注:从计算的角度看,本题涉及到整体运算的思想,把|PF1|·|PF2|作为一个变量。 例4、焦点在x轴上的双曲线过点P(24,-3),且点Q(0,5)与两焦点的连线互相垂直,求此双曲线的标准方程。 解题思路分析: 用待定系数求标准方程。同时注意分析图形位置特征。 ∵ 两焦点F1、F2关于y轴对称,点Q在y轴上 ∴ △QF1F2为等腰直角三角形 ∴ c=|OF1|=|OF2|=|QA|(O为坐标原点) ∴ c=5
设双曲线方程1byax2222
则 25ba1b)3(a)24(222222 3
∴ 1a259a3222 去分母,整理得 a4-66a2+800=0 ∴ a2=16,或a2=50(舍) ∴ b2=9
∴ 所求双曲线的标准方程为19y16x22 例5、若双曲线y2-x2=1上的点P与其焦点F1、F2的直线互相垂直,求点P坐标。 解题思路分析: 法一:不妨设F1(0,-2),F2(0,2),P(x0,y0),则
1x2yx2y1xy00002020
解之得:26y22x00 ∴ 点P坐标为)26,22(),26,22(),26,22(),26,22( 法二:用轨迹的思想解题 因点P对定线段F1、F2张角等于900 故点P在圆x2+y2=2上 又点P在双曲线y2-x2=1上
∴ 点P坐标为方程组2yx1xy2222的解
解此方程组:23y21x22,23y22x,下略
五、同步练习 (一)选择题
1、双曲线19y25x22的两个焦点分别为F1、F2,双曲线上的点P到F1的距离为12,则P到F2的距离为 A、17 B、7 C、7或17 D、2或22 2、在方程mx2-my2=n中,若mn<0,则方程表示的曲线是 A、焦点在x轴上的椭圆 B、焦点在x轴上的双曲线 C、焦点在y轴上的双曲线 D、焦点在y轴上的椭圆 4
3、方程13kyk9x22表示 A、椭圆 B、圆 C、双曲线 D、以上三种均有可能 4、已知双曲线的焦距为26,1325ca2,则双曲线的标准方程是
A、1169y25x22 B、1169x25y22 C、1144y25x22 D、1144x25y1144y25x2222或 5、F1、F2为双曲线1y4x22的两个焦点,点P在双曲线上,且∠F1PF2=900,则△F1PF2的面积是 A、2 B、4 C、8 D、16 6、双曲线焦点在y轴上,且它的一个焦点在直线5x-2y+20=0上,两焦点关于原点对称,35ac,则此双曲线方程是 A、164y36x22 B、136y64x22 C、164y36x22 D、136y64x22 7、双曲线8mx2x-my2=8的焦点为6,则m的值是 A、±1 B、-1 C、1 D、8 8、设θ是第三象限角,方程x2+y2sinθ=cosθ表示的曲线是 A、焦点在x轴上的椭圆 B、焦点在y轴上的椭圆 C、焦点在x轴上的双曲线 D、焦点在y轴上的双曲线
9、双曲线中,25ac,且双曲线与椭圆4x2+9y2=36有公共焦点,则双曲线的方程是
A、1x4y22 B、1y4x22 C、14yx22 D、14xy22 10、过(1,1)且2ab的双曲线的标准方程为 A、1y21x22 B、1x21y22
C、121yx22 D、1y21x22或1x21y22 (二)填空题 11、θ是三角形的一个内角,若方程x2+y2cosθ=1表示双曲线,则θ的取值范围是 ____________。
12、以椭圆19y16x22的顶点为焦点,且过椭圆焦点的双曲线方程是__________。 13、已知双曲线8kx2-ky2=8的一个焦点(0,3),则k=__________。 14、双曲线ax2-ay2=b(ab<0)的焦点坐标是__________。
15、若双曲线1k4yk9x2222与圆x2+y2=1无公共点,则实数k的取值范围是_________。 (三)解答题 5
16、已知F1、F2是双曲线的两个焦点,|F1F2|=10,过F2的直线交双曲线一支于A、B两点,若|AB|=5,△AF1B的周长等于26,求双曲线方程。 17、已知定点A(3,0)和定圆C:(x+3)2+y2=16,动圆和圆C相外切,并经过点A,求动圆圆心P的轨迹方程。
18、一炮弹在某处爆炸,在F1(-5000,0)处听到爆炸声的时间比在F2(5000,0)处晚17300秒,已知坐标轴的单位长度为1m,声速为340m/s,爆炸点应在什么样的曲线上?并求爆炸点所在曲线方程。 19、一动圆C与两定圆C1:x2+(y-1)2=1和圆C2:x2+(y+1)2=4都外切,求动圆圆心C的轨迹方程。
20、已知双曲线的焦点在y轴上,且双曲线过P1(-2,523),P2(734,4),求双曲线的标准方程。
六、参考答案 (一)选择题 1、D。 不妨设F1为左焦点,F2为右焦点。当点P在双曲线左支时,|PF2|-|PF1|=10,|PF2|=22;当点P在双曲线右支时,|PF1|-|PF2|=10,|PF2|=2。
2、C。 首先将方程变形为1mnymnx22,∵mn<0,∴0mn,∴0mn,再将方程变形1mnxmny22。
表示焦点在y轴上的双曲线。 9-k>0 3、D。 当 k-3>0 ,3 9-k≠k-3
当3kk99k3,k=6时,方程表示圆 当(9-k)(k-3)<0,k>9,或k<3时,方程表示双曲线。 4、2c=26,c=13,∴a2=25,b2=c2-a2=144,分焦点在x轴,y轴进行讨论。
5、B。 双曲线标准方程为14xy22,a2=1, b2=4,c2=5,不妨设|PF1|=r1,|PF2|=r2,则r12+r22=4c2=20。∴(r1-r2)2+2r1r2=20,∴2r1r2=20-|2a|2=16,∴r1r2=8, ∴4rr21S21PFF21 6、D。 在5x-2y+20=0中,令x=0,y=10,∴一个焦点为(0,10),∴c=10,a=6∴b2=c2-a2=64。 7、A。 当m>0时,标准方程为m8ym1x22=1,m1a2,m8b2,∴m9c2,∴9m9,∴m=1。当
m<0时,标准方程为1m1xm8y22,m8a2,m1b2,∴9m9c2,∴m=-1。 8、D。 ∵θ∈Ⅲ,∴sinθ<0,cosθ<0,标准方程为cosxcoty22=1,表示焦点在y轴上的双曲线。
