数学奥林匹克竞赛培训
数学奥林匹克之路小学数学竞赛经验分享

数学奥林匹克之路小学数学竞赛经验分享作为小学生,我曾经积极参加数学奥林匹克竞赛,在这个过程中收获了许多经验和教训。
今天,我将分享我的数学竞赛经验,希望能给其他小学生在数学奥林匹克之路上提供一些帮助和启示。
第一,培养对数学的兴趣是关键。
数学竞赛并不仅仅是为了获得好成绩,更重要的是提升自己对数学的兴趣和热爱。
只有对数学有浓厚的兴趣,才能坚持不懈地学习和参加竞赛。
因此,在备战数学竞赛时,我们要培养对数学的兴趣,可以通过解有趣的数学问题、参加数学俱乐部或者找到一位优秀的数学教师进行探讨等方式来激发兴趣。
第二,熟练掌握基础知识是基础。
对于小学生来说,数学竞赛的基础知识通常都是在课堂上学习的内容。
因此,在备战竞赛时,我们要将课本知识牢固掌握,并且进行广泛的练习。
通过反复做题,我们可以逐渐熟悉各种类型的题目,并提高解题的速度和准确度。
第三,注重解题方法和思维能力的培养。
数学竞赛不仅仅考察知识的掌握程度,更注重解题思路和方法的灵活运用。
因此,在备战竞赛时,我们既要搞清楚各种解题方法的原理和步骤,也要学会运用这些方法来解决实际问题。
同时,我们还需要培养灵活的思维能力,学会从不同的角度思考问题,找到问题的本质,从而能够快速有效地解决问题。
第四,保持良好的心态和积极的态度。
数学竞赛是一项长期的过程,充满了挑战和压力。
在备战竞赛时,我们要保持积极的态度,相信自己的能力,并且坚持不懈地努力。
遇到困难和挫折时,要保持乐观的心态,相信自己一定可以战胜困难,取得好的成绩。
第五,多参加模拟竞赛和交流活动。
在备战竞赛过程中,我们可以参加一些模拟竞赛和交流活动,这样既可以检验自己的水平,也可以通过与他人的交流和互动来学习和提高。
通过模拟竞赛,我们可以提前熟悉竞赛的环境和题型,增强自己的比赛经验,为正式竞赛做好准备。
总结起来,数学奥林匹克之路是一条充满挑战和机遇的道路。
在备战竞赛时,我们需要培养对数学的兴趣,扎实掌握基础知识,注重解题方法和思维能力的培养,保持良好的心态和积极的态度,并且多参加模拟竞赛和交流活动。
数学奥林匹克通过参加奥林匹克竞赛激发孩子们的数学兴趣和竞争力

数学奥林匹克通过参加奥林匹克竞赛激发孩子们的数学兴趣和竞争力数学奥林匹克,作为一种具有挑战性和竞争性的数学竞赛,对于激发孩子们的数学兴趣和竞争力具有重要意义。
通过参加奥林匹克竞赛,孩子们可以从中体验到数学的魅力,激发对数学的兴趣和热爱,并通过与其他参赛者的较量不断提高自己的数学能力。
本文将从以下几个方面来探讨数学奥林匹克如何对孩子们的数学兴趣和竞争力产生积极影响。
一、激发数学兴趣数学奥林匹克竞赛的题目通常具有一定的难度,涉及到许多抽象的数学概念和思维方法。
参与奥林匹克竞赛的孩子们需要通过深入思考和解题来应对挑战,这种思维训练不仅能够提高他们的逻辑思维能力,还能够激发他们对数学的兴趣。
在解决问题的过程中,孩子们会产生一种探索和发现的乐趣,从而愿意主动地去学习数学知识,培养数学思维。
二、培养数学思维方式数学奥林匹克竞赛注重培养学生的创新思维和实际解决问题的能力。
相较于传统教学方法,奥林匹克竞赛更加注重培养学生的数学思维方式。
在竞赛中,学生需要运用数学原理和方法,灵活地解决各种问题。
这种思维方式可以帮助他们在日常生活中遇到数学问题时更加从容地解决,培养了他们对于复杂问题的分析和解决能力。
三、增强数学学习动力数学奥林匹克竞赛的激烈竞争环境能够有效地激发孩子们的学习动力。
在参与竞赛的过程中,孩子们会感受到与其他优秀的参赛者竞争的紧张氛围,这种竞争对于他们来说是一种推动力量。
为了取得好成绩,孩子们会更加努力地学习和复习,提高自己的数学水平,同时也会从竞争中汲取到一些学习上的启示和经验,提高自己的学习方法和策略。
四、促进数学交流与合作数学奥林匹克竞赛注重学生之间的交流与合作,鼓励他们分享解题思路和方法。
通过与其他参赛者的交流,孩子们可以学习到不同的解题思路和方法,开阔了他们的数学视野。
同时,通过合作解决问题,孩子们也能够培养团队合作精神,学会与他人协作,共同攻克数学难题。
总结起来,数学奥林匹克竞赛通过其独特的竞争性和挑战性,对于激发孩子们的数学兴趣和竞争力产生了积极的影响。
中国数学奥林匹克介绍

中国数学奥林匹克介绍中国数学奥林匹克,简称为IMO(国际数学奥林匹克),是国际上最具影响力的数学竞赛之一、自1985年起,中国每年都会派遣队伍参加这一盛会。
中国在IMO上取得了非常出色的成绩,多次获得团体奖牌,并培养了众多优秀的数学人才。
中国数学奥林匹克始于1983年,最初是由当时的中国科学院院士陈省身等人发起。
陈省身是中国数学界的重要人物,也是这一竞赛的领导者和推动者。
中国数学奥林匹克的目标是培养和选拔具有创造性思维和解决问题能力的数学人才,提高学生的数学素养,促进数学教育的发展。
中国数学奥林匹克的选拔过程是分层次进行的,包括地区选拔赛、省级选拔赛、国家集训队选拔等。
优秀的学生会经过多轮选拔,最终组成中国队参加国际比赛。
这种选拔制度确保了参赛队伍的质量,使得中国能够派出强大的代表队。
中国数学奥林匹克所包含的题目范围非常广泛,从初等数学到高等数学的内容都有涉及。
题目要求学生具备独立解决问题的能力,包括发现问题、分析问题、归纳总结等。
这对学生的数学素养和思维能力提出了很高的要求,也使得中国队员在解题过程中展现出了扎实的数学基础和创新的思维。
中国数学队在IMO上的成绩一直非常出色。
自1985年以来,中国队一直保持着稳定的优异表现,多次获得团体奖牌。
尤其是近年来,中国队凭借出色的成绩连续蝉联团体冠军。
这些成绩不仅得益于优秀的选手,也离不开中国数学教育的发展和中国数学界对于数学奥林匹克的重视。
中国数学奥林匹克的成功离不开中国政府、学校和家庭的大力支持。
中国政府高度重视数学奥林匹克的培养和选拔工作,为学生参加比赛提供了优秀的培训和支持条件。
许多学校也设立了数学奥林匹克班,为学生提供特殊的培养和训练。
同时,家庭对于学生参与数学奥林匹克的支持和鼓励也非常重要,为学生提供了良好的学习环境和培养机会。
综上所述,中国数学奥林匹克是一个重要的数学竞赛,并且在国际上享有很高的声誉。
通过竞赛的选拔和培养,中国数学奥林匹克不仅推动了数学教育的发展,也培养了一大批具有扎实数学基础和创造力的数学人才。
数学奥林匹克竞赛的体会与思考

• (1)华罗庚教授在1956年就说过“这一工作会不会打 乱学校的工作呢?会不会影响全面发展的原则呢?做得 好,是不会的,……”他告诫大家“应当小心从 事”. • (2)王元教授在“数学竞赛之我见”中说:“国际上 的数学竞赛范围,大体上从小学四年级到大学二年 级.小学生因基础知识太少,这期间的所谓数学竞赛, 其实是智力小测验型,对大学生应强调系统学习,要 求对数学有一个整体了解,因此数学竞赛的重点应是 中学,特别是高中.” • (3)郑毓信教授在《数学教育哲学》一书中引述了香 港大学数学系萧文强先生关于数学奥林匹克竞赛的一 点忧虑:“证诸过去四年的香港经验,虽然每年选拔 了好几名颇富数学机智的年轻人,为香港争得好几面 奖牌,但可没见到如何藉著这项活动,在中学师生中 诱发出那股活泼生气,也没见到如何藉著这项活动营 造出一种数学文化气息.”
(四)周密细致的训练计划
• 数学竞赛涉及的知识面广、思维方法多、能力要 求高,仅靠老师讲几道典型的例题,学生做大量 的习题是远远不够的。老师必须教给学生动的数 学思想和方法,充分调动学生积极性,培养学生 自学能力,引导他们主动学习,而要学习的内容 很多,不同阶段的要求不同,没有周密的计划显 然是不行的,我总体是这样安排的:
3.严肃数学与趣味数学之间
竞赛题既有非常抽象、非常专业化的题目,又有 非常实际、非常生活化的题目,并且无论哪类题 目,命题者都追求内容的现代化、陈述的趣味性、 技巧的独创性,这使得竞赛数学把理论与应用结 合了起来.把形式化与生活趣味化结合了起来。 竞赛数学很多思想来源于高等数学,而基本方法 则植根于初等数学.不需要用到高深的数学工具, 但要有良好的数学素质,如敏锐的数学思考、深 刻的数学分析和精湛的数学构思.
3、高二学年的综合训练
(1)分代数、几何、数论、组合四大块组织若干专题 训练,精选一定数量典型问题,进行练习、讨论、 评讲和归纳,以达到能力提升的目的。 (2)套题训练,包括单元综合训练,一试综合训练、 二试综合训练和联赛模拟训练,其训练量依据学 生实际情况确定。 (3)每年暑假期间要组织高一、高二年级的学生进行 为期25天的强化训练,前15天主要是梳理重点难 点、讨论典型问题,后10天进行综合套题的考试 和评讲(教练组成员每人3套)。
2023年imo国际数学奥林匹克第二天全解答

2023年imo国际数学奥林匹克第二天全解答一、了解IMO国际数学奥林匹克国际数学奥林匹克(International Mathematical Olympiad,简称IMO)是世界上最具影响力的青少年数学竞赛活动。
自1959年起,每年举办一次,吸引了全球范围内的优秀中学生参加。
我国自1985年开始参加IMO,取得了优异的成绩。
二、掌握2023年IMO第二天试题及解答2023年IMO国际数学奥林匹克竞赛已经落幕,第二天试题涵盖了代数、几何、组合、数论等多个数学领域。
以下为部分试题及解答:1.试题一:已知函数$f(x)$满足$f(x+1) + f(x-1) = 2f(x)$,求证:$f(x)$为周期为4的周期函数。
2.试题二:求解不等式$frac{1}{x-1} + frac{1}{x-2} + frac{1}{x-3} + frac{1}{x-4} geqslant 1$的解集。
3.试题三:已知$n$为正整数,求$1^2 + 2^2 + 3^2 + cdots + n^2$与$n(n+1)(2n+1)$的比值。
三、分析试题特点与难点1.试题特点:(1)注重基础,涵盖初中至高中数学知识;(2)题目新颖,需要灵活运用数学方法;(3)考察逻辑思维、分析问题和解决问题的能力。
2.试题难点:(1)题目阅读理解,需要快速抓住关键信息;(2)解题方法多样,需要合理选择和运用;(3)对数学公式和定理的熟练掌握程度要求较高。
四、总结数学竞赛备战策略1.扎实掌握基本概念、公式和定理;2.提高解题技巧,熟练运用数学方法;3.培养逻辑思维能力,提升分析问题和解决问题的水平;4.多做真题,积累经验,提高应试能力;5.参加培训课程或寻找专业指导,提升数学素养。
以上就是关于2023年IMO国际数学奥林匹克第二天的全解答,希望对大家有所帮助。
usamo知识点

usamo知识点在数学竞赛中,USAMO(美国数学奥林匹克竞赛)是一项备受关注的最高级别竞赛。
参加USAMO需要对数学的各个领域有深入的理解和扎实的知识储备。
以下是一些USAMO的重要知识点:1. 不等式:USAMO中经常涉及各种不等式的证明和应用。
学生需要熟悉基本的不等式,如柯西-施瓦茨不等式、阿尔卡西不等式和均值不等式等。
2. 几何:USAMO几何部分通常包含复杂的几何问题。
学生需要熟悉各种几何知识,包括平面几何和立体几何。
重点包括线段和角的性质,相似三角形,圆的性质,解析几何等。
3. 数论:数论在USAMO中也是重要的一部分。
学生需要了解各种数论定理和技巧,包括质数性质,同余定理,欧拉定理和费马小定理等。
题目可能涉及到整数分解,模运算和数列等。
4. 代数:代数在USAMO中也占据重要的位置。
学生需要熟悉代数学的基本理论和方法,包括多项式、方程、组合与数列等内容。
学生需要掌握解方程和多项式性质的技巧。
5. 组合数学:在USAMO中,组合数学可以是一个相对较难的部分。
学生需要善于运用组合与排列的技巧,理解计数原理和概率理论等。
题目可能涉及到集合、排列组合、图论等知识。
6. 梳理知识点,多做题:除了以上的几个主要知识点,在备战USAMO时,多做一些经典的USAMO题目是非常重要的。
这有助于加深对知识点的理解,并提高解题能力。
请注意,USAMO是一项严肃且具有挑战性的竞赛。
想要在USAMO中表现出色,需要一个全面而扎实的数学基础,有足够的练习和思考时间,并不断拓展数学的知识面。
通过培养解决问题的能力和灵活性,参赛者可以更好地应对USAMO 的挑战。
美国中学数学奥林匹克竞赛

美国中学数学奥林匹克竞赛美国中学数学奥林匹克竞赛(American Mathematics Olympiad,简称AMC)是美国最负盛名的中学生数学竞赛之一。
它的主要目的是鼓励学生学习数学,培养学生的创新能力和独立思考能力。
AMC竞赛分为两个阶段: AMC 8和AMC 10/12。
AMC 8是专门针对8年级及以下学生的竞赛,考试内容包括中学数学的基础知识和技能,如数论、代数、几何等。
AMC 10/12则是针对10年级和12年级学生的竞赛,考试内容更加深入,包括更高级的数学知识和技能。
参加AMC竞赛的学生需要先通过学校或地区预赛,然后才有资格参加全国决赛。
全国决赛的前250名学生有资格参加国家奥林匹克数学队(USA Mathematical Olympiad,简称USAMO)的夏令营培训。
培训结束后,由数学奥林匹克队队长挑选出6名学生组成美国国家数学奥林匹克队,参加国际奥林匹克数学竞赛(International Mathematical Olympiad,简称IMO)。
AMC竞赛的历史可以追溯到1950年,当时由美国数学协会(Mathematical Association of America,简称MAA)举办。
随着时间的推移,AMAMC竞赛越来越受到美国中学生的关注,也越来越受到家长和教师的重视。
这主要是因为AMC竞赛能够激发学生的学习兴趣,培养学生的创新思维和独立思考能力。
参加AMC竞赛的学生不仅有机会提升自己的数学水平,还有机会获得各种奖学金和荣誉。
许多大学都对AMC竞赛的优胜者给予特别关注,并为他们提供优惠的录取条件和财务援助。
AMC竞赛不仅是一项竞赛,也是一个学习社区。
学生可以通过参加各种培训课程和夏令营,与同龄人一起学习和交流。
这些活动不仅能提高学生的数学水平,还能丰富学生的学习体验,增强学生的学习兴趣。
总的来说,美国中学数学奥林匹克竞赛是一项对中学生具有很大吸引力的竞赛,它既能激发学生的学习兴趣,又能培养学生的创新思维和独立思考能力。
高一学科竞赛(培优)课程计划
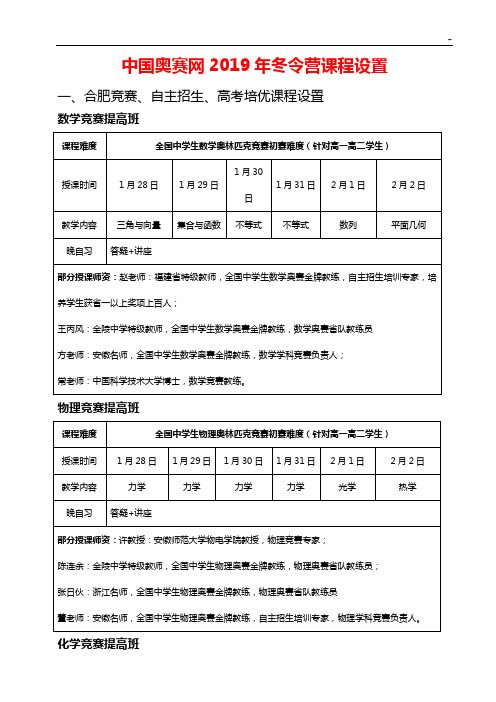
中国奥赛网2019年冬令营课程设置一、合肥竞赛、自主招生、高考培优课程设置
数学竞赛提高班
物理竞赛提高班
化学竞赛提高班
生物竞赛提高班
自主招生班
高考培优理科提高班
高考培优理科冲刺班
高考培优文科冲刺班
电脑制作活动冲刺班
二、南京冬令营竞赛专题精讲+刷题班课程设置数学
物理
化学
三、上课时间、地点
(一)时间:元月27号报到,28日上课,2月2日结束;电脑营1号结束。
(二)地点:培优营:安徽大学老校区(黄山路校区);竞赛冲刺营:南京。
四、费用标准
(一)学科竞赛营、高考培优营学费1980元/每生;
(二)电脑制作营学费3980元/每生;
(三)南京竞赛冲刺营:2380元/每生;
(四)食宿费用:合肥:80元/每生每天(伙食、住宿各40元);南京:160元/天(住宿酒店100元,伙食60元)。
(五)食宿标准:住宿校内招待所、留学生公寓,每间4人;学生食堂统一用餐。
南京酒店上课,住宿标间,酒店桌餐。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数学奥林匹克竞赛培训
数学奥林匹克竞赛(MathematicsOlympiad)是一项国际性的数学竞赛,由教育、科学与文化组织(UNESCO)创建,旨在为全球的青少年提供一个国际性的数学竞赛平台,同时也使他们通过参与竞赛学习深入了解数学,进一步提高学术水平。
参加奥林匹克竞赛的主要目的是通过组织各项竞赛活动,鼓励青少年学习和探索数学,增强学术素养,发展创新能力和提高学习效率。
因此,奥林匹克竞赛的实施和培训也促进了数学素养的提高,有助于锻炼出更多的科学和技术人才。
为了帮助参赛选手更好地参与奥林匹克竞赛,以及在数学学习上获得更大的成就,许多教育机构都提供了专门的奥林匹克数学培训课程。
其中,有一些数学培训课程是针对某个特定领域的,比如说几何、概率论、代数或者微积分,而其他一些则注重提高参赛选手的基本数学功底,为参赛选手提供一个更有效的考试解题思路,使其有更强的参赛能力。
此外,有一些数学培训课程注重发掘参赛选手的数学潜能,培养参赛选手的数学思维和解题能力,帮助参赛选手掌握更丰富的数学知识,思考数学问题,依靠数学的力量解决实际问题。
参加奥林匹克培训既可以提高参赛者的数学功底,也可以激发参赛者的数学学习热情,强化他们对数学的认知,对解决问题的能力,以及对数学学习的兴趣,使他们在奥林匹克数学竞赛中取得更好的成
绩。
参加奥林匹克培训可以有效帮助参赛者提升数学能力,丰富知识储备,拓宽思维,培养数学思维能力,加强实践能力,提高参赛者在奥林匹克竞赛中的表现。
综上所述,为了帮助参赛者在数学奥林匹克竞赛中取得更好成绩,许多教育机构都提供了专门的奥林匹克数学培训课程,旨在通过提高参赛者的数学能力和解题能力,促进参赛者在数学学习上取得更大的进步。
