正交分解法(精选例题)
正交分解理论例题及练习

正交分解理论例题及练习正交分解理论是现代数学中的一个重要概念,它在各个领域都有着广泛的应用。
本文将介绍正交分解理论的基本概念,并提供一些例题和练,以帮助读者更好地理解和应用这一理论。
正交分解理论的基本概念正交分解理论是将一个向量空间拆分成若干个正交子空间的方法。
它的核心思想是利用向量空间中的正交基,将向量空间中的向量表示成各个正交子空间上的分量之和。
在正交分解理论中,一个向量空间可以表示为以下形式:$$V = V_1 \oplus V_2 \oplus \ldots \oplus V_n$$其中,$V$ 是一个向量空间,$V_1, V_2, \ldots, V_n$ 是$V$ 的正交子空间。
例题例题1设向量空间 $V$ 的一组基为 $v_1 = (1, 0)$ 和 $v_2 = (0, 1)$。
将向量 $v = (3, 4)$ 表示为 $v_1$ 和 $v_2$ 的分量之和。
解答:首先,根据正交分解理论,$v$ 可以表示为 $v_1$ 和 $v_2$ 的分量之和。
假设 $v$ 的分量分别为 $x_1 v_1$ 和 $x_2 v_2$,其中$x_1$ 和 $x_2$ 是待定系数。
则有:$$v = x_1 v_1 + x_2 v_2$$代入已知数值,得到:$$(3, 4) = x_1 (1, 0) + x_2 (0, 1)$$由此可得到一个线性方程组:$$\begin{cases} x_1 = 3 \\ x_2 = 4 \end{cases}$$解这个线性方程组,得到解 $x_1 = 3$ 和 $x_2 = 4$。
因此,向量 $v = (3, 4)$ 可以表示为 $(3, 0)$ 和 $(0, 4)$ 的分量之和。
例题2设向量空间 $V$ 的一组基为 $v_1 = (1, 1, 1)$ 和 $v_2 = (1, -1, 0)$。
求向量空间 $V$ 的正交子空间 $V_1$ 和 $V_2$。
解答:根据正交分解理论,我们需要寻找与 $v_1$ 和 $v_2$ 正交的向量。
正交分解法(2)

正交分解法
如图,物体重力为10N,AO绳与顶板间的夹角为45º,
BO绳水平,试用计算法求出AO绳和BO绳所受拉力的大小。
FAOY=FAOcos45=G
A FAO
y FAOY
FAOX O
Bx
FAOX=FBO=G
C
正交分解法
如图,氢气球被水平吹来的风吹成图示的情形,若测得
绳子与水平面的夹角为37˚,已知气球受到空气的浮力为15N,
FN=Fsinα+Gcosα
F
A
α
Fcosα=Gsinα+Ff
y
Ff=μFN
FN
Fcosα
x
Ff Gsinα
F Fsinα
G Gcosα
正交分解法
计算多个共点力的合力时,正交分解法显得简明方便 正交分解法求合力,运用了“欲合先分”的策略,降低了 运算的难度,是解题中的一种重要思想方法。
选择合适的坐标 分解不在坐标上的力 进行同轴的代数和的运算 将两个垂直的力合成
唯一解
F2 < Fsin θ
无解
F> F2 > Fsin θ
两组解
F2 >= F
唯一解
正交分解法
选择一个坐标轴,将力分解为两个轴上的相互垂直的分力
FX= Fcosα
y
Fy
F
Fy= Fsinα
α
o
x
Fx
F2
F
θ
F1
G1
G2 G
从上面两图中可以发现,我们按照力的作用效果把F 和G进行分解所得到的两个分力的方向是相互垂直的, 这种分解力的方法叫做力的正交分解法。
Fx合=F1x+F2x+F3x+…
力的正交分解法

N2 N1
G
y
N2 N1
G
正
x
交 法
四边形法
解:以球为对象 由于球静止 F合=0 N1=Gtan370 N2=G/cos370
解:以球为对象 建立如图坐标 Fx=0 N1 - N2sin370=0 Fy=0
N2cos370 - G=0
物体静止或匀速运动,受力分析如下:
正交分解
例、G=100N,绳子OA、OB所受张力分别多大?
y
F3
F2y F3yF2
300
600 F4x
F3
F3
F3y
F2y
F2
300
600 F4x
F3x
6F002xF1
x
F x F 1 F 2 x F 3 x F 4 x
F4y
F4
12co6s0 033co3s0 04co6s0 0
1133/221/2(N)
4、将坐标轴上的力分别合成,按坐标轴规定的方向求代数和
即:Fx合=F1x+F2x+F3x+...... Fy合=F1y+F2y+F3y+......
5、最后求再求合力F的大小和方向 F合 Fx2合Fy2合
例1:一个物体受到四个力的作用,已知
F1=1N,方向正东;F2=2N,方向东偏北600, F偏3=南600,N求,3 物方3 体向所西受偏的北合30力0;。F4=4N,方向东
A. mg
FN y
B. (mg+Fsin) C. (mg-Fsin) D. Fcos
Ff
F2 x
mg
F1
F
为了求合力进行正交分解,分解是方法,合 成是目的。
正交分解专项练习
G
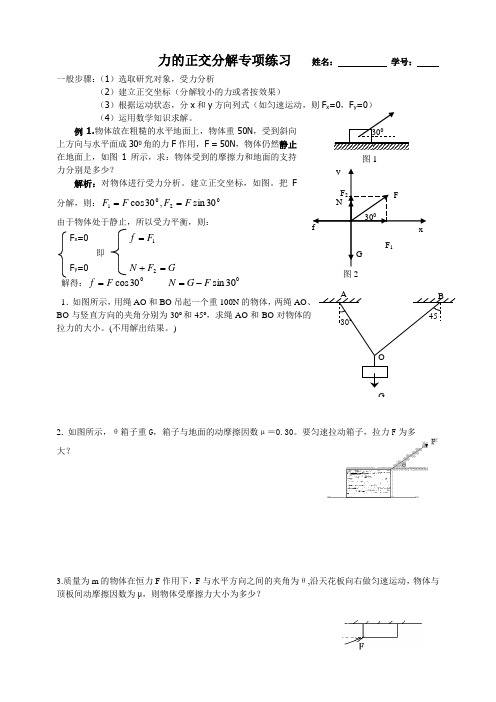
力的正交分解专项练习 姓名: 学号:
一般步骤:(1)选取研究对象,受力分析
(2)建立正交坐标(分解较小的力或者按效果)
(3)根据运动状态,分x 和y 方向列式(如匀速运动,则F x
(4)运用数学知识求解。
例1.物体放在粗糙的水平地面上,物体重
50N ,受到斜向上方向与水平面成300角的力F 作用,F = 50N ,物体仍然静止在地面上,如图
1所示,求:物体受到的摩擦力和地面的支持力分别是多少?
解析:对物体进行受力分析。
建立正交坐标,如图。
把F 分解,则:0
20
130sin ,30cos F F F F == 由于物体处于静止,所以受力平衡,则: F x =0 1F f = 即 F y =0 G F N =+2
解得:0
30cos F f = 0
30sin F G N -=
1.如图所示,用绳AO 和BO 吊起一个重100N 的物体,两绳AO 、
BO 与竖直方向的夹角分别为30o 和45o
,求绳AO 和BO 对物体的拉力的大小。
(不用解出结果。
)
2. 如图所示,θ箱子重G ,箱子与地面的动摩擦因数μ=0.30。
要匀速拉动箱子,拉力F 为多大?
3.质量为m 的物体在恒力F 作用下,F 与水平方向之间的夹角为θ,沿天花板向右做匀速运动,物体与顶板间动摩擦因数为μ,则物体受摩擦力大小为多少?
图1 图2。
4.正交分解法

力的正交分解【课堂探究】一、数学知识准备:二、力的分解1、把一个力分解成_________的过程和方法叫做力的分解。
力的分解是力的合成的___________,同样适用_______________。
2、在实际问题中,如果一个力分解为两个力时,通常根据这个力的_____________来确定分力的方向。
3、分解的步骤:1、根据力的作用效果确定分力的方向;2、画平行四边形定则定分力的大小;3、根据三角形知识求分力的大小和方向.三、力的正交分解法1.定义:将一个力分解为两个 的分力的方法称为正交分解法。
2.目的:将力的合成化简为同向、反向或垂直方向的分力,便于运用代数运算公式解决矢量的运算,“分解”的目的是为了更好地“合成”。
3.适用情况:适用于计算三个或三个以上的力的合成。
4.步骤:(1)建立坐标系:以共点力的作用点为坐标原点,直角坐标系x 轴和y 轴的选择应使尽量多的力在坐标轴上。
(2)正交分解各力:将每一个不在坐标轴上的力分解到x 轴和y 轴上,并求出各分力的大小。
(3)分别求出x 轴、y 轴上各分力的矢量和,即:Fx= Fy=(4)求共点力的合力:=θtan =θcot θ a bc =θsin =θcos合力的大小:F合=三、典型例题例1:已知放在水平面上的物体,受到与水平方向成θ角的推力F 的作用,求:该力对物体产生怎样的作用效果,其分力大小和方向如何?例2:如图所示:将重力为G的光滑圆球用细绳拴在竖直墙壁上,如图,当把绳的长度增长,则绳对球的拉力T和墙对球的弹力N的大小?例3:在同一平面上共点的四个力分别为F1=19N、F2=40N、F3=30N、F4=15N,方向如图所示,求其合力例4:重为100N的物块,放在倾角为。
30光滑斜面上,求重力的垂直斜面和使物块下滑的分力大小。
例6:如图所示,水平地面上的重为180N木块,受到与水平面成。
37斜向上的拉力F作用,F大小为60N。
求:(1)物体受到的支持力的大小;(2)若木块做匀速直线运动,木块与地面的动摩擦因数多大?四、课后作业Fθ1、如图所示:三个共点力,1F =5N ,2F =10N ,3F =15N ,θ=60°,它们的合力的x 轴方向的分量x F 为________N ,y 轴方向的分量y F 为 N ,合力的大小为 N ,合力方向与x 轴正方向夹角为 。
正交分解法专题训练

正交分解法专题训练1、 如图所示,用绳AC 和BC 吊起一个重100 N 的物体,两绳AC 、BC 与竖直方向的夹角分别为30°和45°.求:绳AC 和BC 对物体的拉力的大小2、长为20cm 的轻绳BC 两端固定在天花板上,在中点系上一重60N 的重物,如图所示:(1)当BC 的距离为10cm 时,AB 段绳上的拉力为多少?(2)当BC 的距离为102cm 时.AB 段绳上的拉力为多少?3、如图所示,细绳CO 与竖直方向成30°角,A 、B 两物体用跨过定滑轮的细绳相连.已知物体B 所受的重力为100 N ,地面对物体B 的支持力为80 N .试求:(1)物体A 所受的重力.(2)物体且与地面间的摩擦力.(3)细绳CO 受到的拉力。
4、质量为=5kg 的物体,置于倾角为=37的固定斜面上,刚好匀速下滑,现对物体施加一水平推力F,使物体沿斜面匀速向上运动,求水平推力F 的大小。
5、如图所示,人重300N,物体重200N,地面粗糙,物体静止,当人用100N的力向下拉绳子时,求人对地面的弹力和地面对物体的弹力?6、如图所示,弹簧AB原长为35厘米,A端挂一个重50牛的物体,手执B端,将物体置于倾角为300的斜面上,当物体沿斜面匀速下滑时,弹簧长变为40厘米,当物体匀速上滑时,弹簧长变为50厘米,求弹簧的劲度系数和物体与斜面的动摩擦因数7.如图所示,A、B两物体叠放在水平地面上,已知A、B的质量分别为m A=10kg,m B=20kg,A、B之间,B 与地面之间的动摩擦因数为μ=0.5.一轻绳一端系住物体A,另一端系于墙上,绳与竖直方向的夹角为37°今欲用外力将物体B匀速向右拉出,求所加水平力F的大小,并画出A、B的受力分析图.取(g=10m/s2,sin37°=0.6,cos37°=0.8).8、如图所示,长为5m的细绳两端分别系于竖立在地面上相距为4m的两杆的顶端A、B。
精品!正交分解练习,连这一套就够了
正交分解练习
1.如图所示,用与竖直方向成37°角,大小为100N的力推着一个质量为9kg的木块紧贴在竖直的墙壁上,若木块匀速下滑,求墙对木块的摩擦力的大小和方向以及木块与墙之间的动摩擦因数.(g=10m/s2)
2.如图所示,斜面倾角为θ=37°,在斜面上放着一重为100N的物体,问:
(1)当物块静止时所受摩擦力多大?
(2)如果物体和斜面间的动摩擦因数为0.2,那么让物体下滑,在下滑过程中物体受到的摩擦力多大?
(sin37°=0.6 cos37°=0.8)
3.如图所示,在倾角为θ的光滑斜面上,重为G的物体受到未知水平推力F的作用,使物体静止不动,则:
(1)物体对斜面的压力为多大?
(2)水平推力F为多大?
4.如图所示,轻质弹簧拉着一个质量为6kg的物体静止在倾角θ=30°的光滑斜面上,此时弹簧伸长量x1=10cm.
(1)求弹簧的劲度系数k;
(2)如果将斜面换成粗糙斜面,倾角不变,当弹簧的伸长量x2=15cm时,物体恰沿斜面向上做匀速直线运动,求物体与斜面间的动摩擦因数μ.
正交分解练习
参考答案
一.计算题(共2小题)
1.;2.;。
牛顿第二定律经典例题
α
F
例三、一斜面AB长为5m,倾角为30°,一质量为2kg 的小物体(大小不计)从斜面顶端A点由静止释放, 如图所示。斜面与物体间的动摩擦因数为0.5,求小物 体下滑到斜面底端B时的速度及所用的时间。(g取
10m/s2,sin37=0.6,cos37=0.8)
A
B
沿哪两个方向进行正交分解?
例题四:质量为2kg的物体,静止放于水平面上,现 在物体上施一水平力F,使物体开始沿水平面运动, 运动了10s时,将水平力撤去。若物体运动的速度图 象如图所示,则水平力F= N,物体与水平面 间的动摩擦因数= 。(g取10m/s2)
N
二、一只静止的木箱,质量m=40kg,现以200N斜 向下的力F 推木箱, F 与水平成α=37º ,木箱沿水平地
面运动,木箱与地面间的动摩擦因数µ =0.30。求:木
箱 在 2 秒 末 的 速 度 和 2 秒 内 的 位 移 。 ( g 取 10m/s2 ,
sin37=0.6,cos37=0.8)
正交分解法 1、受力分析 2、沿着两个垂直的方向分解: 沿运动方向+与运动垂直方向 3、列式 运动方向:F合=ma 垂直方向:平衡方程 4、滑动摩擦:f=μN
例一、如图所示,质量为4kg的物体静止于水平面上,
物体与水平面间的动摩擦因数为0.5,物体受到大小为 20N,与水平方向成37°角斜向止的拉力F作用时沿水 平面做匀加速运动,求物体的加速度是多大?(g取 10m/s2,sin37=0.6,cos37=0.8)
正交分解l练习
如图所示,降落伞由于受到水平方向风力 而沿着跟竖直方向成30°角的方向匀速下 降,降落伞和人共重700N,则降落伞所受 的空气阻力为______。
修建房屋时,常用如图所示装置提起建筑材 料,当人向右运动的过程中,建筑材料A被缓 缓提起。此过程中,设人对地面的压力为FN, 人受到的摩擦力为F1,人拉绳的力为F2,则 下列说法正确的是 A.FN、F1和F2都增大 B.FN和F1增大,F2不变 C.FN、F1和F2都减小 D.FN增大,F1减小,F2不变
练习2.如图4-1-5所示,重为40N的物体 与竖直墙面间的摩擦因数为μ =0.4,若 用斜向上的推力F=50N托住物体,物体 处于静止状态,这时物体受到的摩擦力 是多少牛?要使物体匀速下滑,推力的 大小应变为多大?
例2. 如图所示, 斜面倾角为θ ,质量为m的木块 在受一平行于斜面的推力F作用下处于静止状 态,求物体受到的摩擦力。
F
例3.如图所示,木块在不受力时恰能从斜面 上匀速滑下,求:
(1)物体与斜面间的动摩擦因数。 (2)如果要将木块匀速推上该斜面,需加多 大的沿斜面向上的外力?(斜面倾角为θ ,木 块质量m)
Байду номын сангаас
放在斜面上的物体,当受到沿斜面向上 的100N的拉力时,恰好沿斜面向上做匀 速运动;当受到沿斜面向下20N的拉力 时,恰好沿斜面向下做匀速运动;当物 体不受拉力作用时,物体所受的摩擦力 是多大?
2.受力分析的顺序: 重力、弹力、摩擦力
例1.一质量为m的物体,现用一与水平 方向成θ 角的斜向上的拉力拉物体使其 在水平面上做匀速直线运动,物体与地 面间的动摩擦因数为μ ,求拉力的大小 是多少?
练习1.一质量为m的物体,现用一与水 平方向成θ 角的斜向下的推力F推物体 使其在水平面上做匀速直线运动,求物 体与地面间的动摩擦因数为μ 。
力的正交分解法经典习题
正交分解法基本步骤知道这种方法的基本步骤对你非常重要,因为它可以让你清楚每一步该去做什么。
大思路是这样的:1)建立直角坐标系xoy 。
一般选共点力的交点为坐标原点选择坐标方向时可以沿已知力的方向,这样这个方向的已知力就不用分解了。
2)沿x 、y 轴,将各个力依次分解为互相垂直的两个分力,如右图所示。
这一步是正交分解法的精髓所在:为了简化求合力的计算,正交分解法采用了“欲退先进”的战术,分解是为了合成,这样把所有计算限定在直角三角形和一条直线上的矢量计算中,虽然看似多了一步,却使计算变得简单了。
3)在x 、y 轴的方向上,分别求同一直线上几个力的合力。
123x x x x F F F F =+++⋯ 123y y y y F F F F =+++⋯这一步计算只有简单的加减法,方便吧!4)求出x F 和y F 的合力就是要求的多个力的合力了 大小:22x y F F F =+ 方向(与x轴正方向夹角为ϕ):tan /y x F F ϕ= 好吧,我们下面来实践一下,看看我们讲的方法是不是好用!下面我们先来看一道题:你知道合力是多大吗?如图所示,一物体受到110F N =,25F N =,38F N =三个共点力作用。
其中1F 和2F 的夹角为30°,1F 和3F 的夹角为150°。
求这三个共点力的合力。
建立坐标,先分解,再求和体验思路: 首先,我们可以选择三个力的交点为坐标原点,1F 为x轴的正方向建立直角坐标系。
体验过程: 第二步,将1F 、2F 、3F 分别沿x、y轴正交分解得到: 111x y F F F ==10N, =0;22cos30 2.53x F F N ==, 22sin30 2.5y F F N ==; 33cos15043x F F N ==-,33sin304y F F N ==。
第三步:(12310 2.5343x x x x F F F F N =++=+=10-1.53 1230 2.54 6.5y y y y F F F F N =++=++=最后,求出合力22x y F F F =+=9.85N ,tan /0.878y x F F ϕ==,41.3ϕ=︒实 践: 如图所示:同一平面内有三个共点力190F N =,230F N =,360F N =,它们之间互成120°夹角,求这三个力的合力。
