2013高二北师大版数学必修5全册综合测试]

合集下载

北师大版数学高二-必修5试题 1.3.1《等比数列》

1.3.1《等比数列》同步练习一、选择题1. 某数列既成等差数列也成等比数列，那么该数列一定是（） A ．公差不为0的等差数列 B ．公比为1的等比数列 C ．常数数列1,1,1,… D ．以上都不对2．若a 、b 、c 成等差数列，b 、c 、d 成等比数列，111,,c d e 成等差数列，则a 、c 、e 成（）A ．等差数列B ．等比数列C ．既成等差数列又成等比数列D ．以上答案都不是 3．在各项都为正数的等比数列{}n a 中，若569,a a =则3132310log log log a a a +++=（）A. 12B. 10C. 8D.32log 5+4．已知－9，a 1，a 2，－1四个实数成等差数列，－9，b 1，b 2，b 3，－1五个实数成等比数列，则b 2(a 2－a 1)＝（）A ．8B ．－8C ．±8D ．98二、填空题5.在83和272之间插入三个数，使这五个数成等比数列，则插入的三个数的乘积为_____.6．在等差数列{a n }中，若100a =，则有等式()……*12121919,nna a a a a a n n -+++=+++<∈N 成立，类比上述性质，相应地：在等比数列{b n }中，若91b =，则有等式成立.7.在数列｛a n ｝中，若a 1=1,a n +1=2a n +3 (n≥1),则该数列的通项a n =_____.三、解答题8. 设数列{}n a 的前n 项的和14122333n n n S a +=-⨯+，......3,2,1=n 求首项1a 与通项n a .9.已知函数f (x )定义在区间（－1，1）上，f (12)＝－1，且当x ，y ∈(－1，1)时，恒有f (x )－f (y )＝f (x －y 1－xy)，又数列{a n }满足a 1＝12，a n +1＝2a n 1+a n 2，设b n＝1f (a 1)＋1f (a 2)＋…＋1f (a n )． ⑴证明：f (x )在（－1，1）上为奇函数； ⑵求f (a n )的表达式；⑶是否存在正整数m ，使得对任意n ∈N ，都有b n <m －84成立，若存在，求出m 的最小值；若不存在，请说明理由.参考答案1.B 【解析】根据等比数列的特征，非零常数列一定为等比数列，因此次数列的公比一定为1，故选择B.2.B 【解析】由2,2a cb ac b +=+∴=，由222,c c bd d a c =∴=+，由211,d c e =+∴22,a c c ec ae c ce++=∴=，即,,a c e 成等比数列. 3.B 【解析】53132310312103563log log log log ()5log 910a kig a a a a a a a ++====.4.B 【解析】2212221198,9,()8413a a db b a a -+-====∴-=--. 5.216【解析】令五个数为231232212322827827,,,,,36,6,2163232a a a a a a a a a ∴=⨯=∴=∴==6.()……12121717,n n b b b b b b n n -⋅=⋅<∈*N 【解析】利用性质181nnb b -=.7.123n +-【解析】111323,2,323n n n n n n a a a a a ++++=+∴=∴+=+，即123n n a +=-8.解：（I ）21114122333a S a ==-⨯+，解得：12a = ()2111144122333n n n n n n n a S S a a +++++=-=---()11242n n n n a a ++⇒+=+所以数列{}2n na +是公比为4的等比数列所以：()111224n n n a a -+=+⨯得：42n nn a =- （其中n 为正整数）9.解：（1）令x ＝y ＝0，则f (0)＝0，再令x ＝0，得f (0)－f (y )＝f (－y )， ∴f (－y )＝－f (y )，y ∈(－1，1)，∴f (x )在（－1，1）上为奇函数．（2）),1()()()1(,1)21()(1xyyx f y f x f f a f ++=+-==知由 )(2)()()1()12()(21n n n n n n n n n n a f a f a f a a a a f a a f a f =+=⋅++=+=∴+，即2)()(1=+n n a f a f ∴{f (a n )}是以－1为首项，2为公比的等比数列，∴f (a n )＝－2n －1．（3）112212211211)2121211(--+-=---=+⋯+++-=n n n n b ．若48-<m b n 恒成立（n ∈N ＋），则.242421211-->-<+-n n m ，m 即∵n ∈N ＋，∴当n ＝1时，124-n 有最大值4，故m >4．又∵m ∈N ，∴存在m ＝5，使得对任意n ∈N ＋，有48-<m b n ．。

北师大版必修5第三章不等式综合测试题

北师大版必修5第三章不等式综合测试题一、单选题1．若0a b >>，R c ∈，则（）A ．11a b >B ．a c b c +>+C ．22a b <D ．a c b c -<- 2．若关于x 的不等式2210ax ax -+<的解集为∅，则实数a 的取值范围是（） A ．1a > B ．1a ≥ C ．01a <≤ D ．01a ≤≤ 3．已知()440,0a b ab a b +=>>，则4a b +的最小值等于（）A ．6B ．8C ．4D ．54．若实数x ，y 满足约束条件0320x y x x y -≥⎧⎪≤⎨⎪+-≥⎩，则2x y -的最小值为（）A ．.1B ．1-C ．3D ．3-5．若关于x 的不等式28210ax ax ++<的解集是()7,1--，那么a 的值为（） A ．1 B ．2 C ．3 D ．46．若,m n 均为正实数，则“4mn ≥”是“4m n +≥”的（）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件 7．设1x >，则11x x +-的最小值是（） A ．2B ．3 C．D ．4 8．已知0x >，0y > ，且211x y+=，若对任意的正数x ，y ，不等式222x y m m +>+恒成立，则实数m 的取值范围是（）A ．()[),14,-∞-+∞ B ．(][),42,-∞-+∞ C ．()2,4- D ．()4,2- 9．已知0a >，0b >，且满足21a b +=，则31a b +有（） A．最大值为5+B．最小值为5+10．已知f (x )=1212x x ≥⎧⎨-<⎩，，则不等式()220x f x x ⋅+-≤的解集是（） A ．{x |-21x ≤≤}B ．{x |2x <}C ．{x |21x x ≤-≥或}D ．{x |2x ≥-} 11．下列命题正确的是（）A ．函数1y x x=+的最小值是2 B ．若,a b ∈R 且0ab >，则2b a a b +≥ C．y = 的最小值是2D ．函数()4230y x x x=-->的最小值为2-12．已知函数()()2,f x x ax b a b R =++∈的最小值为0，若关于x 的不等式()f x c<的解集为(),4m m +，则实数c 的值为（）A ．9B ．8C ．6D ．4二、填空题 13．234(0)2x x x x++>的最小值为__________. 14．已知,x y R ∈，且22x y -=，则124y x ⎛⎫+ ⎪⎝⎭的最小值为________.15．已知实数x ，y 满足x ，y >0的最大值为_________.16．海伦公式亦叫海伦-秦九韶公式，相传这个公式最早是由古希腊数学家阿基米德得出的，而因为这个公式最早出现在海伦的著作《测地术》中，所以被称为海伦公式，它是利用三角形的三条边的边长直接求三角形面积的公式，表达式为S =其中a ，b ，c 分别是三角形的三边长，2a b c p ++=.已知一根长为10的木棍，截成三段构成一个三角形，若其中有一段的长度为2，则该三角形面积的最大值为___________.三、解答题17．已知关于x 的不等式()2320ax x a R ++>∈. 2（2）当0a >时，求关于x 的不等式2321ax x ax -+>-的解集.18．设矩形()ABCD AB AD >的周长为24m ，把ABC ∆沿AC 向ADC ∆折叠，AB 折过去后交DC 于P ，设AB xcm =，ADP ∆的面积为()f x ．（1）求()f x 的解析式及定义域；（2）求()f x 的最大值．19．如图所示，已知D 是以点A (4，1)，B (－1，－6)，C (－3，2)为顶点的三角形区域(包括边界与内部)．（1）写出表示区域D 的不等式组；（2）设点B (－1，－6)，C (－3，2)在直线4x －3y －a ＝0的异侧，求a 的取值范围． 20．已知函数2()6(0)f x x ax a =-+>．（Ⅰ）关于x 的不等式()0f x <的解集为{|23}x x <<，求()f x y x =在区间[2，4]的最小值；（Ⅱ）解关于x 的不等式1()5f x x a<+． 21．已知p ：实数x 满足x 2﹣4ax +3a 2＜0，其中a ＞0； q ：实数x 满足2＜x ≤3．（1）若a ＝1，且p ∧q 为真，求实数x 的取值范围；（2）若p 是q 的必要不充分条件，求实数a 的取值范围．22．已知二次函数()f x 满足()()12f x f x x +-=()x R ∈，且()01f =（1）求()f x 的解析式；（2）当[]1,2x ∈时，不等式()f x mx ≥恒成立，求实数m 的取值范围；（3）当[]1,1x ∈-时，方程()2f x x m =+有解，求实数m 的取值范围.参考答案1．B【分析】由不等式的基本性质可判断各选项的正误.【详解】对于A 选项，0a b >>，则0ab >，a b ab ab∴>，可得11a b <，A 选项错误；对于B 选项，0a b >>，由不等式的基本性质可得a c b c +>+，B 选项正确；对于C 选项，0a b >>，由不等式的基本性质可得22a b >，C 选项错误；对于D 选项，0a b >>，由不等式的基本性质可得a c b c ->-，D 选项错误.故选：B.2．D【分析】根据题意，讨论二次项系数a 的取值情况，找出满足不等式无解的a 的取值集合即可.【详解】解：当0a =时，10<，此不等式无解；当0a ≠，要使原不等式无解，应满足：{20440a a a >∆=-≤，解得：01a ≤≤.故选：D.3．C【分析】利用基本不等式即可求解.【详解】由基本不等式可得：24442a b a b ab +⎛⎫+=≤ ⎪⎝⎭，即()()214404a b a b +-+≥，所以()()144404a b a b ++-≥⎡⎤⎣⎦，解得44a b +≥或40a b +≤（舍），当且仅当444a b a b ab =⎧⎨+=⎩即212a b =⎧⎪⎨=⎪⎩时等号成立，所以4a b +的最小值等于4，故选：C【点睛】易错点睛：利用基本不等式求最值时，要注意其必须满足的三个条件：（1）“一正二定三相等”“一正”就是各项必须为正数；（2）“二定”就是要求和的最小值，必须把构成和的二项之积转化成定值；要求积的最大值，则必须把构成积的因式的和转化成定值；（3）“三相等”是利用基本不等式求最值时，必须验证等号成立的条件，若不能取等号则这个定值就不是所求的最值，这也是最容易发生错误的地方.4．D【分析】根据实数x ，y 满足约束条件0320x y x x y -≥⎧⎪≤⎨⎪+-≥⎩，画出可行域，记目标函数2z x y =-，平移直线122z y x =-，当直线在y 轴上的截距最大时z 有最小值求解. 【详解】实数x ，y 满足约束条件0320x y x x y -≥⎧⎪≤⎨⎪+-≥⎩的可行域如图所示：记目标函数2z x y =-，平移直线122z y x =-，当直线经过点(3,3)A 时在y 轴上的截距最大，此时对应的z 具有最小值，最小值为3233z =-⋅=-，故选：D.5．C【分析】由题意知方程28210ax ax ++=的两根为7-和1-，利用韦达定理即可求a 的值.【详解】由题意知方程28210ax ax ++=的两根为7-和1-，由根与系数的关系可得()2171a-⨯-=，解得：3a =，故选：C6．A【分析】利用充分条件与必要条件的定义，结合基本不等式判断即可.【详解】 ,m n 均为正实数，若4mn ≥，可得：24m n mn +≥≥；反之不成立，例如,取14,2m n ==时，4m n +≥，但4mn ≥不成立，∴“4mn ≥”是“4m n +≥”的充分不必要条件，故选：A【点睛】判断充分条件与必要条件应注意：首先弄清条件p 和结论q 分别是什么，然后直接依据定义、定理、性质尝试,p q q p ⇒⇒.对于带有否定性的命题或比较难判断的命题，除借助集合思想化抽象为直观外，还可利用原命题和逆否命题、逆命题和否命题的等价性，转化为判断它的等价命题；对于范围问题也可以转化为包含关系来处理.7．B【分析】由基本不等式求得最小值．【详解】∵1x >，得10x ->，∴111131x x -++≥=-，当且仅当111x x -=-，即2x =时等号成立．故选：B.【点睛】易错点睛：利用基本不等式求最值时，要注意其必须满足的三个条件：（1）“一正二定三相等”“一正”就是各项必须为正数；（2）“二定”就是要求和的最小值，必须把构成和的二项之积转化成定值；要求积的最大值，则必须把构成积的因式的和转化成定值；（3）“三相等”是利用基本不等式求最值时，必须验证等号成立的条件，若不能取等号则这个定值就不是所求的最值，这也是最容易发生错误的地方.8．D【分析】不等式222x y m m +>+恒成立，等价于2x y +的最小值大于22m m +，所以先利用基本不等式求出2x y +的最小值，然后解关于m 的不等式即可【详解】解：因为0x >，0y > ，且211x y+=，所以2142(2)2248x y x y x y x y y x ⎛⎫+=++=+++≥+ ⎪⎝⎭，当且仅当4x y y x=，即4,2x y ==时取等号，所以2x y +的最小值的最小值为8，不等式222x y m m +>+恒成立，等价于2x y +的最小值大于22m m +，所以282m m >+，解得42m -<<，故选：D9．B【分析】将代数式2+a b 与31a b +相乘，展开后利用基本不等式可求得31a b+的最值，进而可得出合适的选项.【详解】已知0a >，0b >，且满足21a b +=，()313162555b a a b a b a b a b ⎛⎫∴+=++=++≥=+ ⎪⎝⎭当且仅当a =时，等号成立，因此，31a b+的最小值为5+故选：B.10．B【分析】根据()f x 的定义，分类讨论解不等式．【详解】2x ≥时，不等式为220x x +-≤21x ⇒-<<，无解；2x <，不等式为221720()024x x x -+-≤⇒-+≥，恒成立，∴2x <，综上，不等式的解集为{|2}x x <．故选：B ．11．B【分析】利用基本不等式和对勾函数性质依次判断各个选项即可得到结果.【详解】对于A ，当0x <时，10y x x=+<，A 错误；对于B ，由0ab >知：0b a >，0ab >，2b a a b ∴+≥=（当且仅当b a a b =，即a b =时取等号），B 正确；对于C ，令3t =，则1110333y t t =+≥+=，C 错误；对于D ，44232322y x x x x ⎛⎫=--=-+≤-=- ⎪⎝⎭43x x =，即3x =时取等号），即函数()4230y x x x =-->的最大值为2-，D 错误. 故选：B .【点睛】易错点睛：利用基本不等式求最值时，要注意必须满足的三个条件：“一正二定三相等”.（1）“一正”就是各项必须为正数；（2）“二定”就是要求和的最小值，必须把构成和的二项之积转化成定值；要求积的最大值，则必须把构成积的因式的和转化成定值；（3）“三相等”是利用基本不等式求最值时，必须验证等号成立的条件，若不能取等号则这个定值就不是所求的最值，这也是最容易发生错误的地方12．D【分析】先由()()2,f x x ax b a b R =++∈的最小值为0，得到0∆=，再由()f x c <的解集为(),4m m +，得到()0f x c -=的根为m ，4m +，由根与系数的关系即可求解.【详解】解：()()2,f x x ax b a b R =++∈的值域为[)0,+∞，240a b ∴∆=-=，24a b ∴=， ()22a f x x ⎛⎫=+ ⎪⎝⎭，对称轴为2a x =-， ()f x c <的解集为(),4m m +，()0f x c ∴-=的根为m ，4m +，即2204a c x ax ++-=的根为m ，4m +， 1224x x a m +=-=+，42a m --=， ()242a c f m m ⎛⎫∴==+= ⎪⎝⎭. 故选：D.【点睛】关键点点睛：求解本题的关键在于，根据题中函数的最小值为0，求出()22a f x x ⎛⎫=+ ⎪⎝⎭，再由对应不等式的解集，根据一元二次不等式与一元二次方程之间的关系，即可求解. 13．72【分析】由0x >，化简23423222x x x x x ++=++，再根据基本不等式，即可得解. 【详解】由0x >，可得：234233722222x x x x x ++=++≥=，当且仅当22x x=，即2x =，时取等号，故234(0)2x x x x++>的最小值为72，故答案为：72. 【点睛】本题考查了利用基本不等式求最值，考查了化简计算能力，属于基础题.14．4【分析】将表达式124yx ⎛⎫+ ⎪⎝⎭化为222x y -+，再结合均值不等式求解即可【详解】212224yx x y -⎛⎫+=+ ⎪⎝⎭，因为220,20x y ->>，所以2224x y -+≥=，当且仅当21x y =-=时，取到最小值故答案为：415【分析】平方后结合基本不等式可得22≤，即可得解. 【详解】由题意，241124x y x y +==+≤+=+，当且仅当4x y =时，等号成立，..【点睛】易错点睛：利用基本不等式求最值时，要注意其必须满足的三个条件：（1） “一正”就是各项必须为正数；（2）“二定”就是要求和的最小值，必须把构成和的二项之积转化成定值；要求积的最大值，则必须把构成积的因式的和转化成定值；（3）“三相等”是利用基本不等式求最值时，必须验证等号成立的条件，若不能取等号则这个定值就不是所求的最值，这也是最容易发生错误的地方.16【分析】先根据题意，得到5p =，设2a =，则8+=b c ，根据S =等式，即可求出结果.【详解】由海伦公式可知1052p ==，不妨设2a =，则8+=b c ，则552b c S -+-=≤=当且仅当55b c -=-，即4b c ==时，等号成立.【点睛】本题主要考查基本不等式的应用，熟记基本不等式变形是解题关键.17．（1）25,5=-=-a b （2）3a =时，不等式的解集为{|1}x x ≠；3a >时，不等式的解集为3|,1x x x a ⎧⎫<>⎨⎬⎩⎭或；0<<3a 时，不等式的解集为3|1,x x x a ⎧⎫<>⎨⎬⎩⎭或【分析】（1）当0a <时，根据一元二次不等式的解集，可以知道一元二次方程的根，根据一元二次方程根与系数关系可以求出实数,a b 的值；（2）求出一元二次方程2321ax x ax -+=-的两个根，根据两个大小的关系分类求出关于x 的不等式2321ax x ax -+>-的解集.【详解】（1）当0a <时，因为2320ax x ++>的解集为{}1x b x <<，所以方程2320ax x ++=的两个根为,1(1)b b <，由根与系数关系得：3512215a b a b b a ⎧=-+=-⎧⎪⎪⎪⇒⎨⎨=-⎪⎪⋅=⎩⎪⎩；（2）22321(3)30(3)(1)0ax x ax ax a x ax x -+>-⇒-++>⇒-->，当0a >时，方程2321ax x ax -+=-的两个根分别为：3,1a. 当3a =时，两根相等，故不等式的解集为{|1}x x ≠；当3a >时，31a <，不等式的解集为3|,1x x x a ⎧⎫<>⎨⎬⎩⎭或；当0<<3a 时，31a >，不等式的解集为3|1,x x x a ⎧⎫<>⎨⎬⎩⎭或. 【点睛】本题考查了已知一元二次不等式的解集求参数问题，考查了字母系数一元二次不等式的求解问题，考查了分类讨论思想.18．（1）()()()17212126122f x x x x ⎛⎫=--<< ⎪⎝⎭（2）()f x的最大值为108-. 【分析】（1）利用周长，可以求出AD 的长，利用平面几何的知识可得DP PB ='，再利用勾股定理，可以求出DP 的值，由矩形()ABCD AB AD >的周长为24m ，可求出x 的取值范围，最后利用三角形面积公式求出()f x 的解析式；（2）化简（1）()f x 的解析式，利用基本不等式，可以求出()f x 的最大值．【详解】（1）如下图所示：∵设AB x =，则12AD x =-，又,DP PB AP AB PB AB DP ='='-'=-，即AP x DP =-，∴()()22212x PD x PD -+=-，得 7212PD x=-， ∵AB AD >，∴612x <<，∴ADP ∆的面积()()()1172121261222f x AD DP x x x ⎛⎫=⋅=--<< ⎪⎝⎭．（2）由（1）可得， ()()1727212121086)2(f x x x x x ⎛⎫=--=-+ ⎪⎝⎭ 1086272108722≤-⨯=- 当且仅当72x x=，即62x = ∴()f x 的最大值为108722-62x =．【点睛】本题考查了求函数解析式，考查了基本不等式，考查了数学运算能力.19．（1）7523071104100x y x y x y --≤⎧⎪+-≤⎨⎪++≥⎩；（2）(－18，14)．【分析】（1）根据点的坐标求出直线方程，结合原点所在位置得出不等式组；（2）点B (－1，－6)，C (－3，2)在直线4x －3y －a ＝0的异侧，[4×(－1)－3×(－6)－a ]·[4×(－3)－3×2－a ]<0，即可得解.【详解】（1）直线AB ，AC ，BC 的方程分别为7x －5y －23＝0，x ＋7y －11＝0，4x ＋y ＋10＝0.原点(0，0)在区域D 内，故表示区域D 的不等式组为7523071104100x y x y x y --≤⎧⎪+-≤⎨⎪++≥⎩；（2）根据题意有[4×(－1)－3×(－6)－a ]·[4×(－3)－3×2－a ]<0，即(14－a )(－18－a )<0，解得－18<a <14.故a 的取值范围是(－18，14)．20．（Ⅰ）5；（Ⅱ）答案见解析.【分析】（Ⅰ）根据不等式和方程的关系求出a 的值，从而求出()f x y x =的解析式，求出函数的最小值即可；（Ⅱ）问题转化为()10a x x a a ⎛⎫--< ⎪⎝⎭，通过讨论a 的范围，求出不等式的解集即可．【详解】解：（Ⅰ）不等式()0f x <的解集为{|23}x x << 2∴和3是方程260x ax -+=的根23a +=，解得：5a =故2()56f x x x =-+()665255f x y x x x x x∴==+-⋅-= 当且仅当x =“=”成立故()f x y x=在区间[2，4]的最小值是5；（Ⅱ）1()5f x x a <+即2165x ax x a -+<+，(0)a > 故22(1)0ax a x a -++<，故1()0a x x a a ⎛⎫--< ⎪⎝⎭ 1()0x x a a ⎛⎫∴--< ⎪⎝⎭ ①1a a <即1a >时，1x a a<< ②1a a=即1a =时，不等式无解 ③1a a >即01a <<时，1a x a << 综上：1a >时，不等式的解集是1{|}x x a a<< 1a =时，不等式无解 01a <<时，不等式的解集是1}|{x a x a<<． 21．（1）（2，3）；（2）[1，2]．【分析】（1）求解一元二次不等式，解得命题p 为真的取值范围和q 命题为真的范围取交集即可；（2）命题q 为真对应的x 的范围是命题p 为真对应的x 的范围的子集，即可求得参数范围.【详解】（1）p ：由原不等式得，（x ﹣3a ）（x ﹣a ）＜0，∵a ＞0，所以a ＜x ＜3a ；当a ＝1时，得到1＜x ＜3；q ：实数x 满足2＜x ≤3；若p ∧q 为真，则p 真且q 真，∴实数x 的取值范围是：（2，3）；（2）p 是q 的必要不充分条件，即由p 得不到q ，而由q 能得到p ；∴233a a ≤⎧⎨≥⎩，解得1≤a ≤2； ∴实数a 的取值范围是[1，2]．【点睛】复合命题p ∧q 的真假由命题p ，q 共同决定，当两命题中有一个是假命题时复合后为假命题，由若p 是q 的必要不充分条件可得集合q 是集合p 的真子集.22．（1）()21f x x x =-+；（2）1m ；（3）[]1,5-. 【分析】（1）设二次函数f （x ）的解析式，代入f （x +1）﹣f （x ）＝2x 和f （0）＝1，可求a 、b 、c 的值；（2）由题意得21x x mx -+≥在[]1,2x ∈上恒成立，即min 11m x x ⎛⎫≤+- ⎪⎝⎭，利用对勾函数求[]1,2x ∈的最小值即可得m 的取值范围；（3）由题意得x 2﹣3x +1＝m 在x ∈[﹣1，1]上有解，求出g （x ）＝x 2﹣3x +1，x ∈[﹣1，1]的值域即是m 的取值范围.【详解】（1）设二次函数()2f x ax bx c =++()0a ≠，代入()()12f x f x x +-=和()01f =，得()()221121a x b x c ax bx c x c ⎧++++---=⎪⎨=⎪⎩，化简得()221ax a b x x R c ⎧++=∈⎨=⎩， ∴1a =，1b =-，1c =，∴()21f x x x =-+；（2）当[]1,2x ∈时，不等式()f x mx ≥恒成立，即21x x mx -+≥在[]1,2x ∈上恒成立，即2111x x m x x x-+≤=+-在[]1,2x ∈上恒成立，令()11h x x x=+-, 在[]1,2上递增，()()min 11h x h ∴==，解得1m ；（3）当[]1,1x ∈-时，方程()2f x x m =+有解，即方程231x x m -+=在[]1,1x ∈-上有解；令()231g x x x =-+，在[]1,1-上递减，()()()()min max 11,15g x g g x g ∴==-=-=，则()g x 的值域是[]1,5-，所以，m 的取值范围是[]1,5-.【点睛】方法点睛：（1）恒成立问题求参数的方法：参变分离求函数的最值，讨论法求最值.（2）方程有解求参数的方法：参变分离求函数的值域，讨论法求值域. （3）求解析式的方法：待定系数法，换元法，解方程法，消参法.。

北师大版高二数学必修5质量检测题及答案

高二数学必修5质量检测题姓名：_________班级：________ 得分：________第Ⅰ卷（选择题共60分）一、选择题：本答题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1. 3,…那么A .第12项B .第13项C ．第14项D ．第15项2. 已知数列{a n }中，12n n a a -= (n ≥2)，且a 1=1，则这个数列的第7项为A ．512B ．256C ．128D ．643. 已知等差数列}{n a 中，610416,2,a a a +==则6a 的值是A . 15B . 10 C. 5 D. 84. 数列{n a }的通项公式是n a ＝331n n -(n ∈*N )，则数列{n a }是 A ．递增数列 B ．递减数列C ．常数列D ．不能确定该数列的增减性5.在ABC ∆中，6016A AB ∠=︒=，，面积S =，则AC 等于A.50B.C.100D. 6.对于任意实数a 、b 、c 、d ，以下四个命题中的真命题是A ．若,0,a b c >≠则ac bc >B ．若0,,a b c d >>>则ac bd >C ．若,a b >则11a b< D ．若22,ac bc >则a b > 7. 在等比数列{a n }中，3S =1，6S =4，则101112a a a ++的值是A ．81B ．64C ．32D ．278. 已知等比数列{}n a 满足1223412a a a a +=+=，，则5a =A ．64B ．81C ．128D ．2439.设函数()246,06,0x x x f x x x ⎧-+≥=⎨+<⎩，则不等式()()1f x f > 的解集是A.()()3,13,-+∞ B. ()()3,12,-+∞ C. ()()1,13,-+∞ D. ()(),31,3-∞-10. 用铁丝制作一个面积为1 m 2的直角三角形铁框，铁丝的长度最少是A. 5.2 mB. 5 mC. 4.8 mD. 4.6 m11.已知点P （x ，y ）在不等式组20,10,220x y x y -≤⎧⎪-≤⎨⎪+-≥⎩表示的平面区域上运动，则12z x y =-+的取值范围是 A ．[－1，－1] B ．[－1，1] C ．[1，－1] D ．[1，1]12．某观察站C 与两灯塔A 、B 的距离分别为x 米和3千米，测得灯塔A 在观察站C 的正西方向，灯塔B 在观察站C 西偏南30，若两灯塔A 、B千米，则x 的值为C.或二、填空题：本大题共5小题，每小题6分，共30分．把本大题答案填在第Ⅱ卷题中横线上．13. 不等式2(2)(23)0x x x ---<的解集为14. 已知数列{}n a 的前n 项和23n S n n =-，则其通项公式为=n a ________ 15. 在29和34之间插入2个数，使这4个数成等比数列，则插入的2个数的乘积为 16．已知点（3，1）和（-1，1）在直线320x y a -+=的同侧，则a 的取值范围是17．若2＋22＋ (2)>130，n ∈N*，则n 的最小值为_______.高二数学必修5质量检测题（卷）2009.11第Ⅱ卷（非选择题）二、填空题：本大题共5小题，每小题6分，共30分.把答案填在题中横线上.13． ; 14. .15. . 16. ； 17.__________.三、解答题：本大题共4小题，共60分．解答应写出文字说明、证明过程或演算步骤．18．（本题满分15分）设不等式2430x x -+<的解集为A ，不等式260x x +->的解集为B.（1）求A∩B；（2）若不等式20x ax b ++<的解集为A∩B，求,a b 的值.19. （本题满分15分）在锐角△ABC 中，已知AC =2AB =， 60A ∠=. 求:(1)BC 边的长；（2）分别用正弦定理、余弦定理求B ∠的度数.20. （本题满分15分）已知a ∈R, 解关于x 的不等式：220x x a a ---<21. （本题满分15分）某种汽车购买时费用为16．9万元，每年应交付保险费及汽油费共1万元；汽车的维修费第一年为1千元，以后每年都比上一年增加2千元．（Ⅰ）设使用n 年该车的总费用（包括购车费用）为n S ，试写出n S 的表达式；（Ⅱ）求这种汽车使用多少年报废最合算（即该车使用多少年平均费用最少）.高二数学必修5质量检测题参考答案及评分标准2009.11一、选择题：本答题共12小题，每小题5分，共60分．1. B （根据石油中学魏有柱供题改编）2. D （根据铁一中张爱丽供题改编）3. C （根据金台高中高二数学组供题改编）4.B （根据铁一中周粉粉供题改编）5.A. （根据十二厂中学闫春亮供题改编）6.D （根据金台高中高二数学组供题改编）7. D （根据石油中学夏战灵供题改编）8. B （根据石油中学高建梅供题改编）9.A （ 09天津高考题）10. B （根据教材第94页练习改编）11. B （根据铁一中周粉粉供题改编）12．D （根据金台高中高二数学组及斗鸡中学张永春供题改编）二、填空题：13.{}123或x x x <-<< （根据铁一中孙敏供题改编）;14. 64n -（根据铁一中周粉粉供题改编）;15. 16（根据铁一中孙敏供题改编）; 16．{|}75或a a a <->（根据斗鸡中学张永春、铁一中张爱丽、石油中学高建梅供题改编）; 17．7（根据石油中学夏战灵供题改编）.三、解答题：本大题共5小题，共60分．18．设不等式2430x x -+<的解集为A ，不等式260x x +->的解集为B.（1）求A∩B；（2）若不等式20x ax b ++<的解集为A∩B，求,a b 的值.（根据斗鸡中学张永春、石油中学高建梅等供题改编）解:(1) A={}13x x <<, （3分） B={}32或x x x <->（6分）A∩B ={}23x x << （9分）（2）∵不等式20x ax b ++<的解集为A∩B∴ 23a +=-（11分） 23b ⨯= （13分）得5a =-，6b = （15分）19.在锐角△ABC 中，已知AC =AB =， 60A ∠=. 求:(1)BC 边的长；（2）分别用正弦定理、余弦定理求B ∠的度数. 解：（1）由余弦定理得2222cos BC AB AC AB AC A =+-∠ （3分）=22122+-⨯ =3 （6分）∴BC =（7分）（2）45B ∠= ，能用正弦定理求出B ∠的度数得4分，过程略.能用余弦定理求出B ∠的度数得4分，过程略.（根据铁一中张爱丽供题改编）20. 已知a ∈R, 解关于x 的不等式：220x x a a ---<解：由题意得(1)()0x a x a --+< (3分)∴ 当1a a +<-时,即12a <-时,解集为(1,)a a +- (7分) 当1a a +>-时,即12a >-时,解集为(,1)a a -+ (11分) 当1a a +=-时,即12a =-时,解集为φ (15分) （根据铁一中孙敏、金台高中高二数学组。

2013年高二数学必修五章末归纳整合(北师大版)(2)最新版

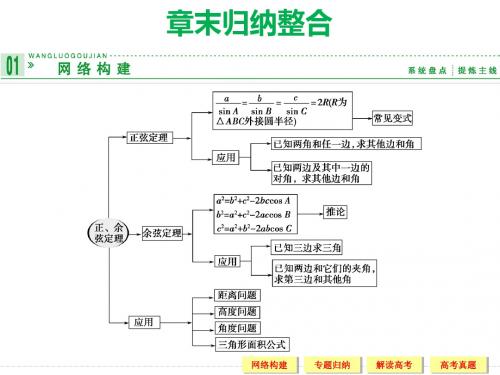
网络构建
专题归纳
解读高考
高考真题
专题三正、余弦定理的综合应用
(1)在解三角形时，常常将正弦定理与余弦定理结合使用，要注意恰当地选择定理，简化运算过程，提高解题速度，同时，要注意与平面几何中的有关性质、定理结合起来，挖掘题目中的隐含条件． (2)利用正弦、余弦定理证明有关三角形的三角函数恒等式和判定三角形的类型，主要是将已知条件中的边、角关系转化为角的关系或边的关系．一般地，利用公式 a＝2Rsin A，b＝2Rsin B，c＝2Rsin C可将边的关系转化为角的三角函数关系，然后利用三角函数恒等式进行化简，其中往往用到三角形内角和定理A＋B＋C＝π.
网络构建
专题归纳
解读高考
高考真题
【例2】在△ABC 中，已知 a＝8，B＝60°，c＝4( 3＋1)，解此三
角形．
[思路探索] 先用余弦定理求出b，然后利用余弦定理的推论或正弦定理求出相应角的余弦值或正弦值，最后确定角的大小．解由余弦定理得：b2＝a2＋c2－2accos B＝
82＋[4( 3＋1)]2－2×8×4( 3＋1)·cos 60°＝
64＋16(4＋2 3)－64( 3＋1)×12＝96，∴b＝4 6.
网络构建
专题归纳
解读高考
高考真题
法一由 cos A＝b2＋2cb2c－a2＝926×＋4166 ×34＋ 132＋－164＝ 22， ∵0°<A<180°，∴A＝45°. 故 C＝180°－A－B＝180°－45°－60°＝75°.
且满足ccooss BC＝－2ab＋c. (1)求角 B 的值；
(2)若 b＝ 19，a＋c＝5，求 a，c 的值．
[思路探索]
cos (1)cos

高二数学必修五模块试题(北师大版含答案和解释)

高二数学必修五模块试题(北师大版含答案和解释)模块学习评价 (时间120分钟，满分150分)一、选择题(本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的) 1．若a＞b＞c，则一定成立的不等式是( ) A．a|c|＞b|c| B．ab＞ac C．a－|c|＞b－|c| D.1a＜1b＜1c 【解析】∵a＞b，∴a－|c|＞b－|c|. 【答案】 C 2．在△ABC中，若sin A∶sin B∶sin C＝3∶2∶4，则cos C的值为( ) A．－14 B.14 C．－23 D.23 【解析】由正弦定理知，a∶b∶c＝sin A∶sin B∶sin C＝3∶2∶4，设a＝3k，b＝2k，c＝4k，(k＞0)，由余弦定理得 cos C＝a2＋b2－c22ab ＝9k2＋4k2－16k22×3k×2k＝－14. 【答案】 A 3．(2013•洋浦高二检测)在△ABC中，若a＝2，b＝23，A＝30°，则B为( ) A．60° B．60°或120° C．30° D．30°或150° 【解析】根据正弦定理得sin B＝bsin Aa＝23×sin30°2＝32，∴B＝60°或120°，∵b>a，故两解都符合题意．【答案】 B 4．不等式ax2＋2x＋c>0的解集是(－2，3)，则a＋c的值是( ) A．10 B．－10 C．14 D．－14 【解析】不等式ax2＋2x＋c>0的解集是(－2，3)，即方程ax2＋2x＋c＝0的解为x＝－2或x＝3. ∴－2＋3＝－2a，－2×3＝ca，∴a＝－2，c＝12，∴a＋c＝10. 【答案】 A 5．设{an}是等差数列，且a2＝－6，a8＝6，Sn是数列{an}的前n项和，则( ) A．S4＜S5 B．S4＝S5 C．S6＜S5 D．S6＝S5 【解析】设公差为d，则a1＋d＝－6，a1＋7d＝6解得d＝2，a1＝－8.则a4＝－2，a5＝0，a6＝2，∴S4＝S5. 【答案】 B 6．(2013•乌鲁木齐高二检测)已知U 为实数集，M＝{x|x2－2x<0}，N＝{x|y＝x－1}，则M∩(∁UN)等于( ) A．{x|0<x<1} B．{x|0<x<2} C．{x|x<1} D．∅【解析】不等式x2－2x<0可化为x(x－2)<0，所以M＝{x|0<x<2}，又因为N＝{x|x≥1}，所以∁UN＝{x|x<1}，M∩(∁UN)＝{x|0<x<2}∩{x|x<1}＝{x|0<x<1}．【答案】 A 7．不等式组（x－y＋5）（x＋y）≥0，0≤x≤3表示的平面区域是( ) A．矩形 B．三角形 C．直角梯形D．等腰梯形【解析】画出图形可知：不等式组（x－y＋5）（x＋y）≥00≤x≤3表示的平面区域是等腰梯形．【答案】 D 8．(2013•惠州高二检测)若AB→•BC→＋AB→2＝0，则△ABC是( ) A．直角三角形 B．锐角三角形 C．钝角三角形 D．等腰直角三角形【解析】由AB→•BC→＋AB→2＝0，得c2＝－ac•cos(π－B)，∴cos B＝ca，根据余弦定理得a2＋c2－b22ac＝ca，整理得a2＝c2＋b2，所以该三角形为直角三角形．【答案】 A 9．等比数列{an}是递增数列，若a5－a1＝60，a4－a2＝24，则公比q为( ) A.12 B．2 C.12或－2 D．2或12 【解析】由已知得a1q4－a1＝60，a1q3－a1q＝24，两式相除得q＝2或12，经检验q＝2或12均满足{an}是递增数列，故选D. 【答案】 D 10．(2013•丰台高二检测)已知数列{an}中，a1＝35，an＝1－1an－1(n≥2)，则a2 012＝( ) A．－12 B．－23 C.35 D.52 【解析】由an＝1－1an－1及a1＝35得a2＝－23，a3＝52，a4＝35，a5＝－23，…，所以数列中的项呈周期出现，周期为3，于是a2 012＝a670×3＋2＝a2＝－23. 【答案】 B 11．(2012•辽宁高考)设变量x，y满足x－y≤10，0≤x＋y≤20，0≤y≤15，则2x＋3y的最大值为( ) A．20 B．35 C．45 D．55 【解析】不等式组表示的区域如图所示，所以过点A(5，15)时2x＋3y 的值最大，此时2x＋3y＝55. 【答案】 D 图1 12．如图1，某汽车运输公司刚买了一批豪华大客车投入营运，据市场分析每辆客车营运的总利润y(单位：10万元)与营运年数x(x∈N)为二次函数关系，若使营运的年平均利润最大，则每辆客车应营运( ) A．3年 B．4年 C．5年 D．6年【解析】由图像知，函数过点(6，11)，可设y＝a(x－6)2＋11，把点(4，7)代入得7＝a(4－6)2＋11，解得a＝－1，∴y＝－(x－6)2＋11＝－x2＋12x－25. ∴平均利润yx＝－x2＋12x－25x＝－(x＋25x)＋12≤－2x×25x＋12＝2.这时x＝25x即x＝5. 【答案】 C 二、填空题(本大题共4小题，每小题5分，共20分，将答案填在题中的横线上) 13．若关于x的不等式x－ax＋1＞0的解集为(－∞，－1)∪(12，＋∞)，则实数a＝________．【解析】由题意知 x＝－1和x＝12是方程(x－a)•(x＋1)＝0的两个根，∴a ＝12. 【答案】12 14．等比数列{an}的前n项和为2n－1，则数列{an2}的前n项和为________．【解析】设{an}的前n项和为Sn，则Sn＝2n－1，∴n≥2时Sn－1＝2n－1－1，∴an＝Sn－Sn－1＝2n－1，n＝1时也适合上式，∴an＝2n－1(n∈N＋)，故an2＝4n －1. 易知{an2}为以1为首项，以4为公比的等比数列，∴其前n 项和为1－4n1－4＝4n－13. 【答案】13(4n－1) 15．设x，y为正实数，且x＋y＝2，则2x＋1y的最小值为________．【解析】2x ＋1y＝(2x＋1y)×1＝(2x＋1y)•(x＋y2)＝32＋yx＋x2y≥32＋2 yx•x2y＝3＋222，当且仅当x＋y＝2，yx＝x2y，即x＝4－22，y＝22－2，时等号成立．【答案】3＋222 16．(2013•哈师大附中高二检测)如图2，在某灾区的搜救现场，一条搜救犬从A点出发沿正北方向行进x m到达B处发现生命迹象，然后向右转105°，行进10 m到达C处发现另一生命迹象，这时它向右转135°回到出发点，那么x＝________．图2 【解析】∠ABC＝180°－105°＝75°，∠BCA＝180°－135°＝45°，∠BAC＝180°－75°－45°＝60°，又AB＝x，BC＝10，∴xsin 45°＝10sin 60°. 得x＝10sin 45°sin 60°＝1063. 【答案】1063 三、解答题(本大题共6小题，共70分．解答应写出文字说明，证明过程或演算步骤) 17．(本小题满分10分)已知a、b、c分别是△ABC的三个内角所对的边，若△ABC面积S△ABC＝32，c＝2，A＝60°，求a、b的值．【解】∵32＝12b×2×sin 60°，∴b＝1，又a2＝b2＋c2－2bccos A，∴a2＝3，即a＝3. 18．(本小题满分12分)(2013•福州高二检测)已知不等式mx2＋nx－1m<0的解集为{x|x<－12，或x>2}． (1)求m，n的值； (2)解关于x的不等式：(2a－1－x)(x＋m)>0，其中a是实数．【解】(1)依题意m<0，－12＋2＝－nm，－12×2＝－1m2得m＝－1，n＝32.(2)原不等式为(2a－1－x)(x－1)>0即[x－(2a－1)](x－1)<0. ①当2a－1<1，即a<1时，原不等式的解集为{x|2a－1<x<1}．②当2a－1＝1即a＝1时，原不等式的解集为∅. ③当2a－1>1即a>1时，原不等式的解集为{x|1<x<2a－1}． 19．(本小题满分12分)某货轮在A处看灯塔B在货轮北偏东75°，距离为126 n mile；在A处看灯塔C在货轮的北偏西30°，距离为83 n mile.货轮由A处向正北航行到D处时，再看灯塔B在北偏东120°，求： (1)A处与D处之间的距离； (2)灯塔C与D处之间的距离．【解】(1)在△ABD中，由已知得∠ADB＝60°，B＝45°. 由正弦定理得 AD＝ABsinBsin∠AD B＝126×2232 ＝24(n mile)． (2)在△ADC中，AC＝83，AD＝24，∠CAD＝30°，由余弦定理得 CD2＝AD2＋AC2－2AD•ACcos 30° ＝242＋(83)2－2×24×83cos 30° ＝3×64，∴CD＝83(n mile)．所以A处与D处之间的距离为24n mile，灯塔C与D处之间的距离为83 n mile. 20．(本小题满分12分)某工厂家具车间造A、B型两类桌子，每张桌子需木工和漆工两道工序完成．已知木工做一张A、B型桌子分别需要1小时和2小时，漆工油漆一张A、B型桌子分别需要3小时和1小时，又知木工、漆工每天工作分别不得超过8小时和9小时，而工厂造一张A、B型桌子分别获利润2千元和3千元，试问工厂每天应生产A、B型桌子各多少张，才能获得利润最大？【解】设每天生产A型桌子x张，B型桌子y张，则x＋2y≤8，3x ＋y≤9，x≥0，y≥0，目标函数为：z＝2x＋3y. 作出可行域：把直线l：2x＋3y＝0向右上方平移至l′的位置时，直线经过可行域上的点M，且与原点距离最大，此时z＝2x＋3y取最大值，解方程x ＋2y＝83x＋y＝9，得M的坐标为(2，3)．故每天应生产A型桌子2张，B型桌子3张才能获得最大利润． 21．(本小题满分12分)(2013•黄冈高二检测)已知等差数列{an}满足：a3＝7，a5＋a7＝26，{an}的前n项和为Sn. (1)求an及Sn； (2)令bn＝1an2－1(n∈N＋)，求数列{bn}的前n项和Tn. 【解】(1)设等差数列{an}的公差为d，因为a3＝7，a5＋a7＝26，所以有a1＋2d＝7，2a1＋10d＝26，解得a1＝3，d＝2，所以an＝3＋2(n－1)＝2n＋1；Sn＝3n＋n（n－1）2×2＝n2＋2n. (2)由(1)知an＝2n＋1，所以bn＝1an2－1＝1（2n＋1）2－1＝14•1n（n＋1）＝14•(1n－1n＋1)，所以Tn＝14•(1－12＋12－13＋…＋1n－1n＋1)＝14•(1－1n＋1)＝n4（n＋1），即数列{bn}的前n项和Tn＝n4（n ＋1）. 22．(本小题满分12分)某投资商到一开发区投资72万元建起一座蔬菜加工厂，第一年共支出12万元，以后每年支出增加4万元，从第一年起每年蔬菜销售收入50万元．设f(n)表示前n年的纯利润总和f(n)＝(前n年的总收入－前n年的总支出－投资额)． (1)该厂从第几年开始盈利？ (2)若干年后，投资商为开发新项目，对该厂有两种处理方案：①年平均纯利润达到最大时，以48万元出售该厂；②纯利润总和达到最大时，以10万元出售该厂，问哪种方案更合算？【解】由题意知， f(n)＝50n－12n＋n（n－1）2×4－72 ＝－2n2＋40n－72. (1)由f(n)＞0，即－2n2＋40n－72＞0，解得2＜n ＜18. 由n∈N＋知，从第三年开始盈利． (2)方案①：年平均纯利润f（n）n＝40－2n＋36n≤16当且仅当n＝6时等号成立．故方案①共获利6×16＋48＝144(万元)，此时n＝6. 方案②：f(n)＝－2(n －10)2＋128.当n＝10，f(n)max＝128. 故方案②共获利128＋10＝138(万元)．比较两种方案，选择第①种方案更合算．。

高中数学模块综合评估1(含解析)北师大版必修5-北师大版高二必修5数学试题

模块综合评估(一)时间：120分钟满分：150分一、选择题(本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合要求的)1．数列1,3,7,15，…的通项公式a n 可能是( C ) A ．2n B ．2n ＋1 C ．2n －1 D ．2n －1解析：取n ＝1时，a 1＝1，排除A 、B ，取n ＝2时，a 2＝3，排除D. 2．已知集合A ＝{x |x 2－2x －3≥0}，B ＝{x |－2≤x <2}，则A ∩B ＝( A ) A ．[－2，－1] B ．[－1,2) C ．[－1,1] D ．[1,2)解析：由已知，可得A ＝{x |x ≥3或x ≤－1}，则A ∩B ＝{x |－2≤x ≤－1}＝[－2，－1]．故选A.3．在△ABC 中，B ＝135°，C ＝15°，a ＝5，则此三角形的最大边长为( A ) A ．5 2 B ．5 3 C ．2 5 D ．3 5解析：依题意，知三角形的最大边为b .由于A ＝30°，根据正弦定理，得b sin B ＝asin A ，所以b ＝a sin B sin A ＝5sin135°sin30°＝5 2. 4．若f (x )＝－x 2＋mx －1的函数值有正值，则m 的取值范围是( A ) A ．m <－2或m >2 B ．－2<m <2 C ．m ≠±2 D．1<m <3解析：因为f (x )＝－x 2＋mx －1有正值，所以Δ＝m 2－4>0，所以m >2或m <－2. 5．已知c <d ，a >b >0，则下列不等式中必成立的一个是( B ) A ．a ＋c >b ＋d B ．a －c >b －d C ．ad >bc D.a c >bd解析：由不等式的性质可知c <d ，∴－c >－d .又a >b >0，∴a ＋(－c )>b ＋(－d )，即a －c >b －d .6．等差数列{a n }满足a 24＋a 27＋2a 4a 7＝9，则其前10项之和为( D ) A ．－9 B ．－15 C ．15 D ．±15解析：因为a 24＋a 27＋2a 4a 7＝(a 4＋a 7)2＝9，所以a 4＋a 7＝±3，所以a 1＋a 10＝±3，所以S 10＝10a 1＋a 102＝±15.7．某学生用一不准确的天平(两臂不等长)称10 g 药品，他先将5 g 的砝码放在左盘，将药品放在右盘使之平衡；然后又将5 g 的砝码放在右盘，将药品放在左盘使之平衡，则此学生实际所得药品( B )A ．小于10 gB ．大于10 gC ．大于等于10 gD ．小于等于10 g解析：设左、右臂长分别为t 1，t 2(t 1≠t 2)，第一次称的药品为x 1 g ，第二次称的药品为x 2 g ，则有5t 1＝x 1t 2，x 2t 1＝5t 2，所以x 1＋x 2＝5⎝ ⎛⎭⎪⎫t 1t 2＋t 2t 1>5×2＝10，即大于10 g.8．已知变量x ，y 满足约束条件⎩⎪⎨⎪⎧x －y ＋2≤0，x ≥1，x ＋y －7≤0，则yx的取值范围是( C )A ．(3,6) B.⎝ ⎛⎭⎪⎫95，3 C.⎣⎢⎡⎦⎥⎤95，6 D ．(3，＋∞)解析：作出可行域，如图阴影部分所示．目标函数z ＝y x ＝y －0x －0的几何意义是可行域内的点(x ，y )与原点(0,0)间连线的斜率．由图可知k OC ≤z ≤k OB .易求得B (1,6)，C ⎝ ⎛⎭⎪⎫52，92，因为k OC ＝95，k OB ＝61＝6，所以95≤z ≤6.9．在如图所示的表格中，如果每格填上一个数后，每一行成等差数列，每一列成等比数列，那么x ＋y ＋z 的值为( B )A ．1B ．2C ．3D ．4解析：由题知表格中第三列成首项为4，公比为12的等比数列，故有x ＝1.根据每行成等差数列得第四列前两个数字依次为5，52，故其公比为12，所以y ＝5×⎝ ⎛⎭⎪⎫123＝58，同理z ＝6×⎝ ⎛⎭⎪⎫124＝38，故x ＋y ＋z ＝2. 10．已知x ，y 为正实数，且x ，a 1，a 2，y 成等差数列，x ，b 1，b 2，y 成等比数列，则a 1＋a 22b 1b 2的取值范围是( C )A ．RB ．(0,4]C ．[4，＋∞) D．(－∞，0]∪[4，＋∞)解析：原式＝x ＋y2xy＝x 2＋2xy ＋y 2xy ＝x y ＋y x ＋2，又∵x ，y >0，∴x y ＋y x ＋2≥2x y ·yx＋2＝4，当且仅当x y ＝y x，即x ＝y 时等号成立．11．若x ，y 满足条件⎩⎪⎨⎪⎧3x －5y ＋6≥0，2x ＋3y －15≤0，y ≥0当且仅当x ＝y ＝3时，z ＝ax ＋y 取得最大值，则实数a 的取值范围是( C )A.⎝ ⎛⎭⎪⎫－23，35B.⎝ ⎛⎭⎪⎫－∞，－35∪⎝ ⎛⎭⎪⎫23，＋∞C.⎝ ⎛⎭⎪⎫－35，23D.⎝ ⎛⎭⎪⎫－∞，－23∪⎝ ⎛⎭⎪⎫35，＋∞解析：直线3x －5y ＋6＝0和直线2x ＋3y －15＝0的斜率分别为k 1＝35，k 2＝－23，且两直线的交点坐标为(3,3)，作出可行域如图所示，当且仅当直线z ＝ax ＋y 经过点(3,3)时，z 取得最大值，则直线z ＝ax ＋y 的斜率－a 满足－23<－a <35，解得－35<a <23，故选C.12．在各项均为正数的等比数列{a n }中，公比q ∈(0,1)．若a 3＋a 5＝5，a 2·a 6＝4，b n ＝log 2a n ，数列{b n }的前n 项和为S n ，则当S 11＋S 22＋…＋S nn取最大值时，n 的值为( C ) A ．8 B ．9 C ．8或9 D ．17解析：因为a 2·a 6＝a 3·a 5＝4，且a 3＋a 5＝5，所以a 3，a 5是方程x 2－5x ＋4＝0的两个根．又因为等比数列{a n }各项均为正数且q ∈(0,1)，所以a 3＝4，a 5＝1.所以q 2＝a 5a 3＝14，所以q ＝12.所以a n ＝4·⎝ ⎛⎭⎪⎫12n －3，所以b n ＝log 2a n ＝5－n .所以S n ＝9－n ·n 2，所以S n n ＝9－n2. T n ＝S 11＋S 22＋…＋S n n ＝14(－n 2＋17n )＝14⎣⎢⎡⎦⎥⎤－⎝ ⎛⎭⎪⎫n －1722＋2894.所以当n ＝8或9时，T n 取得最大值．二、填空题(本大题共4小题，每小题5分，共20分，请把答案填写在题中横线上) 13．在△ABC 中，角A ，B ，C 所对的边分别为a ，b ，c ，若a ＝1，c＝3，C ＝π3，则A＝π6. 解析：由正弦定理，得a sin A ＝c sin C ⇒sin A ＝a sin C c ＝323＝12，所以A ＝π6.14．若数列{a n }的前n 项和S n ＝23a n ＋13，则{a n }的通项公式是a n ＝(－2)n －1.解析：当n ＝1时，由已知S n ＝23a n ＋13，得a 1＝23a 1＋13，即a 1＝1；当n ≥2时，由已知得到S n －1＝23a n －1＋13，所以a n ＝S n －S n －1＝⎝ ⎛⎭⎪⎫23a n ＋13－⎝ ⎛⎭⎪⎫23a n －1＋13＝23a n －23a n －1，所以a n ＝－2a n －1，所以数列{a n }为以1为首项，以－2为公比的等比数列，所以a n ＝(－2)n －1.15．如图，海岸线上有相距5海里的两座灯塔A ，B ，灯塔B 位于灯塔A 的正南方向．海上停泊着两艘轮船，甲船位于灯塔A 的北偏西75°，与A 相距32海里的D 处；乙船位于灯塔B 的北偏西60°方向，与B 相距5海里的C 处，则两艘轮船之间的距离为13海里．解析：如图，连接AC ，由题意知，AB ＝BC ＝5，∠ABC ＝60°，所以△ABC 为等边三角形，则AC ＝5，在△ACD 中，AD ＝32，∠DAC ＝45°，由余弦定理得CD ＝13.16．若a >0，b >0，a ＋b ＝2，则下列不等式对一切满足条件的a ，b 恒成立的是①③④(写出所有正确不等式的编号)．①ab ≤1；②a ＋b ≤2；③a 2＋b 2≥2；④1a ＋1b≥2.解析：两个正数，和为定值，积有最大值，即ab ≤a ＋b24＝1，当且仅当a ＝b 时取等号，故①正确；(a ＋b )2＝a ＋b ＋2ab ＝2＋2ab ≤4，当且仅当a ＝b 时取等号，得a ＋b ≤2，故②错误；由于a 2＋b 22≥a ＋b24＝1，故a 2＋b 2≥2成立，故③正确；1a ＋1b ＝⎝ ⎛⎭⎪⎫1a ＋1b a ＋b2＝1＋a 2b ＋b2a≥1＋1＝2，当且仅当a ＝b 时取等号，故④正确．三、解答题(本大题共6小题，共70分．解答应写出文字说明，证明过程或演算步骤)17．(本小题10分)已知方程ax 2＋bx ＋2＝0的两根为－12和2.(1)求a ，b 的值； (2)解不等式ax 2＋bx －1>0.解：(1)因为方程ax 2＋bx ＋2＝0的两根为－12和2.由根与系数的关系，得⎩⎪⎨⎪⎧－12＋2＝－b a，－12×2＝2a ，解得a ＝－2，b ＝3.(2)易知ax 2＋bx －1>0，即2x 2－3x ＋1<0，解得12<x <1.所以不等式ax 2＋bx －1>0的解集为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪12<x <1. 18．(本小题12分)在△ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，已知A ＝π3，sin B＝3sin C .(1)求tan C 的值；(2)若a ＝7，求△ABC 的面积．解：(1)因为A ＝π3，所以B ＋C ＝2π3，故sin ⎝ ⎛⎭⎪⎫2π3－C ＝3sin C ，所以32cos C ＋12sin C ＝3sin C ，即32cos C ＝52sin C ，得tan C ＝35. (2)由b sin B ＝csin C，sin B ＝3sin C ，得b ＝3c . 在△ABC 中，由余弦定理，得a 2＝b 2＋c 2－2bc cos A ＝9c 2＋c 2－2×(3c )×c ×12＝7c 2，又因为a ＝7，所以c ＝1，b ＝3，所以△ABC 的面积为S ＝12bc sin A ＝334.19．(本小题12分)△ABC 的内角A ，B ，C 所对的边分别为a ，b ，c . (1)若a ，b ，c 成等差数列，证明sin A ＋sin C ＝2sin(A ＋C )； (2)若a ，b ，c 成等比数列，求cos B 的最小值．解：(1)证明：∵a ，b ，c 成等差数列，∴a ＋c ＝2b . 由正弦定理得sin A ＋sin C ＝2sin B .∵sin B ＝sin[π－(A ＋C )]＝sin(A ＋C )，∴sin A ＋sin C ＝2sin(A ＋C )． (2)∵a ，b ，c 成等比数列，∴b 2＝ac .由余弦定理得cos B ＝a 2＋c 2－b 22ac ＝a 2＋c 2－ac 2ac ≥2ac －ac 2ac ＝12，当且仅当a ＝c 时等号成立．∴cos B 的最小值为12.20．(本小题12分)在等差数列{a n }中，已知公差d ＝2，a 2是a 1与a 4的等比中项． (1)求数列{a n }的通项公式； (2)设b n ＝an n ＋12，记T n ＝－b 1＋b 2－b 3＋b 4－…＋(－1)nb n ，求T n .解：(1)由题意知(a 1＋d )2＝a 1(a 1＋3d )，即(a 1＋2)2＝a 1(a 1＋6)，解得a 1＝2，所以数列{a n }的通项公式为a n ＝2n . (2)由题意知b n ＝a n n ＋12＝n (n ＋1)，所以T n ＝－1×2＋2×3－3×4＋…＋(－1)nn ·(n ＋1)．因为b n ＋1－b n ＝2(n ＋1)，可得当n 为偶数时，T n ＝(－b 1＋b 2)＋(－b 3＋b 4)＋...＋(－b n －1＋b n )＝4＋8＋12＋ (2)＝n24＋2n 2＝n n ＋22，当n 为奇数时，T n ＝T n －1＋(－b n )＝n －1n ＋12－n (n ＋1)＝－n ＋122.所以T n＝⎩⎪⎨⎪⎧－n ＋122，n 为奇数，nn ＋22，n 为偶数.21．(本小题12分)某蔬菜基地种植甲、乙两种无公害蔬菜．生产一吨甲种蔬菜需用电力9千瓦时，耗肥4吨，3个工时；生产一吨乙种蔬菜需用电力5千瓦时，耗肥5吨，10个工时，现该基地仅有电力360千瓦时，肥200吨，工时300个．已知生产一吨甲种蔬菜获利700元，生产一吨乙种蔬菜获利1 200元，在上述电力、肥、工时的限制下，问如何安排甲、乙两种蔬菜种植，才能使利润最大？最大利润是多少？解：设种植甲种蔬菜x 吨，乙种蔬菜y 吨，利润为z 元，根据题意可得⎩⎪⎨⎪⎧9x ＋5y ≤360，4x ＋5y ≤200，3x ＋10y ≤300，x ≥0，y ≥0，目标函数为：z ＝700x ＋1 200y ，作出二元一次不等式组表示的平面区域，即可行域，如图，作直线：700x ＋1 200y ＝0，即7x ＋12y ＝0，平移直线，当直线过A 点时目标函数取最大值．解方程组⎩⎪⎨⎪⎧4x ＋5y ＝200，3x ＋10y ＝300，得x ＝20，y ＝24.所以点A 的坐标为(20,24)．所以z max ＝700×20＋1 200×24＝42 800.即种植甲种蔬菜20吨，乙种蔬菜24吨，才能使利润最大，最大利润为42 800元． 22．(本小题12分)设等差数列{a n }的公差为d ，点(a n ，b n )在函数f (x )＝2x的图像上(n ∈N ＋)．(1)证明：数列{b n }为等比数列；(2)若a 1＝1，函数f (x )的图像在点(a 2，b 2)处的切线在x 轴上的截距为2－1ln2，求数列{a n b 2n }的前n 项和S n .解：(1)证明：由已知，b n ＝2a n >0. 当n ≥1时，b n ＋1b n＝2a n ＋1－a n ＝2d. 所以，数列{b n }是首项为2a 1，公比为2d的等比数列．(2)函数f (x )＝2x在(a 2，b 2)处的切线方程为y －2a 2＝(2a 2ln2)(x －a 2)，它在x 轴上的截距为a 2－1ln2.由题意，a 2－1ln2＝2－1ln2.解得a 2＝2.所以，d ＝a 2－a 1＝1，a n ＝n ，b n ＝2n ，a n b 2n ＝n ·4n. 于是，T n ＝1×4＋2×42＋3×43＋…＋(n －1)·4n －1＋n ·4n,4T n ＝1×42＋2×43＋…＋(n －1)×4n＋n ·4n ＋1.因此，T n －4T n ＝4＋42＋…＋4n －n ·4n ＋1＝4n ＋1－43－n ·4n ＋1＝1－3n 4n ＋1－43.所以，T n ＝3n －14n ＋1＋49.。

(常考题)北师大版高中数学必修五第二章《解三角形》测试题(包含答案解析)(3)

一、选择题1．在ABC 中，内角A 、B 、C 所对的边分别为a 、b 、c ，若()sin sin sin c C a A b a B =+-，角C 的角平分线交AB 于点D ，且CD =，3a b =，则c 的值为（）A ．72B ．3C ．3D ．2．在ABC 中，内角,A ,B C 的对边分别为,a ,b c ，已知b =22cos c a b A -=，则a c +的最大值为（）A B ．C ．D3．在△ABC 中，若222a c b -+=，则C ＝( )． A ．45° B ．30°C ．60°D ．120°4．ABC 的内角,,A B C 的对边分别为,,a b c ，分别根据下列条件解三角形，其中有两解的是（）A ．2,4,120a b A ===︒B ．3,2,45a b A ===︒C ． 6,60b c C ===︒D ．4,3,30b c C ===︒5．ABC 的内角,,A B C 的对边分别为,,a b c ，若222sin sin sin sin A C B A C +-=，1b =，则2a -的最小值为（）A ．4-B ．-C ．2-D ．6．在ABC 中，,,a b c 分别为三个内角,,A B C 的对边，若cos cos a A b B =，则ABC 一定是（）A ．等腰三角形B ．直角三角形C ．等腰直角三角形D ．等腰三角形或直角三角形7．在ABC 中，内角,,A B C 所对应的边分别为,,a b c ，若sin cos 0b A B =，且2b ac =，则a cb+ 的值为（）A BC ．2D ．48．在直角梯形ABCD 中，//AB CD ，90ABC ∠=，22AB BC CD ==，则cos DAC ∠=（）A B C D ．109．在ABC 中，内角A ，B ，C 的对边分别为a ，b ，c ，且1a =，cos si 3n 3b c C B -=，则B 的值是（）A ．6π B ．3π C ．23π D ．56π 10．在ABC 中，a ，b ，c 分别为角A ，B ，C 的对边，若3a =，2b =，45B =︒，则A =（）A ．30B ．30或150︒C ．60︒或120︒D ．60︒11．构造如图所示的图形，它是由3个全等的三角形与中间的一个小等边三角形拼成的一个大等边三角形，设2BD AD =，则DEF 与ABC 的面积之比为（）A ．12B ．13C ．15D ．1712．已知ABC 中，角A ，B ，C 的对边分别为a ，b ，c ，2sin sin sin B A C =，13a cc a+=+，则B = （） A ．56π B ．6π C ．3π D ．2π 二、填空题13．已知ABC 的面积为4，2tan 3B =，AB AC >，设M 是边BC 的中点，若5AM =，则BC =___________.14．在ABC 中，点M 是边BC 的中点，3AM =2BC =，则2AC AB +的最大值为___________.15．某小区拟将如图的一直角三角形ABC 区域进行改建：在三边上各选一点连成等边三角形DEF ，在其内建造文化景观.已知207m AB =，107m AC =，则DEF 区域面积（单位：2m ）的最小值大约为______2m .7 2.65≈；3 1.73≈）16．如图，一船自西向东匀速航行，上午10时到达一座灯塔P 的南偏西75︒，距灯塔68海里的M 处，下午2时到达这座灯塔的东南方向N 处，则该船航行的速度为__________海里/小时.17．在三角形ABC 中，a ，b ，c 分别是角A ，B ，C 的对边，222a c b ac +-=，3b =2a c +的最大值为______．18．在ABC 中，若3b =3c =，30B ︒=，则a 等于________.19．ABC 的内角A ，B ，C 的对边分别为a ，b ，c ．已知sin sin 22sin sin b C c B a B C +=，2226b c a +-=，则ABC 的面积为_______． 20．已知a ，b ，c 分别为ABC 三个内角A ，B ，C 的对边，且cos cos sin b C c B a A +=，则A =________. 三、解答题21．在ABC 中，已知边长是5,7,8BC AC AB ===. （1）求角B ；（2）求ABC 的面积；（3）求ABC 外接圆面积.22．在ABC 中，a ，b ，c 分别为角A ，B ，C 的对边，且()()()sin sin sin 3a b A B C c b -+=.（1）求角A ；（2）若ABC 的面积23ABC S =△a 的取值范围.23．在△ABC 中，BC ＝a ，AC ＝b ，且a ，b 是方程22320x x -+=的两根，()2cos 1A B +=.（1）求角C 的度数；（2）求AB 的长.24．ABC 是等边三角形，点D 在边AC 的延长线上，且AD =3CD ，BD 7，求AD 的值和sin ∠ABD 的值25．在△ABC 中，BC =a ，AC =b ，a 、b 是方程22320x x -+=的两个根，且120A B +=︒，求ABC 的面积及AB 的长.26．在△ABC 中，a 、b 、c 分别是∠A 、∠B 、∠C 的对边长，已知2b ac =，且a 2－c 2=ac －bc ，求∠A 的大小及sin b Bc的值【参考答案】***试卷处理标记，请不要删除一、选择题 1．B 解析：B 【分析】利用正弦定理边角互化以及余弦定理求出角C 的值，由ABC ACD BCD S S S =+△△△可得出ab a b =+，结合3a b =可求得a 、b 的值，再利用余弦定理可求得c 的值. 【详解】()sin sin sin c C a A b a B =+-，由正弦定理可得()22c a b a b =+-，可得222a b c ab +-=，由余弦定理可得：2221cos 22a b c C ab +-==，0C π<<，所以3C π=，由ABC ACD BCD S S S =+△△△，有111sin sin sin 232626ab a CD b CD πππ=⋅+⋅，得ab a b =+，所以234b b =，0b >，43b ∴=，34a b ==，由余弦定理可得221616471692cos 3c a b ab C =+--==+. 故选：B. 【点睛】方法点睛：在解三角形的问题中，若已知条件同时含有边和角，但不能直接使用正弦定理或余弦定理得到答案，要选择“边化角”或“角化边”，变换原则如下：（1）若式子中含有正弦的齐次式，优先考虑正弦定理“角化边”；（2）若式子中含有a 、b 、c 的齐次式，优先考虑正弦定理“边化角”；（3）若式子中含有余弦的齐次式，优先考虑余弦定理“角化边”；（4）代数式变形或者三角恒等变换前置；（5）含有面积公式的问题，要考虑结合余弦定理求解；（6）同时出现两个自由角（或三个自由角）时，要用到三角形的内角和定理.2．B解析：B 【分析】由正弦定理化边角，利用诱导公式两角和的正弦公式化简可得B 角，然后用余弦定理得2()33a c ac +-=，再利用基本不等式变形后解不等式得a c +的最大值．【详解】因为22cos c a b A -=，所以由正弦定理得，2sin sin 2sin cos C A B A -=，因为A B C π+=-，所以sin sin()sin cos cos sin C A B A B A B =+=+，所以2sin cos 2cos sin sin 2sin cos A B A B A B A +-=，化简得(2cos 1)sin 0B A -=，因为sin 0A ≠，所以2cos 10B -=，解得1cos 2B =，因为(0,)B π∈，所以3B π=，因为b =222232cos a c ac B a c ac =+-=+-，所以2()33a c ac +-=，所以222313()()()44a c a c a c ≥+-+=+，当且仅当a c =时取等号，所以a c +≤a c +的最大值为故选：B ．【点睛】方法点睛：本题考查主要正弦定理、余弦定理，在三角形问题中出现边角关系时可用正弦定理化边为角，然后由利用三角函数恒等变换公式如诱导公式，两角和与差的正弦公式等化简变形得出所要结论．3．B解析：B 【分析】根据余弦定理，可以求出C 角的余弦值，进而根据C 为三角形内角，解三角方程可以求出C 角．【详解】∵222a c b -+=，∴22222a b c cosC ab +-==. 又∵C 为三角形内角∴30C =︒. 故选B ．【点睛】本题考查余弦定理的应用，属基础题．4．D解析：D 【分析】运用正弦定理公式，可以求出另一边的对角正弦值，最后还要根据三角形的特点：“大角对大边”进行合理排除. 【详解】A. 2,4,120a b A ===︒,由,a b <A B ⇒<所以不存在这样的三角形.B. 3,2,45a b A ===︒,由sin sin sin a b B A B =⇒=,a b >所以只有一个角BC. 6,60b c C ===︒中，同理也只有一个三角形.D. 4,3,30b c C ===︒中2sin sin sin 3c b B C B =⇒=此时b c >，所以出现两个角符合题意，即存在两个三角形. 所以选择D 【点睛】在直接用正弦定理求另外一角中，求出 sin θ后，记得一定要去判断是否会出现两个角.5．A解析：A 【分析】由222sin sin sin sin A C B A C +-=，利用正弦定理和余弦定理，可得6B π=，再根据正弦定理、三角形内角和及两角和的余弦公式，得到2a -4cos 3C π⎛⎫=+ ⎪⎝⎭，借助角C 的范围，即可求得结果. 【详解】222sin sin sin sin A C B A C +-=，∴222a c b +-=，∴2222a c b ac +-=，∴cos 2B =，又0B π<<，∴6B π=，12sin sin sin sin 6b A C B ac π====，∴2sin a A =，2sin c C =，∴24sin a A C -=-4sin()B C C =+-4sin()6C C π=+-14cos 22C C C ⎛⎫=+- ⎪ ⎪⎝⎭2cos C C =-14cos sin 22C C ⎛⎫=- ⎪ ⎪⎝⎭ 4cos 3C π⎛⎫=+ ⎪⎝⎭因为506C π<<，所以7336C πππ<+<，所以当3C ππ+=时，2a -取得最小值，且最小值为4-.故选：A. 【点睛】本题考查了正弦定理和余弦定理的应用、三角形内角和的应用、两角和的余弦公式及余弦型函数的最值问题，考查学生对这些知识的掌握能力，属于中档题.在解有关三角形的题目时，要有意识地考虑用哪个定理更合适，一般地，如果式子中含有角的余弦或边的二次式时，要考虑用余弦定理；如果式子中含有角的正弦或边的一次式时，则考虑用正弦定理.6．D解析：D 【分析】根据cos cos a A b B =，利用正弦定理将边转化为角得到sin cos sin cos A A B B =，然后再利用二倍角的正弦公式化简求解. 【详解】因为cos cos a A b B =，由正弦定理得：sin cos sin cos A A B B =，所以sin 2sin 2A B =，所以22A B =或22A B π=-，即A B =或2A B π+=所以ABC 一定是等腰三角形或直角三角形，故选：D 【点睛】本题主要正弦定理，二倍角公式的应用，属于中档题.7．C解析：C 【分析】利用正弦定理边化角，结合辅助角公式可求得sin 03B π⎛⎫-= ⎪⎝⎭，从而确定3B π=；利用余弦定理构造方程可求得()24+=a c ac ，代入所求式子即可化简得到结果. 【详解】sin cos 0b A B =，()sin sin cos sin sin 2sin sin 03B A A B A B B A B π⎛⎫∴=-=-= ⎪⎝⎭，()0,A π∈，sin 0A ∴≠，sin 03B π⎛⎫∴-= ⎪⎝⎭，又()0,B π∈，3B π∴=.()22222231cos 2222a c ac a cb ac ac B ac ac ac +-+-+-∴====，整理可得：()24+=a c ac ，2a cb+∴====. 故选：C . 【点睛】本题考查解三角形的相关知识，涉及到正弦定理边化角、余弦定理的应用等知识；解决此类问题的关键是能够通过正弦定理，将边的齐次式转化为角的关系，属于常考题型.8．C解析：C 【分析】设1BC CD ==，计算出ACD ∆的三条边长，然后利用余弦定理计算出cos DAC ∠．【详解】如下图所示，不妨设1BC CD ==，则2AB =，过点D 作DE AB ⊥，垂足为点D ，易知四边形BCDE 是正方形，则1BE CD ==，1AE AB BE ∴=-=，在Rt ADE ∆中，AD ==AC在ACD ∆中，由余弦定理得2222cos2AC AD CD DAC AC AD +-∠===⋅，故选C ．【点睛】本题考查余弦定理求角，在利用余弦定理求角时，首先应将三角形的边长求出来，结合余弦定理来求角，考查计算能力，属于中等题．9．C解析：C 【分析】cos sin sin 33B C C B A =-，再由三角恒等变换化简可得sin 3=-B B ，进而可得tan 3B =.【详解】因为1a =cos si 3n 3b c C B -=3cos sin 3b C c B a -=，cos sin sin 33B C C B A =-，又()sin sin sin cos cos sin A B C B C B C =+=+，33in n co c s s os in s 3s n n i i B C B C C B B C =-，化简得sin sin 3sin C B B C =-，因为()0,C π∈，()0,B π∈，所以sin 0C ≠，所以sin 3=B B 即tan 3B = 所以23B π=. 故选：C. 【点睛】本题考查了三角恒等变换及正弦定理的综合应用，考查了运算求解能力与转化化归思想，属于中档题.10．C解析：C 【解析】 ∵3,2,45a b B ===︒∴根据正弦定理sin sin a b A B=，即sin sin a B A b ===∵a b =>=∴()45,135A ∈︒︒ ∴60A =︒或120︒ 故选C11．D解析：D 【分析】由题意得出点D 为AF的中点，由余弦定理得出AB =，结合三角形面积公式得出正确答案. 【详解】2,BD AD AF BD ==，2AF AD ∴=，即点D 为AF 的中点由余弦定理得：2222cos120AB AD BD AD BD ︒⋅-=+解得：AB =)22ABC1()sin 601217sin 602DEFAD S S ︒︒∴== 故选：D 【点睛】本题主要考查了余弦定理以及三角形的面积公式，属于中档题.12．B解析：B 【分析】根据正弦定理，边角互化可得2b ac =，再根据2221a c a c b c a ac+-+-=，利用余弦定理求角.【详解】∵2sin sin sin B A C =，∴21b ac=，∴2221a c a c b c a ac+-+-== ∴cos 2B =，又()0,πB ∈∴6B π=．故选:B ．【点睛】本题考查正弦定理和余弦定理解不等式，重点考查转化的思想，计算能力，属于基础题型.二、填空题13．4【分析】首先利用余弦定理和三角形面积公式建立关于的方程再分别求根据余弦定理求结合条件求得的值【详解】得：解得：①中利用余弦定理②由①②可得解得：或即当时得此时不成立当时得此时成立故故答案为：4【点解析：4【分析】首先利用余弦定理和三角形面积公式，建立关于,a c 的方程，再分别求,a c ，根据余弦定理求b ，结合条件AB AC >，求得BC 的值.【详解】2tan 3B =，得：sin 13B =，cos 13B =11sin 422ABC S ac B ac ===，解得：ac =① ABM中，利用余弦定理222252cos 5424a a a c c B c =+-⋅⋅=+= ② 由①②可得22174ac a c ⎧=⎪⎨+=⎪⎩，解得：2a c ⎧=⎪⎨=⎪⎩4a c =⎧⎪⎨=⎪⎩， AB AC >，即c b >当2a c ==时，2222cos 32b a c ac B =+-=，得b =c b <，不成立，当4,a c == 2222cos 5b a c ac B =+-=，得b =c b >，成立，故4BC a ==.故答案为：4【点睛】易错点点睛：本题的易错点是求得,a c 后，还需满足条件AB AC >这个条件，否则会增根. 14．【分析】用余弦定理表示出求出后利用余弦函数性质可得最大值【详解】记则在中同理在中可得∴设则其中是锐角显然存在使得∴的最大值为故答案为：【点睛】关键点点睛：本题考查余弦定理考查换元法求最值解题方法是用解析：【分析】用余弦定理表示出,AC AB ，求出2AC AB +后利用余弦函数性质可得最大值．【详解】记AMC α∠=，则AMB πα∠=-，在AMC中，2222cos 314AC AM MC AM MC ααα=+-⋅=+-=-，同理在AMB中可得24AB α=+，∴228AB AC +=，设AB x =，AC x =，(0,)2x π∈．则12cos )cos )2AC AB x x x x x x +=+=+=+)x θ=+，其中cos θθ==θ是锐角，显然存在0(0,)22x ππθ=-∈，使得0sin()1x θ+=， ∴2AC AB +的最大值为故答案为：【点睛】关键点点睛：本题考查余弦定理，考查换元法求最值．解题方法是用余弦定理表示出,AB AC ，得出228AB AC +=，利用三角换元法AB x =，AC x =，(0,)2x π∈．这里注意标明x 的取值范围．在下面求最值时需确认最值能取到，然后结合三角函数的性质求最值．15．【分析】设那么在中利用正弦定理求出关于的函数并求出其最大值即可求解【详解】在中可得所以设那么在中由正弦定理可得其中所以当时取到最小值最小值为故面积的最小值故答案为：【点睛】本题考解三角形的实际应用考解析：130【分析】设CED θ∠=，m DE x =，那么6BFE πθ∠=+，cos CE x θ=，在BEF 中，利用正弦定理，求出x 关于θ的函数，并求出其最大值，即可求解.【详解】在Rt ABC △中，AB =，AC =，可得CB =. 所以6ABC π∠=设CED θ∠=，m DE x =，那么6BFE πθ∠=+，cos CE x θ=.在BFE △中，由正弦定理，可得sin sin 66xπθ=+ ⎪⎝⎭，132(cos sin )cos 1021,(3sin 2cos )102122x x xθθθθθ++=+=， 2121101010sin()3sin 2cos 7s 3in()x θαθθθα===+++，其中23tan α=，所以当sin()1θα+=时，x 取到最小值，最小值为103，故DEF 面积的最小值21sin 75375 1.73129.7513023S x π=⨯=≈⨯=≈. 故答案为：130【点睛】本题考解三角形的实际应用，考查正弦定理，三角恒等变换，以及三角函数的性质，属于中档题.本题解题的关键在于设CED θ∠=，m DE x =，进而在BFE △中，得1021cos sin sin 66xx θππθ-=⎛⎫+ ⎪⎝⎭，进而将问题转化为求边x 的最小值问题. 16．【解析】如图在△MNO 中由正弦定理可得则这艘船的航行速度(海里/小时)点睛：(1)测量两个不可到达的点之间的距离问题一般是把求距离问题转化为应用余弦定理求三角形的边长的问题然后把求未知的另外边长问题解析：176 【解析】如图,在△MNO 中，由正弦定理可得，68sin120686346sin 45MN === 则这艘船的航行速度6642v ==(海里/小时). 点睛：(1)测量两个不可到达的点之间的距离问题，一般是把求距离问题转化为应用余弦定理求三角形的边长的问题．然后把求未知的另外边长问题转化为只有一点不能到达的两点距离测量问题，然后运用正弦定理解决．(2)测量从一个可到达的点到一个不可到达的点之间的距离问题，一般可转化为已知两个角和一条边解三角形的问题，从而运用正弦定理解决．17．【分析】由余弦定理可求出角再根据正弦定理即可表示出然后利用消元思想和辅助角公式即可求出的最大值【详解】因为所以而∴∵∴∴其中所以的最大值为当时取得故答案为：【点睛】本题主要考查正余弦定理在解三角形中解析：【分析】由余弦定理可求出角B ，再根据正弦定理即可表示出2a c +，然后利用消元思想和辅助角公式，即可求出2a c +的最大值．【详解】因为222a cb ac +-=，所以2221cos 222a c b ac B ac ac +-===，而0B π<<，∴3B π=．∵2sin sin sin sin 3a b c A B C π====，∴2sin ,2sin a A c C ==．∴222sin 4sin 2sin 4sin 4sin 3a c A C A A A A π⎛⎫+=+=+-=+ ⎪⎝⎭()A ϕ=+，其中tan 2ϕ=．所以2a c +的最大值为2A πϕ=-时取得．故答案为：【点睛】本题主要考查正余弦定理在解三角形中的应用，以及利用三角函数求解三角形中的最值问题，意在考查学生的转化能力和数学运算能力，属于中档题．18．或【分析】由正弦定理求得得到或分类讨论即可求得的值【详解】由正弦定理可得所以因为所以或当时可得；当时此时综上可得或故答案为：或【点睛】本题主要考查了正弦定理的应用其中解答中利用正弦定理求得的值得出的解析：【分析】由正弦定理，求得sin C =，得到60C ︒=或120C ︒=，分类讨论，即可求得a 的值. 【详解】由正弦定理，可得sin sin b c B C =，所以sin 3sin c B C b ⋅===，因为(0,180)C ∈，所以60C ︒=或120C ︒=，当60C ︒=时，90A ︒=，可得a =；当120C ︒=时，30A ︒=，此时a b ==综上可得a =a =故答案为：.【点睛】本题主要考查了正弦定理的应用，其中解答中利用正弦定理求得sin C 的值，得出C 的大小是解答的关键，着重考查分类讨论，以及运算与求解能力. 19．【分析】由正弦定理得由平方关系和余弦定理可得再利用面积公式即可得解【详解】由已知条件及正弦定理可得易知所以又所以所以所以即所以的面积故答案为：【点睛】本题考查了正弦定理余弦定理和三角形面积公式的应用解析：32【分析】由正弦定理得sin A =32bc =，再利用面积公式1sin 2S bc A =即可得解. 【详解】由已知条件及正弦定理可得2sin sin sin sin B C A B C =，易知sin sin 0B C ≠，所以sin 2A =，又2226b c a +-=，所以2223cos 2b c a A bc bc+-==，所以cos 0A >，所以cos A =32bc =，bc =，所以ABC 的面积113sin 2222S bc A ==⨯=．故答案为：32. 【点睛】本题考查了正弦定理、余弦定理和三角形面积公式的应用，属于中档题. 20．【分析】根据正弦定理把已知等式中的边转化为角的正弦利用两角和公式化简求得的值进而求得【详解】由于为三角形内角可得故答案为：【点睛】本题主要考查正弦定理的应用解题的关键是利用正弦定理把等式中的边转化为解析：2π 【分析】根据正弦定理把已知等式中的边转化为角的正弦，利用两角和公式化简求得sin A 的值进【详解】cos cos sin b C c B a A +=，2sin cos sin cos sin()sin sin B C C B B C A A ∴+=+==，sin 0A ≠，sin 1A ∴=，∴由于A 为三角形内角，可得2A π=．故答案为：2π．【点睛】本题主要考查正弦定理的应用．解题的关键是利用正弦定理把等式中的边转化为角的正弦．三、解答题21．（1）3π；（2）3）493π. 【分析】（1）由余弦定理，求得1cos 2B =，即可求得角B 的大小；（2）由三角形的面积公式，即可求得ABC S的面积；（3）由正弦定理，求得2sin AC R B ==. 【详解】（1）由题意，在ABC 中，5BC =，7AC =，8AB =，由余弦定理有2222225871cos 22582BC AB AC B BC AB +-+-===⋅⨯⨯，因为(0,)B π∈，所以3B π=.（2）由三角形的面积公式，可得ABC S=11sin 8522AB BC B ⋅=⨯⨯= （3）由正弦定理，可得72sin sin 3AC R B π===，所以外接圆面积为2493ππ⨯=. 22．（1）30；（2）2a ≥【分析】（1）由正弦定理化角为边可得222b c a +-=，再利用余弦定理即可求出；（2）由面积公式可得8bc =+.（1）由已知结合正弦定理可得()()()3a b a b c c b -+=-，即2223b c a bc +-=，则由余弦定理可得22233cos 2b c bc A bc a +===-， ()0,180A ∈，30A ∴=；（2）11sin 2324ABC S bc A bc ===+△，则843bc =+，由2223234a b c bc bc bc =+-≥-=，当且仅当b c =时等号成立，2a ∴≥.23．（1）23C π=；（2）10AB . 【分析】（1）利用诱导公式可得角C 的余弦值，从而可求C 的大小.（2）利用余弦定理和韦达定理可求AB 的长.【详解】（1）由题设可得()1cos 2C π-=即1cos 2C =-，而C 为三角形内角，故23C π=. （2）由韦达定理可得23,2a b ab +==，由余弦定理可得()2222222cos 10AB a b ab C a b ab a b ab =+-=++=+-=，故10AB. 24．6；32114．【分析】在BCD 中，根据AD =3CD ，BD =27，利用余弦定理求解CD ，在A BD 中,利用正弦定理求解.【详解】如图所示：在等边ABC 中，AD =3CD ，所以AC =2CD ．又BD 7所以BD 2=BC 2+CD 2-2BC ⋅CD ⋅cos ∠BCD ，即)2=(2CD )2+CD 2-2⋅2CD ⋅CD ⋅cos120°，解得CD =2，可得AD=6,由sin 60AD ABD =∠, 得6sin 60ABD =∠，解得sin ∠ABD25．S AB == 【分析】利用韦达定理求出,a b ab +,再利用余弦定理,得到关于c 的方程，解之可得AB 的长；再结合面积公式可得.【详解】,a b 是方程220x-+=的两个根, 2a b ab ∴+==,又因为120A B +=︒则60C =︒,所以由余弦定理得：()(22222222221cos 22222c a b ab c a b c C ab ab -⨯-+--+-====⨯，解得c= 所以AB =ABC的面积11sin 222S ab C ==⨯= 26．3A π=，sin b B c 2= 【分析】由已知条件变形，结合余弦定理可求得A ，由2b ac =得=b a c b，结合正弦定理可求得sin b B c. 【详解】由2b ac =，且a 2－c 2=ac －bc ，得222b c a bc +-=，所以2221cos 22b c a A bc +-==，因为0A π<<，所以3A π=. 因为2b ac =，所以=b ac b ，所以sin sin sin 2b B a B A c b === 故3A π=，sinb Bc =【点睛】关键点点睛：利用正弦定理和余弦定理求解是解题关键.。

高中数学第三章不等式章末综合检测北师大版必修5

—————————— 新学期新成绩新目标新方向 ——————————第三章不等式章末综合检测(三)(时间：120分钟，满分：150分)一、选择题：本题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的． 1．函数y ＝ln （x ＋1）－x 2－3x ＋4的定义域为( ) A ．(－4，－1) B ．(－4，1) C ．(－1，1) D ．(－1，1]解析：选C.由题意知⎩⎪⎨⎪⎧x ＋1＞0，－x 2－3x ＋4＞0⇒－1＜x ＜1.2．若f (x )＝3x 2－x ＋1，g (x )＝2x 2＋x －1，则f (x )与g (x )的大小关系是( ) A ．f (x )>g (x ) B ．f (x )＝g (x ) C ．f (x )<g (x )D ．随x 值的变化而变化解析：选A.因f (x )－g (x )＝x 2－2x ＋2＝(x －1)2＋1>0，故f (x )>g (x )． 3．不等式x －2x ＋3≤2的解集是( ) A ．{x |x ＜－8或x ＞－3} B ．{x |x ≤－8或x ＞－3} C ．{x |－3≤x ≤2} D ．{x |－3＜x ≤2} 解析：选B.原不等式可化为x －2x ＋3－2≤0，即－x －8x ＋3≤0，即(x ＋3)(x ＋8)≥0且x ≠－3，解得：x ≤－8或x ＞－3. 4．已知实数x ，y 满足x 2＋y 2＝1，则(1－xy )(1＋xy )有( ) A ．最小值12和最大值1B ．最小值34和最大值1C ．最小值12和最大值34D ．最小值1解析：选B.因为x 2y 2≤⎝ ⎛⎭⎪⎫x 2＋y 222＝14，当且仅当x 2＝y 2＝12时，等号成立，所以(1－xy )(1＋xy )＝1－x 2y 2≥34.因为x 2y 2≥0，所以34≤1－x 2y 2≤1.5．若不等式4x ＋1x ＋2<0和不等式ax 2＋bx －2>0的解集相同，则a ，b 的值分别为( )A ．－8，－10B ．－4，－9C ．－1，9D ．－1，2解析：选B.因为不等式4x ＋1x ＋2<0的解集为(－2，－14)，所以不等式ax 2＋bx －2>0的解集为(－2，－14)，所以二次方程ax 2＋bx －2＝0的两个根为－2，－14，所以⎩⎪⎨⎪⎧－2＋（－14）＝－ba －2×（－14）＝－2a，所以a ＝－4，b ＝－9.故选B.6．不等式组⎩⎪⎨⎪⎧－2（x －3）＞10，x 2＋7x ＋12≤0的解集为( )A ．[－4，－3]B ．[－4，－2]C ．[－3，－2]D ．∅解析：选A.⎩⎪⎨⎪⎧－2（x －3）＞10，x 2＋7x ＋12≤0⇒⎩⎪⎨⎪⎧x －3＜－5，（x ＋3）（x ＋4）≤0 ⇒⎩⎪⎨⎪⎧x ＜－2，－4≤x ≤－3⇒－4≤x ≤－3. 7．某公司租地建仓库，每月土地费用与仓库到车站距离成反比，而每月货物的运输费用与仓库到车站距离成正比．如果在距离车站10 km 处建仓库，则土地费用和运输费用分别为2万元和8万元，那么要使两项费用之和最小，仓库应建在离车站( ) A ．5 km 处 B ．4 km 处 C ．3 km 处D ．2 km 处解析：选A.设车站到仓库距离为x (x ＞0)，土地费用为y 1，运输费用为y 2，由题意得y 1＝k 1x，y 2＝k 2x ，因为x ＝10时，y 1＝2，y 2＝8，所以k 1＝20，k 2＝45，所以费用之和为y ＝y 1＋y 2＝20x＋45x ≥220x ×45x ＝8，当且仅当20x ＝4x5，即x ＝5时取等号． 8．已知x ，y 满足约束条件⎩⎪⎨⎪⎧x －y ≥0x ＋y －4≤0，y ≥1则z ＝－2x ＋y 的最大值是( )A ．－1B ．－2C ．－5D ．1解析：选A.作出可行域，如图中阴影部分所示，易知在点A (1，1)处，z 取得最大值，故z max ＝－2×1＋1＝－1.9．已知x ＞0，y ＞0.若2y x ＋8x y＞m 2＋2m 恒成立，则实数m 的取值范围是( )A ．m ≥4或m ≤－2B ．m ≥2或m ≤－4C ．－2＜m ＜4D ．－4＜m ＜2解析：选D.因为x ＞0，y ＞0，所以2y x ＋8x y ≥8(当且仅当2y x ＝8x y 时取“＝”)．若2y x ＋8x y＞m2＋2m 恒成立，则m 2＋2m ＜8，解之得－4＜m ＜2.10．已知－1≤x ＋y ≤4，且2≤x －y ≤3，则z ＝2x －3y 的取值范围是( ) A ．[3，8] B ．[3，6] C ．[6，7]D ．[4，5]解析：选A.设2x －3y ＝λ(x ＋y )＋μ(x －y )，则(λ＋μ)x ＋(λ－μ)y ＝2x －3y ，所以⎩⎪⎨⎪⎧λ＋μ＝2，λ－μ＝－3，解得⎩⎪⎨⎪⎧λ＝－12，μ＝52，所以z ＝－12(x ＋y )＋52(x －y )．因为－1≤x ＋y ≤4，所以－2≤－12(x ＋y )≤12.①因为2≤x －y ≤3，所以5≤52(x －y )≤152.②①＋②得，3≤－12(x ＋y )＋52(x －y )≤8，所以z 的取值范围是[3，8]．11．若不等式x 2＋ax ＋1≥0对一切x ∈⎝ ⎛⎦⎥⎤0，12恒成立，则实数a 的最小值为( )A ．0B ．－2C ．－52D ．－3解析：选C.因为不等式x 2＋ax ＋1≥0对一切x ∈⎝ ⎛⎦⎥⎤0，12恒成立，所以对一切x ∈⎝ ⎛⎦⎥⎤0，12，ax ≥－x 2－1，即a ≥－x 2＋1x恒成立．令g (x )＝－x 2＋1x ＝－⎝ ⎛⎭⎪⎫x ＋1x . 易知g (x )＝－⎝ ⎛⎭⎪⎫x ＋1x 在⎝ ⎛⎦⎥⎤0，12内为增函数．所以当x ＝12时，g (x )max ＝－52，所以a 的取值范围是⎣⎢⎡⎭⎪⎫－52，＋∞，即a 的最小值是－52.故选C.12．已知x ，y满足约束条件⎩⎪⎨⎪⎧x －y －1≤0，2x －y －3≥0，若目标函数z ＝ax ＋by (a ＞0，b ＞0)在该约束条件下取到的最小值为25，则a 2＋b 2的最小值为( ) A ．5 B ．4 C. 5D ．2解析：选B.画出约束条件表示的可行域(如图所示)．显然，当直线z ＝ax ＋by 过点A (2，1)时，z 取得最小值，即25＝2a ＋b ，所以25－2a ＝b ，所以a 2＋b 2＝a 2＋(25－2a )2＝5a 2－85a ＋20.构造函数m (a )＝5a 2－85a ＋20(5＞a ＞0)，利用二次函数求最值，显然函数m (a )＝5a 2－85a ＋20的最小值是4×5×20－（85）24×5＝4，即a 2＋b 2的最小值为4.故选B.二、填空题：本题共4小题，每小题5分． 13．函数y ＝2－x －4x(x ＞0)的值域为________．解析：当x ＞0时，y ＝2－⎝⎛⎭⎪⎫x ＋4x ≤2－2x ×4x ＝－2.当且仅当x ＝4x，x ＝2时取等号．答案：(－∞，－2]14．若不等式x 2－4x ＋m <0的解集为空集，则不等式x 2－(m ＋3)x ＋3m <0的解集是________．解析：由题意，知方程x 2－4x ＋m ＝0的判别式Δ＝(－4)2－4m ≤0，解得m ≥4，又x 2－(m ＋3)x ＋3m <0等价于(x －3)(x －m )<0，所以3<x <m . 答案：(3，m )15．已知O 是坐标原点，点A (－1，1)，若点M (x ，y )为平面区域⎩⎪⎨⎪⎧x ＋y ≥2x ≤1y ≤2内的一个动点，则OA →·OM →的取值范围是________．解析：画出满足条件的可行域如图中阴影部分所示，因为OA →＝(－1，1)，OM →＝(x ，y )，所以OA →·OM →＝－x ＋y .取目标函数z ＝－x ＋y ，则y ＝x ＋z .作斜率为1的一族平行线，当直线经过点C (1，1)时，z 取最小值，即z min ＝－1＋1＝0；当直线经过点B (0，2)时，z 取最大值，即z max ＝0＋2＝2，于是0≤z ≤2，即OA →·OM →的取值范围是[0，2]．答案：[0，2]16．已知实数a ，b ，c 满足a ＋b ＋c ＝0，a 2＋b 2＋c 2＝1，则a 的最大值是________．解析：因为a ＋b ＋c ＝0，所以b ＋c ＝－a . 因为a 2＋b 2＋c 2＝1，所以－a 2＋1＝b 2＋c 2＝(b ＋c )2－2bc ＝a 2－2bc ，所以2a 2－1＝2bc ≤b 2＋c 2＝1－a 2，所以3a 2≤2，所以a 2≤23，所以－63≤a ≤63.所以a max ＝63. 答案：63三、解答题：解答应写出文字说明、证明过程或演算步骤．17．(本小题满分10分)已知函数f (x )＝x 2＋2x，解不等式f (x )－f (x －1)＞2x －1.解：由题意可得x 2＋2x －(x －1)2－2x －1＞2x －1，化简得2x （x －1）＜0，即x (x －1)＜0，解得0＜x ＜1.所以原不等式的解集为{x |0＜x ＜1}．18．(本小题满分12分)正数x ，y 满足1x ＋9y＝1.(1)求xy 的最小值； (2)求x ＋2y 的最小值．解：(1)由1＝1x ＋9y≥21x ·9y 得xy ≥36，当且仅当1x ＝9y，即y ＝9x ＝18时取等号，故xy的最小值为36.(2)由题意可得x ＋2y ＝(x ＋2y )·⎝ ⎛⎭⎪⎫1x ＋9y ＝19＋2y x ＋9x y≥19＋22y x ·9xy＝19＋62，当且仅当2y x ＝9x y，即9x 2＝2y 2时取等号，故x ＋2y 的最小值为19＋6 2.19．(本小题满分12分)已知x 、y 、z 是实数，a 、b 、c 是正实数，求证：b ＋c a x 2＋a ＋c by 2＋a ＋b cz 2≥2(xy ＋yz ＋xz )．证明：法一：b ＋c a x 2＋a ＋c b y 2＋a ＋b c z 2－2(xy ＋yz ＋xz )＝b a x 2－2xy ＋a b y 2＋c a x 2－2xz ＋a c z 2＋cby 2－2yz ＋b c z 2＝⎝⎛⎭⎪⎫bax －a b y 2＋⎝⎛⎭⎪⎫c ax －a c z 2＋ ⎝⎛⎭⎪⎫c by －b c z 2≥0. 所以b ＋c a x 2＋a ＋c b y 2＋a ＋b cz 2≥2(xy ＋yz ＋xz )成立．当且仅当a ＝b ＝c 时等号成立．法二：b ＋c a x 2＋a ＋c b y 2＋a ＋b c z 2＝⎝ ⎛⎭⎪⎫b ax 2＋a b y 2＋⎝ ⎛⎭⎪⎫c a x 2＋a c z 2＋⎝ ⎛⎭⎪⎫c b y 2＋b c z 2≥2b a ·abxy ＋2c a ·ac xz ＋2c b ·bcyz ＝2(xy ＋yz ＋xz )．当且仅当a ＝b ＝c 时等号成立． 20．(本小题满分12分)已知函数f (x )＝x 2－2x －8，g (x )＝2x 2－4x －16. (1)求不等式g (x )<0的解集；(2)若对一切x >2，均有f (x )≥(m ＋2)x －m －15恒成立，求实数m 的取值范围．解：(1)g (x )＝2x 2－4x －16<0，所以(2x ＋4)(x －4)<0，所以－2<x <4，所以不等式g (x )<0的解集为{x |－2<x <4}． (2)因为f (x )＝x 2－2x －8.当x >2时，f (x )≥(m ＋2)x －m －15恒成立，所以x 2－2x －8≥(m ＋2)x －m －15，则x 2－4x ＋7≥m (x －1)．所以对一切x >2，均有不等式x 2－4x ＋7x －1≥m 成立．又x 2－4x ＋7x －1＝(x －1)＋4x －1－2≥2（x －1）×4x －1－2＝2(当x ＝3时等号成立)．所以实数m 的取值范围是(－∞，2]．21．(本小题满分12分)一个农民有田2亩，根据他的经验，若种水稻，则每亩每期产量为400千克；若种花生，则每亩每期产量为100千克，但水稻成本较高，每亩每期需240元，而花生只要80元，且花生每千克可卖5元，稻米每千克只卖3元，现在他只能凑足400元，问这位农民对两种作物各种多少亩，才能得到最大利润？解：设水稻种x 亩，花生种y 亩，则由题意得⎩⎪⎨⎪⎧x ＋y ≤2，240x ＋80y ≤400，x ≥0，y ≥0.即⎩⎪⎨⎪⎧x ＋y ≤2，3x ＋y ≤5，x ≥0，y ≥0，画出可行域如图阴影部分所示．而利润P ＝(3×400－240)x ＋(5×100－80)y ＝960x ＋420y (目标函数)，可联立⎩⎪⎨⎪⎧x ＋y ＝2，3x ＋y ＝5，得交点B (1.5，0.5)．故当x ＝1.5，y ＝0.5时，P 最大值＝960×1.5＋420×0.5＝1 650，即水稻种1.5亩，花生种0.5亩时所得到的利润最大．22．(本小题满分12分)已知二次函数f (x )＝ax 2＋bx ＋c (a ，b ，c ∈R )满足：对任意实数x ，都有f (x )≥x ，且当x ∈(1，3)时，有f (x )≤18(x ＋2)2成立．(1)证明：f (2)＝2；(2)若f (－2)＝0，求f (x )的表达式；(3)设g (x )＝f (x )－m 2x ，x ∈[0，＋∞)，若g (x )图像上的点都位于直线y ＝14的上方，求实数m 的取值范围．解：(1)证明：由条件知：f (2)＝4a ＋2b ＋c ≥2恒成立．又因取x ＝2时，f (2)＝4a ＋2b ＋c ≤18(2＋2)2＝2恒成立，所以f (2)＝2.(2)因为⎩⎪⎨⎪⎧4a ＋2b ＋c ＝2，4a －2b ＋c ＝0，所以4a ＋c ＝2b ＝1.所以b ＝12，c ＝1－4a .又f (x )≥x 恒成立，即ax 2＋(b －1)x ＋c ≥0恒成立．所以a ＞0，Δ＝⎝ ⎛⎭⎪⎫12－12－4a (1－4a )≤0，解得：a ＝18，c ＝12.所以f (x )＝18x 2＋12x ＋12.(3)g (x )＝18x 2＋⎝ ⎛⎭⎪⎫12－m 2x ＋12＞14，在x ∈[0，＋∞)上恒成立．即x 2＋4(1－m )x ＋2＞0在x ∈[0，＋∞)上恒成立， ①Δ＜0，即[4(1－m )]2－8＜0. 解得：1－22＜m ＜1＋22. ②⎩⎪⎨⎪⎧Δ≥0，－2（1－m ）≤0，f （0）＞0.解得：m ≤1－22，综上m ∈⎝ ⎛⎭⎪⎫－∞，1＋22.。

北师大版高中数学必修五模块综合测评.docx

模块综合测评(时间120分钟，满分150分)一、选择题(本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的)1．已知等差数列{a n}满足a2＋a4＝4，a3＋a5＝10，则它的前10项的和S10＝()A．138B．135C．95 D．23【解析】由a2＋a4＝4，a3＋a5＝10得a1＝－4，d＝3，所以S10＝10×(2a1＋9d)2＝10×(－8＋27)2＝5×19＝95.【答案】 C2．在△ABC中，已知a、b和锐角A，要使三角形有两解，则应该满足的条件是()A．a＝b sin A B．b sin A＞aC．b sin A＜b＜a D．b sin A＜a＜b【解析】当a＝b sin A时，有一解，当b sin A＜a＜b时，有两解，当a＞b 时有一解．【答案】 D3．已知不等式x2＋ax＋4＜0的解集为空集，则a的取值范围是()A ．－4≤a ≤4B ．－4＜a ＜4C ．a ≤－4或a ≥4D ．a ＜－4或a ＞4【解析】欲使不等式x 2＋ax ＋4＜0的解集为空集，则Δ＝a 2－16≤0，∴－4≤a ≤4.【答案】 A4．已知等差数列的前n 项和为18，若S 3＝1，a n ＋a n －1＋a n －2＝3，则n 的值为( )A ．9B ．21C ．27D ．36【解析】 ∵S 3＝a 1＋a 2＋a 3＝1，又a 1＋a n ＝a 2＋a n －1＝a 3＋a n －2， ∴3(a 1＋a n )＝1＋3，∴a 1＋a n ＝43.又S n ＝n (a 1＋a n )2＝23n ＝18，∴n ＝27，故选C.【答案】 C5．关于x 的不等式ax －b >0的解集是(1，＋∞)，则关于x 的不等式(ax ＋b )(x －3)>0的解集是( )A ．(－∞，－1)∪(3，＋∞)B ．(－1,3)C ．(1,3)D ．(－∞，1)∪(3，＋∞) 【解析】 (ax ＋b )(x －3)>0等价于 ⎩⎨⎧ ax ＋b >0，x －3>0或⎩⎨⎧ax ＋b <0，x －3<0， ∴⎩⎨⎧x >－1，x >3或⎩⎨⎧x <－1，x <3. ∴x ∈(－∞，－1)∪(3，＋∞)．【答案】 A6．“神七”飞天，举国欢庆，据科学计算，运载“神舟七号”飞船的“长征2号”系列火箭，点火1分钟内通过的路程为2 km ，以后每分钟通过的路程比前一分钟增加2 km ，在到达离地面240 km 的高度时，火箭与飞船分离，则这一过程大约需要的时间是( )A ．10分钟B ．13分钟C ．15分钟D ．20分钟【解析】由题设条件知，火箭每分钟通过的路程构成以a 1＝2为首项，公差d ＝2的等差数列，∴n 分钟内通过的路程为S n ＝2n ＋n (n －1)2×2＝n 2＋n ＝n (n ＋1)．检验选项知，n ＝15时，S 15＝240 km.故选C.【答案】 C7．(2016·西安高二检测)在△ABC 中，内角A 、B 、C 满足6sin A ＝4sin B ＝3sin C ，则cos B ＝( )A.154 B ．34 C.31510D ．1116【解析】由6sin A ＝4sin B ＝3sin C 得sin A ∶sin B ∶sin C ＝2∶3∶4，设△ABC 中角A 、B 、C 的对边分别为a ，b ，c ，则由正弦定理知a ∶b ∶c ＝2∶3∶4.不妨设a ＝2k ，b ＝3k ，c ＝4k (k ＞0)，则cos B ＝a 2＋c 2－b 22ac ＝(22＋42－32)k 22×2k ×4k ＝1116.【答案】 D8．(2015·四川高考)设实数x ，y 满足⎩⎨⎧2x ＋y ≤10，x ＋2y ≤14，x ＋y ≥6，则xy 的最大值为( )A.252 B ．492 C ．12D ．16【解析】⎩⎨⎧2x ＋y ≤10，x ＋2y ≤14，x ＋y ≥6表示的可行域如图中阴影部分所示．令S ＝xy ，不妨设在点M (x 0，y 0)处S 取得最大值，且由图象知点M (x 0，y 0)只可能在线段AD ，AB ，BC 上．(1)当M (x 0，y 0)在线段AD 上时，x 0∈[－2,0]，此时S ＝xy ≤0；(2)当M (x 0，y 0)在线段AB 上时，x 0∈[0,2]，S ＝xy ＝x ·14－x 2＝x ⎝ ⎛⎭⎪⎫7－x 2＝－x 22＋7x ＝－12(x －7)2＋492，当x 0＝2时，S max ＝－12(2－7)2＋492＝－252＋492＝12；(3)当M (x 0，y 0)在线段BC 上时，x 0∈[2,4]，S ＝xy ＝x ·(10－2x )＝－2x 2＋10x ＝－2⎝ ⎛⎭⎪⎫x －522＋252，当x 0＝52时，S max ＝252. 综上所述，xy 的最大值为252. 【答案】 A9．y ＝3＋x ＋x 21＋x (x ＞0)的最小值是( )A ．2 3B ．－1＋2 3C ．1＋2 3D ．－2＋2 3【解析】 y ＝3＋x ＋x 21＋x ＝31＋x ＋x ＝31＋x ＋x ＋1－1≥23－1，当且仅当31＋x ＝1＋x ，即x ＝3－1时取等号，故y 有最小值23－1.【答案】 B10．对于每个自然数n ，抛物线y ＝(n 2＋n )x 2－(2n ＋1)x ＋1与x 轴交于A n ，B n 两点，以|A n B n |表示该两点间的距离，则|A 1B 1|＋|A 2B 2|＋…＋|A 2 015B 2 015|的值是( )A.2 0142 015 B ．2 0162 015 C.2 0152 014D ．2 0152 016【解析】 |A n B n |＝|x 1－x 2|＝⎝ ⎛⎭⎪⎫2n ＋1n 2＋n 2－4n 2＋n ＝1n 2＋n ＝1n ·(n ＋1)＝1n －1n ＋1， ∴|A 1B 1|＋|A 2B 2|＋…＋|A 2 015B 2 015|＝⎝ ⎛⎭⎪⎫1－12＋⎝ ⎛⎭⎪⎫12－13＋…＋⎝ ⎛⎭⎪⎫12 015－12 016＝2 0152 016.【答案】 D11．设f (x )＝3ax －2a ＋1，若存在x 0∈(－1,1)使f (x 0)＝0，则实数a 的取值范围是( )A ．－1＜a ＜15 B ．a ＜－1 C ．a ＜－1或a ＞15D ．a ＞15【解析】由于f (x )＝3ax －2a ＋1，故f (x )一定是一条直线，又由题意，存在x 0∈(－1,1)，使得f (x 0)＝0，故直线y ＝3ax －2a ＋1在x ＝－1和x ＝1时的函数值异号，即f (－1)f (1)＜0，得(1－5a )(a ＋1)＜0，解得a ＜－1或a ＞15.【答案】 C12．(2014·福建高考)已知圆C ：(x －a )2＋(y －b )2＝1，平面区域Ω：⎩⎨⎧x ＋y －7≤0，x －y ＋3≥0，y ≥0.若圆心C ∈Ω，且圆C 与x 轴相切，则a 2＋b 2的最大值为( )A ．5B ．29C ．37D ．49【解析】作出可行域，如图，由题意知，圆心为C (a ，b )，半径r ＝1，且圆C 与x 轴相切，所以b ＝1.而直线y ＝1与可行域的交点为A (6,1)，B (－2,1)，目标函数z ＝a 2＋b 2表示点C 到原点距离的平方，所以当点C 与点A 重合时，z 取到最大值，z max ＝37.【答案】 C二、填空题(本大题共4个小题，每小题5分，共20分．将答案填在题中的横线上)13．已知二次函数f (x )＝ax 2－3x ＋2，不等式f (x )＞0的解集为{x |x ＜1或x ＞b }，则b ＝________.【解析】由题意知1，b 是方程ax 2－3x ＋2＝0的两根，由根与系数的关系得⎩⎪⎨⎪⎧1＋b ＝3a ，1×b ＝2a ，∴⎩⎨⎧a ＝1，b ＝2.【答案】 214．在△ABC 中，B ＝120°，AC ＝7，AB ＝5，则△ABC 的面积为________．【解析】设AB ＝c ，BC ＝a ，AC ＝b ，由余弦定理b 2＝a 2＋c 2－2ac cos B ，得49＝a 2＋25－2×5a ⎝ ⎛⎭⎪⎫－12，解得a ＝3，∴S △ABC ＝12ac sin B ＝12×3×5×sin120°＝1534. 【答案】153415．(2015·全国卷Ⅱ)若x ，y 满足约束条件⎩⎨⎧x －y ＋1≥0，x －2y ≤0，x ＋2y －2≤0，则z ＝x ＋y 的最大值为________．【解析】画出可行域如图所示．由⎩⎨⎧x －2y ＝0，x ＋2y －2＝0，得⎩⎪⎨⎪⎧x ＝1，y ＝12.∴A ⎝ ⎛⎭⎪⎫1，12. 由z ＝x ＋y ，得y ＝－x ＋z ，平移直线l 0：x ＋y ＝0. 当直线过点A 时，z 最大，z max ＝1＋12＝32. 【答案】 3216．若a ＞0，b ＞0，且a 2＋14b 2＝1，则a 1＋b 2的最大值为________．【解析】 a 1＋b 2＝12·2a 1＋b 2≤4a 2＋1＋b 24＝54，当且仅当⎩⎨⎧4a 2＝1＋b 2，4a 2＋b 2＝4时等号成立，即a ＝104，b ＝62时成立．【答案】 54三、解答题(本大题共6小题，共70分，解答应写出文字说明，证明过程或演算步骤)17．(本小题满分10分)已知△ABC 的周长为2＋1，且sin A ＋sin B ＝2sin C . (1)求边AB 的长；(2)若△ABC 的面积为16sin C ，求C 的度数．【解】 (1)由题意△ABC 的周长为2＋1，∴AB ＋BC ＋AC ＝2＋1.由正弦定理，得 BC ＋AC ＝2AB ，∴AB ＝1.(2)由△ABC 的面积为12BC ·AC ·sin C ＝16sin C ，得BC ·AC ＝13.由(1)知BC ＋AC ＝2，由余弦定理，得cos C ＝AC 2＋BC 2－AB 22AC ·BC ＝12，∴C ＝60°.18．(本小题满分12分)已知等比数列{a n }中，a 2＝2，a 5＝128，若b n ＝log 2a n ，数列{b n }前n 项的和为S n .(1)若S n ＝35，求n 的值；(2)求不等式S n ＜2b n 的解集. 【导学号：67940089】【解】 (1)由a 2＝a 1q ＝2，a 5＝a 1q 4＝128得q 3＝64， ∴q ＝4，a 1＝12，∴a n ＝a 1q n －1＝12·4n －1＝22n －3， ∴b n ＝log 2a n ＝log 222n －3＝2n －3. ∵b n ＋1－b n ＝[2(n ＋1)－3]－(2n －3)＝2，∴{b 1}是以b 1＝－1为首项，2为公差的等差数列， ∴S n ＝(－1＋2n －3)n 2＝35，n 2－2n －35＝0，(n －7)(n ＋5)＝0，即n ＝7.(2)∵S n －2b n ＝n 2－2n －2(2n －3)＝n 2－6n ＋6＜0， ∴3－3＜n ＜3＋3， ∵n ∈N ＋，∴n ＝2,3,4，即所求不等式的解集为{2,3,4}．19．(本小题满分12分)如图1，矩形ABCD 是机器人踢球的场地，AB ＝170 cm ，AD ＝80 cm ，机器图1人先从AD 中点E 进入场地到点F 处，EF ＝40 cm ，EF ⊥AD .场地内有一小球从点B 向点A 运动，机器人从点F 出发去截小球．现机器人和小球同时出发，它们均作匀速直线运动，并且小球运动的速度是机器人行走速度的2倍．若忽略机器人原地旋转所需的时间，则机器人最快可在何处截住小球？【解】设该机器人最快可在点G 处截住小球，点G 在线段AB 上．连接FG .设FG ＝x cm.根据题意，得BG ＝2x cm.则AG ＝AB －BG ＝(170－2x )cm.连接AF ，在△AEF 中，EF ＝AE ＝40 cm ，EF ⊥AD ，所以∠EAF ＝45°，AF ＝402cm ，于是∠F AG ＝45°.在△AFG 中，由余弦定理，得 FG 2＝AF 2＋AG 2－2AF ·AG cos ∠F AG ，所以x 2＝(402)2＋(170－2x )2－2×402×(170－2x )×cos 45°，解得x 1＝50，x 2＝3703.所以AG ＝170－2x ＝70 cm 或AG ＝－2303cm(不合题意，舍去)．即该机器人最快可在线段AB 上离A 点70 cm 处截住小球． 20．(本小题满分12分)解关于x 的不等式ax 2－2≥2x －ax (a ∈R ).【导学号：67940090】【解】原不等式可化为ax 2＋(a －2)x －2≥0⇒(ax －2)(x ＋1)≥0. (1)当a ＝0时，原不等式化为x ＋1≤0⇒x ≤－1. (2)当a ＞0时，原不等式化为⎝ ⎛⎭⎪⎫x －2a (x ＋1)≥0⇒x ≥2a 或x ≤－1；(3)当a ＜0时，原不等式化为⎝ ⎛⎭⎪⎫x －2a (x ＋1)≤0.①当2a ＞－1，即a ＜－2时，原不等式的解集为－1≤x ≤2a ； ②当2a ＝－1，即a ＝－2时，原不等式的解集为x ＝－1； ③当2a ＜－1，即－2＜a ＜0时，原不等式的解集为2a ≤x ≤－1. 综上所述，当a ＜－2时，原不等式的解集为⎣⎢⎡⎦⎥⎤－1，2a ；当a ＝－2时，原不等式的解集为{－1}；当－2＜a ＜0时，原不等式的解集为⎣⎢⎡⎦⎥⎤2a ，－1；当a ＝0时，原不等式的解集为(－∞，－1]；当a ＞0时，原不等式的解集为(－∞，－1]∪⎣⎢⎡⎭⎪⎫2a ，＋∞.21．(本小题满分12分)某汽车运输公司购买了一批豪华大客车投入运营．据市场分析，每辆客车运营的总利润y (单位：十万元)与运营年数x 满足二次函数的关系：y ＝－a (x －6)2＋11，且该二次函数图像过点(4,7)．问每辆客车运营多少年，运营的年平均利润最大？最大值为多少？(年平均利润＝总利润年数) 【解】设年平均利润为z 十万元，依题意， ∵二次函数y ＝－a (x －6)2＋11的图像过点(4,7)， ∴7＝－a (4－6)2＋11， ∴a ＝1，∴y ＝－(x －6)2＋11，z ＝y x ＝－(x －6)2＋11x＝－x 2＋12x －25x ＝－x －25x ＋12＝－⎝ ⎛⎭⎪⎫x ＋25x ＋12.∵x ＞0，∴x ＋25x ≥10， ∴－⎝ ⎛⎭⎪⎫x ＋25x ≤－10，∴－⎝ ⎛⎭⎪⎫x ＋25x ＋12≤2，∴z ≤2，当且仅当x ＝25x 即x ＝5时，z 有最大值为2十万元．即每辆客车运营5年，运营的年平均利润最大，最大值为2十万元．22．(本小题满分12分)已知数列{a n }是首项为a 1＝14，公比q ＝14的等比数列，设b n ＋2＝3log 14a n (n ∈N ＋)，数列{c n }满足c n ＝a n ·b n .(1)求证：{b n }是等差数列；(2)求数列{c n }的前n 项和S n ；(3)若c n ≤14m 2＋m －1对一切正整数n 恒成立，求实数m 的取值范围.【导学号：67940091】【解】 (1)证明：由题意知，a n ＝⎝ ⎛⎭⎪⎫14n (n ∈N ＋)， ∵b n ＝3log 14a n －2，b 1＝3log 14a 1－2＝1，∴b n ＋1－b n ＝3log 14a n ＋1－3log 14a n ＝3log 14a n ＋1a n＝3log 14q ＝3， ∴数列{b n }是首项b 1＝1，公差d ＝3的等差数列．(2)由(1)知，a n ＝⎝ ⎛⎭⎪⎫14n ，b n ＝3n －2(n ∈N ＋)， ∴c n ＝(3n －2)×⎝ ⎛⎭⎪⎫14n (n ∈N ＋)， ∴S n ＝1×14＋4×⎝ ⎛⎭⎪⎫142＋7×⎝ ⎛⎭⎪⎫143＋…＋(3n －5)×⎝ ⎛⎭⎪⎫14n －1＋(3n －2)×⎝ ⎛⎭⎪⎫14n ；于是14S n ＝1×⎝ ⎛⎭⎪⎫142＋4×⎝ ⎛⎭⎪⎫143＋7×⎝ ⎛⎭⎪⎫144＋…＋(3n －5)×⎝ ⎛⎭⎪⎫14n ＋(3n －2)×⎝ ⎛⎭⎪⎫14n ＋1，两式相减得34S n ＝14＋3⎣⎢⎡⎦⎥⎤⎝ ⎛⎭⎪⎫142＋⎝ ⎛⎭⎪⎫143＋…＋⎝ ⎛⎭⎪⎫14n －(3n －2)×⎝ ⎛⎭⎪⎫14n ＋1＝12－(3n ＋2)×⎝ ⎛⎭⎪⎫14n ＋1. ∴S n ＝23－12n ＋83×⎝ ⎛⎭⎪⎫14n ＋1(n ∈N ＋)． (3)∵c n ＋1－c n ＝(3n ＋1)·⎝ ⎛⎭⎪⎫14n ＋1－(3n －2)·⎝ ⎛⎭⎪⎫14n ＝9(1－n )·⎝ ⎛⎭⎪⎫14n ＋1(n ∈N ＋)， ∴当n ＝1时，c 2＝c 1＝14，当n≥2时，c n＋1＜c n，即c1＝c2＞c3＞c4＞…＞c n，∴当n＝1或2时，c n取得最大值是1 4.又c n≤14m2＋m－1对一切正整数n恒成立，∴14m2＋m－1≥14，即m2＋4m－5≥0，解得m≥1或m≤－5.故实数m的取值范围为{m|m≥1或m≤－5}．。

高中数学章末综合测评3 不等式北师大版必修5-北师大版高二必修5数学试题

章末综合测评(三) 不等式(满分：150分时间：120分钟)一、选择题(本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的)1．若1a <1b <0，则下列不等式：①a ＋b <ab ；②|a |>|b |；③a <b ；④b a ＋a b>2中正确的是( )A ．①②B ．②③C ．①④D ．③④C [由1a <1b<0，得b <a <0，∴②③均不成立，a ＋b <0，ab >0，∴①成立．而b a ＋a b －2＝a －b2ab>0，∴b a ＋ab>2，④成立．故选C ．]2．如果a ，b ，c 满足c <b <a 且ac <0，则下列选项中不一定成立的是( ) A ．ab >ac B ．c (b －a )>0 C ．cb 2<ab 2D ．ac (a －c )<0C [c <b <a ，ac <0⇒a >0，c <0．对于A ：⎭⎪⎬⎪⎫b >c a >0⇒ab >ac ，A 正确．对于B ：⎭⎪⎬⎪⎫b <a ⇒b －a <0c <0⇒c (b －a )>0，B 正确；对于C ：⎭⎪⎬⎪⎫c <a b2≥0⇒cb 2≤ab 2即C 不一定成立，C 错．对于D ：ac <0，a －c >0⇒ac (a －c )<0，D 正确．]3．直线3x ＋2y ＋5＝0把平面分成两个区域，下列各点与原点位于同一区域的是( ) A ．(－3,4) B ．(－4,3) C ．(0，－3)D ．(－3,2)A [当x ＝y ＝0时，3x ＋2y ＋5＝5>0，则原点一侧对应的不等式是3x ＋2y ＋5>0，可以验证仅有点(－3,4)满足3x ＋2y ＋5>0．]4．已知不等式x 2＋ax ＋4＜0的解集为空集，则a 的取值范围是 ( ) A ．－4≤a ≤4 B ．－4＜a ＜4 C ．a ≤－4或a ≥4D ．a ＜－4或a ＞4A [由Δ≤0，知a 2－16≤0，∴－4≤a ≤4．]5．若集合A ＝{x |x 2＋x －6<0}，B ＝⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪x ＋2x －3≤0，则A ∩B 等于( ) A ．(－3,3) B ．[－2,2) C ．(－2,2)D ．[－2,3)B [A ＝{x |－3<x <2}＝(－3,2)，B ＝[－2,3)， ∴A ∩B ＝[－2,2)．]6．已知x ，y 满足约束条件⎩⎪⎨⎪⎧x －y ≥0，x ＋y －4≤0，y ≥1，则z ＝－2x ＋y 的最大值是( )A ．－1B ．－2C ．－5D ．1A [根据题意作出约束条件确定的可行域，如下图．令z ＝－2x ＋y ，则y ＝2x ＋z ，可知在图中A (1,1)处，z ＝－2x ＋y 取到最大值－1，故选A ．]7．已知a >0，x ，y 满足约束条件⎩⎪⎨⎪⎧x ≥1，x ＋y ≤3，y ≥a x －3，若z ＝2x ＋y 的最小值为1，则a＝( )A ．14 B ．12 C ．1D ．2B [作出线性约束条件⎩⎪⎨⎪⎧x ≥1，x ＋y ≤3，y ≥a x －3的可行域．因为y ＝a (x －3)过定点(3,0)，故应如图所示，当过点C (1，－2a )时，z ＝2x ＋y 有最小值，∴2×1－2a ＝1，∴a ＝12．]8．已知a >b ，b >0，a ＋b ＝2，则y ＝1a ＋4b的最小值是( )A ．72B ．4C ．92D ．5C [∵a ＋b ＝2，∴a 2＋b 2＝1，∴y ＝1a ＋4b ＝⎝ ⎛⎭⎪⎫1a ＋4b ⎝ ⎛⎭⎪⎫a 2＋b 2＝52＋2a b ＋b2a，∵a >0，b >0，∴2a b ＋b2a≥22a b ·b 2a ＝2，当且仅当2a b ＝b 2a，且a ＋b ＝2，即a ＝23，b ＝43时取得等号，∴y 的最小值是92，选C ．]9．已知函数f (x )＝⎩⎪⎨⎪⎧x ＋2，x ≤0，－x ＋2，x >0.则不等式f (x )≥x 2的解集是( ) A ．[－1,1] B ．[－2,2] C ．[－2,1] D ．[－1,2]A [f (x )≥x 2⇔⎩⎪⎨⎪⎧x ≤0，x ＋2≥x2或⎩⎪⎨⎪⎧x ＞0－x ＋2≥x2⇔⎩⎪⎨⎪⎧x ≤0，x 2－x －2≤0或⎩⎪⎨⎪⎧x >0x 2＋x －2≤0⇔⎩⎪⎨⎪⎧x ≤0－1≤x ≤2或⎩⎪⎨⎪⎧x >0－2≤x ≤1⇔－1≤x ≤0或0<x ≤1⇔－1≤x ≤1．]10．若不等式(a －2)x 2＋2(a －2)x －4＜0对一切x ∈R 恒成立，则a 的取值范围是( ) A ．(－∞，2] B ．(－2,2) C ．(－2,2]D ．(－∞，－2)C [当a －2＝0，即a ＝2时，原不等式化为－4＜0对一切x ∈R 恒成立．当a －2≠0时，即a ≠2时，由题意，得⎩⎪⎨⎪⎧a －2＜0，Δ＝4a －22＋16a －2＜0，解得－2＜a ＜2．综上所述，a 的取值范围为－2＜a ≤2，故选C ．]11．已知实数x ，y 满足2x ＋y －5＝0，那么x 2＋y 2的最小值为( ) A ． 5 B ．10 C ．2 5D ．210A [∵y ＝5－2x ，∴x 2＋y 2＝x 2＋5－2x 2＝5x 2－20x ＋25＝5x －22＋5，∴当x ＝2时，x 2＋y 2的最小值为5．]12．在平面上，过点P 作直线l 的垂线所得的垂足称为点P 在直线l 上的投影，由区域⎩⎪⎨⎪⎧x －2≤0，x ＋y ≥0，x －3y ＋4≥0中的点在直线x ＋y －2＝0上的投影构成的线段记为AB ，则|AB |＝( )A ．2 2B ．4C ．3 2D ．6C [作出不等式组对应的平面区域如图阴影部分所示，解得Q (－1,1)，R (2，－2)，区域内的点在直线x ＋y －2＝0上的投影构成线段R ′Q ′即AB ，而R ′Q ′＝RQ ，所以|AB |＝|QR | ＝－1－22＋1＋22＝32．]二、填空题(本大题共4小题，每小题5分，共20分．将答案填在题中的横线上) 13．不等式2x 2＋2x －4≤12的解集为．[－3,1] [不等式2x 2＋2x －4≤12化为2x 2＋2x －4≤2－1，∴x 2＋2x －4≤－1， ∴x 2＋2x －3≤0， ∴－3≤x ≤1，∴原不等式的解集为[－3,1]．]14．若实数x ，y 满足x 2＋y 2＋xy ＝1，则x ＋y 的最大值是．233[由x 2＋y 2＋xy ＝1得1＝(x ＋y )2－xy ， ∴(x ＋y )2＝1＋xy ≤1＋⎝ ⎛⎭⎪⎫x ＋y 22，解得－233≤x ＋y ≤233，∴x ＋y 的最大值为233．] 15．要挖一个面积为432 m 2的矩形鱼池，周围两侧分别留出宽分别为3 m 、4 m 的堤堰，要想使占地总面积最小，此时鱼池的长为、宽为．24 m 18 m [设鱼池的长宽分别为x m ，y m ，∴xy ＝432，∴(x ＋6)(y ＋8)＝xy ＋6y ＋8x ＋48＝480＋6y ＋8x ≥480＋248xy ＝768，当且仅当6y ＝8x ，即x ＝18，y ＝24时，等号成立．]16．已知a ，b ∈R ＋且a ＋b ＝1，那么下列不等式：①ab ≤14；②ab ＋1ab ≥174；③a ＋b ≤2；④1a ＋12b≥22中，正确的序号是． ①②③ [∵a ，b ∈R ＋，a ＋b ＝1，∴ab ≤⎝ ⎛⎭⎪⎫a ＋b 22＝14，ab ＋1ab ≥174，(a ＋b )2＝a ＋b＋2ab ≤a ＋b ＋a ＋b ＝2，∴a ＋b ≤2．故①②③正确，∵1a ＋12b ＝a ＋b a ＋a ＋b 2b ＝32＋b a ＋a 2b ≥32＋2b a ·a 2b ＝32＋2，(当且仅当a 2＝2b 2时等号成立)．④不正确．]三、解答题(本大题共6小题，共70分，解答应写出文字说明、证明过程或演算步骤) 17．(本小题满分10分)若函数f (x )＝lg(8＋2x －x 2)的定义域为M ，函数g (x )＝1－2x －1的定义域为N ，求集合M ，N ，M ∩N ． [解] 由8＋2x －x 2>0，即x 2－2x －8<0， ∴(x －4)(x ＋2)<0， ∴－2<x <4． ∴M ＝{x |－2<x <4}．由1－2x －1≥0，得x －3x －1≥0， ∴x ≥3或x <1． ∴N ＝{x |x <1或x ≥3}．∴M ∩N ＝{x |－2<x <1或3≤x <4}．18．(本小题满分12分)当x >3时，求函数y ＝2x 2x －3的值域．[解] ∵x >3，∴x －3>0， ∴y ＝2x 2x －3＝2x －32＋12x －3＋18x －3＝2(x －3)＋18x －3＋12 ≥22x －3·18x －3＋12＝24．当且仅当2(x －3)＝18x －3，即x ＝6时，上式等号成立，∴函数y ＝2x2x －3的值域为[24，＋∞)．19．(本小题满分12分)已知实数x ，y 满足不等式组⎩⎪⎨⎪⎧x ＋2y －4≥0，3x －4y ＋8≥0，2x －y －8≤0，求|x －y |的最大值．[解] 关于x ，y 的不等式组表示的平面区域如图所示．|x －y |＝2·|x －y |2＝2·|x －y |12＋12的几何意义表示区域内的点到直线x －y ＝0的距离的2倍，由图可知点A (4,0)到直线x －y ＝0距离最大，所以|x －y |的最大值为2· |4－0|2＝4．20．(本小题满分12分)某厂准备生产甲、乙两种适销产品，每件销售收入分别为3千元，2千元．甲、乙产品都需要在A ，B 两种设备上加工，在每台A ，B 上加工一件甲产品所需工时分别为1时、2时，加工一件乙产品所需工时分别为2时、1时，A 、B 两种设备每月有效使用工时分别为400时和500时．如何安排生产可使月收入最大？[解] 设甲、乙两种产品的产量分别为x ，y 件，约束条件是⎩⎪⎨⎪⎧x ＋2y ≤4002x ＋y ≤500，x ≥0，y ≥0目标函数是f ＝3x ＋2y ，要求出适当的x ，y 使f ＝3x ＋2y 取得最大值．作出可行域，如图．设3x ＋2y ＝a ，a 是参数，将它变形为y ＝－32x ＋a2，这是斜率为－32，随a 变化的一组直线．当直线与可行域相交且截距a2最大时，目标函数f 取得最大值．由⎩⎪⎨⎪⎧x ＋2y ＝400，2x ＋y ＝500得⎩⎪⎨⎪⎧x ＝200，y ＝100.因此，甲、乙两种产品的每月产量分别为200,100件时，可得最大收入800千元． 21．(本小题满分12分)甲厂以x 千克/小时的速度运输生产某种产品(生产条件要求1≤x ≤10)，每小时可获得利润是100⎝ ⎛⎭⎪⎫5x ＋1－3x 元．(1)要使生产该产品2小时获得的利润不低于 3 000元，求x 的取值范围；(2)要使生产900千克该产品获得的利润最大，问：甲厂应该选取何种生产速度？并求最大利润．[解] (1)根据题意，200⎝ ⎛⎭⎪⎫5x ＋1－3x ≥3 000⇔5x －14－3x≥0，又1≤x ≤10，可解得3≤x ≤10．(2)设利润为y 元，则y ＝900x·100⎝ ⎛⎭⎪⎫5x ＋1－3x ＝9×104－3⎝ ⎛⎭⎪⎫1x －162＋6112，故x ＝6时，y max ＝457 500元．22．(本小题满分12分)已知不等式ax 2－3x ＋6>4的解集为{x |x <1或x >b }， (1)求a ，b 的值；(2)解不等式ax 2－(ac ＋b )x ＋bc <0．[解] (1)由题意知，1和b 是方程ax 2－3x ＋2＝0的两根，则⎩⎪⎨⎪⎧3a ＝1＋b ，2a ＝b ，解得⎩⎪⎨⎪⎧a ＝1b ＝2．(2)不等式ax2－(ac＋b)x＋bc<0，即为x2－(c＋2)x＋2c<0，即(x－2)(x－c)<0．①当c>2时，2<x<c；②当c<2时，c<x<2；③当c＝2时，原不等式无解．综上知，当c>2时，原不等式的解集为{x|2<x<c}；当c<2时，原不等式的解集为{x|c<x<2}；当c＝2时，原不等式的解集为∅．。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

全册综合测试（时间：120分钟满分：150分）第Ⅰ卷（选择题共60分）一、选择题（本大题共12个小题，每小题5分，共60分，每小题有4个选项，其中有且仅有一个是正确的，把正确的选项填在答题卡中） 1.(2011·重庆文，2)设U=R,M={x|x2-2x>0},则CUM=（） A.［0,2］ B.(0,2) C.(-∞,0)∪(2,+∞) D.(-∞,0］∪［2,+∞) ［答案］ A ［解析］该题考查二次不等式求解，集合的补集运算. 由x2-2x>0得x>2或x<0. ∴CUM=［0,2］. 2.已知数列｛an｝为等差数列，且有a2+a3+a10+a11=48,则a6+a7=（） A.21 B.22 C.23 D.24 ［答案］ D ［解析］ a2+a3+a10+a11=2(a6+a7)=48，∴a6+a7=24,故选D. 3.在△ABC中，已知a、b和锐角A,要使三角形有两解，则应满足的条件是（） A.a=bsinA B.bsinA>a C.bsinA［答案］ D ［解析］当a=bsinA时，有一解，当bsinAb时有一解. 4.a∈R,且a2+a<0,那么-a,-a3,a2的大小关系是（） A.a2>-a3>-a B.-a>a2>-a3 C.-a3>a2>-a D.a2>-a>-a3 B ∵a2+a<0,∴-1

令a=-21,-a3=81,a2=41,排除A、C、D，故选B. 5.“神七”飞天，举国欢庆，据科学计算，运载“神舟七号”飞船的“长征2号”系列火箭，点火1分钟内通过的路程为2km,以后每分钟通过的路程比前一分钟增加2km,在到达离地面240km的高度时，火箭与飞船分离，则这一过程大约需要的时间是（） A.10分钟 B.13分钟 C.15分钟 D.20分钟 C 由题设条件知，火箭每分钟通过的路程构成以a1=2为首项，公差d=2的等差

数列，∴n分钟内通过的路程为Sn＝2n+2)1(nn³2＝n2+n=n(n+1).检验选项知，n=15时，S15＝240km.故选C. 6.已知不等式x2+ax+4＜0的解集为空集，则a的取值范围是（） A.-4≤a≤4 B.-4＜a＜4 C.a≤-4或a≥4 D.a＜-4或a＞4 ［答案］ A ［解析］欲使不等式x2+ax+4＜0的解集为空集，则Δ=a2-16≤0，∴-4≤a≤4. 7.（2012²西安模拟）在△ABC中，内角A、B、C满足6sinA=4sinB=3sinC,则cosB=（）

A.415 B.43 C.10153 D.1611 D 由6sinA=4sinB=3sinC得 sinA：sinB：sinC=2：3： 4,设△ABC中角A、B、C的对边分别为a,b,c,则由正弦定理知 a：b：c=2：3：4. 不妨设a=2k,b=3k,c=4k(k>0)

则cosB=acbca2222=kkk422)342(2222=1611. 8.已知等比数列{an}的各项均为正数，公比q≠1,设P=293aa,Q=75aa,则P与Q的大小关系是（） A.P＞Q B.P＜Q C.P=Q D.无法确定 A

由等比数列的性质得，Q=75aa=93aa,

而P=293aa且a3＞0,a9＞0,a3≠a9, ∴293aa＞93aa，即P＞Q. 9.已知△ABC中，AB=3，AC=1且B=30°，则△ABC的面积等于（） A.23 B. 43 C. 23 或3 D. 43 或23 D c=AB=3,b=AC=1,B=30°.

由于csinB=3³21=23， csinB＜b＜c， ∴符合条件的三角形有两个.

∵CcBbsinsin，即Csin3211.

∴sinC=23. ∴C=60°或120°,∵A=90°或30°，S△ABC=23或43. 10.下列函数中，最小值为4的是（） A.y=x+x4 B.y=sinx+xsin4 (0C.y=ex+4e-x D.y=12122xx C 对A选项,x<0时无最小值；对B选项，因为0

又y=sinx+xsin4在sinx∈ (0,1］上为减函数，

所以ymin＝1+14=5；

对D选项，函数y=12122xx≥22, 当且仅当x2+1=2即x=±1时，取“＝”.故选C. 11.一小商贩准备用50元钱在一批发市场购买甲、乙两种小商品，甲每件4元，乙每件7元，甲商品每件卖出去后可赚1元，乙每件卖出去后可赚1.8元.若要使赚的钱最多，那么该商贩购买甲、乙两种商品的件数应分别为（） A.甲7件，乙3件 B.甲9件，乙2件 C.甲4件，乙5件 D.甲2件，乙6件 D 设该商贩购买甲、乙两种商品的件数为x件和y件，此时该商贩赚的钱为z元，则由题意可得

4x+7y≤50 ，z=x+1.8y. x≥0，y≥0 如图所示，经分析可知，要使z最大，则只需通过点（2，6），∴当x=2,y=6时，zmax＝2+1.8³6＝12.8.故选D.

2an,0≤an<21,

12.数列｛an｝满足an+1= 若a1=76,则a20的值为（） 2an-1,21≤an<1. A.76 B. 75 C. 73 D. 71 ［答案］ B ［解析］逐步计算，可得a1=76,a2=712-1=75,

a3=710-1=73,a4=76,a5=75,a6=73,„, 这说明数列｛an}是周期数列，T=3, 而20＝3³6＋2，∴a20=75. 第Ⅱ卷（非选择题共90分）二、填空题（本大题共4个小题，每空4分，共16分，把正确答案填在题中横线上）

13.在等比数列｛an}中，a1+a2+a3+a4=815,a2a3=-89,则11a+21a+31a+41a= .

［答案］ -35

11a+21a+31a+41a=4141aa

aa

+3232aaaa=324321aaaaaa=89815

=-35 (∵a1a4=a2a3). 14.在R上定义运算⊙：a⊙b=ab+2a+b，则满足x⊙（x-2）<0的实数x的取值范围为 . ［答案］（-2，1）［解析］由定义得x（x-2）+2x+x-2<0，即x2+x-2<0,∴-215.若数列｛an｝的通项公式为an=(-1) n(3n-2),则a1+a2+„+a10= . ［答案］ 15 ［解析］ ∵an=(-1) n(3n-2) ∴a1+a2+„+a10=-1+4-7+10-„-25+28 =(-1+4)+(-7+10)+„+(-25+28) =3³5＝15. 16.外国船只除特许外，不得进入离我国海岸线d海里以内的区域，如图所示，设A与B是我们的观测站，A与B的距离为s海里，海岸线是过A、B的直线，一外国船只在P点，在A站测得∠BAP=,同时在B 站测得∠ABP＝β，则与β满足三角不等式为时，就应当向此未经特许的外国船只发出警告，命令其退出我国海域.

d≤)sin(sinsins 如图过P作PQ⊥AB于Q点. QBPQ=tanβ,

∴QB=PQ²cotβ, 同理QA=PQ²cot(π-) =-PQ²cot, ∵QB-QA=s, ∴PQ(cotβ+cot)=s,

∴PQ=sincossincoss=)sin(sinsins,

d≤PQ=)sin(sinsins就要发出警告. 三、解答题（本大题共6个小题，共74分，解答应写出文字说明，证明过程或演算步骤） 17.（本小题满分12分）已知△ABC的周长为2+1，且sinA+sinB=2sinC. （1）求边AB的长；（2）若△ABC的面积为61sinC,求C的度数.

［解析］ (1)由题意△ABC的周长为2+1， ∴AB+BC+AC=2+1.由正弦定理，得 BC+AC=2AB.∴AB=1. (2)由△ABC的面积为21BC²AC²sinC=61sinC,得 BC²AC=31.由（1）知BC+AC=2，

由余弦定理，得cosC=BCACABBCAC2222=21. ∴C=60°. 18.（本小题满分12分）已知a>2,解不等式组 a(x-2)+1>0 (x-1) 2>a(x-2)+1. ∵a>2,原不等式组可化为

x>2-a1 x2-(a+2)x+2a>0 x>2-a1 即 . (x-2)(x-a)>0

而2-a1<2,2-a1-a=-aa2)1(<0. 当a>2时，原不等式的解集为｛x|2-a1a｝. 19.（本小题满分12分）在△ABC中，a,b,c分别是∠A,∠B,∠C的对应边长，已知2sin2A=3cosA.(1)求∠A；

(2)若a=3,求△ABC面积的最大值. ［解析］ (1)∵2sin2A=3cosA, ∴2(1-cos2A)=3cosA, ∴2cos2A+3cosA-2=0,

解得cosA=21,

∵0

(2)∵S△ABC=21bcsinA=43bc, 又∵b2+c2-a2=bc, ∴a2=b2+c2-bc≥2bc-bc=bc, 当且仅当a=b时等号成立，

∴bc≤a2=(3)2=3,∴S△ABC≤433.

即△ABC面积的最大值是433. 20.（本小题满分12分）已知等比数列｛an｝中，a1=64,公比q≠1,a2,a3,a4又分别是某等差数列的第7项，第3项，第1项. (1)求an; (2)设bn=log2an，求数列｛|bn|｝的前n项和Tn. （1）依题意有a2-a4=3(a3-a4), 即2a1q3-3a1q2+a1q=0,∴2q2-3q+1=0.

∵q≠1,∴q=21,故an=64³(21)n-1.

(2)∵bn=log2［64³(21)n-1］=7-n. 7-n (n≤7) ∴|bn|= ， n-7 (n>7)

当n≤7时，Tn=2)13(nn;

当n>7时，Tn=T7+2)6)(7(nn=21+2)6)(7(nn.

2)13(nn (n≤7)