运筹学参考模板
中国科学院研究生院博士学位论文模板

发表文章目录 · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · 19
简历 · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · 21
in Operations Research
摘要
本 文 是 中 国 科 学 院 学 位 论 文 的 LATEX 模 板。 除 了 介 绍 LATEX 文 档 类 CASthesis 的用法外,本文还是一个简要的学位论文写作指南。
关键词: 中科院,学位论文,LATEX 模板
Abstract
This paper is a thesis template of Chinese Academy of Sciences. Besides that the usage of the LATEX document class CASthesis, a brief guideline for writing the thesis is also included.
附录 A 中国科学院研究生院学位论文撰写要求 · · · · · · · · · · · · · · · · · · · · · · · · · 11 A.1 基本要求 · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · 11 A.1.1 硕士学位论文· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · 11 A.1.2 博士学位论文· · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · · 11
迪杰斯特拉算法模板

迪杰斯特拉算法模板摘要:1.迪杰斯特拉算法简介2.算法模板3.算法的应用与优势4.算法的局限性正文:【迪杰斯特拉算法简介】迪杰斯特拉算法(Dijkstra"s algorithm)是一种经典的单源最短路径算法,由荷兰计算机科学家艾兹赫尔·迪杰斯特拉(Edsger W.Dijkstra)于1956 年提出。
该算法主要用于寻找一个有权图中,从源节点到其他所有节点的最短路径。
它在网络科学、运筹学以及计算机科学等领域具有广泛的应用。
【算法模板】迪杰斯特拉算法的核心思想是每次选择距离源节点最近的节点进行扩展,直到找到目标节点或扩展完毕。
算法的具体步骤如下:1.创建一个集合,用于存储已确定最短路径的节点;2.将源节点加入该集合,并将其距离设为0;3.初始化距离数组,将源节点到其他所有节点的距离设为无限大(如正无穷或负无穷),将源节点到自身的距离设为0;4.从未确定最短路径的节点中选择距离最小的节点,将其加入已确定最短路径的节点集合,并更新其他节点的距离;5.重复步骤4,直到找到目标节点或所有节点都已确定最短路径;6.如果所有节点都已确定最短路径,返回距离数组。
【算法的应用与优势】迪杰斯特拉算法在实际应用中具有很多优势,例如:1.可以处理有向图和无向图;2.可以处理存在负权边的图;3.可以处理存在多源节点的图;4.可以处理大规模的图,具有较好的时间复杂性。
【算法的局限性】尽管迪杰斯特拉算法在很多情况下表现优秀,但它也存在一些局限性,如:1.算法的时间复杂度为O(E*logV),其中E 为边数,V 为节点数。
当图规模较大时,计算时间较长;2.算法需要占用较大的内存空间,因为需要存储距离数组和已确定最短路径的节点集合。
总之,迪杰斯特拉算法是一种具有广泛应用和重要意义的单源最短路径算法。
运筹与优化 (一)

小问题
孙子兵法十三篇,你知道几篇?
孙子兵法十三篇
计篇第一 作战篇第二 谋攻篇第三 形篇第四 势篇第五 虚实篇第六 军争篇第七 九变篇第八 行军篇第九 地形篇第十 九地篇第十一 火攻篇第十二 用间篇第十三
小问题
三十六计,你知道几计?
三十六计
定性与定量
思想(谋略)——定性——古代运筹学思想
方法(操作)——定量——现代优化技术
由定性到定量,二者可以结合!
运筹与优化的关系
最优化:把事情做到最好! • 最优化方法的目的在于针对所研究的系统,求得一个合理 运用人力、物力和财力的最佳方案,发挥和提高系统的效 能及效益,最终达到系统的最优目标。 最优化方法主要运用数学方法(定量)研究各种系统的优 化途径及方案,为决策者提供科学决策的依据。 最优化方法是运筹学的最基本内容,最优化上升到科学的 高度就是运筹学。因此,最优化方法也叫运筹学方法。 运筹学并不仅限于优化问题,还有判定问题(回答是否可 以),但有的判定问题也可转化为优化问题。
着整体性的概念和系统分析的思想,在他们的报告中使用了 “Operational Research(OR)”一词,这便是我们所说的运筹学。
运筹学的发展:(国外)
军事需要:运筹学的活动是从二次世界大战初期的军事任务开始的。
当时迫切需要把各项稀少的资源以有效的方式分配给各种不同的军事 经营及在每一经营内的各项活动,所以美国及随后美国的军事管理当 局都号召大批科学家运用科学手段来处理战略与战术问题,实际上这 便是要求他们对种种(军事)经营进行研究,这些科学家小组正是最 早的运筹小组。第二次世界大战期间,“OR”成功地解决了许多重要 作战问题,显示了科学的巨大物质威力,为“OR”后来的发展铺平了 道路。
江西财经大学——运筹学习题集06071015596
第二十章 Decision analysis在下面习题(或习题的一部分)的左边,我们插入符号“A ”(加载宏)表示可以使用以上列出的Excel 加载宏,符号“T ”表示计算后验概率的Excel 模板会有帮助。
几乎所有的习题都可以放不得使用电子表格规划求解。
在题号前带有星号的的问题书后至少给出了部分的答案。
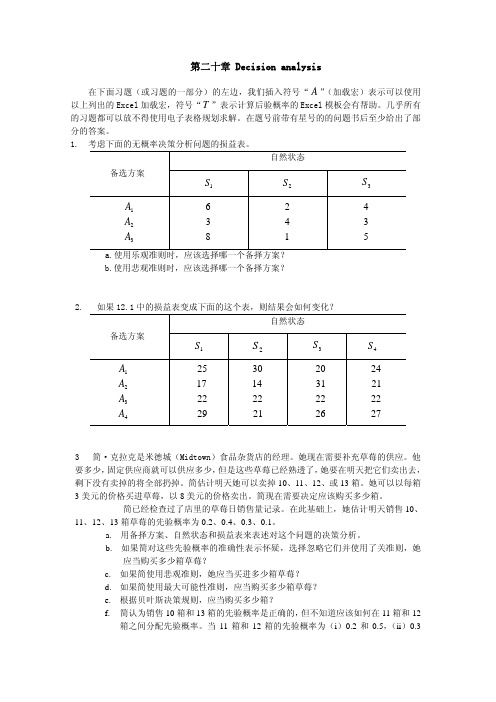
1. 考虑下面的无概率决策分析问题的损益表。
自然状态备选方案1S 2S 3S321A A A 836 142 534 a.使用乐观准则时,应该选择哪一个备择方案? b.使用悲观准则时,应该选择哪一个备择方案?2. 如果12.1中的损益表变成下面的这个表,则结果会如何变化?自然状态备选方案1S2S3S 4S4321A A A A29221725 21221430 26223120 272221243 简·克拉克是米德城(Midtown)食品杂货店的经理。
她现在需要补充草莓的供应。
他要多少,固定供应商就可以供应多少,但是这些草莓已经熟透了,她要在明天把它们卖出去,剩下没有卖掉的将全部扔掉。
简估计明天她可以卖掉10、11、12、或13箱。
她可以以每箱3美元的价格买进草莓,以8美元的价格卖出。
简现在需要决定应该购买多少箱。
简已经检查过了店里的草莓日销售量记录。
在此基础上,她估计明天销售10、11、12、13箱草莓的先验概率为0.2、0.4、0.3、0.1。
a. 用备择方案、自然状态和损益表来表述对这个问题的决策分析。
b. 如果简对这些先验概率的准确性表示怀疑,选择忽略它们并使用了关准则,她应当购买多少箱草莓?c. 如果简使用悲观准则,她应当买进多少箱草莓?d. 如果简使用最大可能性准则,应当购买多少箱草莓?e. 根据贝叶斯决策规则,应当购买多少箱?f. 简认为销售10箱和13箱的先验概率是正确的,但不知道应该如何在11箱和12箱之间分配先验概率。
当11箱和12箱的先验概率为(i )0.2和0.5,(ii )0.3和0.4,(iii )0.5和0.2时重新使用贝叶斯决策规则进行决策。
指派问题的EXCEL求解模板

Ke wo d sg me t rbe y r s Asin n o lm E cl ouintmp  ̄e p x e l t s o e l Ge ea ouintmpae Re u d n ou et g n rl lt s o e lt d n a t l mest n v i
me t ,b t s o v d t ed f r n s i me t r b e n e s i e e t o mu at ov ec n r d ci n e l e n s u o s le i e e t s l a h f a g n n o l m e d t u e ad f r n r l s l et o ta i t ,r ai p o f o h o z O e c mp tr t eg n r ou i nt mp ae o ov n ea sg me t r b e , r h s i me t r b e s l- Ht o u e h t e e a s l t h wi h l o e l ts r li gt s in n o l m f ea sg f s h p o t n n o lm o v p i gp o i e o dt n r n tn . n r vd s n i o s sa t c i f i o
As i n sg me tPr be Soli g E n o lm vn XCEL Te pa e m lt
Z e gHo g n hn nj u
(hn hi e vs nUnvrt A r utr,n ut dC mmec r c S ag a 0 35 Sag aT l io iesy gi l e Id sya o e i i c u r n re a h hnhi 0 3 ) B n 2
运筹学课后习题答案 熊伟(第二版)
v5
v6
v1
0
8.8
8.6
5.6
8
6
v2
0
8
5
13
4
v3
0
3
4.8
12
v4
0
7.8
9
v5
0
9
v6
0
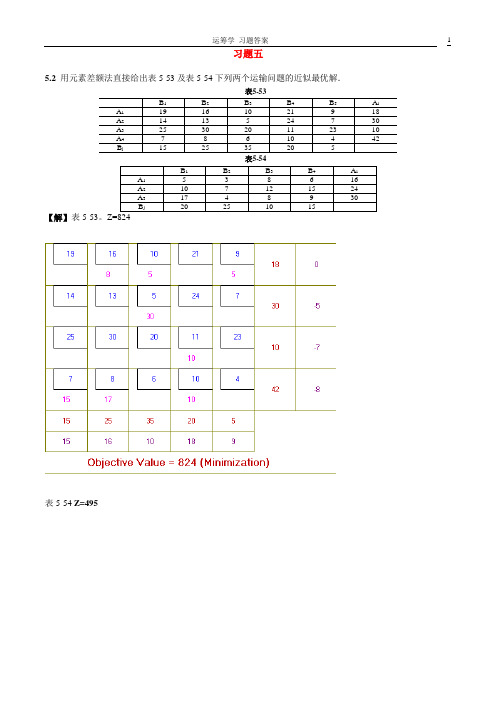
v1、v2、…、v6到各点的最优路线图分别为:
6.9设图6-43是某汽车公司的6个零配件加工厂,边上的数字为两点间的距离(km)。现要在6个工厂中选一个建装配车间。
(1)应选那个工厂使零配件的运输最方便。
距离表C
1
2
3
4
5
6
1
∞
8.8
9
5.6
8
6
2
8.8
∞
10
5
∞
4
3
9
10
∞
3
4.8
14
4
5.6
5
3
∞
12
∞
5
8
∞
4.8
12
∞
9
6
6
4
14
∞
9
∞
在C中行列分别减除对应行列中的最小数,得到距离表C1。
距离表C1
1
2
3
4
5
6
1
∞
3.2
3.4
0
0.6
0.4
2
2.8
∞
6
1
∞
0
3
4
7
∞
0
0
11
4
0.6
2
0
∞
7.2
A到H的最短路PAH={A,B,F,H},{A,C,F,H}最短路长22;A到I的最短路PAI={A,B,F,I},{A,C,F,I}最短路长21。
运筹学试题

兰州大学管理学院试卷运筹学(C)卷管理学院2008级用2010年1月18日用大班号:年级:姓名:学号:(学号后6位)说明:1.本试卷满分为100分。
考试时间为120分钟。
2.所有答案都必须答到试卷上,若试卷上写不完的答案可以另附纸张,但必须在试卷上注明。
直接写在试卷以外的纸张上的答案不计分。
3.答完卷后将考卷和草纸一起交上。
一、名词解释(每题2分,共10分)1. 初始基本可行解多个基本可行解中一个,一般情况下在求最大时取最小的基本可行解,求最小时取最大的基本可行解。
1. 线性规划问题的可行域在线性规划规划问题中,符合所有约束条件约束的解(可行解)的集合,在有解的情况下,它是一个多维的区域。
3.确定性决策在决策问题中,其自然状况完全决定的的决策。
4.剩余量在线性规划问题中,资源限制量大于资源实际利用量的部分。
4.松驰量对于一般规划问题约束条件中实际值小于常数项的部分。
二、单项选择题(从下列各题四个备选答案中选出一个正确答案,答案选错或未选者,该题不得分。
)(每题2分,共10分)3.用图解法求解下列问题:max Z=2x-3ys.t. -x+2y≤2x+2y≤6x-y≤3x+3y≥3x,y>=0其最优解为( C )A.(2,2) B.(4,1)C.(3,0) D.(2,5)4.若运输问题在有条件的总供应量大于总需要量时,( D )。
A.不能求解 B.不存在可行解C.虚设一个需求点再求解 D.虚设一个供应点再求解3.以下叙述中,不正确的是(C)A.树的点数为线数加1 B.树的任意两点间只有一条路C.图的点数大于线数D.任何不连通图都不是树4.在产销平衡运输问题的数学模型中,约束条件的关系是(A)。
A.= B.≤C.≥D.≤,=,≥都有1.线性规划的约束条件为2x1+x2+x3=52x1+2x2+x4=6x1, x2, x3, x4≥0则基本可行解为( A )A.(0, 2, 3, 2) B.(3, 1, -1, 0)C.(0, 0, 6, 5) D.(2, 0, 1, 4)三、判断题(你认为下列命题是否正确,对正确的打“√”;错误的打“×”。
新版石家庄铁道大学交通运输考研经验考研参考书考研真题

若在几十年前,我们的父辈们或许还可以告诉我们,未来从事怎样的职业,会有很好的发展,不至于失业。
而如今,他们大抵再也不能如此讲话了,只因这个世界变化的如此之快,在这变化面前,他们大概比我们还要慌乱,毕竟他们是从传统的时代走来的,这个更新换代如此迅速的世界只会让他们措手不及。
但是,虽然如此,他们却可以告诉我们一条永远也不会过时的生存法则,那就是掌握不断学习的能力。
所以,经过各种分析考量我终于选择了考研这条路,当然,这是只是,千万条路中的一条。
只不过我认为,这条路可操作性比较强,也更符合我们当下国情。
幸运的是,我如愿以偿,考到自己希望的学校。
一年的努力奋斗,让自己从此走上了截然不同的人生道路。
秋冬轮回,又是一年春风吹暖。
在看到录取名单之后,我终于按捺不住发了我一条朋友圈,庆祝考研胜利。
当时收到了很多平时不太联系的同学,发来的询问信息,这也促使我想将我的备考经验写下来,希望真的可以帮助接下来备考的学弟学妹们!因为想要讲的话太多,所以这篇文章会比较长,希望各位能够一点点看完。
或许会从我的经验教训中找到自己的方向以及方法来面对考研。
在结尾处会奉上我的学习资料供大家下载。
石家庄铁道大学交通运输的初试科目为:(101)思想政治理论(204)英语二(302)数学二(833)运筹学(842)(901)材料力学(908)交通运输工程系统分析参考书目:1.《材料力学》(1、2册)(第五版),孙训方等,高等教育出版社;2.《道路交通工程系统分析方法》(第二版),王炜,人民交通出版社2011。
首先简单介绍一下我的英语复习经验。
⑴单词:英语的单词基础一定要打好,如果单词过不了关,那你其他可以看懂吗??单词可以用木糖英语单词闪电版就够了。
也可以用app软件。
但是这样就会导致玩手机(如果你自制力超强),单词的话到考前也不能停止的。
我的单词并没有背好,导致英语后来只有60+,很难过…⑵阅读:阅读分数很高,所以一定要注重,可以听木糖英语的名师讲解,或者木糖英语的课程,阅读最重要的是自己有了自己的方法,有一个属于自己的做题方法可以节省很多时间,如果初次做题还没有什么思路,那就可以多看看真题里面的答案解析考研英语很难,和四六级是完全不同的!大家肯定都听说过,所以阅读暑假就可以开始做了,真题反复摸索,自己安排好时间。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
目录1 绪论 (4)1.1 研究的目的 (4)1.2 研究的主要方法和思路 (4)2 线性规划问题(利润最大化) (4)2.1 问题的提出 (4)2.2 模型的建立 (5)2.2.1 决策变量的设定 (5)2.2.2 目标函数的建立 (5)2.2.3 约束条件的确定 (6)2.2.4 模型的建立 (7)2.3 模型的求解及解的分析 (7)2.3.1 在Excel电子表格中建立线性规划模型 (7)2.3.2 用Excel“规划求解”功能求解线性规划问题 (8)2.3.3 规划模型运算结果的详细解释 (11)3 动态规划问题(资源分配问题) ....................................................... 错误!未定义书签。
3.1问题的提出............................................................................... 错误!未定义书签。
3.2 模型的建立.............................................................................. 错误!未定义书签。
3.2.1 决策变量的设定 ............................................................ 错误!未定义书签。
3.2.2 目标函数的建立 ............................................................ 错误!未定义书签。
3.2.3 约束条件的确定 ............................................................ 错误!未定义书签。
3.2.4 模型的建立.................................................................... 错误!未定义书签。
3.3 模型的求解及解的分析............................................................ 错误!未定义书签。
3.3.1 在Excel电子表格中建立线性规划模型........................ 错误!未定义书签。
3.3.2 用Excel“规划求解”功能求解线性规划问题................... 错误!未定义书签。
4 指派问题............................................................................................ 错误!未定义书签。
4.1 问题的提出.............................................................................. 错误!未定义书签。
4.2 例3问题i的建模和求解......................................................... 错误!未定义书签。
4.2.1 模型的建立.................................................................... 错误!未定义书签。
4.2.2 模型的求解及解的分析 ................................................. 错误!未定义书签。
4.3 例3问题ⅱ的建模和求解.......................................................... 错误!未定义书签。
4.4 例3问题ⅲ的建模和求解......................................................... 错误!未定义书签。
4.5例3问题ⅳ的建模和求解.......................................................... 错误!未定义书签。
4.6 例3问题ⅴ的建模和求解.......................................................... 错误!未定义书签。
5 总结 ................................................................................................... 错误!未定义书签。
1绪论1.1 研究的目的运筹学的应用与计算机软件的开发紧密相连,规模稍大的运筹学模型是无法用手工计算来求解的。
利用计算机求解运筹学问题,不但速度快,而且精确度高,有利于生活中实际问题的处理,因此学习利用计算机求解运筹学问题十分必要。
1.2 研究的主要方法和思路国内目前常用的计算机软件主要有LINDO, LINGO, WinQSB, MATLAB和EXCEL-Risk Solver Platform等求解器。
本文以运用Excel 建模和求解运筹学问题为例,使用Excel“规划求解”功能求解问题。
Microsoft Office Excel 的“规划求解”工具取自德克萨斯大学奥斯汀分校的Leon Lasdon 和克里夫兰州立大学的Alan Waren 共同开发的Generalized Reduced Gradient (GRG2) 非线性最优化代码。
线性和整数规划问题取自Frontline Systems, Inc. 公司的John Watson 和Daniel Fylstra 提供的有界变量单纯形法和分支边界法。
本文以三个常见的运筹学问题来进一步了解使用Excel建模和求解的具体步骤,这三个问题分别是线性规划问题(利润最大化问题)、动态规划问题(资源分配问题)和指派问题。
2 线性规划问题(利润最大化)2.1 问题的提出例1 力浦公司的市场利润最大化问题力浦公司是一家生产外墙涂料的建材公司。
目前生产甲、乙两种规格产品,这两种产品在市场上的单位利润分别是4万元和5万元。
甲、乙产品均需要同时消耗A、B、C三种化工材料,生产1个单位的甲产品需要消耗三种材料的情况是:1单位的A材料、2单位的B材料和1单位的C 材料,而生产1单位的乙产品则需要1单位的A材料、1单位的B材料和3单位的C材料。
当前市场上的甲、乙产品供不应求,但是在每个生产周期(假设一年)内,公司的A、B、C三种原材料资源的储备分别是45单位、80单位和90单位,年终剩余的资源必须无偿调回,而且近期也没有筹集到额外资源的渠道。
面对这种局面,力浦公司如何安排生产计划,以获得最大的市场利润?2.2 模型的建立表1-1 两种产品的有关数据2.2.1 决策变量的设定本问题的决策变量是甲、乙两种产品的产量。
可设:x1为甲产品的产量(单位);x2为乙产品的产量(单位)。
2.2.2 目标函数的建立本问题的目标是市场利润最大。
由于这两种产品在市场上的单位利润分别是4万元和5万元,而甲、乙产品的产量分别为x1和x2,所以市场利润为:z=4x1+5x2(万元)。
2.2.3 约束条件的确定本问题的约束条件共有四个。
第一个约束是原材料A的资源储备限制。
由于生产一单位的甲、乙产品都需要1单位的A材料,所以生产甲、乙产品所需的A材料为x1+x2。
由题意,A材料的资源储备为45单位。
由此可得第一个约束:X1+x2≤45第二个约束是原材料B的资源储备限制。
由于生产一单位的甲产品需要2单位的B材料,而生产一单位的乙产品则需要1单位的B材料,所以生产甲、乙产品所需的B材料为2x1+x2。
由题意,B材料的资源储备为80单位。
由此可得第二个约束:2X1+x2≤80第三个约束是原材料C的资源储备限制。
由于生产一单位的甲产品需要1单位的C材料,而生产一单位的乙产品则需要3单位的C材料,所以生产甲、乙产品所需的C材料为x1+3x2。
由题意,C材料的资源储备为90单位。
由此可得第三个约束:X1+3x2≤90第四个约束是决策变量的非负约束。
由于产量不可能为负值。
所以第四个约束为:X1≥0, x2≥02.2.4 模型的建立Maxz=4x1+5x2X1+x2≤45s.t2X1+x2≤80X1+3x2≤90X1≥0, x2≥02.3 模型的求解及解的分析Excel拥有大量的用户群,其“规划求解”功能强大,可以实现对有多个决策变量的线性规划问题的求解,回避了用线性规划专用软件求解时对操作者的专业要求,同时也克服了笔算的缺点,其操作方法简单、方便、快捷,大大提高了计算的效率和准确性。
2.3.1 在Excel电子表格中建立线性规划模型下图1显示了把表1的数据输入到电子表格的例1 (E和F两列是为输入公式和符号预留的)。
图1-1 把表1输入到数据单元格后的例1的初始表格图1-2 例1完整的电子表格模型变量单元格只需指定,无须输入,且默认初始值是“0”。
图1-3 在Excel界面的编辑栏输入公式2.3.2 用Excel“规划求解”功能求解线性规划问题2.3.2.1 用Excel中的“规划求解”功能求解例1的步骤如下:第一步:在“工具”菜单中,选择“规划求解”选项,弹出“规划求解参数”对话框,如下图1-4所示。
图1-4 “规划求解参数”对话框第二步:在对话框中输入参数所在的单元格地址。
(1)在“设置目标单元格”一栏中,输入表示目标函数值的单元格地址“G12”,并在“等于”一栏中,选择“最大值”单选按钮;(2)在“可变单元格”一栏中,输入决策变量的单元格地址“C12:D12”;(3)在“约束”一栏中,通过单击“添加”按钮,在弹出的“添加”按钮,在弹出的“添加约束”对话框中添加约束条件,如下图5所示。
图1-5 “添加约束”对话框第三步:单击“选项”按钮,在弹出的“规划求解选项”对话框中,可以设定规划求解运算中的有关参数。
本题需选中“采用线性模型”和“假定非负”复选框,其他参数不变,如下图6所示。
图1-6 “规划求解选项”对话框第四步:单击右上角的“求解”按钮,开始进行规划求解。
图1-7 “规划求解参数”对话框22.3.2.2 求解结果这时,规划求解用最优值代替了可变单元格中的初始试验解,“规划求解”最终结果如下图8所示。
力浦公司在最大限度利用现有资源的前提下,可以获得最大的市场利润是202.5万元,甲、乙两种产品均要生产22.5个单位,三种资源的使用情况分别是:材料A使用了45单位,消耗已尽;材料B使用了67.5单位,剩余12.5单位;材料C使用了90单位,消耗已尽。
