三角形的外接圆与内切圆
三角形的内切圆和外接圆
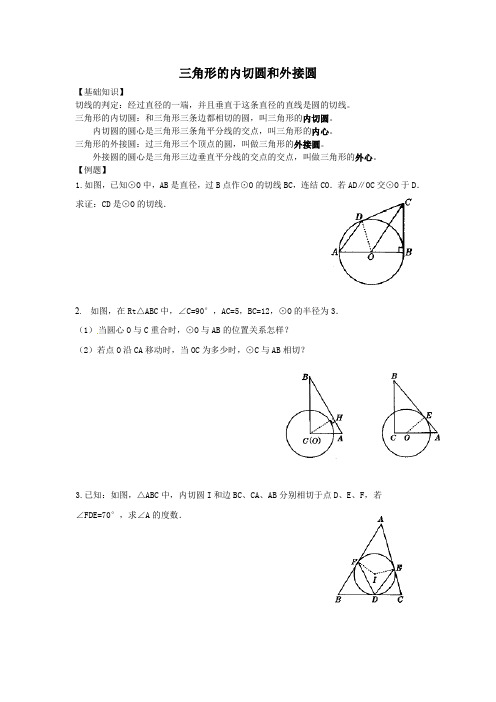
三角形的内切圆和外接圆【基础知识】切线的判定:经过直径的一端,并且垂直于这条直径的直线是圆的切线。
三角形的内切圆:和三角形三条边都相切的圆,叫三角形的内切圆。
内切圆的圆心是三角形三条角平分线的交点,叫三角形的内心。
三角形的外接圆:过三角形三个顶点的圆,叫做三角形的外接圆。
外接圆的圆心是三角形三边垂直平分线的交点的交点,叫做三角形的外心。
【例题】1.如图,已知⊙O中,AB是直径,过B点作⊙O的切线BC,连结CO.若AD∥OC交⊙O于D.求证:CD是⊙O的切线.2.如图,在Rt△ABC中,∠C=90°,AC=5,BC=12,⊙O的半径为3.(1)当圆心O与C重合时,⊙O与AB的位置关系怎样?(2)若点O沿CA移动时,当OC为多少时,⊙C与AB相切?3.已知:如图,△ABC中,内切圆I和边BC、CA、AB分别相切于点D、E、F,若∠FDE=70°,求∠A的度数.4. 如图,正三角形的内切圆半径为1,那么这个正三角形的边长为( )A .2B .3 CD.5. △ABC 中,AB =AC =5,BC =6,求△ABC 的内切圆的半径长。
6. 任意△ABC 中内切圆I 和边BC 、CA 、AB 分别相切于点D 、E 、F. 求证:△DEF 是锐角三角形。
7. 如图,已知ABC ∆内接于⊙O ,AE 切⊙O 于点A ,BC ∥AE ,求证:ABC ∆是等腰三角形.·ABCOEP【巩固练习】1.一个三角形的内心,外心都在三角形内,则这个三角形一定是( ) A 、直角三角形 B 、锐角三角形 C 、钝角三角形 D 、等腰三角形2.如右图,I 是ABC ∆的内心,则下列式子正确的是( ) A 、∠BIC=︒180-2∠A B 、∠BIC=2∠A C 、∠BIC=︒90+∠A/2 D 、∠BIC=︒90-∠A/23.ABC ∆外切于⊙O ,E 、F 、G 分别是⊙O 与各边的切点,则EFG ∆的外心是ABC ∆的 。
三角形的外接圆与内切圆的性质

三角形的外接圆与内切圆的性质在数学几何学中,三角形是一个基本的几何形状。
而三角形的外接圆和内切圆是与三角形紧密相关的两个圆形。
本文将描述三角形的外接圆和内切圆的性质,并探讨它们的关系。
一、三角形的外接圆(Circumcircle)三角形的外接圆是能够完全通过三个顶点的圆。
这意味着三角形的每个顶点都位于圆上。
外接圆的圆心被称为三角形的外心(Circumcenter)。
在外接圆中,三角形的三条边都是圆的切线。
下面是三角形外接圆的性质:1. 外接圆的半径等于三角形任意一边的中线长。
2. 对于直角三角形,外接圆的直径等于斜边的长度。
3. 外接圆的周长等于三角形的周长。
二、三角形的内切圆(Incircle)三角形的内切圆是与三角形的三条边相切的圆。
内切圆的圆心被称为三角形的内心(Incenter)。
在内切圆中,三角形的每条边都是圆的切线。
下面是三角形内切圆的性质:1. 内切圆的半径等于三角形的内角平分线的长度,也等于三角形三个角的内切点到相应边的距离。
2. 内切圆的圆心到三边距离的和等于内切圆的半径。
3. 内切圆的半径与三角形的面积成正比。
面积越大,半径越大。
三、外接圆与内切圆的关系在任何三角形中,外接圆的圆心、内心以及重心(三条中线的交点)三点共线。
这条直线称为欧拉线(Euler Line)。
此外,外接圆和内切圆的半径之间存在着一个特殊的关系。
设R为外接圆的半径,r为内切圆的半径,s为三角形的半周长(即三边之和的一半),则有如下关系式:R = (abc)/(4∆)r = ∆/s其中,a、b、c为三角形的三边长度,∆为三角形的面积。
这两个关系式表明,外接圆的半径与三角形的边长成正比,而内切圆的半径与三角形的面积成正比。
总结:三角形的外接圆与内切圆是与三角形紧密相关的圆形。
外接圆通过三角形的三个顶点,内切圆与三角形的三条边相切。
外接圆和内切圆有着许多重要的性质,包括半径与三角形边长、面积的关系等。
同时,外接圆的圆心、内心和重心三点共线,并且外接圆和内切圆的半径之间存在着特殊的关系。
三角形外接圆与内切圆的关系

三角形外接圆与内切圆的关系在数学中,三角形是一种基础的几何形状,而外接圆和内切圆是与三角形紧密相关的几何概念。
本文将探讨三角形外接圆与内切圆的关系,并介绍它们的性质和特点。
一、外接圆外接圆是指可以完全包围三角形的圆,也就是通过三角形三个顶点的圆。
设三角形的三个顶点分别为A、B、C,连接三个顶点形成的边AB、BC、CA,外接圆的圆心为O,半径为R。
根据外接圆的性质可以得出以下结论:1. 外接圆的半径是三角形三边的中线之积的一半。
即 R = (AB × BC × CA) / (4×S),其中S为三角形的面积。
2. 外接圆的圆心是三角形三个顶点的垂直平分线的交点。
3. 三角形的三条边与圆的切点构成的割线长度相等。
二、内切圆内切圆是指可以切刚好与三角形的三边相切的圆。
设三角形的三个顶点分别为A、B、C,连接三个顶点形成的边AB、BC、CA,内切圆的圆心为I,半径为r。
根据内切圆的性质可以得出以下结论:1. 内切圆的半径可以通过三角形的三条边之和与面积的比值计算得出。
即 r = 2×S / (AB + BC + CA),其中S为三角形的面积。
2. 内切圆的圆心是三角形三个角的角平分线的交点。
3. 内切圆的切点是三角形三条边的垂直平分线的交点。
三、外接圆与内切圆的关系通过观察可以发现,三角形的外接圆和内切圆具有一定的关系。
根据欧拉定理,三角形的外接圆和内切圆的圆心,以及三角形的垂心、重心、外心四点共线,并且这条直线称为欧拉线。
具体而言,外接圆和内切圆的圆心与三角形的垂心、重心、外心四点共线。
垂心是指三角形三个顶点所形成的垂直平分线的交点,重心是指三角形三个顶点与它们所对边中点形成的线段的交点,外心是指三角形三个垂直平分线的交点。
此外,外接圆的半径大于内切圆的半径,且内切圆的圆心位于外接圆的圆心与三角形各顶点之间。
四、应用领域三角形外接圆和内切圆的关系在各个学科和领域中都有广泛的应用。
三角形的外接圆与内切圆的关系

三角形的外接圆与内切圆的关系三角形是几何学中最基本的图形之一,它由三条边和三个内角组成。
而在三角形中,外接圆和内切圆是两个与之密切相关的圆形。
外接圆,正如其名所示,是指可以完整地包围三角形的圆。
它的圆心位于三角形的外部,且圆心到三角形的每个顶点距离相等,这个距离叫做外接圆的半径。
那么,三角形的外接圆与内切圆之间存在着怎样的关系呢?内切圆是指可以刚好与三角形的三条边相切的圆形。
内切圆的圆心位于三角形的内部,且圆心到三角形的每条边的距离相等,这个距离叫做内切圆的半径。
根据三角形的性质,三角形的三条角平分线交于一个点,而这个点恰好是内切圆的圆心。
由此可见,三角形的内切圆与角平分线有紧密的关系。
除此之外,三角形的外接圆和内切圆还存在着一些相互关系。
首先,两个圆的圆心和三角形的顶点是共线的,也就是说它们在同一条直线上。
此外,三角形的任意一条边都是两个圆的切线,也可以说两个圆与三角形的每条边相切。
这一属性对于解决一些与圆有关的几何问题非常有用。
进一步地,我们还可以通过三角形的边长和角度来确定外接圆和内切圆的半径。
对于外接圆而言,其半径等于三角形的边长之积除以四倍三角形的面积。
而内切圆的半径则等于三角形的面积除以半周长(半周长等于三边之和的一半)。
利用外接圆和内切圆的性质,我们可以解决一些实际问题,比如计算三角形的面积、判断三角形的类型等。
在工程学、建筑学以及地理学等领域,对三角形的外接圆和内切圆的关系有着广泛的应用。
综上所述,三角形的外接圆与内切圆存在着紧密的关系。
两个圆的圆心和三角形的顶点共线,圆与三角形的顶点和边存在相切关系。
通过三角形的边长和角度,我们可以推导出外接圆和内切圆的半径。
这些性质不仅仅是几何学的基础知识,还在实际中有着重要的应用和意义。
几何中的三角形内切圆与外接圆

几何中的三角形内切圆与外接圆在几何中的三角形中,内切圆和外接圆是两个重要的概念。
本文将详细介绍三角形内切圆和外接圆的定义、性质以及相关推论,进一步探讨它们在几何中的应用。
一、三角形内切圆首先,我们来定义三角形内切圆。
在一个三角形中,如果存在一个圆,这个圆与三角形的三条边都有且仅有一个公共点,那么这个圆就是三角形的内切圆。
三角形的内切圆有以下性质:1. 内切圆的圆心与三角形的三条角平分线的交点重合。
根据这个性质,我们可以很容易地找到内切圆的圆心。
2. 内切圆的半径等于三角形三边长度之和的一半再除以周长。
3. 三角形三个顶点与内切圆的切点构成的切线互相垂直。
二、三角形外接圆接下来,我们来定义三角形外接圆。
在一个三角形中,如果存在一个圆,这个圆与三角形的三条边的延长线相交于圆上,那么这个圆就是三角形的外接圆。
三角形的外接圆有以下性质:1. 外接圆的圆心是三角形三个顶点的垂直平分线的交点。
2. 外接圆的半径等于三角形任意一条边的长度的一半再除以正弦定理中的正弦值。
3. 三角形的三条边分别是外接圆与相应角的切线。
三、应用与推论三角形内切圆和外接圆在几何中有广泛的应用。
它们不仅帮助我们理解和解决一些几何问题,还在实际生活中有很多实际应用。
1. 运用内切圆或外接圆,我们可以求解三角形的面积。
通过计算内切圆的半径和外接圆的半径,结合数学公式,可以得到三角形的面积。
2. 内切圆和外接圆还可以帮助我们进行几何证明。
在证明过程中,利用内切圆和外接圆的性质,可以简化证明的步骤,提高证明的效率。
3. 三角形内切圆和外接圆的概念还在工程和建筑设计中有很多应用。
例如,在建筑设计中,设计师可以利用内切圆和外接圆的性质来确定柱子和梁的位置和角度。
通过对三角形内切圆和外接圆的了解,我们可以进一步探索几何学中的更多知识和应用。
这些概念和性质不仅仅是理论上的,它们在实际生活中也有着很多实际应用和意义。
综上所述,三角形内切圆和外接圆是几何中重要的概念和性质。
三角形的外接圆和内切圆

三角形的外接圆和内切圆三角形是几何学中最基本的图形之一,它有许多引人注目的性质和特点。
其中,外接圆和内切圆是三角形中常见的两种圆,它们与三角形的关系引起了广泛的研究和应用。
一、外接圆外接圆是一个与三角形的三条边都相切的圆。
对于任意给定的三角形,它都存在一个唯一的外接圆。
外接圆有许多特点,其中一些被广泛应用于几何学和其它相关领域。
首先,外接圆的圆心是三角形三边的垂直平分线的交点。
也就是说,如果我们将三角形的三条边分别延长,然后找到它们垂直平分线的交点,这个交点就是外接圆的圆心。
其次,外接圆的半径等于三角形的边长的一半除以正弦值的倒数。
这个性质被称为外接圆定理,可以用来计算外接圆的半径。
再次,外接圆的直径等于三角形的任一边的长度除以正弦值。
这个性质被称为外接圆直径定理,也是计算外接圆直径的一个重要公式。
此外,外接圆对于三角形的角度关系也有一定的影响。
例如,对于直角三角形来说,外接圆的直径等于斜边的长度,这个性质被广泛应用于解决直角三角形相关的问题。
二、内切圆内切圆是一个与三角形的三条边都相切的圆。
与外接圆类似,任意给定的三角形都存在一个唯一的内切圆。
内切圆同样具有一些重要的性质和应用。
首先,内切圆的圆心是三角形的内角平分线的交点。
也就是说,如果我们将三角形的三个内角的平分线延长,这三条延长线的交点就是内切圆的圆心。
其次,内切圆的半径可以通过三角形的面积和半周长来计算。
内切圆半径公式为:r = Δ / s,其中Δ 表示三角形的面积,s 表示三角形的半周长。
再次,内切圆与三角形的边长和内角关系也有重要的性质。
例如,内切圆的半径等于三角形任意一条边的长度乘以正切值的倒数。
最后,内切圆还有一个重要的性质,即它与三角形的三条边的交点构成三角形的角平分线。
这个性质有助于解决一些与角平分线相关的问题。
结论三角形的外接圆和内切圆是在几何学中经常遇到的两种圆形。
它们分别与三角形的三个顶点或三个内角相切,具有许多有趣的性质和应用。
三角形的外接圆和内切圆的性质与计算

三角形的外接圆和内切圆的性质与计算三角形是几何学中最基本的图形之一,而三角形的外接圆和内切圆又是三角形的重要性质之一。
本文将详细探讨三角形的外接圆和内切圆的性质,并介绍如何计算它们。
【一、三角形的外接圆】外接圆是指可以与三角形的三个顶点相切的圆。
具体而言,三角形的外接圆满足以下性质:1. 外接圆的圆心位于三角形的垂直平分线的交点。
即三角形的三条垂直平分线的交点是外接圆的圆心。
2. 外接圆的半径等于三角形三边的中线的一半。
其中,中线是连接三角形的一个顶点和对立边中点的线段。
3. 外接圆的直径等于三角形的外角平分线的长度。
在计算外接圆时,我们可以利用以下公式:1. 外接圆的圆心坐标可以通过三角形的顶点坐标计算得出。
假设三角形的三个顶点坐标分别为A(x1,y1)、B(x2,y2)和C(x3,y3)。
外接圆的圆心坐标为:圆心横坐标 = (x1 + x2 + x3) / 3圆心纵坐标 = (y1 + y2 + y3) / 32. 外接圆的半径可以通过三角形的顶点坐标计算得出。
假设外接圆的半径为R。
则R的长度等于三角形任意一条边的一半,可以使用以下公式计算:R = (a + b + c) / (4 * S)其中,a、b、c分别为三角形的三条边长,S为三角形的面积,可以使用海伦公式或其他计算方法得出。
【二、三角形的内切圆】内切圆是指可以与三角形的三条边相切的圆。
具体而言,三角形的内切圆满足以下性质:1. 内切圆的圆心位于三角形的内角平分线的交点。
即三角形的三条内角平分线的交点是内切圆的圆心。
2. 内切圆的半径等于三角形的面积除以半周长。
其中,半周长等于三角形的周长除以2。
在计算内切圆时,我们可以利用以下公式:1. 内切圆的圆心坐标可以通过三角形的顶点坐标计算得出。
假设三角形的三个顶点坐标分别为A(x1,y1)、B(x2,y2)和C(x3,y3)。
内切圆的圆心坐标为:圆心横坐标 = (a * x1 + b * x2 + c * x3) / (a + b + c)圆心纵坐标 = (a * y1 + b * y2 + c * y3) / (a + b + c)其中,a、b、c分别为三角形的三条边长。
三角形内切圆与外接圆的性质

三角形内切圆与外接圆的性质在几何学中,三角形是最为基本和重要的图形之一。
三角形内切圆和外接圆是与三角形密切相关的圆。
本文将探讨三角形内切圆和外接圆的性质,包括内切圆和外接圆的定义、性质及其在数学和实际问题中的应用。
一、内切圆的性质内切圆是指与三角形的三条边都相切于一点的圆。
它有以下几个性质:1. 内切圆的圆心与三角形的内心重合。
内心是三角形内部的一个特殊点,它是三角形三条内角平分线的交点。
由于内切圆与三角形的三边都相切,所以内切圆的圆心一定与三角形的内心重合。
2. 内切圆的半径等于三角形三条边的内切线的和。
内切线是指从三角形的顶点到内切圆的切点所连的线段。
内切圆的半径等于三条内切线的和,即r = s - a + s - b + s - c,其中r是内切圆的半径,a、b、c分别是三角形的三边长,s是三角形半周长。
3. 内切圆与三角形的三条边的切点连成的线段垂直于各边。
这是内切圆性质的一个重要结论,可由内切圆的切线与半径的性质得出。
二、外接圆的性质外接圆是指能够同时与三角形的三个顶点相切的圆。
它有以下几个性质:1. 外接圆的圆心在三角形的外心上。
外心是三角形外接圆的圆心,它是三角形三条外角平分线的交点。
因为外接圆与三角形的三个顶点相切,所以外接圆的圆心一定在三角形的外心上。
2. 外接圆的半径等于三角形三边长的乘积的二倍除以三角形的面积。
外接圆半径R的计算公式为R = (abc) / 4A,其中a、b、c是三角形的三边长,A是三角形的面积。
3. 三角形的三个外角等于外接圆圆心对应角的两倍。
外接圆通过三角形的三个顶点,相应角即为三角形的外角,该外角等于外接圆圆心对应角的两倍。
三、应用和意义三角形内切圆和外接圆在数学和实际问题中具有广泛的应用。
其中,内切圆和外接圆的性质可以用于解决与三角形相关的几何问题,如求解三角形的面积、周长等。
此外,内切圆和外接圆还与其他数学分支有着密切的关系。
比如,在代数学中,可以通过求解三角形内切圆和外接圆的性质,解决关于三角函数的各种问题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三角形的外接圆与内切圆
三角形是几何学中最基本的图形之一,与之相关的几何定理也非常多。
其中,三角形的外接圆和内切圆是两个重要的概念。
本文将探讨
这两个圆的性质及其与三角形的关系。
一、三角形的外接圆
外接圆,即能够完全包围三角形的圆,是指与三角形三边上的各个
顶点都相切的圆。
首先,我们来看一下外接圆的性质。
1. 外接圆的圆心:
三角形的外接圆的圆心恰好位于三角形的三条边的垂直平分线的交
点处,称为"外心"。
2. 外接圆的半径:
外接圆的半径等于三角形边长的一半的倒数,即 R = (a*b*c) / (4*Δ),其中 a、b、c分别为三角形的三边长,Δ为三角形的面积。
3. 外接圆的特点:
外接圆与三角形的三条边互相相切,因此,任意一条边的中点如果
与另外两条边的中点相连,则这条线段恰好是外接圆的直径。
二、三角形的内切圆
内切圆,顾名思义,是能够与三角形内接的圆,也就是恰好与三角
形的三条边相切的圆。
接下来,我们来了解一下内切圆的性质。
1. 内切圆的圆心:
三角形的内切圆的圆心位于三角形三条边的角平分线的交点处,称为"内心"。
2. 内切圆的半径:
内切圆的半径等于三角形面积与半周长(s = (a+b+c)/2)之比(r = Δ / s)。
3. 内切圆的特点:
内切圆与三角形的三条边互相相切,而且三角形的三条边的切点恰好是内切圆的圆心。
三、外接圆与内切圆的关系
外接圆和内切圆是紧密相关的,它们之间存在一些有趣的关系。
1. 欧拉定理:
三角形的外心、内心和重心三点共线,而且重心将外心和内心分成两个倍长的线段。
2. 内接圆与外接圆的半径关系:
内切圆与外接圆的半径满足关系式:R = 2r,其中 R为外接圆的半径,r为内切圆的半径。
3. 内接圆与外接圆的位置关系:
无论三角形的形状如何变化,内切圆始终位于外接圆的内部。
四、应用举例
外接圆和内切圆的概念在实际应用中也有很多重要的应用。
例如,在工程建设中,外接圆和内切圆的关系可以用来设计合适的桥梁、隧道和弧形道路的曲线。
在航空航天领域,外接圆和内切圆的概念可以用来确定航线和飞行轨道的最佳路径。
总结:
三角形的外接圆和内切圆具有重要的几何性质和应用价值。
外接圆是能够完全包围三角形的圆,其圆心位于三角形三边的垂直平分线的交点处。
内切圆是能够与三角形内接的圆,其圆心位于三角形三边的角平分线的交点处。
外接圆和内切圆之间存在一些有趣的关系,同时在工程和航空领域中也有着广泛的应用。
理解和掌握外接圆和内切圆的性质对于深入研究和应用三角形的几何定理具有重要意义。
