LINGO练习题-1及答案 - 360文档中心

lingo1

3、运输方案要在满足物质需求和装载条件下安排从各供应点到各需求点的运量和路线，使其运输费用最低。 4、生产计划要按产品工艺流程和顾客需求，制定原料、零件、部件等订购、投产的日程和数量，尽量降低成本使利润最高。
解决方案：
1、依赖过去的经验判断面临的问题。 2、做大量的实验反复比较。 3.数学建模。

优化模型的三要素：
1、决策变量
2、目标函数 3、约束条件
优化模型
概念：在工程技术、经济管理、科学研究和日常生活等诸多领域中，人们经常遇到的一类决策问题：在一系列客观或主观限制条件下，寻求使所关注的某个或多个指标达到最大（或最小）的决策。
1、结构设计要在满足强度要求的条件下选择材料的尺寸，使其总重量最轻。
2、资源分配在有限资源约束下制定各用户的分配数量，使资源产生的总效益最大。

lingo模型参考习题

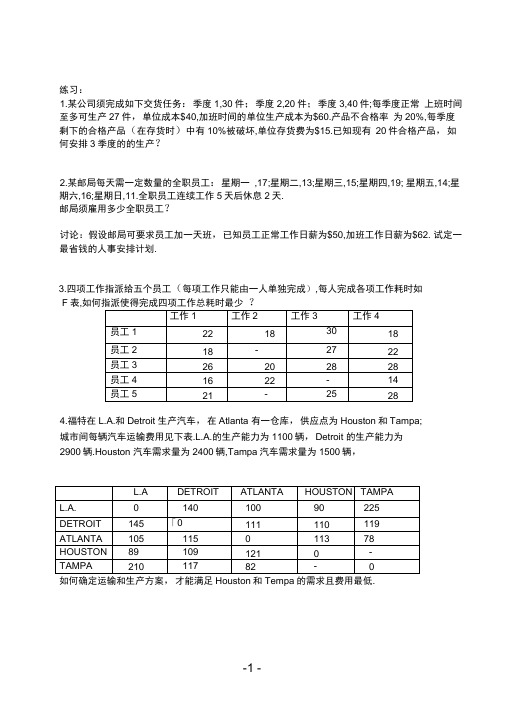
练习：1.某公司须完成如下交货任务：季度1,30件；季度2,20件；季度3,40件;每季度正常上班时间至多可生产27件，单位成本$40,加班时间的单位生产成本为$60.产品不合格率为20%,每季度剩下的合格产品（在存货时）中有10%被破坏,单位存货费为$15.已知现有20件合格产品，如何安排3季度的的生产？2.某邮局每天需一定数量的全职员工：星期一,17;星期二,13;星期三,15;星期四,19; 星期五,14;星期六,16;星期日,11.全职员工连续工作5天后休息2天.邮局须雇用多少全职员工？讨论：假设邮局可要求员工加一天班，已知员工正常工作日薪为$50,加班工作日薪为$62. 试定一最省钱的人事安排计划.3.四项工作指派给五个员工（每项工作只能由一人单独完成）,每人完成各项工作耗时如F表,如何指派使得完成四项工作总耗时最少4.福特在L.A.和Detroit 生产汽车，在Atlanta 有一仓库，供应点为Houston和Tampa;城市间每辆汽车运输费用见下表.L.A.的生产能力为1100辆，Detroit 的生产能力为2900辆.Houston 汽车需求量为2400辆,Tampa汽车需求量为1500辆，如何确定运输和生产方案，才能满足Houston和Tempa的需求且费用最低.5.设有三个化肥厂供应四个地区的农用化肥.假定等量的化肥在这些地区使用效果相同.各化肥厂年产量，各地区年需要量及从各化肥厂到各地区运送单位化肥的运价（万元/6」ndianapolis 航空公司计划每天从Indianapolis 飞6个航班,计划目的地为：New试帮该公司确定航线和相应的航班次数7.某种机器可在高低两种不同的负荷下进行生产，设机器在高负荷下生产的年产量函数为:y=8x,（x:投入生产的机器台数）,年完好率为0.7;机器在低负荷下生产的年产量函数为:y=5x,（x:投入生产的机器台数）,年完好率为0.9;假定开始生产时完好的机器数量为1000台，试问每年如何安排机器在高，低负荷下的生产，使在五年内生产的产品总产量最咼.讨论：如果5年末完好机器数必为500台,又将如何？8.某工厂要对一种产品制定今后四个时期的生产计划，据估计在今后四个时期内，市场对于该产品的需求量如表所示，假定该厂生产每批产品的固定成本为3（千元）,若不生产为0;每单位产品成本为1（千元）;每个时期生产能力所允许的最大生产批量为不超过6个单位;每个时期末未售出的产品，每单位需存储费0.5（千元）.还假定在第一个时期的初始储存量为0,第四个时期之末的库存量也为0.试问如何安排各个时期的生产与库存，才能在满足市场需要的条件下，使总成本最小.9. Bran east 航空公司须为每天飞行于New York和Chicago的航班配备空姐。

Lingo精选题目及参考答案

Lingo 精选题目及答案答题要求：将Lingo 程序复制到Word 文档中，并且附上最终结果。

1、简单线性规划求解（目标函数）2134maxx x z += s.t.（约束条件）⎪⎪⎩⎪⎪⎨⎧≥≤≤+≤+0,781022122121x x x x x x x2、整数规划求解219040Max x x z +=⎪⎩⎪⎨⎧≥≤+≤+0,702075679212121x x x x x x 3、0-1规划求解Max 432215.18.04.0x x x x f +++=10106234321≤+++x x x x10,,,4321或=x x x x4、非线性规划求解||4||3||2||min 4321x x x x z +++=s.t. ⎪⎪⎩⎪⎪⎨⎧-=+--=-+-=+--2132130432143214321x x x x x x x x x x x x5、集合综合应用产生一个集合5052--=x x y ，（10,...,2,1=x ），求y 前6个数的和S 1，后6个数的和S 2，第2~8个数中的最小值S 3，最大值S 4。

6、综合题要求列出具体的目标函数和约束条件，然后附上Lingo 程序和最终结果。

6.1 指派问题有四个工人，要指派他们分别完成4项工作，每人做各项工作所消耗的时间如下表：问指派哪个人去完成哪项工作，可使总的消耗时间为最小？6.2 分配问题某两个煤厂A1，A2每月进煤数量分别为60t和100t，联合供应3个居民区B1,B2,B3。

3个居民区每月对煤的需求量依次分别为50t，70t，40t，煤厂A1离3个居民区B1,B2,B3的距离依次分别为10km,5km,6km,煤厂A2离3个居民区B1,B2,B3的距离分别为4km,8km,12km。

问如何分配供煤量使得运输量（即t·km）达到最小？1、model:max=4*x1+3*x2;2*x1+x2<10;x1+x2<8;x2<7;end2、model:max=40*x1+90*x2;9*x1+7*x2<56;7*x1+20*x2<70;@gin(x1);@gin(x2);end3、model:max=x1^2+0.4*x2+0.8*x3+1.5*x4;3*x1+2*x2+6*x3+10*x4<10;@bin(x1); @bin(x2);@bin(x3); @bin(x4);end4、model:max=@abs(x1)+2*@abs(x2)+3*@abs(x3)+4*@abs(x4);x1-x2-x3+x4=0;x1-x2+x3-3*x4=1;x1-x2-2*x3+3*x4=-1/2;end5、model:sets:jihe/1..10/:y;ss/1..4/:S;endsets!由于y和s中部分有负数，所以要先去掉这个约束;@for(jihe:@free(y));@for(ss(i):@free(S));!产生元素;@for (jihe(x):y(x)=x^2-5*x-50); S(1)=@sum (jihe(i)|i#le#6:y(i)); S(2)=@sum (jihe(i)|i#ge#5:y(i));S(3)=@min (jihe(i)|i#ge#2 #and# i#le#8:y(i)); S(4)=@max (jihe(i)|i#ge#2 #and# i#le#8:y(i)); end6.1、设：第i 个工人做第j 项工作用时ij t ，标志变量ij f 定义如下：⎩⎨⎧=其他件工作个工人去做第指派第01j i f ijmin∑∑==⨯4141i j ij ijt fs.t. 141=∑=i ijf()4,3,2,1=j 每份工作都有一人做∑==411j ijf()4,3,2,1=i 每人都只做一项工作model : sets :work/A B C D/;worker/jia yi bing ding/; time(worker,work):t,f; endsets!目标函数可以用[obj]标志出，也可以省略；[obj] min =@sum (time(i,j):t(i,j)*f(i,j)); data :!可以直接复制表格，但是在最后要有分号; t=; e !每份工作都有一人做;@for (work(j):@sum (time(i,j):f(i,j))=1); !每人都只做一项工作;@for (worker(i):@sum (time(i,j):f(i,j))=1); !让f 取0-1值，此条件可以省略；!@for(time(i,j):@bin(f(i,j))); end6.2设：煤厂进煤量i s ，居民区需求量为i d ，煤厂i 距居民区j 的距离为ij L ，煤厂i 供给居民区j 的煤量为ij g那么可以列出如下优化方程式∑∑==⨯=3121min j i ij ij L gs.t ()3,2,121==∑=j d gi jij()2,131=≤∑=i s gj iijmodel : sets :supply/1,2/:s; demand/1,2,3/:d;link(supply,demand):road,sd; endsets data :road=10 5 6 4 8 12; d=50 70 40; s=60 100; enddata[obj] min =@sum (link(i,j):road(i,j)*sd(i,j)); @for (demand(i):@sum (supply(j):sd(j,i))=d(i)); @for (supply(i):@sum (demand(j):sd(i,j))<s(i));end1．线性规划模型。

Lingo精选题目及答案

Lingo 精选题目及答案答题要求：将Lingo 程序复制到Word 文档中，并且附上最终结果。

1、简单线性规划求解（目标函数）2134maxx x z += s.t.（约束条件）⎪⎪⎩⎪⎪⎨⎧≥≤≤+≤+0,781022122121x x x x x x x2、整数规划求解219040Max x x z +=⎪⎩⎪⎨⎧≥≤+≤+0,702075679212121x x x x x x 3、0-1规划求解Max 432215.18.04.0x x x x f +++=10106234321≤+++x x x x10,,,4321或=x x x x4、非线性规划求解||4||3||2||min 4321x x x x z +++=s.t. ⎪⎪⎩⎪⎪⎨⎧-=+--=-+-=+--2132130432143214321x x x x x x x x x x x x5、集合综合应用产生一个集合5052--=x x y ，（10,...,2,1=x ），求y 前6个数的和S 1，后6个数的和S 2，第2~8个数中的最小值S 3，最大值S 4。

6、综合题要求列出具体的目标函数和约束条件，然后附上Lingo 程序和最终结果。

6.1 指派问题6.2 分配问题某两个煤厂A1，A2每月进煤数量分别为60t和100t，联合供应3个居民区B1,B2,B3。

3个居民区每月对煤的需求量依次分别为50t，70t，40t，煤厂A1离3个居民区B1,B2,B3的距离依次分别为10km,5km,6km,煤厂A2离3个居民区B1,B2,B3的距离分别为4km,8km,12km。

问如何分配供煤量使得运输量（即t·km）达到最小？1、model:max=4*x1+3*x2;2*x1+x2<10;x1+x2<8;x2<7;end2、model:max=40*x1+90*x2;9*x1+7*x2<56;7*x1+20*x2<70;@gin(x1);@gin(x2);end3、model:max=x1^2+0.4*x2+0.8*x3+1.5*x4;3*x1+2*x2+6*x3+10*x4<10;@bin(x1); @bin(x2);@bin(x3); @bin(x4);end4、model:max=@abs(x1)+2*@abs(x2)+3*@abs(x3)+4*@abs(x4);x1-x2-x3+x4=0;x1-x2+x3-3*x4=1;x1-x2-2*x3+3*x4=-1/2;end5、model:sets:jihe/1..10/:y;ss/1..4/:S;endsets!由于y和s中部分有负数，所以要先去掉这个约束;@for(jihe:@free(y));@for(ss(i):@free(S));!产生元素;@for (jihe(x):y(x)=x^2-5*x-50); S(1)=@sum (jihe(i)|i#le#6:y(i)); S(2)=@sum (jihe(i)|i#ge#5:y(i));S(3)=@min (jihe(i)|i#ge#2 #and# i#le#8:y(i)); S(4)=@max (jihe(i)|i#ge#2 #and# i#le#8:y(i)); end6.1、设：第i 个工人做第j 项工作用时ij t ，标志变量ij f 定义如下：⎩⎨⎧=其他件工作个工人去做第指派第01j i f ijmin∑∑==⨯4141i j ij ijt fs.t. 141=∑=i ijf()4,3,2,1=j 每份工作都有一人做∑==411j ijf()4,3,2,1=i 每人都只做一项工作model : sets :work/A B C D/;worker/jia yi bing ding/; time(worker,work):t,f; endsets!目标函数可以用[obj]标志出，也可以省略；[obj] min =@sum (time(i,j):t(i,j)*f(i,j)); data :!可以直接复制表格，但是在最后要有分号; t=; e !每份工作都有一人做;@for (work(j):@sum (time(i,j):f(i,j))=1); !每人都只做一项工作;@for (worker(i):@sum (time(i,j):f(i,j))=1); !让f 取0-1值，此条件可以省略；!@for(time(i,j):@bin(f(i,j))); end6.2设：煤厂进煤量i s ，居民区需求量为i d ，煤厂i 距居民区j 的距离为ij L ，煤厂i 供给居民区j 的煤量为ij g那么可以列出如下优化方程式∑∑==⨯=3121min j i ij ij L gs.t ()3,2,121==∑=j d gi jij()2,131=≤∑=i s gj iijmodel : sets :supply/1,2/:s; demand/1,2,3/:d;link(supply,demand):road,sd; endsets data :road=10 5 6 4 8 12; d=50 70 40; s=60 100; enddata[obj] min =@sum (link(i,j):road(i,j)*sd(i,j)); @for (demand(i):@sum (supply(j):sd(j,i))=d(i)); @for (supply(i):@sum (demand(j):sd(i,j))<s(i));end1．线性规划模型。

Lingo解目标规划

不考虑目标，运输问题的数学模型为：
设xij 表示从第i个产地向第j个销地的运量。则： min z cij xij
i 1 j 1 3 4
x
j 1 3
4
ij
ai , i 1,2,3 b j , j 1,2,3,4
x
i 1
ij
xij 0
Lingo代码：
sets: cd/1..3/:a; xd/1..4/:b; links(cd,xd):c,x; endsets data: a=300 200 400; b=200 100 450 250; c=5 2 6 7 3546 4 5 2 3; enddata min=@sum(links(i,j):c(i,j)*x(i,j)); @for(cd(i):@sum(xd(j):x(i,j))<=a(i)); @for(xd(j):@sum(cd(i):x(i,j))>=b(j));
整数线性规划一般形式：
max(min) z c j x j
j 1
n
( a )
n (b) aij x j ( , )bi j 1 (c ) xj 0 x , x , , x 中部分或全部取整数 ( d ) n 1 2
Lingo代码
min=d31; 2*x1+x2<=11; x1-x2+d11-d12=0; x1+2*x2+d21-d22=10; 8*x1+10*x2+d31-d32=56; d12=0; d21+d22=0;
例2：
min z p1d1 p2 d 2 p3 (2d 3 d 4 )
5 11

LINGO_1_

华中农业大学建模基地
LINGO实验 LINGO实验
－注意事项－注意事项－
在模型的开头可以用“ 对模型命名；在模型的开头可以用“TITLE” 对模型命名；变量可以放在约束右端；变量可以放在约束右端；每行（目标，约束，说明语句）后增加 “；”；每行（目标，约束，说明语句）开头都是函数调用；＠开头都是函数调用；上下界限定用@BND（）不计入模型的约束，也不能（）,不计入模型的约束上下界限定用（）不计入模型的约束，给出其松紧判断和敏感性分析; 给出其松紧判断和敏感性分析缺省假定所有变量非负；可在模型的“ 缺省假定所有变量非负；可在模型的“END”语句后用语句后用 “@FREE（） ”将变量的非负假定取消; （）将变量的非负假定取消变量说明：（）;对整型变量说明对0-1变量说明：@BIN（）对整型变量说明：@GIN 变量说明（）对整型变量说明：（）；模型由一系列语句组成，适当缩进，增强可读性。模型由一系列语句组成，适当缩进，增强可读性。
华中农业大学建模基地
LINGO实验 LINGO实验
－求解器状态窗口－求解器状态窗口－
LP，QP，ILP，IQP，PILP，，，，，， PIQP，NLP，INLP，PINLP ，，，变量数量模型类型当前解状态当前目标函数值 Ob Infe Ite T 约束不满足的总量目前为止的迭代次数 T Type Obj N B-and-B Global Multistart N 非零系数数量可直接求解的变量不作为决策变量。策变量。 Class T N In 约束数量 "Global Optimum", "Local Optimum", "Feasible", "Infeasible“(不可行不可行), 不可行 "Unbounded“(无界无界), 无界 "Interrupted“(中断中断), 中断 "Undetermined“(未确定未确定) 未确定

lingo练习

数学规划模型及lingo 求解练习： 1.考虑下述不平衡指派问题。

现有7个人指派给他们5项任务，效率矩阵如下表。

约定：①一个任务只能被一个人完成；②一个人在某时刻只能做一项任务；③所（1） lingo 代码求解，给出最优指派以及最优值； 1. 模型的建立：设：题干中有i 个人共要完成j 件事情，可建立以下模型：i=1,2,3…..m j=1,2,3…..n=0或1xij=1:指派第i 人做第j 事 xij=0: 不指派第i 人做第j 事（ cij ）称为系数矩阵。

2. 详细代码： Model: SETS:Chandi/1..7/:cl; Xiaodi/1..5/:xl;ChanXiao(Chandi,Xiaodi):c,x; ENDSETS DATA:c=2 15 13 1 8 10 4 14 15 7 9 14 16 13 8 7 8 11 9 4 8 4 15 8 6 12 4 6 8 13 5 16 8 5 10;m nij iji=1j=1min =c x Z •∑∑11nijj x==∑11miji x==∑ijx[obj] min=@sum(ChanXiao:c*x);@for(Chandi(i):@sum(Xiaodi(j):x(i,j))<1); @for(Xiaodi(j):@sum(Chandi(i):x(i,j))=1);@for(Chandi(i):@sum(Xiaodi(j):c(i,j)*x(i,j))<Cmax); @for(ChanXiao(i,j):@bin(x(i,j))); End（2）目标是任务尽早完工。

建立数学规划模型，并编写lingo 代码求解，给出最优指派以及最优值； 1.模拟建立：设：题干中有i 个人共要完成j 件事情，可建立以下模型： min max Z C =•j=1,2,3,….ni=1,2,3,….mi=1,2,3…..m 0或1xij=1:指派第i 人做第j 事 xij=0: 不指派第i 人做第j 事（ cij ）称为系数矩阵。

Lingo精选题目及答案

Lingo 精选题目及答案答题要求：将Lingo 程序复制到Word 文档中，并且附上最终结果。

1、简单线性规划求解（目标函数）2134maxx x z += s.t.（约束条件）⎪⎪⎩⎪⎪⎨⎧≥≤≤+≤+0,781022122121x x x x x x x2、整数规划求解219040Max x x z +=⎪⎩⎪⎨⎧≥≤+≤+0,702075679212121x x x x x x 3、0-1规划求解Max 432215.18.04.0x x x x f +++=10106234321≤+++x x x x10,,,4321或=x x x x4、非线性规划求解||4||3||2||min 4321x x x x z +++=s.t. ⎪⎪⎩⎪⎪⎨⎧-=+--=-+-=+--2132130432143214321x x x x x x x x x x x x5、集合综合应用产生一个集合5052--=x x y ，（10,...,2,1=x ），求y 前6个数的和S 1，后6个数的和S 2，第2~8个数中的最小值S 3，最大值S 4。

6、综合题要求列出具体的目标函数和约束条件，然后附上Lingo 程序和最终结果。

6.1 指派问题有四个工人，要指派他们分别完成4项工作，每人做各项工作所消耗的时间如下表：问指派哪个人去完成哪项工作，可使总的消耗时间为最小？6.2 分配问题某两个煤厂A1，A2每月进煤数量分别为60t和100t，联合供应3个居民区B1,B2,B3。

3个居民区每月对煤的需求量依次分别为50t，70t，40t，煤厂A1离3个居民区B1,B2,B3的距离依次分别为10km,5km,6km,煤厂A2离3个居民区B1,B2,B3的距离分别为4km,8km,12km。

问如何分配供煤量使得运输量（即t·km）达到最小？1、model:max=4*x1+3*x2;2*x1+x2<10;x1+x2<8;x2<7;end2、model:max=40*x1+90*x2;9*x1+7*x2<56;7*x1+20*x2<70;@gin(x1);@gin(x2);end3、model:max=x1^2+0.4*x2+0.8*x3+1.5*x4;3*x1+2*x2+6*x3+10*x4<10;@bin(x1); @bin(x2);@bin(x3); @bin(x4);end4、model:max=@abs(x1)+2*@abs(x2)+3*@abs(x3)+4*@abs(x4);x1-x2-x3+x4=0;x1-x2+x3-3*x4=1;x1-x2-2*x3+3*x4=-1/2;end5、model:sets:jihe/1..10/:y;ss/1..4/:S;endsets!由于y和s中部分有负数，所以要先去掉这个约束;@for(jihe:@free(y));@for(ss(i):@free(S));!产生元素;@for (jihe(x):y(x)=x^2-5*x-50); S(1)=@sum (jihe(i)|i#le#6:y(i)); S(2)=@sum (jihe(i)|i#ge#5:y(i));S(3)=@min (jihe(i)|i#ge#2 #and# i#le#8:y(i)); S(4)=@max (jihe(i)|i#ge#2 #and# i#le#8:y(i)); end6.1、设：第i 个工人做第j 项工作用时ij t ，标志变量ij f 定义如下：⎩⎨⎧=其他件工作个工人去做第指派第01j i f ijmin∑∑==⨯4141i j ij ijt fs.t. 141=∑=i ijf()4,3,2,1=j 每份工作都有一人做∑==411j ijf()4,3,2,1=i 每人都只做一项工作model : sets :work/A B C D/;worker/jia yi bing ding/; time(worker,work):t,f; endsets!目标函数可以用[obj]标志出，也可以省略；[obj] min =@sum (time(i,j):t(i,j)*f(i,j)); data :!可以直接复制表格，但是在最后要有分号; t=; e !每份工作都有一人做;@for (work(j):@sum (time(i,j):f(i,j))=1); !每人都只做一项工作;@for (worker(i):@sum (time(i,j):f(i,j))=1); !让f 取0-1值，此条件可以省略；!@for(time(i,j):@bin(f(i,j))); end6.2设：煤厂进煤量i s ，居民区需求量为i d ，煤厂i 距居民区j 的距离为ij L ，煤厂i 供给居民区j 的煤量为ij g那么可以列出如下优化方程式∑∑==⨯=3121min j i ij ij L gs.t ()3,2,121==∑=j d gi jij()2,131=≤∑=i s gj iijmodel : sets :supply/1,2/:s; demand/1,2,3/:d;link(supply,demand):road,sd; endsets data :road=10 5 6 4 8 12; d=50 70 40; s=60 100; enddata[obj] min =@sum (link(i,j):road(i,j)*sd(i,j)); @for (demand(i):@sum (supply(j):sd(j,i))=d(i)); @for (supply(i):@sum (demand(j):sd(i,j))<s(i));end1．线性规划模型。