中国利率期限结构中的宏观经济风险_省略_析_基于宏观_金融模型的研究途径_孙皓
基于主成分分析我国利率期限结构及其影响因素
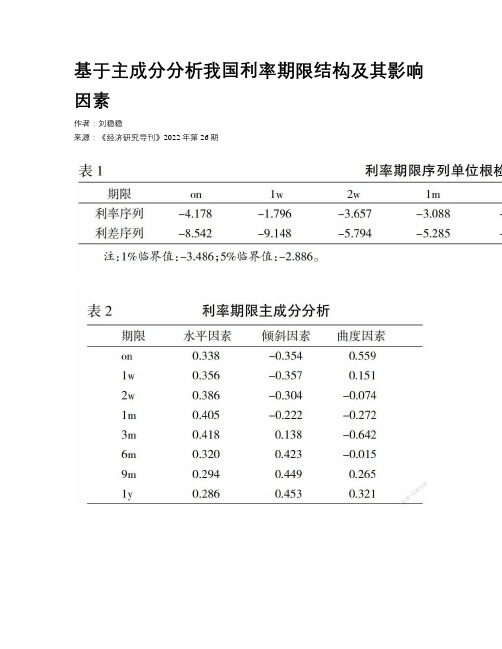
基于主成分分析我国利率期限结构及其影响因素作者:***来源:《经济研究导刊》2022年第26期摘要:上海银行间同业拆放利率(SHIBOR)作为我国基准利率,自运行以来不断发展完善。
以其为研究对象,通过主成分分析提取出3个可反映利率期限结构变动96%以上变动的特征要素,即“水平”、“倾斜”及“曲度”因素;另加入宏观经济变量,利用结构向量自回归(SVAR)模型,发现实体经济因素的冲击主要导致利率期限结构水平变动及倾斜变动,货币政策冲击对利率期限结构曲度变动有一定影响。
关键词:主成分分析;利率期限结构;结构向量自回归;影响因素中图分类号:F832.0 文献标志码:A 文章编号:1673-291X(2022)26-0074-04引言上海银行间同业拆放利率(SHIBOR)自2007年1月4日起正式运行,并不断发展和完善,努力培育成我国货币市场的基准利率,进一步推进了我国利率市场化的改革。
戴国强和李良松(2010)指出,利率作为一个重要的经济变量,不仅是金融产品定价和金融宏观调控的基础,而且其利率期限结构的变动及包含的宏观信息可为央行依据宏观经济走势制定相应利率政策提供直接支持[1]。
在宏观经济发展阶段中,价格水平、货币政策等多种宏观经济因素与利率有着重要的联系。
Litterman和Scheinkman(1991)以美国国债市场为研究对象,首次利用主成分分析法,考察了债券收益率与系统风险因素及非系统风险因素之间的关系,分析其在利率期限结构变化中的作用,且将其归结为水平因素、倾斜因素和曲度因素3种[2]。
刘金全等(2007)利用VAR模型研究宏观因素对不同期限的银行间短期拆借利率水平的影响,得出宏观经济冲击对短期利率水平存在显著的影响[3]。
张笑峰、郭菊娥(2012)对SHIBOR利率期限结构的变动影响因素及其作用机理进行了探讨,发现宏观经济中,物价水平是导致利率期限结构中水平移动的主要因素[4]。
本文利用主成分分析方法对SHIBOR利率期限结构变动因素分析,将SHIBOR利率期限结构的复杂变动用三种特征要素的变化来反映,并基于SVAR模型,分析各种宏观经济变量变化对SHIBOR利率期限结构变动特征要素的冲击效应。
中国市场利率期限结构的静态估计

中国市场利率期限结构的静态估计在金融领域,利率期限结构是指同一借款人在不同期限内借款的利率水平。
它是衡量市场对未来经济发展和通胀预期的一种指标。
了解利率期限结构对于制定金融政策、投资决策和风险管理都具有重要意义。
本文将探讨中国市场利率期限结构的静态估计。
一、利率期限结构的定义利率期限结构通常采用年化利率来表示,是不同到期日的债券或贷款的利率之间的比较。
由于市场对未来经济状况的预期和风险因素的考虑,不同期限的借款利率往往存在差异。
研究利率期限结构可以帮助我们理解市场对未来经济发展的预期和对风险的评估。
二、中国市场利率期限结构的特点中国市场利率期限结构在一定程度上受到宏观经济因素和政府干预的影响。
经济增长、通胀率、货币政策和市场流动性等因素都会对利率期限结构产生影响。
此外,政府在货币市场的干预也会对利率形成产生一定的影响。
三、利率期限结构的静态估计方法静态估计是指一次性对利率期限结构进行估计,通常使用拟合现有利率数据的数学模型来实现。
在中国市场,常用的静态估计方法包括线性插值法、平均值法和平滑曲线法。
这些方法可以根据市场上的利率数据,对不同期限的利率进行估计,以获得整体的利率期限结构。
四、中国市场利率期限结构的实证研究许多学者对中国市场的利率期限结构进行了实证研究。
这些研究通过对历史的利率数据进行建模和分析,旨在揭示市场对未来经济走势的预期。
实证研究的结果显示,中国市场的利率期限结构具有一定的特点,例如常常出现上升的利率期限结构、长期利率较高等。
五、利率期限结构的影响因素中国市场利率期限结构的形成受到多种因素的影响。
宏观经济因素如经济增长、通胀率等是影响利率期限结构的重要因素。
货币政策和市场流动性也会对利率形成产生影响。
此外,市场预期和投资者风险偏好也是决定利率期限结构的重要因素。
六、利率期限结构的应用利率期限结构可以为金融机构和投资者提供重要参考信息。
它不仅可以用于制定货币政策、评估利率风险,还可以用于决策债券投资和利率衍生品交易。
利率期限结构(应用)

• (4)利率期限结构动态模型 • 基本利率期限结构动态模型根据利率期限结构模
型的推导过程,可以分为两种类型:第一种类型就是 一般均衡模型(Equilibriummodel),根据市场的均衡 条件求出利率所必须遵循的一个过程,在这些模型 中,相关的经济变量是输入变量,利率水平是输出变 量;另一种类型是无套利模型(No arbitrage model), 通过相关债券等资产之间必须满足的无套利条件 进行分析,此时利率水平是一个输入变量,相关金融 工具的价格是输出变量.必须特别指出的是,这些模 型都是建立在风险中性世界中,所描述的均是风险 中性世界中的利率变动行为.而实证检验都是利用 现实世界的利率数据进行的.因此,在将现实世界中 的估计结果运用于衍生产品定价时,必须先利用模 型相对应的风险价格通过Girsanov定理将现实世 界转换为风险中性世界,然后再利用风险中性世界 中的相应结果进行定价.
• (6)利率期限结构研究现状总结性分析
利率期限结构
• 利率期限结构(term structure),是某个时点 不同期限的利率所组成的一条曲线.因为在 某个时点,零息票债券的到期收益率等于该 时期的利率,所以利率期限结构也可以表示 为某个时点零息票债券的收益率曲线(yield curve).它是资产定价、金融产品设计、保 值和风险管理、套利以及投机等的基准.因 此,对利率期限结构问题的研究一直是金融 领域的一个基本课题.
(2)利率期限结构静态估计 当市场上存在的债券种类有限时(特别对债券
市场不发达国家而言),如何根据有效的债券价格资 料对整个利率期限结构进行估计,是进行债券研究 的一个重要内容.不同的学者提出了不同的估计方 法,其核心就是对贴现函数δ(m)的估计.郑振龙和林 海利用McCulloch样条函数和息票剥离法对我国 市场利率期限结构进行了静态估计,构造出中国真 正的市场利率期限结构.朱世武和陈健恒则使用 Nelson-Siege-Svensson方法对我国交易所市场 的利率期限结构进行了估计.郑振龙和林海估计出 中国债券市场的违约风险溢酬并进行了分析.林海 和郑振龙对中国市场利率的流动性溢酬进行了估 计和分析.林海和郑振龙对这些问题进行了统一和 归纳,并分析了其在中国金融市场的具体运用.
中国系统性金融风险研究

中国系统性金融风险研究作者:周皓何碧清赵靖沙楠来源:《中国经济报告》2019年第04期【提;;要】本文借鉴国内外系统性金融风险的学术研究成果,从宏观和微观两个层面度量了中国系统性金融风险的动态变化,并以此为基础讨论中国宏观经济走势与相关政策。
最新测算结果表明,2019年上半年中国宏观层面系统性金融风险指标较2018年水平大幅下降,处于历史较低水平,但微观层面指标仍然高企。
2018年年中以来的政策转向是近期宏观经济企稳的主要原因,民营企业融资等问题得到部分缓解。
但经济周期的滞后效应以及支持民营企业、小微企业融资的政策负担均可能使银行业不良贷款较快显现,构成经济复苏中的潜在风险。
我们认为,中国经济同时面对内、外两方面的压力,但主要矛盾还是在内部,解决内部结构性、导向性的问题是抵御外部风险冲击的最有效手段,中长期的经济政策仍必须以改革和开放作为主线。
例如进一步确立民营经济的重要地位、构建竞争中性的营商环境等,同时以中短期的宏观周期性宽松政策稳定国内经济走势、对冲外部贸易摩擦的负面影响,为正处于关键期、攻坚期的改革和开放赢得足够的时间窗口。
【关键词】系统性金融风险;金融巨灾风险指标;系统性预期损失值;条件在险价值;系统性风险指標一、背景介绍供给侧结构性改革和防控系统性金融风险是自2016年以来中国经济和金融工作的政策主线,在持续两年高强度的“去杠杆”和“防风险”工作后,部分企业遭遇了融资困难,信用违约不断发生,金融市场股权质押流动性风险凸显,叠加中美贸易摩擦影响,中国实体经济与金融市场在2018年全年都处于高风险、高波动的环境中。
在2018年中国经济面对的各项问题和矛盾中,非公有制经济在中国经济社会发展中的作用和地位这一主题受到了最广泛的关注和讨论。
习近平总书记主持召开民营企业座谈会并发表重要讲话,肯定了民营经济“五六七八九”的贡献,并明确表示将毫不动摇地鼓励、支持、引导非公有制经济发展,将为非公有制经济发展营造良好环境和提供更多机会。
中国实际利率与通胀预期的期限结构——基于无套利宏观金融模型的研究

作者: 曾耿明[1];牛霖琳[1]
作者机构: [1]厦门大学王亚南经济研究院,福建厦门361005
出版物刊名: 金融研究
页码: 24-37页
年卷期: 2013年 第1期
主题词: 利率期限结构;实际利率;通胀预期
摘要:国债市场中隐含的实际利率和通胀预期的信息对于指导我国的货币政策和投资者决策具有重要的参考价值。
本文通过采用简约型无套利宏观金融模型,第一次从中国银行间国债收益率曲线中分解出债券市场实际利率和通胀预期的整个期限结构。
本文模型推断结果发现在2005年1月到2012年4月的样本时间内银行间国债市场的实际利率长期处于负值,反映出近年来货币政策偏于宽松和利率市场化机制未完善的问题。
通过对本文分解的通胀预期和其它同类通胀预期指标比较分析,发现通过本文方法获得的通胀预期很好地反映了债券市场通胀预期的水平和变化趋势,也吻合通货膨胀的周期变化。
同时因本文方法能够推断不同期限的通胀预期,相比已有的单一期限通胀预期指标,能够为政策制定者和市场投资者提供更为丰富的决策信息。
利率期限结构、宏观经济及资本市场之间的关系研究

·50·
经济学与管理学研究
周 亮 利率期限结构、宏观经济及资本市场之间的关系研究
仿射利率期限结构模型,利用蒙特卡罗模拟对我国 国债进行定价预测,并与 Longstaff-Schwartz 模型、 Vasicek 模型、Cox-Inger-soll-Ross 模型的定价效果 进行实证比较,结果表明多因子模型要优于单因子 模型,双因子模型要略优于三因子模型[5]。李宏瑾 (2012)通过协整分析方法对我国利率期限结构的预 期假说进行检验后发现,各期限国债利率存在着长 期均衡的协整关系,隔夜及 1 月期短端利率始终是 其他各期限利率的 Granger 原因,反之则不成立[6]。 文忠桥 (2013) 利用粒子群算法模拟 Nelson原Siegel 模型,通过构建参数的 AR(2)模型对利率期限结构 进行预测,结果发现样本内的预测结果比较理想,但 样本外的预测绩效不佳[7]。陈映洲、张健(2015)比较 了 LSCC(动态 Svensson)模型与 LSC(动态 NelsonSiegel) 模型对利率期限结构的拟合与预测能力,结 果发现动态 Svensson(LSCC)模型具有更加显著的 拟合能力和预测能力,能够更好地反映国债利率期 限结构的动态特征[8]。赵晶、张洋、丁志国(2015)选 取了 6 个利率期限结构模型采用均方差和平均绝对 误差对实证效果进行判别后发现,DL 模型在针对中 国市场和美国市场数据的拟合与预测方面能力均 十分突出且效果稳定,指数样条模型次之,而其他 模型则在利率期限结构特征的刻画效果方面存在 更强的数据依赖与能力不足问题[9]。陈浪南、郑衡亮 (2015) 则采用因子模型分析了我国的利率期限结 构,并提取了水平因子和斜率因子,发现这两个因 子能够较好地解释我国国债利率市场的短期和长 期期限特征[10]。
我国利率期限结构的静态分析和动态特征
我国利率期限结构的静态分析和动态特征摘要:利率期限结构反映的是利率和到期期限之间的关系。
文章利用指数样条法估计出我国上交所国债的利率期限结构,对其进行静态的分析,得到上交所国债利率期限结构统计特征。
同时,应用主成分分析方法研究国债利率期限结构的动态特征,发现水平因素、斜度因素和凸度因素对我国国债即期利率曲线变动的解释能力分别达到51.28%、26.63%和10.86%,累计贡献率达到88.77%,不同因素对各个到期期限即期利率的影响程度也有所不同。
关键词:利率期限结构指数样条法主成分分析一、引言利率期限结构是某个时点不同期限的利率所组成的一条曲线,它是资产定价、金融产品设计、保值和风险管理、套利以及投机等金融活动的基础。
对利率期限结构的估计是资产定价领域一个基础性的研究问题。
随着我国债券市场的发展、金融创新的不断深入以及利率市场化进程的逐步推进,利率期限结构问题研究的重要性日益凸现出来。
在一个存在零息票债券的市场上,我们通过直接求出这些零息票债券的到期收益率就可以估计出某个时点的利率期限结构并进行分析。
但是如果不存在零息票债券或者数量十分有限,那么这种方法就受到很大的限制,中国债券市场就是如此。
在中国债券市场上,大部分债券都是息票债券,零息票债券的数量很少。
上海证券交易所和银行同业间债券交易市场上交易的国债都是息票债券。
因此,我们就不能通过求到期收益率的方法来估计利率期限结构,而只能采取其他的估计方法。
在本文我们使用Vasicek(1982)提出的指数样条估计方法,利用我国上交所2002~2005年国债现货市场的交易数据,估计出我国国债利率期限结构的一个时间序列数据。
有了即期利率这一基准利率曲线,我们就可以用其给国债、公司债以及其他利率金融产品进行定价,为投资者提供投资参考和依据。
但是,我们知道,由于各种宏观经济因素及国债市场本身众多的因素处于不断的变动之中,即期利率曲线也在不断的发生着变化。
利率的变化会导致利率金融产品尤其是固定收益证券价格的变化。
利率期限结构的宏观经济预测作用
论坛 ( C F 4 0 ) 青年论坛第 3 9期 双 周 内部 研 讨 会 与会 代 表 的 有 益 讨 论 ; 感 谢 匿 名 审 稿 人 的宝 贵建 议 ; 本 文仅 代 表 个 人 观 点 , 与 所 在
益率 曲线 的斜 率 ( 也 即长 短期 利率 之差 ) 观察 而得 。 利率 期 限结 构 有助 于市 场参 与者 和货 币政策 当局 准确 判断 未来宏 观 经济 运行 的 状况 , 观 察货
币政 策 的实 际效 果 , 提高 货 币决策 的可 靠性 和有 效性 。正 是 由于利率 期 限结 构包 含 了未来 经 济增 长 和通 货 膨胀 走 势 的 重要 信 息 , 因此很 多 国家 的货 币政 策 制定 者 非 常关 注 收 益 率 曲线 的变 动情
要。 在宏 观 层 面上 , 无 风 险的利 率期 限结 构还具 有宏 观经 济指 示器 的作 用 。自 F i s h e r ( 1 9 3 0 ) 开 创性 地将 名义 利 率分解 为实 际利 率与 预期 通货 膨胀 率 后 . 经 济学 家 们认 识 到 , 实 际利 率 的 高低 直接 决 定经 济主 体 的消费 和投 资决策 , 而 经济决 策则 主要 取决 于 长期而 非短 期利 率水 平 。 因而 , 利率 期 限 结构包 含 了大量 有关 未来 经 济增长 、 投资、 消 费 以及通 货膨胀 等 方面 的信 息 , 这 些信 息 可 融 评 论 2 0 1 3 年第 3 期 理性 预 期 理论 认 为经 济个 体 在做 经 济决 策 之前 , 会努 力 搜集 有 关未 来 经 济前 景 的信 息 , 这 些 信息 提供 了关 于未 来 资产 收益 的详尽 资 料 , 而 一旦 经 济个 体 利用 这 些信 息 做 出投 资决 策 . 这些 信 息必 将 反 映在 其投 资 行为 上 , 而 所有 拥有 这 些 信息 的投 资者 在市 场 上相 互 作 用 , 均衡 的结果 则 是 这些 信息 反 映在 均衡 价格 中。如果 经 济系 统确 实是 理性 预期 的 , 那 么 就完 全有 可 能从 均衡 价格 中过 滤 出关 于未来经 济前 景的信 息 , 当然 也包 括经济增 长 的信 息 。就这个 意义上讲 , 市场就 是 F a m a ( 1 9 7 0 )
利率的风险结构与期限结构
流动性风险
在某些情况下,投资者可 能难以将手中的债券以合 理的价格出售。
利率风险的测量
久期
衡量利率变动对债券价格 的影响程度。久期越长, 利率变动对债券价格的影 响越大。
凸性
描述债券价格与利率变动 的非线性关系。凸性越大 ,非线性影响越显著。
敏感性分析
通过分析不同利率变动情 景下债券价格的变动范围 ,评估利率风险。
经济预测
通过对利率期限结构的分析,可 以预测未来经济走势和货币政策 走向,从而为投资决策提供依据 。
03
利率风险与期限结构的关系
利率风险对期限结构的影响
利率变动对长期债券的影响更大
长期债券的利率敏感性更高,因此利率的小幅变动可能会对长期债券的价格产 生较大影响。
利率风险可能导致期限结构扭曲
如果预期利率下降,长期债券的价格可能会上涨,导致期限结构变得平坦或向 下倾斜。
利率期限结构的实证01 Nhomakorabea利率期限结构的历史表现
通过对历史数据的分析,可以观察到不同期限的债券收益率之间存在一
定的相关性,长期债券收益率通常高于短期债券收益率。
02 03
利率期限结构的经济因素分析
影响利率期限结构的经济因素包括经济增长率、通货膨胀率、货币政策 等,这些因素的变化会影响市场预期和债券供需关系,进而影响利率期 限结构。
利率的风险结构与期 限结构
• 利率的风险结构 • 利率的期限结构 • 利率风险与期限结构的关系 • 利率风险管理与期限结构策略
目录
01
利率的风险结构
利率风险的来源
01
02
03
市场风险
由于市场利率变动,导致 债券价格波动,从而影响 投资组合的收益。
利率期限结构宏观金融模型研究新进展
利率期限结构宏观金融模型研究新进展*朱 波 文兴易内容提要:传统利率期限结构理论主要研究收益率曲线的形状及其形成原因,而现代利率期限结构理论主要讨论利率的动态演变过程。
尽管无套利仿射期限结构模型能很好地拟合收益率曲线的动态行为,但无法对潜因子进行经济解释。
近年来,现代利率期限结构理论领域的一个重大进展是,在无套利仿射期限结构模型基础上同时对期限结构因子与宏观经济变量进行建模,对微观金融结构与宏观经济结构之间的交互作用机制进行分析,利率期限结构宏观金融模型得到飞速发展,本文对近几年的最新进展做一综述。
关键词:利率期限结构 宏观金融模型 无套利仿射期限结构模型 近年来,利率期限结构宏观金融模型及货币政策含义受到众多学者和政策制定者的高度重视。
国外关于利率期限结构理论的研究可以分为传统利率期限结构理论和现代利率期限结构理论。
传统利率期限结构理论包括纯粹预期理论、流动性升水理论、市场分割理论和优先偏好理论,主要研究收益率曲线的形状及形成原因。
现代利率期限结构理论以无套利框架下的动态期限结构理论为主,重在研究利率的动态演变过程,常用的模型框架是无套利仿射期限结构模型(A ffine Term S tructure M odels, ATSM)。
近年来,现代利率期限结构理论领域的一个重大进展是,在无套利仿射期限结构模型基础上同时对期限结构因子与宏观经济变量进行建模,对微观金融结构与宏观经济结构之间的交互作用机制进行分析,利率期限结构宏观金融模型(M acro-fi-nance M odel of the Inte rest Term Structure)得到飞速发展。
一、宏观金融模型的基本思想在很长一段时间内,微观金融和宏观经济对利率的分析视角之间存在巨大的差异。
金融经济学家认为短期利率是由一组不可直接观察的潜因子(多个风险因子)所驱动的,而宏观经济学家则认为短期利率是由中央银行设定的。
对长期利率而言,宏观经济学家认为长期利率是未来短期利率的预期(预期假说),而金融经济学家却认为长期利率的变动反映的是“风险溢价”的变化。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
经济评论 2011年第3期ECONOMIC REVIEW No.3 2011中国利率期限结构中的宏观经济风险因素分析———基于宏观-金融模型的研究途径孙 皓 石柱鲜*
摘要:本文应用宏观-金融模型对我国利率期限结构动态过程中的时变宏观经济风险价格进行定量估计,在此基础上,对利率期限结构的预期成分和风险溢价成分进行分解,并且模拟了宏观经济对利率期限结构的冲击效应。研究结果表明,我国利率期限结构中存在着显著的时变宏观经济风险价格;不同期限利率可以明显地分解出预期成分和风险溢价成分,风险溢价成分的变动具有“阶段性”特点;宏观经济冲击在短期内对利率期限结构的整体水平与坡度均有明显影响,在长期内则仅对整体水平的影响较为明显。因此,我国利率期限结构可以体现出宏观经济形势的变化,应该进一步提高利率期限结构在货币政策制定中的作用。关键词:利率期限结构 宏观经济 宏观-金融模型
一、引言利率期限结构中包含丰富的经济信息,其变化是金融市场与宏观经济运行关联状态的重要表现。Ang和Piazzesi(2002)提出的无套利向量自回归模型(no-arbitragevectorautoregressionmodel)不但为描述利率期限结构与宏观经济之间的关联机制进行了新尝试,也为宏观-金融模型(macro-financemodel)的构建提供了一般框架。随着研究的深入,宏观-金融模型已经成为宏观经济学和金融学领域实证研究的有效分析工具。宏观-金融模型是利率期限结构模型与宏观经济模型的联合模型,它既可以看成带有利率期限结构约束的宏观经济模型,也可以看成考虑了宏观经济因素的利率期限结构模型。宏观-金融模型中的宏观经济模块主要由总需求方程、总供给方程和货币政策方程组成,金融模块的基础是仿射利率期限结构模型。利用宏观-金融模型可以通过脉冲响应函数、方差分解等技术定量分析宏观经济与利率期限结构的动态相关性。国外学者应用宏观-金融模型对各国经济进行了大量实证研究,取得了较好效果。例如,Rudebush和Wu(2003)建立了一个包含两个不可观测变量的宏观-金融模型对美国经济进行研究,模型中的两个不可观测变量在宏观经济模块中可以分别解释为中长期的通货膨胀率目标与宏观经济波动变量,在金融模块中可以分别解释为利率期限结构的水平因子和斜率因子;Ichiue(2004)建立了一个仅包含可观测变量的宏观-金融模型对美国经济进行研究,产出变量、通货膨胀变量、利率变量和利差变量是宏观经济模块中的可观测变量,这些变量被假定服从向量自回归(VAR)过程;Oda和Suzuki(2007)建立了一个包含三个不可观测变量的宏观-金融模型对日本经济进行研究,宏观经济模块中的不可观测变量可以分别解释为具有时变性质的自
36*孙皓,清华大学国情研究中心,邮政编码:100084,电子信箱:sunh2002@163.com;石柱鲜,吉林大学数量经济研究中心,邮政编码:130012,电子信箱:shizhux@eyou.com。本文得到教育部人文社会科学重点研究基地项目“中国经济转轨时期增长轨迹与特征的实证研究”(05JJD790006)、国家社科基金项目“中日韩三国经济周期波动及其主要影响因素的比较研究”(06BGJ021)和教育部青年基金项目“潜在产出与自然利率在我国经济周期波动分析中的应用研究”(08JC790044)的资助。感谢匿名审稿人的宝贵意见,当然文责自负。然利率(naturalinterestrate)、隐性通货膨胀目标(implicitinflationtarget)和潜在产出增长率;Lemke(2008)建立了一个包含两个不可观测变量的宏观-金融模型对欧洲经济进行研究,宏观经济模块中的不可观测变量可以分别解释为具有时变性质的自然利率和潜在产出。这些学者的研究结果均表明,不同设定形式的宏观-金融模型可以很好地拟合各个国家和地区的实际数据,应用该模型能够对相关经济问题进行分析与解释。近年来,国内学者也应用宏观-金融模型对我国的经济问题进行了探索性研究,并且得到一些有价值的实证结论。例如,石柱鲜等(2008)的研究认为,我国利率期限结构可以对经济增长率、通货膨胀率和短期利率的变动做出预测,并且这些宏观经济变量也能够对利率期限结构产生影响;魏玺(2008)的研究认为,我国利率期限结构中的水平因子、斜率因子和曲率因子与产出和通货膨胀率等宏观经济因素具有相关性。但是,这些研究在宏观-金融模型的设定形式、估计方法等方面仍然存在改进空间,应用模型对经济问题的分析视角也可以进一步丰富。本文借鉴国内外学者的研究成果,应用时变宏观经济风险价格(riskprice)条件下的宏观-金融模型对我国利率期限结构中的宏观经济风险因素进行实证分析。文章的第二部分描述宏观-金融模型的基本结构并对模型进行估计;第三部分计算宏观经济风险价格的估计值,并且对利率期限结构的预期成分和风险溢价成分进行分解;第四部分对宏观经济对利率期限结构的冲击效应进行分析;最后部分为研究结论。
二、宏观-金融模型及其估计我们首先描述宏观-金融模型的基本结构,然后对模型进行估计,并且对利率的拟合效果进行评价。(一)宏观-金融模型参照Oda和Suzuki(2007)的研究框架,我们对宏观-金融模型的基本结构进行描述。宏观经济模块为一个包括产出-利率空间的总需求函数(IS曲线)、物价-产出空间的总供给函数(AS曲线)和货币政策反应函数(Taylor规则)的新凯恩斯宏观经济模型,具体形式如下:xt=a1Etxt+1+1-a1xt-1-a 2it-Etπt+1-rnt+εISt(1)πt=b1Etπt+1+1-b1πt-1+b2xt+εASt(2)it=c1it-1+1-c1rnt+π*t+c2πt-π*t+c3xt+εMPt(3)Δynt=Δynt-1+εPGt(4)rnt=1-d1rnt-1+d1a-12Δynt+d2(5)π*t=π*t-1+d3πt-1-π*t-1-d4i′(6)
i′=it-c1it-1-1-c1rnt+π*t-1+c2π-π*t+c3xt(7)其中,xt为产出缺口;πt为通货膨胀率;it为短期名义利率;Δynt为实际产出对数的一阶差分;rnt为时变的
自然利率;π*t为时变的隐性通货膨胀目标①;i′为基于π*t-1的利率调整误差;εISt、εASt、εMPt和εPGt分别为反映需
求冲击、供给冲击、货币政策冲击和潜在产出冲击的随机扰动项,分别服从N0,σ
IS2、N0,σAS2、
N0,σMP2和N0,σPG2。a1、a 2、b1、b2、c1、c2、c3、d1、d2、d3、d4、σIS、σAS、σMP和σPG均为正,是需要估计的参数。
(1)~(3)式分别为总需求、总供给和货币政策方程。(1)式刻画了包含产出缺口“前瞻”性成分与“后顾”性成分加权平均值的“混合型”IS曲线,“前瞻”与“后顾”性成分所占权重分别为a1和(1-a1),产出缺口与实际利率缺口间负向替代关系的替代系数为-a2;(2)式刻画了包含通货膨胀率“前瞻”性成分与“后顾”性成分加权平均值的“混合型”AS曲线,“前瞻”与“后顾”性成分所占权重分别为b1和(1-b1),通货膨胀率与产出缺口间正向替代关系的替代系数为b2;(3)式刻画了具有利率内生性的Taylor规则,短期利率平滑性的平滑系数为c1,短期利率对通货膨胀缺口和产出缺口的反应系数分别为c2和c3。(4)~(7)式分别描述了不可观测变量潜在产出增长率、自然利率和隐性通货膨胀目标的动态过程。(4)式假定Δynt为一个自回归过程;(5)式为通过考虑潜在产出增长率稳态情形而得到的自然利率rnt的动态
37①标准Taylor规则中的π*为中央银行设定的通货膨胀目标,这里的隐性通货膨胀目标π*t可以看成私人部门预期的长期
均衡通货膨胀率(Bekaert,etal.,2005;OdaandSuzuki,2007)。过程方程;(6)式和(7)式假定隐性通货膨胀目标π*t取决于历史值π*t-1,通货膨胀缺口πt-1-π*t-1和基于π*t-1的利率调整误差i′。同时,按照Fuhrer(2000)、Amato和Laubach(2003)的分析,如果令a2表示消费跨期替代的弹性(elasticityofintertemporalsubstitution),结构参数a 2可以用2a1-1a2替换。
下面介绍金融模块的具体形式。金融模块是以仿射利率期限结构模型为基础的。假定宏观经济风险价格可以表示为:Λt=λ0+λ1Ft(8)其中,Λt是4×1向量,表示宏观经济风险价格;λ0为4×1向量;λ1为4×6矩阵。λ0和λ1的具体结构如下:
λ0=λIS0λAS0λMP0λΔPG0,λ1=λIS1λAS,IS1λMP,IS100λΔPG,IS1λIS,AS1λAS1λMP,AS100λΔPG,AS1λIS,MP1λAS,MP1λMP100λΔPG,MP1λIS,ΔPG1λAS,ΔPG1λMP,ΔPG100λΔPG1(9)如果将Ft定义为向量xt,πt,it,rnt,π*t,Δynt′,则利用Sim(2000)的方法,Ft可以表示为如下自回归过
程:Ft=CF+ψFFt-1+FεFt(10)其中,CF为6×1系数向量;ψF为6×6系数矩阵;F为6×4系数矩阵。这样,不同期限利率在仿射利率期限结构模型的框架下,可以表示为:
ij,t=Ajj+B′jjFt+εjt(11)
Aj-Aj-1=B′j-1CF-F·λ0+12B′j-1FF′Bj-1+A1, j≥2(12)
B′j=B′j-1ψF-F·λ1+B′1, j≥2(13)
A1=0,B′1=0,0,1,0,0,0′(14)
其中,j为利率的期限长度;εjt为利率的理论值与实际值误差,并且被假定服从如下自回归过程:
εjt=αjεjt-1+ujt(15)其中,ujt服从N0,σj2。
这样,(8)~(15)式就构成了宏观-金融模型中的金融模块,λ0和λ1中的元素、αj和σj为需要估计的参数。(二)模型估计估计宏观-金融模型的时候,实际产出yt以实际GDP来度量(利用线性插值法进行季度数据与月度数
据转换),通货膨胀率πt以消费价格指数度量,不同期限利率选自银行间同业拆借市场月度利率,样本数据
来源于《经济景气统计月报》、《中国人民银行统计季报》,区间是1996年1月-2010年3月。本文以周为单位度量利率期限(一个月按4周计算),研究对象为7天(2~7天)、30天(21~30天)、60天(31~60天)、90天(61~90天)、120天(91~120天)利率,则文中这些利率对应的期限分别为1周、4周、8周、12周和16周。我们经过X-12方法对数据序列进行了季节调整,以剔除季节因素和非规则因素的影响。参照Ang等(2003)以及Lemke(2008)等学者思路,我们分两个步骤估计宏观-金融模型。第一步,估计宏观经济模块所表述的状态空间模型;第二步,在宏观经济模块参数估计值的基础上,对不同期限利率理论值与实际值误差的平方和进行最小化计算,估计金融模块的未知参数。宏观-金融模型的参数估计结果如表1所示。表1显示,模型整体效果良好,参数的大部分估计值显著。宏观经济模块的参数估计值符号与预期符号相同,这说明新凯恩斯理论所描述的经济规律可以解释我国宏观经济的实际运行情况。从宏观经济模块中的具体方程来看,总需求方程中的a 2估计值为0.0055,模型中a 2前面的系数符号为负,因此实际利率缺口和产出缺口之间的替代系数为-0.0055,两者间具有负向替代关系;总供给方程中的b2估计值为0.0031,表明产38
