华东师大版九上数学第3课时 坡度问题
华师大版2020-2021年九年级数学上册导学案:24.4 第3课时 坡度问题【含答案】

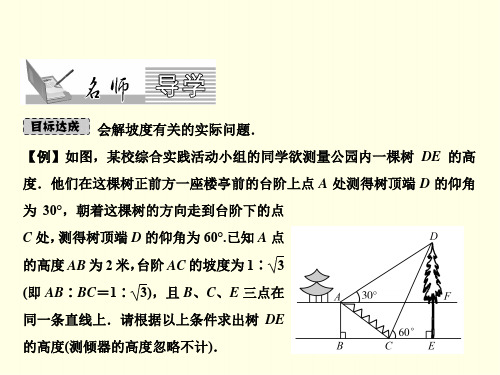
华师大版2020-2021年九年级数学上册导学案第24章 解直角三角形24.4解直角三角形 第3课时 坡度问题学习目标:1.理解坡度、坡角的概念(重点).2.能够解决与坡度、坡角有关的实际问题(难点).自主学习一、新知预习在修路、挖河、开渠和筑坝时,设计图纸上都要注明斜坡的倾斜程度.如图,坡面的铅垂高度h 和水平长度l 的比叫做坡面的______(或坡比),记作i ,即i=l h.坡度通常写成1:m 的形式,如i=1:6.坡面与水平面的夹角叫做______,记作α,有i=lh=tan α.显然,坡度越大,坡角α就越____,坡面就越____. 合作探究一、探究过程探究点1:利用坡度、坡角解决实际问题 【典例精析】例 水库大坝的横断面是梯形,坝顶宽6 m ,坝高23 m ,斜坡AB 的坡度i=1∶3 ,斜坡CD 的坡度i ’=1∶2.5 , 则斜坡CD 的坡面角α,坝底宽AD 和斜坡AB 的长应设计为多少(参考数据:tan18.4°≈31)?【归纳总结】根据坡度的定义i =hl ,解题时需先求得水平距离l 和铅直高度h .【针对训练】1.(1)一斜坡的坡角为30°,则它的坡度为 ;(2)如果一个坡度为1∶2.5,则这个坡角为 (用计算器计算,结果精确到0.1°); (3)等腰梯形的较小底长为3,腰长为5,高为4,则另一个底长为 ,坡度为 ; (4)堤坝横断面是等腰梯形(如图所示).若AB=10 m,CD=4 m,高h=4 m,则坡度i= ,AD= m.第1题图 第2题图2如图,在平面上种植树木时,要求株距(相邻两树间的水平距离)为4m ,如果在坡度为0.75的山坡上种树,也要求株距为4m ,那么相邻两树间的坡面距离为( ) A .5m B .6m C .7m D .8m二、课堂小结坡度、坡比问题图解坡面的垂直高度h 和水平宽度l 的比值叫做坡面的坡度(或坡比),坡面与水平面的夹角α叫做坡角,显然tan α=_______.当堂检测1.如图是拦水坝的横断面,斜坡AB 的水平宽度AC 为6米,斜面坡度为1:3,则斜坡AB 的长为( ) A .210米B .3米C .6米D .12米第1题图 第2题图2.如图,在坡度为1:2的山坡上种树,要求相邻两棵树的水平距离是6m ,则斜坡上相邻两棵树的坡面距离是( ) A .3m B .3m C .12m D .6m3.小明沿着坡度为1:的斜坡向上行走了10米,则他的垂直高度上升了 米.4. 如图,给高为3米,坡度为1∶1.5的楼梯表面铺地毯.已知每级楼梯宽度为1.5米,地毯的价格为每平方米8元,则铺完整个楼梯共需______元.第4题图第5题图5.一座拦河大坝的横截面如图所示,已知AB=20 m,斜坡AB的坡比是1∶2,斜坡DC的坡比是3∶4,则DC的长是米.6.如图,A,B两地被大山阻隔,由A地到B地需要先爬坡到山顶C地,再下坡到B地,已知坡面AC的坡度i=1:,坡面BC的坡角∠CBA=45°,BC=4千米.若修建一条穿山隧道AB,则隧道打通后与打通前相比,从A地到B地的路程约缩短多少千米(结果精确到0.01千米.参考数据:≈1.414,≈1.732)?能力提升7.某校教学楼后面紧邻着一个山坡,坡上面是一块平地,如图所示,BC∥AD,BE⊥AD,斜坡AB长为26米,斜坡AB的坡度i=12∶5,为了减缓坡面防山体滑坡,保障安全,学校决定对该斜坡进行改造,经地质人员勘测,当坡角不超过50°时,可确保山体不滑坡.(1)求改造前坡顶到地面的距离BE的长;(2)如果改造时保持坡脚A不动,坡顶B沿BC向左移11米到F点处,问这样改造能确保安全吗(参考数据:tan48.8°≈1.14)?参考答案自主学习 一、新知预习坡度 坡角 大 陡 合作探究一、探究过程 【典例精析】例 解:如图,作BE ⊥AD 于E ,CF ⊥AD 于F.∵斜坡AB 的坡度i =1:3,∴tanA =,∴α≈18.4°.∴=.∴AE =69m.∴AB =≈72.7(m ).∵斜坡CD 的坡度i ′=1∶2.5,∴tan ∠D ==.∴=.∴DF =57.5m.∴AD =AE +EF +DF =69+6+57.5=132.5(m ).故斜坡AB 的坡面角α约为18.4°,坝底宽AD 的长是132.5m ,斜坡AB 的长是72.7m .【针对训练】1.(1)1∶3(2)21.8 (3)9 4∶3 (4)4∶3 52.A 二、课堂小结 h ∶l 当堂检测1. A2.B3.54.905.6. 解:作CD ⊥AB 于点D ,在Rt △BCD 中,∵∠CBA =45°,BC =4千米,∴CD = BD =4千米.∵坡面AC 的坡度i =1:,∴31=.∴AD =CD =4.∴AC ==8千米.∵AB =AD +BD ,∴AB =(4+4)千米.又∵AC +CB =(8+4)千米,∴AC +CB ﹣AB =8+4﹣4﹣4≈2.73(千米).答:隧道打通后与打通前相比,从A 地到B 地的路程约缩短2.73千米.7. 解:(1)设AE =5x ,∵斜坡AB 的坡比为i =12∶5,∴BE =12x ,由勾股定理,得AE 2+ BE 2=AB 2,即(5x )2+(12x )2=262,解得x =2,∴BE =12x =24米.(2)如图,作FH⊥AD于H,连接F A.由(1)知AE=10米.由题意,得AH=11+10=21(米).在Rt△AFH中,tan∠F AH==≈1.14,则∠F AH≈48.8°.∵48.8°<50°,∴这样改造能确保安全.。
初中数学九上《坡比、坡度问题》华东师大版

(2) AD=AG+GH+HD=6.4+6+6.4=18.8(m)
S SHMED SABCD
6 29.4 5.2 6 18.8 3.2 92.04 39.68 52.36(m2)
2
2
答:增加部分的横断面积52.36 m2
解后反思
利用解直角三角形的知识解决实际问题 的一般过程是:
(1)将实际问题抽象为数学问题(画出平面图 形,转化为解直角三角形的问题); (2)根据条件的特点,适当选用锐角三角形函 数等去解直角三角形; (3)得到数学问题的答案; (4)得到实际问题的答案.
10:53
B如C图为:6m是,一堤海高堤为的3横.2断m: ,面为为了梯提形: 高AB海C堤D,的已拦知水堤能顶力宽, 需要将海堤加高2m,并且保持堤顶宽度不变,迎水坡 CD的坡度也不变。但是背水坡的坡度由原来的i=1:2改 成i=1:2.5(有关数据在图上已注明)。
②修一条长为100米的渠道要挖去的土方数.
分析: 1.将实际问题转化为数学问题. 2.要求S等腰梯形ABCD,首先要求出AD,
如何利用条件求AD? 3.土方数=S·l
10:53
∴AE=1.5×0.6=0.9(米). ∵等腰梯形ABCD, ∴FD=AE=0.9(米). ∴AD=2×0.9+0.5=2.3(米).
在Rt△BCF中,同理可得: BF
4.2
7.90(米)
∴AB=AE+EF+BF
tan 28
≈6.72+12.51+7.90≈27.1(米).
答: 路基下底的宽约为27.1米.
12.51米
D
C
4.2米
初三上数学课件(华东师大)-坡度与坡角
h
坡度 (或坡比),记作 i,即 i= l .坡度一般写成 1∶m 的形式.坡面
与水平面的夹角叫做 坡角 ,记作 α,有 i=hl = tanα α 就 越大 ,坡面就 越陡 .
.坡度越大,坡角
1.下列对坡度的描述正确的是( B )
A.坡度是指斜坡与水平线夹角的度数
B.坡度是指斜坡的铅垂高度与水平宽度的比
解:(1)∵FD∥CG,∴∠BDF=∠BAC=45°,∵斜坡 AB 长 60 2米,D 是 AB 的中点,∴BD=30 2米,∴DF=BD·cos∠BDF=30 2× 22=30(米), BF=DF=30 米.∵斜坡 BE 的坡比为 3∶1,∴BEFF= 13,∴EF=10 3米, ∴DE=DF-EF=(30-10 3)米,∴休闲平台 DE 的长是(30-10 3)米; (2)设 GH=x 米,则 MH=GH-GM=(x-30)米,DM=AG+AP=33+30 =63(米),在 Rt△DMH 中,tan30°=MDMH,即x-6330= 33,解得 x=30+21 3, ∴建筑物 GH 的高为(30+21 3)米.
11.为邓小平诞辰 110 周年献礼,广安市政府 对城市建设进行了整改.如图,斜坡 AB 长 60 2 米,坡角(即∠BAC)为 45°,BC⊥AC,现计划 在斜坡中点 D 处挖去部分斜坡,修建一个平行 于水平线 CA 的休闲平台 DE 和一条新的斜坡 BE(下面两个小题结果都保留根号). (1)若修建的斜坡 BE 的坡比为 3∶1,求休闲平台 DE 的长; (2)一座建筑物 GH 距离 A 点 33 米远(即 AG=33 米),小亮在 D 点测得建筑 物顶部 H 的仰角(即∠HDM)为 30°.点 B、C、A、G、H 在同一个平面内, 点 C、A、G 在同一条直线上,且 HG⊥CG,问建筑物 GH 高为多少米?
华东师大版九年级数学上册《24章 解直角三角形 24.4 解直角三角形 坡比、坡度问题》教学案例_10

A C ┌24.2解直角三角形第3课时 解直角三角形的应用——坡度、坡角教学设计学习目标1、理解坡度、坡角的概念2、继续巩固解直角三角形的知识,提高学生的应用能力。
学习重难点重点: 锐角三角函数在解直角三角形中的灵活运用难点:要求学生善于将某些实际问题中的数量关系,归结为直角三角形中元素之间的关系,从而解决问题.自主学习A 、情境导入分组练习,互问互答,巩固勾股定理和锐角三角函数定义等内容,回顾仰角与俯角等概念。
在修路、挖河、开渠和筑坝时,设计图纸上都要注明斜坡的倾斜程度,何为倾斜程度呢?B 、明确目标使学生养成“先画图,再求解”的习惯;灵活运用坡度、坡角在实际问题情境下的应用,以及熟练应用直角三角形的边角关系。
C 、自主学习自学课本,理解坡度、坡角的概念,并能熟练应用于实际问题中,时间为10分钟。
合作探究看完课本后,对于课本中的例4,有不懂的地方,同桌之间交流,再解决不了得地方小组讨论解决,然后自己做完课后练习题,同桌之间相互检查,做错的地方相互讨论指正。
E 、展示反馈由小组中的一名同学,回答练习题答案,其他同学根据自己的答案指出异同点。
F 、精讲点拨内容总结 坡角是斜坡与水平线的夹角;坡度是指斜坡上任意一点的高度与水平距离的比值。
坡角与坡度之间的关系是:i =lh =tan a 。
坡度越大,坡角就越大,坡面就越陡。
方法归纳在涉及梯形问题时,常常首先把梯形分割成我们熟悉的三角形、平行四边形,再借助这些熟悉图形的性质与特征来加以研究。
G 、课堂小结坡度、坡角的的概念,坡度与坡角的关系,以及它们在实际问题中的实际应用。
H 、达标检测1、如图,有一斜坡AB 长40m ,坡顶离地面的高度为20m,求此斜坡的倾斜角. B2.如图,水库大坝的截面是梯形ABCD,坝顶AD=6m,坡长CD=8m.坡底BC=30m,∠ADC=135°.(1)求坡角∠ABC 的大小;(2)如果坝长100m,那么修建这个大坝共需多少土石方(结果精确到0.01m3 ).I 、 拓展提高3.如图,沿水库拦水坝的背水坡将坝面加宽两米,坡度由原来的1:2改成1:2.5,已知原背水坡长BD=13.4米, 求: (1)原背水坡的坡角 和加宽后的背水坡的坡角 ; (2)加宽后水坝的横截面面积增加了多少?(精确到0.01)AB C DB A E F。
九年级数学上册第24章4解直角三角形第3课时解直角三角形的应用_坡度坡角同步练习新版华东师大版

24.4 第3课时 解直角三角形的应用——坡度、坡角知识点 1 坡度与坡角1.以下对坡度的描述正确的是( ) A. 坡度是指坡面与水平面夹角的度数B. 坡度是指坡面的铅垂高度与水平长度的比C. 坡度是指坡面的水平长度与铅垂高度的比D. 坡度是指坡面的水平长度与坡长的比2.若斜坡AB 的坡角为56°19′,坡度i ≈3∶2,则( ) A .sin56°19′≈1.5 B .cos56°19′≈1.5 C .tan56°19′≈1.5 D .tan56°19′≈233.如果坡角的余弦值为31010,那么坡度为( )A .1∶10B .3∶10C .1∶3D .3∶1 4.[2017·济南]如图24-4-24,为了测量山坡护坡石坝的坡度(坡面的铅垂高度与水平长度的比称为坡度),把一根长5 m 的竹竿AC 斜靠在石坝旁,量出竹竿上距离竹竿底端1 m 处的点D 离地面的高度DE =0.6 m ,又量得竿底与坝脚的距离AB =3 m ,则石坝的坡度为( )A. 34 B .3 C. 35D .4图24-4-245.如图24-4-25,小明爬一土坡,他从A 处爬到B 处所走的直线距离AB =4米,此时,他离地面的高度h =2米,则这个土坡的坡角为________.图24-4-255.如图24-4-25,小明爬一土坡,他从A 处爬到B 处所走的直线距离AB =4米,此时,他离地面的高度h =2米,则这个土坡的坡角为________.6.[教材例4变式]渠道的横断面如图24-4-26,渠口宽AD =4 m ,渠底宽BC =2 m ,AD ∥BC ,AB =CD ,渠深1 m ,求渠壁的坡度和坡角α .图24-4-26知识点 2 坡面距离、坡面的水平距离(或铅垂高度) 7.[2017·温州]如图24-4-27,一辆小车沿倾斜角为α的斜坡向上行驶13米,已知cos α=1213,则小车上升的高度是( )A .5米B .6米C .6.5米D .12米图24-4-278.如图24-4-28是拦水坝的横断面,斜坡AB 的水平长度为12米,坡面坡度为1∶2,则斜坡AB 的长为( )A .4 3米B .6 5米C .12 5米D .24米图24-4-289.如图24-4-29,在坡度为1∶2的山坡上种树,要使株距(相邻两棵树的水平距离)是6 m ,则斜坡上相邻两棵树的坡面距离是( )A .6 mB .3 5 mC .3 mD .12 m图24-4-2910.[2017·泰州]小明沿着坡度i 为1∶3的直路向上走了50 m ,则小明沿垂直方向升高了______m.11.某地下车库的入口处有一斜坡AB ,其坡度i =5∶12,且AB =26 m ,则车库的深度为___________________m.12.如图24-4-30,一人乘雪橇沿坡度为1∶3的斜坡笔直滑下,滑下的距离s (米)与时间t (秒)之间的关系式为s =10t +2t 2.若滑到坡底的时间为4秒,求此人下降的高度为多少米.图24-4-3013.[教材练习变式][2017·重庆]如图24-4-31(示意图),已知点C 与某建筑物底端B 相距306米(点C 与点B 在同一水平面上),某同学从点C 出发,沿同一剖面的斜坡CD 行走195米至坡顶D 处,斜坡CD 的坡度(或坡比)i =1∶2.4,在D 处测得该建筑物顶端A 的俯角为20°,则该建筑物AB 的高度为(精确到0.1米,参考数据:sin20°≈0.342,cos20°≈0.940,tan20°≈0.364)( )A .29.1米B .31.9米C .45.9米D .95.9米图24-4-3114.如图24-4-32所示,小刚早晨起来去爬山,他从山脚沿坡度为1∶1的坡面前进了100 m 到达B 点,后又沿坡角为60°的坡面前进了200 m 到达山顶C 点,则此山高为__________m.图24-4-3215.[2016·泸州]如图24-4-33,为了测量出楼房AC 的高度,从距离楼底C 处60 3米的点D (点D 与楼底C 在同一水平面上)出发,沿坡面坡度i =1∶3的斜坡DB 前进30米到达点B ,在点B 处测得楼顶A 的仰角为53°,求楼房AC 的高度.(K参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈43,计算结果用根号表示,不取近似值 )K图24-4-3316.[2017·黔东南州]如图24-4-34,某校教学楼AB 后方有一斜坡,已知斜坡CD 的长为12米,坡角α为60°.根据有关部门的规定,当∠α≤39°时,才能避免滑坡危险,学校为了消除安全隐患,决定对斜坡CD 进行改造,在保持坡脚C 不动的情况下,学校至少要把坡顶D 向后水平移动多少米才能保证教学楼的安全?(结果取整数,参考数据:sin39°≈0.63,cos39°≈0.78,tan39°≈0.81,2≈1.41,3≈1.73,5≈2.24)图24-4-3417.如图24-4-35,某人在山坡坡脚C 处测得一座建筑物顶点A 的仰角为60°,沿山坡向上走到P 处再测得该建筑物顶点A 的仰角为45°.已知BC =90米,且B ,C ,D 在同一条直线上,坡面坡度为12(即tan ∠PCD =12).(1)求该建筑物的高度(即AB 的长);(2)求此人所在位置点P 的铅垂高度(测倾器的高度忽略不计,结果保留根号).图24-4-35教师详答1.B 2.C 3.C 4.B 5.30°6.解:分别过点A ,D 作AE ⊥BC 于点E ,DF ⊥BC 于点F . ∵AD ∥BC ,∴四边形AEFD 为矩形, ∴EF =AD ,AE =DF . 又∵AB =DC ,∴Rt △ABE ≌Rt △DCF , ∴BE =CF .∵AD =4 m ,BC =2 m , ∴BE =CF =1 m ,∴渠壁的坡度i =1∶1, 即tan α=1, ∴α=45°.答:渠壁的坡度为1∶1, 坡角α为45°.7.A [解析] 如图,假设AC =13米,作CB ⊥AB 于点B , ∵cos α=1213=ABAC ,∴AB =12(米),∴BC =AC 2-AB 2=132-122=5(米), ∴小车上升的高度是5米. 故选A.8.B [解析] 在Rt △ABC 中,∵BC AC =i =12,AC =12米,∴BC =6米.根据勾股定理,得AB =AC 2+BC 2=6 5米.故选B. 9.B10.25 [解析] 如图,过点B 作BE ⊥AC 于点E , ∵坡度i =1∶3, ∴tan A =1∶3=33, ∴∠A =30°. ∵AB =50 m , ∴BE =12AB =25 m ,∴小明沿垂直方向升高了25 m. 故答案为25.11.1012.解:如图,由题意知t =4时,s =72,i =1∶ 3.设BC =x ,则AC =3x , 由勾股定理得AB =2x =72, ∴x =36, ∴BC =36,∴此人下降的高度为36米.13.A [解析] 作DE ⊥BC 于点E ,作AF ⊥DE 于点F ,如图. 设DE =x 米,则CE =2.4x 米,由勾股定理,得 x 2+(2.4x )2=1952, 解得x =75,∴DE =75米,CE =2.4x =180米, EB =BC -CE =306-180=126(米). ∵AF ∥DG ,∴∠1=∠ADG =20°,∴tan ∠1=tan ∠ADG ≈0.364.∵AF =EB =126米,tan ∠1=DF AF≈0.364, ∴DF ≈0.364AF =0.364×126≈45.86(米), ∴AB =FE =DE -DF ≈75-45.86≈29.1(米). 故选A.14. (50 2+100 3)15.解:过点B 作BE ⊥CD 于点E ,BF ⊥AC 于点F ,则四边形CEBF 是矩形. ∵斜面DB 的坡度i =1∶3,∴∠BDE =30°. 在Rt △BED 中,BD =30,∴BE =BD ·sin30°=15,ED =BD ·cos30°=15 3, ∴BF =CE =CD -ED =45 3. 在Rt △AFB 中,∠ABF =53°,∴AF =BF ·tan ∠ABF ≈45 3×43=60 3,∴AC =AF +FC =AF +BE ≈60 3+15. 答:楼房AC 的高度约为(60 3+15)米. 16.[解析] 假设点D 水平移动到点D ′的位置时,恰好有∠D ′CE =39°,过点D 作DE ⊥AC 于点E ,过点D ′作D ′E ′⊥AC 于点E ′,根据锐角三角函数的定义求出DE ,CE ,CE ′的长,进而可得出结论.解:假设点D 水平移动到D ′的位置时,恰好有∠D ′CE =39°,过点D 作DE ⊥AC 于点E ,过点D′作D′E′⊥AC于点E′,∵CD=12米,∠DCE=60°,∴DE=CD·sin60°=12×32=6 3(米),CE=CD·cos60°=12×12=6(米).∵DE⊥AC,D′E′⊥AC,DD′∥CE′,∴四边形DEE′D′是矩形,∴D′E′=DE=6 3米.∵∠D′CE′=39°,∴CE′=D′E′tan39°≈6 30.81≈12.8(米),∴EE′=CE′-CE≈12.8-6=6.8≈7(米),∴DD′=EE′≈7米.答:学校至少要把坡顶D向后水平移动7米才能保证教学楼的安全.17.解:(1)在Rt△ABC中,BC=90,∠ACB=60°,∴AB=BC·tan60°=90 3.答:该建筑物的高度为90 3米.(2)过点P作PE⊥BD于点E,PF⊥AB于点F,则四边形BEPF是矩形,∴PE=BF,PF=BE.设PE=x,则BF=PE=x.在Rt△PCE中, tan∠PCD=PECE=12,∴CE=2x.∵AF=AB-BF=90 3-x,PF=BE=BC+CE=90+2x,且在Rt△APF中,∠APF=45°,∴AF=PF,即90 3-x=90+2x.解得x=30 3-30.答:此人所在位置点P的铅垂高度为(30 3-30)米.。
24.4解直角三角形第3课时坡度、坡角课件

第24章 解直角三角形
24.4 第3课时 坡度、坡角的问题
洛阳市双语实验学校
知识回顾
解直角三角形的依据
(1)三边之间的关系: a2+b2=c2(勾股定理);
(2)两锐角之间的关系:∠ A+ ∠ B= 90º
B
(3)边角之间的关系
自动扶梯与地面所成的夹角为θ,则tanθ的值为_____
4.如下图,河堤的横断面中,堤高BC是5米,迎水斜坡
AB的长丝13米,那么斜坡AB的坡度是( C )
A.1:3
B.1:2.6
C.1:2.4
D.1:2
B
C
A
中考链接
如走i=图了1:,0.4小6的5明千斜从米坡点到向A达上处点走出了B发,1,s千i沿米nα着达=坡到角点153为C.α问,的小然斜明后坡从又向A沿上点着到坡点度C上为 升的高度CD是多少千米(结果保留根号)?
3.得到数学问题的答案;
4.得到实际问题的答案.
课堂小结
3.
4.
洛阳市双语实验学校
再见!
洛阳市双语实验学校
自学内容: 课本115页
A
6
i 1 : 3B
C
i=1:2.5
23
D
坡面
α 水平面
铅垂高度(h)
1.坡度(或坡比): 坡度通常写成1: m 的形式.
2.坡角: 坡面与水平面的夹角叫做坡角,记作α.
3.坡度与坡角的关系:
1、斜坡的坡度是1 : 3 ,则坡角α=___3_0__度。 2、斜坡的坡角是450 ,则坡比是 __1_:_1___。
B
【解】
A
C
α
FD
九年级数学上册第24章解直角三角形24.4解直角三角形第3课时坡问题教案新版华东师大版12
九年级数学上册第24章解直角三角形24.4解直角三角形第3课时坡问题教案新版华东师大版121.理解并掌握坡度、坡比的定义;2.学会用坡度、坡比解决实际问题.(重点、难点)一、情境导入在现实生活中,测量某些量可以采取不同的方法,某斜面的截面如图所示,两位同学分别选取不同的点进行测量.从F 处进行测量和从A 处进行测量的数据如图所示.你能否通过所学知识求得该坡面的铅直高度?二、合作探究探究点:与坡度或坡角有关的实际问题一辆汽车从坡底走到坡顶共用30s ,车速是2m/s ,汽车行驶的水平距离是40m ,则这个斜坡的坡度是________.解析:坡面距离为30×2=60m ,水平距离为40m ,∴铅直高度为602-402=205(m),∴坡度i =205∶40=5∶2.方法总结:根据坡度的定义i =h l,解题时需先求得水平距离l 和铅直高度h . 如图所示,在平面上种植树木时,要求株距(相邻两树间的水平距离)为4m ,如果在坡度为0.75的山坡上种树,也要求株距为4m ,那么相邻两树间的坡面距离为( )A .5mB .6mC .7mD .8m解析:由题知,水平距离l =4m ,i =0.75,∴铅直高度h =l ·i =4×0.75=3(m),∴坡面距离为32+42=5(m).故选A.方法总结:解此类题,首先根据坡度的定义,求得水平距离或铅直高度,再根据勾股定理,求得坡面距离.如图所示,给高为3米,坡度为1∶1.5的楼梯表面铺地毯.已知每级楼梯长度为1.5米,地毯的价格为每平方米8元,则铺完整个楼梯共需多少元?解析:由于楼梯的长度已知,所以要求地毯的总面积,需求地毯的总长度,由题意知,地毯的总长度为BC 与AC 的和,而由坡度的定义知BC AC =11.5,所以AC 可求.解:∵BC AC =11.5,∴AC =1.5BC =1.5×3=4.5(米).∴AC +BC =4.5+3=7.5(米).∴地毯的总面积为1.5×7.5=11.25(平方米). ∴需要的钱数为8×11.25=90(元). 答:铺完整个楼梯共需90元.三、板书设计坡度(坡比)的问题:坡面的铅直高度h 和水平宽度l 的比叫坡度(或坡比),即i =tan α=ih,坡面与水平面的夹角α叫坡角.本课时主要培养学生分析问题、解决问题的能力;渗透数形结合的数学思想和方法.进一步感知坡度、坡角与实际生活的密切联系,认识将知识应用于实践的意义.。
【华东师大版】九年级数学上册 同步练习第24章解直角三角形第3课时解直角三角形的应用_坡度坡角
24.4 第3课时 解直角三角形的应用——坡度、坡角知识点 1 坡度与坡角1.以下对坡度的描述正确的是( ) A. 坡度是指坡面与水平面夹角的度数B. 坡度是指坡面的铅垂高度与水平长度的比C. 坡度是指坡面的水平长度与铅垂高度的比D. 坡度是指坡面的水平长度与坡长的比2.若斜坡AB 的坡角为56°19′,坡度i ≈3∶2,则( ) A .sin56°19′≈1.5 B .cos56°19′≈1.5 C .tan56°19′≈1.5 D .tan56°19′≈233.如果坡角的余弦值为31010,那么坡度为( )A .1∶10B .3∶10C .1∶3D .3∶1 4.[2017·济南]如图24-4-24,为了测量山坡护坡石坝的坡度(坡面的铅垂高度与水平长度的比称为坡度),把一根长5 m 的竹竿AC 斜靠在石坝旁,量出竹竿上距离竹竿底端1 m 处的点D 离地面的高度DE =0.6 m ,又量得竿底与坝脚的距离AB =3 m ,则石坝的坡度为( )A. 34 B .3 C. 35D .4图24-4-245.如图24-4-25,小明爬一土坡,他从A 处爬到B 处所走的直线距离AB =4米,此时,他离地面的高度h =2米,则这个土坡的坡角为________.图24-4-255.如图24-4-25,小明爬一土坡,他从A 处爬到B 处所走的直线距离AB =4米,此时,他离地面的高度h =2米,则这个土坡的坡角为________.6.[教材例4变式]渠道的横断面如图24-4-26,渠口宽AD =4 m ,渠底宽BC =2 m ,AD ∥BC ,AB =CD ,渠深1 m ,求渠壁的坡度和坡角α .图24-4-26知识点 2 坡面距离、坡面的水平距离(或铅垂高度) 7.[2017·温州]如图24-4-27,一辆小车沿倾斜角为α的斜坡向上行驶13米,已知cos α=1213,则小车上升的高度是( )A .5米B .6米C .6.5米D .12米图24-4-278.如图24-4-28是拦水坝的横断面,斜坡AB 的水平长度为12米,坡面坡度为1∶2,则斜坡AB 的长为( )A .4 3米B .6 5米C .12 5米D .24米图24-4-289.如图24-4-29,在坡度为1∶2的山坡上种树,要使株距(相邻两棵树的水平距离)是6 m ,则斜坡上相邻两棵树的坡面距离是( )A .6 mB .3 5 mC .3 mD .12 m图24-4-2910.[2017·泰州]小明沿着坡度i 为1∶3的直路向上走了50 m ,则小明沿垂直方向升高了______m.11.某地下车库的入口处有一斜坡AB ,其坡度i =5∶12,且AB =26 m ,则车库的深度为___________________m.12.如图24-4-30,一人乘雪橇沿坡度为1∶3的斜坡笔直滑下,滑下的距离s (米)与时间t (秒)之间的关系式为s =10t +2t 2.若滑到坡底的时间为4秒,求此人下降的高度为多少米.图24-4-3013.[教材练习变式][2017·重庆]如图24-4-31(示意图),已知点C 与某建筑物底端B 相距306米(点C 与点B 在同一水平面上),某同学从点C 出发,沿同一剖面的斜坡CD 行走195米至坡顶D 处,斜坡CD 的坡度(或坡比)i =1∶2.4,在D 处测得该建筑物顶端A 的俯角为20°,则该建筑物AB 的高度为(精确到0.1米,参考数据:sin20°≈0.342,cos20°≈0.940,tan20°≈0.364)( )A .29.1米B .31.9米C .45.9米D .95.9米图24-4-3114.如图24-4-32所示,小刚早晨起来去爬山,他从山脚沿坡度为1∶1的坡面前进了100 m 到达B 点,后又沿坡角为60°的坡面前进了200 m 到达山顶C 点,则此山高为__________m.15.[2016·泸州]如图24-4-33,为了测量出楼房AC 的高度,从距离楼底C 处60 3米的点D (点D 与楼底C 在同一水平面上)出发,沿坡面坡度i =1∶3的斜坡DB 前进30米到达点B ,在点B 处测得楼顶A 的仰角为53°,求楼房AC 的高度.(K参考数据:sin53°≈0.8,cos53°≈0.6,tan53°≈43,计算结果用根号表示,不取近似值 )K图24-4-3316.[2017·黔东南州]如图24-4-34,某校教学楼AB 后方有一斜坡,已知斜坡CD 的长为12米,坡角α为60°.根据有关部门的规定,当∠α≤39°时,才能避免滑坡危险,学校为了消除安全隐患,决定对斜坡CD 进行改造,在保持坡脚C 不动的情况下,学校至少要把坡顶D 向后水平移动多少米才能保证教学楼的安全?(结果取整数,参考数据:sin39°≈0.63,cos39°≈0.78,tan39°≈0.81,2≈1.41,3≈1.73,5≈2.24)图24-4-3417.如图24-4-35,某人在山坡坡脚C 处测得一座建筑物顶点A 的仰角为60°,沿山坡向上走到P 处再测得该建筑物顶点A 的仰角为45°.已知BC =90米,且B ,C ,D 在同一条直线上,坡面坡度为12(即tan ∠PCD =12).(1)求该建筑物的高度(即AB 的长);(2)求此人所在位置点P 的铅垂高度(测倾器的高度忽略不计,结果保留根号).图24-4-35教师详答1.B 2.C 3.C 4.B 5.30°6.解:分别过点A ,D 作AE ⊥BC 于点E ,DF ⊥BC 于点F . ∵AD ∥BC ,∴四边形AEFD 为矩形, ∴EF =AD ,AE =DF . 又∵AB =DC ,∴Rt △ABE ≌Rt △DCF , ∴BE =CF .∵AD =4 m ,BC =2 m , ∴BE =CF =1 m ,∴渠壁的坡度i =1∶1, 即tan α=1, ∴α=45°.答:渠壁的坡度为1∶1, 坡角α为45°.7.A [解析] 如图,假设AC =13米,作CB ⊥AB 于点B , ∵cos α=1213=ABAC ,∴AB =12(米),∴BC =AC 2-AB 2=132-122=5(米), ∴小车上升的高度是5米. 故选A.8.B [解析] 在Rt △ABC 中,∵BC AC =i =12,AC =12米,∴BC =6米.根据勾股定理,得AB =AC 2+BC 2=6 5米.故选B. 9.B10.25 [解析] 如图,过点B 作BE ⊥AC 于点E , ∵坡度i =1∶3, ∴tan A =1∶3=33, ∴∠A =30°. ∵AB =50 m , ∴BE =12AB =25 m ,∴小明沿垂直方向升高了25 m. 故答案为25.11.1012.解:如图,由题意知t =4时,s =72,i =1∶ 3.设BC =x ,则AC =3x , 由勾股定理得AB =2x =72, ∴x =36, ∴BC =36,∴此人下降的高度为36米.13.A [解析] 作DE ⊥BC 于点E ,作AF ⊥DE 于点F ,如图. 设DE =x 米,则CE =2.4x 米,由勾股定理,得 x 2+(2.4x )2=1952, 解得x =75,∴DE =75米,CE =2.4x =180米, EB =BC -CE =306-180=126(米). ∵AF ∥DG ,∴∠1=∠ADG =20°,∴tan ∠1=tan ∠ADG ≈0.364.∵AF =EB =126米,tan ∠1=DF AF≈0.364, ∴DF ≈0.364AF =0.364×126≈45.86(米), ∴AB =FE =DE -DF ≈75-45.86≈29.1(米). 故选A.14. (50 2+100 3)15.解:过点B 作BE ⊥CD 于点E ,BF ⊥AC 于点F ,则四边形CEBF 是矩形. ∵斜面DB 的坡度i =1∶3,∴∠BDE =30°. 在Rt △BED 中,BD =30,∴BE =BD ·sin30°=15,ED =BD ·cos30°=15 3, ∴BF =CE =CD -ED =45 3. 在Rt △AFB 中,∠ABF =53°,∴AF =BF ·tan ∠ABF ≈45 3×43=60 3,∴AC =AF +FC =AF +BE ≈60 3+15. 答:楼房AC 的高度约为(60 3+15)米. 16.[解析] 假设点D 水平移动到点D ′的位置时,恰好有∠D ′CE =39°,过点D 作DE ⊥AC 于点E ,过点D ′作D ′E ′⊥AC 于点E ′,根据锐角三角函数的定义求出DE ,CE ,CE ′的长,进而可得出结论.解:假设点D 水平移动到D ′的位置时,恰好有∠D ′CE =39°,过点D 作DE ⊥AC 于点E ,过点D′作D′E′⊥AC于点E′,∵CD=12米,∠DCE=60°,∴DE=CD·sin60°=12×32=6 3(米),CE=CD·cos60°=12×12=6(米).∵DE⊥AC,D′E′⊥AC,DD′∥CE′,∴四边形DEE′D′是矩形,∴D′E′=DE=6 3米.∵∠D′CE′=39°,∴CE′=D′E′tan39°≈6 30.81≈12.8(米),∴EE′=CE′-CE≈12.8-6=6.8≈7(米),∴DD′=EE′≈7米.答:学校至少要把坡顶D向后水平移动7米才能保证教学楼的安全.17.解:(1)在Rt△ABC中,BC=90,∠ACB=60°,∴AB=BC·tan60°=90 3.答:该建筑物的高度为90 3米.(2)过点P作PE⊥BD于点E,PF⊥AB于点F,则四边形BEPF是矩形,∴PE=BF,PF=BE.设PE=x,则BF=PE=x.在Rt△PCE中, tan∠PCD=PECE=12,∴CE=2x.∵AF=AB-BF=90 3-x,PF=BE=BC+CE=90+2x,且在Rt△APF中,∠APF=45°,∴AF=PF,即90 3-x=90+2x.解得x=30 3-30.答:此人所在位置点P的铅垂高度为(30 3-30)米.。
初中数学华东师大版九年级上册坡比、坡度问题 课件PPT
BC AC1、坡角来自i= h : l 坡面 h
α 水平面 l
坡面与水平面的夹角叫做坡角,记作α 。
2、坡度(或坡比)
如图所示,坡面的铅垂高度(h)和水平长度(l)
的比叫做坡面的坡度(或坡比),记作i, 即 i=—h— l
坡度通常写成1∶m的形式,如i=1∶6.
3、坡度与坡角的关系
ih l tan 坡度等于坡角的正切值
初中数学华东师大版九年级上册 《坡比、坡度问题》
类型:获奖课件PPT
——坡度、坡角
温故知新
三边之间关系 锐角之间关系
边角之间关系 (以锐角A为例)
a2+b2=c2(勾股定理)
∠A+∠B=90º
sin
A
A的对边 斜边
BC AB
cos
A
A的邻边 斜边
AC AB
tan
A
A的对边 A的邻边
温故知新
特殊角的三角函数值
快速抢答:(看谁又快又准!说出角的度 数)
例1 例2
1、斜坡的坡度是 √3:1 则坡角α=__6_0___度。
2、斜坡的坡角是450 ,则坡比是 1_:__1____。
3、斜坡长是12米,坡高6米,则坡比是1__:___3_
_。
h α
L
九年级数学上册24.4解直角三角形第3课时坡度坡角在解直角三角形中的应用作业课件华东师大版
一、选择题(每小题 6 分,共 12 分) 8.在平昌冬奥会上,一运动员乘滑雪板沿坡比 为 1∶ 3 的斜坡笔直滑下,滑下的距离 s(m)与 时间 t(s)间的关系为 s=10t+2t2.若滑到坡底的时 间为 4 s,则此人下降的高度为( C ) A.72 m B.36 3 m C.36 m D.18 3 m
解:延长 BC 交 OP 于点 H. ∵斜坡 AP 的坡度为 1∶2.4,∴APDD =152 ,设 AD=5k,则 PD=12k, 由勾股定理,得 AP=13k, ∴13k=26,解得 k=2,∴AD=10,∵BC⊥AC,AC∥PO,∴BH⊥PO, ∴四边形 ADHC 是矩形,CH=AD=10,AC=DH,∵∠BPD=45°, ∴PH=BH,设 BC=x,则 x+10=24+DH,∴AC=DH=x-14,在 Rt△ABC 中,tan 76°=ABCC ,即x-x14 ≈4.01. 解得 x≈18.7,经检验 x≈18.7 是原方程的解. 答:纪念碑 BC 的高度约为 18.7 m
解:由题意知,AH=10 m,BC=10 m,在 Rt△ABC 中,∵∠ CAB=45°, ∴AB=BC=10 m,在 Rt△DBC 中,∵∠CDB=30°,∴DB
= tan
BC ∠CDB
=10
3
m.
∵DH=AH-DA=AH-(DB-AB)=10-10 3 +10=20- 10 3 ≈2.7 m,∵2.7 m<3 m, ∴建筑物需要拆除
第10题图
11.某居民楼紧挨一座山坡 AB,经过地质人员 勘测,当坡度不超过 45°时,可以确保山体不滑 坡,如图所示,已知 AE∥BD,斜坡 AB 的坡角 ∠ABD=60°,为防止滑坡,现对山坡进行改造, 改造后,斜坡 BC 与地面 BD 成 45°角,AC=10 m.则斜坡 BC=_3_3_.3_ m(结果精确到 0.1 m,参考 数据: 2 =1.41, 3 ≈1.73).
