九年级中考复习专题训练：二次函数与几何(无答案)

合集下载

九年级数学中考二轮专项复习：二次函数与几何综合(含答案)

中考数学二轮专项复习：二次函数与几何综合（含答案）1.如图,已知直线y 1=21x +b 和抛物线y 2=-45x 2+ax +b 都经过点B （0,1）和点C ,过点C 作CM ⊥x轴于点M ,且CM =25.第1题图（1）求出抛物线的解析式;（2）动点P 从点O 出发,以每秒1个单位长度的速度,沿OM 向点M运动,过点P 作PE ⊥x 轴分别交抛物线和直线于点E ,F .当点P 运动多少秒时,四边形EFMC 为菱形?（3）在（2）的条件下,在直线AC 上是否存在一点Q ,使得以点E 、F 、Q 为顶点的三角形与△AMC 相似,若存在,请直接写出点Q 的坐标;若不存在,请说明理由.解：（1）把B (0,1)代入y 1=21x +b ,得b =1,∴y 1=21x +1,把y =25代入y 1=21x +1得x =3, ∴C （3,25）,把B (0,1),C （3,25）代入y 2=-45x 2+ax +b 得,⎪⎩⎪⎨⎧=++-=2534451b a b ,解得⎪⎩⎪⎨⎧==4171a b , ∴y 2=-45x 2+417x +1.（2）∵四边形EFMC 为菱形, 则EF =FM =CM =25, 设P (t ,0),则EP =-45t 2+417t +1,FP =21t +1,MP =3-t ,则EF =EP -FP =-45t 2+417t +1-21t -1=-45t 2+415t , FM =10545222+-=+t t PM PF ,∴-45t 2+415t=25①,105452+-t t =25②, 解①得t =1或t =2,解②得t =1或t =3,要使①,②同时成立,则t =1, 当点P 运动1秒时,四边形EFMC 为菱形; （3）存在,点Q 的坐标为（2,2）或（6,4）. 【解法提示】由（2）可知t =1,∴点F 的横坐标为1, 将x =1代入y 1=21x +1中,得y 1=23, 将x =1代入y 2=-45x 2+417x +1中,得y 2=4. ∴点E （1,4）,F （1,23）, 将y =0代入y 1=21x +1中,得x =-2,∴点A 的坐标为（-2,0）, ①如解图,过点E 作EQ 1⊥CF ,∵四边形EFMC 为菱形,∴∠ECF =∠ACM ,FE =EC ,∴∠EFC =∠ECF =∠ACM ,又∵∠EQ 1F =∠AMC =90°,∴△EQ 1F ∽△AMC ,∵EF =EC ,EQ 1⊥CF ,∴Q 1为CF 的中点,∵F （1,23）,C （3,25）, ∴点Q 1的坐标为（2,2）;第1题解图②如解图,过点E 作EQ 2//x 轴,交直线BC 于点Q 2,∵EQ 2//x 轴,∴∠EQ 2F =∠CAM ,∠Q 2EF =∠FP A =90°,∴∠Q 2EF =∠AMC =90°,∴△EQ 2F ∽△MAC ,又∵E （1,4）,∴设Q 2（x ,4）, 将y =4代入y 1=21x +1,得x =6, ∴点Q 2的坐标为（6,4）;综上所述,点Q 的坐标为（2,2）或（6,4）.2.如图，一次函数y ＝21x ＋1的图象与x 轴交于点A ，与y 轴交于点B ，二次函数y ＝21x 2＋bx ＋c 的图象与一次函数y ＝21x ＋1的图象交于B 、C 两点，与x 轴交于D 、E 两点且D 点坐标为(1，0)．第2题图（1）求二次函数的解析式；（2）若抛物线上存在点P ，使S △BDC ＝S △PBC ，求出P 点坐标(不与已知点重合)；（3）在x 轴上存在点N ，平面内存在点M ，使得B 、N 、C 、M 为顶点构成矩形，请直接写出M 点坐标．解：（1）将x ＝0代入y ＝21x ＋1中，得：y ＝1， ∴B (0，1)，将B (0，1)，D (1，0)的坐标代入y ＝21x 2＋bx ＋c 得：⎪⎩⎪⎨⎧=++=0211c b c ，解得⎪⎩⎪⎨⎧=-=123c b ， ∴二次函数的解析式为y ＝21x 2－23x ＋1；（2）如解图①，过点D 作DF ∥y 轴交AC 于点F ，过点P 作PG ∥y 轴交AC 于点G ，第2题解图①将x ＝1代入直线BC 的解析式得：y ＝23，即F (1，23)，设点P (x ，21x 2－23x ＋1)，则G (x ，21x ＋1)， ∴GP ＝⎪⎭⎫⎝⎛+--+123211212x x x ＝x x 2212+-.∵△PBC 的面积＝△DBC 的面积， ∴DF ＝GP ，即x x 2212+-＝23，当x x 2212+-＝-23时，解得x ＝2＋7或x ＝2－7，∴点P 的坐标为(2＋7，277+)或(2－7，277-)，当x x 2212+-＝23时，解得x ＝3或x ＝1(舍去)，∴点P 的坐标为(3，1)，综上所述，点P 的坐标为(3，1)或(2＋7，277+)或(2－7，277-)；（3）点M 的坐标为(3，4)，(1，4)，(23，－2)或(29，2)．【解法提示】如解图②所示：当∠CBN ＝90°时，则BN 的解析式为y ＝－2x ＋1，将直线BC 的解析式与抛物线的解析式联立得：⎪⎪⎩⎪⎪⎨⎧+-=+=123211212x x y x y ，解得⎩⎨⎧==10y x ，或⎩⎨⎧==34y x ，∴点C 的坐标为(4，3)，将y ＝0代入直线BN 的解析式得：－2x ＋1＝0，解得x ＝21，∴点N 的坐标为(21，0)，设点M 的坐标为(x ，y )， ∵四边形BNMC 为矩形，∴202421x +=+，21230y +=+，解得x ＝29，y ＝2，∴点M 的坐标为(29，2)；第2题解图②如解图③所示：当∠CNM ＝90°时，第2题解图③设CN 的解析式为y ＝－2x ＋n ，将点C 的坐标代入得：－8＋n ＝3，解得n ＝11，∴CN 的解析式为y ＝－2x ＋11，将y ＝0代入得－2x ＋11＝0，解得x ＝211， ∴点N 的坐标为(211，0)，设点M 的坐标为(x ，y )， ∵四边形BMNC 为矩形， ∴2422110x +=+，23201y +=+，解得x ＝23，y ＝－2，∴点M 的坐标为(23，－2)；如解图④所示：当∠BNC ＝90°时，过点C 作CF ⊥x 轴，垂足为F ，第2题解图④设ON ＝a ，则NF ＝4－a ，∵∠BNO ＋∠OBN ＝90°，∠BNO ＋∠CNF ＝90°，∴∠OBN ＝∠CNF ，又∵∠BON ＝∠CFN ， ∴△BON ∽△NFC ， ∴NF OB CF ON =，即3a ＝a-41，解得：a ＝1或a ＝3，当a ＝1时，点N 的坐标为(1，0)，设点M 的坐标为(x ，y )， ∵四边形BNCM 为矩形， ∴21240x +=+，20231y+=+，解得x ＝3，y ＝4， ∴点M 的坐标为(3，4)；当a ＝3时，点N 的坐标为(3，0 )，设点M 的坐标为(x ，y )， ∵四边形BNCM 为矩形， ∴23240x +=+，20231y+=+，解得x ＝1，y ＝4， ∴点M 的坐标为(1，4)，综上所述，点M 的坐标为(3，4)，(1，4)，(23，－2)或(29，2)．3. 如图,在平面直角坐标系中,点O 为坐标原点,抛物线y =ax 2-bx +5与x 轴交于A 、B 两点(点A 在点B 的左侧),与y 轴交点为C ,直线y =-x -2经过点A ,交抛物线于点D ,交y 轴于点E ,连接CD ,并且∠ADC =45°.第3题图（1）求抛物线的解析式;（2）过点A 的直线AF 与抛物线的另一个交点为F ,sin ∠BAF =55,求点F 的坐标; （3）在（2）的条件下,点P 是直线AF 下方抛物线上一点,过点P 作PQ ⊥AF ,垂足为Q ,若PE =EQ ,求点P 的坐标.解：（1）当x =0时,y =ax 2+bx-5=-5,则C （0,-5）, 当y =0时,-x -2=0,则A （-2,0）, 当x =0时,y =-x -2=0,则E （0,-2）, ∴OA =OE ,∴△OAE 为等腰直角三角形,∴∠OAE =45°, ∵∠ADC =45°, ∴CD //x 轴,∴△CDE 为等腰直角三角形, ∴CD =CE =3,∴D （3,-5）,把A （-2,0）,D （3,-5）代入y =ax 2+bx -5,得⎩⎨⎧-=-+=--55390524b a b a ,解得⎪⎪⎩⎪⎪⎨⎧-==2321b a ,∴抛物线的解析式为y =21x 2-23x -5；（2）设直线AF 交y 轴于G ,如解图①, 在Rt △AOG 中,sin ∠OAG =5155==AG OG ,第3题解图①G设OG=t,AG=5t,∴OA=22)5(tt-=2t,∴2t=2,解得t=1,∴G（0,1）,易得直线AG的解析式为y=21x+1,联立⎪⎪⎩⎪⎪⎨⎧--=+=523211212xxyxy,解得⎩⎨⎧==⎩⎨⎧=-=462yxyx或,∴点F的坐标为（6,4）;（3）作EM⊥PQ于M,如解图②,∵PQ⊥AF,∴设PQ的解析式为y=-2x+m,第3题解图②∵EM//AF,∴EM的解析式为y=21x-2,联立⎪⎩⎪⎨⎧+-=+=mxyxy2121,解得⎪⎪⎩⎪⎪⎨⎧+=-=54515252mymx,则Q （54515252+-m m ，）,设点P 的坐标为（a ,b ）,∵EQ =EP ,∴QM =PM ,∴M 点的坐标为[21(a +52m -52),21(b +5451+m )], 把M [21(a +52m -52),21(b +5451+m )]代入y =21x -2 得41(a +52m -52)-2=21(b +5451+m ), ∴b =21a -5,即P （a ,21a -5）,把P （a ,21a -5）代入y =21x 2-23x -5得21a 2-23a -5=21a -5,解得a 1=0,a 2=4, ∴P 点坐标为（0,-5）或（4,-3）.类型二等腰三角形的存在性问题4. 如图，抛物线y ＝－12x 2＋bx ＋c 与x 轴交于A (－1，0)、B 两点，与y 轴交于点C (0，2)，抛物线的对称轴交x 轴于点D .第4题图（1）求抛物线的解析式；（2）求sin ∠ABC 的值；（3）在抛物线的对称轴上是否存在点P ，使△PCD 是以CD 为腰的等腰三角形，如果存在，直接写出点P 的坐标；如果不存在，请说明理由．解：（1）将点A (－1，0)，C (0，2)代入抛物线y ＝－12x 2＋bx ＋c 中，得 ⎩⎨⎧－12－b ＋c ＝0c ＝2，解得⎩⎨⎧b ＝32c ＝2， ∴抛物线的解析式为y ＝－12x 2＋32x ＋2；（2）令y ＝－12x 2＋32x ＋2＝0，解得x 1＝－1，x 2＝4， ∴点B 的坐标为(4，0)，在Rt △BOC 中，BC ＝22OB OC +＝2242+＝52， ∴sin ∠ABC ＝BC OC＝522＝55；（3）存在，点P 坐标为(23，25)或(23，－25)或(23，4)．【解法提示】由抛物线y ＝－21x 2＋23x ＋2得对称轴为直线x ＝23， ∴点D 的坐标为(23，0)． ∴CD ＝22OD OC +＝22232⎪⎭⎫⎝⎛+＝25.∵点P 在对称轴x ＝23上，且△PCD 是以CD 为腰的等腰三角形， ∴当点D 为顶点时，有DP ＝CD ＝25，此时点P 的坐标为(23，25)或(23，－25)；当点C 为顶点时，如解图，连接CP ，则CP ＝CD ，过点C 作CG ⊥DP 于点G ，则DG ＝PG ， ∵DG ＝2， ∴PG ＝2，PD ＝4， ∴点P 的坐标为(32，4)．第4题解图综上所述，存在点P 使△PCD 是以CD 为腰的等腰三角形，点P 的坐标为(32，25)或(32，－25)或(32，4)．5.如图①，在平面直角坐标系中，抛物线()02≠++=a c bx ax y 与直线3333+=x y 交于A 和E ⎪⎪⎭⎫⎝⎛3354，两点，与x 轴交于点B （3,0），与y 轴交于点C （0，3-），对称轴与x 轴交于点D ，顶点为点H .（1）求抛物线的解析式；（2）点P 为抛物线上的一动点，且位于直线AE 下方，过点P 作PM ∥y 轴交直线AE 于点M ，求线段PM 的最大值；（3）如图②，连接CD ，将（1）中抛物线沿射线CD 平移得到新抛物线y ’，y ’经过点D ，y ’的顶点为点F ，在直线HF 上，是否存在点Q ，使△DHQ 为等腰三角形？若存在，请求出点Q 的坐标；若不存在，请说明理由.图① 图②第5题图解：：（1）将点B （3,0）、C （0，3-）、E （4，335）的坐标代入c bx ax y ++=2中，得⎪⎪⎪⎩⎪⎪⎪⎨⎧=++-==++3354163039c b a c c b a ，解得⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧-=-==333233c b a ， ∴抛物线的解析式为3332332--=x x y ；（2）令y =0，即03332332=--x x ，解得x 1=-1,x 2=3, ∴点A （-1,0），设直线AE 的解析式为t kx y +=，将点A 、E 的坐标代入得⎪⎩⎪⎨⎧=+=+-33540t k t k ，解得⎪⎪⎩⎪⎪⎨⎧==3333t k ， ∴直线AE 的解析式为3333+=x y ，设点P 的坐标为（m ，3332332--m m ），则点M 的坐标为（m ，3333+m ），且-1＜m ＜4. ∴PM =（3333+m ）-（3332332--m m ） =3343332++-m m =1232523332+⎪⎭⎫ ⎝⎛--m ， ∵33-＜0，1＜m ＜4. ∴当m =23时，PM 有最大值，其最大值为12325；（1）存在，由（1）易得H （1，334-），D （1,0）， ∵将（1）中抛物线沿射线CD 平移得到新抛物线y'，y'经过点D ，y'的顶点为点F ， ∴F （2，33-），易得直线HF 的解析式为3373-=x y ，设点Q 的坐标为（n ，3373-n ）， ∴DQ 2=()35216433731222+-=⎪⎪⎭⎫ ⎝⎛-+-n n n n ， HQ 2=()48433433731222+-=⎪⎪⎭⎫ ⎝⎛+-+-n n n n ， DH 2=3163342=⎪⎪⎭⎫ ⎝⎛-，当DQ =HQ 时，DQ 2=HQ 2，则3521642+-n n =4842+-n n ，解得35=n ，∴点Q （33235-，）；当DQ =DH 时，DQ 2=DH 2，则3521642+-n n =316，解得n =3或1， ∵点H 与点Q 不重合， ∴n =1（舍去），∴Q （3323，）；当HQ =DH 时，HQ 2=DH 2，则4842+-n n =316，解得n =3321+或3321-， ∴Q （3321+，3342-）或Q （3321-，3342--）；综上所述，存在点Q ，使得△DHQ 为等腰三角形，点Q 的坐标为（33235-，）或（3323，）或（3321+，3342-）或（3321-，3342--）. 类型三直角三角形的存在性问题6. 如图，已知抛物线y ＝ax 2＋bx ＋c (a ≠0)的对称轴为直线x ＝－1，且经过A (1，0)，C (0，3)两点，与x 轴的另一个交点为B .第6题图(1)若直线y ＝mx ＋n 经过B ，C 两点，求抛物线和直线BC 的解析式；(2)在抛物线的对称轴x ＝－1上找一点M ，使点M 到点A 的距离与到点C 的距离之和最小，求点M 的坐标；(3)设点P 为抛物线的对称轴x ＝－1上的一个动点，求使△BPC 为直角三角形的点P 的坐标．解：（1）由题意得⎪⎪⎩⎪⎪⎨⎧==++-=-3012c c b a a b，解得⎪⎩⎪⎨⎧=-=-=321c b a ，∴抛物线的解析式为y ＝－x 2－2x ＋3.∵对称轴为直线x ＝－1，抛物线经过A (1，0)， ∴B (－3，0)．设直线BC 的解析式y ＝mx ＋n ，把B (－3，0)，C (0，3)分别代入y ＝mx ＋n 得⎩⎨⎧==+-303n n m ，解得⎩⎨⎧==31n m ， ∴直线BC 的解析式为y ＝x ＋3；（2）如解图，连接MA ，第6题解图∵MA ＝MB ，∴MA ＋MC ＝MB ＋MC .∴使MA ＋MC 最小的点M 应为直线BC 与对称轴x ＝－1的交点．设直线BC 与对称轴x ＝－1的交点为M ，把x ＝－1代入直线y ＝x ＋3，得y ＝2. ∴M (－1，2);（3）设P (－1，t )，∵B (－3，0)，C (0，3)，∴BC 2＝18， PB 2＝(－1＋3)2＋t 2＝4＋t 2， PC 2＝(－1)2＋(t －3)2＝t 2－6t ＋10.①若B 为直角顶点，则BC 2＋PB 2＝PC 2，即18＋4＋t 2＝t 2－6t ＋10，解得t ＝－2； ②若C 为直角顶点，则BC 2＋PC 2＝PB 2，即18＋t 2－6t ＋10＝4＋t 2，解得t ＝4； ③若P 为直角顶点，则PB 2＋PC 2＝BC 2，即：4＋t 2＋t 2－6t ＋10＝18，解得t 1＝3＋172，t 2＝3－172.综上所述，满足条件的点P 共有四个，分别为：P 1(－1，－2)，P 2(－1，4)，P 3(－1，3＋172)，P 4(－1，3－172)．7. 如图,抛物线y ＝－43x 2＋bx ＋c 经过A (3,0),C (－1,0)两点,与y 轴交于B 点．第7题图备用图（1）求抛物线的解析式;（2） D 为第一象限抛物线上的一点,连接CD 交AB 于点E ,当CE ＝2ED 时,求点D 的坐标; （3）点P 以每秒3个单位长度的速度从点O 出发,沿O →B →A 匀速运动,同时点Q 以每秒1个单位长度的速度从点C 出发,沿C →A 匀速运动,运动时间为t 秒,当一个点到达终点时,另一个点也随之停止运动,是否存在t ,使以A 、P 、Q 为顶点的三角形为直角三角形,若存在,直接写出t 的值;若不存在,说明理由．解：（1）∵抛物线y ＝c bx x ++-234经过A (3,0)、C (-1,0)两点,∴⎪⎪⎩⎪⎪⎨⎧=+--=++⨯-034033342c b c b ，解得⎪⎩⎪⎨⎧==438c b ,∴抛物线的解析式为y ＝438342++-x x ; （2）如解图,作DF ∥AC 交AB 于点F ,第7题解图∴∠EAC ＝∠EFD ,∠ECA ＝∠EDF , ∴△ACE ∽△FDE , ∴FD AC ＝DE CE ＝DE 2DE ＝12, ∵AC ＝4,∴FD ＝2,设D (x ,y ),则F (x -2,y ), 令x ＝0,得y ＝4, ∴B (0,4),过点F 作FM ⊥x 轴于点M , ∴△AMF ∽△AOB , ∴AM OA ＝FM OB , ∴3－（x －2）3＝y 4＝－43x 2＋83x ＋44,解得x 1＝1,x 2＝2, ∴y 1＝163,y 2＝4, ∴D 1(1,163),D 2(2,4);（3）存在．t 1＝－1＋136,t 2＝1,t 3＝74,t 4＝114. 【解法提示】∵当P 在OB 上时,OP ＝3t ,CQ ＝t , ∴AQ ＝4-t ,要使△APQ 是直角三角形,则需①∠AQP ＝90°,此时点Q 与点O 重合,CQ ＝1,则t ＝1; ②∠APQ ＝90°,此时△PQO ∽△APO , ∴OQ OP ＝OPOA ,即(3t )2＝(1-t )·3,解得t 1＝13－16,t 2＝－13－16(负根舍去)．当点P 在AB 上,在Rt △AOB 中,OA ＝3,OB ＝4,易得AB ＝5, 则此时AP ＝9-3t ,AQ ＝4-t , ③当∠PQA ＝90°时,则PQ ⊥AO ,∴cos ∠P AQ ＝QA AP ＝OA AB ,即4－t 9－3t ＝35,解得t ＝74;④当∠QP A＝90°时,则△APQ∽△AOB,∴APAO＝AQAB,即9－3t3＝4－t5,解得t＝114.综上所述,t的值为1或13－16或74或114.8.如图，抛物线cbxaxy++=2与x轴交于点A（-3,0），B（1,0），与y轴交于点C（0,3），顶点为D.（1）求抛物线的表达式及点D的坐标；（2）如图①，在x轴上找一点E，使得△CDE的周长最小，求点E的坐标；（3）如图②，F为直线AC上的动点，在抛物线上是否存在点P，使得△AFP为等腰直角三角形？若存在，求出点P的坐标；若不存在，请说明理由．图①图②第8题图解：（1）∵A，B，C三点在抛物线上，∴,321339⎪⎩⎪⎨⎧=-=-=⎪⎩⎪⎨⎧=++=+-=cbaccbacba，解得∴抛物线的表达式y＝－x2－2x＋3，∵y＝－x2－2x＋3=()412++-x，∴点D的坐标为（-1,4）；（2）如解图①，作点C关于x轴的对称点M，则M(0，－3)，连接DM，DM与x轴的交点为E，连接CE，此时△CDE的周长最小，第8题解图①设直线DM 的解析式为y ＝kx ＋b (k ≠0)，将D (－1，4)，M (0，－3)代入y ＝kx ＋b ，得⎩⎨⎧-==+-34b b k ，解得⎩⎨⎧-=-=37b k ， ∴直线DM 的解析式为y ＝－7x －3，令y ＝0，则y ＝－7x －3＝0，解得x ＝－37，∴点E 的坐标为(－37，0)．（3）存在．由（1）知，OA ＝OC ＝3，∠AOC ＝90°， ∴∠CAB ＝45°，如解图②，第8题解图②①当∠AFP ＝90°时，即∠AF 1P 1＝90°，∴点P 1既在x 轴上，又在抛物线上，则点P 1与点B 重合，点P 1的坐标为(1，0)； ②当∠F AP ＝90°时，即∠F 2AP 2＝90°，则∠P 2AO ＝45°，设AP 2与y 轴的交点为点N ，∴OA ＝ON ＝3，则N (0，－3)， ∴直线AP 2的解析式为y ＝－x －3，联立抛物线与直线AP 2的解析式，得方程组⎩⎨⎧+--=--=3232x x y x y ，解得⎩⎨⎧=-=03y x 或⎩⎨⎧-==52y x ，∵A (－3，0)， ∴P 2(2，－5)；③当∠APF ＝90°时，即∠AP 3F 3＝90°，点P 3既在x 轴上，又在抛物线上，则点P 3与点B 重合，点P 3的坐标为(1，0)．综上所述，抛物线上存在点P ，使得△AFP 为等腰直角三角形，其坐标为P (1，0)或(2，－5)．类型四特殊四边形的存在性问题9. 如图，抛物线y ＝ax 2＋bx ＋c (a ≠0)与y 轴交于点C (0，4)，与x 轴交于点A 和点B ，其中点A 的坐标为(－2，0)，抛物线的对称轴x ＝1与抛物线交于点D ，与直线BC 交于点E . (1)求抛物线的解析式；(2)若点F 是直线BC 上方的抛物线上的一个动点，是否存在点F ，使四边形ABFC 的面积为17？若存在，求出点F 的坐标；若不存在，请说明理由；(3)平行于DE 的一条直线l 与直线BC 相交于点P ，与抛物线相交于点Q ，若以D 、E 、P 、Q 为顶点的四边形是平行四边形，求点P 的坐标．第9题图解：（1）∵点A (－2，0)与点B 关于直线x ＝1对称，∴B (4，0)，将点A ，B ，C 的坐标代入函数解析式，得⎪⎩⎪⎨⎧==++=+-40416024c c b a c b a ，解得⎪⎪⎩⎪⎪⎨⎧==-=4121c b a ，∴抛物线的解析式为y ＝21-x 2＋x ＋4；（2）不存在点F ，使四边形ABFC 的面积为17，理由如下：∵B (4，0)，C (0，4)， ∴BC 的解析式为y ＝－x ＋4，如解图，过点F 作x 轴垂线，交BC 于G ，设F 点的坐标为(m ，21-m 2＋m ＋4)，则G (m ，-m ＋4)，∴FG ＝(21-m 2＋m ＋4)－(－m ＋4)＝21-m 2＋2m ，∴S 四边形ABFC ＝S △ABC ＋S △BCF ＝21AB ·y C ＋21FG ·(x B －x C )＝21×6×4＋12×4(21-m 2＋2m )＝17，整理得m 2－4m ＋5＝0， ∵b 2－4ac ＝16－4×1×5＝－4<0. ∴方程无解， ∴F 点不存在；第9题解图（3）当x ＝1时，21-x 2＋x ＋4＝29，即D (1，29)．当x ＝1时，－x ＋4＝3，即E (1，3)， ∴DE ＝92－3＝32.设Q 点坐标为(m ，－12m 2＋m ＋4)，则P (m ，－m ＋4)． ∴|PQ |＝|(－12m 2＋m ＋4)－(－m ＋4)|＝|－12m 2＋2m |. 由PQ ∥DE ，PQ ＝DE 得|－12m 2＋2m |＝32，∴－12m 2＋2m ＝32或－12m 2＋2m ＝－32，解得m 1＝1(PQ 与DE 重合，舍去)，m 2＝3或m 3＝2＋7，m 4＝2－7.∴P 点坐标为(3，1)或(2＋7，2－7)或(2－7，2＋7)．10．如图，经过点A （3,3）的抛物线bx ax y +=2与x 轴交于点B （4,0）和原点O ，P 为二次函数上一动点，过P 作x 轴垂线，垂足为D (x'，0)(x'>0)，并与直线OA 交于点C .（1）求抛物线的表达式；（2）当点P 在线段OA 上方时，过P 作x 轴的平行线与线段OA 相交于点E ，求△PCE 周长的最大值及此时P 点的坐标；（3）当PC ＝CO 时，求P 点坐标．第10题图解：（1）∵A （3,3），B （4,0）两点在抛物线bx ax y +=2上，∴,4160393⎩⎨⎧+=+=b a b a 解得,41⎩⎨⎧=-=b a ∴抛物线的表达式为x x y 42+-=；（2）如解图①，设点P 的坐标为(x ，－x 2＋4x )，第10题解图①∵点A 坐标为(3，3)；∴∠AOB ＝45°，∴OD ＝CD ＝x ，∴PC ＝PD －CD ＝－x 2＋4x －x ＝－x 2＋3x ，∵PE ∥x 轴，∴△PCE是等腰直角三角形，∴当PC取最大值时，△PCE周长最大．∵PE与线段OA相交，∴0≤x≤1，由PC＝－x2＋3x＝－(x－32)2＋94可知，抛物线的对称轴为直线x＝32，且在对称轴左侧PC随x的增大而增大，∴当x＝1时，PC最大，PC的最大值为－1＋3＝2，∴PE＝2，CE＝2，∴△PCE的周长为CP＋PE＋CE＝4＋2，∴△PCE周长的最大值为4＋2，把x＝1代入y＝－x2＋4x，得y＝－1＋4＝3，∴点P的坐标为(1，3)；（3）设点P坐标为(x，－x2＋4x)，则点C坐标为(x，x)，如解图②，D2第10题解图②①当点P在点C上方时，P1C1＝－x2＋4x－x＝－x2＋3x，OC12x，∵P1C1＝OC1，∴－x2＋3x2x，解得x1＝32x2＝0(舍去)．把x＝32代入y＝－x2＋4x得，y＝－(32)2＋4(32)＝1＋2，∴P1(32，1＋2)，②当点P在点C下方时，P2C2＝x－(－x2＋4x)＝x2－3x，OC22x，∵P2C2＝OC2，∴x2－3x2x，解得x1＝32x2＝0(舍去)，把x ＝3＋2代入y ＝－x 2＋4x 得y ＝－(3＋2)2＋4(3＋2)＝1－22，∴P 2(3＋2，1－22)．综上所述，P 点坐标为(3－2，1＋22)或(3＋2，1－22)．11.如图，抛物线y ＝ax 2＋bx ＋c 的图象与x 轴分别交于A ，B 两点，与y 轴交于点C ，其中点A (－1，0)、C (0，5)、D (1，8)在抛物线上，M 为抛物线的顶点．（1）求抛物线的解析式；（2）求△MCB 的面积；（3）在抛物线上是否存在点P ，使△P AB 的面积等于△MCB 的面积？若存在，求出所有符合条件的点P 的坐标；若不存在，请说明理由．第11题图解：（1）∵A (－1，0)，C (0，5)，D (1，8)三点在抛物线y ＝ax 2＋bx ＋c 上，∴⎪⎩⎪⎨⎧++==+-=c b a c c b a 850，解得⎪⎩⎪⎨⎧==-=541c b a ， ∴抛物线的解析式为y ＝－x 2＋4x ＋5；（2）如解图，过点M 作MN ∥y 轴交BC 于点N ， ∴S △MCB ＝S △MCN ＋S △MNB ＝12MN ·OB .∵y＝－x2＋4x＋5＝－(x－5)(x＋1)＝－(x－2)2＋9，∴M(2，9)，B(5，0)，由B，C两点的坐标易求得直线BC的解析式为：y＝－x＋5，当x＝2时，y＝－2＋5＝3，则N(2，3)，则MN＝9－3＝6，则S△MCB＝12×6×5＝15；第11题解图（3）在抛物线上存在点P，使△P AB的面积等于△MCB的面积．∵A(－1，0)，B(5，0)，∴AB＝6，∵S△P AB＝S△MCB，∴12×6×|y P|＝15，∴|y P|＝5，即y P＝±5.当y P＝5时，－x2＋4x＋5＝5，解得x1＝0，x2＝4；当y P＝－5时，－x2＋4x＋5＝－5，解得x3＝2＋14，x4＝2－14.故在抛物线上存在点P1(0，5)，P2(4，5)，P3(2＋14，－5)，P4(2－14，－5)，使△P AB的面积等于△MCB的面积．精品Word 可修改欢迎下载。

最新九年级中考数学复习：二次函数综合题(面积问题)专题训练

(2)如图1，过点作 y轴且交直线于点，求线段的最大值；
(3)如图2，连接，，是否存在点，使得三角形的面积等于，若存在，求出此时点的坐标；若不存在，请说明理由．
答案
1．(1)①m= ，D( ， )；②
(2)( ， )
2．(1) ；点G（，）
(ห้องสมุดไป่ตู้)存在，点P的坐标为（，﹣1）
17．如图，抛物线与x轴交于A，B两点，与y轴交于C点，连接AC，已知B(﹣1，0)，且抛物线经过点D(2，﹣2)．
(1)求抛物线的表达式；
(2)若点E是抛物线上第四象限内的一点，且，求点E的坐标；
(3)若点P是y轴上一点，以P，A，C三点为顶点的三角形是等腰三角形，求P点的坐标．
18．如图，抛物线y＝x2+bx+c与x轴交于A，B两点（点A在点B左侧），与y轴交于点C(0，3)．
(3)点P为线段OC上一个动点，过点P作y轴的平行线交抛物线于点M，交x轴于点N，问是否存在这样的点P，使得四边形ABPM是等腰梯形？若存在，求出此时点P的坐标；若不存在，请说明理由．
11．如图①，抛物线y＝ax2＋bx＋C（a≠0）经过点A（﹣4，0），点B（2，0）和点C（0，﹣4），它的对称轴为直线l，顶点为D．
（1）若AB＝5，求抛物线的解析式；
（2）若经过点C和定点M的直线与该抛物线交于另一点D，且S△ACM＝S△ADM（“S”表示面积）．
①求定点M的坐标；
②连接BD交y轴于点E，连接AE，若∠AEO＝∠BDC，求a的值．
15．抛物线的对称轴为直线，该抛物线与x轴的两个交点分别为A和B，与y轴的交点为C，其中．
(3)点D的坐标为（2，1），最大距离为．

中考数学总复习_题型专项(八)二次函数与几何图形综合题_类型_探究图形面积数量关系及最值等问题试题

2－2x＋6＝3，得x＝，∴F(，3)．⎪⎪⎩⎩2FM HL33－HK2题型专项(八)二次函数与几何图形综合题类型1探究图形面积数量关系及最值等问题1．(2016·贵港模拟)如图甲，四边形OABC的边OA，OC分别在x轴，y轴的正半轴上，顶点在B点的抛物线交x轴于点A，D，交y轴于点C.已知A(3，0)，D(－1，0)，C(0，3)．(1)求抛物线的解析式及顶点B的坐标；(2)设△AOC沿x轴正方向平移t个单位长度错误!＜t≤3)时，AOC与△ABC重叠部分的面积为S，求S与t 之间的函数关系式，并指出t的取值范围；3(3)当0＜t≤时，求S的最大值．解：(1)设抛物线的解析式为y＝a(x－3)(x＋1)．∵将C(0，3)代入，得－3a＝3，解得a＝－1.∴y＝－x2＋2x＋3.∵y＝－x2＋2x＋3＝－(x－1)2＋4，∴B(1，4)．(2)设直线AB的解析式为y＝kx＋b.⎧3k＋b＝0，⎧k＝－2，∵将A(3，0)，B(1，4)代入y＝kx＋b得⎨解得⎨⎪k＋b＝4，⎪b＝6，∴y＝－2x＋6.过点C作射线CF∥x轴交AB于点F.∵将y＝3代入直线AB的解析式得：3322图13①当0＜t≤时，如图1所示．设△AOC平移到△PNM的位置，PM交AB于点H，MN交AC于点G.则ON＝AP＝t，过点H作LK⊥x轴于点K，交CF于点L.由△AHP∽△FHM，得AP HK t HK＝，即＝.解得HK＝2t.－t1113∴S＝△SMNP－△SG NA－△SHAP＝2×3×3－2(3－t)2－2t×2t＝－2t2＋3t.2 ⎧⎪－ t 2＋3t （0<t≤ ）， ⎨⎪⎩t 2－3t ＋（ <t≤3）. AG 3 5⎪ ⎪ ⎩ ⎩ ＝ .∴PG＝ 5|y P |＝ 5d.2 ∴ 5d ＝6＋d ，解得 d ＝ .2 2 图 23②当＜t≤3 时，如图 2 所示：设△AOC 平移到△PQR 的位置，RQ 交 AB 于点 I ，交 AC 于点 V.∵直线 AC 的解析式为 y ＝－x ＋3，直线 AB 的解析式为 y ＝－2x ＋6， ∴V(t ，t ＋3)，I(t ，－2t ＋6)．∴IV ＝－2t ＋6－(－t ＋3)＝－t ＋3，AQ ＝3－t.1 1 1 9∴S ＝△S IVA ＝2AQ·IV＝2(3－t)2＝2t 2－3t ＋2.3 3 2 2综上所述，S ＝ 1 9 3 2 2 2 3 3 3 3 3(3)当 0＜x≤2时，S ＝－2t 2＋3t ＝－2(t －1)2＋2，当 t ＝1 时，S 最大＝2.2．(2016·十堰模拟)如图 1，在平面直角坐标系中，抛物线 y ＝ax 2＋bx ＋3(a≠0)经过点 A(－1，0)和点 B(3， 0)．(1)求抛物线的解析式，并写出顶点 D 的坐标；(2)若点 P 在直线 x ＝2 上运动，当点 P 到直线 AD 的距离 d 等于点 P 到 x 轴的距离时，求 d 的值；(3)如图 2，直线 AC ：y ＝－x ＋m 经过点 A ，交 y 轴于点 C.探究：在 x 轴上方的抛物线上是否存在点 M ，使得 △S C DA ＝△2S ACM ？若存在，求点 M 的坐标；若不存在，请说明理由．解：(1)∵抛物线 y ＝ax 2＋bx ＋3(a ≠0)经过点 A(－1，0)和点 B(3，0)，⎧a －b ＋3＝0， ⎧a ＝－1， ∴⎨ 解得⎨⎪9a ＋3b ＋3＝0， ⎪b ＝2.∴y ＝－x 2＋2x ＋3＝－(x －1)2＋4.∴D(1，4)．(2)设 P(2，y P )，过 P 作 PE⊥AD 于点 E ，设直线 AD 与直线 x ＝2 交于点 G ，则 PE ＝d ＝|y P |，直线 AD 的解析式为 y ＝2x ＋2， ∴G(2，6)．∴PG＝6－y P .AN 3∵sin ∠AGP ＝＝，∴ PE 1 PG 5①若点 P 在第一象限，则 PG ＝6－d ，3 5－3∴ 5d ＝6－d ，解得 d ＝ .②若点 P 在第四象限，则 PG ＝6＋d ，3 5＋323 5－3 3 5＋3∴d 的值为或 .( 3)∵直线 AC 过点 A ，所以可求得直线 AC ： y ＝－x －1.过点 D 作 DE∥AC，交 y 轴于点 E ，可求得直线 DE ：y ＝－x ＋5.⎧⎪⎧⎪x1＝，x2＝22⎪⎩⎪⎩y1＝.y2＝2222⎧⎪3⎪⎩3⎪⎩∴所求抛物线解析式为y＝x2－x－4.BC ABAB44过点E作EF⊥AB于点F，则sin∠EDF＝sin∠CBA＝＝.∴＝.∴E(0，5)．∴EC的中点F(0，2)．∴过点F平行于AC的直线为y＝－x＋2.⎧⎪y＝－x＋2，∴⎨⎪⎩y＝－x2＋2x＋3.3－133＋13，解得⎨或⎨1＋131－13.(舍去)3－131＋13∴M(，)．3．(2016·玉林模拟)已知抛物线y＝ax2＋bx＋c与x轴交于A，B两点，与y轴交于点C.其中点A在x轴的负半轴上，点C在y轴的负半轴上，线段OA，OC的长(OA＜OC)是方程x2－5x＋4＝0的两个根，且抛物线的对称轴是直线x＝1.(1)求A，B，C三点的坐标；(2)求此抛物线的解析式；(3)若点D是线段AB上的一个动点(与点A，B不重合)，过点D作DE∥BC交AC于点E，连接CD，设BD的长为△m，CDE的面积为S，求S与m的函数关系式，并写出自变量m的取值范围．S是否存在最大值？若存在，求出最大值并求此时D点坐标；若不存在，请说明理由．解：(1)∵OA，OC的长是x2－5x＋4＝0的根，OA＜OC，∴OA＝1，OC＝4.∵点A在x轴的负半轴，点C在y轴的负半轴，∴A(－1，0)，C(0，－4)．∵抛物线y＝ax2＋bx＋c的对称轴为x＝1，∴由对称性可得B点坐标为(3，0)．∴A，B，C三点坐标分别是A(－1，0)，B(3，0)，C(0，－4)．(2)∵点C(0，－4)在抛物线y＝ax2＋bx＋c图象上，∴c＝－4.将A(－1，0)，B(3，0)代入y＝ax2＋bx－4，得⎧a－b－4＝0，⎨解得⎪9a＋3b－4＝0.4a＝，⎨8b＝－.4833(3)根据题意，BD＝m，则AD＝4－m.在△R t OBC中，BC＝OB2＋OC2＝5.DE AD∵DE∥△B C，∴ADE∽△ABC.∴＝.AD·BC5（4－m）20－5m∴DE＝＝＝.OC4EF4BC5DE55 5 4 ∵S ＝－ (m －2)2＋2，a ＝－＜0，4 4 20－5m∴EF ＝ DE ＝ × ＝4－m.1 1 1∴S △CDE ＝△S ADC －△S ADE ＝2(4－m)×4－2(4－m)(4－m)＝－2m 2＋2m(0＜m ＜4)．1 12 2∴ 当 m ＝2 时，S 有最大值 2. ∴点 D 的坐标为(1，0)．。

九年级二次函数与几何.doc

辅导讲义
学员编号：年级：九年级课时数：
学员姓名：辅导科目：学科教师：
授课
类型
(二次函数与几何)
（二次函数与几何的类型）
（中考链接）
授课日期时段
教学内容
一、同步知识梳理
1、二次函数概念：形如（a≠0,a,b,c为常数）的函数叫x的二次函数.
2、二次函数的图象与性质：
二次函数y=-x2+6x+3的图象开口方向,顶点坐标为_________,对称轴
为_________.当x=时,函数有值，为.当x时，y的值随x的增大而增大.它是由y=-x2向平移个单位，再向平移个单位得到的．
3、抛物线与x轴的交点个数：
抛物线与x轴的交点有个，抛物线与x轴的交点有个，抛物线y=x2+2x+1与x轴的交点有个.
总结：抛物线与x轴的交点个数由决定.
4、抛物线的图象与a、b、c及b2-4ac的关系.
解法一：设抛物线的对称轴交x轴于点E.
∵ED∥y轴,∴∠OC′M=∠EDM,∠C′OM=∠DEM
∴△C′OM∽△DEM.
∴
∴ ，∴m= ．
解法二：设直线C′D的关系式为y=kx+n,
则，解得n= 2, ∴ .
∴当y= 0时，，
.∴ .
二、专题过关
1、如图，直线交轴于A点，交轴于B点，过A、B两点的抛物线交轴于另一点C（3,0）.
∴平移了个单位
题型三、二次函数与几何图形的综合应用
例题、如图，抛物线与x轴交于A、B两点，与y轴交于C点，四边形OBHC为矩形，CH的延长线交抛物线于点D（5，2），连结BC、AD.
（1）求C点的坐标及抛物线的关系式；
（2）将△BCH绕点B按顺时针旋转90°后再沿x轴对折得到△BEF（点C与点E对应），判断点E是否落在抛物线上，并说明理由；

数学：二次函数与几何综合(九年级训练考试卷)

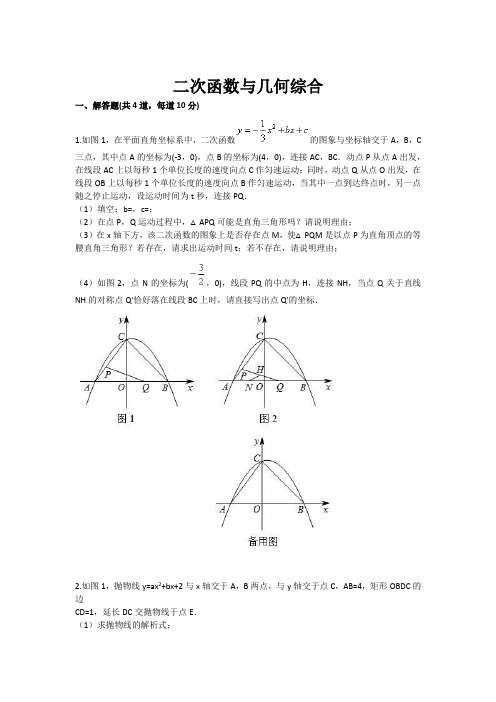
二次函数与几何综合一、解答题(共4道，每道10分)1.如图1，在平面直角坐标系中，二次函数的图象与坐标轴交于A，B，C 三点，其中点A的坐标为(-3，0)，点B的坐标为(4，0)，连接AC，BC．动点P从点A出发，在线段AC上以每秒1个单位长度的速度向点C作匀速运动；同时，动点Q从点O出发，在线段OB上以每秒1个单位长度的速度向点B作匀速运动，当其中一点到达终点时，另一点随之停止运动，设运动时间为t秒，连接PQ．（1）填空：b=，c=；（2）在点P，Q运动过程中，△APQ可能是直角三角形吗？请说明理由；（3）在x轴下方，该二次函数的图象上是否存在点M，使△PQM是以点P为直角顶点的等腰直角三角形？若存在，请求出运动时间t；若不存在，请说明理由；（4）如图2，点N的坐标为(，0)，线段PQ的中点为H，连接NH，当点Q关于直线NH的对称点Q′恰好落在线段BC上时，请直接写出点Q′的坐标．2.如图1，抛物线y=ax2+bx+2与x轴交于A，B两点，与y轴交于点C，AB=4，矩形OBDC的边CD=1，延长DC交抛物线于点E．（1）求抛物线的解析式；（2）如图2，点P是直线EO上方抛物线上的一个动点，过点P作y轴的平行线交直线EO 于点G，作PH⊥EO，垂足为H．设PH的长为l，点P的横坐标为m，求l与m的函数关系式（不必写出m的取值范围），并求出l的最大值；（3）如果点N是抛物线对称轴上的一点，抛物线上是否存在点M，使得以M，A，C，N为顶点的四边形是平行四边形？若存在，直接写出所有满足条件的点M的坐标；若不存在，请说明理由．3.如图，抛物线y=ax2+bx-2的对称轴是直线x=1，与x轴交于A，B两点，与y轴交于点C，点A的坐标为(-2，0)，点P为抛物线上的一个动点，过点P作PD⊥x轴于点D，交直线BC 于点E．（1）求抛物线的解析式；（2）若点P在第一象限内，当OD=4PE时，求四边形POBE的面积；（3）在（2）的条件下，若点M为直线BC上一点，点N为平面直角坐标系内一点，是否存在这样的点M和点N，使得以点B，D，M，N为顶点的四边形是菱形？若存在，直接写出点N的坐标；若不存在，请说明理由．（温馨提示：考生可以根据题意，在备用图中补充图形，以便探究）4.如图1，若直线l：y=-2x+4交x轴于点A，交y轴于点B，将△AOB绕点O逆时针旋转90°得到△COD．过点A，B，D的抛物线h：y=ax2+bx+4．（1）求抛物线h的表达式；（2）若与y轴平行的直线m以1秒钟一个单位长度的速度从y轴向左平移，交线段CD于点M，交抛物线h于点N，求线段MN的最大值；（3）如图2，点E为抛物线h的顶点，点P是抛物线h在第二象限上的一动点（不与点D，B重合），连接PE，以PE为边作图示一侧的正方形PEFG，随着点P的运动，正方形的大小、位置也随之改变．当顶点F或G恰好落在y轴上时，直接写出对应的点P的坐标．。

九年级中考《二次函数与几何图形综合题》基础巩固+变式练习拓展与提升专题练习

《二次函数与几何图形综合题》基础巩固+变式练习拓展与提升专题练习

1.(原题)如图，抛物线y＝ax2＋bx＋c(a≠0)与x轴交于点A、B(1，0)，与y轴交于点C，直线y＝12x－2经过点A、C.抛物线的顶点为D，对称轴为直线l. (1)求抛物线的解析式； (2)求顶点D的坐标与对称轴l；

2.(变式一)如图，抛物线y＝ax2＋bx＋c(a≠0)与x轴交于点A、B(1，0)，与y轴交于点C，直线y＝12x－2经过点A、C.抛物线的顶点为D，对称轴为直线l. (1)求抛物线的解析式； (2)设点E为x轴上一点，且AE＝CE，求点E的坐标； 3.(变式二)如图，抛物线y＝ax2＋bx＋c(a≠0)与x轴交于点A、B(1，0)，与y轴交于点C，直线y＝12x－2经过点A、C.抛物线的顶点为D，对称轴为直线l. (1)求抛物线的解析式； (2)设点G是y轴上一点，是否存在点G，使得GD＋GB的值最小？若存在，求出点G的坐标；若不存在，请说明理由；

4.(变式三)如图，抛物线y＝ax2＋bx＋c(a≠0)与x轴交于点A、B(1，0)，与y轴交于点C，直线y＝12x－2经过点A、C.抛物线的顶点为D，对称轴为直线l. (1)求抛物线的解析式； (2)在对称轴l上是否存在一点F，使得△BCF的周长最小？若存在，求出点F的坐标及△BCF周长的最小值；若不存在，请说明理由； 5.(变式四)如图，抛物线y＝ax2＋bx＋c(a≠0)与x轴交于点A、B(1，0)，与y轴交于点C，直线y＝12x－2经过点A、C.抛物线的顶点为D，对称轴为直线l. (1)求抛物线的解析式； (2)若点H是抛物线上位于AC上方的一点，过点H作y轴的平行线，交AC于点K，设点H的横坐标为h，线段HK＝d. ①求d关于h的函数关系式； ②求d的最大值及此时H点的坐标；

6.（原题）在平面直角坐标系中，已知抛物线y＝－ 12x2＋bx＋c(b，c为常数)的顶点为P，等腰直角三角形ABC的顶点A的坐标为(0，－1)，C的坐标为(4，3)，直角顶点B在第四象限． (1)如图，若该抛物线过A，B两点，求抛物线的函数表达式； (2)平移(1)中的抛物线，使顶点P在直线AC上滑动，且与AC交于另一点Q.若点M在直线AC下方，且为平移前(1)中的抛物线上的点．当以PQ为直角边，M，P，Q三点为顶点的三角形是等腰直角三角形时，求出所有符合条件的点M的坐标；

初三数学二次函数专题训练(含答案)-[1]

(完整word版)初三数学二次函数专题训练(含答案)-(word版可编辑修改) 编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（(完整word版)初三数学二次函数专题训练(含答案)-(word版可编辑修改)）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为(完整word版)初三数学二次函数专题训练(含答案)-(word版可编辑修改)的全部内容。

二次函数专题训练（含答案）一、填空题1.把抛物线221x y -=向左平移2个单位得抛物线 ,接着再向下平移3个单位，得抛物线 .2.函数x x y +-=22图象的对称轴是，最大值是 .3。

正方形边长为3,如果边长增加x 面积就增加y,那么y 与x 之间的函数关系是。

4。

二次函数6822-+-=x x y ，通过配方化为k h x a y +-=2)(的形为 .5.二次函数c ax y +=2（c 不为零），当x 取x 1，x 2（x 1≠x 2）时，函数值相等，则x 1与x 2的关系是。

6.抛物线c bx ax y ++=2当b=0时，对称轴是，当a ，b 同号时,对称轴在y 轴侧，当a ，b 异号时,对称轴在y 轴侧。

7.抛物线3)1(22-+-=x y 开口 ,对称轴是，顶点坐标是 .如果y 随x 的增大而减小,那么x 的取值范围是 .8.若a 0，则函数522-+=ax x y 图象的顶点在第象限;当x 4a -时,函数值随x 的增大而 .9.二次函数c bx ax y ++=2（a ≠0）当a0时，图象的开口a 0时,图象的开口 ,顶点坐标是。

10。

抛物线2)(21h x y --=,开口 ,顶点坐标是，对称轴是 .11。

2023年中考数学高频考点专题训练--二次函数与动态几何综合题

2023年中考数学高频考点专题训练--二次函数与动态几何综合题1．如图，已知抛物线y=−43x2+bx+c经过A(0,4)，B(3,0)两点，与x轴负半轴交于点C，连接AC、AB．（1）求该抛物线的解析式；（2）D、E分别为AC、AB的中点，连接DE，P为DE上的动点，PQ⊥BC，垂足为Q，QN⊥AB，垂足为N，连接PN．①当△PQN与△ABC相似时，求点P的坐标；②是否存在点P，使得PQ=NQ，若存在，直接写出点P的坐标，若不存在，请说明理由．2．如图，抛物线y= 12x2+bx+c与y轴交于点C（0，﹣4），与x轴交于点A、B，且B点的坐标为（2，0）．（1）求抛物线的解析式；（2）若点P是AB上的一个动点，过点P作PE∥AC交BC于点E，连接CP，求∥PCE面积最大时P点的坐标；（3）在（2）的条件下，若点D为OA的中点，点M是线段AC上一点，当∥OMD为等腰三角形时，连接MP、ME，把∥MPE沿着PE翻折，点M的对应点为点N，直接写出点N的坐标．3．已知抛物线y=−12x2+mx+m+12与x轴交于点A，B（点A在点B的左侧），与y轴交于点C（0，−52），点P为抛物线在直线AC上方图象上一动点．（1）求抛物线的解析式；（2）求∥PAC面积的最大值，并求此时点P的坐标；（3）在（2）的条件下，抛物线y=−12x2+mx+m+12在点A、B之间的部分（含点A、B）沿x轴向下翻折，得到图象G．现将图象G沿直线AC平移，得到新的图象M与线段PC只有一个交点，求图象M的顶点横坐标n的取值范围．4．如图，抛物线y= −14x2+bx+c与x轴交于点A（2，0），交y轴于点B（0，52）．直线y=kx−32过点A与y轴交于点C，与抛物线的另一个交点是D．（1）求抛物线y= −14x2+bx+c与直线y=kx −32的解析式；（2）设点P是直线AD上方的抛物线上一动点（不与点A、D重合），过点P作y轴的平行线，交直线AD于点M，作DE∥y轴于点E．探究：是否存在这样的点P，使四边形PMEC是平行四边形？若存在请求出点P的坐标；若不存在，请说明理由；（3）在（2）的条件下，作PN∥AD于点N，设∥PMN的周长为l，点P的横坐标为x，求l与x 的函数关系式，并求出l的最大值．5．如图，抛物线y＝ax2+bx+2（a≠0）与x轴交于A（﹣1，0）、B（4，0）两点，与y轴交于点C．（1）求抛物线的解析式；（2）当点P是直线BC下方的抛物线上一点，且S∥PBC＝2S∥ABC时，求点P的坐标；（3）点P（﹣2，﹣3），点E是抛物线上一点，点F是抛物线对称轴上一点，是否存在这样的点E和点F，使得以点B、P、E、F为顶点的四边形是平行四边形？若存在，请直接写出点F的坐标；若不存在，请说明理由．6．如图，抛物线y=ax2+bx+2交x轴于点A(-3，0)和点B(1，0)，交y轴于点C.（1）求这个抛物线的函数表达式.（2）点D的坐标为(-1，0)，点P为第二象限内抛物线上的一个动点，求四边形ADCP面积的最大值.（3）点M为抛物线对称轴上的点，问：在抛物线上是否存在点N，使∥MNO为等腰直角三角形，且∥MNO为直角？若存在，请直接写出点N的坐标；若不存在，请说明理由.7．已知二次函数y=ax2+bx+c的图象过点(−1，0)，且对任意实数x，都有4x−12≤ax2+bx+c≤2x2−8x+6．（1）求该二次函数的解析式；（2）若（1）中二次函数图象与x轴的正半轴交点为A，与y轴交点为C；点M是（1）中二次函数图象上的动点．问在x轴上是否存在点N，使得以A、C、M、N为顶点的四边形是平行四边形．若存在，求出所有满足条件的点N的坐标；若不存在，请说明理由．8．如图，在平面直角坐标系中，点O为坐标原点，点A在第一象限，点B在x轴正半轴上，AO=AB，OB=4，tan∥AOB=2，点C是线段OA的中点.（1）求点C的坐标；（2）若点P是x轴上的一个动点，使得∥APO=∥CBO，抛物线y=ax2+bx经过点A、点P，求这条抛物线的函数解析式；（3）在（2）的条件下，点M是抛物线图象上的一个动点，以M为圆心的圆与直线OA相切，切点为点N，点A关于直线MN的对称点为点D.请你探索：是否存在这样的点M，使得∥MAD∥∥AOB？若存在，请直接写出点M的坐标；若不存在，请说明理由.9．如图，抛物线y=x2+bx+c与x轴交于点A，B，与y轴交于点C，其中点A在y轴的左侧，点C 在x轴的下方，且OA=OC=5．（1）求抛物线对应的函数解析式；（2）点P为抛物线对称轴上的一动点，当PB+PC的值最小时，求点P的坐标；（3）在（2）条件下，点E为抛物线的对称轴上的动点，点F为抛物线上的动点，以点P、E、F 为顶点作四边形PEFM，当四边形PEFM为正方形时，请直接写出坐标为整数的点M的坐标．10．综合与探究如图，已知抛物线y=ax2+2x+c(a≠0)与x轴负半轴交于点A(−1，0)，与y轴交于点C(0，3)，抛物线的顶点为D，直线y＝x＋b与抛物线交于A，F两点，过点D作DE∥y轴交直线AF于点E．（1）求抛物线和直线AF的解析式；（2）在直线AF上方的抛物线上有一点P，使S△PAE=3S△PDE，求点P的坐标；（3）若点M为抛物线上一动点，试探究在直线AF上是否存在一点N，使得以D，E，M，N为顶点的四边形是平行四边形？若存在，请直接写出点N的坐标；若不存在，请说明理由．11．如图，在平面直角坐标系中，抛物线y=ax2+bx+c的对称轴为x=2，与y轴交于点A与x轴交于点E、B，且点A(0，5)，B(5，0)，过点A作AC平行于x轴，交抛物线于点C，点P为抛物线上的点，且在AC的上方，作PD平行于y轴交AB于点D．（1）求二次函数的解析式；（2）当点P在何位置时，四边形APCD的面积最大？并求出最大面积；（3）在抛物线上是否存在点Q，使得以点A、C、D、Q为顶点的四边形为平行四边形，如果存在，请写出点Q，D的坐标，如果不存在，请说明理由．12．如图1，抛物线y＝ax2+bx﹣4a经过A（﹣1，0）、C（0，4）两点，与x轴交于另一点B．（1）求抛物线的解析式；（2）如图2，点P为第一象限抛物线上一点，满足到线段CB距离最大，求点P坐标；（3）如图3，若抛物线的对称轴EF（E为抛物线顶点）与线段BC相交于点F，M为线段BC上的任意一点，过点M作MN∥EF交抛物线于点N，以E，F，M，N为顶点的四边形能否为平行四边形？若能，求点N的坐标；若不能，请说明理由．13．已知抛物线y=−12x2+32x+2，与x轴交于两点A，B（点A在点B的左侧），与y轴交于点C．（1）求点A，B和点C的坐标；（2）已知P是线段BC上的一个动点．①若PQ⊥x轴，交抛物线于点Q，当BP+PQ取最大值时，求点P的坐标；②求√2AP+PB的最小值．14．已知二次函数y=﹣x2+2x+m.（1）如果二次函数的图象与x轴有两个交点，求m的取值范围；（2）如图，二次函数的图象过点A（-1，0），与y轴交于点C，求直线BC与这个二次函数的解析式；（3）在直线BC上方的抛物线上有一动点D，DE ⊥x轴于E点，交BC于F，当DF最大时，求点D的坐标，并写出DF最大值.15．如图，抛物线y=12x2+32x+2与x轴交于A、B两点（点A在点B的左边），与y轴交于点C，连接BC．（1）求点A、B、C的坐标．（2）点P为AB上的动点（点A、O、B除外），过点P作直线PN∥x轴，交抛物线于点N，交直线BC于点M．设点P到原点的值为t，MN的长度为s，求s与t的函数关系式．（3）在（2）的条件下，试求出在点P运动的过程中，由点O、P、N围成的三角形与Rt∥COB 相似时点P的坐标．16．如图，抛物线y＝ax2+bx+4交x轴于A（﹣3，0），B（4，0）两点，与y轴交于点C，连接AC，BC.点P是第一象限内抛物线上的一个动点，点P的横坐标为m，过点P作PM∥x轴，垂足为点M，PM交BC于点Q.（1）求此抛物线的表达式：（2）过点P作PN∥BC，垂足为点N，请用含m的代数式表示线段PN的长，并求出当m为何值时PN有最大值，最大值是多少？（3）试探究点P在运动过程中，是否存在这样的点Q，使得以A，C，Q为顶点的三角形是等腰三角形.若存在，请求出此时点Q的坐标，若不存在，请说明理由.答案解析部分1．【答案】（1）解：将A(0,4),B(3,0)代入抛物线的解析式得：{c=4−12+3b+c=0，解得：b=83,c=4．∴抛物线的解析式为：y=−43x2+83x+4．（2）解：①如图1所示：∵令y=0，−43x2+83x+4=0解得：x1=−1,x2=3，∴C(−1,0)．∴BC=4,AB=√32+42=5．∵D、E分别为AC、AB的中点，∴DE//BC．∴ADDC=AFFO=1．∴PQ=FO=2．∵PQ⊥BC,QN⊥AB，∴∠PQN+∠NQB=90°，∠NQB+∠QBN=90°．∴∠PQN=∠QBN．∴当PQQN=ABCB或POQN=CBAB时，△PQN与△ABC相似．∵当PQQN=ABCB时，2QN=54，解得：QN=8 5．∵QNQB=OAAB=45，∴QB=54QN=54×85=2．∴OQ=3−2=1．∴点P的坐标为(1,2)．当PQQN=CBAB时，2QN=45，解得：QN=2.5．∵QNQB=OAAB=45，∴QB=54QN=54×52=258．∴OB−BQ=−1 8，∴点P的坐标为(−18,2)．综上所述点P的坐标为：(1,2)或(−18,2)．②如图2所示：∵PQ=QN,PQ=2，∴QN=2．∵QN⊥AB，∴∠QNB=90°，∵由（2）可知OA=4,AB=5，∴sin∠ABO=4 5．∴QNQB=45，即2QB=45，解得：QB=52．∴OQ =OB −QB =3−52=12． ∴P(12,2) ．2．【答案】（1）解：根据题意得：{c =−42+2b +c =0 ，解得： {b =1c =−4，所以该抛物线的解析式为：y= 12x 2+x ﹣4；（2）解：令y=0，即 12 x 2+x ﹣4=0，解得x 1=﹣4，x 2=2，∴A （﹣4，0），S ∥ABC = 12 AB•OC=12设P 点坐标为（x ，0），则PB=2﹣x ． ∵PE∥BC ，∴∥BPE=∥BAC ，∥BEP=∥BCA ， ∴∥PBE∥∥BAC ，∴S △PBE S △ABC=（ PB AB ）2，即 S△PBE 12 =（ 2−x 6 ）2，化简得：S ∥PBE = 13（2﹣x ）2． S ∥PCE =S ∥PCB ﹣S ∥PBE = 12 PB•OC ﹣S ∥PBE = 12 ×（2﹣x ）×4﹣ 13 （2﹣x ）2=﹣ 13 x 2﹣ 23 x+ 83 =﹣ 13 （x+1）2+3∴当x=﹣1时，S ∥PCE 的最大值为3．（3）解：由（2）已知A （﹣4，0）， ∵点D 为0A 中点， ∴D （﹣2，0），设直线AC 的解析式为y=mx+n ，把A （﹣4，0）、C （0，﹣4）分别代入得： {−4m +n =0n =−4 ，解得 {m =−1n =−4 ，∴直线AC 的解析式为y=﹣x ﹣4．∵PE∥AC ，所以可设直线PE 的解析式为y=﹣x+a ，将P （﹣1，0）代入y=﹣x ﹣a 得a=﹣1，所以直线PE 的解析式为y=﹣x ﹣1．设直线BC 的解析式为y=kx+a′，将B （2，0）、C （0，﹣4）代入y=kx+a′得 {2k +a′=0a′=−4 ，解得k=2，a′=﹣4．所以直线BC 的解析式为y=2x ﹣4．由2x ﹣4=﹣x ﹣1得x=1，将x=1代入y=2x ﹣4得y=﹣2， ∴E 点坐标为（1，﹣2）． ①当MD=OD 时，如图1：∵AD=MD=AD ，OA=OC ，∥DAM=∥OAC ， ∴∥ADM∥∥AOC ，∴∥ADM=∥AOC=90°，即DM∥x 轴，∴M 的横坐标为﹣2，将x=﹣2代入y=﹣x ﹣4，得y=﹣2．所以此时M 的坐标为（﹣2，﹣2）； ∵M 和E 点纵坐标相等， ∴ME∥x 轴， ∴∥PEM=45°．由翻折得∥ENM=2∥PEM=90°，即NE∥y 轴， ∴EN=ME=3， ∵E （1，﹣2）， ∴N （1，1）．②当DM=OM 时，过点M 作MG∥x 轴交于点，如图2：易知DG=OG=1，即G点与P点重合，M的横坐标为﹣1，将x=﹣1代入y=﹣x﹣4，得y=﹣3．∴M（﹣1，﹣3）．∵ME= √(−1−1)2+(−3+2)2= √5，EB= √(1−2)2+22= √5，∴ME=EB，∵PB=3，PM=3，即PB=PM，又∵PE=PE，∴∥BPE∥∥MPE，∴∥BEP=∥MEP，∴点N与点B重合，∴N（2，0）；③当OD=OM时，设点O到AC的最短距离为h，则OA•OC=h•AC∵AC= √OA2+OC2= √42+42=4 √2，∴h= 4×44√2=2 √2，∵h＞OD，∴OD≠OM．此时等腰∥OMD不存在．综上所述，N点的坐标分别为（1，1）或（2，0）．3．【答案】（1）解：将点C（0，−52）代入抛物线解析式得：m+12=−52，解得：m=−3，∴抛物线解析式为：y=−12x2−3x−52；（2）解：∵抛物线与x轴交于A、B两点，∴令0=−12x2−3x−52，解得：x1=−5，x2=−1，∴A、B坐标分别为：A(−5，0)，B(−1，0)，设直线AC的解析式为：y=kx+b(k≠0)，将A(−5，0)和C(0，−52)代入得：{−5k+b=0b=−52，解得：{k=−12b=−52，∴直线AC的解析式为：y=−12x−52，如图所示，过P点作PQ∥x轴，交AC于Q点，∵P点在位于直线AC上方的抛物线上，∴设P(a，−12a2−3a−52)，则Q(a，−12a−52)，其中−5<a<0，∴PQ=y P−y Q=−12a2−3a−52−(−12a−52)=−12a2−52a，∵S△PAC=12PQ(x C−x A)，∴S△PAC=12(−12a2−52a)×[0−(−5)]=−54(a+52)2+12516，∵−54<0，∴抛物线开口向下，当a=−52时，S△PAC取得的最大值，最大值为12516，此时，将a=−52代入抛物线解析式得：y=158，∴当P(−52，158)时，S△PAC取得的最大值，最大值为12516；（3）解：如图所示，抛物线y=−12x2+mx+m+12在点A、B之间的部分（含点A、B）沿x轴向下翻折，得到图象G ．由（1）可知，原抛物线顶点坐标为(−3，2)，∴沿x 轴向下翻折后，图象G 的顶点坐标为(−3，−2)，图象G 的解析式为：y =12x 2+3x +52；∵图象G 沿着直线AC 平移，∴作直线BS∥AC ，交PC 于S 点，则随着平移过程，点B 在直线BS 上运动，分如下情况讨论：①当图象G 沿直线AC 平移至B 点恰好经过S 点时，如图中M 1所示，此时，平移后的图象M 恰好与线段PC 有一个交点，即为S 点，由（2）知，P(−52，158)，以及直线AC 的解析式为y =−12x −52，∴设直线BS 的解析式为：y =−12x +b ，将B(−1，0)代入得：b =−12，∴直线BS 的解析式为：y =−12x −12；设直线PC 的解析式为：y =kx +b(k ≠0)，将P(−52，158)，C(0，−52)代入得：{−52k +b =158b =−52，解得：{k =−74b =−52，∴直线PC 的解析式为：y =−74x −52；联立{y =−12x −12y =−74x −52，解得：{x =−85y =310，即：S 点的坐标为S(−85，310)，∴此时点B(−1，0)平移至S(−85，310)，等同于向左平移35个单位，向上平移310个单位，即：当平移后的图象M 与线段PC 恰好仅有一个交点时，可由原图像G 向左平移35个单位，向上平移310个单位， ∵原图像G 的顶点坐标为：(−3，−2)， ∴平移后图象M 1的顶点的横坐标n =−3−35=−185； ②当图象G 沿直线AC 平移至恰好经过C 点时，如图中M 2所示，设图象G 与直线AC 的交点为R ，联立{y =12x 2+3x +52y =−12x −52，解得：{x =−5y =0或{x =−2y =−32， ∴点R 的坐标为：R(−2，−32)，由R(−2，−32)平移至C(0，−52)，等同于向右平移2个单位，向下平移1个单位，∴当平移后的图象M 与线段PC 恰好仅有一个交点时，可由原图像G 向右平移2个单位，向下平移1各单位，∵原图像G 的顶点坐标为：(−3，−2)，∴平移后图象M 2的顶点的横坐标n =−3+2=−1；∴当图象G 在M 1和M 2之间平移时，均能满足与线段PC 有且仅有一个交点，此时，图象M 的顶点横坐标n 的取值范围为：−185≤n ≤−1； ③当图象G 沿直线AC 平移至A 点恰好经过C 点时，如图中M 3所示，此时，由A(−5，0)平移至C(0，−52)，等同于向右平移5个单位，向下平移52个单位，即：原图像G 向右平移5个单位，向下平移52个单位，得到图象M 3，∵原图像G 的顶点坐标为：(−3，−2)，∴平移后图象M 3的顶点的横坐标n =−3+5=2；综上所述，当新的图象M 与线段PC 只有一个交点时，图象M 的顶点横坐标n 的取值范围为：−185≤n ≤−1或n =2． 4．【答案】（1）解：∵y= −14x 2+bx+c 经过点A （2，0）和B （0， 52 ），∴由此得 {−1+2b +c =0c =52，解得 {b =−34c =52． ∴抛物线的解析式是y= −14x 2﹣ 34 x+ 52 ，∵直线y=kx ﹣ 32 经过点A （2，0）∴2k ﹣ 32 =0，解得：k= 34，∴直线的解析式是y= 34 x ﹣ 32（2）解：设P 的坐标是（x ， −14 x 2﹣ 34 x+ 52 ），则M 的坐标是（x ， 34 x ﹣ 32 ）∴PM=（ −14 x 2﹣ 34 x+ 52 ）﹣（ 34 x ﹣ 32 ）=﹣ 14 x 2﹣ 32 x+4，解方程 {y =−14x 2−34x +52y =34x −32得： {x =−8y =−712， {x =2y =0 ， ∵点D 在第三象限，则点D 的坐标是（﹣8，﹣7 12 ），由y= 34 x ﹣ 32得点C 的坐标是（0，﹣32）， ∴CE=﹣ 32 ﹣（﹣7 12）=6，由于PM∥y 轴，要使四边形PMEC 是平行四边形，必有PM=CE ，即﹣ 14 x 2﹣ 32 x+4=6解这个方程得：x 1=﹣2，x 2=﹣4，符合﹣8＜x ＜2，当x=﹣2时，y=﹣ 14 ×（﹣2）2﹣ 34 ×（﹣2）+ 52=3，当x=﹣4时，y=﹣ 14 ×（﹣4）2﹣ 34 ×（﹣4）+ 52= 32 ，因此，直线AD 上方的抛物线上存在这样的点P ，使四边形PMEC 是平行四边形，点P 的坐标是（﹣2，3）和（﹣4， 32）（3）解：在Rt∥CDE 中，DE=8，CE=6 由勾股定理得：DC= √82+62 ∴∥CDE 的周长是24， ∵PM∥y 轴， ∵∥PMN=∥DCE ， ∵∥PNM=∥DEC ， ∴∥PMN∥∥CDE ，∴△PMN 的周长△CDE 的周长 = PM DC ，即 l 24 = −14x 2−32x+410，化简整理得：l 与x 的函数关系式是：l=﹣ 35 x 2﹣ 185 x+ 485，l=﹣ 35 x 2﹣ 185 x+ 485 =﹣ 35（x+3）2+15，∵﹣ 35＜0，∴l 有最大值，当x=﹣3时，l 的最大值是15．5．【答案】（1）解：∵y ＝ax 2+bx+2（a≠0）与x 轴交于A （﹣1，0）、B （4，0）， ∴{a −b +2=016a +4b +2=0 ，解得 {a =−12b =32 ， ∴抛物线的解析式为：y =−12 x 2+32x+2．（2）解：∵A （﹣1，0）、B （4，0）， ∴AB ＝5，由抛物线的解析式可得，C （0，2），∴OC ＝2，l BC ：y =−12x+2．∴S ∥PBC ＝2S ∥ABC ＝2 ×12•AB•OC ＝5×2＝10．在x 轴上取点M （﹣6，0），则MB ＝10，∴S ∥MBC =12 •MB•OC =12×2×10= 10．过点M 作BC 的平行线MN ，交抛物线于点P 1，P 2，∴l MN ：y =−12 x ﹣3．联立 {y =−12x 2+32x +2y =−12x −3，解得 {x =2+√14y =−4−√142 ，或 {x =2−√14y =−4+√142，∴P 1（2 +√14 ，﹣4 −√142 ），P 2（2 −√14 ，﹣4 +√142）．（3）解：由抛物线解析式可得，抛物线对称轴为直线x =32．∵点F 是抛物线对称轴上一点， ∴设点F 的坐标为（ 32，t ）．若以点B 、P 、E 、F 为顶点的四边形是平行四边形，需要分以下两种情况： ①当BP 为边时，如图，由平行四边形的性质可知，E1（32+6，t+3），E2（32−6，t﹣3），∵点E在抛物线y =−12x2+32x+2上，∴t+3 =−12×（32+6）2+32×（32+6）+2，解得t =−1438，t﹣3 =−12×（32−6）2+32×（32−6）+2，解得t =−1378，∴F的坐标为（32，−1438）或（32，−1378）．②当BP为对角线时，BP的中点为（1，−3 2），∵F（32，t），∴E（−12，﹣t﹣3），∴﹣t﹣3 =−12×（−12）2+32×（−12）+2，解得t =−338，∴F（32，−338）．综上，点F的坐标为（32，−1438）或（32，−1378）或（32，−338）．6．【答案】（1）解：抛物线的表达式为：y=a(x+3)(x-1)=a(x2+2x-3)=ax2+2ax-3a，即-3a=2，解得：a=- 2 3，故抛物线的表达式为：y=- 23x2- 43x+2，则点C(0，2)，函数的对称轴为：x=1（2）解：连接OP，设点P(x，- 23x2- 43x+2)，则S=S四边形ADCP=S∥APO+S∥CPO-S∥ODC= 12×AO×y P+ 12×OC×|x P|- 12×CO×OD = 12×3×(- 23x2- 43x+2) +12×2×(-x)- 12×2×1=-x2-3x+2，∵-1＜0，故S有最大值，当x=- 32时，S的最大值为174（3）解：存在，理由：∥MNO为等腰直角三角形，且∥MNO为直角时，点N的位置如下图所示：①当点N在x轴上方时，点N的位置为N1、N2，N1的情况(∥M1N1O)：设点N1的坐标为(x，- 23x2- 43x+2)，则M1E=x+1，过点N1作x轴的垂线交x轴于点F，过点M1作x轴的平行线交N1F于点E，∵∥FN1O+∥M1N1E=90°，∥M1N1E+∥EM1N1=90°，∴∥EM1N1=∥FN1O，∥M1N1E=∥N1OF=90°，ON1=M1N1，∴∥M1N1E∥∥N1OF(AAS)，∴M1E=N1F，即：x+1=- 23x2- 43x+2，解得：x=−7±√734(舍去负值)，则点N1( −7+√734，−3+√734)；N2的情况(∥M2N2O)：同理可得：点N 2( −1−√734 ， −3+√734)； ②当点N 在x 轴下方时，点N 的位置为N 3、N 4，同理可得：点N 3、N 4的坐标分别为：( −7−√734 ， −3−√734 )、( −1+√734 ， −3−√734)；综上，点N 的坐标为：( −7+√734 ， −3+√734 )或( −1−√734 ， −3+√734 )或( −7−√734， −3−√734 )或( −1+√734 ， −3−√734). 7．【答案】（1）解：令 4x −12=2x 2−8x +6 ，解得 x 1=x 2=3 ，当 x =3 时， 4x −12=2x 2−8x +6=0 ，∴y =ax 2+bx +c 必过 (3，0) ，又∵y =ax 2+bx +c 必过 (−1，0) ，∴{a −b +c =09a +3b +c =0,⇒,{b =−2a c =−3a， ∴y =ax 2−2ax −3a ，即 4x −12≤ax 2−2ax −3a ，即可看成二次函数 y =ax 2−2ax −3a 与一次函数 y =4x −12 仅有一个交点，且整体位于 y =4x −12 的上方∴a >0 ，∴ 4x −12=ax 2−2ax −3a 有两个相等的实数根∴ Δ=0∴(2a +4)2−4a(12−3a)=0 ，∴(a −1)2=0 ，∴a =1 ，∴b =−2 ， c =−3 ，∴y =x 2−2x −3 ．（2）解：由（1）可知： A(3，0) ， C(0，−3) ，设 M(m ，m 2−2m −3)，N(n ，0) ，①当 AC 为对角线时， {x A +x C =x M +x N y A +y C =y n +y N∴{3+0=m +n 0+(−3)=m 2−2m −3+0，解得 m 1=0 （舍）， m 2=2 ， ∴n =1 ，即 N 1(1，0) ．②当AM为对角线时，{x A+x M=x C+x Ny A +yM=yC+yN∴{3+m=0+n0+m2−2m−3=−3+0，解得m1=0（舍）m2=2，∴n=5，即N2(5，0)．③当AN为对角线时，{x A+x N=x C+x My A +yN=yC+yM∴{3+n=0+m0+0=−3+m2−2m−3，解得m1=1+√7，m2=1−√7，∴n=√7−2或n=−2−√7，∴N3(√7−2，0)，N4(−2−√7，0)．综上所述：N点坐标为(1，0)或(5，0)或(√7−2，0)或(−2−√7，0)．8．【答案】（1）解：过点A作AD∥OB于点D，过点C作CE∥OB于点E，∵AO=AB，∴AD是∥AOB的中线，∴OD= 12OB=2，∵tan∥AOB=2，∴ADOD=2，∴AD=4，∵CE∥AD，点C是AO的中点，∴CE是∥AOD的中位线，∴CE= 12AD=2，OE=12OD=1，∴C的坐标为（1，2）；（2）解：由（1）可知：CE=2，BE=3，A的坐标为（2，4），∴tan∥CBE= CEBE=23，∵∥APO=∥CBO，∴tan∥APO=tan∥CBO= 23， ∴AD PD = 23， ∴PD=6，设P 的坐标为（x ，0），∵D （2，0），∴PD=|x ﹣2|，∴|x ﹣2|=6，∴x=8或x=﹣4，∴P （8，0）或（﹣4，0）；当P 的坐标为（8，0）时，把A （2，4）和（8，0）代入y=ax 2+bx ，∴{4=4a +b 0=64a +8b，解得： {a =−13b =83， ∴抛物线的解析式为：y=﹣ 13 x 2+ 83x ，当P 的坐标为（﹣4，0）时，把A （2，4）和P （﹣4，0）代入y=ax 2+bx ，∴{4=4a +2b 0=16a −4b ，解得： {a =13b =43， ∴抛物线的解析式为：y= 13 x 2+ 43x ，综上所述，抛物线的解析式为：y=﹣ 13 x 2+ 83 x 或y= 13 x 2+ 43x ；（3）解：∵M 为圆心，N 为切点，∴MN∥OA ，∵D 点是A 点关于MN 的对称点，∴∥MAD 是等腰三角形，MA=MD当∥MAD∥∥AOB 时，∵∥AOB 是等腰三角形，∴∥MAD=∥AOB ，当抛物线的解析式为y=﹣ 13 x 2+ 83x 时，如图2，①若点N在A的上方时，此时∥MAN=∥AOB，∴AM∥x轴，∴M的纵坐标为4，∴把y=4代入y=﹣13x2+ 83x，解得：x=2（舍去）或x=6，∴M的坐标为（6，4），②当点N在点A的下方时，此时∥MDA=∥AOB，∴DM∥x轴，过点A作AE∥DM于点E，交于x轴于点F，设D点横坐标为a，∴DE=2-a，∵tan∥MDA=tan∥AOB=2，∴AE=2DE=4-2a，∴点M的纵坐标为2a，∴由勾股定理可知：AD= √5（2-a），OA=2 √5，∴OADM=OBAD，解2√5DM=4√5(2−a)，∴DM= 5(2−a)2，设M的横坐标为x，∴x-a= 5(2−a)2∴x= 10−3a2，∴M（10−3a2，2a）把M（10−3a2，2a）代入y=﹣13x2+ 83x，得：2a=- 13×(10−3a2)2+ 83×(10−3a2)解得：a=2或a=- 10 3，∴当a=2时，M（2，4）舍去当a=- 103时，M（10，-203）当抛物线的解析式为y= 13x2+ 43x时，如图4，若点N在点A的上方时，此时∥MAN=∥AOB，延长MA交x轴于点F，∵∥MAN=∥OAF，∴∥AOB=∥OAF，∴FA=FO，过点F作FG∥OA于点G，∵A（2，4），∴由勾股定理可求得：AO=2 √5，∴OG= 12AO= √5 ， ∵tan∥AOB= CF OG∴GF=2 √5 ，∴由勾股定理可求得：OF=5，∴F 的坐标为（5，0），设直线MA 的解析式为：y=mx+n ，把A （2，4）和F （5，0）代入y=mx+n ，∴{4=2m +n 0=5m +n，解得： {m =−43n =203， ∴直线MA 的解析式为：y=﹣ 43 + 203，联立 {y =13x 2+43x y =−43x +203， ∴解得：x=2（舍去）或x=﹣10，把x=﹣10代入y=﹣ 43 + 203， ∴y=20，∴M （﹣10，20），若点N 在点A 的下方时，此时∥MAN=∥AOB ，∴AM∥x 轴，∴M 的纵坐标为4，把y=4代入y= 13 x 2+ 43x ， ∴x=﹣6或x=2（舍去），∴M （﹣6，4），综上所述，存在这样的点M （6，4）或（10，- 203）或（﹣10，20）或（﹣6，4），使得∥MAD∥∥AOB9．【答案】（1）解：由题意，可得A （﹣5，0），C （0，﹣5）．∵抛物线y=x 2+bx+c 过点A ，点C ，∴{25−5b +c =0c =−5，∴抛物线对应的函数解析式为y=x 2+4x ﹣5；（2）解：∵y=x 2+4x ﹣5=（x+2）2﹣9，∴对称轴是直线x=﹣2．∵抛物线y=x 2+4x ﹣5与x 轴交于点A ，B ，∴点A ，B 关于直线x=﹣2对称．连结AC ，交对称轴于点P ，此时PB+PC 的值最小．设直线AC 的解析式为y=mx+n ，则 {−5m +n =0n =−5，解得 {m =−1n =−5 ， ∴直线AC 的解析式为y=﹣x ﹣5，当x=﹣2时，y=﹣3，∴点P 的坐标为（﹣2，﹣3）（3）解：在（2）条件下，点P 的坐标为（﹣2，﹣3）．设F （x ，x 2+4x ﹣5），∵四边形PEFM 为正方形，∴E （﹣2，x 2+4x ﹣5），M （x ，﹣3），PM=PE ，∴|x+2|=|x 2+4x ﹣5+3|，∴x 2+4x ﹣2=x+2，或x 2+4x ﹣2=﹣x ﹣2，整理得x 2+3x ﹣4=0，或x 2+5x=0，解得x 1=﹣4，x 2=1，x 3=0，x 4=﹣5，∴M （﹣4，﹣3）或M （1，﹣3）或M （0，﹣3）或M （﹣5，﹣3）10．【答案】（1）解：将A(−1，0)和C(0，3)代入y =ax 2+2x +c(a ≠0)，得{a −2+c =0c =3，∴抛物线解析式为y=−x2+2x+3，将A(−1，0)代入y＝x＋b，得：－1＋b＝0，解得b＝1，∴直线AF的解析式为y＝x＋1（2）解：y=−x2+2x+3=−(x−1)2+4，∴D(1，4)，对于直线y＝x＋1，令x＝1，则y＝2，故E(1，2)，∴DE＝4－2＝2．过点P作x轴的垂线，交AF于点H，过点P作PG∥AF于点G，过点P作PK∥DE于点K，连接PA和PD，如图所示：设P(m，−m2+2m+3)，则H(m，m+1)，∴PH=(−m2+2m+3)−(m+1)=−m2+m+2，对于直线y＝x＋1，令x＝0，则y＝1，由交点得出∥FAB＝45°，∴∥PHG＝45°，即∥PHG为等腰直角三角形，故有PG=√22PH=√22(−m2+m+2)，延长DE交x轴于点Q，则Q(1，0)，∴AQ＝2，即AE=√2AQ=2√2，∴S△PAE=12AE⋅PG=12×2√2×√22(−m2+m+2)=−m2+m+2，∵P(m，−m2+m+3)，K(1，−m2+m+3)，∴PK=|1−m|，∴S△PDE=12DE⋅PK=12×2×|1−m|=|1−m|，由S△PAE=3S△PDE，得−m2+m+2=3|1−m|，解得m1=2−√3，m2=2+√3（不合题意，舍去），m3=−1+√6，m4=−1−√6（不合题意，舍去），将m1=2−√3代入−m2+2m+3，得−m2+2m+3=2√3，则得点P的坐标为P(2−√3，2√3)；将m3=−1+√6代入−m2+2m+3，得−m2+2m+3=4√6−6，则得点P的坐标为P(−1+√6，4√6−6)；综上所述，点P的坐标为P(2−√3，2√3)或P(−1+√6，4√6−6)（3）解：存在，N1(0，1)，N2(2，3)，N3(1+√172，3+√172)，N4(1−√172，3−√172)11．【答案】（1）解：∵抛物线y=ax2+bx+c的对称轴为x=2，∴−b2a=2，∴b=−4a，∴抛物线解析式为y=ax2−4ax+c，∵点A(0，5)，B(5，0)，∴{c=525a−5b+c=0，∴{a=−1c=5，∴二次函数的解析式为y=−x2+4x+5；（2）解：∵AC//x轴，点A(0，5)，当y=5时，−x2+4x+5=5，∴x1=0，x2=4，∴C(4，5)，∴AC=4，设直线AB的解析式为y=mx+n，∵A(0，5)，B(5，0)，由点A、B的坐标得，直线AB的解析式为y=−x+5；设P(m，−m2+4m+5)，∴D(m，−m+5)，∴PD=−m2+4m+5+m−5=−m2+5m，∵AC=4，∴S四边形APCD =12AC⋅PD=2(−m2+5m)=−2(m−52)2+252∴当m=52时，四边形APCD的面积最大，∴即点P(52，354)时，四边形APCD的面积最大为252；（3）解：(3)设P(n，−n2+4n+5)则D(n，−n+5)①当AC为平行四边形的边，如图，∴AC∥DQ，AC=DQ，∴点Q的纵坐标为−n+5，又∵点Q在抛物线上，∴−x2+4x+5=−n+5，解得x=2±√4+n，∴点Q的坐标为(2+√4+n，−n+5)或(2−√4+n，−n+5)，当Q点坐标为(2+√4+n，−n+5)时，∵AC =4，∴DQ =2+√4+n −n =4， ∴4+n =(n +2)2，解得n =0或n =−3，∵点P 在第一象限，且在AC 的上方， ∴0<n <4， ∴此时不符合题意；当Q 点坐标为(2−√4+n ，−n +5)时， ∵AC =4，∴DQ =n −2+√4+n =4，∴4+n =(6−n)2，即n 2−13n +32=0解得n =13+√412或n =13−√412，∵点P 在第一象限，且在AC 的上方， ∴0<n <4，∴n =13−√412∴D 点坐标为(13−√412，√41−32)，Q 点坐标为(2−√42−2√412，√41−32)②AC 为平行四边形的对角线时，如图，连接DQ 交AC 于点M ， ∴AM =CM ，DM =QM ， ∵A(0，5)，C(4，5)， ∴M 的坐标为(2，5)，设点Q 的坐标为(t ，−t 2+4t +5)，∴{t+n2=2−t 2+4t+5−n+52=5，解得{t =1n =3或{t =4n =0，同理可得0<n <4， ∴{t =1n =3， ∴点D 的坐标为（3，2），点Q 的坐标为（1，8）；综上所述，存在Q 使得以A 、C 、D 、Q 为顶点的四边形为平行四边形，此时D 、Q 的坐标分别为(13−√412，√41−32)，(2−√42−2√412，√41−32)或（3，2），（1，8）． 12．【答案】（1）解：由题意得 {a −b −4a =0−4a =4 ，解得 {a =−1b =3．∴抛物线的解析式：y ＝﹣x 2+3x+4．（2）解：由B （4，0）、C （0，4）可知，直线BC ：y ＝﹣x+4；如图1，过点P 作PQ//y 轴，交直线BC 于Q ，设P （x ，﹣x 2+3x+4），则Q （x ，﹣x+4）；∴PQ ＝（﹣x 2+3x+4）﹣（﹣x+4）＝﹣x 2+4x ；S ∥PCB ＝ 12 PQ•OB ＝ 12 ×（﹣x 2+4x ）×4＝﹣2（x ﹣2）2+8；∴当P （2，6）时，∥PCB 的面积最大；（3）解：存在．抛物线y ＝﹣x 2+3x+4的顶点坐标E (32,254) ，直线BC ：y ＝﹣x+4；当 x =32 时，F (32,52) ，∴.EF =154．如图2，过点M 作MN∥EF ，交直线BC 于M ，设N （x ，﹣x 2+3x+4），则M （x ，﹣x+4）；由题意点N 在第一象限，∴MN ＝（﹣x 2+3x+4）﹣（﹣x+4）＝﹣x 2+4x ；当EF 与NM 平行且相等时，四边形EFMN 是平行四边形，由﹣x 2+4x =154时，解得 x 1=52,x 2=32 （不合题意，舍去）．当 x =52 时， y =−(52)2+3×52+4=214，∴N （ 52， 214 ）．∴点N 坐标为（ 52， 214 ）．13．【答案】（1）令 y =0 ，则 −12x 2+32x +2=0 ，解得 x 1=−1 ， x 2=4 ．∴A 点坐标为 (−1,0) ，B 点坐标为 (4,0) ．令 x =0 ，则 y =2 ． ∴C 点坐标为 (0,2) ．（2）①设： l BC :y =mx +n ，将 B(4,0) ， C(0,2) 分别代入得， {0=4m +n 2=n ，解得 {m =−12n =2，故 l BC :y =−12x +2 ．可设 P(t,−12t +2) ， 0≤t ≤4 ，则 Q(t,−12t 2+32t +2) ，且Q 在P 上方．所以 PQ =−12t 2+32t +2−(−12t +2)=−12t 2+2t ．又 BP =√(4−t)2+(−12t +2)2=√52(4−t) ．故 BP +PQ =√52(4−t)+(−12t 2+2t)=−12t 2+(2−√52)t +2√5 ．当 t =2−√52 时取得最大值，此时 P(2−√52,1+√54) ．②如图，延长AC至点D，使得CD=CB，连接BD，作DE⊥y轴于点E，过点P作PH⊥BD于点H．由AC2=12+22=5，BC2=22+42=20，AB2=(−1−4)2=25，所以AC2+BC2=AB2，∠ACB=90°．则△BDC是等腰直角三角形，∠CBD=45°．√2AP+PB=√2(AP+PBsin45°)=√2(AP+PH)，由垂线段最短可知，当A，P，H共线时(AP+PH)取得最小值．∵∠BCD=∠DEC=∠COB=90°，∵∠DCE+∠BCO=∠BCO+∠CBO=90°，∴∠DCE=∠CBO．∴△CDE≌△BCO．∴DE=CO=2，CE=BO=4．可得点D的坐标为(2,6)．∴BD=√(2−4)2+(6−0)2=2√10，=12BD⋅AH，代入可得12×5×6=12×2√10⋅AH，S△ABD=12AB⋅yD，故有√2AP+PB=√2(AP+PH)≥√2AH=3√5．解得AH=3√102所以√2AP+PB的最小值为3√5．14．【答案】（1）解：当抛物线与x轴有两个交点时，∆>0，即4+4m>0，∴m>-1；（2）解：∵点A(-1，0)在抛物线y=-x2+2x+m上，∴-1-2+m=0，∴m=3，∴抛物线解析式为y=-x 2+2x+3，且C(0，3)，当x=0时，-x 2+2x+3=0，解得x=-1，或x=3， ∴B （3,0），设直线BC 的解析式为y=kx+b ，将B(3，0)，C(0，3)代入y=kx+b 中，得: {3k +b =0b =3 ，解得 {k =−1b =3，∴直线AB 的解析式为y=-x+3;（3）解：点D 在抛物线上，设坐标为（x ，-x 2+2x+3），F 在直线AB 上，坐标为（x ，-x+3），∴DF=-x 2+2x+3-(-x+3)=-x 2+3x= −(x −32)2+94，∴当 x =32 时，DF 最大，为 94 ，此时D 的坐标为（ 32,154 ）.15．【答案】（1）解：∵点A 、B 、C 在二次函数图象上 ∴把x=0代入 y =12x 2+32x +2 ，得y=2把y=0代入 y =12x 2+32x +2 ，得x 1=﹣1，x 2=4，∴A （﹣1，0），B （4，0），C （0，2）；（2）解：设直线BC 的解析式为y=kx+b （k≠0），把B （4，0），C （0，2）代入，得 {4k +b =0b =2 ， {k =−12b =2 ∴直线BC 的解析式为 y =12x +2∵OP=t∴P （t ，0），M （t ，﹣ 12 t+2），N （t ，﹣ 12 t 2+ 32 t+2），如图，∴S 1=N 1P 1﹣M 1P 1=﹣ 12 t 2+ 32 t+2﹣（﹣ 12 t+2）=﹣ 12t 2+2t （0＜t ＜4），S2=M2P2﹣N2P2=﹣12t+2﹣（﹣12t2+ 32t+2）= 12t2﹣2t（﹣1＜t＜0），（3）解：如图，①若∥OPN∥∥OCB，当OP与OC是对应边时，则OPOC=NPBO，即t2=−12t2+32t+24化简得：t2+t﹣4=0，解得：t1=−1+√172，t2=−1−√172（不合题意，舍去）②若∥OPN∥∥OBC，当OP与OB是对应边时，则OPOB=PNCO，即t4=−12t2+32t+24化简得：t2﹣2t﹣4=0解得：t3=1+ √5，t4=1﹣√5（不合题意，舍去）∴符合题意的点P的坐标为（−1+√172，0）和（1+ √5，0）．16．【答案】（1）解：由二次函数交点式表达式得：y＝a（x+3）（x﹣4）＝a（x2﹣x﹣12）＝ax2﹣ax ﹣12a，即：﹣12a＝4，解得：a＝﹣1 3，则抛物线的表达式为y=−13x2+13x+4，（2）设点P（m，﹣13m2+ 13m+4），则点Q（m，﹣m+4），∵OB＝OC，∴∥ABC＝∥OCB＝45°＝∥PQN，PN＝PQsin∥PQN＝√22（﹣13m2+ 13m+4+m﹣4）＝﹣√26（m﹣2）2+ 2√23，∵﹣√26＜0，∴PN有最大值，当m＝2时，PN的最大值为2√23.（3）存在，理由：点A 、B 、C 的坐标分别为（﹣3，0）、（4，0）、（0，4），则AC ＝5，AB ＝7，BC ＝4 √2 ，∥OBC ＝∥OCB ＝45°，将点B （4，0）、C （0，4）的坐标代入一次函数表达式：y ＝kx+b 得 {0=4k +b b =4 解得 {k =−1b =4∴直线BC 的解析式为y ＝﹣x+4…①，设直线AC 的解析式为y=mx+n把点A （﹣3，0）、C （0，4）代入得 {0=−3m +n n =4解得 {m =43n =4∴直线AC 的表达式为：y ＝ 43x+4，设直线AC 的中点为K （﹣ 32 ，2），过点M 与CA 垂直直线的表达式中的k 值为﹣ 34 ，设过点K 与直线AC 垂直直线的表达式为y ＝﹣ 34 x+q把K （﹣ 32 ，2）代入得2=﹣ 34 ×（﹣ 32 ）+q解得q= 78∴y ＝﹣ 34 x+ 78 …②，①当AC ＝AQ 时，如图1，则AC ＝AQ ＝5，设：QM ＝MB ＝n ，则AM ＝7﹣n ，由勾股定理得：（7﹣n ）2+n 2＝25，解得：n ＝3或4（舍去4），故点Q （1，3），②当AC＝CQ时，如图1，CQ＝5，则BQ＝BC﹣CQ＝4 √2﹣5，则QM＝MB＝8−5√22，故点Q（5√22，8−5√22）.③当CQ＝AQ时，联立①②，{y=−x+4y=−34x+78，解得，x＝252（舍去），综上所述点Q的坐标为：Q（1，3）或Q（5√22，8−5√22）.。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

专题：二次函数与几何综合
一.二次函数与面积
1. 如图，已知二次函数238322xxy与x轴交于A、B两点，点A在B的左边，与y轴交于点C，
点P在第一象限的抛物线上，且在对称轴右边.若4PACS,求点P拍的坐标.

二.二次函数与全等
2.如图，已知抛物线342xxy与x轴交于A、B两点，与y轴交于点C，连接AC，将直线AC向右
平移交抛物线于点P，交x轴于点Q，且∠CPQ=135°，求直线PQ的表达式.

三．二次函数与勾股定理
3.如图，抛物线42xy与x轴交于A，B两点，点Q为抛物线在第二象限上的一点，且∠AQB=90°，
求点Q的坐标.
四.二次函数与等腰三角形
4.如图，抛物线29)1(212xy与x轴交于点A ，B，点C（2，m）在抛物线上，点P在y轴的正
半轴上，且△BCP为等腰三角形，求点P的坐标.

五.二次函数与平行四边形
5.如图，抛物线23212xxy与x轴交于A，B两点，D为y轴上一点，E为抛物线上一点，是否存
在这样的点D和E，使以A，D，B，E为顶点的四边形为平行四边形？若存在，求出D，E的坐标；若
不存在，请说明理由.
六．二次函数与矩形
6.如图，抛物线322xxy的图像与x轴交于A，B两点（点A在点B的左边），与y轴交于点C，
点D为抛物线动的顶点.
（1）求点A，B，C的坐标；

（2）设点H是第二象限内抛物线上的一点，且△HAB的面积是6，求点H的坐标；
（3）点M为线段AB上一点（点M不与点A，B重合），过点M作x轴的垂线，与直线AC交于点E，与
抛物线交于点P，过点P作PQ∥AB交抛物线于点Q，过点Q作QN⊥x轴于点N，若点P在点Q左边，
当矩形PMNQ的周长最大时，求△AEM的面积.
七. 二次函数与菱形
7.如图，已知抛物线cbxxy2与x轴交于A，B，AB=2，与y轴交于点C，对称轴为直线2x，对
称轴交x轴于点M.

（1）求抛物线的函数表达式；
（2）设P为对称轴上一动点，求△APC周长的最小值；
（3）设D为抛物线上一点，E为对称轴上一点，若以A，B，D，E为顶点的四边形是菱形，则点D的
坐标为 .

八. 二次函数与正方形
8.如图，抛物线221212xxy经过点C（-3，h），CD⊥x轴，垂足为D，Rt△AOB≌Rt△CDA，点A，
B分别在x轴和y轴上，在对称轴右侧的抛物线上是否存在两点P、Q，使四边形ABPQ是正方形？若
存在，求出点P、Q的坐标;若不存在，说明理由.

九．二次函数与梯形
9.如图，抛物线1232xxy与x轴交于点A，B，与y轴交于点C，在抛物线上是否存在点P，使
得以A，C，B,P为顶点的四边形是直角梯形？若存在，求出点P的坐标；若不存在，请说明理由.

十．二次函数与圆
10.如图，已知二次函数)0(12aaxy的图像过点A（-2，2），一次函数bkkbkxy,,0(是常数
)
的图像经过点B（0，2）.
（1）求a的值并写出二次函数的表达式；
（2）求b的值；
（3）设直线l与二次函数图像交于M，N，过点M作MC垂直x轴于点C，求证：MB=MC；
（4）在（3）的条件下，请判断以线段MN为直径的圆与x轴的位置关系，并说明理由.
小练习：
1.如图，点A在x轴上，OA=4，将线段OA绕点O顺时针旋转120°至OB位置.
（1）求点B的坐标；
（2）求经过A，O,B的抛物线解析式；
（3）在此抛物线的对称轴上，是否存在点P，使得以P,O,B为顶点的三角形是等腰三角形？若存在，
求点P的坐标，若不存在，请说明理由.

2.如图，一次函数221xy分别交y轴，x轴于A，B两点，抛物线cbxxy2过A，B两点.
点N为抛物线上一个动点，过点N作x轴的垂线交直线AB于M，作NE∥x轴交AB于点E，设点N的
横坐标为x，△NEM的周长为L.

（1）求这个抛物线的解析式；
（2）当点N为直线AB上方的抛物线上动点（不与A，B两点重合），求L与x的函数关系，并求L的
最大值；
（3）当点N在抛物线上运动时，△MNE与△OAB是否全等？若全等，请直接写出点N的坐标；若不全
等，请说明理由.

3.已知抛物线kkxkxy322交x轴于A，B两点（A在B的左边），交y轴于C点，且y有最大值4.
（1）求抛物线的解析式；
（2）在抛物线上是否存在点P，使△PBC是直角三角形？若存在，求出P点坐标，若不存在，说明理
由.
4.如图，已知二次函数)0(32:21aaaxaxyL和二次函数)0(1)1(:22axayL图像的顶点
分别为M,N，与y轴分别交于点E，F.

（1）函数)0(322aaaxaxy的最小值为＿＿＿＿；当二次函数 21,LL的y值同时随着x的增
大而减小，x的取值范围是＿＿＿＿；

（2）当EF=MN时，求a的值，并判断四边形ENFM的形状.（直接写出，不必证明）；
（3）若二次函数2L的图像与x轴的右交点为A（m,0），当△AMN为等腰三角形时。求方程
01)1(2xa
的解.

5.如图，已知抛物线cbxaxy2，经过A（-1,0），B（3,0），C（0,3）三点，直线l是抛物线的对
称轴.

（1）求抛物线的函数关系式；
（2）设点P直线l上的一个动点，当△PAC的周长最小时，求点P的坐标;
（3）在直线l上是否存在点M，使△MAC为等腰三角形？若存在，求出点M的坐标，若不存在，请说
明理由.

（4）设过点A的直线与抛物线在第一象限的交点为N，当△ACN的面积为815时，求直线AN的解析式;