二次函数动点问题解答方法技巧分析报告
二次函数动点问题

二次函数中的动点问题探究【解题方法和策略】二次函数中直角三角形解题思路:(1)分类讨论:按直角顶点进行讨论(2)勾股定理(3)相似三角形,经常用K 型相似二次函数中等腰三角形解题思路:(一)代数方法:(1)求出或用变量(或者用未知数)表示出三角形三条边的长(2)根据题意确定三边中某两边的相等关系,等到方程或方程组(3)解方程或方程组,若方程有解,则解即为所求,写出坐标即可;若无解,则不存在满足题意的三角形(二)几何方法:找到满足条件的等腰三角形两圆一线:1.如果知道底边是定长,可以做出底边中垂线找到所需的点2.如果一腰是定长,则分别以定长的两个端点为圆心,找到需要的点;二次函数中等腰直角三角形问题:根据题意分情况讨论边的情况,根据等腰三角形“三线合一”以及“直角三角形斜边中线等于斜边一半”解题【典型例题】一、二次函数中直角三角形【例1】如图,已知直线112y x =+与y 轴交于点A,与x 轴交于点D,抛物线212y x bx c =++与直线交于A、E(4,m)两点,与x 轴交于B、C 两点,且B 点坐标为(1,0).⑴求该抛物线的解析式;⑵设动点P 在x 轴上移动,当△PAE 是直角三角形时,求点P 的坐标..【例2】如图,直线y=2x﹣10分别与x轴,y轴交于点A,B,点C为OB的中点,抛物线y=﹣x2+bx+c经过A,C两点.(1)求抛物线的函数表达式;(2)点D是直线AB上方的抛物线上的一点,且△ABD的面积为.①求点D的坐标;②点P为抛物线上一点,若△APD是以PD为直角边的直角三角形,求点P到抛物线的对称轴的距离.【练习1】如图,已知关于x的二次函数y=﹣x2+bx+c(c>0)的图象与x轴相交于A、B两点(点A在点B的左侧),与y轴交于点C,且OB=OC=3,顶点为M.(1)求出二次函数的关系式;(2)点P为线段MB上的一个动点,过点P作x轴的垂线PD,垂足为D.若OD=m,△PCD 的面积为S,求S关于m的函数关系式,并写出m的取值范围;(3)探索线段MB上是否存在点P,使得△PCD为直角三角形?如果存在,求出P的坐标;如果不存在,请说明理由.二、二次函数中等腰三角形【例3】如图1,点A在x轴上,OA=4,将线段OA绕点O顺时针旋转120°至OB的位置.(1)求点B的坐标;(2)求经过A、O、B的抛物线的解析式;(3)在此抛物线的对称轴上,是否存在点P,使得以点P、O、B为顶点的三角形是等腰三角形?若存在,求点P的坐标;若不存在,请说明理由.【例4】如图1,在平面直角坐标系中,抛物线y=﹣x2+bx+c与x轴交与点A(﹣3,0),点B(9,0),与y轴交与点C,顶点为D,连接AD、DB,点P为线段AD上一动点.(1)求抛物线的解析式;(2)如图2,抛物线对称轴与x轴交与点G,E为OG的中点,F为点C关于DG对称的对称点,过点P分别作直线EF、DG的垂线,垂足为M、N,连接MN,当△PMN为等腰三角形时,求此时EM的长.【练习2】在平面直角坐标xOy中,(如图)正方形OABC的边长为4,边OA在x轴的正半轴上,边OC在y轴的正半轴上,点D是OC的中点,BE⊥DB交x轴于点E.(1)求经过点D、B、E的抛物线的解析式;(2)将∠DBE绕点B旋转一定的角度后,边BE交线段OA于点F,边BD交y轴于点G,交(1)中的抛物线于M(不与点B重合),如果点M的横坐标为,那么结论OF=DG能成立吗?请说明理由;(3)过(2)中的点F的直线交射线CB于点P,交(1)中的抛物线在第一象限的部分于点Q,且使△PFE为等腰三角形,求Q点的坐标.三、二次函数中等腰直角三角形【例5】如图,在直角坐标系中,已知点A(﹣1,0)、B(0,2),将线段AB绕点A按逆时针方向旋转90°至AC.(1)点C的坐标为;(2)若二次函数y=x2﹣ax﹣2的图象经过点C.①求二次函数y=x2﹣ax﹣2的关系式;②在此二次函数的图象上是否存在点P(点C除外),使△ABP是以AB为直角边的等腰直角三角形?若存在,求出所有点P的坐标;若不存在,请说明理由.【例6】如图,二次函数y=x2+bx+c的图象经过A(1,0),B(﹣3,0)两点,与y轴交于点C,过点A的直线与y轴交干点D,与抛物线交于点M,且tan∠BAM=1.(1)求该二次函数的解析式;(2)P为抛物线上一动点,E为直线AD上一动点,是否存在点P,使以点A、P、E为顶点的三角形为等腰直角三角形?若存在,请求出所有点P的坐标;若不存在,请说明理由.【练习3】已知如图,在平面直角坐标系xOy中,二次函数y=﹣x2+bx+c的图象经过点A (4,0),C(0,2)(1)求抛物线的表达式;(2)如图2,在抛物线上是否存在一点P,使△ACP是以AC为斜边的等腰直角三角形?若存在,求点P的坐标,若不存在请说明理由.【例7】如图,矩形OABC的边OA、OC分别在x、y轴的正半轴上,且OA=1,OC=2,以O为直角顶点作Rt△COD,OD=3,已知二次函数y=ax2+bx﹣的图象过D、B两点.(1)求二次函数的解析式;(2)如图1,连接BD,在BD下方的抛物线是否存在点M,使得四边形BCDM的面积S最大?若存在,请求出S的最大值及点M的坐标,若不存在,请说明理由;(3)如图2,E为射线DB上的一点,过E作EH⊥x轴于H,点P为抛物线对称轴上一点,且在x轴上方,点Q在第二象限的抛物线上,是否存在P、Q使得以P、O、Q为顶点的三角形与△DEH全等?若存在,请直接写出点Q的坐标,如果不存在,请说明理由.【练习4】如图,二次函数y=ax2+c的图象交x轴于A、B两点,点A坐标为(﹣1,0),顶点C的坐标为(0,﹣2),点D在x轴上,过点D作直线l垂直于x轴,设点D的横坐标为m(m>1).(1)求二次函数的函数关系式和点B的坐标;(2)二次函数y=ax2+c的图象上有一点Q,当△ODQ是以点D为直角顶点的等腰直角三角形时,求m的值;(3)在直线l上有一点P(点P在第一象限),使得以点P、D、B为顶点的三角形与以点B、C、O为顶点的三角形全等,求点P的坐标.课后作业:1.如图,已知二次函数y=ax2+2x+3的图象与x轴交于点A、点B(点B在x轴的正半轴上),与y轴交于点C,其顶点为D,直线DC的函数关系式为y=kx+3,又tan∠OBC=1.(1)求a,k的值.(2)探究:在该二次函数的图象上是否存在点P(点P与B、C不重合),使得△PBC是以BC为一条直角边的直角三角形?若存在,求出P的坐标;若不存在,请说明理由.2.如图,在平面直角坐标系中,O 是坐标原点,点A、B 的坐标分别为)3,0(A 和)0,5(B ,连结AB .(1)现将AOB △绕点O 按逆时针方向旋转90°,得到COD ∆,(点A 落到点C 处),请画出COD ∆,并求经过B 、C 、D 三点的抛物线对应的函数关系式;(2)将(1)中抛物线向右平移两个单位,点B 的对应点为点E ,平移后的抛物线与原抛物线相交于点F .P 为平移后的抛物线对称轴上一个动点,连结PF PE 、,当PF PE -取得最大值时,求点P 的坐标;(3)在(2)的条件下,当点P 在抛物线对称轴上运动时,是否存在点P 使EPF ∆为直角三角形?如果存在,请求出点P 的坐标;如果不存在,请说明理由.3.已知抛物线y =ax 2+bx +c 经过A (-1,0)、B (3,0)、C (0,3)三点,直线l 是抛物线的对称轴.(1)求抛物线的函数关系式;(2)设点P 是直线l 上的一个动点,当△PAC 的周长最小时,求点P 的坐标;(3)在直线l 上是否存在点M ,使△MAC 为等腰三角形,若存在,直接写出所有符合条件的点M 的坐标;若不存在,请说明理由.4.如图,在直角坐标系中,已知点A(﹣1,0)、B(0,2),将线段AB绕点A按逆时针方向旋转90°至AC.(1)点C的坐标为;(2)若二次函数y=x2﹣ax﹣2的图象经过点C.①求二次函数y=x2﹣ax﹣2的关系式;②当﹣1≤x≤4时,直接写出函数值y对应的取值范围;③在此二次函数的图象上是否存在点P(点C除外),使△ABP是以AB为直角边的等腰直角三角形?若存在,求出所有点P的坐标;若不存在,请说明理由.。
二次函数的动点问题(等腰、直角三角形的存在性问题)
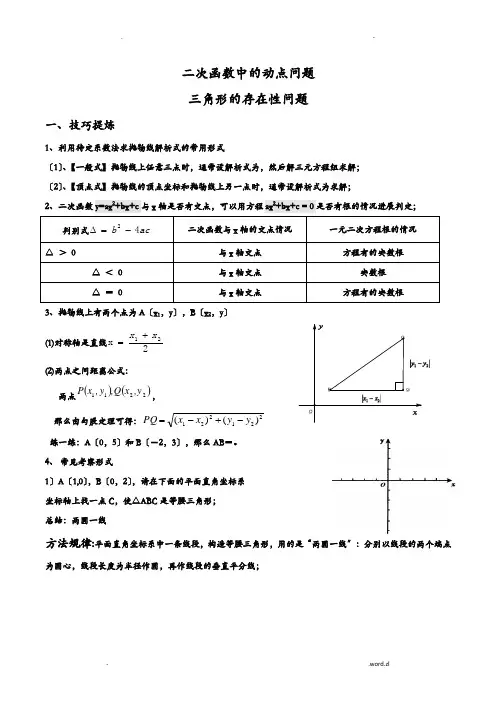
_ Q_ G_P_ O二次函数中的动点问题 三角形的存在性问题一、技巧提炼1、利用待定系数法求抛物线解析式的常用形式〔1〕、【一般式】抛物线上任意三点时,通常设解析式为,然后解三元方程组求解; 〔2〕、【顶点式】抛物线的顶点坐标和抛物线上另一点时,通常设解析式为求解;2、二次函数y=ax 2+bx+c 与x 轴是否有交点,可以用方程ax 2+bx+c = 0是否有根的情况进展判定;判别式ac b 42-=∆ 二次函数与x 轴的交点情况一元二次方程根的情况 △ > 0与x 轴交点 方程有的实数根△ < 0 与x 轴交点 实数根 △ = 0与x 轴交点方程有的实数根3、抛物线上有两个点为A 〔x 1,y 〕,B 〔x 2,y 〕 (1)对称轴是直线2x 21x x +=(2)两点之间距离公式: 两点()()2211y ,x Q ,y ,x P , 那么由勾股定理可得:221221)()(y y x x PQ -+-=练一练:A 〔0,5〕和B 〔-2,3〕,那么AB =。
4、 常见考察形式1〕A 〔1,0〕,B 〔0,2〕,请在下面的平面直角坐标系 坐标轴上找一点C ,使△ABC 是等腰三角形; 总结:两圆一线方法规律:平面直角坐标系中一条线段,构造等腰三角形,用的是“两圆一线〞:分别以线段的两个端点为圆心,线段长度为半径作圆,再作线段的垂直平分线;2〕A 〔-2,0〕,B 〔1,3〕,请在平面直角坐标系中坐标轴 上找一点C ,使△ABC 是直角三角形;总结: 两线一圆方法规律{平面直角坐标系中一条线段,构造直角三角形,用的是“两线一圆〞:分别过线段的两个端点作线段的垂线,再以线段为直径作圆; 5、求三角形的面积:〔1〕直接用面积公式计算;〔2〕割补法;〔3〕铅垂高法; 如图,过△ABC 的三个顶点分别作出与水平线垂直的三条直线, 外侧两条直线之间的距离叫△ABC 的“水平宽〞〔a 〕,中间的 这条直线在△ABC 内部线段的长度叫△ABC 的“铅垂高〞〔h 〕. 我们可得出一种计算三角形面积的新方法:S △ABC =12ah ,即三角形面积等于水平宽与铅垂高乘积的一半。
初中数学丨二次函数的动点问题总结例题解析,两个问题一次解决

初中数学丨二次函数的动点问题总结例题解析,两个问题一次解决动点问题一直是初中热点,近几年往往考查探究运动中的特殊性:等腰三角形、直角三角形、相似三角形、平行四边形、梯形、特殊角或其三角函数、线段或面积的最值。
今天老师针对初中数学的二次函数及动点问题整理了这篇文章,并通过中考真题的详细讲解让同学们掌握所有知识点。
内容较长,由于篇幅限制,上传不完整,老师已整理好word打印版,需要的同学或家长可以在文末免费获取。
也可以关注后,发送私信“学习”来免费领取。
动点问题题型方法归纳总结动态几何特点——问题背景是特殊图形,考查问题也是特殊图形,所以要把握好一般与特殊的关系;分析过程中,特别要关注图形的特性(特殊角、特殊图形的性质、图形的特殊位置。
)共同点:1.特殊四边形为背景2.点动带线动得出动三角形;3.探究动三角形问题(相似、等腰三角形、面积函数关系式);4.求直线、抛物线解析式;5.探究存在性问题时,先画出图形,再根据图形性质探究答案。
解法四:数学往往有两个思考方向:代数和几何,有时可以独立思考,有时需要综合运用。
代数讨论:计算出△PQB三边长度,均用 t 表示,在讨论分析R t△PHQ中用勾股定理计算PQ长度,而PB、BQ长度都可以直接用 t 表示,进行分组讨论即可计算。
点评:此题综合性较强,涉及函数、相似性等代数、几何知识,1,2小题不难,第3小题是比较常规的关于等腰三角形的分类讨论,需要注意的事在进行讨论并且得出结论后应当检验,在本题中若求出的 t 值与题目中的0<t<1矛盾,应舍去点评:这是一道涉及二次函数、方程、几何知识的综合压轴题,有一定的能力要求,第3小题是一个最值问题,解此类题时需数形结合方可较轻松的解决问题。
由于文章篇幅限制,完整word版老师已整理好,内容免费获取方式如下:关注后,发送私信“学习”即可免费获取。
除以上内容,老师还整理了关于初中数学各模块题型的精讲,上面展示的题型库+配套练习,课堂中关于如何学好数学的视频课,希望你们认真领会并按照课程中所讲坚持下去,必见成效。
中考必考二次函数动点问题出题方向和结题思路

中考二次函数压轴题———解题通法研究几个自定义概念:① 三角形基本模型:有一边在X 轴或Y 上,或有一边平行于X 轴或Y 轴的三角形称为三角形基本模型。
② 动点(或不确定点)坐标“一母示”:借助于动点或不确定点所在函数图象的解析式,用一个字母把该点坐标表示出来,简称“设横表纵”。
如:动点P 在y=2x+1上, 就可设 P (t, 2t+1).若动点P在y=2321x x -+,则可设为P(t,2321t t -+)当然若动点M 在X 轴上,则设为(t, 0).若动点M 在Y轴上,设为(0,t).③ 动三角形:至少有一边的长度是不确定的,是运动变化的。
或至少有一个顶点是运动,变化的三角形称为动三角形。
④ 动线段:其长度是运动,变化,不确定的线段称为动线段。
⑤ 定三角形:三边的长度固定,或三个顶点固定的三角形称为定三角形。
⑥ 定直线:其函数关系式是确定的,不含参数的直线称为定直线。
如:y=3x-6。
⑦ X 标,Y 标:为了记忆和阐述某些问题的方便,我们把横坐标称为x 标,纵坐标称为y 标。
⑧ 直接动点:相关平面图形(如三角形,四边形,梯形等)上的动点称为直接动点,与之共线的问题中的点叫间接动点。
动点坐标“一母示”是针对直接动点坐标而言的。
1.求证“两线段相等”的问题:借助于函数解析式,先把动点坐标用一个字母表示出来;然后看两线段的长度是什么距离(即是“点点”距离,还是“点轴距离”,还是“点线距离”,再运用两点之间的距离公式或点到x 轴(y 轴)的距离公式或点到直线的距离公式,分别把两条线段的长度表示出来,分别把它们进行化简,即可证得两线段相等。
2、“平行于y 轴的动线段长度的最大值”的问题:由于平行于y 轴的线段上各个点的横坐标相等(常设为t ),借助于两个端点所在的函数图象解析式,把两个端点的纵坐标分别用含有字母t 的代数式表示出来,再由两个端点的高低情况,运用平行于y 轴的线段长度计算公式-y y 下上,把动线段的长度就表示成为一个自变量为t ,且开口向下的二次函数解析式,利用二次函数的性质,即可求得动线段长度的最大值及端点坐标。
二次函数动点问题的解题思路

2023年12月下半月㊀解法探究㊀㊀㊀㊀二次函数动点问题的解题思路◉江苏省连云港市海头初级中学㊀王小路㊀㊀摘要:二次函数动点问题难度较大,常作为测试中的压轴题,分值较高.部分学生常因不得法㊁无明确的解题思路,失分较为严重.授课中应结合学情以及经验,做好二次函数动点问题教学设计,展示习题情境以及解题思路,给类似问题的解答提供针对性解题指引.关键词:二次函数;动点问题;解题思路㊀㊀二次函数动点问题对学生的想象能力要求较高[1].解决该类习题需从题干以及图形出发寻找突破口,尤其应注重 化动为静 ,全面考虑各种满足题设条件的情境.1求解参数范围图1例1㊀(2021年 河南 统考中考真题)如图1,抛物线y =x 2+m x 和直线y =-x +b 交于点A (2,0)和点B .(1)求m 和b 的值;(2)求点B 的坐标,并结合图象写出不等式x 2+m x >-x +b 的解集;(3)M 为直线A B 上的一个动点,将点M 向左平移3个单位长度得到点N .当线段MN 和抛物线只有一个公共点时,直接写出点M 的横坐标x M 的取值范围.思路剖析:问题(1)将点A 坐标分别代入到抛物线和直线解析式中,构建两个方程求出m 和b 的值;问题(2)将抛物线和直线解析式联立求出点B 的坐标,运用数形结合法求出不等式的解集;问题(3)先确定线段MN 的长度和方向,以点M 为研究对象,从点A 右侧开始逐渐沿着直线A B 运动,分析不同情况下MN 和抛物线的交点,得出结论.解:(1)将点A (2,0)分别代入到抛物线和直线解析中,得4+2m =0,-2+b =0,{解得m =-2,b =2.{(2)由(1)得抛物线为y =x 2-2x ,其顶点坐标为(1,-1);直线为y =-x +2.联立y =x 2-2x ,y =-x +2,{解得x =-1,y =3,{或x =2,y =0,{所以点B 的坐标为(-1,3).不等式x 2+m x >-x +b 表示抛物线y =x 2-2x 在直线y =-x +2的上方,对应的解集为x <-1或x >2.(3)由题意可得,A ,B 两点的水平距离为3.根据题意,直线MN 为一条与x 轴平行的直线,且线段MN 的长为3.由于M 为动点,坐标未知,因此,需要分类讨论.①当点M 在点A 的右侧,线段M N 和抛物线只有一个公共点时,线段M N 经过抛物线的顶点(1,-1).令-x +2=-1,解得x =3,此时x M =3.②当点M 在线段A B 上时,要想满足题意,则应满足-1ɤx M <2.③当点M 在点B 的左侧,则线段MN 和抛物线不会有交点.综上分析,满足题意的x M 的取值范围为-1ɤx M <2或x M =3.点评:例1情境较为复杂,吃透题设情境,准确判断线段MN 的走向,以点A 和点B 为分类讨论的界限是解题的关键.2求解点的坐标图2例2㊀如图2,已知抛物线y =-14x 2+32x +4和坐标轴分别交于A ,B ,C 三点,其中点M 在直线B C 下方的抛物线上运动,则当øA B C =øM C B 时,点M 的坐标为.思路剖析:由øA B C 为锐角,知点M 只能在直线B C 下方右侧抛物线上.先假设出点M ,作出辅助线,运用øA B C =øM C B 得出线段C N 和N B 的相等关系,再设出O N 的长,借助勾股定理求出点N 的坐标.最后,在此基础上求出直线C N 的解析式,与抛物线解析式联立解出点M 的坐标.解:对于抛物线y =-14x 2+32x +4,令x =0,得y =4,所以点C (0,4);令y =0,解得x 1=-2,x 2=38解法探究2023年12月下半月㊀㊀㊀8,则A (-2,0),B (8,0).因此O A =2,O C =4,O B =8.在直角三角形C O B 中,由勾股定理可得B C =42+82=45.图3设点M 的位置如图3所示,连接C M 和x 轴交于点N .由øA B C =øM C B ,则C N =N B .令O N =x ,则C N =N B =8-x .在直角三角形C O N 中,由勾股定理可得x 2+42=(8-x )2,解得x =3,则点N (3,0).设直线C N 的解析式为y =k x +4,将N (3,0)代入得k =-43,则C N 的解析式为y =-43x +4.将其和抛物线y =-14x 2+32x +4联立,解得x 1=0(舍去),x 2=343.将x =343代入y =-43x +4,得y =-1009.综上,点M 的坐标为(343,-1009).点评:根据题意假设出点M 的位置,将给出的角度关系转化为线段间的相等关系,灵活运用勾股定理求出点N 的坐标,求出直线表达式后与抛物线解析式联立求得最终结果.3求解最值问题图4例3㊀(2022年 广东 统考中考真题)如图4,抛物线y =x 2+b x +c (b ,c 是常数)的顶点为C ,与x 轴交于A ,B 两点,A (1,0),AB =4,P 为线段A B 上的动点,过点P 作P Q ʊBC 交A C 于点Q .(1)求该抛物线的解析式;(2)求әC P Q 面积的最大值,并求此时点P 的坐标.思路剖析:问题(1)根据已知条件求出点B 的坐标,运用待定系数法即可求出结果.问题(2)首先求出抛物线顶点C 的坐标,使用待定系数法分别求出直线B C 和A C 的解析式,然后根据P Q 和B C 的平行关系,设出直线P Q 解析式,求出点P 的坐标,最后结合图形通过图形面积关系表示出әC P Q 的面积,运用二次函数性质,求出最值.解:(1)由A (1,0),A B =4,得到B (-3,0).由抛物线过A ,B 两点,将两点坐标代入抛物线解析式得1+b +c =0,9-3b +c =0,{解得b =2,c =-3,{则抛物线的解析式为y =x 2+2x -3.(2)由(1)可得y =x 2+2x -3=(x +1)2-4,则点C (-1,-4).根据A ,B ,C 三点的坐标,容易求得直线B C 的解析式为y =-2x -6,直线A C 的解析式为y =2x -2.由P Q ʊB C ,设直线P Q 的解析式为y =-2x +m ,令y =0,解得x =m 2,则点P 的坐标为(m2,0).联立y =-2x +m ,y =2x -2,{解得x =m +24,y =m -22,ìîíïïïï所以点的坐标为Q(m +24,m -22).又点P 是线段A B 上的动点,则-3<m2<1,解得-6<m <2.由图4可知S әC P Q =S әA P C -S әA P Q ,而S әA P C =12|y C ||A P |,S әA P Q =12|y Q ||A P |,则S әC P Q =12ˑ4ˑ(1-m2)-12ˑ(1-m2)ˑ(-m -22)=-18(m +2)2+2.由二次函数性质可得,当m =-2时,S әC P Q 取得最大值2,此时点P 的坐标为(-1,0).点评:该题综合性较强,求解时需认真观察图形,既要注重数形结合,又要会运用已知条件进行灵活转化,适当设出参数,搭建已知与未知参数之间的桥梁,化陌生为熟悉[2].4总结上述三道例题情境较为典型,解题思路具有较强的代表性.从解题过程不难看出,二次函数动点问题的思路灵活多变,需在深刻理解题意的基础上,敢于大胆假设,借助所学知识 化动为静 ,运用题设条件抽丝剥茧,严谨推理,认真计算,得出结果[3].参考文献:[1]王微.初中数学二次函数动点问题教学模式分析[J ].数理天地(初中版),2023(9):46G48.[2]单小燕.二次函数动点问题的解法及教学策略探究[J ].数学之友,2022,36(22):4G6.[3]冯玲玉.初中数学动点问题的教学策略研究 以二次函数为例[J ].数理天地(初中版),2022(16):36G38.Z48。
中考数学解题方法与技巧---二次函数动点问题解答方法技巧

动点问题题型方法归纳总结
动态几何特点----问题背景是特殊图形,考查问题也是特殊图形,所以要把握好 一般与特殊的关系;分析过程中,特别要关注图形的特性(特殊角、特殊图形 的性质、图形的特殊位置。) 动点问题一直是中考热点,近几年考查探究运动中的特殊性:等腰三角形、直 角三角形、 相似三角形、平行四边形、梯形、特殊角或 其三角函数、线段或面积的最值。 下面就此问题的常见题型作简单介绍,解题方法、关键给以点拨。
2 / 26
07
动点个数 两个 问题背景 特殊菱形两边上移动
考查难点 探究相似三角形
①菱形性质 ②特殊角三角函数 考 ③求直线、抛物线解析式 点 ④⑤相不似等三式角形
08
09
一个
两个
特殊直角梯形三边 抛物线中特殊直角梯形底
上移动
边上移动
探究三角形面积函 探究等腰三角形 数关系式
①求直线解析式 ①求抛物线顶点坐标
(1)求抛物线C1 关于原点对称的抛物线C2 的解析式; (2)设抛物线C1 的顶点为 M ,抛物线C2 与 x 轴分别交 于的M速CD,N度AD沿的两水面点平积(方为点向SC分.别在若向点点右DA、的向,左左点侧运D)动,同顶;时与点以此为每同N秒时,1,四点个边单M形位, 点上运N动同,时直以到每点秒A2与个点单D位重的合速为度止沿.坚求直出方四向边分形别向M下DN、向A 的面积S 与运动时间t之间的关系式,并写出自变量t的取 值范围; (并求3)出当此t最为大何值值;时,四边形 MDNA的面积 S 有最大值, (求出4)此在时运t动的过值程;中若,不四能边,形请M说D明NA理能由否.形成矩形?若能,
中考数学解题方法与技巧
---函数解题思路方法总结
⑴ 求二次函数的图象与 轴的交点坐标,需转化为一元二次方程; x
二次函数动点问题解答方法技巧(含例解标准答案)
下面就此问题的常见题型作简单介绍,解题方法、关键给以点拨。
二、抛物线上动点
5、(湖北十堰市)如图①,已知抛物线 (a≠0)与 轴交于点A(1,0)和点B(-3,0),与y轴交于点C.
(1)求抛物线的解析式;
(2)设抛物线的对称轴与 轴交于点M,问在对称轴上是否存在点P,使△CMP为等腰三角形?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
(3)当 为何值时,四边形 的面积 有最大值,并求出此最大值;
(4)在运动过程中,四边形 能否形成矩形?若能,求出此时 的值;若不能,请说明理由.
[解](1)点 ,点 ,点 关于原点的对称点分别为 , , .
设抛物线 的解析式是
,
则
解得
所以所求抛物线的解析式是 .
(2)由(1)可计算得点 .
过点 作 ,垂足为 .
⑶ 根据图象的位置判断二次函数ax²+bx+c=0中a,b,c的符号,或由二次函数中a,b,c的符号判断图象的位置,要数形结合;
⑷ 二次函数的图象关于对称轴对称,可利用这一性质,求和已知一点对称的点坐标,或已知与x轴的一个交点坐标,可由对称性求出另一个交点坐标.
⑸ 与二次函数有关的还有二次三项式,二次三项式ax²+bx+c﹙a≠0﹚本身就是所含字母x的二次函数;下面以a>0时为例,揭示二次函数、二次三项式和一元二次方程之间的内在联系:
当运动到时刻 时, , .
根据中心对称的性质 ,所以四边形 是平行四边形.
所以 .
所以,四边形 的面积 .
因为运动至点 与点 重合为止,据题意可知 .
所以,所求关系式是 , 的取值范围是 .
(3) ,( ).
二次函数动点经典例题+练习(附解析)
二次函数中的动点问题动点问题题型方法归纳总结:几何特点----问题背景是特殊图形,考查问题也是特殊图形,所以要把握好一般与特殊的关系;分析过程中,特别要关注图形的特性(特殊角、特殊图形的性质、图形的特殊位置。
) 动点问题一直是中考热点,近几年考查探究运动中的特殊性:等腰三角形、直角三角形、 相似三角形、平行四边形、梯形、特殊角或其三角函数、线段或面积的最值。
下面就此问题的常见题型作简单介绍,在解题方法给以点拨。
例:如图①, 已知抛物线32++=bx ax y (a ≠0)与x 轴交于点A (1,0)和点B (-3,0),与y 轴交于点C .(1) 求抛物线的解析式;(2) 设抛物线的对称轴与x 轴交于点M ,问在对称轴上是否存在点P ,使△CMP 为等腰三角形?若存在,请直接写出所有符合条件的点P 的坐标;若不存在,请说明理由.(3) 如图②,若点E 为第二象限抛物线上一动点,连接BE 、CE ,求四边形BOCE 面积的最大值,并求此时E 点的坐标.注意:第(2)问按等腰三角形顶点位置分类讨论画图再由图形性质求点P 坐标----①C 为顶点时,以C 为圆心CM 为半径画弧,与对称轴交点即为所求点P ,②M 为顶点时,以M 为圆心MC 为半径画弧,与对称轴交点即为所求点P ,③P 为顶点时,线段MC 的垂直平分线与对称轴交点即为所求点P 。
第(3)问方法一,先写出面积函数关系式,再求最大值(涉及二次函数最值); 方法二,先求与BC 平行且与抛物线相切点的坐标(涉及简单二元二次方程组),再求面积。
二次函数的动点问题1.如图,已知抛物线1C 与坐标轴的交点依次是(40)A -,,(20)B -,,(08)E ,.(1)求抛物线1C 关于原点对称的抛物线2C 的解析式; (2)设抛物线1C 的顶点为M ,抛物线2C 与x 轴分别交于C D ,两点(点C 在点D 的左侧),顶点为N ,四边形MDNA 的面积为S .若点A ,点D 同时以每秒1个单位的速度沿水平方向分别向右、向左运动;与此同时,点M ,点N 同时以每秒2个单位的速度沿坚直方向分别向下、向上运动,直到点A 与点D 重合为止.求出四边形MDNA 的面积S 与运动时间t 之间的关系式,并写出自变量t 的取值范围;(3)当t 为何值时,四边形MDNA 的面积S 有最大值,并求出此最大值;(4)在运动过程中,四边形MDNA 能否形成矩形?若能,求出此时t 的值;若不能,请说明理由.[解] (1)点(40)A -,,点(20)B -,,点(08)E ,关于原点的对称点分别为(40)D ,,(20)C ,,(08)F -,.设抛物线2C 的解析式是2(0)y ax bx c a =++≠,则16404208a b c a b c c ++=⎧⎪++=⎨⎪=-⎩,,. 解得168a b c =-⎧⎪=⎨⎪=-⎩,,.所以所求抛物线的解析式是268y x x =-+-. (2)由(1)可计算得点(31)(31)M N --,,,.过点N 作NH AD ⊥,垂足为H .当运动到时刻t 时,282AD OD t ==-,12NH t =+. 根据中心对称的性质OA OD OM ON ==,,所以四边形MDNA 是平行四边形. 所以2ADN S S =△.所以,四边形MDNA 的面积2(82)(12)4148S t t t t =-+=-++. 因为运动至点A 与点D 重合为止,据题意可知04t <≤.所以,所求关系式是24148S t t =-++,t 的取值范围是04t <≤. (3)781444S t ⎛⎫=--+ ⎪⎝⎭,(04t <≤).所以74t =时,S 有最大值814. 提示:也可用顶点坐标公式来求.(4)在运动过程中四边形MDNA 能形成矩形.由(2)知四边形MDNA 是平行四边形,对角线是AD MN ,,所以当AD MN =时四边形MDNA 是矩形.所以OD ON =.所以2222OD ON OH NH ==+.所以22420t t +-=.解之得1222t t ==,(舍). 所以在运动过程中四边形MDNA可以形成矩形,此时2t =.[点评]本题以二次函数为背景,结合动态问题、存在性问题、最值问题,是一道较传统的压轴题,能力要求较高。
二次函数动点问题
二次函数动点问题动点问题是中考中的热点也是难点,这类问题的关键在于不要被动点牵着鼻子走,而是要根据图形的特性先确定要求的点的位置再根据几何关系求出点的坐标。
对于涉及函数的动点问题,还应考虑到借助代数的方法,通过建立方程、构建函数模型等方法来求解。
比较典型的动点问题类型一般有:求等腰三角形、直角三角形、相似三角形、平行四边形、梯形、特殊角(或其三角函数)的存在性、求线段或面积的最值等。
类型一:求线段或面积的最值要点:求面积或线段的最值时,关键在于将长度或面积用代数式表示出来,构建一个函数关系式,再利用函数关系式求出最值。
例1 如图1,已知抛物线经过坐标原点O 和x 轴上另一点E ,顶点M 的坐标为 (2,4);矩形ABCD 的顶点A 与点O 重合,AD 、AB 分别在x 轴、y 轴上,且AD=2,AB=3. (1)求该抛物线的函数关系式;(2)将矩形ABCD 以每秒1个单位长度的速度从图1所示的位置沿x 轴的正方向匀速平行移动,同时一动点P 也以相同的速度.....从点A 出发向B 匀速移动,设它们运动的时间为t 秒(0≤t ≤3),直线AB 与该抛物线的交点为N (如图2所示) ① 当t=时,判断点P 是否在直线ME 上,并说明理由;② 设以P 、N 、C 、D 为顶点的多边形面积为S ,试问S 是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由.25图2BCOA D EMyxPN· 图1BCO (A )DE Myx类型二:等腰三角形或直角三角形的存在性要点:证明等腰三角形或直角三角形的存在性需要注意分类讨论,即讨论直角顶点或者两腰的情况。
例2 如图,已知抛物线y=ax2+bx+c的顶点坐标为Q(2,-1),且与y轴交于点C(0,3),与x轴交于A、B两点(点A在点B的右侧),点P是该抛物线上一个动点,从点C沿抛物线向点A 运动(点P与A不重合),过点P作PD∥y轴,交AC于点D.(1)求该抛物线的函数关系式;(2)当△ADP是直角三角形时,求点P的坐标.例3 已知:如图,在平面直角坐标系xOy中,矩形OABC的边OA在y轴的正半轴上,OC 在x轴的正半轴上,OA=2,OC=3,过原点O作 AOC的平分线交AB于点D,连接DC,过点D作DE⊥DC,交OA于点E.(1)求过点E、D、C的抛物线的解析式;(2)将△EDC绕点D按顺时针方向旋转后,角的一边与y轴的正半轴交于点F,另一边与线段OC交于点G.如果DF与(1)中的抛物线交于另一点M,点M的横坐标为65,那么EF=2GO是否成立?若成立,请给予证明;若不成立,请说明理由;(3)对于(2)中的点G,在位于第一象限内的该抛物线上是否存在点Q,使得直线GQ与AB的交点P与点C、G构成的△PCG是等腰三角形?若存在,请求出点Q的坐标;若不存在成立,请说明理由.要点:证明相似三角形的存在性时,本质是要注意三角形的内角的变化情况。
二次函数动点问题(共9张PPT)
•〔3〕连接CP,在第一象限的抛物线上是否存在一点R,使△RPM与△RMB的 面积相等?假设存在,求出点R的坐标;假设不存在,说明理由.
3、二次函数中四边形问题:
①抛物线上的点能否构成平行四边形; ②抛物线上的点能否构成矩形、菱形或正方形。
解二次函数动点问题 解题方法及解题步骤
•解题方法:
•一般的,在二次函数动点问题中应用的解题方法: 待定系数法、数形结合、分类讨论、联系与转化、图像 的平移
变化等思想方法,并且要与平面图形的性质有机结 合,从而使得复 杂的、综合的二次函数动点问题化整为零,逐一击破。
①习抛题物 从线局〔上部3的到〕点整能体求否的构联〔成系平更2行清〕四晰中边,形列面;出相积应的S关〔系平式;方单位〕与t时间〔秒〕的函数关系式及面积S取 〔1〕求最正方大形A值BC时D的P边点长.的坐标.
〔2〕在BC上方的抛物线上是否存在一点K,使四边形ABKC的面积最大?假设存在,求出K点的坐标及最大面积;
x
图① 〔2〕设点P是直线l上的一个动点,当△PAC是以AC为斜边的Rt△时,求点P的坐标;
例1抛物线y=ax2+bx+c经过A〔-1,0〕、B〔3,0〕、C〔0,3〕三点,直线l是抛物线的对称轴.
②习题各个量、未知量的联系,对习题进展解剖,使
〔0,3〕三点,对称轴与抛物线相交于点P、与直线BC相交于点M.
二次函数动点问题
解二次函数动点问题 应用知识点
•二次函数动点问题所包含的知识点及考点:
1、二次函数中最短问题:
①是否存在一点到某两点的距离和为最短;
②是否存在一点使某三角形周长最短;
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实用文档 标准文案 函数解题思路方法总结: ⑴ 求二次函数的图象与x轴的交点坐标,需转化为一元二次方程; ⑵ 求二次函数的最大(小)值需要利用配方法将二次函数由一般式转化为顶点式; ⑶ 根据图象的位置判断二次函数ax²+bx+c=0中a,b,c的符号,或由二次函数中
a,b,c的符号判断图象的位置,要数形结合; ⑷ 二次函数的图象关于对称轴对称,可利用这一性质,求和已知一点对称的点坐标,或已知与x轴的一个交点坐标,可由对称性求出另一个交点坐标.
⑸ 与二次函数有关的还有二次三项式,二次三项式ax²+bx+c﹙a≠0﹚本身就是所含字母x的二次函数;下面以a>0时为例,揭示二次函数、二次三项式和一元二次方程之间的内在联系:
二、 抛物线上动点 5、(湖北十堰市)如图①, 已知抛物线32bxaxy(a≠0)与x轴交于点A(1,0)和点B (-3,0),与y轴交于点C. (1) 求抛物线的解析式; (2) 设抛物线的对称轴与x轴交于点M ,问在对称轴上是否存在点P,使△CMP为等腰三角形?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由. (3) 如图②,若点E为第二象限抛物线上一动点,连接BE、CE,求四边形BOCE面积的最大值,并求此时E点的坐标. 实用文档
标准文案
注意:第(2)问按等腰三角形顶点位置分类讨论画图再由图形性质求点P坐标----①C为顶点时,以C为圆心CM为半径画弧,与对称轴交点即为所求点P,②M为顶点时,以M为圆心MC为半径画弧,与对称轴交点即为所求点P,③P为顶点时,线段MC的垂直平分线与对称轴交点即为所求点P。 第(3)问方法一,先写出面积函数关系式,再求最大值(涉及二次函数最值); 方法二,先求与BC平行且与抛物线相切点的坐标(涉及简单二元二次方程组),再求面积。
07 08 09 动点个数 两个 一个 两个
问题背景 特殊菱形两边上移动 特殊直角梯形三边上移动 抛物线中特殊直角梯形底边上移动
考查难点 探究相似三角形 探究三角形面积函数关系式 探究等腰三角形
考 点 ①菱形性质 ②特殊角三角函数 ③求直线、抛物线解析式 ④相似三角形 ⑤不等式 ①求直线解析式 ②四边形面积的表示 ③动三角形面积函数④矩形性质 ①求抛物线顶点坐标 ②探究平行四边形 ③探究动三角形面积是定值 ④探究等腰三角形存在性 实用文档
标准文案 共同点: ⑤探究存在性问题时,先画出图形,再根据图形性质探究答案。 二次函数的动态问题(动点)
1.如图,已知抛物线1C与坐标轴的交点依次是(40)A,,(20)B,,(08)E,. (1)求抛物线1C关于原点对称的抛物线2C的解析式; (2)设抛物线1C的顶点为M,抛物线2C与x轴分别交于CD,两点(点C在点D的左侧),顶点为N,四边形MDNA的面积为S.若点A,点D同时以每秒1个单位的速度沿水平方向分别向右、向左运动;与此同时,点M,点N同时以每秒2个单位的速度沿坚直方向分别向下、向上运动,直到点A与点D重合为止.求出四边形MDNA的面积S与运动时间t之间的关系式,并写出自变量t的取值范围;
(3)当t为何值时,四边形MDNA的面积S有最大值,并求出此最大值; (4)在运动过程中,四边形MDNA能否形成矩形?若能,求出此时t的值;若不能,请说明理由.
[解] (1)点(40)A,,点(20)B,,点(08)E,
关于原点的对称点分别为(40)D,,(20)C,,(08)F,.
设抛物线2C的解析式是 2(0)yaxbxca
,
特 点 ①菱形是含60°的特殊菱形; △AOB是底角为30°的等腰三角形。 ②一个动点速度是参数字母。 ③探究相似三角形时,按对应角不同分类讨论;先画图,再探究。 ④通过相似三角形过度,转化相似比得出方程。 ⑤利用a、t范围,运用不等式求出a、t的值。 ①观察图形构造特征适当割补表示面积 ②动点按到拐点时间分段分类 ③画出矩形必备条件的图形探究其存在性 ①直角梯形是特殊的(一底角是45°) ②点动带动线动 ③线动中的特殊性(两个交点D、E是定点;动线段PF长度是定值,PF=OA) ④通过相似三角形过度,转化相似比得出方程。 ⑤探究等腰三角形时,先画图,再探究(按边相等分类讨论)
①特殊四边形为背景; ②点动带线动得出动三角形; ③探究动三角形问题(相似、等腰三角形、面积函数关系式); ④求直线、抛物线解析式; 实用文档
标准文案 则16404208abcabcc,,.解得168abc,,. 所以所求抛物线的解析式是268yxx. (2)由(1)可计算得点(31)(31)MN,,,. 过点N作NHAD,垂足为H. 当运动到时刻t时,282ADODt,12NHt. 根据中心对称的性质OAODOMON,,所以四边形MDNA是平行四边形.
所以2ADNSS△.
所以,四边形MDNA的面积2(82)(12)4148Stttt. 因为运动至点A与点D重合为止,据题意可知04t≤. 所以,所求关系式是24148Stt,t的取值范围是04t≤.
(3)781444St,(04t≤).所以74t时,S有最大值814. 提示:也可用顶点坐标公式来求. (4)在运动过程中四边形MDNA能形成矩形. 由(2)知四边形MDNA是平行四边形,对角线是ADMN,,所以当ADMN时四边形MDNA是矩形.
所以ODON.所以2222ODONOHNH.
所以22420tt.解之得126262tt,(舍). 所以在运动过程中四边形MDNA可以形成矩形,此时62t. [点评]本题以二次函数为背景,结合动态问题、存在性问题、最值问题,是一道较传统的压轴题,能力要求较高。
2. (06福建龙岩卷)如图,已知抛物线234yxbxc与坐标轴交于ABC,,三点,
点A的横坐标为1,过点(03)C,的直线334yxt与x轴交于点Q,点P是线段BC上的一个动点,PHOB于点H.若5PBt,且01t. (1)确定bc,的值:__________bc,;
(2)写出点BQP,,的坐标(其中QP,用含t的式子表示): (______)(______)(______)BQP,,,,,; 实用文档 标准文案 (3)依点P的变化,是否存在t的值,使PQB△为等腰三角形?若存在,求出所有t的值;若不存在,说明理由. [解] (1)94b 3c
(2)(40)B, (40)Qt, (443)Ptt, (3)存在t的值,有以下三种情况 ①当PQPB时 PHOB,则GHHB 4444ttt 13t
②当PBQB时,得445tt 49t ③当PQQB时,如图解法一:过Q作QDBP,又PQQB
则522BPBDt又BDQBOC△∽△ BDBQBOBC544245tt3257t 解法二:作RtOBC△斜边中线OE 则522BCOEBEBE,,此时OEBPQB△∽△
BEOBBQPB
542
445tt
32
57t
解法三:在RtPHQ△中有222QHPHPQ 222(84)(3)(44)ttt2
57320tt
32057tt,(舍去)
又01t当13t或49或3257时,PQB△为等腰三角形. 解法四: 数学往往有两个思考方向:代数和几何,有时可以独立思考,有时需要综合运用。 代数讨论:计算出△PQB三边长度,均用t表示,再讨论分析Rt△PHQ中用勾股定理计算PQ长度,而PB、BQ长度都可以直接直接用t表示,进行分组讨论即可计算。 [点评]此题综合性较强,涉及函数、相似性等代数、几何知识,1、2小题不难,第3小题是比较常规的关于等腰三角形的分类讨论,需要注意的是在进行讨论并且得出结论后应当检验,在本题中若求出的t值与题目中的01t矛盾,应舍去
3.如图1,已知直线12yx与抛物线2164yx交于AB,两点.
y C
A O
Q H B
P x C
O P
Q D
B
C O P
Q E
B
C O P
Q HB 实用文档
标准文案 (1)求AB,两点的坐标; (2)求线段AB的垂直平分线的解析式; (3)如图2,取与线段AB等长的一根橡皮筋,端点分别固定在AB,两处.用铅笔拉着这根橡皮筋使笔尖P在直线AB上方的抛物线上移动,动点P将与AB,构成无数个三角形,这些三角形中是否存在一个面积最大的三角形?如果存在,求出最大面积,并指出此时P点的坐标;如果不存在,请简要说明理由.
[解] (1)解:依题意得216412yxyx解之得12126432xxyy (63)(42)AB,,, (2)作AB的垂直平分线交x轴,y轴于CD,两点,交AB于M(如图1) 由(1)可知:3525OAOB 55AB
1522OMABOB 过B作BEx⊥轴,E为垂足 由BEOOCM△∽△,得:54OCOMOCOBOE,, 同理:55500242ODCD,,,, 设CD的解析式为(0)ykxbk y x O y x O P A 图2 图1 B B A y x O 图1 D M A C B
第26题 E
