Chap2.1数列的极限
《数列的极限》课件

单调有界定理
总结词
如果一个数列单调增加或单调减少,且存在上界或下界,则该数列存在极限。
详细描述
单调有界定理是数列极限存在性定理中的一个重要推论,它表明如果一个数列单调增加或单调减少,并且存在上 界或下界,那么这个数列存在极限。这是因为单调性保证了数列不会无限增大或减小,而有界性则保证了数列不 会趋于无穷大或无穷小。
数列的极限
目录
CONTENTS
• 数列极限的定义 • 数列极限的性质 • 数列极限的存在性定理 • 数列极限的应用 • 数列极限的证明方法
01 数列极限的定义
CHAPTER
定义及性质
定义
对于数列${ a_{n}}$,如果当$n$趋于无穷大时,$a_{n}$趋于某个常数$a$,则称数列${ a_{n}}$收敛 于$a$。
05 数列极限的证明方法
CHAPTER
定义法
总结词
通过直接使用数列极限的定义来证明数列的极限。
详细描述
定义法是最基本的证明数列极限的方法,它基于数列 极限的定义,通过直接计算数列的项与极限值之间的 差的绝对值,并证明这个差可以任意小,从而证明数 列的极限。
柯西收敛准则证明法
总结词
利用柯西收敛准则来证明数列的极限。
性质
极限的唯一性、四则运算法则、夹逼准则等。
收敛与发散
收敛
当数列的项逐渐接近一个常数时,该 数列称为收敛的。
发散
如果数列的项没有收敛到任何值,则 该数列称为发散的。
收敛的几何意义
几何解释
在数轴上,如果一个数列的项逐渐接 近一个点,那么这个数列就是收敛的 ,而这个点就是它的极限。
举例
考虑数列${ 1, -1, 1, -1, ldots }$,该 数列在$x=0$处收敛,因为当$n$趋 于无穷大时,该数列的项逐渐接近0 。
高等数学第2章第1节数列极限的概念

第二章 数列极限引 言为了掌握变量的变化规律,往往需要从它的变化过程来判断它的变化趋势.例如有这么一个变量,它开始是1,然后为1111,,,,,234n如此,一直无尽地变下去,虽然无尽止,但它的变化有一个趋势,这个趋势就是在它的变化过程中越来越接近于零.我们就说,这个变量的极限为0.在高等数学中,有很多重要的概念和方法都和极限有关(如导数、微分、积分、级数等),并且在实际问题中极限也占有重要的地位.例如求圆的面积和圆周长(已知:2,2S r l r ππ==),但这两个公式从何而来?要知道,获得这些结果并不容易!人们最初只知道求多边形的面积和求直线段的长度.然而,要定义这种从多边形到圆的过渡就要求人们在观念上,在思考方法上来一个突破.问题的困难何在?多边形的面积其所以为好求,是因为它的周界是一些直线段,我们可以把它分解为许多三角形.而圆呢?周界处处是弯曲的,困难就在这个“曲”字上面.在这里我们面临着“曲”与“直”这样一对矛盾.在形而上学看来,曲就是曲,直就是直,非此即彼,辩证唯物主义认为,在一定条件下,曲与直的矛盾可以相互转化.恩格斯深刻提出:“高等数学的主要基础之一是这样一个矛盾,在一定的条件下直线和曲线应当是一回事”.整个圆周是曲的,每一小段圆弧却可以近似看成是直的;就是说,在很小的一段上可以近似地“以直代曲”,即以弦代替圆弧.执照这种辩证思想,我们把圆周分成许多的小段,比方说,分成n 个等长的小段,代替圆而先考虑其内接正n 边形.易知,正n 边形周长为2sinn l nR nπ=显然,这个n l 不会等于l .然而,从几何直观上可以看出,只要正n 边形的边数不断增加.这些正多边形的周长将随着边数的增加而不断地接近于圆周长.N 越大,近似程度越高.但是,不论n 多么大,这样算出来的总还只是多边形的周长.无论如何它只是周长的近似值,而不是精确值.问题并没有最后解决.为了从近似值过渡到精确值,我们自然让n 无限地增大,记为n →∞.直观上很明显,当n →∞时,n l l →,记成lim n n l l →∞=.——极限思想.即圆周长是其内接正多边形周长的极限.这种方法是我国刘微(张晋)早在第3世纪就提出来了,称为“割圆术”.其方法就是——无限分割.以直代曲;其思想在于“极限”.除之以外,象曲边梯形面积的计算均源于“极限”思想.所以,我们有必要对极限作深入研究.§1 数列极限的概念一 什么是数列1 数列的定义数列就是“一列数”,但这“一列数”并不是任意的一列数,而是有一定的规律,有一定次序性,具体讲数列可定义如下;若函数f 的定义域为全体正整数集合N +,则称:f N R +→为数列.注:1)根据函数的记号,数列也可记为(),f n n N +∈;2)记()n f n a =,则数列()f n 就可写作为:12,,,,n a a a ,简记为{}n a ,即{}{}()|n f n n N a +∈=;3)不严格的说法:说()f n 是一个数列.2 数列的例子(1)(1)111:1,,,,234n n ⎧⎫---⎨⎬⎩⎭;(2)11111:2,1,1,1,435n ⎧⎫++++⎨⎬⎩⎭ (3){}2:1,4,9,16,25,n ;(4){}11(1):2,0,2,0,2,n ++-二、什么是数列极限1.引言对于这个问题,先看一个例子:古代哲学家庄周所著的《庄子. 天下篇》引用过一句话:“一尺之棰,日取其半,万世不竭”.把每天截下的部分的长度列出如下(单位为尺):第1天截下12, 第2天截下2111222⋅=,第3天截下23111222⋅=,第n 天截下1111222n n -⋅=,得到一个数列:231111,,,,,2222n 不难看出,数列12n ⎧⎫⎨⎬⎩⎭的通项12n 随着n 的无限增大而无限地接近于零. 一般地说,对于数列{}n a ,若当n 无限增大时,n a 能无限地接近某一个常数a ,则称此数列为收敛数列,常数a 称为它的极限.不具有这种特性的数列就不是收敛的数列,或称为发散数列.据此可以说,数列12n ⎧⎫⎨⎬⎩⎭是收敛数列,0是它的极限. 数列{}{}21,1(1)n n ++-都是发散的数列.需要提出的是,上面关于“收敛数列”的说法,并不是严格的定义,而仅是一种“描述性”的说法,如何用数学语言把它精确地定义下来.还有待进一步分析.以11n ⎧⎫+⎨⎬⎩⎭为例,可观察出该数列具以下特性: 随着n 的无限增大,11n a n =+无限地接近于1→随着n 的无限增大,11n+与1的距离无限减少→随着n 的无限增大,1|11|n +-无限减少→1|11|n+-会任意小,只要n 充分大. 如:要使1|11|0.1n +-<,只要10n >即可; 要使1|11|0.01n+-<,只要100n >即可;任给无论多么小的正数ε,都会存在数列的一项N a ,从该项之后()n N >,1|11|n ε⎛⎫+-< ⎪⎝⎭.即0,N ε∀>∃,当n N >时,1|11|n ε⎛⎫+-< ⎪⎝⎭.如何找N?(或N存在吗?)解上面的数学式子即得:1n ε>,取1[]1N ε=+即可.这样0,ε∀>当n N >时,111|11|n n N ε⎛⎫+-=<< ⎪⎝⎭.综上所述,数列11n ⎧⎫+⎨⎬⎩⎭的通项11n +随n 的无限增大,11n+无限接近于1,即是对任意给定正数ε,总存在正整数N,当n N >时,有1|11|n ε⎛⎫+-< ⎪⎝⎭.此即11n ⎧⎫+⎨⎬⎩⎭以1为极限的精确定义,记作1lim 11n n →∞⎛⎫+= ⎪⎝⎭或1,11n n →∞+→. 2.数列极限的定义定义1 设{}n a 为数列,a 为实数,若对任给的正数ε,总存在正整数N,使得当n N >时有||n a a ε-<, 则称数列{}n a 收敛于a,实数a 称为数列{}n a 的极限,并记作lim n n a a →∞=或()n a a n →→∞.(读作:当n 趋于无穷大时,n a 的极限等于a 或n a 趋于a). 由于n 限于取正整数,所以在数列极限的记号中把n →+∞写成n →∞,即lim n n a a →∞=或()n a a n →→∞.若数列{}n a 没有极限,则称{}n a 不收敛,或称{}n a 为发散数列. [问题]:如何表述{}n a 没有极限? 3.举例说明如何用N ε-定义来验证数列极限 要证,lim a a n n =∞→关键是:对任正数ε,解不等式ε<-a a n找出n 的范围,进而确定. (1) 直接解不等式 ε<-a a n例1 证明1(1)lim 0(0)n n nαα+→∞-=> 同理可证:12(1)lim 0n n n +→∞-=,13(1)lim 0,n n n+→∞-= . (2)适当放大),)((k n nAn a a =≤-ϕ转化为解不等式εϕ<)(n . 例2 证明 lim 0(||1)nn q q →∞=<.同理可证:1lim 02n n →∞⎛⎫= ⎪⎝⎭,12lim 0,lim(1)0,,23n nn n n →∞→∞⎛⎫⎛⎫-=-= ⎪ ⎪⎝⎭⎝⎭ .例3.证明 321lim097n n n →∞-=+.例4.证明 223lim 33n n n →∞=-. 例5.证明1n =,其中0a >.4 关于数列的极限的N ε-定义的几点说明 (1) 关于ε:①ε的任意性.定义1中的正数ε的作用在于衡量数列通项n a 与常数a 的接近程度,ε越小,表示接近得越好;而正数ε可以任意小,说明n a 与常数a 可以接近到任何程度;②ε的暂时固定性.尽管ε有其任意性,但一经给出,就暂时地被确定下来,以便依靠它来求出N;③ε的多值性.ε既是任意小的正数,那么2,3,2εεε等等,同样也是任意小的正数,因此定义1中的不等式||n a a ε-<中的ε可用2,3,2εεε等来代替.从而“||n a a ε-<”可用“||n a a ε-≤”代替;④正由于ε是任意小正数,我们可以限定ε小于一个确定的正数.(2) 关于N:① 相应性,一般地,N随ε的变小而变大,因此常把N定作()N ε,来强调N是依赖于ε的;ε一经给定,就可以找到一个N;②N多值性.N的相应性并不意味着N是由ε唯一确定的,因为对给定的ε,若100N =时能使得当n N >时,有||n a a ε-<,则101N =或更大的数时此不等式自然成立.所以N不是唯一的.事实上,在许多场合下,最重要的是N的存在性,而不是它的值有多大.基于此,在实际使用中的N也不必限于自然数,只要N是正数即可;而且把“n N >”改为“n N ≥”也无妨.(3)数列极限的几何理解:在定义1中,“当n N >时有||n a a ε-<”⇔“当n N >时有n a a a εε-<<+” ⇔“当n N >时有(),(;)n a a a U a εεε∈-+=” ⇔所有下标大于N的项n a 都落在邻域(;)U a ε内;而在(;)U a ε之外,数列{}n a 中的项至多只有N个(有限个).反之,任给0ε>,若在(;)U a ε之外数列{}n a 中的项只有有限个,设这有限个项的最大下标为N,则当n N >时有(;)n a U a ε∈,即当n N >时有||n a a ε-<,由此写出数列极限的一种等价定义(邻域定义): 定义1' 任给0ε>,若在(;)U a ε之外数列{}n a 中的项只有有限个,则称数列{}n a 收敛于极限a.由此可见:1)若存在某个00ε>,使得数列{}n a 中有无穷多个项落在0(;)U a ε之外,则{}n a 一定不以a 为极限;2)数列是否有极限,只与它从某一项之后的变化趋势有关,而与它前面的有限项无关. 所以,在讨论数列极限时,可以添加、去掉或改变它的有限项的数值,对收敛性和极限都不会发生影响.例1 证明{}2n 和{}(1)n-都是发散数列.例2.设lim lim n n n n x y a →∞→∞==,作数列如下:{}1122:,,,,,,,n n n z x y x y x y . 证明 lim n n z a →∞=.例3.设{}n a 为给定的数列,{}n b 为对{}n a 增加、减少或改变有限项之后得到的数列.证明:数列{}n b 与{}n a 同时收敛或发散,且在收敛时两者的极限相等.三、无穷小数列在所有收敛数列中,在一类重要的数列,称为无穷小数列,其定义如下: 定义2 若lim 0n n a →∞=,则称{}n a 为无穷小数列.如1211(1)1,,,2n n n n n +⎧⎫-⎧⎫⎧⎫⎧⎫⎨⎬⎨⎬⎨⎬⎨⎬⎩⎭⎩⎭⎩⎭⎩⎭都是无穷小数列.数列{}n a 收敛于a 的充要条件:定理2.1 数列{}n a 收敛于a 的充要条件是{}n a a -为无穷小数列. 作业 P27 2(2)(3),3(1)(4)(6),4,5(1),6。
《数列的极限 》课件

在微积分中的应用
定积分与不定积分
定积分和不定积分是微积分的重要组成部分,它们的 计算和证明都涉及到数列极限的应用。例如,在计算 定积分时,需要用到极限来估计积分的误差;在证明 不定积分的性质时,也需要用到数列极限。
04
无穷小与无穷大
无穷小的性质
无穷小是极限为0的变量。
1
2
无穷小具有可交换性、可结合性、可分解性。
3
无穷小是相对于自变量变化的趋势,可以是x趋 向于无穷大或x趋向于某一常数。
无穷大的性质
无穷大是极限不存在的变量。
无穷大具有可交换性、可结合性、可分解性。
无穷大可以是正无穷大或负无穷大,取决于自变 量的变化趋势。
《数列的极限》PPT课件
• 数列极限的定义 • 数列极限的性质 • 数列极限的存在性 • 无穷小与无穷大 • 数列极限的应用
01
数列极限的定义
定义及性质
定义
数列的极限是指当数列的项数n趋于 无穷大时,数列的项x_n趋于某一固 定值A的性质。
性质
极限具有唯一性、有界性、局部保号 性、局部不等式性质等。
级数理论
级数是微积分的一个重要分支,它与数列极限有着密切 的联系。通过数列极限,我们可以研究级数的收敛性和 求和问题,如利用比较审敛法、p-级数等。
在实际问题中的应用
金融数学
在金融数学中,许多问题涉及到数列极限的应用。例如,在研究资产价格的波动时,我们需要用到大数定律和中 心极限定理等数列极限的知识。
闭区间套定理
总结词
闭区间套定理表明,如果一个数列的项落在 不断缩小的闭区间内,则该数列收敛。
第2章极限与连续

第2章 极限与连续2.1 数列的极限1. 数列及其极限一、数列极限的描述性定义1.依照某种规律排列的一串数叫做数列。
数列中的每一个数叫做数列的项。
数列中的一般项称为通项,用x n 表示。
2.看几个数列的实例: 1,4,9,16,25,…,n 2,… 1,0,-1,0,1,0,-1,0,1,…3.数列可以看成为自变量取正整数值n 的函数 即:x n =f(n)4.数列的极限对于数列x 1,x 2,x 3,…,x n ,…,当项数n 无限增大时,它的通项x n 无限趋近于某一个常数a ,则称a 为数列{x n }的极限。
记作 a x n n =+∞→lim 或x n →a(n →+∞)5.具有极限的数列称为收敛数列,没有极限的数列称为发散数列 例如:⑴ ,21,,41,21,11-n ⑵ ,1)1(,,45,34,23,2n n n +---⑶ ,1,,43,32,21+n n⑷ 1,-4,9,-16,25,-36,…,(-1)n+1n 2,… 其中,⑴⑶是收敛数列,⑵⑷是发散数列。
[几点说明]1.数列的收敛与否与这个数列的增减性无关例如上面的收敛数列中,⑴是递减数列,⑶是递增数列。
常数列一定是收敛数列。
2.收敛的数列一定有界,但有界的数列不一定收敛。
3.收敛数列的极限有的可以达到,有的不能达到。
例如,常数列可以达到它的极限,但上面的例子都不能达到它们的极限。
二、数列极限的精确定义 1.无限趋近于a 的意义是指:⑴随着n 的增大,数列的项x n 与a 之间的距离越来越小⑵只要n 足够大,数列的项x n 与a 之间的距离可以小于给定的任何正数 ⑶无论你给定一个多小的正数,都一定可以在数列中找到一项x N ,使这一项后面所有的项与a 之间的距离小于你给定的那个正数。
定义2.1对于给定的无论怎样小的正数ε,总存在一个自然数N ,使得当n >N 时,不等式|x n -a|<ε成立,那么,就称a 是数列{x n }的极限。
第二章--数列极限习题解答

第2章 数列极限§2.1 数列极限的概念一 基本内容一、数列极限的定义lim 0,0,n n n a A N n N a A εε→∞=⇔∀>∃>∍>⇒-<“”.在用-N ε定义证明极限时有两种方法.1 分析法由不等式n a a ε-<寻找n 与ε的关系,从而求N 的方法称为分析法. 2 综合法由n a a -经放大得到n 的简易表达式,从而求出N 的方法称为综合法. 二、数列发散的定义0000lim 0, 0, , n n n a a N n N a a εε→∞≠⇔∃>∀>∃>∍-≥“”.数列{}n a 发散, lim n n a a a →∞⇔∀≠00, 0, (, )a U a εε⇔∀∃>∍“外有{}n a 的无穷多项”. 三、无穷小数列数列{}n a 称为无穷小lim 0n n a →∞⇔=.性质(1) 无穷小的和差仍是无穷小; (2) 无穷小的积仍是无穷小; (3) 无穷小与有界量的积仍是无穷小; (4) lim ()n n n a a a a →∞=⇔-为无穷小.二 习题解答1 设1(1)nn a n+-=,1,2,,0n a ==.(1) 对下列ε分别求出极限定义中相应的N ,10.1ε=,20.01ε=,30.001ε=;(2) 对123,,εεε可找到相应的N ,这是否证明了n a 趋于0?应该怎样做才对?(3) 对给定的ε,是否只能找到一个N ?解:(1) 因为1(1)20n n a a n n +--=-≤,所以2n ε>时,n a a ε-<,故10.1ε=时,20N =;20.01ε=时,200N =;30.001ε=时,2000N =.(2) 对123,,εεε可找到相应的N ,这不能证明n a 趋于0.必须是0ε∀>,2N ε⎡⎤=⎢⎥⎣⎦,当n N >时,0n a ε-<,才能证明n a 的极限为0.(3) 因为lim 00,0,0n n n a N n N a εε→∞=⇔∀>∃>∍>⇒-<“”,而1n N >+时,亦有0n a ε-<,故N 的选取不唯一.2 按-N ε定义证明.(1) lim11n nn →∞=+.证:因为11111n n n n -=<++,所以0ε∀>,取1N ε⎡⎤=⎢⎥⎣⎦,当n N >时, 11nn ε-<+, 故lim 11n nn →∞=+. (2) 2233lim 212n n n n →∞+=-.证:因为222223323212124232n n n n n n n n n n +++-=<<--+-,所以0ε∀>,取1max 3,N ε⎧⎫⎡⎤=⎨⎬⎢⎥⎣⎦⎩⎭,当n N >时,2233212n n n ε+-<-,故2233lim 212n n n n →∞+=-. (3) !lim 0n n n n→∞=.证:因为!12310n n n n n n n n n ⋅⋅⋅⋅-=<⋅⋅⋅⋅,所以0ε∀>,取1N ε⎡⎤=⎢⎥⎣⎦,当n N>时,!0n n nε-<,故!lim 0n n n n →∞=.(4) limsin 0n nπ→∞=.证:因为sin 0sin n n n πππ-=<,所以0ε∀>,取N πε⎡⎤=⎢⎥⎣⎦,当n N >时,sin 0n πε-<,故limsin 0n n π→∞=.(5) lim 0n n na→∞=(1)a >.证:设1a h =+,则10a h >⇒>,且当2n >时,21(1)(1)2n n a h n n h =+>-,于是2222440(1)(2)n n n n a a n h n n h nh -=<=<-+-,所以0ε∀>,取24max 2,N h ε⎧⎫⎡⎤=⎨⎬⎢⎥⎣⎦⎩⎭,当n N >时,0n n aε-<,故lim 0n n na →∞=.3 指出哪些是无穷小数列?(1) n.解:因为1lim0(0)n n αα→∞=>,所以0n=.故是无穷小数列. (2) n解:因为1(1)n a >,所以1n =.故非无穷小数列.(3) 31limn n →∞. 解:因为1lim 0(0)n n αα→∞=>,所以31lim 0n n →∞=.故31n ⎧⎫⎨⎬⎩⎭是无穷小数列.(4) 1lim 3n n →∞.解:因为lim 0(||1)n n q q →∞=<,所以1lim 03nn →∞=.故13n ⎧⎫⎨⎬⎩⎭是无穷小数列.(5)n解:因为lim 0(||1)n n q q→∞=<,所以0n =.故⎧⎫是无穷小数列. (6) n解:因为1(1)na >,所以1n =.故非无穷小数列.4 证明:若lim n n a a →∞=,则k N +∀∈,lim n k n a a +→∞=.证:因为lim n n a a →∞=,所以0ε∀>,0N ∃>,n n N a a ε∍>⇒-<“”,于是当n N >时,k N +∀∈,n k a a ε+-<,故lim n k n a a +→∞=.5 用定义证明(1) 数列1n ⎧⎫⎨⎬⎩⎭不以1为极限.证:取012ε=,则2N ∀>,取01n N =+,则011112N n N ->>+,故数列1n ⎧⎫⎨⎬⎩⎭不以1为极限.(2) 数列{}(1)nn -发散.3n >证:a R ∀∈,0a =时,取01ε=,则2N ∀>,取02n N =,则(1)0021n n N --=>,当0a ≠时,取01ε=,则||N a ∀>,取02n N =,则(1)02||1n n a N a N --≥->>,故数列{}(1)nn -发散.6 证明数列{}n a 收敛于n a a a ⇔-为无穷小数列,并用此结论证明(1)lim 11n n n →∞⎧⎫-+=⎨⎬⎩⎭. 证:()⇒设{}n a 收敛于a ,则lim n n a a →∞=,即0,0,n N n N a a εε∀>∃>∍>⇒-<“”,于是lim 0n n a a →∞-=,即n a a -为无穷小数列.()⇐设n a a -为无穷小数列,则lim 0n n a a →∞-=,于是0,0,()0n N n N a a εε∀>∃>∍>⇒--<“”,即lim n n a a →∞=.因为(1)111n n n -+-=,而1n ⎧⎫⎨⎬⎩⎭是无穷小数列,所以 (1)lim 11n n n →∞⎧⎫-+=⎨⎬⎩⎭.7 证明若lim n n a a →∞=,则lim n n a a →∞=,举例说明反不成立.证:因为lim n n a a →∞=,所以0ε∀>,0N ∃>,n n N a a ε∍>⇒-<“”,此时亦有||||n n a a a a ε-<-<,故lim n n a a →∞=.反之不成立,例如:(1)nn a =-,lim 1n n a →∞=,但lim n n a →∞不存在.8 用-N ε语言证明. (1)lim0n →∞=.证:0=<,所以0ε∀>,取21N ε⎡⎤=⎢⎥⎣⎦,则n N >0ε<,故lim0n →∞=.(2) 312lim0n nn →∞+++=.证:因为33212(1)1022n n n n n n n n n +++++-=<=,所以0ε∀>,取1N ε⎡⎤=⎢⎥⎣⎦,则n N >时,3120n n ε+++-<,故312lim 0n nn→∞+++=. (3) lim 1n n a →∞=,其中1, n n n n a n n -⎧⎪=⎪⎪⎩为偶数为奇数.证:当2n k =时,1111n n a n n--=-=;当21n k =+时, 111n a n-===<, 所以0ε∀>,取1N ε⎡⎤=⎢⎥⎣⎦,则n N >时,1n a ε-<,故lim 1n n a →∞=.9 设,1n n a ∀≥-,lim 0n n a →∞=,用-N ε语言证明1n =.1n a=≤.证:因为lim 0n n a →∞=,所以0ε∀>,0N ∃>,n n N a ε∍>⇒<“”,而1n a ≤,于是n N >1ε<,故1n =.10 利用上题结果求极限.(1)) limnn→∞.解:n==3322n--()22999222n nn nn=<=,故)3limnn→∞=.(2)n.解:=,所以1122-=-12n=<,故1n=.(3)n.解:因为=,11-=-=<<1n=<.故1n=.(4)n.提示:=.解:==,=<=故0n=.§2.2 收敛数列的性质一基本内容一、收敛数列的一般性质性质1 (唯一性) 若数列{}n a收敛,则极限唯一.性质2 (有界性) 若数列{}n a收敛,则必有界.性质3 (保号性) 若数列{}n a收敛,且lim0nna A→∞=>,则0,0nN n N a∃>∍>⇒>“”.性质3'(保号性) 如果limnna A→∞=,又, 0nn a∀>,则0A≥.性质4 (有序性) 设lim,nna A→∞=lim,nnb B→∞=(1) 若A B >,则0, n n N n N a b ∃>∍>⇒>“”; (2) 若0, n n N n N a b ∃>∍>⇒>“”,则A B ≥. 性质5 (夹逼性) 设lim lim n n n n a b l →∞→∞==,且数列{}n c 满足00, n n n N n N a c b ∃>∍>⇒≤≤“”,则{}n c 收敛,且lim n n c l →∞=.二、收敛数列的四则运算定理1 若{},{}n n a b 收敛,则{}, {}, {}, (lim 0)n n n n n n n n n n a a b a b a b b b →∞⎧⎫+-⋅≠⎨⎬⎩⎭也收敛,且(1) lim{}lim lim n n n n n n n a b a b →∞→∞→∞+=+;(2) lim{}lim lim n n n n n n n a b a b →∞→∞→∞-=-;(3) lim{}lim lim n n n n n n n a b a b →∞→∞→∞⋅=⋅;(4) lim lim lim nn n n n nn a a b b →∞→∞→∞=.三、数列与其子列的关系数列{}k n 是自然数集的一个无穷子集,且严格单调上升,则数列12,,,,k n n n a a a 称为数{}n a 列的子列,记作{}k n a .定理2 数列{}n a 收敛{}n a ⇔的任一个子列都收敛,且极限相同.二 习题解答1 求下列极限.(1) 32331lim 423n n n n n →∞++++.解:323323311311lim lim 2342344n n n n n n n n n n→∞→∞++++==++++. (2) 212lim n nn→∞+.解:221212limlim 0n n n n n n →∞→∞+⎛⎫=+= ⎪⎝⎭. (3) 11(2)3lim (2)3n nn n n ++→∞-+-+.解:111121(2)31333lim lim (2)33213nn n n n n n n +++→∞→∞-⎛⎫+ ⎪-+⎝⎭==-+-⎛⎫+ ⎪⎝⎭. (4))lim n n →∞.解:)1lim2n n n n →∞-===. (5))lim10n n→∞+.解:)lim10lim 1lim 2lim 10n n n n n n n n →∞→∞+=+++ 10=.(6) 22111222lim 111333n n n →∞++++++. 解:2211122111112222lim lim 211111133333113n n n n n n →∞→∞⎛⎫- ⎪⎝⎭+++-==⎛⎫+++- ⎪⎝⎭-.2 设lim n n a a →∞=,lim n n b b →∞=,且a b <,证明0,n n N n N a b ∃>∍>⇒<“”.证:因为lim n n a a →∞=,lim n n b b →∞=,且a b <,所以取2b aε-=,则110,2n b aN n N a a -∃>∍>⇒-<“”, 220,2n b aN n N b b -∃>∍>⇒-<“”,取12max{,}N N N =,则n N >时,2n n a ba b +<<,故结论成立.3 设{}n a 为无穷小数列,{}n b 有界,证明{}n n a b 为无穷小数列.证:因为{}n b 有界,所以0,,n M n b M ∃>∍∀≤“”,又{}n a 为无穷小数列,所以0,0,n N n N a Mεε∀>∃>∍>⇒<“”,于是n N >时, n n a b M Mεε<⋅=,故{}n n a b 为无穷小数列.4 求下列极限.(1) 111lim 1223(1)n n n →∞⎛⎫+++⎪⋅⋅+⎝⎭.解:111lim 1223(1)n n n →∞⎛⎫+++⎪⋅⋅+⎝⎭11111lim 12231n n n →∞⎛⎫=-+-++- ⎪+⎝⎭1lim 111n n →∞⎛⎫=-= ⎪+⎝⎭. (2)22)nn →∞⋅. 解:22)nn →∞⋅2111222lim22n n +++→∞==.(3) 21321lim 222nn n →∞-⎛⎫+++⎪⎝⎭. 解:设21321222n n n S -=+++,则13212122nn n S --=+++.于是 212222112222n n n n S --=++++-1112112122123122212n n n nn n ----=+⋅-=---, 所以21321lim 3222n n n →∞-⎛⎫+++= ⎪⎝⎭.(4)n .解:因为,而2n ≥1≤=, 又1n =,所以1n =. (5) 222111lim (1)(2)n n n n →∞⎛⎫+++ ⎪+⎝⎭. 解:因为2222211111(2)(1)(2)n n n n n n n ++≤+++≤+,而21lim 0(2)n n n →∞+=,21lim0n n n →∞+=,所以222111lim 0(1)(2)n n n n→∞⎛⎫+++= ⎪+⎝⎭. (6) 2lim nn →∞⎛⎫++. 解:2n≤++++,而1n n ==,1n n ==,所以2lim 1nn →∞⎛⎫++=+. (7) 2lim nn →∞⎛⎫++-. 解:同上得 2lim 1n n →∞⎛⎫+=-.(8) n n n→∞++.解:因为1n n ++≤<1n nn →∞++=. (9) n解:n≤1n =,1n ,所以1n .5 设{}n a 与{}n b 一个是收敛数列,一个发散数列,证明{}n n a b ±是发散数列.又问{}n n a b ⋅和(0)n n n a b b ⎧⎫≠⎨⎬⎩⎭是否必为发散数列.证:不妨设数列{}n a 发散,数列{}n b 收敛,假设数列{}n n a b ±收敛,则{}{}n n n n a b b a ±=收敛,但{}n a 发散,矛盾,故{}n n a b ±发散.此结论对{}n n a b ⋅和(0)n n n a b b ⎧⎫≠⎨⎬⎩⎭不成立,例如1n a n =,n b =0n n a b =→,0n na b =→.6 证明下列数列发散.(1) (1)1n n n ⎧⎫-⎨⎬+⎩⎭.证:因为n 为奇数时,lim(1)11nn nn →∞-=-+,n 为偶数时, lim(1)11n n nn →∞-=+, 所以(1)1n n n ⎧⎫-⎨⎬+⎩⎭发散.(2) {}(1)nn -.证:因为n 为奇数时,{}(1)nn -发散,所以{}(1)nn -发散.(3) cos 4n π⎧⎫⎨⎬⎩⎭.证:因为8n k =时,limcoslimcos214n k n k ππ→∞→∞==,84n k =+时, limcoslimcos(21)14n k n k ππ→∞→∞=+=-, 所以cos 4n π⎧⎫⎨⎬⎩⎭发散.7 判断下列结论是否成立(若成立,给出证明;若不成立,举出反例) . (1) 若{}21k a -和{}2k a 都收敛,则{}n a 收敛;(2) 若{}{}{}32313,,k k k a a a --都收敛,且极限相同,则{}n a 收敛. 解:(1)结论不成立,例如:(1)n n a =-,(2) 结论成立.实因:{}{}{}32313,,k k k a a a --都收敛,且极限相同,不妨设32313lim lim lim k k k n n n a a a a --→∞→∞→∞===,则113222313330,0,0,0,k k k K k K a a K k K a a K k K a a εεεε--⎧∃>∍>⇒-<⎪∀>∃>∍>⇒-<⎨⎪∃>∍>⇒-<⎩“”“”“”,取123max{,,}N K K K =,则n N >时,n a a ε-<,故{}n a 收敛.8 求下列极限.(1) 1321lim 242n n n →∞-⋅⋅⋅. 解:因为1n =时,12≤,假设n k =时结论成立,即13210242n n -<⋅⋅⋅<,则1n k =+时,132121242(1)2(1)k k k k++⋅⋅⋅++==<<所以13210242n n -<⋅⋅⋅<,故1321lim 0242n n n →∞-⋅⋅⋅=.(2) 1!lim!np n p n =→∞∑.解:因为1!!(2)(2)!(1)!!2(1)!!n p n p n n n n n n =<<--+-+<-+∑,所以1!211!np p n n =<<+∑,故1!lim 1!np n p n =→∞=∑.(3) lim (1)n n n αα→∞⎡⎤+-⎣⎦,01α<<.解:因为10α-<,所以11(1)n n αα--+<,从而111(1)(1)(1)(1)n n n n n n n ααααα---+=++<+=+,于是10(1)n n n ααα-<+-<,而1lim 0n n α-→∞=,所以lim (1)0n n n αα→∞⎡⎤+-=⎣⎦.(4) 22lim(1)(1)(1)nn ααα→∞+++,1α<. 解:因为22(1)(1)(1)nααα+++22(1)(1)(1)(1)1nααααα-+++=-1211n αα+-=-, 所以221lim(1)(1)(1)1n n αααα→∞+++=-.9 设12,,,m a a a 为m 个正数,证明{}12max ,,,m na a a =.证:设{}12max ,,,m a a a M =,则n M ≤≤,而1n =,所以{}12max ,,,m n M a a a ==.10 设lim n n a a →∞=,证明(1) []limn n na a n→∞=.证:因为1[]n n n na na na -<≤,所以[]1n n n na a a n n-<≤,而lim n n a a →∞=,1lim n n a a n →∞⎛⎫-= ⎪⎝⎭,故[]lim n n na a n →∞=. (2) 若0a >,0n a >,则1n =.证:因为lim 0n n a a →∞=>,所以取2aε=,则 0,2n aN nN a a ∃>∍>⇒-<“”,从而322n a a a <<1n =.§2.3 数列极限存在的条件一 基本内容一、单调有界定理定义1 数列{}n a 1, n n n a a +⇔∀≥,数列{}n a 1, n n n a a +⇔∀≤.数列{}n a 1, n n n a a +⇔∀>(严格单调上升), 数列{}n a 1, n n n a a +⇔∀<(严格单调下降). 定理1 单调有界数列必有极限.推论 如果lim n n a a →∞=且{}n a 单调上升,则, n n a a ∀≤;如果lim n n a a →∞=且{}n a 单调下降,则, n n a a ∀≥.二、柯西收敛准则数列{}n a 收敛0, 0, ,m n N m n N a a εε⇔∀>∃>∍>⇒-<“”.> 0, 0, n+p n N p n N a a εε⇔∀∃>∍∀⇒-<“, >”. 数列{}n a 发散0000>0, >0, >, , - 00n +p n N n N p a a εε⇔∃∀∃∃∍≥0“”.二 习题解答1 利用1lim 1nn e n →∞⎛⎫+= ⎪⎝⎭求下列极限.(1) 1lim 1n n n →∞⎛⎫- ⎪⎝⎭.解:1111lim 1lim 1nnn n n n e --→∞→∞⎛⎫⎛⎫⎛⎫-=+= ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭⎝⎭. (2) 11lim 1n n n +→∞⎛⎫+ ⎪⎝⎭.解:1111lim 1lim 1lim 1n nn n n e n n n +→∞→∞→∞⎛⎫⎛⎫⎛⎫+=+⋅+= ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭. (3) 1lim 11nn n →∞⎛⎫+ ⎪+⎝⎭. 解:11111lim 1lim 1lim 1111nn n n n e n n n +-→∞→∞→∞⎛⎫⎛⎫⎛⎫+=++= ⎪ ⎪ ⎪+++⎝⎭⎝⎭⎝⎭. (4) 1lim 12nn n →∞⎛⎫+ ⎪⎝⎭.解:12211lim 1lim 122nnn n n n →∞→∞⎛⎫⎛⎫⎛⎫+=+ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭(5) 21lim 1nn n →∞⎛⎫+ ⎪⎝⎭.解:212211lim 1lim 11nn nn n n n →∞→∞⎛⎫⎛⎫⎛⎫ ⎪+=+= ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭. (6) 211lim 1nn n n →∞⎛⎫++ ⎪⎝⎭, 提示:21111n n n +<-.解:因为211111111nnnn n n n ⎛⎫⎛⎫⎛⎫+≤++≤+ ⎪ ⎪ ⎪-⎝⎭⎝⎭⎝⎭,所以211lim 1nn e n n →∞⎛⎫++= ⎪⎝⎭.2 试问下面的解题方法是否正确? 求lim 2n n →∞.解:设2n n a =及lim n n a a →∞=,由于12n n a a -=,两边取极限()n →∞得2a a =,所以0a =.解:给出的解题方法错误.实因在{}n a 的极限存在时,才能设lim n n a a →∞=,而lim 2nn →∞发散,所以出现了错误的结论.3 证明下列数列极限存在,并求其值. (1)设1a =1n a +=1,2,n =.解:因为12a =,假设n k =时2k a <,则1n k =+时,12k a +=从而,2n n a ∀<.又1,n n n a a +∀=>,所以{}n a ,于是由单调有界定理知{}n a 收敛.设lim n n a a →∞=,对等式1n a +=a =由此得2a =,0a =(舍去),故lim 2n n a →∞=.(2) 设1a =(0)c >,1n a +=,1,2,n =.解:因为1a ,假设n k =时k a ,则1n k =+时,1k a +== 从而,n n a ∀.又 2,021(21)14n n n a a c ∀<<+-<+,于是2,nn n a a c ∀-<,所以1,n n n a a +∀=,即{}n a . 由单调有界定理知{}n a 收敛,设lim n n a a →∞=,对等式1n a +=两边取极限得a =,解之得a =,a =舍去), 故lim n n a →∞=.(3) 设!nn c a n =(0)c >,1,2,n =.解:当[]n c >时,()[]110123[][]1123[]nc n c c a c c n c n+<=<⋅⋅⋅⋅⋅⋅+⋅⋅⋅⋅⋅⋅, 而[]11lim0123[]c n c c n+→∞⋅=⋅⋅⋅⋅,故lim 0!nn c n →∞=.4 利用11nn ⎧⎫⎪⎪⎛⎫+⎨⎬ ⎪⎝⎭⎪⎪⎩⎭为递增数列的结论,证明111nn ⎧⎫⎪⎪⎛⎫+⎨⎬ ⎪+⎝⎭⎪⎪⎩⎭为递增数列. 证:因为11nn ⎧⎫⎪⎪⎛⎫+⎨⎬ ⎪⎝⎭⎪⎪⎩⎭,所以2111,1121n n n n n ++⎛⎫⎛⎫∀+>+ ⎪ ⎪++⎝⎭⎝⎭,于是 11111111111n n n n n +-⎛⎫⎛⎫⎛⎫+=++ ⎪ ⎪ ⎪+++⎝⎭⎝⎭⎝⎭21111121n n n +-⎛⎫⎛⎫<++ ⎪ ⎪++⎝⎭⎝⎭11111111221n n n n +-⎛⎫⎛⎫⎛⎫=+++ ⎪ ⎪⎪+++⎝⎭⎝⎭⎝⎭121(1)(3)12(2)n n n n n +++⎛⎫=+ ⎪++⎝⎭1221431244n n n n n n +++⎛⎫=+⋅ ⎪+++⎝⎭1112n n +⎛⎫<+ ⎪+⎝⎭,故111nn ⎧⎫⎪⎪⎛⎫+⎨⎬ ⎪+⎝⎭⎪⎪⎩⎭ .5 应用柯西收敛准则,证明下列数列{}n a 收敛.(1) 2sin1sin 2sin 222n n na =+++. 证:因为12sin(1)sin(2)sin()222n n n pn n n p +++++++++ 12111111111222222n n n p n p n n ++++⎛⎫≤+++=-<< ⎪⎝⎭, 所以0ε∀>,取1max 1,N ε⎧⎫=⎨⎬⎩⎭,当n N >时,0p ∀>,12sin(1)sin(2)sin()222n n n pn n n p ε+++++++++<, 故由柯西收敛准则知{}n a 收敛.(2) 222111123n a n =++++. 证:因为222111(1)(2)()n n n p ++++++111(1)(1)(2)(1)()n n n n n p n p <+++++++-+111n n p n <-<+, 所以0ε∀>,取1N ε=,当n N >时,0p ∀>,222111(1)(2)()n n n p ε+++<+++,故由柯西收敛准则知{}n a 收敛.6 证明:若单调数列{}n a 含有一个收敛子列,则{}n a 收敛.证:不妨设{}n a ,且有收敛子列{}k n a ,记lim k n n a a →∞=,则{}kn a ,且,kn k aa ∀≤.于是,k k n k a a a ∀≤≤,即{}n a 有上界,故由单调有界定理知结论成立.(1)n >7 证明:若0n a >,且1lim 1n n n ar a →∞+=>,则lim 0n n a →∞=.证:因为0n a >,且1lim 1n n n a r a →∞+=>,所以取012r ε-=,则110,2n n a r N n N r a +-∃>∍>⇒-<“”.即121n n a a r +<+.因为改变数列的有限项不改变数列的敛散性,所以不妨设120,1n n a n a r +∀><+,于是11211121201n n n n n n a a a a a a a a a r ----⎛⎫<=⋅⋅⋅⋅< ⎪+⎝⎭,而112lim 01n n a r -→∞⎛⎫= ⎪+⎝⎭,故由夹逼性定理知lim 0n n a →∞=. 8 证明:若{}n a 为递增(递减)有界数列,则{}lim sup n n n a a →∞=,{}()inf n a .又问逆命题是否成立.证:设{}n a ,因为{}n a 有界,从而有上确界,设{}sup n a a =,则,n n a a ∀≤,且0,0,N N a a εε∀>∃>∍>-“”,由单调性知n N >时,N n a a a a a εε-<≤≤<+,即n a a ε-<,故{}lim sup n n n a a a →∞==.同理可证{}n a 时,{}lim inf n n n a a →∞=.9 利用不等式11(1)()n n n b a n a b a ++->+-,(0)b a >>,证明111n n +⎧⎫⎪⎪⎛⎫+⎨⎬ ⎪⎝⎭⎪⎪⎩⎭为递减数列,并由此推出11nn ⎧⎫⎪⎪⎛⎫+⎨⎬ ⎪⎝⎭⎪⎪⎩⎭为有界数列.证:当0b a >>时,1n ∀≥有1111()()n n n n n n b a b a b ab a b a ++---=-++++()(1)n b a n a >-+,于是1122(1)(1)()n n n n n b n b n a b a a a aa ++++⎛⎫>+-+=- ⎪⎝⎭.取111a n =++,11b n=+,则422(1)(1)(1)(2)2n b n n n n a a n n n +++-=-++3232441144n n n n n n+++=>++, 从而12n n b a ++>,即()()1211111n n nn +++>++,故()111n n +⎧⎫+⎨⎬⎩⎭. 而121111(11)4n n n n +⎛⎫⎛⎫+<+<+= ⎪ ⎪⎝⎭⎝⎭,故11nn ⎧⎫⎪⎪⎛⎫+⎨⎬ ⎪⎝⎭⎪⎪⎩⎭有界.10 证明:13, 1nn e n n ⎛⎫∀-+< ⎪⎝⎭.证:因为()111n n +⎧⎫+⎨⎬⎩⎭,且()11lim 1n n e n +→∞+=,又()11nn ⎧⎫+⎨⎬⎩⎭, 且()1lim 1n n e n →∞+=,所以()()11111n n e n n ++<<+,于是()()()1111111n n n e n n n +-+<+-+()3111ne n n n n=+<<.故结论成立.11 给定两个正数11,a b 11()a b <,令11,2n nn n a b a b +++=(1,2,)n =, 证明lim n n a →∞、lim n n b →∞存在且相等.证:因为11,2n nn n a b n a b +++∀==,所以 1,{}n n n nn n n a b a a n a a a +++∀=≤=⇒ 且有上界1b ;1,{}n n n n b b b +∀=≥=⇒ 且有下界1a ,故由单调有界定理知lim n n a →∞、lim n n b →∞存在.设lim n n a a →∞=,lim n n b b →∞=,在等式12n n n a b a ++=两边取极限得2a ba +=,从而ab =,故结论成立.12 设{}n a 为有界数列,记{}1sup ,,n n n a a a +=,{}1inf ,,n n n a a a +=,证明 (1) {}n a 为递减有界数列,{}n a 为递增有界数列,且,,n m m n a a ∀≤.证:因为{}{}1121,sup ,,sup ,,n n n n n n n a a a a a a ++++∀=≥=,所以,而{}{}1121,inf ,,inf ,,n n n n n n n a a a a a a ++++∀=≤=,所以{}n a,于是当m n >时,n n m a a a ≤≤;当m n =时,n n m a a a ≤=;当m n <时,n m m a a a ≤≤.故结论成立.(2) 设lim , lim n n n n a a a a →∞→∞==,则a a ≤.证:在不等式n m a a ≤两边取极限即知结论成立. (3) {}n a 收敛a a ⇔=.证:()⇒设lim n n a →∞,则0,0N ε∀>∃>,2n n N a a ε∍>⇒-<“”,即,22n n N a a a εε∀>-<<+, 从而2n a a ε≤+,2n a a ε≥-,于是022a a a a εεε⎛⎫≤-≤+--= ⎪⎝⎭,故由ε的任意性知a a =.总练习题21 求下列数列的极限. (1) n解:因为3<=1n =,所以由夹逼性定理知3n =.(2) 5lim n n n e→∞.解:因为55550160(11)n n nn n nnn n n n e C C CC <<=<++++ 5(1)(2)(3)(4)(5)6!n n n n n n n =-----, 而5lim 0(1)(2)(3)(4)(5)6!n n n n n n n n →∞=-----,所以由夹逼性定理知 5lim 0n n n e→∞=. (3) lim n →∞.解:limn →∞limlimn n →∞→∞=- 0n n =-=.2 证明:(1) 2lim 0n n n q →∞=(1)q <.证:当0q =,结论显然成立,当0q ≠时,由1q <知11q>,令11h q =+,则3331(1)(1)(2)6n n n h h C h n n n q=+>=--,于是2236(1)(2)nn n q n n n h <--.而2223366(1)(2)(1)(2)nn n n q n n n h n n n h -<<----,又236lim 0(1)(2)n n n n n h →∞=--, 所以2lim 0n n n q →∞=.(2) ln lim0n nn α→∞=(1)α≥.证:因为2222ln 220n n n n n αααααα<<=,而22lim 0n n α→∞=,所以ln lim 0n nn α→∞=. 6n >(3)0n =.证:因为0(1)n n <=⋅⋅-111111223(1)n n n nn++++⋅⋅-<=,所以0<且0n =,故结论成立.3 设lim n n a a →∞=,证明(1) 12lim nn a a a a n→∞+++=,又问此等式能否反过来推出lim n n a a →∞=.证:因为lim n n a a →∞=,所以10,0N ε∀>∃>,12n n N a a ε∍>⇒-<“”,固定1N ,设112N M a a a a a a =-+-++-,则1n N >时, 12122na a a n N M M a nn n n εε+++--≤+⋅<+. 而lim 0n Mn →∞=,所以就上述2,0N ε∃>,22M n N n ε∍>⇒<“”,取 12max{,}N N N =,则n N >时,1222na a a a nεεε+++-<+=,故12lim nn a a a a n→∞+++=.反之不成立,例如(1)n n a =-,12lim 0n n a a an→∞+++=,但{}n a 发散.(2) 若,0n n a∀>,则n a .证:因为lim n n a a →∞=,所以当0a =时,由平均不等式得120na a a n +++≤,从而0n a =.当0a ≠时,11lim n na a →∞=,则121111lim n n a a a n a→∞+++=, 于是12lim111n n na a a a →∞=+++,而1212111nn na a a nna a a +++≤≤+++,所以n a .4 应用上题结论证明下列各题.(1) 1112lim 0n n n→∞+++=. 证:因为1lim 0n →∞=,所以1112lim0n n n→∞+++=. (2) 1n =(0)a >.证:设1a a =,1,1n n a ∀>=,则lim 1n n a →∞=,于是111lim n n x→∞=⋅⋅⋅=.(3) 1n =.证:设11a =,1,n nn a n ∀>=,则lim 1n n a →∞=,于是12n n n n ⋅⋅⋅=-. n(4)n=.证:设1nan=,则lim0nna→∞=,于是nn n=⋅⋅=.(5)ne =.证:因为1lim1nnen→∞⎛⎫+=⎪⎝⎭,所以(1)limnnnnen→∞+=,于是由3(2)题的结论得nnen⋅⋅=.ne=,从而lim1n n nnen→∞==+.(6) 1nnn→∞++=.证:因为1n,所以31nnn→∞+=.(7) 若1lim nnnbab+→∞=,(0)nb>,则na=.证:设11a b=,11,nnnbn ab-∀>=,则1lim lim nnn nnba ab→∞→∞-==,于是1nn nnab-=⋅⋅=.5 证明:若{}n a为递增数列,为{}n b递减数列,且lim()0n nna b→∞-=,则limnna→∞与limnnb→∞都存在且相等.证:因为{}na,{}n b,所以数列{}n na b-.又lim()0n nna b→∞-=,于是sup{}0n na b-=,从而sup{}0n n n n n na b a b a b-≤-=⇒≤.由此知{}n a有上界1b,{}n b有下界1a,故lim nna→∞与limnnb→∞都存在.设limnna a→∞=,limnnb b→∞=,则lim lim lim()limn n n n nn n n na a a ab b b→∞→∞→∞→∞==--==,综上可知结论成立.6 利用单调有界数列必有极限的证明下列极限收敛,并求其极限.(1)116,na a+==(1,2,,)n=.解:因为165a=>,假设n k=时,5ka>,则1n k=+时,15ka+=>=,所以{}na有下界5.又1,n nn a a+∀=,所以{}na,由单调有界定理知{}na收敛.设limnna a→∞=,在等式1na+=a=解之得5a=,故lim5nna→∞=为所求.(2)115,na a+==(1,2,,)n=.解:因为156a=<,假设n k=时,6ka<,则1n k=+时,16na+==,所以{}na有上界.又1,n nn a a+∀=>,从而{}na,由单调有界定理知{}na收敛.设limnna a→∞=,在等式1na+=两边取极限得a,解之得6a=,故lim6nna→∞=为所求.(3)112,na a+==(1,2,,)n=.解:因为12a=n k=时,ka<1n k=+时,1ka+===,所以{}na有上界.又nn1,nn a+∀=na==>,所以{}na,由单调有界定理知{}na收敛.设limnna a→∞=,在等式1na+=两边取极限得a=,解之得a,故limnna→∞=为所求.(4)11144,23n nna a aa+⎛⎫==+⎪+⎝⎭(1,2,,)n=.解:因为141a=>,假设n k=时,1ka>,则1n k=+时,114141123213k kka aa+⎛⎫⎛⎫=+>+=⎪ ⎪++⎝⎭⎝⎭.所以{}na有下界.又141412323nn n nn n naa a aa a a+⎛⎫⎛⎫=+<+⎪ ⎪++⎝⎭⎝⎭()()11122n n n na a a a=+<+=,所以{}na,由单调有界定理知{}na收敛.设limnna a→∞=,在等式11423n nna aa+⎛⎫=+⎪+⎝⎭两边取极限得1423a aa⎛⎫=+⎪+⎝⎭,解之得1a=,故lim1nna→∞=为所求.(5)11313,1nnnaa aa+-==+(1,2,,)n=.解:因为131a=>,假设n k=时,1ka>,则1n k=+时,131122111k k kkk ka a aaa a+-++-==>++.所以{}na有下界.又21313121111n n n nn n n nn n na a a aa a a aa a a+---+-==+-=++++2(1)1nn nnaa aa-=-<+,所以{}na,由单调有界定理知{}na收敛.设limnna a→∞=,在等式1311nnnaaa+-=+取极限得311aaa-=+,解之得1a=,故lim1nna→∞=为所求.7 设数列{}n a满足0M∃>,对一切n∀,21321n n nA a a a a a a M-=-+-++-≤,证明数列{}n a与{}n A都收敛.证:因为n∀,21321n n nA a a a a a a M-=-+-++-≤,所以{}nA有上界,又{}nA,故由单调有界定理知{}nA收敛.于是,由柯西收敛准则知,0,0Nε∀>∃>,,n p nn N A A pε+∍>⇒-<∀“”,即12n n n pA A Aε++++++<.从而n N>时,21321()()()n p n n n n n n p n pa a a a a a a a+++++++--=-+-++-21321n n n n n p n pa a a a a aε++++++-≤-+-++-<,故由柯西收敛准则知{}n a收敛.8 设0a>,0σ>,112a aaσ⎛⎫=+⎪⎝⎭,112n nna aaσ+⎛⎫=+⎪⎝⎭,1,2,n=.证明数列{}na解:因为112a aaσ⎛⎫=+>⎪⎝⎭,假设n k=时,ka1n k=+时112k kka aaσ+⎛⎫=+⎪⎝⎭所以{}n a有下界.又11122n n n n a a a a σ+⎛⎫⎛=+< ⎪ ⎝⎝⎭(()1122n n n n a a a a <<+=, 所以{}n a ,由单调有界定理知{}n a 收敛.设lim n n a a →∞=,在等式112n n n a a a σ+⎛⎫=+ ⎪⎝⎭两边取极限得12a a a σ⎛⎫=+ ⎪⎝⎭,解之得a = 故lim n n a →∞9 设110a b >>,记112n n n a ba --+=,11112n n n n n ab b a b ----=+,2,3,n =.证明数列{}n a 与{}n b证:因为11111122n n n n n n n n a b a b a b a b ------+=≥=+,所以 ,n n n a b ∀≥.于是n ∀,122n n n n n n a b a a a a +++=≤=,又 n ∀,12221111n n n n n nn n n na b b b a b a b b b +==≥=+++ , 从而{}n a 且有下界1b ,{}n b 且有上界1a ,故{}n a ,{}n b 收敛.设lim n n a a →∞=,lim n n b b →∞=,在等式112n n n a b a --+=,11112n n n n n a b b a b ----=+两边取极限得2a b a +=,2abb a b=+,从而得a b =.又111111111122n n n n n n n n n n a b a ba b a b a b a b --------+=⋅===+,所以11ab a b =,故lim lim n n n n a b →∞→∞==.10 按柯西收敛准则叙述数列{}n a 发散的充分必要条件,并用它证明下列数列{}n a 是发散的.(1) (1)n n a n =-; (2) sin2n n a π=. 解:{}n a 发散0000,0,,N n m N ε⇔∃>∀>∃>,000n m a a ε∍->“”.(1) 取01ε=,则0N ∀>,取001,3n N m N =+=+,于是00,n m N >,且00041n m a a ε-=>=,故{}(1)n n -发散.(2) 取01ε=,则0N ∀>,取002,2n N m N ππ=+=-,于是00,n m N >,且00021n m a a ε-=>=,故sin 2n π⎧⎫⎨⎬⎩⎭发散.11 设lim n n b b →∞=,lim n n a a →∞=,记{}max ,n n n S a b =,{}min ,n n n T a b =,1,2,n =.证明 (1) {}lim max , n n S a b →∞=; (2) {}lim min , n n T a b →∞=.提示:参考第一章总练习题1. 证:(1) 因为{}()max ,2n n n n n n n a b a b S a b -++==,所以{}()lim max , 2n n a b a b S a b →∞-++==.(2) 因为{}()min ,2n n n n n n n a b a b T a b --+==,所以{}()lim min , 2n n a b a b S a b →∞--+==.12 证明下列不等式. (1) k n ∀<,k N ∈,111112121112!3!nn n n n ⎛⎫⎛⎫⎛⎫⎛⎫+>+-+--+ ⎪ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭1121111!k k n n n -⎛⎫⎛⎫⎛⎫+--- ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭. 证:因为k n ∀<,122111111nn n n n n C C C n n n n ⎛⎫+=++++ ⎪⎝⎭1221111k n n n kC C C n n n >++++ 21(1)1(1)(1)112!!kn n n n n k n n n k n ---+=+⋅+⋅++, 所以()()()()111112121112!3!n n n n n+>+-+--+ ()()()1112111!k k n n n-+---. (2) 证明:()()11111nn e n n++<<+.证:因为()111n n +⎧⎫+⎨⎬⎩⎭,且()11lim 1n n e n +→∞+=, 所以()111n e n+<+.又()11n n ⎧⎫+⎨⎬⎩⎭ ,且()1lim 1n n e n →∞+=,所以()11ne n +<.故()()11111n n e n n++<<+. (3) e e ⋅<<. 证:nn ⋅⋅== ()11nn ⎧⎫+⎨⎬⎩⎭ ⇒ . 而n e =,于是,n e ∀<e <.又n n +⋅⋅=所以()111n n +⎧⎫+⎨⎬⎩⎭⇒ , 而n e =,所以,n e ∀>.从而 1111(1)!!(1)n n n n n n n n n e n e e n n n nn ++-++>⇒>⋅>+,e ⋅>⋅e e ⋅<<. (4) 证明:11122!3!!e n >++++.证:因为 ()1,1mm e m∀>+, 当m n >时,()()()()111112211112!!n e m n m m m->+-++---,令m →∞,则11122!3!!e n >++++. (5) 证明:()1111122!3!!nn n +<++++. 证:()122111111nn n n n nC C C nn n n +=++++ 2(1)(1)2111112!!n n n n n n n n n n--⋅=+⋅+⋅++⋅()()()()111112211112!!n n n n n n-=+-++---11122!3!!n <++++.(6) 证明:()111lim 22!3!!n e n →∞++++=. 证:因为()1111122!3!!ne n n +<++++<,而()1lim 1nn e n→∞+=,所以()111lim 22!3!!n e n →∞++++=. 13 求极限0n x ≥ ⎝.解:当01x ≤≤时,21132nnx x ⎛⎫≤++≤ ⎪⎝⎭,所以此时nn。
2.1数列极限
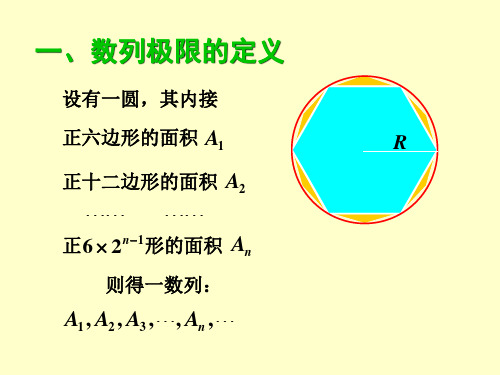
设有一圆,其内接
正六边形的面积 A1
R
正十二边形的面积 A2
正6 2n1形的面积 An
则得一数列:
A1 , A2 , A3 ,, An ,
显然,An却不会等于圆面积,但是,这些正多 边形的面积必将随着边数的增加而不断接近圆的面
积,这个“不断接近”的过程就是一个极限的过程。 而且,当 n 时,An无限接近于圆的面积。
证
反证法 设
lim
n
xn
a, lim n
xn
b,
且a b
取
b
2
a
,由定义有
自然数N1,当
n
N1 时
xn
a
ba 2
a
ba 2
x
a
ba 2
(1)
自然数N2, 当 n N2 时
ba
ba
ba
xn b 2 b 2 x b 2 (2)
取 N max{N1, N2}, 当 n N 时,(1)与(2)同时成立
1
xn
1
; 10000
显然 1 , 1 , 1 一个比一个小,但毕竟是确定数。 10 100 10000
一般地,要使 xn 1 ( 可以任意小), 只要
n
1
1
即可,即从第[
1
1]
项开始,以后所有项
都满足 xn 1 .
同理可观察数列(2),用数学语言表达为:
定义2 设{xn}是一个数列,a为一个确定的数。若
2 ,,
,1 (1)n , ;
n
23
n
(3) {2n},
即 2,4,6, ,2n, ;
1 (1)n
(4) {
2.1 数列及其极限
2.1 数列及其极限当前讲授一、数列的概念引例公元前四世纪,我国春秋战国时期的哲学家庄子在《庄子·天下篇》一书中有一段富有哲理的名句:“一尺之棰,日取其半,万世不竭”.它用一个很朴素、很形象的例子说明了物质的无限可分性.我们把逐日取下的棰的长度顺次排列出来,便得到一串按一定顺序排列的无穷多个数,,,……,,…….这一串数就构成了一个数列.定义:称按一定顺序排列起来的无穷多个数,,,…,,…为数列,其中的第项为数列的通项或一般项.数列常简记为.说明:数列可以理解为正整数的函数,从而也可以写成,它的定义域是全体正整数.例如,引例中的数列的通项可以写为.定义:对于数列,若有成立,则称数列单调增加;若有成立,则称数列单调减少.单调增加和单调减少的数列统称为单调数列.对于数列,若存在正数,使得对于所有的,都有,则称数列有界,否则称数列为无界.二、数列的极限定义:当无限增大时,如果数列的一般项能无限接近于某个确定的常数,则称数列以为极限或称数列收敛于,记为或其中表示无限增大.如果时,不能无限接近于某一个确定的常数,则称数列发散或不收敛.典型例题例2.1.1 观察下列数列的敛散性,并在收敛时求出其极限.(1) ;(2) ;(3) ;(4) ;(5) ;(6) .解(1) ∵时,一般项无限接近于0,∴,即数列收敛于0.(2) ∵时,一般项无限接近于0,∴,即数列收敛于0.(3) ∵这个数列的特点是正项和负项交错排列,在变大的过程中,数列的取值虽然会在0点两侧来回变动,但会分别在两侧越来越接近0,当时,能无限接近0,∴,即数列收敛于0.(4) 这个数列的特点也是正项和负项交错排列.因为这个数列总在1和之间来回取值,没有一个确定的趋向,所以此数列发散,即极限不存在.(5) 当时,一般项也无限增大,可记为,所以数列发散,即极限不存在.(6) 这个数列是常数列.显然,,即常数列收敛于.几点说明:(1) 数列的极限反映了数列的变化趋势.例如数列的极限反映出该数列的变化趋势.(2) 以零为极限的变量称为无穷小量,例如,因为,,,所以、、都是当时的无穷小量.(3) 绝对值无限变大的变量称为无穷大量,例是时的无穷大量.如果我们再分细一点,当时,相应的取值在数轴上是沿轴正向运动,无限变大,而相应的取值在数轴上是沿轴负向运动,绝对值无限变大,可分别记为和.三、收敛数列的基本性质性质1(极限的唯一性) 若数列收敛,则其极限唯一.性质2(收敛数列的有界性) 收敛数列必然有界.性质2的逆命题是不成立的,即有界数列未必收敛.例2.1.1中的数列就是一个有界数列,但它是发散的.注意:数列有界是数列收敛的必要条件,而不是充分条件.思考无界数列是否收敛?无界数列不满足收敛的必要条件,所以是发散的.例如数列的项排列为,显然此数列无界,所以它是发散的.性质3(保号性)(1)设,若(或),则存在正整数,使得时,(或).(2)设,若存在正整数,使得时,(或),则(或).性质3中的第(1)条是说,若数列的极限大于零,则该数列从某项开始,后面所有的项全大于零;若数列的极限小于零,则该数列从某项开始,后面所有的项全小于零.简述为:当充分大时,数列的项与其极限值保持相同的符号.性质3中的第(2)条是说,若收敛数列从某项开始,后面所有的项全大于零,则其极限一定不会是负数;若收敛数列从某项开始,后面所有的项全小于零,则其极限一定不会是正数.四、数列极限的运算法则及存在法则1、四则运算法则设,,则(1);(简述为:代数和的极限等于极限的代数和)(2);(简述为:乘积的极限等于极限的乘积)(3)(此时).(简述为:商的极限等于极限的商,但要求分母的极限不为零)其中(1)和(2)可推广至有限项的情形.推论设,则(1),为常数,即常数因子可以提到极限号外.(2),为正整数.在中令是常数列即可推得(1).对于任意正整数,有.注意:四则运算法则的应用前提是及均存在.例如,,但不能写为:.2、极限存在的两个准则准则1(夹逼定理)若数列,,满足不等式,且,,则数列收敛,且.准则2单调有界数列必有极限.根据此准则,运用一定的技巧,我们可以证明数列是收敛的,且,是一个无理数.它的值是,通常取.指数函数和自然对数函数中的底数就是这个常数.说明:(1) 这是一个非常重要的极限类型,将作为公式应用.括号内的变量是趋向1的,指数趋向于,记作“”,以后遇到“”型极限可考虑使用它.(2) 此极限式更一般的形式为,若在自变量的某一变化过程中,,即是无穷小量,则.例如,.典型例题例 2.1.2求下列数列的极限:(1) ;(2) ;(3) ;(4) ;解(1) .(2) .(3) .(4).以上四个极限题有共同之处,都是求分式的极限,且当时,分子分母均是无穷大量.我们把这种类型的极限叫做无穷大比无穷大型,记为.例 2.1.3求下列极限:(1) ;(2) .解(1) .(2) ∵,即,而,,由夹逼定理,即得.例 2.1.4在下列式子中,错误的选项是().(A) ;(B) ;(C) ;(D) .分析此题4个选项均为“”型极限,所以考虑利用重要极限.解(1) ∵.∴(A)正确.(2) ∵.∴(B)正确.(3).∴(C)正确.(4) ∵,∴(D)不正确.也可以这样求极限:.备注:本题用到初等数学中的公式:,.小结(1)数列极限的概念;(2)无穷小量和无穷大量的概念;(3)收敛数列的基本性质;(4)数列极限的四则运算法则;(5)数列极限存在的两个准则;(6)重要极限及其在解“”型极限题中的应用.。
高数讲义系列之二
高数讲义系列之二高数讲义系列之二第二章极限与连续2.1数列的极限1、数列:按照某一规律排列的无穷多个数,叫无穷数列,记为{a n}=a1,a2,a3…a n…,其中每一个数叫做数列的项,第n项a n叫数列的通项。
2、观察一组数列,当项数n无限增大时,a n是否无限趋近于一个常数①0,1/2,1/22…1/2n-1… 该数列数值越来越趋近于0,极限等于0②1,-1/2,1/3,-1/4…(-1)n+11/n…该数列数值越来越趋近于0,极限等于0③1,1/2,2/3,3/4…n/n+1…该数列数值越来越趋近于1,极限等于1④1,-1,1,-1…(-1)n+1…该数列数值越来越趋近的数不唯一,极限不存在⑤1,3,5,7…2n-1…该数列数值越来越趋近无穷大,极限不存在(或∞)3、数列极限的定义:对于数列{a n},当项数n趋近无穷大时(n→∞),若通项a n无限接近于一个确定的常数A(a n→A),则A是{a n}的极限。
记为:lim a n = A 含义是:n→∞,a n→A注意:①极限是一个常数,极限是A,并不表示取到了A,而是无限趋近于A。
②极限不存在有两种情况:1)无穷大2)不唯一③常数的极限在任何情况下都等于常数本身。
④若极限存在,则数列收敛,若极限不存在,则数列发散。
4、几个常用极限①n→∞, q n→0 (|q|<1),即-1与1之间的数乘无穷大次方趋近于0②n→∞,a开n次方→1 (a>0),即大于0的数开无穷次方趋近于1③n→∞,a→a,即常数的极限在任何情况下都等于常数本身。
作业:习题2-1(P21):1、22.2 数项级数的基本概念1、数项级数的定义:给定一个数列:{u n}=u1,u2,u3…u n…,将所有项相加:∑u n= u1+u2+u3+…+u n+…形成的式子叫数项无穷级数,简称级数,u n是一般项或通项。
2、级数与数列的区别与联系:①数列关注的是某一项的值,级数关注的是所有项的和。
第二章 数列极限
注 5 “ ε − N ”定义的否定叙述: lim an ≠ a ⇔ ∃ε 0 > 0 , ∀N ∈ N * , ∃n0 > N 使
an0 − a ≥ ε 0 。
按定义验证 lim an ≠ a 的关键是求出不等式组(视 N 为定数,视 n 0 、 ε 0 为待求数)
n →∞
n0 > N , an0 − a ≥ ε 0
显然看出 lim
n →∞
。 关) ,使 an0 − a ≥ ε 0 ” 验证分析:取 ε 0 =
1 , 200
an0 − a ≥ ε 0 ; an0 − a ≥ ε 0 ; an0 − a ≥ ε 0 ;
对 N = 1 , ∃ n0 = 201 > N ⇒ 对 N = 10 , ∃ n0 = 210 > N ⇒
定义 1*: lim an = a ⇔ ∀ε > 0 ,在区间 ( a − ε , a + ε ) 之外至多有 {an } 的有限项。
n →∞
lim an ≠ a ⇔ ∃ ε 0 > 0 ,在区间 (a − ε 0 , a + ε 0 ) 之外有 {an } 的无限项。
n →∞
四
收敛与发散的概念
数列{ an }收敛 ⇔ { an }存在有限极限;
( a − ε , a + ε ) 之外至多有 {an } 的有限项,则称 {an } 收敛于 a ,记作 lim an = a 。
n →∞
注 2 在区间 ( a − ε , a + ε ) 之外至多有 {an } 的有限项 ⇔ ∃N , ∀n > N ,有 an − a < ε 。 事实上: “⇐” 已知 ∃N ,∀n > N 有 a − ε < an < a + ε ,这说明在区间 ( a − ε , a + ε ) 之外至多
