凸函数不等式在几何凸函数中的移植
凸函数几个等价定义

本科生毕业论文题目凸函数的几个等价定义系别班级姓名学号答辩时间年月学院目录摘要 (4)1凸函数的定义 (6)2凸函数的等价定义和性质 (6)2.1凸函数的等价定义 (6)2.2凸函数的性质 (7)3凸函数等价定义和性质的应用举例 (10)3.1一些集合上的凸函数举例 (10)3.2运用凸函数等价定义证明不等式 (11)总结 (16)参考文献 (17)谢辞 (18)凸函数的几个等价定义摘要凸函数是一类重要的函数,它的概念最早见于Jensen在1905年的著述中。
它在纯粹数学和应用数学的众多领域中具有广泛的应用,现已成为数学规划、对策论、数理经济学、变分学和最优控制等学科的理论基础和有力工具。
为了理论上的突破,加强它们在实践中的应用,产生了广义凸函数。
本文主要归纳了凸函数的几个常见定义和性质以及它们在不等式证明等几个方面的应用。
关键词:凸函数;等价性;不等式Several equivalent of convex function definedAbstractConvex function is a kind of important function, it is the concept of the earliest Jensen in 1905 in the works. It in pure mathematics and applied mathematics of many fields has wide application, it has become the mathematical programming, the game theory and mathematical economics, variational learn and optimal control subjects such as theoretical basis and powerful tools. In order to theoretical breakthrough, strengthen them in practical application, produced the generalized convex function. This paper mainly summarizes the convex function of several common definition and characteristics and their inequation and so on several aspects in the application. [Key wards]Convex functions; Equivalence; Inequality.凸函数是一种性质特殊的函数,在许多数学分支中,经常可以看到有关的应用,例如在数学分析、函数论、泛函分析、最优化理论等当中。
凸函数的一个Hadamard型不等式

凸函数的一个 < B C B F B 1 C 型不等式
赵伟珍 ! ! 李爱军
" 河南理工大学 数学与信息科学学院 ! 河南 焦作 !* # ( * " " "
摘!要! 通过对两个积分式做变量代换和利用拉格 朗 日 中 值 定 理 # 得出了一个关于凸函数的 < B C B F B 1 C型 不 等式 & 推广了前人的成果 $ 关键词 ! 凸函数 & 变量代换 & 积分 < B C B F B 1 C 不等式 & 中图分类号 ! " # ‘ % ’ !!!!! 文献标识码 ! +!!!! 文章编号 ! % " " & # " ! % ! " " ’ " % " % ! ) " !
( ! " % J " % , 0 ’ # 2O + / 4 + (@ % 2 * 4C * " 5 % ?A , " ) # ’ * " ( S 9* 9 =
# ; <+‘ b 0 ? 4 N J 0 5 G+ ? 4 D 5 !> ]
! #< # # " , 0 B 1 2 F 0 5 2 . P+ @ ? 0 C3 B 2 J 0 F B 2 ? A H B 5 C G 5 P . 1 F B 2 ? A H 0 5 B 57 . @ 2 0 A J 5 ? A= 5 ? L 0 1 H ? 2 : ? B . N D .* ( * " % " 9 J ? 5 B Q Q Q M M ’ 3 7 ( # 4 ) # b ? 2 JL B 1 ? B / @ 0 H D / H 2 ? 2 D 2 ? . 5 2 . ? 5 2 0 1 B @ 0 D B 2 ? . 5B 5 CD H ? 5 B 1 B 5 0F 0 B 5 4 L B @ D 0 2 J 0 . 1 0 F# K 0. / 4 E W E> E E ( # 2 B ? 5. 5 0 ? 5 0 D B @ ? 2 . P< B C B F B 1 C H 2 0 P . 1 A . 5 L 0 UP D 5 A 2 ? . 5 H K J ? A J 0 5 0 1 B @ ? N 0 HK . 1 O HC . 5 0/ 2 J 0 1 0 C 0 A 0 H 4 W M M Q E M Q H . 1 H 8 ’ ) 8 % * 4 + ( A . 5 L 0 UP D 5 A 2 ? . 5)< B C B F B 1 C ? 5 0 D B @ ? 2 L B 1 ? B / @ 0H D / H 2 ? 2 D 2 ? . 5) ? 5 2 0 1 B 2 0 W M E 9: ! 责任编辑 ! 李潜生 "
4.2 凸性与拐点
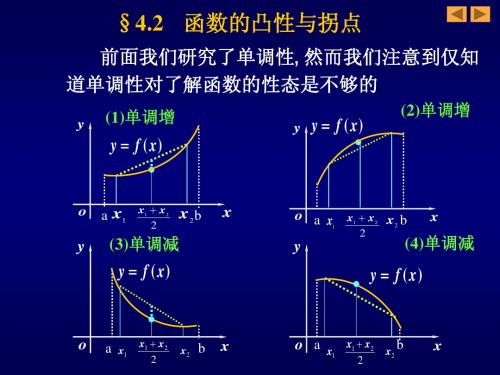
f ''(ξ ) f ( x) = f ( x0 ) + f '( x0 )( x − x0 ) + ( x − x0 )2 2!
y
其中 ξ 介于 x0 与 x 之间 由于 f ″(ξ) ≥ 0 , 可知 ξ
凸函数
f ( x) ≥ f ( x0 ) + f '( x0 )( x − x0 )
o
x0
x
(3)
y
凸函数
y 凹函数
o
a
b x
o
a
b
x
凹凸函数的另一重要特征: 凹凸函数的另一重要特征 凸函数的切线斜率 f ′(x) 单调增加 凹函数的切线斜率 f ′(x)单调减少 单调减少 一阶充分条件) 定理 (一阶充分条件 一阶充分条件 上连续, 内可导, 若 f (x)在 [a, b] 上连续 (a , b)内可导 且 f ′(x)在 在 内可导 在 (a , b)内单调增加 或减少 则 f (x) 在[a , b]是凸函数 内单调增加(或减少 内单调增加 或减少), 是凸函数 (凹函数 ) 凹函数
即
f ( x + h) + f ( x − h) − 2 f ( x) > 0
f ( x + h) + f ( x − h) − 2 f ( x) ⇒ 0 ≤ lim h→0 h2
洛
1 f ' ( x + h) − f ' ( x − h) lim 2 h→0 2h
f' ( x + h) − f' ( x) f' ( x − h) − f' ( x) 1 = lim + 2 h→0 h (−h)
利用函数的凹凸性证明不等式

利用函数的凹凸性证明不等式使用函数的凹凸性证明不等式的方法,通常分为以下三个步骤:1.确定使用的函数是凸函数还是凹函数,以及其定义域。
2.利用函数的凹凸性得出基本不等式或者推导得到不等式。
3.根据不等式左右两边的定义域,进一步讨论如何得出不等式的证明。
以下是一个示例:要证明不等式$(a+b)^2\\leq 2(a^2+b^2)$。
1.确定使用的函数是凸函数还是凹函数,以及其定义域。
函数$f(x)=x^2$在实数域上是凸函数。
我们可以令$a,b$为实数。
2.利用函数的凹凸性得出基本不等式或者推导得到不等式。
由$f(x)$的凸性可得,对于任意两个实数$a,b$和$\\lambda\\in(0,1)$,有:$$f(\\lambda a+(1-\\lambda)b)\\leq\\lambda f(a)+(1-\\lambda)f(b)$$将$\\lambda$取为$\\dfrac12$,$a,b$代入,得到:$$f\\left(\\dfrac{a+b}{2}\\right)\\leq\\dfrac{f(a)+f(b)}{2}$$即:$$\\left(\\dfrac{a+b}{2}\\right)^2\\leq\\dfrac{a^2+b^2} {2}$$化简可得:$$a^2+2ab+b^2\\leq 2a^2+2b^2$$即:$$(a+b)^2\\leq 2(a^2+b^2)$$3.根据不等式左右两边的定义域,进一步讨论如何得出不等式的证明。
由于$a$和$b$都是实数,所以$(a+b)^2$和$2(a^2+b^2)$都存在并且有意义。
因此,不等式成立。
综上所述,我们使用函数的凸性证明了不等式$(a+b)^2\\leq 2(a^2+b^2)$。
凸函数的性质及其在证明不等式中的应用

凸函数的性质及其在证明不等式中的应用数学计算机科学学院摘要:凸函数是一类重要的函数.凸函数在不等式的研究中尤为重要,而不等式最终归结为研究函数的特性,这就需要来研究凸函数了.本篇文章论述了凸函数、对数凸函数的定义、引理、定理和性质及其常用的一些判别方法(根据凸函数,对数凸函数的已知的定理、定义、性质,Jensen不等式等一些方法来判断函数是否是凸函数);本文还试就凸函数的等价定义、性质和在证明不等式中的应用等问题作一初步的探讨,以便进一步了解凸函数的性质及其在证明不等式时的作用;并浅谈了一下凸函数在不等式证明中的一些应用(如上述利用凸函数以及对数凸函数的定理,定义,性质,Jensen不等式来证明一些不等式),推广并证明了一些不等式(三角不等式,Jensen不等式等),得到了新的结果.关键词:凸函数;对数凸函数;Jensen不等式;Hadamard不等式;应用Nature of Convex Function and its Application in ProvingInequalitiesChen Huifei, College of Mathematics and Computer ScienceAbstract : Convex function is a kind of important function. Convex function is particularly important in the study of the inequality, and the study of the inequality is reduced to study the characteristics of the convex function,whichmakes it necessary to study convex functions.We discuss definition, lemma, theorem and the nature of some commonly used discriminant methods of the convex function and the logarithmic convex function in this paper(According to known theorems, definitions, nature, Jensen inequality and other methods of convex function and the logarithmic convex function to recognize whether the function is a convex function); In this paper we also try to discuss the equivalent definition and nature of the convex function and the issue of its application in demonstration inequalities of convex function in order to have a better understanding of the nature and role of the convex function in proving inequalities; we also try to discuss some applications of convex function in proving inequalities(Convex function and the use of these convex function theorem, definition, nature, Jensen inequality to prove Inequality). We also have promoted and proved some inequality (Triangle inequality, Jensen inequality) and reached new results.Key words : Convex function;Logarithmic convex function ; Jensen inequality; Hadamard Inequality;Application1引言在很多数学问题的分析与证明中,我们都需要用到凸函数,例如在数学分析、函数论、泛函分析、最优化理论等当中.凸函数是一类重要的函数.凸函数在不等式的研究中尤为重要,而不等式最终归结为研究函数的特性,这就需要来研究凸函数了.常用的凸函数有两种,一种叫上凸函数,即曲线位于每一点切线的下方或曲线上任意两点间的弧段总在这两点连线上方的函数;另一种叫下凸函数,即曲线位于每一点切线的上方或曲线上任意两点间的弧段总在这两点连线下方的函数.本文试就凸函数的等价定义、性质和在证明不等式中的应用等问题作一初步的探讨,以便进一步了解凸函数的性质及其作用.2 概念2.1 凸函数的定义上面对凸函数作了直观的描述,我们用分析式子给出其精确定义.定义[1]2.1设函数()f x 在区间[,]a b 上有定义,若对[,]a b 上任意两点12,x x 和正数λ∈(0,1),总有1212[(1)]()(1)()f x x f x f x λλλλ+-≤+- (A)则f 为区间[,]a b 上的凸函数.(同时也称为上凸函数,若是不等号反向则称为下凸函.)定义[1]2.2 若函数()f x 在D 上是正的,且ln ()f x 在D 上是下凸函数,则称()f x 是D 上的对数下凸函数这时, 对于任意,x y D ∈ 和(0,1)λ∈,有ln [(1)]ln ()(1)ln ()f x y f x f y λλλλ+-≤+-. 即(1)[(1)]()()f x y f x f y λλλλ-+-≤ (B)如果(2) 中的不等号反向,则称()f x 是D 上的对数上凸函数.2.2 对数凸函数的性质 我们已经有了凸函数以及对数凸函数的定义,现在我们来看一下对数的一些引理,定理及其性质等.定理 2.1[2] (对数下(上) 凸函数的判定定理) 设()f x 是D 上的正值函数,且在D 上有二阶导数,则()f x 在D 上为对数下(上) 凸函数的充要条件为对于任意x ∈D ,有2()()(())0(0)f x f x f x '''-≥≤先证下引理引理 2.1[2] (1) 若()g x 是[,]a b 上的下(上) 凸函数,则()()g x f x e = 为[,]a b e e 上的对数下(上) 凸函数.(2) 若()f x 是[,]c d 上的对数下(上) 凸函数,则()ln ()g x f x =为[ln ,ln ]c d 上的下(上) 凸数.证明(1) 任取12,[,]c d x x e e ∈,由()g x 在[,]c d 上是下凸函数,对任意01λ<<有()()121212[(1)]()(1)()121()()112[(1)][][]()()g x x g x g x g x g x f x x e e e e f x f x λλλλλλλλλλ+-+---+-=≤==(2)任取12,[ln ,ln ]x x c d ∈ ,由()f x 是[,]c d 上的对数下凸函数,对任意01λ<<有11212121212[(1)]ln [(1)]ln[()][()]ln ()(1)ln ()()(1)()g x x f x x f x f x f x f x g x g x λλλλλλλλλλ-+-=+-≤=+-=+-所以()g x 为区间[ln ,ln ]c d 上的下凸函数. (用类似方法可证上凸的情形)下证定理2.1[2] “⇐” 设[,]D c d =,()ln ()g x f x =,则 ()()[ln ()]()f xg x f x f x '''==,22()()[()]()()f x f x f x g x f x '''-''= 所以()g x 是为区间[ln ,ln ]c d 上的下凸函数,根据引理1 得()ln ()()g x f x e e f x ==为[ c ,d] 上的对数下凸函数“⇒” 若()f x 为[,]c d 上的对数下凸函数,由引理1 得()ln ()g x f x =为区间[ln ,ln ]c d 上的下凸函数,从而()0g x ''≥ ,对()ln ()g x f x =求二阶导数即得2()()(())0f x f x f x '''-≥. (用类似方法可证上凸的情形) .推论2.1[2] 设12(),()f x f x 是D 上的对数下(上) 凸函数,则1212()(),()()f x f x f x f x +也是D 上的对数下(上) 凸函数证明:设1212()()(),,,(0,1)g x f x f x x x D λ=+∀∈∈121122121111112221221121122212((1))((1))((1))()()()()[()()][()()]()()g x x f x x f x x f x f x f x fx f x f x f x f x g x g x λλλλλλλλλλλλλλ----+-=+-++-≤+≤+⨯+= 其中(A) 由..H older 不等式得到根据定义 2.2 得出1121()()f x f x +是D 上的对数下凸函数.122112[()()]()()()()f x f x f x f x f x f x '''=+12211212[()()]()()2()()()()f x f x f x f x f x f x f x f x ''''''''=++2121212222221111222[()()][()()]{[()()]}(){()()[()]}(){()()[()]}0f x f x f x f x f x f x f x f x f x f x f x f x f x f x '''-=''''''-+-≥根据定理2.1 得12(),()f x f x 是D 上的对数下凸函数. (用类似方法可证上凸的情形)用数学归纳法可将推论1 推广到有限情形.推论 2.2[2] 设()f x 是定义在D 上的正值函数,1) 若()f x 是对数下凸函数,则1()f x 在区间D 上是对数上凸函数. 2) 若()f x 是对数上凸函数,则1()f x 在区间D 上是对数下凸函数. 证明 1) 设1()()x f x φ=22322224241()()()2(())()(),()[]()()()()()2(())()()()(())()()[()][][][]()()()f x f x f x f x x x f x f x f x f x f x f x f x f x f x f x x x x f x f x f x φφφφφ''''-''''==-=-'''''''--'''-=--=-显然是小于0的,所以1()()x f x φ=是对数上凸函数,同理可证2) . 定理 2.2[2] (Jensen 型不等式) 设()f x 是D 上的正值对数下凸函数, 12,01, (1)i i n x D λλλλ∈<<+++=12112212(...)()()...()n n n n f x x x f x f x f x λλλλλλ+++≤ (*)若()f x 是D 上的正值对数上凸函数,则(*) 中不等号反向.证明 (用数学归纳法) 当2n =时,由定义2.2 知不等式(*) 成立. 假设n k =时不等式(*) 成立,即121122121(...)()()...()(1,0)kkk k k i i i f x x x f x f x f x λλλλλλλλ=+++≤=>∑ ,(1,2,...,1),i x D i k ∈=+设1(1,0)ki i i λλ==>∑111211121111221111111121111211[...()()]()()...()()()()...()()()k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k x x f x x x x x f x f x f x f f x f x f x f x f x λλλλλλλλλλλλλλλλλλλλλλλλλλλ-+-+++--++++++-++-+++++++++≤+≤++ 所以当1n k =+时,不等式(*) 成立,从而对于一切自然数(2)n n ≥ 不等式(*) 成立. 用同样方法可证明上凸情形.当然这里的定理对凸函数也是成立的.在下面的运算性质中有介绍.也就是下面的Jensen 不等式 1,Jensen 不等式 2.引理 2.2[2] (凸函数的Hadamard 不等式) 设()x φ是区间D 上的下凸函数则对于任意,.a b D a b ∈≤有11()[()()]22b a a b x dx a b b aφφφφ+⎛⎫≤≤+ ⎪-⎝⎭⎰ (#) 若()x φ是区间D 上的上凸函数,则对于任意,.a b D a b ∈≤,(#)中不等号反向.定理 2.3[2] ( Hadamard 型不等式) 设():[,](0,)f x a b →+∞对数下凸函数,则11()()[()()]2ln ()ln ()b a a b f f x dx f b f a b a f a f b +≤≤---⎰ () 若():[,](0,)f x a b →+∞对数下凸函数,则(5) 中不等号反向.证明 由引理2.1 和引理2.2有1ln ()ln ()11ln ()()lim lim lim n f a bb f x n a a n i f a n n n b a f x dx e dx e n +∆→∞=+∆→∞→∞-==≥=∑⎰⎰nn 由平均值i=1(b-a )e (b-a )11(ln ())()2lim ()ln ()()()()2n i b ai f a b n n b a a n a b lmf b a e f x dxa b b a e b a f =-+∆-→∞+∑==-+≥-=-⎰1b-a (b-a)e (其中b a ∆=-)又令()ln ()x f x φ=,根据定义2.1,对于a x b <<,有()()()()()a b x b x a x b aφφφ-+-≤- ()()()()()()ln ()()()()()()()()()()()exp()|()()[]()()ln ()ln (b a x b a a b x b x a b b b b f x x b a a a a a b a a b b a a b b b b a b aa ab a f x dx edx e dx e dx b a b a e e dx e x b a b a b a b a e e b a f b f a φφφφφφφφφφφφφφφφφ-⎡⎤⎢⎥-⎣⎦-+------==≤--⎡⎤==⎢⎥--⎣⎦--=-=--⎰⎰⎰⎰⎰[()()])f b f a - 定理得证.2.3[3] 凸函数的性质 在讨论了一些对数凸函数的定理,引理,我们来看一看凸函数的运算性质以及它们实用的定理:(1) 若()f x 与()g x 均为区间[,]a b 上的凸函数,则()f x +()g x 也是区间[,]a b 上的凸函数.(2)若()f x 与()g x 为区间[,]a b 上的凸函数,则ⅰ)0λ≥,则()f x λ是[,]a b 上的凸函数;ⅱ)0λ<,则()f x λ是[,]a b 上的凹函数.(3) 设()f x 与()g x 都是[,]a b 上的非负单调递增的凸函数,则()()()h x f x g x =也是[,]a b 上的凸函数.证明:对任意12,x x ∈[,]a b 且12x x <和任意λ∈(0,1),因()f x 与()g x 在[,]a b 上单调递增,故 :1212[()()][()()]0f x f x g x g x --≥即: 12211122()()()()()()()()f x g x f x g x f x g x f x g x +≤+ (1) 又因为()f x 与()g x 在[,]a b 上的凸函数,故1212[(1)]()(1)()f x x f x f x λλλλ+-≤+-,2121g(x +(1-)x )g(x )+(1-)g(x )λλλλ≤ 而()0,()0f x g x ≥≥,设将上面两个不等式相乘,可得2122222211211[(1)][(1)]()()(1)[()()()()](1)()()f x x g x g x f x f x g x f x g x f x g x λλλλλλλλ+-+-≤+-++-又由⑴知21212222211211[(1)][(1)]()()(1)[()()()()(1)()()]f x x g x x g x f x f x g x f x g x f x g x λλλλλλλ+-+-≤+-++-=1122(1)()()()()f x g x f x g x λλ-+由凸函数的定义知:()()()h x f x g x =是[,]a b 上的凸函数.注:1°()f x 与()g x 非负不能少,2°(),()f x g x 单调递增不能少. (4)[4][5] 设()u ϕ是单调递增的凸函数,()u f x =是凸函数,则复合函数[()]f x ϕ也是凸函数.对于其他情况也有类似的情况的命题,如下列:我们也可以看一下单值有反函数的函数的反函数与自身的凸凹性的关系. 如下表:(5) 若()f x 为区间I 的凸函数,且()f x 不是常数,则()f x 在I 部不能达到最大值.2.4[3] 凸函数的等价定义和判定设函数f 在区间(,)a b 上有定义,则下列命题彼此互相等价:(1)对任意12,x x ∈(,)a b 及任意恒有1212[(1)]()(1)()f x x f x f x λλλλ+-≤+-(2)对任意i x ∈(,)a b 及任意i p >0. 1,2,...,i n =. 11n i i p -=∑ 恒有11()n ni i i i i i f p x p f x ==⎛⎫≤ ⎪⎝⎭∑∑ (3)对任意1,2,(,)x x x a b ∈, 12x x x <<,恒有12121212()()()()()()f x f x f x f x f x f x x x x x x x---≤≤--- (4)在(,)a b 上曲线在其每一点处具有不垂直于x 轴的左、右切线,并且曲线在左、右切线之上.(5)若在(,)a b 存在单调递增的函数()x ϕ.以及0x ∈(,)a b ,使得对任意(,)x a b ∈,恒有00()()()xx f x f x t dt ϕ-=⎰,(6)对任意12,x x ∈(,)a b ,12x x <,恒有21121221()()1()22x x x x f x f x f f t dt x x ++⎛⎫≤≤ ⎪-⎝⎭⎰ (7)对任意12,(,)x x a b ∈,恒有1212()()22x x f x f x f ++⎛⎫≤ ⎪⎝⎭对于凸函数定义等价性的证明,可参看[4]及[5].对于等价定义(5)事实上,我们也有类似的这样一个定理: 定理 2.4 设函数f 在[,]a b 上连续,在(,)a b 上可导,则f 在[,]a b 上为上(下)凸函数(严格上(下)凸函数)的一个必要充分条件f '是在(,)a b 上递增(减)(严格递增(减)).证明 先证条件是必要的.设()12,(,)x x a b ⊂.只要x x '与满足12x x x x '<<<,由于等价定义(3)可知12121212()()()()()()f x f x f x f x f x f x x x x x x x '---≤≤'--- 在上式中令12,x x x x +-'→→,得211221()()()()f x f x f x f x x x -''≤≤-. 在是严格上凸函数的情形,我们取一点*x 满足*12x x x <<,从而得出**1212**12()()()()()()f x f x f x f x f x f x x x x x--''≤<≤--. 这样就得出了严格的不等式12()()f x f x ''<,必要性得证.再证充分性.设f '是在(,)a b 上递增.对任何()12,x x x ∈,由Lagrange 中值定理,可只存在()12,x x ξ∈与()12,x x η∈,使得11()()()f x f x f x x ξ-'=-,22()()()f x f x f x x η-'=- 因为x ξη<<,所以()()f f ξη''≤.从而有1212()()()()f x f x f x f x x x x x--≤--所以,可知函数f 在[,]a b 上为上凸函数.容易看出,当f '严格递增时,()()f f ξη''<.上述不等式中成立着严格的不等号,从而函数f 在[,]a b 上是严格的上凸函数.同理可以证明下凸时的情景.当函数f 在[,]a b 有二阶导数时,我们有下列应用起来就会更方便的定理 定理 2.5 设函数f 在[,]a b 上连续,f 在(,)a b 有二阶导数,则f 在[,]a b 上为上凸函数(下凸函数)的充分条件0(0)f f ''''≥≤在(,)a b 成立;而f 在[,]a b 上为严格上(下)凸函数的充分必要条件是0(0)f f ''''≥≤在(,)a b 成立并且在(,)a b 的任何开的子区间f ''不恒等于0.证明 第一个结论,由于0f ''≥得出f '在(,)a b 上递增再由定理4可得出.同理可证明下凸时的情景; 第二个结论,先证充分性 由于0f ''≥在(,)a b 成立并且在(,)a b 的任何开的子区间f ''不恒等于0.对任意12,(,)x x a b ∈,12x x <,又由于2121()()()x x f x f x f x dx ''''=+⎰,所以21()()f x f x ''>.所以函数f 在[,]a b 上为严格的凸函数.充分性得证.再证必要性(反证法) 因为函数f 在[,]a b 上为严格凸函数,对任意12,(,)x x a b ∈,12x x <,则21()()f x f x ''>,而由于2121()()()x x f x f x f x dx ''''=+⎰,若是有一个(,)a b 的子区间恒等于0.不妨设为(,)(,)a b ξη⊂,对任意(,)x ξη∈,()0f x ''=.则由于21()()()x x f f f x dx ηξ''''=+⎰,()()f f ξη''=,这与已知条件相矛盾.所以,必要性得证.同理可证明下凸时的情景. 所以,定理得证.关于凸函数的判定有很多,应用围最广的是Jensen 不等式. Jensen 不等式 1 设()f x 在区间I 上有定义,()f x 为凸函数,当且仅当12,,...,n x x x I ∀∈1212...()()...()n n x x x f x f x f x f n n ++++++⎛⎫≤⎪⎝⎭(J1) 此外,当且仅当12...n x x x === 时,上式等号成立(证明略请参考附[1]). Jensen 不等式 2 12,,...,[,]n x x x a b ∀∈,12,,...,0n λλλ>,且11ni i λ==∑,1.则()f x 为凸函数的充要条件为:11()()n ni i i i i i f x f x λλ==≤∑∑ (J2)此外,上式当且仅当12...n x x x === 时,等号成立.(证明略请参考附[1]). 这里对任意12,,...,0n βββ>,若是令1ii nii βλβ==∑,那么就有1111()nni i i i i i n n i i i i x f x f ββββ====⎛⎫ ⎪ ⎪≤⎪ ⎪⎝⎭∑∑∑∑ (J3) 每个凸函数都有一个Jensen 不等式,Jensen 不等式的应用围甚广,既可用于求解不等式问题,又可用于证明不等式定理,应用Jensen 不等式解题的关键有两条:一是必须先判明函数的上(下)凸性,二是直接应用Jensen 不等式有困难时,可以根据命题的特点,选择恰当的上凸函数和下凸函数,然后再进行解答.3 凸函数以及对数凸函数的应用在许多证明题中,我们常常遇到一些不等式的证明,其中有一类不等式利用凸函数的性质来证明可以非常简洁、巧妙.证明不等式是凸函数的一个重要应用领域,但关键是构造能够解决问题的凸函数.例 1[1] 利用凸函数证明调和平均值H ≤几何平均值G ≤对数平均值L ≤指数平均值E ≤算术平均值A.证明:事实上,我们可以用凸函数理论证明,对任意0(1,2,...,)ix i n = 有1212 (111)...nnx x x n nx x x +++≤≤+++ (2)只要将不等式各部分同时取对数,这时左边的不等式可变为121111...1111ln (ln ln ...ln )n nx x x n n x x x +++-≤----.从而由函数()ln f x x =-在(0,)+∞上的(严格)凸性可得;右边的不等式可直接由()ln g x x =上的(0,)+∞(严格)下凸性可得.(具体证明可参看[2])为了证明例1 中的连不等式,我们先来看下面两个小题:(1) 设0(1,2,...,)i a i n >=且不全相等,0(1,2,...,)i p i n >=有不等式链11111ln ln exp exp n n nii i i i i i i i i nn n ii i i i n i i p a p a p a a p p p a ======⎛⎫⎛⎫ ⎪ ⎪ ⎪≤≤ ⎪ ⎪ ⎪ ⎪⎪⎝⎭⎝⎭∑∑∑∑∑∑ (3) 证:凸函数()ln f x x =-的Jensen 不等式:取0i q >,11ni i q ==∑,0(1,2,...,).i a i n >=得11ln ln n n i i i i i i q a q a ==-≤-∑∑ [4] 111ln ln nn i i i i i i q q a a ==-≤-∑∑ (5)在[4]中令1i ini ii ip a q p a ==∑得 1111exp ln nn niiii ni i i i iii ip p p a p a a a ====⎛⎫≤ ⎪⎝⎭∑∑∑∑ (6)又由(4),(5)可得 1111in nq i i i n i i i i ia q a q a ===≤≤∑∏∑ (7)在此令1ini i i p q p ==∑,可得111111ln exp nn ni i i i ii i i n n n ii i i i i i p p a p a p p p a ======⎛⎫ ⎪≤≤ ⎪ ⎪ ⎪⎝⎭∑∑∑∑∑∑ (8) 联立(6),(8)既得证 (3).(2) 设()()f x p x 与在[,]a b 上正的连续函数且()f x ≠常数,在⑻中作代换i b a p p a i n -⎛⎫=+ ⎪⎝⎭,i b a a f a i n -⎛⎫=+ ⎪⎝⎭并在“∑”号后均乘b a n -,由0b a ->,不改变原不等号方向.令n →∞ 便得(3)的积分形式:ln ln exp exp b bb ba aa ab b bba aa ap fdx pdxp fdx pfdx f p p pdx pdxdx dx f f ⎛⎫⎛⎫ ⎪⎪ ⎪≤≤≤ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎰⎰⎰⎰⎰⎰⎰⎰(3)'在(3)'中令()1,()p x f x x ==()11ln ln ln ln 2b ab a b a b ab a e ----+⎛⎫≤≤≤⎪-⎝⎭再联立(2),得出H G L E A ≤≤≤≤.例 2 (1)在锐角ABC ∆中,证明1cos cos cos 2A B C ++≤, (2)12,,...,n a a a 设为正数,证明恒成立12...n a a a n +++≥. 证明 (1)令()cos()f x x =-,(0,)x π∈.由于()cos()0f x x ''=>,(0,)2x π∈.所以()f x 在(0,)2x π∈上凸函数,所以由于(J1)()()()()33f A f B f C A B Cf ++++≥,即cos()cos()cos()s()33A B C A B C co ---++≥-1()2=-即1cos cos cos 2A B C ++≤;(2) 令()ln ,(0,)g x x x =-∈+∞,所以21()0,(0,)g x x x''=>∈+∞, 故()g x 是在(0,)+∞上的上凸函数.也是根据(J1)121212121212()()...()...()ln ln ...ln ...ln()ln ln ...ln ...ln()n nn nn n g a g a g a a a a g n n a a a a a a n na a a a a a n n++++++≥++++++-≥-++++++≤即即从而,有12...n a a a n+++≥.下面我们再看一个用对数凸函数证明的不等式题. 例 3[2]10,0,12ni i i πλλ=<<>=∑i 设x ,则12112212sin(...)sin sin ...sin n n n n x x x x x x λλλλλλ+++≥ (&)12112212cos(...)cos cos ...cos n n n n x x x x x x λλλλλλ+++≥(%)证明 设()sin()f x x =,由于2()()[()]10f x f x f x '''-=-<,故sin()x 是(0,)2π上的对数凸函数,同理cos()x 也是(0,)2π上对数凸函数.根据定理2即可得(&),(%).例 4 设()f x 在[,]a b 上可积,且()m f x M ≤≤,()t ϕ是在[,]m M 上的连续下凸函数,则11()(())b b a a f x dx f x dx b a b a ϕϕ⎛⎫≥ ⎪--⎝⎭⎰⎰. 证明 令,()k n k f f a b a n ⎛⎫=+- ⎪⎝⎭,,1()k n x b a n ∆=-.由于()t ϕ是凸函数,故有1,2,,1,2,,...()()...()n n n n n n n n f f f f f f n n ϕϕϕϕ++++++⎛⎫≥⎪⎝⎭. 由定积分的定义,上式就相当于,,,,11()n ni n i n i n i ni i f f b a b a ϕϕ==⎛⎫∆∆ ⎪ ⎪≥-- ⎪⎪⎝⎭∑∑,,1()k n x b a n ∆=- 在上式中令n →∞时, 则有11()(())b b a a f x dx f x dx b a b a ϕϕ⎛⎫≥⎪--⎝⎭⎰⎰. 命题得证.例 5[7]设,i i a b R +∈,111,2,...,,,n n i i i i i n a b ====∑∑则21112nni i i i i ia a ab ==≥+∑∑.证明 记1ni i s a ==∑,11ni i a s ==∑,将21112nni i i i i i a a a b ==≥+∑∑变为11121n ii i ia b s a =≥+∑,那么取11i ib a +作为函数1()1f x x =+,则由于3()2(1)0f x x -''=+>,再令i i i b x a =,i i a sλ=所以根据凸函数性质和(J3)得出11111211ni n i i i i i i a b s x a λ==≥=++∑∑结论本文主要讨论了凸函数以及对数凸函数一类重要的函数的概念,包括它们的一些定义,性质,定理,引理和它们在证明一些不等式的重要应用.本文介绍了Jensen不等式,Hadamard不等式,叙述了一些定理,引理,性质并给出了它们的证明,并指出它们在判断凸函数的应用.本文还试就凸函数的等价定义、性质和在证明不等式中的应用等问题作一初步的探讨,以便进一步了解凸函数的性质及其在证明不等式时的作用.最后举出了一些例题来具体的来体现凸函数以及对数凸函数在不等式证明的应用.参考文献:[1]汪文珑.数学分析选讲[M].文理学院数学系,2001[2] 琼.对数凸函数的Jensen型和Hadamard型不等式[J].学报,,2005,3[3]查良凇.凸函数及其在不等式证明中的应用[J].工贸职业技术学院学报,,2005,3[4]燕建梁,喜善.凸函数的性质及其在不等式证明中的应用[J].教育学院学报,,2002,4[5]T.M菲赫金哥尔茨普.微积分教程[M].1965: 290-300[6]常庚哲,史济怀.数学分析教程(上册)(M).高等教育,2003:167-176[7]碧荣.凸函数及其性质在不等式证明中的应用[J].广西师学院学报,,2004,2[8]白景华.图函数的性质、等价定义及应用[J].大学学报,,2003,2[9]Satish Shirali, Harkrishan L. Vasudeva. Mathematical analysis[M]. Alpha Science International Ltd., c2006.[10]Tom M. Apostol.Mathematical analysis[M].China Machine Press, 2004.致这是本人的第一篇论文,所以在多方面没有指导老师金洪老师的指导是很难进行下去的.老师从我的选题开始便给予了很大帮助,在以后的开题,开题报告,初稿的资料搜索,初稿出来后的校正,进一步的改进都给予了极大帮助,使我在论文的完成进程中得以较为平坦地进行下去.在论文的写作的进行中,我同组等同学也给了我很多帮助.在此表示感.也在此对我们的学校师大学以及我校资料室提供这样一个学习环境和帮助,表示感.也感那在身后的帮助.。
Jensen不等式
Jensen不等式
在区间[ a , b ]我们可以取分割点
由(6)式知
再取极限 n → ∞ ,我们就有积分形式的Jensen不等式。
Jensen不等式
Jensen不等式一 若p满足 ,且f为一凸函数,则
更一般情形则将区间[ a , b ]代换为任意可测集合A ( Jensen3
图4
几何意义与物理意义
质量中心
几何意义与物理意义
图5
质量中心落在阴影区域H内部
几何意义与物理意义
通过 ( x1 , f ( x1 )), ( xn , f ( xn )) 两点之弦方程式为
质量中心在弦下
推广到n维空间
例如设z = f ( x , y )为一向上凹之曲面,则(7)式可推广为
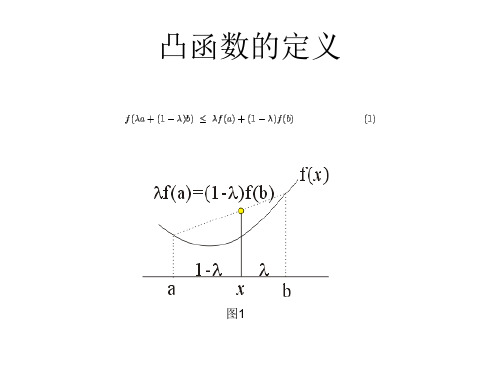
凸函数的定义
图1
凸函数的定义
凸函数的定义
图2
凸函数性质的推广—Jensen不等式
将(1)式推广至一般情形。
其中
,
,
,
,令
凸函数性质的推广—Jensen不等式
则(4)式可改写为
这就是Jensen不等式之一形式。 若取特殊的 pi ,例如: 则(6)式可表为
几何意义与物理意义
质量中心:
或
几何意义与物理意义
关于L-几何凸函数的不等式初探
A ei i a y S u y o e m e rcCo v xFu c i n Pr l n r t d f g o m L t i n e n to
众所周知, 凸函数是一个重要 的数学概念, 在不等式研究中,凸函数所发挥 的作用是无可替代 的【J J, 类 比凸函数的概念, 3中提 出了如下几何 凸函数的概念 : 文[ ]
设 厂 在 区间 D( R 上 有定 义,如 果对 于任 意 的 l 2 ) ) , ∈D 和 t 0 1,都 有 X E(, ) /( ) f( +(一t (2 ≤t ) 1 ) x) f () 1 则说 厂 在 D上是几何凸函数, ) 如果() 1中不等号反 向, 则说 ) D上是几何 凹函数.并建立了几何凸 在
W U a . a Gu ng y o
( uh uSno g co lQuh u3 4 0 , hn ) Q zo e ir hSh o, zo 2 0 6 C ia Hi
Ab t a t On y e o o v x f n to s d fn d i e wa s g o t c c n e u ci n s r c : e tp fc n e u ci n i e e n a n w y a L e mer o v x f n t .M o e v r ei s o i i o r o e ,a s r f e i e u l is f r t i n y e o e me r o v x f n t n a e e t b i d n q ai e o h s o e tp fg o ti c n e u ci r sa l he ,wh c s g n r l ai n o a o s i e u lt s f r t c o s ih i e e ai t f fm u n q ai e z o i o
凸集和凸函数和凸规划-课件
凸集---定义
01
线性组合 (linear Combination)
单击此处添加小标题
02
仿射组合 (Affine Combination)
单击此处添加小标题
03
凸组合 (Convex Combination)
单击此处添加小标题
04
凸锥组合 (Convex Cone Combination)
单击此处添加小标题
第3讲 凸集、凸函数、凸规划
凸集 (Convex Set) 凸函数 (Convex Function) 凸规划 (Convex Programming) 凸性(Convexity)是最优化理论必须涉及到基本概念.具有凸性的非线性规划模型是一类特殊的重要模型,它在最优化的理论证明及算法研究中具有非常重要的作用.
则有:
即点
属于超球,
所以超球为凸集.
凸集----举例
(1)
任意多个凸集的交集为凸集.
(2)
设
是凸集,
是一实数,
则下面的
集合是凸集:
凸集-----性质
(3)
推论:
设
是凸集,
则
也是凸集,
其中
是实数.
(4)
S 是凸集当且仅当S中任意有限个点的凸 组合仍然在S中.P23,定理2.9
凸集-----性质
注:定理4提供了一个判别可微函数是否为凸 函数的依据.
凸函数
定理4-----
01
几何
02
解释
03
一个可微函数
04
是凸函数当且
05
仅当函数图形
06
上任一点处的
07
切平面位于曲
08
面的下方.
数学均值不等式的证明方法
数学均值不等式的证明方法一、凸函数的性质法:凸函数是指曲线所在区间上的任意两点连线的部分都位于曲线的上方。
我们可以证明,如果函数f(x)在区间[a,b]上是凸函数,则有如下均值不等式成立:f((a+b)/2) ≤ (1/(b-a)) ∫[a,b] f(x) dx ≤ (f(a) + f(b))/2通过利用凸函数的性质,我们可以推广到更一般的形式:f((a₁x₁+a₂x₂+...+aₙxₙ)/(a₁+a₂+...+aₙ))≤(a₁f(x₁)+a₂f(x₂)+...+aₙf(xₙ))/(a₁+a₂+...+aₙ)其中,a₁,a₂,...,aₙ是非负实数,且满足a₁+a₂+...+aₙ≠0,x₁,x₂,...,xₙ是函数f(x)的定义域上的任意n个值。
二、Cauchy-Schwarz不等式的证明法:Cauchy-Schwarz不等式是数学中最常用的不等式之一,它的一般形式可以写为:(a₁b₁+a₂b₂+...+aₙbₙ),≤√((a₁²+a₂²+...+aₙ²)(b₁²+b₂²+...+bₙ²))其中,a₁,a₂,...,aₙ和b₁,b₂,...,bₙ是任意实数。
利用这个不等式,我们可以证明数学均值不等式中的特例。
例如,我们可以通过Cauchy-Schwarz不等式来证明算术平均数大于等于几何平均数的不等式:(a₁+a₂+...+aₙ)/n≥√(a₁a₂...aₙ)三、归纳法和递推法:在证明数学均值不等式时,可以利用归纳法和递推法构造一些递推关系式,从而推导出不等式的成立。
例如,在证明幂平均不等式时,我们可以先证明对于n=2的情况成立,即:(a²+b²)/2≥(√(a²)+√(b²))/2然后,通过递推关系式:(a₁^n+a₂^n)/2≥(√(a₁^n)+√(a₂^n))/2(a₁^(n+1)+a₂^(n+1))/2≥(√(a₁^(n+1))+√(a₂^(n+1)))/2不断迭代,可以得到幂平均不等式在任意正整数n下成立。
严格拟凸 和凸函数
严格拟凸和凸函数
严格拟凸函数和凸函数是两种不同的数学概念,它们在几何和优化理论中有重要的应用。
1. 凸函数:在凸分析中,凸函数是一个函数,其定义域为凸集,且对定义域内的任意两点x和y,以及任意实数λ∈[0,1],都有
f((1−λ)x+λy)≤(1−λ)f(x)+λf(y)。
特别地,当上述不等式为严格不等式时,我们称f为严格凸函数。
2. 严格拟凸函数:在数学中,特别是优化理论中,严格拟凸函数是一种特殊的函数。
如果一个函数在凸集的每一点都有切线,并且在凸集的边界上,函数值小于等于切线的高度,那么这个函数就是严格拟凸的。
总之,凸函数和严格拟凸函数在数学和工程领域都有重要的应用。
