8.3.1棱柱棱锥棱台的表面积和体积
高中数学 第八章 立体几何初步 8.3.1 棱柱、棱锥、棱台的表面积和体积习题(含解析)新人教A版必

8.3简单几何体的表面积与体积8.3.1棱柱、棱锥、棱台的表面积和体积课后篇巩固提升基础达标练1.(多选题)长方体ABCD-A1B1C1D1的长、宽、高分别为3,2,1,则()A.长方体的表面积为20B.长方体的体积为6C.沿长方体的表面从A到C1的最短距离为3D.沿长方体的表面从A到C1的最短距离为22×(3×2+3×1+2×1)=22,A错误.长方体的体积为3×2×1=6,B正确.如图①所示,在长方体ABCD-A1B1C1D1中,AB=3,BC=2,BB1=1.在表面上求最短距离可把几何体展开成平面图形,如图②所示,将侧面ABB1A1和侧面BCC1B1展开,则有AC1=,即当经过侧面ABB1A1和侧面BCC1B1时的最短距离是;如图③所示,将侧面ABB1A1和底面A1B1C1D1展开,则有AC1==3,即当经过侧面ABB1A1和底面A1B1C1D1时的最短距离是3;如图④所示,将侧面ADD1A1和底面A1B1C1D1展开,则有AC1==2,即当经过侧面ADD1A1和底面A1B1C1D1时的最短距离是2.因为3<2,所以沿长方体表面从A到C1的最短距离是3,C正确,D不正确.2.如图所示,正方体ABCD-A1B1C1D1的棱长为1,则三棱锥D-ACD1的体积是()A. B. C. D.1D-ACD1的体积等于三棱锥D1-ACD的体积,三棱锥D1-ACD的底面ACD是直角边长为1的等腰直角三角形,高D1D=1,∴三棱锥D-ACD1的体积为V=×1×1×1=.3.一个正四棱锥的底面边长为2,高为,则该正四棱锥的表面积为()A.8B.12C.16D.20=2,所以该四棱锥的表面积为22+4××2×2=12.4.正方体的棱长为2,以其所有面的中心为顶点的多面体的体积为()A.3πB.C.πD.1,由图可知,该几何体由两个四棱锥构成,并且这两个四棱锥体积相等.四棱锥的底面为正方形,且边长为,故底面积为()2=2;四棱锥的高为1,则四棱锥的体积为×2×1=.故几何体的体积为2×.5.正三棱锥的底面周长为6,侧面都是直角三角形,则此棱锥的体积为()A. B. C. D.,正三棱锥的底面周长为6,所以正三棱锥的底面边长为2,侧面均为直角三角形,可知侧棱长均为,三条侧棱两两垂直,所以此三棱锥的体积为.6.(2020全国高一课时练习)如图,长方体ABCD-A1B1C1D1的体积是120,E为CC1的中点,则三棱锥E-BCD的体积是.ABCD-A1B1C1D1的体积为120,所以AB·BC·CC1=120,因为E为CC1的中点,所以CE=CC1,由长方体的性质知CC1⊥底面ABCD,所以CE是三棱锥E-BCD的底面BCD上的高,所以三棱锥E-BCD的体积V=AB·BC·CE=AB·BC·CC1=×120=10.7.正四棱柱的一条体对角线长为9,表面积为144,适合这些条件的正四棱柱有个.a,高为h,由题意得这个方程组有两个解,所以适合条件的正四棱柱有2个.8.已知某几何体是由两个全等的长方体和一个三棱柱组合而成,如图所示,其中长方体的长、宽、高分别为4,3,3,三棱柱底面是直角边分别为4,3的直角三角形,侧棱长为3,则此几何体的体积是,表面积是.V=4×6×3+×4×3×3=90,表面积S=2(4×6+4×3+6×3)-3×3+×4×3×2+×3+3×4=138.9.在正四棱锥S-ABCD中,点O是底面中心,SO=2,侧棱SA=2,则该棱锥的体积为.侧棱SA=2,高SO=2,∴AO==2,因此,底面正方形的边长AB=AO=4,底面积为AB2=16.该棱锥的体积为V=AB2·SO=×16×2=.10.有一个正四棱台形状的油槽,可以装油190 L,假如它的两底面边长分别等于60 cm和40 cm,则它的深度为 cm.S',S.由V=(S++S')h,得h==75(cm).能力提升练1.(2020某某某某检测)我国古代名著《X丘建算经》中记载:“今有方锥下广二丈,高三丈,欲斩末为方亭,令上方六尺,问亭方几何?”大致意思为“有一个正四棱锥下底面边长为二丈,高三丈,现从上面截去一段,使之成为正四棱台状方亭,且正四棱台的上底面边长为六尺,问该正四棱台的体积是多少立方尺?”(注:1丈=10尺)()A.1 946立方尺B.3 892立方尺C.7 784立方尺D.11 676立方尺,正四棱锥的高为30,所截得正四棱台的下底面棱长为20,上底面棱长为6, 设棱台的高为OO1=h,由△PA1O1∽△PAO可得,解得h=21,可得正四棱台的体积为×21×(62+202+6×20)=3892(立方尺),故选B.2.(2020某某某某检测)如图所示,在上、下底面对应边的比为1∶2的三棱台中,过上底面的一边A1B1和AC,BC的中点F,E作一个平面A1B1EF,记平面分三棱台两部分的体积为V1(三棱柱A1B1C1-FEC),V2两部分,那么V1∶V2=.h,上底面的面积是S,则下底面的面积是4S,∴V棱台=h(S+4S+2S)=Sh,V1=Sh,∴.∶43.(2020全国高一课时练习)如图,AA1,BB1,CC1相交于点O,形成两个顶点相对、底面水平的三棱锥容器,AO=A1O,BO=B1O,CO=C1O.设三棱锥高均为1,若上面三棱锥中装有高度为0.5的液体,且液体能流入下面的三棱锥,则液体流下去后液面高度为.,流下去后,液体上方空出的三棱锥的体积为三棱锥体积的.设空出的三棱锥的高为x,则,所以x=,所以液面高度为1-.-4.已知一个三棱柱的三视图如图所示,求这个三棱柱的侧面积.,该三棱柱的底面为正三角形,各侧面为矩形,侧棱长为4cm,如图所示.因为正三角形ABC和正三角形A'B'C'的高为2cm,所以正三角形ABC的边长AB==4(cm).故三棱柱的侧面积为S侧=4×4×3=48(cm2).5.一个正三棱锥P-ABC的底面边长为a,高为h.一个正三棱柱A1B1C1-A0B0C0的顶点A1,B1,C1分别在三条棱上,A0,B0,C0分别在底面△ABC上,何时此三棱柱的侧面积取到最大值?O,连接PO,图略,则PO为三棱锥的高,设A1,B1,C1所在的底面与PO交于O1点,则,令A1B1=x,而PO=h,则PO1=x,于是OO1=h-PO1=h-x=h.所以所求三棱柱的侧面积为S=3x·h(a-x)x=.当x=时,S有最大值为ah,此时O1为PO的中点,即A1,B1,C1分别是三条棱的中点.素养培优练在正三棱台ABC-A1B1C1中,已知AB=10,棱台一个侧面梯形的面积为,O1,O分别为上、下底面正三角形的中心,连接A1O1,AO并延长,分别交B1C1,BC于点D1,D,∠D1DA=60°,求上底面的边长.AB=10,∴AD=AB=5,OD=AD=.设上底面的边长为x(x>0),则O1D1=x.如图所示,连接O1O,过D1作D1H⊥AD于点H,则四边形OHD1O1为矩形,且OH=O1D1=x.∴DH=OD-OH=x,在Rt△D1DH中,D1D==2x.∵四边形B1C1CB的面积为(B1C1+BC)·D1D,∴(x+10)×2x,即40=(x+10)(10-x),∴x=2,故上底面的边长为2.。
棱柱、棱锥、棱台的表面积和体积 课件

柱体、锥体、台体的体积
棱柱
棱柱
棱锥
棱台
棱台
的体
积
棱锥
各面面积之和
V Sh
V 1 (S SS S)h 3
V 1 Sh 3
再见
棱柱
棱柱 展开图
侧面积等于侧面各个 平行四边形的面积和. 表面积等于底面积与 侧面积的和.
棱锥 棱台
新知探究
棱锥展开图
侧面积等于侧面各个三 角形的面积和; 表面积等于底面积与侧 面积的和.
棱台展开图
侧面积等于侧面各个梯 形的面积和; 表面积等于底面积与侧 面积的和.
新知探究
例1 已知棱长为a,各面均为等边三角形的四面体P-ABC,求它的表面积.
可温 以故 为而 师知 矣新 !,
新知探究
1. 棱柱、棱锥、棱台的表面积
如何求正方体和长方体的表面积?
几何体表面积
展开图
平面图形面积
如何求棱柱、棱锥、棱台的表面积?
一般地,我们可以把多面体展成平面图形,利用平面图形求面积 的方法,求多面体的表面积.
新知探究
多面体的表面积就是围成多面体各个面的面积的和. 棱柱、棱锥、棱台的表面积就是围成它们的各个面的面积的和, 也就是展开图的面积.
的体积差,得到棱台的体积公式
V棱台
1 3
(S
SS S)h
其中S′,S分别为棱台的上、下底面面积,h为棱台的高.
D
C
A
B
h
棱台的高是指两 底面之间的距离,即 从上底面上任意一点 向下底面作垂线,这 点与垂足之间的距离.
新知探究
你能推导棱台的体积公式吗?
过棱锥的顶点P作两底面的垂线,垂足为O′,O , 设PO′=x,
8.棱柱、棱锥、棱台的表面积和体积-【新教材】2021学年人教A版(2019)高中数学必修第二册课件

棱柱、棱锥、棱台的体积
几何体
体积公式
棱柱 V棱柱=③ Sh (其中S为棱柱的底面积,h为棱柱的高)
棱锥 V棱锥=④ Sh (其中S为棱锥的底面积,h为棱锥的高)
棱台 V棱台=⑤
(S'+
+S)h (其中S',S分别为棱台的上、下底面面积,h为棱台的高)
棱柱、棱锥、棱台的体积公式之间的关系
判断正误,正确的画“√” ,错误的画“ ✕” .
在三棱柱ABC-A1B1C1中,∠BAC=90°,其正视图和侧视图都是边长为1的正方形,
俯视图是直角边长为1的等腰直角三角形.设点M,N,P分别是棱AB,BC,B1C1的中
点,则三棱锥P-A1MN的体积是
.
思路点拨 把三棱锥P-A1MN的体积转化为三棱锥A1-PMN的体积,再转化为三棱锥P-AMN 的体积.
运用“等体积转换法”求三棱锥的体积
在平面几何中,可利用“等积变换”求三角形的面积,通常有两种方案:一是同 一三角形选不同的边作为底边所得面积相等;二是不同的三角形利用“等底同高” 或“等高同底”得到的三角形面积相等.在空间图形中能否借鉴平面几何的“等积 变换”求三棱锥的体积呢?
如图所示,正方体ABCD-A1B1C1D1的棱长为1,E为线段B1C上的一点,在求三棱锥 A-DED1的体积时,随着E点的变化,底面DED1的面积在变化,点A到底面DED1的距离 也在变化,导致体积难求.
8. 棱柱、棱锥、棱台的表面积和体积 -【新 教材】2 020-20 21学年 人教A 版(201 9)高 中数学 必修第 二册课 件
8. 棱柱、棱锥、棱台的表面积和体积 -【新 教材】2 020-20 21学年 人教A 版(201 9)高 中数学 必修第 二册课 件
学案4:8.3.1 棱柱、棱锥、棱台的表面积和体积
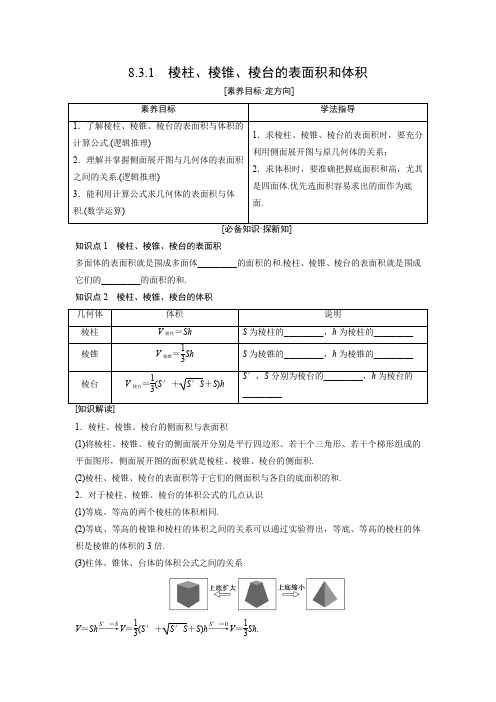
8.3.1 棱柱、棱锥、棱台的表面积和体积[素养目标·定方向]素养目标学法指导1.了解棱柱、棱锥、棱台的表面积与体积的计算公式.(逻辑推理)2.理解并掌握侧面展开图与几何体的表面积之间的关系.(逻辑推理)3.能利用计算公式求几何体的表面积与体积.(数学运算)1.求棱柱、棱锥、棱台的表面积时,要充分利用侧面展开图与原几何体的关系; 2.求体积时,要准确把握底面积和高,尤其是四面体.优先选面积容易求出的面作为底面.[必备知识·探新知]知识点1 棱柱、棱锥、棱台的表面积多面体的表面积就是围成多面体_________的面积的和.棱柱、棱锥、棱台的表面积就是围成它们的_________的面积的和. 知识点2 棱柱、棱锥、棱台的体积 几何体 体积 说明棱柱 V 棱柱=Sh S 为棱柱的_________,h 为棱柱的_________ 棱锥 V 棱锥=13ShS 为棱锥的_________,h 为棱锥的_________ 棱台V 棱台=13(S ′+S ′S +S )hS ′,S 分别为棱台的_________,h 为棱台的_________[知识解读]1.棱柱、棱锥、棱台的侧面积与表面积(1)将棱柱、棱锥、棱台的侧面展开分别是平行四边形、若干个三角形、若干个梯形组成的平面图形,侧面展开图的面积就是棱柱、棱锥、棱台的侧面积. (2)棱柱、棱锥、棱台的表面积等于它们的侧面积与各自的底面积的和. 2.对于棱柱、棱锥、棱台的体积公式的几点认识 (1)等底、等高的两个棱柱的体积相同.(2)等底、等高的棱锥和棱柱的体积之间的关系可以通过实验得出,等底、等高的棱柱的体积是棱锥的体积的3倍.(3)柱体、锥体、台体的体积公式之间的关系V =Sh ――→S ′=S V =13(S ′+S ′S +S )h ――→S ′=0V =13Sh .(4)求棱台的体积可转化为求棱锥的体积.根据棱台的定义进行“补形”,还原为棱锥,采用“大棱锥”减去“小棱锥”的方法求棱台的体积.[关键能力·攻重难]题型探究题型一棱柱、棱锥、棱台的侧面积和表面积典例1现有一个底面是菱形的直四棱柱,它的体对角线长为9和15,高是5,求该直四棱柱的侧面积、表面积.[归纳提升]棱柱、棱锥、棱台的表面积求法(1)多面体的表面积是各个面的面积之和.(2)棱柱、棱锥、棱台的表面积等于它们的侧面积与各自底面积的和.【对点练习1】已知棱长均为5,底面为正方形的四棱锥S-ABCD如图所示,求它的侧面积、表面积.题型二 棱柱、棱锥、棱台的体积典例2 (1)已知高为3的三棱柱ABC -A 1B 1C 1的底面是边长为1的正三角形,如图所示,则三棱锥B 1-ABC 的体积为( )A .14B .12C .36D .34(2)正四棱台两底面边长分别为20 cm 和10 cm ,侧面面积为780 cm 2.求其体积.【对点练习2】 如图,已知正方体ABCD -A 1B 1C 1D 1的棱长为1,则四棱锥A 1-BB 1D 1D 的体积为_______.题型三 求体积的等积法与分割法典例3 (1)如图,已知ABCD -A 1B 1C 1D 1是棱长为a 的正方体,E 为AA 1的中点,F 为CC 1上一点,求三棱锥A 1-D 1EF 的体积.(2)如图,在多面体ABCDEF中,已知四边形ABCD是边长为4的正方形,EF∥AB,EF=2,EF上任意一点到平面ABCD的距离均为3,求该多面体的体积.[归纳提升]求几何体体积的常用方法公式法直接代入公式求解等积法例如四面体的任何一个面都可以作为底面,只需选用底面积和高都易求的形式即可补体法将几何体补成易求解的几何体,如棱锥补成棱柱,三棱柱补成四棱柱等分割法将几何体分割成易求解的几部分,分别求体积11111离d.参考答案[必备知识·探新知]知识点1 棱柱、棱锥、棱台的表面积 各个面 各个面知识点2 棱柱、棱锥、棱台的体积底面积 高 底面积 高 上、下底面面积 高[关键能力·攻重难]题型探究题型一 棱柱、棱锥、棱台的侧面积和表面积典例1 解:如图,设底面对角线AC =a ,BD =b ,交点为O ,体对角线A 1C =15,B 1D =9, ∴a 2+52=152,b 2+52=92, ∴a 2=200,b 2=56. ∵该直四棱柱的底面是菱形, ∴AB 2=⎝⎛⎭⎫AC 22+⎝⎛⎭⎫BD 22=a 2+b 24=200+564=64,∴AB =8.∴直四棱柱的侧面积S 侧=4×8×5=160.∴直四棱柱的底面积S 底=12AC ·BD =207.∴直四棱柱的表面积S 表=160+2×207=160+407. 【对点练习1】 解:∵四棱锥S -ABCD 的各棱长均为5, ∴各侧面都是全等的正三角形.设E 为AB 的中点,连接SE ,则SE ⊥AB , ∴S 侧=4S △SAB =4×12AB ×SE =2×5×52-⎝⎛⎭⎫522=253,S 表=S 侧+S 底=253+25=25(3+1).题型二 棱柱、棱锥、棱台的体积 典例2 (1)【答案】 D【解析】设三棱锥B 1-ABC 的高为h ,则V 三棱锥B 1-ABC =13S △ABC h =13×34×3=34.(2)解:正四棱台的大致图形如图所示,其中A 1B 1=10 cm ,AB =20 cm ,取A 1B 1的中点E 1,AB 的中点E ,则E 1E 为斜高.设O 1,O 分别是上、下底面的中心,则四边形EOO 1E 1为直角梯形.∵S 侧=4×12×(10+20)×EE 1=780(cm 2),∴EE 1=13 cm.在直角梯形EOO 1E 1中,O 1E 1=12A 1B 1=5 cm ,OE =12AB =10 cm ,∴O 1O =132-(10-5)2=12(cm). 故该正四棱台的体积为V =13×12×(102+202+10×20)=2 800(cm 3).【对点练习2】 【答案】13【解析】由题意可知四棱锥A 1-BB 1D 1D 的底面是矩形,边长为1和2, 四棱锥的高为12A 1C 1=22,则四棱锥A 1-BB 1D 1D 的体积为V =13×1×2×22=13.题型三 求体积的等积法与分割法典例3 解:(1)由V 三棱锥A 1-D 1EF =V 三棱锥F -A 1D 1E , ∵S △A 1D 1E =12EA 1·A 1D 1=14a 2,又三棱锥F -A 1D 1E 的高为CD =a , ∴V 三棱锥F -A 1D 1E =13×a ×14a 2=112a 3,∴V 三棱锥A 1-D 1EF =112a 3.(2)如图,连接EB ,EC ,AC .V 四棱锥E -ABCD =13×42×3=16.∵AB =2EF ,EF ∥AB , ∴S △EAB =2S △BEF .∴V 三棱锥F -EBC =V 三棱锥C -EFB =12V 三棱锥C -ABE =12V 三棱锥E -ABC =12×12V 四棱锥E -ABCD =4. ∴多面体的体积V =V 四棱锥E -ABCD +V 三棱锥F -EBC =16+4=20.【对点练习3】 解:在三棱锥A 1-ABD 中,AB =AD =AA 1=a ,A 1B =BD =A 1D =2a , ∵VA 1-ABD =VA -A 1BD ,∴13×12a 2×a =13×12×2a ×32×2a ×d . 解得d =33a .∴A 到平面A 1BD 的距离为33a .。
棱柱、棱锥、棱台的表面积和体积(教学课件)高一数学同步备课系列(人教A版2019 必修第二册)

∴S上底面
3 2
6
2 6 3 cm 2 .
4
S下底面 6
3 2
6 54 3 cm 2 .
4
F
'
A
'
D'
B
'
C
'
E
D
F
A
S侧面
E
'
1
6 (2 6) 21 24 21cm 2 .
2
C
B
2
因此,正六棱台的表面积为 S表 60 3 24 21(cm ).
直棱柱 = ℎ + 2S底面积 (为底面周长, ℎ为高)
(2)斜棱柱的侧面积为多少?如何计算它的表面积?
斜棱柱侧 = (为直截面的周长, 为棱长)
斜棱柱 = L + 2S底面积 (为直截面的周长, 为棱长)
侧面
矩形
底面
多边形
直棱柱
棱
柱
的
表
面
积
侧面
四边形
斜棱柱
底面
多边形
(3)棱锥的侧面展开图是什么?如何计算它的表面积?
所占空间的大小.
多面体的表面积就是围成多面体各个面的面积的和.棱柱、棱锥、棱台的
表面积就是围成它们的各个面的面积的和.
问题1:在初中已经学过了正方体和长方体的表面积,
你知道正方体和长方体的展开图与其表面积的关系吗?
问题1:在初中已经学过了正方体和长方体的表面积,
你知道正方体和长方体的展开图与其表面积的关系吗?
如果棱锥的底面面积为,高为ℎ,那么该棱锥的体积
1
棱锥 = 3 ℎ.
棱锥的高是指从顶点
棱柱、棱锥、棱台的表面积和体积 高一数学人教A版(2019)必修第二册

解:如图示,由题意知
V长方体ABCDABCD 11 0.5 0.5 (m3 ).
V棱锥P-ABCD
1 11 0.5 3
1 6
(m3 ).
∴这个漏斗的容积为
V组合体
1 2
1 6
2 3
(m3 ).
D' A' D A
P
C' B'
C
B
练习
- - - - - - - - - - 教材116页
3. 某广场设置了一些石凳供大家休息,这些石凳是由正方体截去八个一样
过点P作PE⊥AB,垂直为E,则 AE=3,
P
∴PE PB2 BE2 52 32 4.
∴S△PAB
1 2
64
12.
因此,正四棱锥P-ABCD的表面积为
D
C
A
E
B
∴SPABCD 4S△PAB S ABCD 4 12 62 84.
练习
- - - - - - - - - - 教材116页
多面体的表面积就是围成多面体各个面的面积的和.棱柱、棱锥、棱 台的表面积就是围成它们的各个面的面积ຫໍສະໝຸດ 和.常见平面图形的面积公式:
S三角形
1 2
底 高.
S平行四边形 底 高.
S梯形
(上底+下底) 高
1. 2
例1 如图示,四面体P-ABC各棱长均为a,求它的表面积. 解:∵∆ABC是正三角形,其边长为a.
的四面体得到的. 如果被截正方体的棱长是50cm,那么石凳的体积是多少?
解:如图示,由题意知正方体的棱长为0.5m,则有
V正方体ABCD ABCD
1 (m3). 8
D' A'
棱柱、棱锥、棱台的表面积与体积
=
1 2
na h'
探究新知 LOGO
③棱台的表面积 棱台的表面积 = 侧面积+底面积.
h'
棱台
1.正棱台的上底面的周长为c',下底面的周长为c,斜高为h',
正棱台的侧面积是
1 S正棱台侧 = 2
c + c'
h'
例题讲解 LOGO
例1 如图,四面体P-ABC各棱长均为a,求它的表面积.
解:∵∆PBC是正三角形,其边长为a,
探究新知 LOGO
1. 多面体的展开图和表面积
问题1展在开初图中已 面经积学与过其正表方面体积和有长什方么体关的系表?面积,你知道正方体和长方体的展 开图的样子吗?
几何体表面积 展开图
平面图形面积
空间问题
平面问题
转化思想
探究新知 LOGO
多面体的表面积就是围成多面体各个面的面积的和.
也就是说求多面体的表面积关 键在于知道展开图是怎么样的!
(429年~500年)
探究新知 LOGO
探究棱锥与同底等高的棱柱体积之间的关系:
A
C
B
A
C
B
如果一个棱柱和一个棱锥的底面积相等,高也相等,那么,棱柱的体积 是棱锥的体积的3倍.
探究新知 LOGO
②棱锥的体积公式 一般地,如果棱锥的底面面积为S,高为h,那么这个棱锥的体积
棱锥的高是指从顶点向底面作垂线, 顶点与垂足之间的距离.
注意:三棱锥的顶点和底面可以根据需要变换,四面体的每一个面都可以作为底面,可以 求点到面的距离. ——等体积法
探究新知 ③棱台的体积公式
LOGO
由于棱台是由棱锥截成的,因此可以利用两个棱锥的
棱柱、棱锥、棱台的表面积和体积-高中数学必修第二册课件
∴VA1-ABC=13S△ABC·h=13Sh,
课 堂 小
学
结
探 新
VC-A1B1C1=13S△A1B1C1·h=43Sh.
·
提 素
知
养
合 作
又 V 台=13h(S+4S+2S)=73Sh,
课
探 究
∴VB-A1B1C=V 台-VA1-ABC-VC-A1B1C1
时 分 层
释 疑 难
=73Sh-S3h-43Sh=23Sh,
究
分
层
释 的表面积有关问题的关键.
作
疑
业
难
返 首 页
·
32
·
情
课
境
堂
导 学
2.计算棱柱、棱锥、棱台的体积,关键是根据条件找出相应的
小 结
·
探
提
新 底面面积和高,要充分运用多面体的有关截面,将空间问题转化为平 素
知
养
面问题.
合
作
课
探 究
3.在几何体的体积计算中,注意体会“分割思想”、“补体思
时 分
层
释 想”及“等价转化思想”.
作
疑
业
难
返 首 页
·
33
·
情
课
境
堂
导
小
学
1.如图所示,正方体 ABCD-A1B1C1D1 的棱长为 1,则三棱锥 结
·
探
提
新 知
D1-ACD 的体积是(
)
素 养
合 作 探
A.16
究
B.13
课 时 分
层
释 疑 难
C.12
D.1
作 业
返 首 页
2020-2021学年新教材人教A版必修第二册 8.3.1 棱柱、棱锥、棱台的表面积和体积
则
a2+a2+l 2=9,
2a 2+4al=144,
所以 la==74,,或
a=6, l=3.
所以S侧=4×4×7=112(cm2)或S侧=4×6×3=72(cm2).
答案:112或72
【补偿训练】 1.现有一个底面是菱形的直四棱柱,它的体对角线长为9和15,高是5,求该
直四棱柱的侧面积.
2.若正方体的棱长为 2 ,则以该正方体各个面的中心为顶点的凸多面体的表 面积为 ( )
【定向训练】
1.正三棱锥的底面边长为a,高为 6 a,则此棱锥的侧面积等于 ( )
6
A. 3 a2 4
B. 3 a2 2
C. 3 3 a2 4
D. 3 3 a2 2
2.一个正四棱柱的体对角线的长是9 cm,全面积等于144 cm2,则这个棱柱的侧面
积为________ cm2.
【解析】设底面边长,侧棱长分别为a cm,l cm,
【知识延拓】 如图,三棱台ABC -A1B1C1中,AB∶A1B1=1∶2,求三棱锥A1 -ABC,三棱锥B -
A1B1C,三棱锥C -A1B1C1的体积之比.
【思路探究】
【规律方法】三棱柱、三棱台可以分割成三个三棱锥,分割后可求锥体的体积 和柱体或台体的体积关系,割补法在立体几何中是一种重要的方法.
【类题通法】 棱锥的表面积求法 (1)要求锥体的侧面积及表面积,要利用已知条件寻求公式中所需的条件,一般 用锥体的高、斜高、底面边心距等量组成的直角三角形求解相应的量. (2)空间几何体的表面积运算,一般是转化为平面几何图形的运算,往往通过解 三角形来完成. 提醒:(1)多面体的侧面积是各个侧面的面积之和. (2)组合体的表面积应注意重合部分的处理.
8.3.1棱柱、棱锥、棱台的表面积和体积-导学案【新教材】
8.3.1棱柱、棱锥、棱台的表面积和体积一、知识梳理1. 棱柱、棱锥、棱台的表面积:多面体的表面积为____________.2. 棱柱、棱锥、棱台的体积:⑴=_____V 棱柱,⑵=_____V 棱锥,⑶=_____V 棱台.二、重点题型知识点一 : 棱柱、棱锥、棱台的表面积1.已知正六棱柱的高为6,底面边长为4,则它的表面积为( )A .48(3+3)B .48(3+23)C .24(6+2)D .1442.已知四棱台的上、下底面分别是边长为4和8的正方形,侧面是腰长为8的等腰梯形,则该四棱台的表面积为________.3.如图,已知正三棱锥S -ABC 的侧面积是底面积的2倍,正三棱锥的高SO =3,求此正三棱锥的表面积.知识点二 : 棱柱、棱锥、棱台的体积4.正三棱锥的底面周长为6,侧面都是直角三角形,则此棱锥的体积为( ) A .423 B . 2 C .223 D .235.设正六棱锥(底面为正六边形,顶点在底面的正投影为底面中心)的底面边长为1,侧棱长为5,那么它的体积为( )A .6 3B . 3C .2 3D .26.正四棱台两底面边长分别为20 cm 和10 cm ,侧面面积为780 cm 2,求其体积.三、巩固练习1.如图,ABC -A ′B ′C ′是体积为1的棱柱,则四棱锥C -AA ′B ′B 的体积是( )A .13B .12C .23D .342.棱锥的一个平行于底面的截面把棱锥的高分成1∶2(从顶点到截面与从截面到底面)两部分,那么这个截面把棱锥的侧面分成两部分的面积之比等于( )A .1∶9B .1∶8C .1∶4D .1∶3 3.正方体的棱长为2,以其所有面的中心为顶点的多面体的体积为( ) A .3π B .43 C .32πD .14.一个封闭的正三棱柱容器,高为3,内装水若干(如图1,底面处于水平状态).将容器放倒(如图2,一个侧面处于水平状态),这时水面所在的平面与各棱交点E ,F ,F 1,E 1分别为所在棱的中点,则图1中水面的高度为( )A .3B .2C .332D .945.若正四棱锥的底面边长为2 2 cm ,体积为8 cm 3,则它的侧面面积为________. 6.(一题两空)已知棱长为1,各面均为等边三角形的四面体,则它的表面积是________,体积是________.7.已知正四棱锥(底面为正方形,顶点在底面的正投影为正方形的中心)底面正方形的边长为4 cm ,高与斜高夹角为30°,则斜高为________;侧面积为________;全面积为________. 8.如图,在棱长为a 的正方体ABCD -A 1B 1C 1D 1中,则点A 到平面A 1BD 的距离d =________.8.3.1棱柱、棱锥、棱台的表面积和体积 答案一、知识梳理1.各个面的面积的和。
