哈工大结构动力学例题第三讲
哈工大建筑力学第3章(第2 3节) 力偶 力偶矩(2学时)

第三章力系简化的基础知识林国昌§3-2 力对点的矩A o o4力对物体具有转动效果,转动效果与三个因素有关:(1)力F 的大小;(2)转动中心O 到力F 作用线的距离d ;(3)力F 使扳手转动的方向。
注意:距离d 是转动中心O 到力F 作用线的垂直距离。
5力对点的矩:力对点的矩是力使物体绕点转动效果的度量,它是一个代数量,其绝对值等于力的大小与力臂之积。
正负规定:力使物体绕矩心逆时针转动时取正号,反之取负号。
符号表示:)(F M O Fd=±力矩的单位:牛顿•米(N •m)1.在门位置上施力,门很容易转动2.从门位置依序至位置施力,转动越不易ABC转轴OO 'OO’C B A 3-2 力对点的矩转动效果与三个因素有关:(1)力F 的大小;(2)转动中心O 到力F 作用线的距离d ;(3)力F 使扳手转动的方向。
7M O (F ) = ±2ΔOAB 面积=±Fd力对点的矩还可以用矩心为顶点,以力矢量为底边所构成的三角形的面积的2倍来表示,即:三角形ΔOAB 底边:力矢量F 三角形ΔOAB 的高:力臂d 力矩的单位:牛顿•米(N •m)注意:距离d 是转动中心O 到力F 作用线的垂直距离。
§3-3 力偶· 力偶矩林国昌103-3 力偶· 力偶矩一、力偶(F ,F ′)FF ′力偶实例由物理学可知:作用在物体上同一点的两个力,可以合成为作用在该点的合力。
合力:是作用在同一点上的各力的矢量和。
13a)力偶没有合力;b)力偶不能与一个力等效,也不能用一个力来平衡;c)力偶只能与力偶等效,也只能与力偶平衡。
力偶的性质1:力偶与力同属于机械作用的范畴,但又不同于力。
力与力偶分别是力学中的两个基本参量!3-3-1力偶•力偶的第一个性质143-3-1力偶•力偶的第二个性质力对物体具有转动效果,力使物体绕点转动的效果用力对点的矩来度量。
力偶对物体也有转动效果,力偶使物体转动的效果用力偶矩来度量。
结构动力学习题解答

(4)
将(4)式代入方程(3)可以求得:
A= h
(ω
2
n
−ω
2 2
)
= + 4n ω 2 nω
2 2
6F
;
L 6 K − mω
(
2 2
)
+ 9C ω
2
2
α = arctg
ω n −ω
2
2
= arctg
3Cω 6 K − mω 2
;
(2) 求 f (t ) = δ (t ) 的解; 将 f (t ) = δ (t ) 代入方程(1)得
∑ M ,得到系统的运动微分方程;
(3) 求解该方程所对应的特征方程的特征根,得到该系统的固有频率。 3、 拉格朗日方程法: 适用范围:所有的单自由度系统的振动。 解题步骤: (1)设系统的广义坐标为 θ ,写出系统对于坐标 θ 的动能 T 和势能 U 的 表 达 式 ; 进一步写求出拉格朗日函数的表达式:L=T-U ; (2)由格朗日方程
U= r 2 1 1 1 1⎛ K A ϕ A 2 + K B ϕ B 2 = K Aϕ A 2 + K B ϕ B 2 = ⎜ K A + K B A 2 2 2 2 2⎜ rB ⎝
(
)
⎞ 2 ⎟ϕ ; ⎟ A ⎠
系统的机械能为
T +U = r 2 1 1⎛ ̇ A2 + ⎜ K A + K B A (m A + m B )rA 2ϕ 4 2⎜ rB 2 ⎝
ωn =
=
1 rA
;
1.8 已知图1-37所示振动系统中,匀质杆长为 L,质量为 m,两弹簧刚度皆为 K,阻尼系
̇ = 0时 数为 C,求当初始条件 θ 0 = θ 0
动力学I第三章部分(1)习题解答
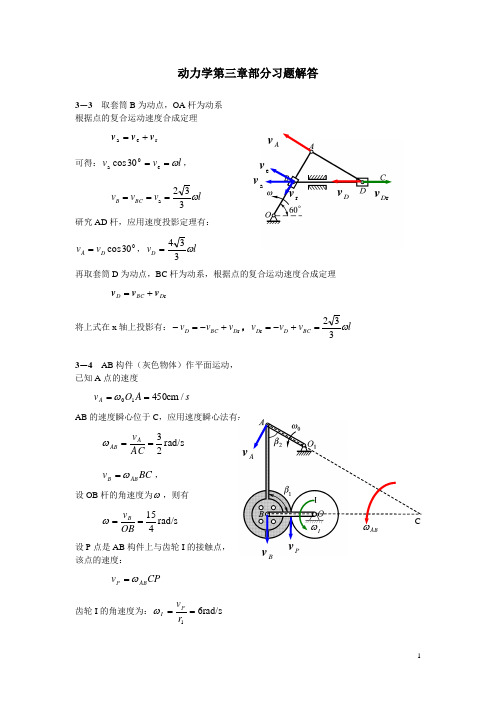
动力学第三章部分习题解答3-3 取套筒B 为动点,OA 杆为动系 根据点的复合运动速度合成定理r e a v v v +=可得:l v v ω==e 0a 30cos ,l v v v BC B ω332a === 研究AD 杆,应用速度投影定理有:030cos D A v v =,l v D ω334=再取套筒D 为动点,BC 杆为动系,根据点的复合运动速度合成定理r D BC D v v v +=将上式在x 轴上投影有:r D BC D v v v +-=-,l v v v BC D D ω332r =+-=3-4 AB 构件(灰色物体)作平面运动, 已知A 点的速度s A O v A /0cm 4510==ωAB 的速度瞬心位于C ,应用速度瞬心法有:rad/s 23==AC v A AB ω BC v AB B ω=,设OB 杆的角速度为ω,则有rad/s 415==OB v B ω 设P 点是AB 构件上与齿轮I 的接触点, 该点的速度:CP v AB P ω=齿轮I 的角速度为:rad/s 61==r v PI ω a v e vr vA vDv rD v A vB P v CAB ωI ω3-6 AB 杆作平面运动,取A 为基点 根据基点法公式有:BA A B v v v +=将上式在AB 连线上投影,可得0,01==B O B v ω因此,041ωω==AB v A AB因为B 点作圆周运动,此时速度为零,因此只有切向加速度(方向如图)。
根据加速度基点法公式n t BA BAA B aaa a ++=将上式在AB 连线上投影,可得n060cos BA A B a a a +=-,r a B 205.2ω-=201231ωα-==B O a B B O (瞬时针)3-7 齿轮II 作平面运动,取A 为基点有nt BA BA A B a a a a ++= n t 1BA BA a a a a ++=将上式在x 投影有:n 1cos BA a a a -=-β由此求得:212n 2cos 2r a a r a BAII βω+==再将基点法公式在y 轴上投影有:2t2sin r a a II BA αβ==,由此求得22sin r a II βα=再研究齿轮II 上的圆心,取A 为基点n t n t2222A O AO A O O aaa aa++=+将上式在y 轴上投影有2sin 2t t 22βαa r a a II AO O ===, B vBAv A vAa Ba t BA an BA atBA anBA axyt2A Oa n 2AO a xyn 2O a t 2Oa由此解得:)(2sin 2121t 221r r a r r a OO O +=+=βα再将基点法公式在x 轴上投影有:n1n22A O O a a a -=- 由此解得:2cos 1n2a a a O -=β,又因为221n 212)(O O O r r a ω+= 由此可得:)(2cos 21121r r a a O O +-±=βω3-9 卷筒作平面运动,C 为速度瞬心, 其上D 点的速度为v ,卷筒的角速度为r R vDC v -==ω 角加速度为rR ar R v -=-==&&ωα 卷筒O 点的速度为:rR vRR v O -==ω O 点作直线运动,其加速度为 rR aRr R R v v a O O -=-==&&研究卷筒,取O 为基点,求B 点的加速度。
结构动力学习题.ppt
22
1
2
5.5556
EI ma 3
2
1
2
EI 5.5556 ma3
2.357
EI ma3
1
A(1) 2
A(1) 1
1
12
11m1
12m2
1 11m1 12m2
1.15321 0.306 0.5
2
A(2) 2
A(2) 1
1
22
m 0
t1
F t1 sin (t )d F t1 sin (t )d
m 0
mt1 0
F
m
1
cos(t
) t1 0
F
mt1
1
cos(t
)
1
2
sin (t
)
t1 0
F
m 2
(cos (t
t1 )
cos t
1 2
3a 16
23a3 192 EI
12
21
1 EI
1 2
2a
a 2
1 2
3a 16
3a3 64 EI
结构动力学习题
1 11m1 22m2
11m1 22m2
2
4
11 22
2 12
0.012 0.01072 0.01465m
结构动力学习题
14-8 求图示结构在阻尼比为=0.05时的自振频率和周期。 并求当初始位移为10mm,初始速度为0.1m/s时的振幅值 和 t=1s时的位移值。
结构动力学习题解答

Ai ), Ai +1
2πζ 1−ζ 2
1
进一步推导有
δ =
,
结构动力学习题解答
因为 ζ 较小, 所以有
ζ =
δ 。 2π
方法二:共振法求单自由度系统的阻尼比。 (1)通过实验,绘出系统的幅频曲线, 如下图:
单自由度系统的幅频曲线 (2)分析以上幅频曲线图,得到:
β 1, 2 = β max / 2 = 2ζ / 4 ;
Wc = 0 、
W d = − πω
c
A2 、
W f = −π F0 sin α ;
(2) 由机械能守恒定理得,弹性力、阻尼力和激振力在一个周期内所作功为零, 即: 于是 进一步得:
Wc + Wd + W f = 0 ; π F0 sin α - πω c A 2 = 0
A = F0 sin α cω ;
x = Ae − n t sin (ω d t + ϕ ) ;
将其代入方程(6)可以求得:
A= h ;ϕ = 0 ; mω d h e − n t sin (ω d t ) mω d
1 1 J Aω A 2 + J B ω B 2 2 2
C
T=
2⎞ 2⎞ ⎛ 1⎛ ⎜ m ArA ⎟ω A2 + 1 ⎜ mB rB ⎟ω B 2 = 1 (m A + mB )rA 2ω A 2 ; ⎟ ⎟ 2⎜ 2⎜ 4 ⎝ 2 ⎠ ⎝ 2 ⎠
A B D
5
结构动力学习题解答
图 1-36 系统的势能为:
∑ M ,得到系统的运动微分方程;
(3) 求解该方程所对应的特征方程的特征根,得到该系统的固有频率。 3、 拉格朗日方程法: 适用范围:所有的单自由度系统的振动。 解题步骤: (1)设系统的广义坐标为 θ ,写出系统对于坐标 θ 的动能 T 和势能 U 的 表 达 式 ; 进一步写求出拉格朗日函数的表达式:L=T-U ; (2)由格朗日方程
第3章 习题解答 哈工大习题册
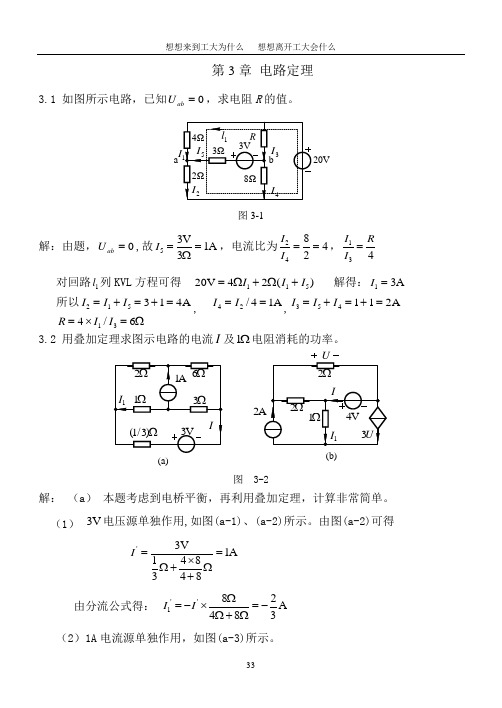
第3章 电路定理3.1 如图所示电路,已知0=ab U ,求电阻R 的值。
a图3-1解:由题,0=ab U ,故53V1A 3I ==Ω,电流比为24842I I ==,134I R I =对回路1l 列KVL 方程可得 11520V 42()I I I =Ω+Ω+ 解得:13AI =所以215314A I I I =+=+=, 42/41A I I ==,354112A I I I =+=+=134/6R I I =⨯=Ω3.2 用叠加定理求图示电路的电流I 及1Ω电阻消耗的功率。
(a)(b)2图 3-2解: (a ) 本题考虑到电桥平衡,再利用叠加定理,计算非常简单。
(1) 3V 电压源单独作用,如图(a-1)、(a-2)所示。
由图(a-2)可得'3V1A 148348I ==⨯Ω+Ω+由分流公式得: ''182A 483I I Ω=-⨯=-Ω+Ω(2)1A 电流源单独作用,如图(a-3)所示。
考虑到电桥平衡,0I ''=,133(1A)A 134I ''=-⨯=-+ (3)叠加:1A I I I '''=+=,11117/12A I I I '''=+=-2111 2.007WP I Ω=⨯=(a-1)(a-2)(a-3)(b )(1)4V 电压源单独作用,如图(b-1)所示。
24V 2V 22U Ω'=⨯=Ω+Ω,136A I U ''=-=-,125A I I I '''=+=- (2)2A 电流源单独作用,如图(b-2)所示。
'2I '(b-1)(b-2)222A 2V 22U Ω⨯Ω''=⨯=Ω+Ω,22/21A I U ''''== 对节点②列KCL 方程得1234A I U ''''=-=-对节点③列KCL 方程得235A I I U ''''''=-=- (3) 叠加 '"1116A 4A=10A I I I =+=---'"5A 5A=10A I I I =+=---2111100W P I Ω=⨯Ω=注释:不能用各独立源单独作用时电阻消耗的功率之和来计算电阻在电路中消耗的功率。
【哈工大 结构动力学】SD 第10章 多自由度体系2020
11
以上分析方法就是代数方程中的特征值分析,自振频率相应 于特征值,而振型即是特征向量。
得到体系的N 个自振频率和振型后,可以把振型和自振频率
分别写成矩阵的形式,
1 2 N
1 0 0
0
2
0
或
1,2,3
T
n
jqj(t)
j
2.0jjqj(t )
j
2 j
qj(t
)
T j
M
Mj
I
ug(t )
振型分解法仅需知道各振型阻尼比 ξ,不需要知道阻尼矩阵[C]
定义振型参与系数γj
j
jT M I
Mj
jT M I jT M j
基本性质
[] 1
两边同时除以振型参与系数γj ,得到:(j=1,2,…N)
得到三个根 :
B1 0.3515, B2 1.6066, B3 3.5420
利用关系式
Bn n2 600
可得结构的三个自振频率:
12 210.88
1 14.522
22 963.96 2 31.048 (rad / s)
32 2125.20
3 46.100
19
算例10-1
求振型 : (K n 2 M ) n 0
7
将位移向量{u}和加速度向量{ü}代入无阻尼自由振动方程:
u 2 sin( t ) u s in ( t )
M u K u 0
( 2 M K ) sin( t ) 0
因为sin(ωt+θ)为任意的,可以消去,因此,
(K 2 M ) 0
上式是关于{φ}的N阶齐次线性方程组,表征了振型和自振
结构动力学习题解答
由
d (T + U ) = 0 得系统运动微分方程 dt
1 (m 2 ⎛ ̇̇ A + ⎜ K + m B )r A 2 ϕ ⎜ ⎝ + K
A
A
B
rA 2 ⎞ ⎟ϕ rB 2 ⎟ ⎠
A
= 0;
因此系统的固有频率为:
⎛ r 2 2⎜ K A + K B A 2 ⎜ rB ⎝ (m A + m B )rA 2 ⎞ ⎟ ⎟ ⎠ ⎛ r 2 2⎜ K A + K B A 2 ⎜ rB ⎝ (m A + m B ) ⎞ ⎟ ⎟ ⎠
̇̇ + 3C θ ̇ + 6 K θ = 6 F sin ω t θ m m mL
(2)
6
结构动力学习题解答
令 2n =
3C 6K 6F ;ω n2 = ;h = ; m m mL
得
̇̇ + 2nθ ̇ + ω 2θ = h sin ω t θ n
(3)
设方程(3)的稳态解为
x = A sin(ω t − α )
̇̇ = hδ ( t ) ; θ 0
然后积分求初始速度
̇̇ d t = θ̇0 = θ 0
0+ 0+ 0+
∫
0
∫ hδ ( t ) d t = h ∫ δ ( t ) d t = h
0 0 0+
;
再积分求初位移
̇̇ d t == h )d t = 0 ; θ0 = θ 0
0+
∫
0
∫
0
̇̇ 、 θ̇ 和 θ 的瞬态响应 这样方程(6)的解就是系统对于初始条件 θ 0 0 0
哈工大结构力学PPT课件(2024版)
2021
9
七、图示桁架C杆的内力是 F
c
a
F
a
a
a aa
2021
10
八、图示结构A端的弯矩(以下边受拉为正) MAC为:
A: -Fl B: Fl C: -2Fl D: 2Fl
F
Fl
Fl
A
C
l
l
2021
(D)
11
九、图示结构中,N F E _ 4F_ , N F D _ 0_ .
A B
F CE
习题讨论
2021
1
一、对图示体系进行几何组成分析。 几无 何多 不余 变约 体束 系的
2021
2
几 何 可 变 体 系
2021
3
二、图示结构跨中截面的弯矩 (下侧受拉为正)是:
A: ql2 8cos, B: ql2 8cos
C: ql2 8cos2 , D: ql2 8cos2
q
B
A
C
l/2
m
m
(A)
(B)
2021(C)
(D)6
五、图示结构AB杆A端的剪力FQAB为 -M/a
。
F/2 F
F/2 A
a/4
a/4
a/4 M
a/4 B
a
2021
7
六、改正图示结构的M图。
m/2
m/4
m
m/2 2a
a
a
2021
8
Fa
F
0.5 Pa
1.5 Fa
1.5 FPa
1.5a
2.5a
1.5a
2F
1a 1a
4F
10.5F
2F b a
结构动力学-第一章
2019/9/16
38
2019/9/16
39
2019/9/16
40
2019/9/16
41
2019/9/16
42
2019/9/16
43
三. 自由度的确定
广义坐标法:广义坐标个数即为自由度个数; 有限元法:独立结点位移数即为自由度数; 集中质量法:独立质量位移数即为自由度数;
11
l3 3EI
柔度系数
my(t) 3 EI l3y( Nhomakorabea)
P(t)
2019/9/16
柔度法步骤: 1.在质量上沿位移正向加惯性力; 2.求外力和惯性力引起的位移; 3.令该位移等于体系位移。
49
二、刚度法
P(t)
m
1
my(t)
y(t)
l EI
y
k11
k11 y(t )
k11y(t) P(t) my(t)
变分法(Hamilton原理)以及lagrange等。
我们这节课主要介绍达朗泊尔原理建立的动力学微分方程,用能量法建立 微分方程的方法在以后的章节中介绍。
达朗泊尔原理
质点系运动的任意瞬时,除了实际作用于每个质点的主动力和约束反力外, 在加上假象的惯性力,则在该瞬时质点系处于假象的平衡状态。
m P(t) my(t)
结构动力学
2019/9/16
1/
思考问题
1,结构动力学和静力学的区别和联系在哪里?
运动方程为:
m y(t) c y(t) k y(t) p(t)
静力学方程为:
k y p
201所9/9/以16 两者的区别在于:动力学问题多了惯性力项以及由运动产生的阻尼力。 2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
§6.2.5轴向振型的正交性
1. 对照轴向变形,给出剪切、扭转运动方程、振 型、频率、正交性表达式。 2. 不同荷载工况讨论:集中力、分布力、力偶、 分布力偶、支座扰动。 3. 求解不同支座形式自由振动。 4. 坐标方向改变会是方程发生怎样的改变? 5. 无质量杆件在梁上会发生怎样的情况? 6. 梁上有质量块怎么办?分别来做,然后相加, 行吗?作用在质点上的荷载P如何分配?
现在,应该很清楚,对于实际结构求解具有无限自由度分布质 量体系固有频率和振型的经典方法不可行。这些问题可以通过 把实际结构离散化为有限自由度体系来进行分析,我们将在下 一章讨论这个问题。
§6.2.2 梁的弯曲-考虑轴力的影响
§6.2.3 梁的弯曲-振型的正交性
§6.2.4 轴向变形的自由振动
例题 E6-1 简支梁 研究图E6-1a所示的等截面简支梁,该梁的四 个边界条件为
(0) 0 ( L) 0
M (0) EI '' (0) 0 M ( L) EI '' ( L) 0 ( a) (b)
图E6-1 简支梁的振动分析 (a)简支梁的基本特性; (b)前三个振型及其频率
例题 E6-2 悬臂梁 在前一例题中,简支梁的自由振动的分析 并无困难,因为简支梁的振型只含有形状函数表达式(6-30)中 的一项。为了提供更有代表性的例子,用以说明需要全部四项 分析方法,考虑图E6-2a所示的悬臂梁。
图E6-2 悬臂梁的振动分析 ( a )悬臂梁的特性;( b ) 前三个振型和相应的频率; (c)图解法求解频率方程
(6-18)
(6-24)
E6-2
例题 E6-4 两个构件的刚架 为了说明多构件体系自由振动分析 的方法,考虑图E6-4a所示的两个构件的刚架。正如图中所示, 两个构件都是等截面的;然而,它们可以具有不同的性质。
图E6-4 简单两杆刚架 (a)刚架的构造;(b)作用在梁上的力
(6-21)
(6-24)
例题 E6-3 在自由端有刚性质量的悬臂梁 在此例中,利用了与例E6-2相同的等截面 悬臂梁,不同的是在自由端固接一个转动惯量为j1的刚性集中质量m1,如图E6-3a所 示。
图E6-3 在端点有集中质量的梁 (a)梁的性质; (b) 作用在端点质量上的力
E6-3
E6-2 E6-3a
E6-3b
