PID and Hinf control HDD
Dynamics and PID control

Tuning of your PID controller I. “Trial & error” approach (online)
(a) P-part: Increase controller gain (Kc) until the process starts oscillating or the input saturates (b) Decrease the gain (~ factor 2) (c) I-part: Reduce the integral time (τI) until the process starts oscillating (d) Increase a bit (~ factor 2) (e) Possible D-part: Increase τD and see if there is any improvement
• Oct. 2009: /wiki/Controller_(control_theory)
– Controller gain (Kc) should be such that controller counteracts changes in output – Need negative sign around the loop -> With negative feedback: Sign of Controller gain (Kc) is same as sign of process gain (k) – Alternatively, always use Kc positive and select between • ”Reverse acting” when k is positive (standard case) – because MV (u) should go down when CV (y) goes up • ”Direct acting” when k is negative • WARNING: Some reverse these definitions (e.g. wikipedia)
最新PID控制及其应用.pdf
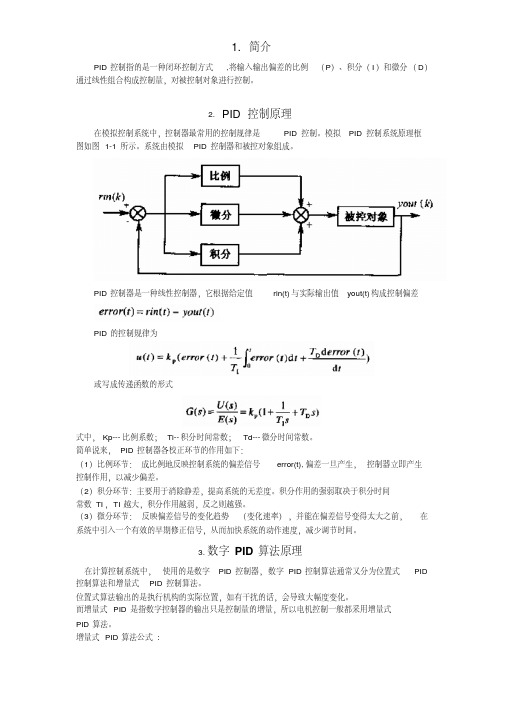
1. 简介PID控制指的是一种闭环控制方式,将输入输出偏差的比例(P)、积分(I)和微分(D)通过线性组合构成控制量,对被控制对象进行控制。
2.PID控制原理在模拟控制系统中,控制器最常用的控制规律是PID控制。
模拟PID控制系统原理框图如图1-1所示。
系统由模拟PID控制器和被控对象组成。
PID控制器是一种线性控制器,它根据给定值rin(t)与实际输出值yout(t)构成控制偏差PID的控制规律为或写成传递函数的形式式中,Kp---比例系数;Ti--积分时间常数;Td---微分时间常数。
简单说来,PID控制器各校正环节的作用如下:(1)比例环节:成比例地反映控制系统的偏差信号error(t),偏差一旦产生,控制器立即产生控制作用,以减少偏差。
(2)积分环节:主要用于消除静差,提高系统的无差度。
积分作用的强弱取决于积分时间常数TI,TI越大,积分作用越弱,反之则越强。
(3)微分环节:反映偏差信号的变化趋势(变化速率),并能在偏差信号变得太大之前,在系统中引入一个有效的早期修正信号,从而加快系统的动作速度,减少调节时间。
3.数字PID算法原理在计算控制系统中,使用的是数字PID控制器,数字PID控制算法通常又分为位置式PID 控制算法和增量式PID控制算法。
位置式算法输出的是执行机构的实际位置,如有干扰的话,会导致大幅度变化。
而增量式PID是指数字控制器的输出只是控制量的增量,所以电机控制一般都采用增量式PID算法。
增量式PID算法公式:----△u( k ) = K p△e(k)+Kie(k)+Kd[△e(k)-△e(k-1)]----△e(k) = e(k) – e(k-1)-----△e(k-1) = e(k-1) – e(k-2)-----e(k) = r(k) – c(k) (因在速度控制导通角上开始是从大变小,所以该公式须变成c(k)-r(k))参数说明:k--------------采样序号, k = 0, 1, 2----;r(t)-----------速度给定值;c(t)-----------速度实际输出值;△u( k )------第K次采样时刻的计算机输出增量值;e(k)----------第K次采样时刻输入的偏差值;e(k-1)--------第(k-1)次采样时刻输入的偏差值;K I-------------积分系数,K I = K P*T/T I;K D------------微分系数,K D = K P*T D/T;T--------------采样调期;Kp------------比例系数;T I-------------积分时间常数T D------------微分时间常数4.PID 控制参数整定方法PID 控制参数的自动整定分两步进行,第一步是初始确定PID 控制参数;第二步是在初定的PID 控制参数基础上,根据直线电机控制系统的响应过程和控制目标期望值,修正初定的PID 参数,直至电机系统的控制指标符合所需求为止.在数字控制系统中,采样周期T 是一个比较重要的因素,采样周期的选取,应与PID 参数的整定综合考虑,选取采样周期时,一般应考虑下列几个因素:(1)采样周期应远小于对象的扰动信号的周期。
对pid控制的认识

对pid控制的认识
PID控制是一种常见的自动控制算法,它可以对被控对象的输出进行调节,使其保持在设定值或者一定的范围之内。
PID控制算法由三个部分组成:比例控制、积分控制和微分控制。
比例控制是PID控制的基础,主要作用是根据误差的大小来控制输出量。
当偏差越大时,输出信号的变化也越大,从而加快了被控对象的响应速度。
但是,这种控制方式存在一个问题,就是当偏差较小时,输出信号的变化很小,可能会导致被控对象在设定值附近产生较大的振荡。
为了解决这个问题,引入积分控制。
积分控制是根据误差的历史累计值进行控制,当偏差累积较大时,输出信号的变化也会增加。
这种控制方式具有较好的稳定性,能够消除系统偏差和残留误差,但也会导致过度调节,从而引起系统的震荡。
将上述三个部分组合起来,就构成了完整的PID控制算法。
在实际应用中,需要对每个控制算法的参数进行调整,以达到最优的控制效果。
总之,PID控制算法是一种常见的自动控制算法,应用广泛,具有良好的稳定性和响应速度。
但是,在实际应用中需要深入了解控制对象的特点,进行合理的参数调整,才能达到最优的控制效果。
pid控制公式

pid控制公式标题:全面理解与应用PID控制器的公式摘要:PID控制器是工业自动化领域中最常用的控制器之一,它通过比较实际输出与期望输出之间的差异,并根据比例、积分和微分项来计算控制信号,以实现对系统的精确控制。
本文将深入探讨PID控制器的公式,包括比例、积分和微分项的含义、作用以及如何平衡它们以达到最佳控制效果。
此外,我们还将讨论一些常见的优化方法和实际应用案例,以帮助读者更好地理解和应用PID控制器的公式。
1. 引言- 介绍PID控制器的基本原理和应用领域- 强调PID控制器在工业自动化中的重要性和广泛应用2. PID控制器的公式概述- 解释PID控制器的三个基本项:比例项、积分项和微分项- 描述它们在控制过程中的作用和影响- 强调PID控制器的线性组合形式:控制信号= Kp * e + Ki * ∫e dt + Kd * de/dt3. 比例项(Proportional Term)- 定义比例项,并解释其作用和意义- 探讨比例增益Kp的选择标准和对控制系统的影响- 提供一些实际应用中常见的经验法则和调节方法4. 积分项(Integral Term)- 解释积分项的概念和功能- 讨论积分时间常数Ti的选择和影响- 引导读者如何解决积分饱和和积分过度响应的问题5. 微分项(Derivative Term)- 介绍微分项的作用和意义- 讨论微分时间常数Td的选择和影响- 强调微分项对系统稳定性和抗干扰能力的重要性6. PID控制器的参数调优- 介绍常见的PID参数整定方法,如经验法则、试验法等- 探讨自动整定算法和优化方法的原理和应用- 提供一些实际应用中常用的调参技巧和策略7. 实际应用案例- 提供一些实际控制系统中使用PID控制器的案例分析- 分析不同实际场景下的PID参数选择和调优策略- 讨论PID控制器在各个行业中的广泛应用和效果展示8. 结论- 总结文章的主要观点和要点- 强调PID控制器的公式对于实现稳定、准确和高效的控制具有重要性- 建议读者在实际应用中充分理解公式并结合优化方法进行合理调整结语:本文通过对PID控制器的公式进行深入探讨,帮助读者全面理解PID控制器的原理、作用及应用。
PID控制原理详解及实例说明

PID控制原理详解及实例说明PID控制是一种常用的控制算法,它能够在工业控制系统中实现对各种参数的精确控制。
PID分别代表比例(proportional)、积分(integral)和微分(derivative),这三个参数共同决定了控制系统的输出。
在本文中,我们将详细介绍PID控制的原理,并通过一个实例来说明PID控制的应用。
**PID控制原理**PID控制算法的基本原理是通过反馈来调节控制系统的输出值,使其与期望值尽可能接近。
PID控制器根据当前的误差值(e),积分项(i)和微分项(d)来计算控制输出(u)。
具体来说,控制输出可以表示为以下公式:\[ u(t)=K_p \cdote(t)+K_i\cdot\int{e(t)dt}+K_d\cdot\frac{de(t)}{dt} \]其中,\(K_p\)、\(K_i\)和\(K_d\)分别是比例增益、积分增益和微分增益。
比例项用于根据误差信号的大小来调整输出,积分项用于修正系统的静态误差,微分项用于预测误差的变化趋势。
通过调节这三个参数的数值,可以使PID控制器在不同的控制情况下获得最佳性能。
**实例说明**为了更好地理解PID控制的应用,我们以一个简单的温度控制系统为例进行说明。
假设我们需要设计一个PID控制器来维持一个恒定的温度值,控制系统的输入是一个加热元件的功率,输出是系统的温度。
首先,我们需要建立一个数学模型来描述系统的动态特性。
假设系统的温度动态可以由以下微分方程描述:\[ \tau \cdot \frac{dT(t)}{dt}+T(t)=K \cdot P(t) \]其中,\(T(t)\)代表系统的温度,\(P(t)\)代表加热元件的功率,\(\tau\)代表系统的时间常数,\(K\)代表系统的传递函数。
接下来,我们可以根据这个数学模型来设计PID控制器。
首先,我们需要对系统进行参数调试,确定合适的比例增益\(K_p\)、积分增益\(K_i\)和微分增益\(K_d\)。
pid控制实例

pid控制实例PID控制技术,即比例积分微分控制,是工业控制系统中最常用的控制方法之一。
它以一定的比例来反馈系统的输出,以及积分和微分时间来补偿系统的响应。
这些参数设定将直接影响系统的控制精度和稳定性。
本文重点讨论如何应用PID控制技术,以及如何设定PID 参数,以了解PID控制的工作原理。
PID控制技术是由三个参数构成的:比例系数(Kp)、积分系数(Ki)和微分系数(Kd)。
它们是PID控制器的重要组成部分,它们的取值决定了系统的响应性能。
比例系数Kp表示系统的灵敏度,它决定了输出变化的大小。
积分系数Ki是系统控制精度的决定因素,通过增大积分系数Ki可以减少系统积分误差。
微分系数Kd是系统控制稳定性的决定因素,通过增大微分系数Kd可以减少系统的微分震动。
PID控制具有良好的功能,可以满足工业控制系统的要求。
例如,它可以用于温度控制、速度控制、压力控制等,并拥有良好的适应性和可扩展性。
对于复杂的控制问题,PID控制可以很好地满足要求。
这里将介绍一个使用PID控制的示例,即温度控制。
首先,我们需要建立一个温度控制循环系统,包括一个可调节温度探头、一个温控器、一个PID控制器和被控制物。
然后,调节温度探头将反馈被控制对象的当前温度值,并将其发送给温控器和PID控制器;PID控制器计算出控制信号,并传递给温度控制器,从而实现温度的控制。
此外,调节PID控制参数也是温度控制的一部分。
根据系统的需要,调节PID参数可以提高控制精度,抑制抖动,提高系统稳定性。
比如,通过调节比例系数Kp,可以改变系统的控制精度;而通过调节Ki和Kd,可以减少积分误差和微分抖动,从而提高系统稳定性。
综上所述,PID控制是一种常用的控制方法,它可以满足工业控制系统的要求,并且具有很好的性能。
此外,它还可以提供良好的控制精度,抑制误差和抖动,从而使系统更加稳定可靠。
为了使PID控制技术发挥最大作用,应该正确设定PID参数。
PID概念
1.PID工程控制和数学物理方面PID(比例积分微分)英文全称为Proportion Integration Differentiation,它是一个数学物理术语。
目前工业自动化水平已成为衡量各行各业现代化水平的一个重要标志。
同时,控制理论的发展也经历了古典控制理论、现代控制理论和智能控制理论三个阶段。
智能控制的典型实例是模糊全自动洗衣机等。
自动控制系统可分为开环控制系统和闭环控制系统。
一个控制系统包括控制器、传感器、变送器、执行机构、输入输出接口。
控制器的输出经过输出接口、执行机构,加到被控系统上;控制系统的被控量,经过传感器,变送器,通过输入接口送到控制器。
不同的控制系统,其传感器、变送器、执行机构是不一样的。
比如压力控制系统要采用压力传感器。
电加热控制系统的传感器是温度传感器。
目前,PID控制及其控制器或智能PID控制器(仪表)已经很多,产品已在工程实际中得到了广泛的应用,有各种各样的PID控制器产品,各大公司均开发了具有PID参数自整定功能的智能调节器(intelligent regulator),其中PID控制器参数的自动调整是通过智能化调整或自校正、自适应算法来实现。
有利用PID控制实现的压力、温度、流量、液位控制器,能实现PID控制功能的可编程控制器(P LC),还有可实现PID控制的PC系统等等。
可编程控制器(PLC) 是利用其闭环控制模块来实现PID控制,而可编程控制器(PLC)可以直接与ControlNet相连,如Ro ckwell的PLC-5等。
还有可以实现PID控制功能的控制器,如Rockwell 的Logix 产品系列,它可以直接与ControlNet相连,利用网络来实现其远程控制功能。
1、开环控制系统开环控制系统(open-loop control system)是指被控对象的输出(被控制量)对控制器(controller)的输出没有影响。
在这种控制系统中,不依赖将被控量反送回来以形成任何闭环回路。
pid
PID——温控、变频 PID(Proportional, Integral and Derivative)是闭环控制中最常用的一种算法,在包括温控、水泵、张力、伺服阀、运控等行业得到了广泛的应用,但因为每个应用的对象特性都不一样,这就要求调试工程师允分了解PID的控制原理,只有这样我们才能把PID的应用好。
PID原理: PID 是由比例、微分、积分三个部分组成的,在实际应用中经常只使用其中的一项或者两项,如P、PI、PD、PID等。
从控制原理来说,当一个控制对象,我们希望控制的输出达到我们设定的值,我们通常会使用开环或者闭环控制,如果控制对象的响应很稳定不会受到其它环节的影响,我们可以选用开环控制。
反之如果被控对象受到设定值、负载或者源端的影响而产生波动,我们应该选用闭环控制。
下图是一个温控的原理图: PID执行周期(1/10秒) 〔范例〕比例控制(P):比例控制是最常用的控制手段之一,这也是最符合人的感观的一种控制,比方说我们控制一个加热器的恒温100度,当开始加热时,离目标温度相差比较远,这时我们通常会加大加热,使温度快速上升,当温度超过100度时,我们则关闭输出,通常我们会使用这样一个函数 e(t) = SP – y(t); u(t) = e(t)*P SP——设定值 e(t)——误差值 y(t)——反馈值 u(t)——输出值 P——比例系数滞后性不是很大的控制对象使用比例控制方式就可以满足控制要求,但很多被控对象中因为有滞后性。
比方说塑胶挤出机,如果设定温度是200度,当采用比例方式控制时,如果P选择比较大,则会出现当温度达到200度输出为0后,温度仍然会止不住的向上爬升,比方说升至230度,当温度超过200度太多后又开始回落,尽管这时输出开始出力加热,但温度仍然会向下跌落一定的温度才会止跌回升,比方说降至170度,最后整个系统会稳定在一定的范围内进行振荡。
如果这个振荡的幅度是允许的比方说家用电器的控制,那则可以选用比例控制,很多传统的家用空调和我们常会发现家用空调始终是间歇工作的,当开始制冷时我们通常会感到越来越冷,当空调停止时又会感到温度越来越高,它采用的则是比例控制比例值太小时的控制效果图:如果比例值太小,反馈值始终到不了设定值(静态误差)就达到了平衡(如果是加热的话就是说散热与P*e(t)加热达到了一个平衡)比例值太大时的控制效果图:如果比例值太大,则被控对象会出上图所示的振荡,当然振荡点不一定是在设定值,而会根据被控对象的不同或者P值的大小而在某个位置进行振荡。
pid控制实例
pid控制实例
PID控制是一种机械自动控制方式,它以某种信号(反馈信号)来反映出位置,并可以根据预设的参考值(设定值)来调整此位置。
在传统的机械控制中,反馈信号是检测位置的一种简单的方式,但PID控制的实现可以使得控制的精度更高。
一般来说,PID控制技术由“比例”(Kp)、“积分”(Ki)、“微分”(Kd)三个控制参数组成,每个参数分别调节系统的运动速度,偏移量和抗扰力等。
Kp调节系统的运动速度,Ki调节系统的偏移量,Kd 调节系统的抗扰力。
下面以一个机器人实例来说明PID控制的方法。
机器人的设备包括电机、编码器和电控板等。
为了保证机器人的稳定运行,需要进行PID控制。
首先,机器人的编码器检测机器人的位置,并将数据发送给电控板。
电控板会根据预设参考值,来计算出控制参数Kp、Ki和Kd。
然后,根据实际位置与参考值的差小,控制电机的转速,实现机器人的位置控制。
此外,PID控制算法可以根据系统变化情况而自动调节,而不需要人工干预。
这使得机器人的控制更加精确和智能化。
综上所述,PID控制技术是一种重要的机械自动控制技术,它可以实现系统控制的精度和智能化。
它是机械工程中,许多设备的重要控制方式,应用范围非常广泛,已经深受使用者的喜爱。
- 1 -。
PID控制详细介绍
C
c
u (n m) 阀门的开度极限 C
执行器进入深度饱和
34
4.3.3 积分饱和现象与抗积分饱和的措施 积分饱和现象
图4.2 加热器出口水温控制系统
35
4.3.3 积分饱和现象与抗积分饱和的措施
图4-2所示加热器水 温控制系统为消除残 差采用了 PI调节
调节阀选用气开式, 调节器为反作用方式。
23
4.3.2 比例积分的调节规律
u0 0
图4.9 PI 调节器对过程负荷变化的响应
负荷变化前(t<t0)被控系统稳 定,控制偏差为零,调节器输出保 持某恒定值。
24
4.3.2 比例积分的调节规律
图4.9 PI 调节器对过程负荷变化的响应
t=t0时刻,系统负荷发生阶跃变化 , P调节立即响应偏差变化,产生正的
输出:偏差的比例(P)、积分(I)和微分(D)的线性组 合
u(t
)
Kc
(e(t)
1 TI
t 0
e(t)dt
TD
de(t ) ) dt
式中 Kc —— 比例系数
TI —— 积分时间常数
TD —— 微分时间常数
4
4.l PID控制的特点 PID控制具有以下优点:
①原理简单,使用方便。 ②适应性强,可以广泛应用于化工、热工、
调节过程中的超调趋势随比例增益的增大和 积分时间的减小而增大,因此PI调节的比例 增益要设置得比纯P调节小,对积分时间的 设置也应有一定的限制。
29
4.3.2 比例积分的调节规律
PI调节在比例带不变的情况下,减小积分时间 TI,将使控制系统稳定性降低、振荡加剧、调 节过程加快、振荡频率升高。
图4.10 PI控制系统不同积分时间的响应过程
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Technische Universiteit Eindhoven, The Netherlands University of California, San Diego, CA, USA
Reduction of flow induced vibrations in hard disk drives by active control of dual-stage suspensions
A.P. Teerhuis & S.J.M. Cools
Reportnumber: DCT-2003/60
Supervisors: Dr. Ir. R.A. de Callafon (UCSD) Prof. Dr. Ir. M. Steinbuch (TUE)
Technische Universiteit Eindhoven Department of Mechanical Engineering Section Control Systems Technology, Power Transmissions P.O. Box 513 5600 MB, Eindhoven
The Netherlands Contents 1 Introduction 1
1.1 Design of a Hard Disk Drive ................... 1
1.2 Goal of this research ....................... 2 ............................. 1.3 Approach 3
Non-collocated control 6
2.1 Introduction ............................ 6 2.2 Model identification ....................... 7
2.3 Prediction error method ..................... 8
2.4 Experimentally found models .................. 9
2.5 Designing a non-collocated controller based on experimental data ................................ 9
2.5.1 Designing a suitable discrete Ha-controller ....... 10 .................... 2.6 Reducing controller order 14
3 Collocated controller design 20
............................ 3.1 Introduction 20
..................... 3.2 The experimental setup 21
3.2.1 Experiments on non-flying suspensions ......... 21
3.2.2 Experiments and model fitting for flying suspensions . 21 ...................... 3.3 Designing a controller 23
3.3.1 Designing a PD-controller ................ 23
3.3.2 Designing an Hz-controller ................ 25
..................... 3.4 Implementing controllers 26
....................... 3.4.1 PD-controller 26
....................... 3.4.2 Hz-controller 26
4 Conclusion 2 9 CONTENTS 2
A Design of an analog PID-controller 32
........... A.l Dynamic behaviour of the PID-controller
32
.................. A.2 Electronic design and analysis 34
...................... A.2.1 Electric circuit 34
..................... A.2.2 Network analysis 34
....... A.3 Tuning of the controller and the frequency range 36 Abstract
The trend in future generation Hard Disk Drives (HDD) is to contain more data and access this data faster. The latter is achieved by increasing the rotational speed of the disks. This, however, also increases the wind inside the HDD housing, generated by the rotating disks. In this report, we focus on two control strategies to decrease the effects of these wind disturbances (windage) on the data read-out of a HDD with a dual-stage suspension. The suspension is produced with two (coupled) piezo elements. Experimentally found models form the basis for the robust controllers. In the first part, non-collocated control is used to decrease windage ef- fects. The readlwrite head is used to detect small position errors and the controller will actuate both piezos of the suspension at the same time. This method will show a great decrease within the range where windage plays the most significant role. However, this method relies on discrete position errors, so the bandwith of this controller is limited. The second part discusses the collocated control for windage. In this case the two piezos, present on the suspension, will be decoupled and used for both actuation and sensing. A new experimental model has to be found
on which a new robust controller is designed and implemented. The general idea is to make the (mechanically weak) suspension behave stiffer. Also this method of control shows an improvement in the region where windage is active. Chapter - 1
Introduction
1.1 Design of a Hard Disk
Drive
In this report, new control strategies are proposed that deal with a specific type of disturbances which occur inside a hard disk drive. Before getting into details, a short introduction in the terminology and the principles of a hard disk drive is given.
Magnetic head Rigid arm with suspension
Figure 1.1: Basic features of an Hard Disk Drive The Hard Disk Drive (HDD) consist of a stack of disks on a rotating spindle. Each separate disk contains data on both sides. This data is posi- tioned on tracks. A magnetic element, hovering (or flying) over the surface
of the disk, reads out the data. When the disks are rotating, a thin layer of air is rotating with the disks. This boundary layer between the magnetic head and the disk (typically 5-15 nm) forms an air bearing on which the
