特色作图计算题
人教版小学五年级专项作图题

作图题1、画出下列轴对称图形的一条对称轴。
2、分别画出将向上平移3格、向右平移8格后得到的图形。
(6%)3、逆时针旋转90度后的图形。
(6%)A4、画出下面图形的轴对称图形。
10、计算下面每个图形的面积.1、平行四边形的底是3.5厘米,高是5厘米.2、三角形的底是10.2分米,高是5分米.3、梯形的上底是4.3厘米,下底是7.7厘米,高是5厘米.12.找出下列数中的合数,并把它们分解质因数。
202945539110211713.求下面各组数的最大公约数。
50和7578和26 6和1136和5414.求下面各组数的最小公倍数。
15和2035和42 8、24和3645、60和7515. 求42和70的最大公约数和最小公倍数.求66和165的最大公约数和最小公倍数.16、求13,39和91的最大公约数和最小公倍数.30,40和60的最小公倍数是它们的最大公约数17、求32,48和60的最大公约数和最小公倍数.18 、分解质因数.28,50 分解质因数.84,9219、在括号里填上适当的数.①11与()的积是合数②97与()的积是质数③23与()的积是偶数④17与()的积能被3整除⑤13与()的积能被5整除⑥29与()的积能被2、3整除⑦37与()的积能被3、5整除⑧41与()的积能被2、3、5整除20、分解质因数①180②507③108④5621、求出下列各数的最大公约数和最小公倍数。
22、24、20和36的最小公倍数是它们最大公约数的多少倍?22、把下面的分数化成最简分数.23、通分并比较分数的大小.24、把下面各组分数通分。
11 24和2372712和1315512、78和11163 5、910和11151512、423和74511112、356和272025、用分数表示下面每个算式的商(能约分的要约分,假分数要化成整数或带分数)。
2÷3=12÷30=15÷7=28÷54=42÷14=26、(1)分数化成小数(除不尽的保留两位小数)。
有关光的计算题和作图题

有关光的计算题和作图题一.光的反射。
请注意:入射角指的是入射光线与法线的夹角,反射角指的是反射光线与法线的夹角,它们都是要与法线发生关系,所以计算角度或者要求作光路图,一定要想办法先作法线。
(1)告诉入射角,求反射角,以及与镜面夹角的问题。
角。
如果入射角增大10,反射角也增大10。
反之亦然。
入射光线与镜面的夹角=900-入射角。
实际上就是求入射角的余角。
反射光线与镜面的夹角=900-反射角。
实际上就是求反射角的余角如果告诉了光线与镜面的夹角,求入射角或者反射角,其实也一样。
只要把握住互余和相200,那么反射角是多少度?方法:∵入射角与镜面夹角是200,∴入射角是900-200=700。
又由于反射角等于入射角,所以反射角也为700。
练习1:已知反射光线与镜面的夹角是500,那么入射角为练习2:已知入射角是300,那么,反射光线与镜面的夹角为练习3:已知入射光线跟平面镜的夹角是300,则它的反射光线与法线的夹角为★练习4:一束光射到平面镜上,当入射角增大100时,反射光线与入射光线垂直,则原来的入射角是(2)告诉入射光线和反射光线的夹角,如何作出平面镜的位置,如何求出各种角度思路:已经知道入射光线和反射光线,那么,作出它们的角平分线就是它们的法线。
(因为入射角=反射角)然后,通过入射点作法线的垂线,就是平面镜的位置。
例:已知入射光线和反射光线的夹角为1000,请问平面镜该如何放置?作出它的位置,并求出入射光线与镜面的夹角。
思路:①先作入射光线和反射光线的角平分线,角平分线就是他们的法线。
可以知道,入射角就等于1000的一半,即500②再通过入射点作法线的垂线,就是镜面的位置。
③入射光线与镜面的夹角,就是入射光线的余角。
∴它=900-600=300(3)绕入射点顺时针或者逆时针转动平面镜的这类题目例:一条光线垂直射向平面镜,若平面镜饶入射点转动,求此时入射光线与反射光线的夹角。
分析:转动前,入射光线,法线和反射光线重合在一起。
作图和计算练习试卷

作图和计算练习试卷班级 姓名一、作图:1、如图10所示,重为10牛的A 物体放在水平地面上,用力的图示法画出物体对地面的压力。
2、 如图8所示,重为6牛的物体静止在水平面上,用力的图示法在图中画出它对水平面的压力。
3、 如图9所示,重为2牛的小球漂浮在水面上,用力的图示法画出小球受到的浮力。
4、如图10所示,甲、乙两个完全相同的容器,分别装有水和盐水,画出密度计放入这两种液体中静止时大致的位置。
5、如图11所示,两端开口的玻璃管底部用橡皮膜封住,装有适量的水,将其分别放入水、盐水和酒精中,当管内外液面恰好相平时,的画出橡皮膜大致的形状。
6、小球重为16牛,对斜面的压力为8牛,请用力的图示法画出斜面受到小球的压力。
7、、画出双通管下端薄膜的大致形状。
二、浮力计算: 1.把体积为3×10 4米3的小球全部浸入盛有水的容器内,求小球受到的浮力F 浮。
2.漂浮在水面的物体排开水的体积为5×10-3米3,求物体的重力。
图10 图11 图8图9第17题图 第18题图3、质量为7.8千克的实心铁块浸没在水中,求:(1)铁块排开水的体积;(2)铁块所受的浮力。
(铁的密度为7.8×103千克/米3)4、一物体浸没在水中,排开水的体积为2×10-3米3。
求:此物体受到的浮力F浮。
5、小海同学游泳时排开水的体积为0.05米3,求他受到的浮力。
三、压力与压强:1、一辆坦克的质量为3×104千克,每条履带的着地面积5米2,求它对水平地面的压力和压强各为多大?3、、一个底面积为0.01米2的轻质容器内装有2.5×10-3米3的酒精,酒精深度为0.3米。
(已知ρ酒=0.8×103千克 / 米3)求:(1)酒精的质量m。
(2)酒精对容器底部的压力F、压强P。
3、一个质量为54克的实心小球,放入装满水的溢水杯中,溢出水的质量为20克。
求:(1)实心球受到的浮力。
作图专项练习题

作图专项练习题本文将为读者提供一些练习题,旨在帮助提高作图技巧和解题能力。
下面列出了五个涉及不同图形和几何问题的作图练习题。
1. 作图题一:画一个半径为5厘米的圆。
解答:首先,在纸上用直尺画一个5厘米的长线段。
然后,取一个圆规,将其中一只脚放在线段的一个端点上,另一只脚在该线段上移动,画出一个圆。
2. 作图题二:画一个边长为6厘米的正方形。
解答:使用直尺,画一个6厘米长的线段。
然后,将直尺对齐这条线段的一个端点,画一条与这条线段垂直且长度也为6厘米的线段。
再将直尺对齐这两个端点,分别画出另外两条边,使其构成一个闭合的正方形。
3. 作图题三:画一个等边三角形。
解答:使用规定好的长度的线段,比如10厘米,作为三角形的边长。
首先,画出一个10厘米长的水平线段。
然后,从水平线段的一个端点出发,以10厘米为半径作一个圆弧。
接下来,以另一个端点出发,同样以10厘米为半径作一个圆弧。
最后,将两个圆弧相交的点与水平线段的另一个端点连接,得到一个等边三角形。
4. 作图题四:画一个半径为4厘米的圆与一个边长为5厘米的正方形相切。
解答:首先,按照上面提到的方法画出一个半径为4厘米的圆。
然后,使用直尺在这个圆的周围画一个正方形,要保证正方形的每条边与圆相切。
画正方形的时候,可以利用圆规的两只脚,一只脚固定在圆上,另一只脚画线。
5. 作图题五:画一个等腰直角三角形。
解答:首先,使用直尺画一条直线作为三角形的底边。
然后,以底边的一个端点为中心,以任意长度作一个圆弧。
接下来,在另一个端点处,再以相同的长度作一个圆弧。
最后,用直尺连接两个圆弧的交点和底边上的端点,得到一个等腰直角三角形。
通过这些作图练习题,读者可以巩固对几何图形的理解,提高作图技巧,并且为解决更复杂的图形问题打下基础。
应当反复练习,直到能够熟练运用不同的作图方法来解决各种几何问题。
中考数学作图题60例
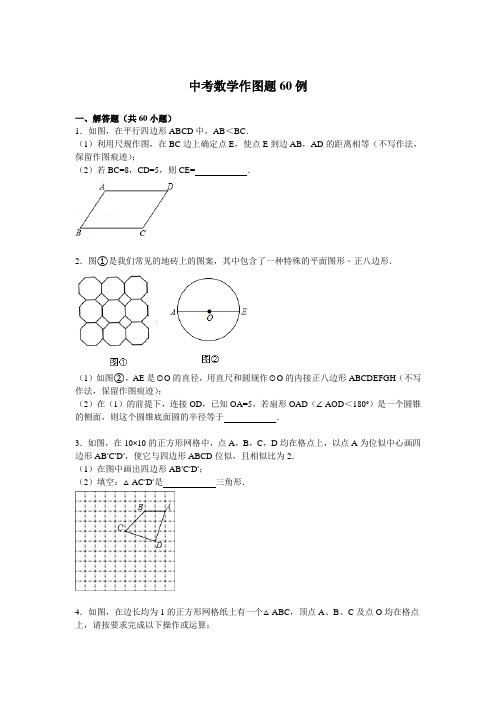
中考数学作图题60例一、解答题(共60小题)1.如图,在平行四边形ABCD中,AB<BC.(1)利用尺规作图,在BC边上确定点E,使点E到边AB,AD的距离相等(不写作法,保留作图痕迹);(2)若BC=8,CD=5,则CE=.2.图①是我们常见的地砖上的图案,其中包含了一种特殊的平面图形﹣正八边形.(1)如图②,AE是⊙O的直径,用直尺和圆规作⊙O的内接正八边形ABCDEFGH(不写作法,保留作图痕迹);(2)在(1)的前提下,连接OD,已知OA=5,若扇形OAD(∠AOD<180°)是一个圆锥的侧面,则这个圆锥底面圆的半径等于.3.如图,在10×10的正方形网格中,点A,B,C,D均在格点上,以点A为位似中心画四边形AB′C′D′,使它与四边形ABCD位似,且相似比为2.(1)在图中画出四边形AB′C′D′;(2)填空:△AC′D′是三角形.4.如图,在边长均为1的正方形网格纸上有一个△ABC,顶点A、B、C及点O均在格点上,请按要求完成以下操作或运算:(1)将△ABC向上平移4个单位,得到△A1B1C1(不写作法,但要标出字母);(2)将△ABC绕点O旋转180°,得到△A2B2C2(不写作法,但要标出字母);(3)求点A绕着点O旋转到点A2所经过的路径长.5.已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).(1)画出△ABC向下平移4个单位长度得到的△A1B1C1,点C1的坐标是;(2)以点B为位似中心,在网格内画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比为2:1,点C2的坐标是;(3)△A2B2C2的面积是平方单位.6.如图,一条公路的转弯处是一段圆弧().(1)用直尺和圆规作出所在圆的圆心O;(要求保留作图痕迹,不写作法)(2)若的中点C到弦AB的距离为20m,AB=80m,求所在圆的半径.7.各顶点都在方格纸格点(横竖格子线的交错点)上的多边形称为格点多边形.如何计算它的面积?奥地利数学家皮克(G•Pick,1859~1942年)证明了格点多边形的面积公式S=a+b﹣1,其中a表示多边形内部的格点数,b表示多边形边界上的格点数,S表示多边形的面积.如图,a=4,b=6,S=4+×6﹣1=6(1)请在图中画一个格点正方形,使它的内部只含有4个格点,并写出它的面积.(2)请在图乙中画一个格点三角形,使它的面积为,且每条边上除顶点外无其它格点.(注:图甲、图乙在答题纸上)8.如图,△ABC是直角三角形,∠ACB=90°.(1)尺规作图:作⊙C,使它与AB相切于点D,与AC相交于点E,保留作图痕迹,不写作法,请标明字母.(2)在你按(1)中要求所作的图中,若BC=3,∠A=30°,求的长.9.如图,在△ABC中,∠C=60°,∠A=40°.(1)用尺规作图作AB的垂直平分线,交AC于点D,交AB于点E(保留作图痕迹,不要求写作法和证明);(2)求证:BD平分∠CBA.10.用圆规、直尺作图,不写作法,但要保留作图痕迹.已知:线段c,直线l及l外一点A.求作:Rt△ABC,使直角边为AC(AC⊥l,垂足为C),斜边AB=c.11.在平面直角坐标系中,△ABC的三个顶点坐标分别为A(2,﹣4),B(3,﹣2),C(6,﹣3).(1)画出△ABC关于x轴对称的△A1B1C1;(2)以M点为位似中心,在网格中画出△A1B1C1的位似图形△A2B2C2,使△A2B2C2与△A1B1C1的相似比为2:1.12.在边长为1的小正方形组成的方格纸中,若多边形的各顶点都在方格纸的格点(横竖格子线的交错点)上,这样的多边形称为格点多边形.记格点多边形内的格点数为a,边界上的格点数为b,则格点多边形的面积可表示为S=ma+nb﹣1,其中m,n为常数.(1)在下面的方格中各画出一个面积为6的格点多边形,依次为三角形、平行四边形(非菱形)、菱形;(2)利用(1)中的格点多边形确定m,n的值.13.如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣1,1),B(﹣3,1),C(﹣1,4).(1)画出△ABC关于y轴对称的△A1B1C1;(2)将△ABC绕着点B顺时针旋转90°后得到△A2BC2,请在图中画出△A2BC2,并求出线段BC旋转过程中所扫过的面积(结果保留π).14.如图,在边长为4的正方形ABCD中,请画出以A为一个顶点,另外两个顶点在正方形ABCD的边上,且含边长为3的所有大小不同的等腰三角形.(要求:只要画出示意图,并在所画等腰三角形长为3的边上标注数字3)15.⊙O为△ABC的外接圆,请仅用无刻度的直尺,根据下列条件分别在图1,图2中画出一条弦,使这条弦将△ABC分成面积相等的两部分(保留作图痕迹,不写作法).(1)如图1,AC=BC;(2)如图2,直线l与⊙O相切于点P,且l∥BC.16.如图,在方格网中已知格点△ABC和点O.(1)画△A′B′C′和△ABC关于点O成中心对称;(2)请在方格网中标出所有使以点A、O、C′、D为顶点的四边形是平行四边形的D点.17.下列网格中的六边形ABCDEF是由边长为6的正方形左上角剪去边长为2的正方形所得,该六边形按一定的方法可剪拼成一个正方形.(1)根据剪拼前后图形的面积关系求出拼成的正方形的边长;(2)如图甲,把六边形ABCDEF沿EH,BG剪成①②③三部分,请在图甲中画出将②③与①拼成的正方形,然后标出②③变动后的位置,并指出②③属于旋转、平移和轴对称中的哪一种变换;(3)在图乙中画出一种与图甲不同位置的两条裁剪线,并在图乙中画出将此六边形剪拼成的正方形.18.如图,已知△ABC,∠C=Rt∠,AC<BC.D为BC上一点,且到A,B两点的距离相等.(1)用直尺和圆规,作出点D的位置(不写作法,保留作图痕迹);(2)连结AD,若∠B=37°,求∠CAD的度数.19.如图,在图中求作⊙P,使⊙P满足以线段MN为弦且圆心P到∠AOB两边的距离相等.(要求:尺规作图,不写作法,保留作图痕迹,并把作图痕迹用黑色签字笔加黑)20.如图,△ABC三个顶点的坐标分别为A(2,4),B(1,1),C(4,3).(1)请画出△ABC关于x轴对称的△A1B1C1,并写出点A1的坐标;(2)请画出△ABC绕点B逆时针旋转90°后的△A2BC2;(3)求出(2)中C点旋转到C2点所经过的路径长(记过保留根号和π).21.如图,已知在△ABC中,∠A=90°(1)请用圆规和直尺作出⊙P,使圆心P在AC边上,且与AB,BC两边都相切(保留作图痕迹,不写作法和证明).(2)若∠B=60°,AB=3,求⊙P的面积.22.如图,在△ABC中,AB=AC,∠DAC是△ABC的一个外角.实验与操作:根据要求进行尺规作图,并在图中标明相应字母(保留作图痕迹,不写作法)(1)作∠DAC的平分线AM;(2)作线段AC的垂直平分线,与AM交于点F,与BC边交于点E,连接AE,CF.猜想并证明:判断四边形AECF的形状并加以证明.23.如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(3,2)、B(3,5)、C (1,2).(1)在平面直角坐标系中画出△ABC关于x轴对称的△A1B1C1;(2)把△ABC绕点A顺时针旋转一定的角度,得图中的△AB2C2,点C2在AB上.①旋转角为多少度?②写出点B2的坐标.24.如图,在△ABC中,∠ACB=90°,AC=BC=AD.(1)作∠A的平分线交CD于E;(2)过B作CD的垂线,垂足为F;(3)请写出图中两对全等三角形(不添加任何字母),并选择其中一对加以证明.25.图1、图2是两张形状、大小完全相同的方格纸,方格纸中的每个小正方形的边长均为1,每个小正方形的顶点叫做格点.(1)在图1中画出等腰直角三角形MON,使点N在格点上,且∠MON=90°;(2)在图2中以格点为顶点画一个正方形ABCD,使正方形ABCD面积等于(1)中等腰直角三角形MON面积的4倍,并将正方形ABCD分割成以格点为顶点的四个全等的直角三角形和一个正方形,且正方形ABCD面积没有剩余(画出一种即可).26.如图,△ABC各顶点的坐标分别是A(﹣2,﹣4),B(0,﹣4),C(1,﹣1).(1)在图中画出△ABC向左平移3个单位后的△A1B1C1;(2)在图中画出△ABC绕原点O逆时针旋转90°后的△A2B2C2;(3)在(2)的条件下,AC边扫过的面积是.27.如图,AC是⊙O的直径,点B在⊙O上,∠ACB=30°(1)利用尺规作∠ABC的平分线BD,交AC于点E,交⊙O于点D,连接CD(保留作图痕迹,不写作法)(2)在(1)所作的图形中,求△ABE与△CDE的面积之比.28.如图,将△ABC在网格中(网格中每个小正方形的边长均为1)依次进行位似变换、轴对称变换和平移变换后得到△A3B3C3.(1)△ABC与△A1B1C1的位似比等于;(2)在网格中画出△A1B1C1关于y轴的轴对称图形△A2B2C2;(3)请写出△A3B3C3是由△A2B2C2怎样平移得到的?(4)设点P(x,y)为△ABC内一点,依次经过上述三次变换后,点P的对应点的坐标为.29.如图,△ABC是等腰三角形,AB=AC,请你用尺规作图将△ABC分成两个全等的三角形,并说明这两个三角形全等的理由.(保留作图痕迹,不写作法)30.如图,已知锐角△ABC.(1)过点A作BC边的垂线MN,交BC于点D(用尺规作图法,保留作图痕迹,不要求写作法);(2)在(1)的条件下,若BC=5,AD=4,tan∠BAD=,求DC的长.31.如图,在平面直角坐标系中,△ABC的三个顶点坐标为A(﹣3,4),B(﹣4,2),C (﹣2,1),且△A1B1C1与△ABC关于原点O成中心对称.(1)画出△A1B1C1,并写出A1的坐标;(2)P(a,b)是△ABC的AC边上一点,△ABC经平移后点P的对称点P′(a+3,b+1),请画出平移后的△A2B2C2.32.如图,已知BD平分∠ABF,且交AE于点D,(1)求作:∠BAE的平分线AP(要求:尺规作图,保留作图痕迹,不写作法);(2)设AP交BD于点O,交BF于点C,连接CD,当AC⊥BD时,求证:四边形ABCD 是菱形.33.如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点三角形ABC(项点是网格线的交点).(1)先将△ABC竖直向上平移6个单位,再水平向右平移3个单位得到△A1B1C1,请画出△A1B1C1;(2)将△A1B1C1绕B1点顺时针旋转90°,得△A2B1C2,请画出△A2B1C2;(3)线段B1C1变换到B1C2的过程中扫过区域的面积为.34.如图,在边长为1个单位长度的小正方形网格中,给出了△ABC(顶点是网格线的交点).(1)请画出△ABC关于直线l对称的△A1B1C1;(2)将线段AC向左平移3个单位,再向下平移5个单位,画出平移得到的线段A2C2,并以它为一边作一个格点△A2B2C2,使A2B2=C2B2.35.阅读下面材料:在数学课上,老师提出如下问题:小芸的作法如下:老师说:“小芸的作法正确.”请回答:小芸的作图依据是.36.如图,C,D分别是线段AB,AC的中点,分别以点C,D为圆心,BC长为半径画弧,两弧交于点M,测量∠AMB的度数,结果为()A.80°B.90°C.100°D.105°37.已知在Rt△ABC中,∠ACB=90°,现按如下步骤作图:①分别以A,C为圆心,a为半径(a>AC)作弧,两弧分别交于M,N两点;②过M,N两点作直线MN交AB于点D,交AC于点E;③将△ADE绕点E顺时针旋转180°,设点D的像为点F.(1)请在图中直线标出点F并连接CF;(2)求证:四边形BCFD是平行四边形;(3)当∠B为多少度时,四边形BCFD是菱形.38.在每个小正方形的边长为1的网格中.点A,B,D均在格点上,点E、F分别为线段BC、DB上的动点,且BE=DF.(Ⅰ)如图①,当BE=时,计算AE+AF的值等于(Ⅱ)当AE+AF取得最小值时,请在如图②所示的网格中,用无刻度的直尺,画出线段AE,AF,并简要说明点E和点F的位置如何找到的(不要求证明).39.设ω是一个平面图形,如果用直尺和圆规经过有限步作图(简称尺规作图),画出一个正方形与ω的面积相等(简称等积),那么这样的等积转化称为ω的“化方”.(1)阅读填空如图①,已知矩形ABCD,延长AD到E,使DE=DC,以AE为直径作半圆.延长CD交半圆于点H,以DH为边作正方形DFGH,则正方形DFGH与矩形ABCD等积.理由:连接AH,EH.∵AE为直径,∴∠AHE=90°,∴∠HAE+∠HEA=90°.∵DH⊥AE,∴∠ADH=∠EDH=90°∴∠HAD+∠AHD=90°∴∠AHD=∠HED,∴△ADH∽.∴,即DH2=AD×DE.又∵DE=DC∴DH2=,即正方形DFGH与矩形ABCD等积.(2)操作实践平行四边形的“化方”思路是,先把平行四边形转化为等积的矩形,再把矩形转化为等积的正方形.如图②,请用尺规作图作出与▱ABCD等积的矩形(不要求写具体作法,保留作图痕迹).(3)解决问题三角形的“化方”思路是:先把三角形转化为等积的(填写图形名称),再转化为等积的正方形.如图③,△ABC的顶点在正方形网格的格点上,请作出与△ABC等积的正方形的一条边(不要求写具体作法,保留作图痕迹,不通过计算△ABC面积作图).(4)拓展探究n边形(n>3)的“化方”思路之一是:把n边形转化为等积的n﹣1边形,…,直至转化为等积的三角形,从而可以化方.如图④,四边形ABCD的顶点在正方形网格的格点上,请作出与四边形ABCD等积的三角形(不要求写具体作法,保留作图痕迹,不通过计算四边形ABCD面积作图).40.定义:数学活动课上,乐老师给出如下定义:有一组对边相等而另一组对边不相等的凸四边形叫做对等四边形.理解:(1)如图1,已知A、B、C在格点(小正方形的顶点)上,请在方格图中画出以格点为顶点,AB、BC为边的两个对等四边形ABCD;(2)如图2,在圆内接四边形ABCD中,AB是⊙O的直径,AC=BD.求证:四边形ABCD 是对等四边形;(3)如图3,在Rt△PBC中,∠PCB=90°,BC=11,tan∠PBC=,点A在BP边上,且AB=13.用圆规在PC上找到符合条件的点D,使四边形ABCD为对等四边形,并求出CD 的长.41.如图,已知△ABC,按如下步骤作图:①以A为圆心,AB长为半径画弧;②以C为圆心,CB长为半径画弧,两弧相交于点D;③连接BD,与AC交于点E,连接AD,CD.(1)求证:△ABC≌△ADC;(2)若∠BAC=30°,∠BCA=45°,AC=4,求BE的长.42.如图,已知△ABC,AB<BC,用尺规作图的方法在BC上取一点P,使得PA+PC=BC,则下列选项正确的是()A.B.C.D.43.数学活动课上,四位同学围绕作图问题:“如图,已知直线l和l外一点P,用直尺和圆规作直线PQ,使PQ⊥l于点Q.”分别作出了下列四个图形.其中作法错误的是()A.B.C.D.44.在平面直角坐标系中,点A的坐标是(0,3),点B在x轴上,将△AOB绕点A逆时针旋转90°得到△AEF,点O、B的对应点分别是点E、F.(1)若点B的坐标是(﹣4,0),请在图中画出△AEF,并写出点E、F的坐标.(2)当点F落在x轴的上方时,试写出一个符合条件的点B的坐标.45.如图,正方形网格中,每个小正方形的边长都是一个单位长度,在平面直角坐标系内,△ABC的三个顶点坐标分别为A(2,﹣4),B(4,﹣4),C(1,﹣1).(1)画出△ABC关于y轴对称的△A1B1C1,直接写出点A1的坐标;(2)画出△ABC绕点O逆时针旋转90°后的△A2B2C2;(3)在(2)的条件下,求线段BC扫过的面积(结果保留π).46.如图,已知△ABC三个顶点坐标分别是A(1,3),B(4,1),C(4,4).(1)请按要求画图:①画出△ABC向左平移5个单位长度后得到的△A1B1C1;②画出△ABC绕着原点O顺时针旋转90°后得到的△A2B2C2.(2)请写出直线B1C1与直线B2C2的交点坐标.47.如图,△ABC在平面直角坐标系内,顶点的坐标分别为A(﹣1,5),B(﹣4,1),C (﹣1,1)将△ABC绕点A逆时针旋转90°,得到△AB′C′,点B,C的对应点分别为点B′,C′,(1)画出△AB′C′;(2)写出点B′,C′的坐标;(3)求出在△ABC旋转的过程中,点C经过的路径长.48.如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(1,4),B(4,2),C (3,5)(每个方格的边长均为1个单位长度).(1)请画出△A1B1C1,使△A1B1C1与△ABC关于x轴对称;(2)将△ABC绕点O逆时针旋转90°,画出旋转后得到的△A2B2C2,并直接写出点B旋转到点B2所经过的路径长.49.数学课上,老师让学生尺规作图画Rt△ABC,使其斜边AB=c,一条直角边BC=a.小明的作法如图所示,你认为这种作法中判断∠ACB是直角的依据是()A.勾股定理B.直径所对的圆周角是直角C.勾股定理的逆定理D.90°的圆周角所对的弦是直径50.如图,已知△ABC,请用尺规过点A作一条直线,使其将△ABC分成面积相等的两部分.(保留作图痕迹,不写作法)51.如图,将线段AB放在边长为1的小正方形网格,点A点B均落在格点上,请用无刻度直尺在线段AB上画出点P,使AP=,并保留作图痕迹.(备注:本题只是找点不是证明,∴只需连接一对角线就行)52.图①,图②,图③都是4×4的正方形网格,每个小正方形的顶点称为格点,每个小正方形的边长均为1.在图①,图②中已画出线段AB,在图③中已画出点A.按下列要求画图:(1)在图①中,以格点为顶点,AB为一边画一个等腰三角形;(2)在图②中,以格点为顶点,AB为一边画一个正方形;(3)在图③中,以点A为一个顶点,另外三个顶点也在格点上,画一个面积最大的正方形.53.“综合与实践”学习活动准备制作一组三角形,记这些三角形的三边分别为a,b,c,并且这些三角形三边的长度为大于1且小于5的整数个单位长度.(1)用记号(a,b,c)(a≤b≤c)表示一个满足条件的三角形,如(2,3,3)表示边长分别为2,3,3个单位长度的一个三角形.请列举出所有满足条件的三角形.(2)用直尺和圆规作出三边满足a<b<c的三角形(用给定的单位长度,不写作法,保留作图痕迹).54.手工课上,老师要求同学们将边长为4cm的正方形纸片恰好剪成六个等腰直角三角形,聪明的你请在下列四个正方形中画出不同的剪裁线,并直接写出每种不同分割后得到的最小等腰直角三角形面积(注:不同的分法,面积可以相等)55.如图是甲、乙两张不同的矩形纸片,将它们分别沿着虚线剪开后,各自要拼一个与原来面积相等的正方形,则()A.甲、乙都可以B.甲、乙都不可以C.甲不可以、乙可以D.甲可以、乙不可以56.将正方形纸片以适当的方式折叠一次,沿折痕剪开后得到两块小纸片,用这两块小纸片拼接成一个新的多边形(不重叠、无缝隙),给出以下结论:①可以拼成等腰直角三角形;②可以拼成对角互补的四边形;③可以拼成五边形;④可以拼成六边形.其中所有正确结论的序号是.57.如图所示,将正方形纸片三次对折后,沿图中AB线剪掉一个等腰直角三角形,展开铺平得到的图形是()A.B.C.D.58.一张菱形纸片按如图1、图2依次对折后,再按如图3打出一个圆形小孔,则展开铺平后的图案是()A.B.C.D.59.如图,在4×4的正方形网格中,每个小正方形的顶点称为格点,左上角阴影部分是一个以格点为顶点的正方形(简称格点正方形).若再作一个格点正方形,并涂上阴影,使这两个格点正方形无重叠面积,且组成的图形是轴对称图形,又是中心对称图形,则这个格点正方形的作法共有()A.2种B.3种C.4种D.5种60.如图,在边上为1个单位长度的小正方形网格中:(1)画出△ABC向上平移6个单位长度,再向右平移5个单位长度后的△A1B1C1.(2)以点B为位似中心,将△ABC放大为原来的2倍,得到△A2B2C2,请在网格中画出△A2B2C2.(3)求△CC1C2的面积.2015年全国中考数学作图题60例参考答案与试题解析一、解答题(共60小题)1.如图,在平行四边形ABCD中,AB<BC.(1)利用尺规作图,在BC边上确定点E,使点E到边AB,AD的距离相等(不写作法,保留作图痕迹);(2)若BC=8,CD=5,则CE=3.考点:作图—复杂作图;平行四边形的性质.专题:作图题.分析:(1)根据角平分线上的点到角的两边距离相等知作出∠A的平分线即可;(2)根据平行四边形的性质可知AB=CD=5,AD∥BC,再根据角平分线的性质和平行线的性质得到∠BAE=∠BEA,再根据等腰三角形的性质和线段的和差关系即可求解.解答:解:(1)如图所示:E点即为所求.(2)∵四边形ABCD是平行四边形,∴AB=CD=5,AD∥BC,∴∠DAE=∠AEB,∵AE是∠A的平分线,∴∠DAE=∠BAE,∴∠BAE=∠BEA,∴BE=BA=5,∴CE=BC﹣BE=3.故答案为:3.点评:考查了作图﹣复杂作图,关键是作一个角的角平分线,同时考查了平行四边形的性质,角平分线的性质,平行线的性质和等腰三角形的性质的知识点.2.图①是我们常见的地砖上的图案,其中包含了一种特殊的平面图形﹣正八边形.(1)如图②,AE是⊙O的直径,用直尺和圆规作⊙O的内接正八边形ABCDEFGH(不写作法,保留作图痕迹);(2)在(1)的前提下,连接OD,已知OA=5,若扇形OAD(∠AOD<180°)是一个圆锥的侧面,则这个圆锥底面圆的半径等于.考点:正多边形和圆;圆锥的计算;作图—复杂作图.专题:作图题.分析:(1)作AE的垂直平分线交⊙O于C,G,作∠AOG,∠EOG的角平分线,分别交⊙O于H,F,反向延长FO,HO,分别交⊙O于D,B顺次连接A,B,C,D,E,F,G,H,八边形ABCDEFGH即为所求;(2)由八边形ABCDEFGH是正八边形,求得∠AOD=3=135°得到的长=,设这个圆锥底面圆的半径为R,根据圆的周长的公式即可求得结论.解答:(1)如图所示,八边形ABCDEFGH即为所求,(2)∵八边形ABCDEFGH是正八边形,∴∠AOD=3=135°,∵OA=5,∴的长=,设这个圆锥底面圆的半径为R,∴2πR=,∴R=,即这个圆锥底面圆的半径为.故答案为:.点评:本题考查了尺规作图,圆内接八边形的性质,弧长的计算,圆的周长公式的应用,会求八边形的内角的度数是解题的关键.3.如图,在10×10的正方形网格中,点A,B,C,D均在格点上,以点A为位似中心画四边形AB′C′D′,使它与四边形ABCD位似,且相似比为2.(1)在图中画出四边形AB′C′D′;(2)填空:△AC′D′是等腰直角三角形.考点:作图-位似变换.专题:作图题.分析:(1)延长AB到B′,使AB′=2AB,得到B的对应点B′,同样得到C、D的对应点C′,D′,再顺次连接即可;(2)利用勾股定理求出AC′2=42+82=80,AD′2=62+22=40,C′D′2=62+22=40,那么AD′=C′D′,AD′2+C′D′2=AC′2,即可判定△AC′D′是等腰直角三角形.解答:解:(1)如图所示:(2)∵AC′2=42+82=16+64=80,AD′2=62+22=36+4=40,C′D′2=62+22=36+4=40,∴AD′=C′D′,AD′2+C′D′2=AC′2,∴△AC′D′是等腰直角三角形.故答案为:等腰直角.点评:本题考查了作图﹣位似变换.画位似图形的一般步骤为:①确定位似中心,②分别连接并延长位似中心和能代表原图的关键点;③根据相似比,确定能代表所作的位似图形的关键点;顺次连接上述各点,得到放大或缩小的图形.同时考查了勾股定理及其逆定理等知识.熟练掌握网格结构以及位似变换的定义是解题的关键.4.如图,在边长均为1的正方形网格纸上有一个△ABC,顶点A、B、C及点O均在格点上,请按要求完成以下操作或运算:(1)将△ABC向上平移4个单位,得到△A1B1C1(不写作法,但要标出字母);(2)将△ABC绕点O旋转180°,得到△A2B2C2(不写作法,但要标出字母);(3)求点A绕着点O旋转到点A2所经过的路径长.考点:作图-旋转变换;弧长的计算;作图-平移变换.专题:作图题.分析:(1)根据图形平移的性质画出平移后的△A1B1C1即可;(2)根据图形旋转的性质画出△ABC绕点O旋转180°后得到的△A2B2C2;(3)根据弧长的计算公式列式即可求解.解答:解:(1)△A1B1C1如图所示;(2)△A2B2C2如图所示:(3)∵OA=4,∠AOA2=180°,∴点A绕着点O旋转到点A2所经过的路径长为=4π.点评:本题考查了利用旋转变换作图,利用平移变换作图,熟练掌握网格结构准确找出对应点的位置是解题的关键.也考查了弧长的计算.5.已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).(1)画出△ABC向下平移4个单位长度得到的△A1B1C1,点C1的坐标是(2,﹣2);(2)以点B为位似中心,在网格内画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比为2:1,点C2的坐标是(1,0);(3)△A2B2C2的面积是10平方单位.考点:作图-位似变换;作图-平移变换.专题:作图题.分析:(1)利用平移的性质得出平移后图象进而得出答案;(2)利用位似图形的性质得出对应点位置即可;(3)利用等腰直角三角形的性质得出△A2B2C2的面积.解答:解:(1)如图所示:C1(2,﹣2);故答案为:(2,﹣2);(2)如图所示:C2(1,0);故答案为:(1,0);(3)∵A2C22=20,B2C=20,A2B2=40,∴△A2B2C2是等腰直角三角形,∴△A2B2C2的面积是:×20=10平方单位.故答案为:10.点评:此题主要考查了位似图形的性质以及平移的性质和三角形面积求法等知识,得出对应点坐标是解题关键.6.如图,一条公路的转弯处是一段圆弧().(1)用直尺和圆规作出所在圆的圆心O;(要求保留作图痕迹,不写作法)(2)若的中点C到弦AB的距离为20m,AB=80m,求所在圆的半径.考点:作图—复杂作图;勾股定理;垂径定理的应用.专题:作图题.分析:(1)连结AC、BC,分别作AC和BC的垂直平分线,两垂直平分线的交点为点O,如图1;(2)连接OA,OC,OC交AB于D,如图2,根据垂径定理的推论,由C为的中点得到OC⊥AB,AD=BD=AB=40,则CD=20,设⊙O的半径为r,在Rt△OAD中利用勾股定理得到r2=(r﹣20)2+402,然后解方程即可.解答:解:(1)如图1,点O为所求;(2)连接OA,OC,OC交AB于D,如图2,∵C为的中点,∴OC⊥AB,∴AD=BD=AB=40,设⊙O的半径为r,则OA=r,OD=OD﹣CD=r﹣20,在Rt△OAD中,∵OA2=OD2+BD2,∴r2=(r﹣20)2+402,解得r=50,即所在圆的半径是50m.点评:本题考查了作图﹣复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法;解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.也考查了勾股定理和垂径定理.7.各顶点都在方格纸格点(横竖格子线的交错点)上的多边形称为格点多边形.如何计算它的面积?奥地利数学家皮克(G•Pick,1859~1942年)证明了格点多边形的面积公式S=a+b﹣1,其中a表示多边形内部的格点数,b表示多边形边界上的格点数,S表示多边形的面积.如图,a=4,b=6,S=4+×6﹣1=6(1)请在图中画一个格点正方形,使它的内部只含有4个格点,并写出它的面积.(2)请在图乙中画一个格点三角形,使它的面积为,且每条边上除顶点外无其它格点.(注:图甲、图乙在答题纸上)考点:作图—应用与设计作图.专题:作图题.分析:(1)根据皮克公式画图计算即可;(2)根据题意可知a=3,b=3,画出满足题意的图形即可.解答:解:(1)如图所示,a=4,b=4,S=4+×4﹣1=5;(2)因为S=,b=3,所以a=3,如图所示,点评:本题考查了应用与设计作图,关键是理解皮克公式,根据题意求出a、b的值.8.如图,△ABC是直角三角形,∠ACB=90°.(1)尺规作图:作⊙C,使它与AB相切于点D,与AC相交于点E,保留作图痕迹,不写作法,请标明字母.(2)在你按(1)中要求所作的图中,若BC=3,∠A=30°,求的长.考点:作图—复杂作图;切线的性质;弧长的计算.专题:作图题.分析:(1)过点C作AB的垂线,垂足为点D,然后以C点为圆心,CD为半径作圆即可;(2)先根据切线的性质得∠ADC=90°,则利用互余可计算出∠DCE=90°﹣∠A=60°,∠BCD=90°﹣∠ACD=30°,再在Rt△BCD中利用∠BCD的余弦可计算出CD=,然后根据弧长公式求解.解答:解:(1)如图,⊙C为所求;(2)∵⊙C切AB于D,∴CD⊥AB,∴∠ADC=90°,∴∠DCE=90°﹣∠A=90°﹣30°=60°,∴∠BCD=90°﹣∠ACD=30°,在Rt△BCD中,∵cos∠BCD=,∴CD=3cos30°=,∴的长==π.点评:本题考查了作图﹣复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法;解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.也考查了切线的性质和弧长公式.9.如图,在△ABC中,∠C=60°,∠A=40°.(1)用尺规作图作AB的垂直平分线,交AC于点D,交AB于点E(保留作图痕迹,不要求写作法和证明);(2)求证:BD平分∠CBA.。
2021年人教版小学数学三年级上册第七单元专项—《作图题》【含答案】

2021年人教版小学数学三年级上册第七单元专项—《作图题》1.画一画。
下面方格纸上每小格的边长按1厘米计算,在方格中画一个长是5厘米宽是2厘米的长方形;再画一个边长是3厘米的正方形。
2.请你在方格纸上画3个不同形状的四边形。
3.请用彩色描边这些图形的边线。
4.画一个边长为2厘米的正方形和一个周长为10厘米的长方形。
5.用4个长3厘米、宽1厘米的长方形拼不同的长方形,拼成的哪种形状的图形周长最短,请你画出来。
6.按要求画一画。
(每个小正方形的边长为1厘米)(1)在下面的方格纸上画一个长6厘米、宽4厘米的长方形。
(2)在下面的方格纸上画一个周长为16厘米的正方形。
7.下面的方格纸中,每个小方格的边长都是1厘米,按要求画图。
(1)宽2厘米,长是宽的3倍的长方形。
(2)和上面长方形周长相等的正方形。
8.下面每个方格的边长是1厘米。
在方格纸上画一个周长是14厘米的长方形,并在这个长方形中画一个最大的正方形。
9.在下面的方格纸上画一个长1分米,宽20毫米的长方形。
10.在方格中分别画1个长方形和1个正方形,使它们的周长都是20厘米。
(小正方形边长看作1厘米)11.下面是一张方格纸,每个小方格的边长是1厘米,请在这张方格纸上画出所有周长是12厘米的长方形。
(边长是整厘米数)12.在下面方格纸上画一个周长是16厘米的正方形,再画一个周长是24厘米的长方形(每个小方格的边长为1厘米)。
13.在边长为1厘米的方格纸上,画周长都是16厘米的长方形,有几种画法,试一试。
14.下面每个方格表示边长1厘米的正方形,在下面的格子图中画周长是20厘米的长方形和正方形各一个。
15.下面每个小方格都是边长1厘米的小正方形,请在下图中画一个周长18厘米的长方形和一个周长24厘米的正方形。
答案1.见详解【分析】每小格的边长按1厘米计算,则长方形的长画5个小格,宽画2个小格即可;再画一个边长是3厘米的正方形,则正方形的四条边都画3个小格即可。
【小升初】2020六年级下册数学总复习试题-按指定的条件画图专项练 全国版(含答案)

按指定的条件画图一、作图题1.画一个长方形,使它的长是3厘米,宽是2厘米.2.操作题:将三角形按2:1的比例放大,画出放大后的图形,并画出放大后的三角形的对称轴.3.下面图形各有几条对称轴,画出来4.(2015•绵阳)画出如图的对称轴.5.请按下面的做法折一折,剪一剪,展开后的图形像什么?标出它的对称轴。
6.画一个边长为4厘米的正方形,在里面画一个最大的圆.7.画出下面图形的对称轴.8.下面的在方格图中分别画出面积是12平方厘米的三角形、平行四边形和梯形.9.画一画,在下面的方格中画出4个面积都等于5个方格大小的不同形状的图形。
10.画出下面图形的对称轴.11.画一个周长为10厘米的长方形。
12.(2013秋•寿县校级期中)在方格纸上画出面积为10cm2的平行四边形、梯形、三角形各一个.(每个方格代表1cm2)13.画一个周长是24厘米,长与宽的比是3:1的长方形.14.以A点为圆心画一个r=2cm的圆,并在圆上画出两条互相垂直的对称轴.15.如图中每个小方格的边长表示1厘米.先在图中画一个周长是18厘米、宽4厘米的长方形.再把这个长方形内的方格分别涂上黑色和蓝色,使黑色方格的面积是蓝色方格面积的3倍.(先计算,再操作)16.在如图格子里画一个周长是12厘米的长方形和一个正方形(每格表示1厘米)17.画出下面轴对称图形的对称轴.(只画一条)18.画出下面图形的对称轴.19.画出下面图形的对称轴.20.画出下面图形的对称轴.21.画出下面每个图形的对称轴.22.下面图形各有几条对称轴,画一画23.①请在图1中画出三角形ABC中AB边上的高,并以AB边和AC边为平行四边形的两条邻边画一个平行四边形.②请在图2中以A1B1边为平行四边形的底边,画一个和三角形A1B1C1面积相等的平行四边形.24.下面图形是由4张完全一样的正方形卡片拼成的.请你画出这个图形的一条对称轴.25.在下面的方格中画一个长方形,周长是20cm,宽是长的2,再把所画的长方形分成面积比为1:2 的3两个长方形.26.按要求在方格纸上画图.(每小格的边长表示1厘米)①底为4厘米的等腰三角形.②高为3厘米的钝角三角形.27.下面每个小方格边长是1cm,请你画一个长是4cm,宽是3cm的长方形;画一个底是4cm,高是3cm 的平行四边形;画一个底是8cm,这条边上的高是3cm的三角形.28.下面每个小方格表示1平方厘米,按要求在方格纸上画图.(i)画一个面积24平方厘米,高4厘米的平行四边形.(ii)画一个面积9平方厘米,高3厘米的三角形.29.画一个边长是2厘米的正方形。
浙教版科学七下期中复习-作图题和计算题

龟兔赛跑10000米长跑时,兔子前一个小时 的速度是10米/秒,后来他看看乌龟还没来, 又睡了5个小时,等他醒后用20米/秒的速度 跑了4个小时冲刺到终点,那么问,兔子在整 个比赛中的平均速度是多少?
解: 总路程=10000米=10千米 总时间=1小时+5小时+4小时=10小时 所以平均速度=10千米÷10小时
1,关于声速和光速的计算
海底的深度为4千米,发出的超声波6秒后 得到回应,问该超声波的速度是多少? 解:V=S/T
=4000米×2÷6秒
=1333.33米/秒 答:~~~ 太阳的第一缕阳光假设,到达地球用了8分钟, 你能估算出日地之间的距离吗?
2。关于平均速度的计算 小明前5秒的速度是8米/秒,后3秒的速度是 10米/秒,那么小明整段路的平均速度是多少? 1平均速度 =( 8+10 )÷2 =9米/秒 2总路程 =5×8+3×10 =70米 平均速度=70米 ÷8秒=8.75米/秒
一,关于光学
1,光的反射 已知,入射光线和反射光线分 别经过点A和点B,作出它们的 光路图 B
A
A1
已知两条反射光线,试找出它的入射光 线和发光点 入射光线是由发 光点发出的,而 A 反射光线好象是 由发光点的像点 发出的
A1
2,平面镜成像
作出箭头在镜 子中所成的像
错!!!
画出湖边小 亭的倒影
质量为0.5吨的木板车,在平直的公路上匀速 行驶,板车受到的阻力是车重的1/10,问运 输工人拉板车的拉力是多大? 解:已知质量M=0.5 ×1000=500千克
那么车重呢? 车重=500千克×9.8牛/千克
=4900牛
那么小车的 阻力f=4900 ×1/10=490牛 阻力呢? 那么对车 F = f =490牛 的拉力呢?
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1 1.(06)(本小题满分4分) 请阅读下列材料: 问题:现有5个边长为1的正方形,排列形式如图1,请把它们分割后拼接成一个新的正方形.要求:画出分割线并在正方形网格图(图中每个小正方形的边长均为1)中用实线画出拼接成的新正方形.
小东同学的做法是:设新正方形的边长为(0)xx.依题意,割补前后图形的面积相等,有
25x,解得5x.由此可知新正方形的边长等于两个正方形组
成的矩形对角线的长.于是,画出如图2所示的分割线,拼出如图3所示的新正方形.
请你参考小东同学的做法,解决如下问题: 现有10个边长为1的正方形,排列形式如图4,请把它们分割后拼接成一个新的正方形.要求:在图4中画出分割线,并在图5的正方形网格图(图中每个小正方形的边长均为1)中用实线画出拼接成的新正方形. 说明:直接画出图形,不要求写分析过程. 解:
解:所画图形如图所示.
图1 图2 图3
图4 图5
图4 图5 2
2.请阅读下列材料: 问题:现有5个边长为1的正方形,排列形式如图1,请把它们分割后拼接成一个新的正方形.要求:画出分割线并在正方形网格图(图中每个小正方形的边长均为1)中用实线画出拼接成的新正方形. 小东同学的做法是:设新正方形的边长为x(x >0). 依题意,割补前后图形面积相等, 有52x, 解得5x.由此可知新正方形的边长等于两个小正方形组成的矩形对角线的长.于是,画出如图2所示的分割线,拼出如图3所示的新正方形.
请你参考小东同学的做法,解决如下问题: (1) 如图4,是由边长为1的5个小正方形组成,请你通过分割,把它拼成一个正方形(在图4上画出分割线,在图4的右侧画出拼成的正方形简图); (2)如图5,是由边长分别为a和b的两个正方形组成,请你通过分割,把它拼成一个正方形(在图5上画出分割线,在图5的右侧画出拼成的正方形简图).
解:
图3图2图1图3图2图1
ba-b
ba 3
3.阅读并操作: 如图①,这是由十个边长为1的小正方形组成的一个图形,对这个图形进行适当分割(如图②),然后拼接成新的图形(如图③).拼接时不重叠、无空隙,并且拼接后新图形的顶点在所给正方形网格图中的格点上(网格图中每个小正方形边长都为1).
图① 图② 图③ 请你参照上述操作过程,将由图①所得到的符合要求的新图形画在下边的正方形网格图中. (1)新图形为平行四边形; (2)新图形为等腰梯形.
解:(1) (2) 4.(本小题满分5分) 小明想把一个三角形拼接成面积与它相等的矩形. 他先进行了如下部分操作,如图1所示: ①取△ABC的边AB、AC的中点D、E,联结DE; ②过点A作AF⊥DE于点F; (1)请你帮小明完成图1的操作,把△ABC拼接成面积与它相等的矩形. (2)若把一个三角形通过类似的操作拼接成一个与原三角形面积相等的正方形,那么原三角形的一边与这边上的高之间的数量关系是________________. (3)在下面所给的网格中画出符合(2)中条件的三角形,并将其拼接成面积与它相等的正方形. 4
ABC
DDCBA②
②①①
②①②①
ABCDDCBA①②①②①②②①
ABC
图3图2图1
解:(1)
(2)若要拼接成正方形,原三角形的一边与这一边上的高之间的数量关系是1:2或2:1 (3)画对一种情况的一个图给1分
或 5.现场学习题 问题背景:在△ABC中,AB、BC、AC三边的长分别为2、13、17,求这个三角形的面积. 小辉同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图1所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.
NM②①
②①FED
CB
A 5 (1)请你将△ABC的面积直接填写在横线上.________ 思维拓展:
(2)我们把上述求△ABC面积的方法叫做构图法.若△ABC三边的长分别为2a、25a、26a (0)a,请利用图2的正方形网格(每个小正方形的边长为a)画出相应的△ABC,并求出它的面积是: . 探索创新:
(3)若△ABC三边的长分别为224mn、2216mn、222mn (0,,)mnomn ,请运用构图法在图3指定区域内画出示意图,并求出△ABC的面积为: . (1) 25.
(2) 面积:23a. (3)面积:3mn.
6.(10)阅读下列材料: 小贝遇到一个有趣的问题:在矩形ABCD中,8ADcm,6ABcm. 现有一动点P按下列方式在矩形内运动:它从A点出发,沿着与AB边夹角为45的方向作直线运动,每次碰到矩形的一边,就会改变运动方向,沿着与 这条边夹角为45的方向作直线运动,并且它一直按照这种 方式不停地运动,即当P点碰到BC边,沿与BC边夹角
为45的方向作直线运动,当P点碰到CD边,再沿着与CD 边夹角为45的方向作直线运动,…,如图1所示.问P点 第一次与D点重合前...与边相碰几次,P点第一次与D点重合.. 时.所经过的路径的总长是多少. 小贝的思考是这样开始的 : 如图2,将 矩形ABCD沿直线CD折叠,得到矩形 11ABCD.由轴对称的知识,发现232PPPE, 11PAPE. 请你参考小贝的思路解决下列问题: (1)P点第一次与D点重合..前.与边相碰 次;P点从A点出发到第一次与D点重合..时.所经过的路径的总长是 cm; (2) 进一步探究:改变矩形ABCD中AD、AB的长,且满足ADAB.动点P从A 点出发,按照阅读材料中动点的运动方式,并满足前后连续两次与边相碰的位 置在矩形ABCD相邻的两边上. 若P点第一次与B点重合..前.与边相碰7次,则 :ABAD的值为 . 图2ABCACB4m2m2mnn2n图3图1
图2 6
解:(1)5,242; (2)4:5. 解题思路示意图:
7.如图1,已知等边△ABC的边长为1,D、E、F分别是AB、BC、AC边上的点(均不与点A、B、C重合),记△DEF的周长为p. (1)若D、E、F分别是AB、BC、AC边上的中点,则p=_______; (2)若D、E、F分别是AB、BC、AC边上任意点,则p的取值范围是 . 小亮和小明对第(2)问中的最小值进行了讨论,小亮先提出了自己的想法:将ABC△以AC边
为轴翻折一次得1ABC△,再将1ABC△以1BC为轴翻折一次得11ABC△,如图2所示. 则由轴对称的
性质可知,112DFFEEDp,根据两点之间线段最短,可得2pDD. 老师听了后说:“你的想法很好,但2DD的长度会因点D的位置变化而变化,所以还得不出我们想要的结果.”小明接过老师的话说:“那我们继续再翻折3次就可以了”.请参考他们的想法,写出你的答案.
解: 8. (08)(本小题满分4分) 已知等边三角形纸片ABC的边长为8,D为AB边上的点,过点D作DGBC∥交AC于点G.DEBC于点E,过点G作GFBC于点F,把三角形纸片ABC分别沿DGDEGF,,按图1
所示方式折叠,点ABC,,分别落在点A,B,C处.若点A,B,C在矩形DEFG内或其边上,且互不重合,此时我们称ABC△(即图中阴影部分)为“重叠三角形”.
ABDFCE1图ABDF
CE
1F1A
1B2D1D
1E
2图 7
(1)若把三角形纸片ABC放在等边三角形网格中(图中每个小三角形都是边长为1的等边三角形),点ABCD,,,恰好落在网格图中的格点上.如图2所示,请直接写出此时重叠三角形ABC的面积;
(2)实验探究:设AD的长为m,若重叠三角形ABC存在.试用含m的代数式表示重叠三角形ABC
的面积,并写出m的取值范围(直接写出结果,备用图供实验,探究使用).
解:(1)重叠三角形ABC的面积为 ; (2)用含m的代数式表示重叠三角形ABC的面积为 ;m的取值范围为 .
【解析】 ⑴ 重叠三角形ABC的面积为3. ⑵ 用含m的代数式表示重叠三角形ABC的面积为23(4)m; m的取值范围为843m≤
9. 如图1,在△ABC中,已知∠BAC=45°,AD⊥BC于D,BD=2,DC=3,求AD的长. 小萍同学灵活运用轴对称知识,将图形进行翻折变换如图1.她分别以AB、AC为对称轴,画出△ABD、△ACD的轴对称图形,D点的对称点为E、F,延长EB、FC相交于G点,得到四边形AEGF是正方形.设AD=x,利用勾股定理,建立关于x的方程模型,求出x的值. (1)请你帮小萍求出x的值. (2) 参考小萍的思路,探究并解答新问题: 如图2,在△ABC中,∠BAC=30°,AD⊥BC于D,AD=4.请你按照小萍的方法画图,得到四边形AEGF,求△BGC的周长.(画图所用字母与图1中的字母对应)
图1 图2
A G
C F B C E B
D A 图1 A G C F B C E B
D A 图2
A C B 备用图 A C B
备用图
