东莞市2016-2017七校联考高二下文数试题

广东省中山市2016-2017学年高二下期末统一考试数学(文)试题(有答案)AKwAUq

中山市高二级2016—2017学年度第二学期期末统一考试高二数学试卷（文科）本试卷共4页，22小题，满分150分．考试用时120分钟．注意事项：1、答卷前，考生务必用2B铅笔在答题卡“考生号”处填涂考生号，用黑色字迹钢笔或签字笔将自己姓名、考生号、试室号、座位号填写在答题卡上．2、选择题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案，答案不能答在试卷上．3、非选择题必须用黑色字迹钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内相应位置上．如需改动，先划掉原来的答案，然后再写上新的答案．不准使用铅笔和涂改液．不按以上要求作答的答案无效．4、考生必须保持答题卡的整洁．考试结束，将答题卡交回，试卷不用上交．一、选择题（本大题共12小题，每小题5分，共60分．在每小题给出的四个备选项中，只有一项是符合题目要求的．）1. 抛物线的焦点坐标为A. B. C. D.【答案】D【解析】因为抛物线x2=4y，所以p=2，所以抛物线x2=4y的焦点坐标为（0，1）．故选D．2. 若复数满足，则A. B. C. D.【答案】C【解析】，故选C.3. 命题“R，”的否定为A. R，B. R，C. R，D. R，【答案】D【解析】“R，”的否定为R，,故选D.4. 某研究型学习小组调查研究学生使用智能手机对学习的影响．部分统计数据如下表：使用智能手机不使用智能手机总计学习成绩优秀 4 8 12学习成绩不优秀16 2 18总计20 10 30附表：P(K2≥k0) 0.15 0.10 0.05 0.025 0.010 0.005 0.001 k0 2.072 2.706 3.841 5.024 6.635 7.879 10.828经计算的观测值为10，则下列选项正确的是( )A. 有99.5%的把握认为使用智能手机对学习有影响B. 有99.5%的把握认为使用智能手机对学习无影响C. 在犯错误的概率不超过0.001的前提下认为使用智能手机对学习有影响D. 在犯错误的概率不超过0.001的前提下认为使用智能手机对学习无影响【答案】A【解析】因为7.879＜K2=10＜10.828，对照数表知，有99.5%的把握认为使用智能手机对学习有影响．故选：A．5. 用反证法证明：若整系数一元二次方程有有理数根，那么中至少有一个是偶数．下列假设正确的是A. 假设都是偶数；B. 假设都不是偶数C. 假设至多有一个偶数D. 假设至多有两个偶数【答案】B【解析】试题分析：“中至少有一个是偶数”包括一个、两个或三个偶数三种情况，其否定应为不存在偶数，即“假设都不是偶数”，故选B.考点：命题的否定.6. 函数的单调递减区间是A. B.C. ，D.【答案】A【解析】函数y=x2﹣lnx的定义域为（0，+∞）．令y′=2x﹣= ，解得，∴函数y=x2﹣lnx的单调递减区间是．故选：A ．点睛：求函数的单调区间的“两个”方法方法一(1)确定函数y＝f(x)的定义域；(2)求导数y′＝f′(x)；(3)解不等式f′(x)>0，解集在定义域内的部分为单调递增区间；(4)解不等式f′(x)<0，解集在定义域内的部分为单调递减区间．方法二(1)确定函数y＝f(x)的定义域；(2)求导数y′＝f′(x)，令f′(x)＝0，解此方程，求出在定义区间内的一切实根；(3)把函数f(x)的间断点(即f(x)的无定义点)的横坐标和上面的各实数根按由小到大的顺序排列起来，然后用这些点把函数f(x)的定义区间分成若干个小区间；(4)确定f′(x)在各个区间内的符号，根据符号判定函数在每个相应区间内的单调性7. 执行如图所示的程序框图，若输出的的值为64，则判断框内应填入的条件是A. B. C. D ．【答案】A【解析】由题意得，模拟执行程序框图，可得：，满足条件，；满足条件，；满足条件，；满足条件，；由题意，此时应不满足套件，推出循环，输出的值为，结合选项可得判断框内填入的条件可以是，故选A.8. 已知F为双曲线的一个焦点，则点F到C的一条渐近线的距离为A. B. 3 C. D.【答案】A【解析】双曲线的a= ，b= ，c= ，则可设F（，0），设双曲线的一条渐近线方程为y=x，则F到渐近线的距离为d==，故选A．9. 下表提供了某厂节能降耗技术改造后在生产A产品过程中记录的产量x(吨)与相应的生产能耗y(吨)的几组对应数据，根据表中提供的数据，求出y关于x的线性回归方程为＝0.7x＋0.35，则下列结论错误的是x 3 4 5 6y 2.5 t 4 4.5A. 产品的生产能耗与产量呈正相关B. t的值是3.15C. 回归直线一定过(4.5,3.5)D. A产品每多生产1吨，则相应的生产能耗约增加0.7吨【答案】B【解析】由题意，故选：B．10. 中国有个名句“运筹帷幄之中，决胜千里之外.”其中的“筹”原意是指《孙子算经》中记载的算筹，古代是用算筹来进行计算，算筹是将几寸长的小竹棍摆在平面上进行运算，算筹的摆放形式有纵横两种形式，如下表表示一个多位数时，像阿拉伯计数一样，把各个数位的数码从左到右排列，但各位数码的筹式需要纵横相间，个位，百位，万位数用纵式表示，十位，千位，十万位用横式表示，以此类推，例如6613用算筹表示就是：，则9117用算筹可表示为A. B.C. D.【答案】A【解析】试题分析：由定义知: 千位9为横式；百位1为纵式；十位1为横式；个位7为纵式，选A考点：新定义11. 设，分别为双曲线：的左右焦点，点关于渐近线的对称点恰好落在以为圆心,为半径圆上,则双曲线的离心率为A. B. C. D.【答案】C【解析】由题意，F1（0，﹣c），F2（0，c），一条渐近线方程为y= x，则F2到渐近线的距离为=b．设F2关于渐近线的对称点为M，F2M与渐近线交于A，∴|MF2|=2b，A为F2M的中点，又0是F1F2的中点，∴OA∥F1M，∴∠F1MF2为直角，∴△MF1F2为直角三角形，∴由勾股定理得4c2=c2+4b2∴3c2=4（c2﹣a2），∴c2=4a2，即c=2a，e=2．故答案为：C ．点睛：解决椭圆和双曲线的离心率的求值及范围问题其关键就是确立一个关于a，b，c的方程或不等式，再根据a，b，c的关系消掉b得到a，c的关系式，建立关于a，b，c的方程或不等式，要充分利用椭圆和双曲线的几何性质、点的坐标的范围等.12. 大衍数列，来源于中国古代著作《乾坤谱》中对易传“大衍之数五十”的推论．其前10项为：0、2、4、8、12、18、24、32、40、50．通项公式：，如果把这个数列排成如图形状，并记表示第m行中从左向右第n个数，则的值为A. 1200B. 1280C. 3528D. 3612【答案】D【解析】由题意，则A（10，4）为数列{a n}的第92+4=85项，∴A（10，4）的值为=3612，故选D ．点睛：本题取材于中国古代著作《乾坤谱》中对易传“大衍之数五十”的推论，明确对应数列中的第几项，然后根据求出此项即可.本题的关键是正确理解树形图，明确项数.二、填空题（本大题共4小题，每小题5分，共20分，把答案填在答题卡相应横线上）13. 一质点做直线运动，它所经过的路程和时间的关系是s=3t2+t，则t=2时的瞬时速度为_________.【答案】13【解析】s=3t2+t的导函数s′=6t+1，∴s′（2）=6×2+1=13∴t=2时的瞬时速度为13故答案为1314. 已知是函数的一个极值点，则实数____________【答案】12【解析】f′（x）= +2x﹣10（x＞0）．∵x=3是函数f（x）=alnx+x2﹣10x的一个极值点，∴f′（3）= +6﹣10=0，解得a=12．∴f′（x）=∴0＜x＜2或x＞3时，f′（x）＞0，3＞x＞2时，f′（x）＜0，∴x=3是函数f（x）=12lnx+x2﹣10x的一个极小值点，故答案为：12．15. 双曲线上一点P到它的一个焦点的距离等于3，那么点P与两个焦点所构成的三角形的周长等于________________.【答案】42【解析】双曲线的a=8，b=6，则c=10，设P到它的上焦点F的距离等于3，由于3＞c﹣a=2，3＜c+a=18，则P为上支上一点，则由双曲线的定义可得PF'﹣PF=2a=16，（F'为下焦点）．则有PF'=19．则点P与两个焦点所构成三角形的周长为PF+PF'+FF'=3+19+20=42．故答案为42．16. 已知函数，如果对任意的，都有成立，则实数a的取值范围是__________.【答案】【解析】求导函数，可得g′（x）= ﹣2= ，x∈[，2]，g′（x）＜0，∴g（x）min=g（2）=ln2﹣4，∵f（x）=2x+a，∴f（x）在[，2]上单调递增，∴f（x）max=f（2）=4+a，∵如果存在，使得对任意的，都有f（x1）≤g（x2）成立，∴4+a≤ln2﹣4，∴a≤故答案为点睛：导数问题经常会遇见恒成立的问题：①根据参变分离，转化为不含参数的函数的最值问题；②若就可讨论参数不同取值下的函数的单调性和极值以及最值，最终转化为，若恒成立，转化为;③若恒成立，可转化为.三、解答题（本大题共6小题，共70分，解答须写出文字说明、证明过程和演算步骤．）17. 已知复数()，且为纯虚数.（1）求复数；（2）若，求复数的模.【答案】(1);(2).【解析】试题分析：（1）化为标准形式，根据纯虚数概念确定复数z；（2）先化简，然后求模即可.试题解析：(1)∵为纯虚数，∴∴，所以(2),∴.点睛：复数代数形式运算问题的常见类型及解题策略：①复数的乘法．复数的乘法类似于多项式的四则运算，可将含有虚数单位的看作一类同类项，不含的看作另一类同类项，分别合并即可．②复数的除法．除法的关键是分子分母同乘以分母的共轭复数，解题中要注意把的幂写成最简形式．③利用复数相等求参数．．18. 已知，设：实数满足，：实数满足．（1）若，且为真，求实数的取值范围；（2）若是的充分不必要条件，求实数的取值范围．【答案】(1);(2).【解析】试题分析：（1）为真时实数的取值范围是，为真时实数x的取值范围是，然后求交集即可；（2）是的充分不必要条件即即是的充分不必要条件，易得：且. 试题解析：（1）由得当时，，即为真时实数的取值范围是.由，得，即为真时实数x的取值范围是因为为真，所以真且真，所以实数的取值范围是.（2）由得，所以，为真时实数的取值范围是.因为是的充分不必要条件，即是的充分不必要条件所以且所以实数的取值范围为：.19. 为了研究一种昆虫的产卵数和温度是否有关，现收集了7组观测数据列于下表中，并做出了散点图，发现样本点并没有分布在某个带状区域内，两个变量并不呈现线性相关关系，现分别用模型①与模型；②作为产卵数和温度的回归方程来建立两个变量之间的关系.温度20 22 24 26 28 30 32 产卵数个 6 10 21 24 64 113 322400 484 576 676 784 900 10241.792.303.04 3.184.16 4.735.7726 692 80 3.571157.54 0.43 0.32 0.00012其中，，，，附：对于一组数据，，……，其回归直线的斜率和截距的最小二乘估计分别为：，（1）根据表中数据，分别建立两个模型下关于的回归方程；并在两个模型下分别估计温度为时的产卵数.（与估计值均精确到小数点后两位）（参考数据：）（2）若模型①、②的相关指数计算分别为，请根据相关指数判断哪个模型的拟合效果更好.【答案】(1)详见解析;(2)模型②的拟合效果更好.【解析】试题分析：（1）利用表中数据，建立两个模型下关于的回归方程；（2）因为，所以模型②的拟合效果更好.试题解析：（1）对于模型①：设，则其中，所以，当时，估计产卵数为对于模型②：设，则其中，所以，当时，估计产卵数为（2）因为，所以模型②的拟合效果更好.点睛：求解回归方程问题的三个易误点：①易混淆相关关系与函数关系，两者的区别是函数关系是一种确定的关系，而相关关系是一种非确定的关系，函数关系是一种因果关系，而相关关系不一定是因果关系，也可能是伴随关系．②回归分析中易误认为样本数据必在回归直线上，实质上回归直线必过(， )点，可能所有的样本数据点都不在直线上．③利用回归方程分析问题时，所得的数据易误认为准确值，而实质上是预测值(期望值)．20. 已知椭圆：的右焦点为，右顶点为，设离心率为，且满足，其中为坐标原点．（1）求椭圆的方程；（2）过点的直线l与椭圆交于M，N两点，求△OMN面积的最大值．【答案】（1）；（2）.【解析】试题分析：（1）根据，解得c值，即可得椭圆的方程；（Ⅱ）联立l与椭圆C的方程，得,得，．所以，又O到l的距离．所以△OMN的面积求最值即可.试题解析：（Ⅰ）设椭圆的焦半距为c，则|OF| = c，|OA| = a，|AF| =．所以，其中，又，联立解得，．所以椭圆C的方程是．（Ⅱ）由题意直线不能与x轴垂直，否则将无法构成三角形．当直线l与x轴不垂直时，设其斜率为k，那么l的方程为．联立l与椭圆C的方程，消去y，得．于是直线与椭圆有两个交点的充要条件是Δ=，这显然大于0．设点，．由根与系数的关系得，．所以，又O到l的距离．所以△OMN的面积．，那么，当且仅当t = 3时取等．所以△OMN面积的最大值是．点睛:本题主要考查直线与圆锥曲线位置关系，所使用方法为韦达定理法：因直线的方程是一次的，圆锥曲线的方程是二次的，故直线与圆锥曲线的问题常转化为方程组关系问题，最终转化为一元二次方程问题，故用韦达定理及判别式是解决圆锥曲线问题的重点方法之一，尤其是弦中点问题，弦长问题，可用韦达定理直接解决，但应注意不要忽视判别式的作用．21. 设函数.（1）若曲线在点处的切线与直线垂直，求的单调区间（其中为自然对数的底数）；（2）若对任意恒成立，求的取值范围.【答案】(1) 的单调减区间为,单调增区间为;(2) .【解析】试题分析：（1）由，解不等式得到单调区间；（2）根据题意，构造，在上单调递减，转化为恒成立问题，求得k的取值范围.试题解析：（1）由，知，且，……1分因为曲线在点处的切线与直线垂直，所以，所以，得，所以，令，得，在上单调递减；令，得，在上单调递增，综上，的单调减区间为,单调增区间为.（2）因为，恒成立，则有，对恒成立，令，则在上单调递减，所以在上恒成立，所以恒成立，令，则.所以的取值范围是.点睛：本题主要考查了利用导数研究函数的单调性和极值、最值，考查了化归转化的思想，属于难题.不等式恒成立，可以变量集中后构造新函数ｇ（ｘ），则此函数在上单调递减，进而转化为在上恒成立，最终变量分离求最值即可．....................................22. 对于命题：存在一个常数，使得不等式对任意正数，恒成立.（1）试给出这个常数的值；（2）在（1）所得结论的条件下证明命题；（3）对于上述命题，某同学正确地猜想了命题：“存在一个常数，使得不等式对任意正数，，恒成立．”观察命题与命题的规律，请猜想与正数，，，相关的命题．【答案】(1);(2)详见解析;(3)详见解析.【解析】试题分析：（1）取特值，定常数的值；（2）利用分析法证明命题P;(3).猜想结论：存在一个常数，使得不等式对任意正数，，，恒成立.试题解析：（1）令得：，故；（2）先证明.∵，，要证上式，只要证，即证即证，这显然成立.∴.再证明.∵，，要证上式，只要证，即证即证，这显然成立.∴.（3）猜想结论：存在一个常数，使得不等式对任意正数，，，恒成立.。

2016-2017高二数学期末试卷

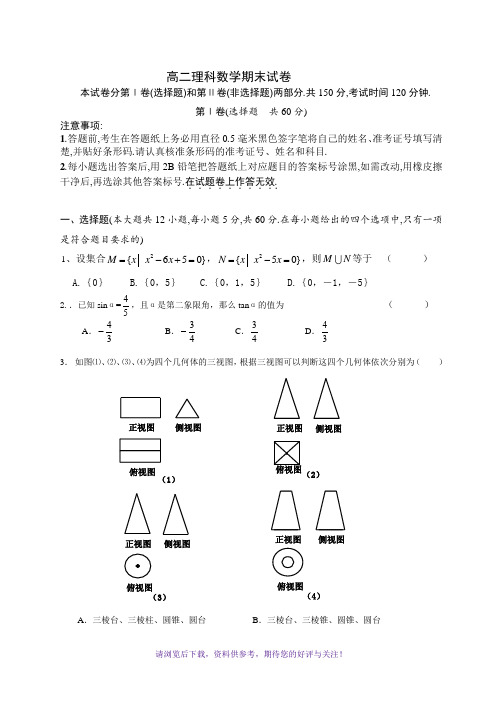
（4）（3）（1）俯视图俯视图俯视图侧视图侧视图侧视图侧视图正视图正视图正视图正视图（2）俯视图·高二理科数学期末试卷本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.共150分,考试时间120分钟.第Ⅰ卷(选择题共60分)注意事项:1.答题前,考生在答题纸上务必用直径0.5毫米黑色签字笔将自己的姓名、准考证号填写清楚,并贴好条形码.请认真核准条形码的准考证号、姓名和科目.2.每小题选出答案后,用2B 铅笔把答题纸上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号.在试题卷上作答无效．．．．．．．．．.．一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1、设集合2{650}M xx x =-+=，2{50}N x x x =-=，则M N 等于（）A.｛0｝B.｛0，5｝C.｛0，1，5｝D.｛0，－1，－5｝2.．已知sin α=54，且α是第二象限角，那么tan α的值为（）A ．34- B ．43- C ．43D ．343．如图⑴、⑵、⑶、⑷为四个几何体的三视图，根据三视图可以判断这四个几何体依次分别为（）A ．三棱台、三棱柱、圆锥、圆台B ．三棱台、三棱锥、圆锥、圆台C ．三棱柱、正四棱锥、圆锥、圆台D ．三棱柱、三棱台、圆锥、圆台4.执行如图所示的程序框图，输出的k 值为 ( )A ．3B ．4C ．5D ．65.直线3x+4y-13=0与圆1)3()2(22=-+-y x 的位置关系是： ( ) A. 相离; B. 相交; C. 相切; D. 无法判定.6.已知数列{a n }中，a 1＝1，a n ＋1＝a n ＋3，若a n ＝2 017，则n ＝( )A ．667B ．668C ．669D ．6737．设原命题“若p 则q ”真而逆命题假，则p 是q 的（）Ａ．充分不必要条件Ｂ．必要不充分条件Ｃ．充要条件Ｄ．既不充分又不必要条件8.设,x y 满足约束条件12x y y x y +≤⎧⎪≤⎨⎪≥-⎩,则3z x y =+的最大值为（）A ． 5 B. 3 C. 7 D. -89．一组数据的平均数、众数和方差都是2，则这组数可以是( )A ．2，2，3，1B ．2，3，－1，2，4C ．2，2，2，2，2，2D ．2，4，0，210. .三个数a ＝70.3，b ＝0.37，c ＝ln 0.3大小的顺序是( )A ．a>b>cB ．a>c>bC ．b>a>cD ．c>a>b11. . 平面向量a 与b 的夹角为60°，a ＝(2,0)，|b |＝1，则|a ＋2b |等于( )A. 3B ．23C ．4D ．1212.设12,F F 是双曲线2222:1(0,0)x y C a b a b-=>>的两个焦点,P 是C 上一点,若a PF PF 6||||21=+,且12PF F ∆的最小内角为30,则C 的离心率为（）A ．2B ．23 C ．3D ．26 第Ⅱ卷(非选择题共90分)注意事项:1.答题前,考生先在答题纸上用直径0.5毫米黑色签字笔将自己的姓名、准考证号填写清楚,然后贴好条形码.请认真核准条形码上的准考证号、姓名和科目.2.第Ⅱ卷共6页,请用直径0.5毫米黑色签字笔在答题纸上各题的答题区域内作答,在试题．．．卷上作答无效．．．．．．.．二、填空题(本大题共4小题,每小题5分,共20分)13 . 已知sin ⎝⎛⎭⎫x ＋π4＝35，则sin 2x ＝________． 14. 若关于x 的不等式240x x a ≥－－在[1,3]上恒成立，则实数a 的取值范围为_______.15．已知，，求=16. 已知球O 的面上四点A 、B 、C 、D ，DA ABC ⊥平面，AB BC ⊥，DA=AB=BC=3则球O 的体积等于 .三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤)17. ．甲、乙两位同学从A 、B 、C 、D 共4所高校中，任选两所参加自主招生考试（并且只能选两所高校），但同学甲特别喜欢A 高校，他除选A 高校外，再在余下的3所中随机选1所；同学乙对4所高校没有偏爱，在4所高校中随机选2所．（1）求乙同学选中D 高校的概率；（2）求甲、乙两名同学恰有一人选中D 高校的概率．18. 设()f x a b =⋅.向量(2sin 21),(2cos 21)a x x b x x ωωωω=+=-. (Ⅰ) 当1,(0,)2x πω=∈时,求函数()f x 的值域;(Ⅱ)当1ω=-时,求函数()f x 的单调递减区间.19. 已知数列{}n a 是等差数列，且253619,25a a a a +=+=．（1）求数列{}n a 的通项公式；（2）若数列{}n n a b -是首项为2，公比为2的等比数列，求数列{}n b 的前n 项和n S ．20. 在△ABC 中，角A 、B 、C 的对边分别为a 、b 、c ，且b cos C ＝(3a －c )cos B.(1)求cos B 的值；(2)若BA →·BC →＝2，且b ＝22，求a 和c 的值．21.如图，椭圆C ：2222+1x y a b=(a ＞b ＞0)的离心率为12，其左焦点到点P (2，1)的距离为10．不过原点O 的直线l 与C 相交于A ，B 两点，且线段AB 被直线OP 平分．(Ⅰ)求椭圆C 的方程；(Ⅱ) 求∆ABP 的面积取最大时直线l 的方程．22. 如图，四棱锥P-ABCD 中，PA ⊥底面ABCD ，四边形ABCD 中，AB ⊥AD ，AB+AD=4，CD=2，︒=∠45CDA ．（I ）求证：平面PAB ⊥平面PAD ；（II ）设AB=AP ．（i ）若直线PB 与平面PCD 所成的角为︒30，求线段AB 的长；（ii ）在线段AD 上是否存在一个点G ，使得点G 到点P ，B ，C ，D 的距离都相等？说明理由。

广东中山市普通高中2016-2017学年下学期高二数学4月月

中山市普通高中2016-2017学年下学期高二数学4月月考试题06第Ⅰ卷一、选择题：（共10小题，每小题5分，共50分） 1.已知集合}4,3,2{},3,2,1{M ==N ,则（）}4,1{.}3,2{...=⋃=⋂⊆⊆N M D N M C M N B N M A2．“0a =”是 “函数ln ||y x a =-为偶函数”的（） A ．充要条件 B.充分不必要条件 C. 必要不充分条件 D.既不充分又不必要条件3．若函数2()1x af x x +=+在1x =处取极值，则a =（）A ．1B ．3C ．2D ．4 4. 函数x y 32x +=的零点所在的一个区间为（） A.(-2,-1) B. (-1,0) C. (0,1) D. (1,2) 5.计算：（）A ．12-B ．12 C．6．在△ABC 中，若C b a cos 2=，则△ABC 是（） A ．等边三角形 B ．等腰三角形C ．直角三角形D ．斜三角形7．已知椭圆的长轴长是短轴长的2倍，则椭圆的离心率等于（） A ．13B．3C ．12D．28．设函数f(x)在定义域内可导，y=f(x)的图象如图1所示，则导函数y=f '(x)可能为（）ABCD9．函数f (x )＝x 3－3x +1在闭区间[-3，0]上的最大值、最小值分别是（）A 1，－1B 3，-17C 1，－17D 9，－1910．定义在R 上的函数)(x f 满足=)(x f ⎩⎨⎧>---≤-0),2()1(0),1(log 2x x f x f x x ，则(2013)f 的值为（）A.1-B.0C.1D.2第II 卷（非选择题共100分）二、填空题：（共4小题，每小题5分，共20分） 11．函数2()x f x x e =⋅的单调递增区间是 .12．执行右边的程序框图，输入的T =.13．如果数列1121222,1,(1)n n n n n n n a a a a a a a n a a ++++--===≥｛｝满足且，则3a 为，通项为 .14．已知函数f (x )＝x 3＋bx 2＋cx ，其导函数y ＝f ′(x )的图象经过点(1,0)，(2,0)，如图所示．则下列说法中不正确．．．的编号是__________．(写出所有不正确说法的编号)(1)当x ＝32时函数取得极小值；(2)f (x )有两个极值点； (3)c ＝6；(4)当x ＝1时函数取得极大值．三、解答题：（共6小题，共80分）解答应写出文字说明，证明过程或演算步骤。

广东省中山市2016-2017学年高二下期末统一考试数学(文)试题(有答案)AKwAUq (1)

中山市高二级2016—2017学年度第二学期期末统一考试高二数学试卷（文科）本试卷共4页，22小题，满分150分．考试用时120分钟．注意事项：1、答卷前，考生务必用2B铅笔在答题卡“考生号”处填涂考生号，用黑色字迹钢笔或签字笔将自己姓名、考生号、试室号、座位号填写在答题卡上．2、选择题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案，答案不能答在试卷上．3、非选择题必须用黑色字迹钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内相应位置上．如需改动，先划掉原来的答案，然后再写上新的答案．不准使用铅笔和涂改液．不按以上要求作答的答案无效．4、考生必须保持答题卡的整洁．考试结束，将答题卡交回，试卷不用上交．一、选择题（本大题共12小题，每小题5分，共60分．在每小题给出的四个备选项中，只有一项是符合题目要求的．）1. 抛物线的焦点坐标为A. B. C. D.【答案】D【解析】因为抛物线x2=4y，所以p=2，所以抛物线x2=4y的焦点坐标为（0，1）．故选D．2. 若复数满足，则A. B. C. D.【答案】C【解析】，故选C.3. 命题“R，”的否定为A. R，B. R，C. R，D. R，【答案】D【解析】“R，”的否定为R，,故选D.4. 某研究型学习小组调查研究学生使用智能手机对学习的影响．部分统计数据如下表：使用智能手机不使用智能手机总计学习成绩优秀 4 8 12学习成绩不优秀16 2 18总计20 10 30附表：P(K2≥k0) 0.15 0.10 0.05 0.025 0.010 0.005 0.001 k0 2.072 2.706 3.841 5.024 6.635 7.879 10.828经计算的观测值为10，则下列选项正确的是( )A. 有99.5%的把握认为使用智能手机对学习有影响B. 有99.5%的把握认为使用智能手机对学习无影响C. 在犯错误的概率不超过0.001的前提下认为使用智能手机对学习有影响D. 在犯错误的概率不超过0.001的前提下认为使用智能手机对学习无影响【答案】A【解析】因为7.879＜K2=10＜10.828，对照数表知，有99.5%的把握认为使用智能手机对学习有影响．故选：A．5. 用反证法证明：若整系数一元二次方程有有理数根，那么中至少有一个是偶数．下列假设正确的是A. 假设都是偶数；B. 假设都不是偶数C. 假设至多有一个偶数D. 假设至多有两个偶数【答案】B【解析】试题分析：“中至少有一个是偶数”包括一个、两个或三个偶数三种情况，其否定应为不存在偶数，即“假设都不是偶数”，故选B.考点：命题的否定.6. 函数的单调递减区间是A. B.C. ，D.【答案】A【解析】函数y=x2﹣lnx的定义域为（0，+∞）．令y′=2x﹣= ，解得，∴函数y=x2﹣lnx的单调递减区间是．故选：A ．点睛：求函数的单调区间的“两个”方法方法一(1)确定函数y＝f(x)的定义域；(2)求导数y′＝f′(x)；(3)解不等式f′(x)>0，解集在定义域内的部分为单调递增区间；(4)解不等式f′(x)<0，解集在定义域内的部分为单调递减区间．方法二(1)确定函数y＝f(x)的定义域；(2)求导数y′＝f′(x)，令f′(x)＝0，解此方程，求出在定义区间内的一切实根；(3)把函数f(x)的间断点(即f(x)的无定义点)的横坐标和上面的各实数根按由小到大的顺序排列起来，然后用这些点把函数f(x)的定义区间分成若干个小区间；(4)确定f′(x)在各个区间内的符号，根据符号判定函数在每个相应区间内的单调性7. 执行如图所示的程序框图，若输出的的值为64，则判断框内应填入的条件是A. B. C. D ．【答案】A【解析】由题意得，模拟执行程序框图，可得：，满足条件，；满足条件，；满足条件，；满足条件，；由题意，此时应不满足套件，推出循环，输出的值为，结合选项可得判断框内填入的条件可以是，故选A.8. 已知F为双曲线的一个焦点，则点F到C的一条渐近线的距离为A. B. 3 C. D.【答案】A【解析】双曲线的a= ，b= ，c= ，则可设F（，0），设双曲线的一条渐近线方程为y=x，则F到渐近线的距离为d==，故选A．9. 下表提供了某厂节能降耗技术改造后在生产A产品过程中记录的产量x(吨)与相应的生产能耗y(吨)的几组对应数据，根据表中提供的数据，求出y关于x的线性回归方程为＝0.7x＋0.35，则下列结论错误的是x 3 4 5 6y 2.5 t 4 4.5A. 产品的生产能耗与产量呈正相关B. t的值是3.15C. 回归直线一定过(4.5,3.5)D. A产品每多生产1吨，则相应的生产能耗约增加0.7吨【答案】B【解析】由题意，故选：B．10. 中国有个名句“运筹帷幄之中，决胜千里之外.”其中的“筹”原意是指《孙子算经》中记载的算筹，古代是用算筹来进行计算，算筹是将几寸长的小竹棍摆在平面上进行运算，算筹的摆放形式有纵横两种形式，如下表表示一个多位数时，像阿拉伯计数一样，把各个数位的数码从左到右排列，但各位数码的筹式需要纵横相间，个位，百位，万位数用纵式表示，十位，千位，十万位用横式表示，以此类推，例如6613用算筹表示就是：，则9117用算筹可表示为A. B.C. D.【答案】A【解析】试题分析：由定义知: 千位9为横式；百位1为纵式；十位1为横式；个位7为纵式，选A考点：新定义11. 设，分别为双曲线：的左右焦点，点关于渐近线的对称点恰好落在以为圆心,为半径圆上,则双曲线的离心率为A. B. C. D.【答案】C【解析】由题意，F1（0，﹣c），F2（0，c），一条渐近线方程为y= x，则F2到渐近线的距离为=b．设F2关于渐近线的对称点为M，F2M与渐近线交于A，∴|MF2|=2b，A为F2M的中点，又0是F1F2的中点，∴OA∥F1M，∴∠F1MF2为直角，∴△MF1F2为直角三角形，∴由勾股定理得4c2=c2+4b2∴3c2=4（c2﹣a2），∴c2=4a2，即c=2a，e=2．故答案为：C ．点睛：解决椭圆和双曲线的离心率的求值及范围问题其关键就是确立一个关于a，b，c的方程或不等式，再根据a，b，c的关系消掉b得到a，c的关系式，建立关于a，b，c的方程或不等式，要充分利用椭圆和双曲线的几何性质、点的坐标的范围等.12. 大衍数列，来源于中国古代著作《乾坤谱》中对易传“大衍之数五十”的推论．其前10项为：0、2、4、8、12、18、24、32、40、50．通项公式：，如果把这个数列排成如图形状，并记表示第m行中从左向右第n个数，则的值为A. 1200B. 1280C. 3528D. 3612【答案】D【解析】由题意，则A（10，4）为数列{a n}的第92+4=85项，∴A（10，4）的值为=3612，故选D ．点睛：本题取材于中国古代著作《乾坤谱》中对易传“大衍之数五十”的推论，明确对应数列中的第几项，然后根据求出此项即可.本题的关键是正确理解树形图，明确项数.二、填空题（本大题共4小题，每小题5分，共20分，把答案填在答题卡相应横线上）13. 一质点做直线运动，它所经过的路程和时间的关系是s=3t2+t，则t=2时的瞬时速度为_________.【答案】13【解析】s=3t2+t的导函数s′=6t+1，∴s′（2）=6×2+1=13∴t=2时的瞬时速度为13故答案为1314. 已知是函数的一个极值点，则实数____________【答案】12【解析】f′（x）= +2x﹣10（x＞0）．∵x=3是函数f（x）=alnx+x2﹣10x的一个极值点，∴f′（3）= +6﹣10=0，解得a=12．∴f′（x）=∴0＜x＜2或x＞3时，f′（x）＞0，3＞x＞2时，f′（x）＜0，∴x=3是函数f（x）=12lnx+x2﹣10x的一个极小值点，故答案为：12．15. 双曲线上一点P到它的一个焦点的距离等于3，那么点P与两个焦点所构成的三角形的周长等于________________.【答案】42【解析】双曲线的a=8，b=6，则c=10，设P到它的上焦点F的距离等于3，由于3＞c﹣a=2，3＜c+a=18，则P为上支上一点，则由双曲线的定义可得PF'﹣PF=2a=16，（F'为下焦点）．则有PF'=19．则点P与两个焦点所构成三角形的周长为PF+PF'+FF'=3+19+20=42．故答案为42．16. 已知函数，如果对任意的，都有成立，则实数a的取值范围是__________.【答案】【解析】求导函数，可得g′（x）= ﹣2= ，x∈[，2]，g′（x）＜0，∴g（x）min=g（2）=ln2﹣4，∵f（x）=2x+a，∴f（x）在[，2]上单调递增，∴f（x）max=f（2）=4+a，∵如果存在，使得对任意的，都有f（x1）≤g（x2）成立，∴4+a≤ln2﹣4，∴a≤故答案为点睛：导数问题经常会遇见恒成立的问题：①根据参变分离，转化为不含参数的函数的最值问题；②若就可讨论参数不同取值下的函数的单调性和极值以及最值，最终转化为，若恒成立，转化为;③若恒成立，可转化为.三、解答题（本大题共6小题，共70分，解答须写出文字说明、证明过程和演算步骤．）17. 已知复数()，且为纯虚数.（1）求复数；（2）若，求复数的模.【答案】(1);(2).【解析】试题分析：（1）化为标准形式，根据纯虚数概念确定复数z；（2）先化简，然后求模即可.试题解析：(1)∵为纯虚数，∴∴，所以(2),∴.点睛：复数代数形式运算问题的常见类型及解题策略：①复数的乘法．复数的乘法类似于多项式的四则运算，可将含有虚数单位的看作一类同类项，不含的看作另一类同类项，分别合并即可．②复数的除法．除法的关键是分子分母同乘以分母的共轭复数，解题中要注意把的幂写成最简形式．③利用复数相等求参数．．18. 已知，设：实数满足，：实数满足．（1）若，且为真，求实数的取值范围；（2）若是的充分不必要条件，求实数的取值范围．【答案】(1);(2).【解析】试题分析：（1）为真时实数的取值范围是，为真时实数x的取值范围是，然后求交集即可；（2）是的充分不必要条件即即是的充分不必要条件，易得：且. 试题解析：（1）由得当时，，即为真时实数的取值范围是.由，得，即为真时实数x的取值范围是因为为真，所以真且真，所以实数的取值范围是.（2）由得，所以，为真时实数的取值范围是.因为是的充分不必要条件，即是的充分不必要条件所以且所以实数的取值范围为：.19. 为了研究一种昆虫的产卵数和温度是否有关，现收集了7组观测数据列于下表中，并做出了散点图，发现样本点并没有分布在某个带状区域内，两个变量并不呈现线性相关关系，现分别用模型①与模型；②作为产卵数和温度的回归方程来建立两个变量之间的关系.温度20 22 24 26 28 30 32 产卵数个 6 10 21 24 64 113 322400 484 576 676 784 900 10241.792.303.04 3.184.16 4.735.7726 692 80 3.571157.54 0.43 0.32 0.00012其中，，，，附：对于一组数据，，……，其回归直线的斜率和截距的最小二乘估计分别为：，（1）根据表中数据，分别建立两个模型下关于的回归方程；并在两个模型下分别估计温度为时的产卵数.（与估计值均精确到小数点后两位）（参考数据：）（2）若模型①、②的相关指数计算分别为，请根据相关指数判断哪个模型的拟合效果更好.【答案】(1)详见解析;(2)模型②的拟合效果更好.【解析】试题分析：（1）利用表中数据，建立两个模型下关于的回归方程；（2）因为，所以模型②的拟合效果更好.试题解析：（1）对于模型①：设，则其中，所以，当时，估计产卵数为对于模型②：设，则其中，所以，当时，估计产卵数为（2）因为，所以模型②的拟合效果更好.点睛：求解回归方程问题的三个易误点：①易混淆相关关系与函数关系，两者的区别是函数关系是一种确定的关系，而相关关系是一种非确定的关系，函数关系是一种因果关系，而相关关系不一定是因果关系，也可能是伴随关系．②回归分析中易误认为样本数据必在回归直线上，实质上回归直线必过(， )点，可能所有的样本数据点都不在直线上．③利用回归方程分析问题时，所得的数据易误认为准确值，而实质上是预测值(期望值)．20. 已知椭圆：的右焦点为，右顶点为，设离心率为，且满足，其中为坐标原点．（1）求椭圆的方程；（2）过点的直线l与椭圆交于M，N两点，求△OMN面积的最大值．【答案】（1）；（2）.【解析】试题分析：（1）根据，解得c值，即可得椭圆的方程；（Ⅱ）联立l与椭圆C的方程，得,得，．所以，又O到l的距离．所以△OMN的面积求最值即可.试题解析：（Ⅰ）设椭圆的焦半距为c，则|OF| = c，|OA| = a，|AF| =．所以，其中，又，联立解得，．所以椭圆C的方程是．（Ⅱ）由题意直线不能与x轴垂直，否则将无法构成三角形．当直线l与x轴不垂直时，设其斜率为k，那么l的方程为．联立l与椭圆C的方程，消去y，得．于是直线与椭圆有两个交点的充要条件是Δ=，这显然大于0．设点，．由根与系数的关系得，．所以，又O到l的距离．所以△OMN的面积．，那么，当且仅当t = 3时取等．所以△OMN面积的最大值是．点睛:本题主要考查直线与圆锥曲线位置关系，所使用方法为韦达定理法：因直线的方程是一次的，圆锥曲线的方程是二次的，故直线与圆锥曲线的问题常转化为方程组关系问题，最终转化为一元二次方程问题，故用韦达定理及判别式是解决圆锥曲线问题的重点方法之一，尤其是弦中点问题，弦长问题，可用韦达定理直接解决，但应注意不要忽视判别式的作用．21. 设函数.（1）若曲线在点处的切线与直线垂直，求的单调区间（其中为自然对数的底数）；（2）若对任意恒成立，求的取值范围.【答案】(1) 的单调减区间为,单调增区间为;(2) .【解析】试题分析：（1）由，解不等式得到单调区间；（2）根据题意，构造，在上单调递减，转化为恒成立问题，求得k的取值范围.试题解析：（1）由，知，且，……1分因为曲线在点处的切线与直线垂直，所以，所以，得，所以，令，得，在上单调递减；令，得，在上单调递增，综上，的单调减区间为,单调增区间为.（2）因为，恒成立，则有，对恒成立，令，则在上单调递减，所以在上恒成立，所以恒成立，令，则.所以的取值范围是.点睛：本题主要考查了利用导数研究函数的单调性和极值、最值，考查了化归转化的思想，属于难题.不等式恒成立，可以变量集中后构造新函数ｇ（ｘ），则此函数在上单调递减，进而转化为在上恒成立，最终变量分离求最值即可．....................................22. 对于命题：存在一个常数，使得不等式对任意正数，恒成立.（1）试给出这个常数的值；（2）在（1）所得结论的条件下证明命题；（3）对于上述命题，某同学正确地猜想了命题：“存在一个常数，使得不等式对任意正数，，恒成立．”观察命题与命题的规律，请猜想与正数，，，相关的命题．【答案】(1);(2)详见解析;(3)详见解析.【解析】试题分析：（1）取特值，定常数的值；（2）利用分析法证明命题P;(3).猜想结论：存在一个常数，使得不等式对任意正数，，，恒成立.试题解析：（1）令得：，故；（2）先证明.∵，，要证上式，只要证，即证即证，这显然成立.∴.再证明.∵，，要证上式，只要证，即证即证，这显然成立.∴.（3）猜想结论：存在一个常数，使得不等式对任意正数，，，恒成立.。

2016-2017年高二下期中考理科数学试题及答案

普宁二中(èr zhōnɡ)2016--2017学年度第二(dìèr)学期期中考高二级理科(lǐkē)数学试卷命题(mìng tí)人：陈木茂审题人：舒有汉祝考试(kǎoshì)顺利！一.选择题（本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的.）1.已知集合，则=（）.A. B. C. D.2.已知a，b是实数，则“a＞2且b＞2”是“a+b＞4且ab＞4”的（）.A．充分不必要条件 B．必要不充分条件C．充要条件 D．既不充分也不必要条件3.曲线在处的切线斜率为（）.A．1 B. C．2 D．4.已知函数则函数的零点所在区间为（）.A. B. C． D．a的公差为5.已知等差数列的前n项和为，且,则数列{}n（）.A.3B.4C.5D.66. 已知向量若则( ).A ．1B ．C ．D ．7. 阅读右边程序框图，则输出结果的值为（）. A ． B ． C. 0 D.8. 已知变量(bi ànli àng)满足(m ǎnz ú)约束条件则的取值范围(f ànw éi)是（）.A. B. C. D.9．函数(h ánsh ù)的图象(t ú xi àn ɡ)大致是（）.10.等腰直角三角形ABC 中，∠C=90°，AC=BC=1，点M ，N 分别是AB ，BC 中点，点P 是△ABC （含边界）内任意一点，则的取值范围是（）.A ．B ．C ．D ．11.已知函数的图像过点，为函数的导函数，为自然对数的底数，若，下恒成立，则不等式的解集为（）.开始s= 0 ,n= 1是否n n = +1输出 s 结束?71 0 2 ≤ n 3= s + s sinA． B． C．D．12．如图,网格纸上正方形小格的边长为1,图中粗线画出的是某几何体的三视图,则该几何体的体积为（）.A. B.C. D. 4二.填空题（本大题共4个小题，每小题5分，共20分.）13.观察下列各式：=125，=625，=3125，…，则的末三位数字为．14.已知复数(fùshù)满足(mǎnzú)，则．15.已知数列(shùliè)的前项和，，则．16.公元前3世纪(shìjì)，古希腊欧几里得在《几何原本》里提出：“球的体积（V）与它的直径(zhíjìng)（d）的立方成正比”，此即（）.与此类似，我们可以得到：(1)正四面体（所有棱长都相等的四面体）的体积（V）与它的棱长（a）的立方成正比，即；(2)正方体（正六面体）的体积（V）与它的棱长（a）的立方成正比，即；(3)正八面体（所有棱长都相等的八面体）的体积（V）与它的棱长（a）的立方成正比，即，那么．三、解答题（本大题共6小题，共70分，解答时应写出文字说明、证明过程或演算步骤.)17．（本小题满分12分）设函数.f x的单调递减区间；(6分)（1）求函数()（2）在△中，,,分别为内角,,的对边,,,,求△ABC的面积.(6分)18.（本小题满分12分）2017年元旦假期期间，调查公司在高速公路某服务区从七座以下小型汽车中按进服务区的先后每间隔50辆就抽取一辆的抽样方法抽取了40名驾驶员进行询问调查，将他们在某段高速公路的车速（km/t）分成六段：后得到如图的频率分布直方图．（1）该调查公司在采样中，用到的是什么(shén me)抽样方法？(2分)（2）求这40辆小型车辆车速(chē sù)的众数和中位数的估计值；(4分)（3）若从车速(chē sù)在的车辆(chēliàng)中任意抽取2辆，求车速(chē sù)在的车辆至少有一辆的概率.(6分)19.（本题满分12分）已知四棱锥S－ABCD的底面ABCD是边长为1正方形，SA⊥底面ABCD，E是SC上的任意一点．(1)求证：平面EBD⊥平面SAC；(5分)(2) 当SA的值为多少时，二面角B－SC－D的大小为120°？(7分)20.（本小题满分12分）设抛物线过点.（1）求抛物线C的方程；(3分)（2）过点作相互垂直的两条直线，，曲线C与交于点,,与l交于点,.证明：；(6分)2（3）在（2）中，我们得到关于抛物线的一个优美结论.请你写出关于椭圆的一个相类似的结论（不需证明）. (3分)21.（本小题满分12分）已知函数(hánshù)f x(1)求函数在点处的切线(qiēxiàn)方程；(3分) (2)求函数()单调(dāndiào)增区间；(3分)(3)若存在(cúnzài)，使得求实数(shìshù)的取值范围.(6分)22.（本题满分10分）选修4-5: 不等式选讲设函数. （1）解不等式；(5分) （2）若，使得，求实数的取值范围.(5分)2016-2017年高二下学期期中考理科数学参考答案一、选择题 1 2 3 4 5 6 7 8 9 10 11 12 C ADBCCBDCABB二、填空题13、125 14、15、5 16.三、解答题 17.解：（1）∵ …3分……………4分由，Z 知，∈k Z ……5分所以()f x 的单调递减区间为（∈k Z ） ……………6分（2）即又，所以，故，从而 ……8分由余弦定理(y ú xi án d ìn ɡ l ǐ)，得， …………9分又8b c +=，所以(su ǒy ǐ)…………10分由△ABC的面积(miàn jī)公式. …12分18. 解：（1）系统抽样……………………2分（2）众数的估计值为最高的矩形的中点(zhōnɡ diǎn)，即众数的估计值等于…4分设图中虚线(xūxiàn)所对应的车速为，则中位数的估计值为：，解得即中位数的估计值为77.5…………………6分(3) 从图中可知，车速在的车辆数为：（辆）………7分车速在[65,70)的车辆数为：（辆）…………………8分设“车速在[65,70)的车辆至少有一辆”为事件A,这是一个古典概型，记车速在[60,65)的车辆设为，车速在[65,70)的车辆为，则所有基本事件有：共15种…………………10分其中两辆车的车速均不在[65,70)的事件仅有一种，即车速在[65,70)的车辆至少有一辆的共14种，所以车速在的[65,70)车辆至少有一辆的概率为.故从车速在[60,70)的车辆中任意抽取2辆，车速在[65,70)的车辆至少有一辆的概率为.……12分19.证明：(1)∵SA⊥平面ABCD，BD⊂平面ABCD，∴SA⊥BD，…1分∵四边形ABCD是正方形，…2分∴AC⊥BD，…3分∴BD⊥平面SAC，…4分∵BD⊂平面EBD，∴平面EBD⊥平面SAC. …5分解：(2)设SA＝a，以A为原点，AB、AD、AS所在直线分别为x、y、z轴建立空间直角坐标系，……6分∵AB＝1，则C(1,1,0)，S(0,0，a)，B(1,0,0)，D(0,1,0)，∴＝(1,1，－a )，＝(1,0，－a )，＝(0,1，－a )，…………7分设平面(píngmiàn)SBC 、平面(píngmiàn)SCD 的法向量(xiàngliàng)分别为n 1＝(x 1，y 1，z 1)，n 2＝(x 2，y 2，z 2)，则∴y 1＝0，从而(cóng ér)可取x 1＝a ，则z 1＝1，∴n 1＝(a,0,1)， ……8分∴x 2＝0，从而(cóng ér)可取y 2＝a ，则z 2＝1，∴n 2＝(0，a,1)，…………9分 ∴cos 〈n 1，n 2〉＝1a 2＋1，要使二面角B －SC －D 为120°，则1a 2＋1＝12，即a ＝1. …11分即当SA ＝1时，二面角B －SC －D 的大小为120°. …………12分20.解：（1）把点)22,2( M 代入抛物线方程得所以曲线C 的方程为. ……………3分（2）显然直线1l ，2l 的斜率存在且不等于，不妨设1l 的方程为，，，由得，由韦达定理得：，， ……………5分因为曲线C 与1l 交于点1P ,2P 且1l 过焦点，所以， ……………7分同理可得， ……………8分所以. ……………9分（3）若1l ，2l 是过椭圆(tu ǒyu án)22:143x y Γ+=的焦点且相互垂直的两条直线(zh íxi àn)，其中椭圆与1l 交于点1P ,2P ,与2l 交于点1Q ,2Q ，则. ……………………12分说明(shu ōm íng):（只写出定值，没有(m éi y ǒu)指出定值为扣1分）21.解：⑴因为(y īn w èi)函数，所以，， (2)分又因为，所以函数()f x 在点(0,(0))f 处的切线方程为． (3)分 ⑵由⑴，．因为当时，总有在上是增函数， (4)分又(0)0f '=，所以不等式的解集为， (5)分故函数()f x 的单调增区间为(0,)∞+． …………6分⑶因为存在12,[1,1]x x ∈-，使得成立，而当时，，所以只要即可． …………7分又因为，，的变化情况如下表所示：()f x '()f x减函数极小值增函数所以()f x 在上是减函数，在上是增函数，所以(su ǒy ǐ)当时，的最小值， …………8分()f x 的最大值为和中的最大值．……9分因为(y īn w èi)，令，因为(y īn w èi)，所以(su ǒy ǐ)1()2ln g a a a a=--在上是增函数． …………10分而，故当时，，即；当时，，即． …………11分所以(su ǒy ǐ)，当1a >时，，即，函数在上是增函数，解得；当时，，即，函数在上是减函数，解得．综上可知，所求的取值范围为． (12)分22.解：（1）当时，，0)(>x f ，即，∴2-<x ；数学试题第11页共4页当时，， 0)(>x f ，即，解得，又21x -≤≤，∴；当时，， 0)(>x f ，即，不成立，∴.综上，不等式0)(>x f 的解集为. --------5分（2），∴. ∵R x ∈∃0，使得20()27f x m m +>，∴，整理得：，解得：，因此(y īnc ǐ)m 的取值范围(f ànw éi)是.--------10分内容总结（1）普宁二中2016--2017学年度第二学期期中考高二级理科数学试卷命题人：陈木茂审题人：舒有汉祝考试顺利（2）(3分) (2)求函数单调增区间（3）7分车速在的车辆数为：（辆）。

广东省中山市2016-2017学年高二下学期期末统一考试数

中山市高二级2016—2017学年度第二学期期末统一考试高二数学试卷（文科）本试卷共4页，22小题，满分150分．考试用时120分钟．注意事项：1、答卷前，考生务必用2B 铅笔在答题卡“考生号”处填涂考生号，用黑色字迹钢笔或签字笔将自己姓名、考生号、试室号、座位号填写在答题卡上．2、选择题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其它答案，答案不能答在试卷上．3、非选择题必须用黑色字迹钢笔或签字笔作答，答案必须写在答题卡各题目指定区域内相应位置上．如需改动，先划掉原来的答案，然后再写上新的答案．不准使用铅笔和涂改液．不按以上要求作答的答案无效．4、考生必须保持答题卡的整洁．考试结束，将答题卡交回，试卷不用上交．一、选择题（本大题共12小题，每小题5分，共60分．在每小题给出的四个备选项中，只有一项是符合题目要求的．） 1. 抛物线214y x =的焦点坐标为 A ．(10)-， B ．(10)，C ．(01)-，D ．(01)，2. 若复数z 满足2z i i z -=-⋅，则z =A ．1i -+B ．1i -C ．1i +D ．1i -- 3. 命题“0x ∃∈R ，20010x x -+≤”的否定为A ． 0x ∃∈R ，20010x x -+≤B ． 0x ∃∈R ，20010x x -+>C ． x ∀∈R ，210x x -+≤D ． x ∀∈R ，210x x -+>4．某研究型学习小组调查研究学生使用智能手机对学习的影响．部分统计数据如下表：附表：经计算2K 的观测值为10，则下列选项正确的是 ( ) A ．有99.5%的把握认为使用智能手机对学习有影响 B ．有99.5%的把握认为使用智能手机对学习无影响C ．在犯错误的概率不超过0.001的前提下认为使用智能手机对学习有影响D ．在犯错误的概率不超过0.001的前提下认为使用智能手机对学习无影响5. 用反证法证明：若整系数一元二次方程20(0)ax bx c a ++=≠有有理数根，那么,,a b c 中至少有一个是偶数．下列假设正确的是A ．假设,,a b c 都是偶数；B ．假设,,a b c 都不是偶数C ．假设,,a b c 至多有一个偶数D ．假设,,a b c 至多有两个偶数 6．函数2()ln f x x x =-的单调递减区间是A. ⎛ ⎝⎦B.⎫+∞⎪⎪⎣⎭C. ,2⎛-∞-⎝⎦，0,2⎛⎝⎦ D.22⎡-⎢⎣⎦7.执行如图所示的程序框图，若输出的S 的值为64，则判断框内应填入的条件是A ．3?k ≤B ．3?k <C ．4?k ≤D ．4?k >8. 已知F 为双曲线22:133x y C -=的一个焦点，则点F 到C 的一条渐近线的距离为AB ．3C ．D ．69．下表提供了某厂节能降耗技术改造后在生产A 产品过程中记录的产量x (吨)与相应的生产能耗y (吨)的几组对应数据，根据表中提供的数据，求出y 关于x 的线性回归方程为y ＝0.7x ＋0.35，则下列结论错误的是A. B ．t 的值是3.15C ．回归直线一定过(4.5,3.5)D ．A 产品每多生产1吨，则相应的生产能耗约增加0.7吨10．中国有个名句“运筹帷幄之中，决胜千里之外.”其中的“筹”原意是指《孙子算经》中记载的算筹，古代是用算筹来进行计算，算筹是将几寸长的小竹棍摆在平面上进行运算，算筹的摆放形式有纵横两种形式，如下表表示一个多位数时，像阿拉伯计数一样，把各个数位的数码从左到右排列，但各位数码的筹式需要纵横相间，个位，百位，万位数用纵式表示，十位，千位，十万位用横式表示，以此类推，例如6613用算筹表示就是：，则9117用算筹可表示为A.B． C ．D．11. 设1F ，2F 分别为双曲线：22221(0,0)x y a b a b-=>>的左右焦点，点2F 关于渐近线的对称点恰好落在以1F 为圆心,1OF 为半径圆上,则双曲线的离心率为A ．3BC ．2D12. 大衍数列，来源于中国古代著作《乾坤谱》中对易传“大衍之数五十”的推论．其前10项为：0、2、4、8、12、18、24、32、40、50．通项公式：221,2,2n n n a n n ⎧-⎪⎪=⎨⎪⎪⎩为奇数为偶数，如果把这个数列{}n a 排成如图形状，并记,A m n （）表示第m 行中从左向右第n 个数，则10,4A （）的值为A ．1200B ．1280C ．3528D ． 3612二、填空题（本大题共4小题，每小题5分，共20分，把答案填在答题卡相应横线上） 13. 一质点做直线运动，它所经过的路程和时间的关系是s =3t 2+t ，则t =2时的瞬时速度为 .14. 已知3x =是函数2ln 10y a x x x =+-的一个极值点，则实数a =15. 双曲线2216436y x -=上一点P 到它的一个焦点的距离等于3，那么点P 与两个焦点所构123456789纵式横式成的三角形的周长等于 .16. 已知函数()()2,ln 2f x x a g x x x =+=-，如果对任意的121,,22x x ⎡⎤∈⎢⎥⎣⎦，都有()()12f x g x ≤成立，则实数a 的取值范围是 .三、解答题（本大题共6小题，共70分，解答须写出文字说明、证明过程和演算步骤．） 17. （本小题满分10分）已知复数3z bi =+(b R ∈)，且(13)i z +⋅为纯虚数. （1）求复数z ；（2）若2ziω=+，求复数ω的模.18.（本小题满分12分）已知0>a ，设p ：实数x 满足22430x ax a -+<，q ：实数x 满足2(3)1x -<．（1）若1=a ，且q p ∧为真，求实数x 的取值范围；（2）若p ⌝是q ⌝的充分不必要条件，求实数a 的取值范围．19.（本小题满分12分）为了研究一种昆虫的产卵数y 和温度x 是否有关，现收集了7组观测数据列于下表中，并做出了散点图，发现样本点并没有分布在某个带状区域内，两个变量并不呈现线性相关关系，现分别用模型①212y C x C =+与模型；②34C x C y e +=作为产卵数y 和温度x 的回归方程来建立两个变量之间的关系.其中2i i t x =，7117i i t t ==∑，ln i i z y =，7117i i z z ==∑，附：对于一组数据11(,)μν，22(,)μν，……(,)n n μν，其回归直线v βμα=+的斜率和截距的最小二乘估计分别为：121()()()nii i nii μμννβμμ==--=-∑∑，ανβμ=-（1）根据表中数据，分别建立两个模型下y 关于x 的回归方程；并在两个模型下分别估计温度为30C时的产卵数.（1234,,,C C C C 与估计值均精确到小数点后两位）（参考数据：4.65 4.855.05104.58,127.74,156.02e e e ≈≈≈）（2）若模型①、②的相关指数计算分别为22120.82,0.96.R R ==，请根据相关指数判断哪个模型的拟合效果更好.20.（本小题满分12分）已知椭圆C ：2221(3x y a a +=>的右焦点为F ，右顶点为A ，设离心率为e ，且满足113e OF OA AF +=，其中O 为坐标原点．（1）求椭圆C 的方程；（2）过点(0,1)的直线l 与椭圆交于M ，N 两点，求△OMN 面积的最大值． 21. （本小题满分12分）设函数()ln ,kf x x k R x=+∈. （1）若曲线()y f x =在点()(),e f e 处的切线与直线20x -=垂直，求()f x 的单调区间（其中e 为自然对数的底数）；（2）若对任意()()1212120,x x f x f x x x >>-<-恒成立，求k 的取值范围.22. （本小题满分12分）对于命题P ：存在一个常数M ，使得不等式2222a b a bM a b b a a b b a+≤≤+++++对任意正数a ，b 恒成立.（1）试给出这个常数M 的值；（2）在（1）所得结论的条件下证明命题P ；（3）对于上述命题，某同学正确地猜想了命题Q ：“存在一个常数M ，使得不等式333333a b c a b cM a b b c c a a b b c c a++≤≤++++++++对任意正数a ，b ，c 恒成立．”观察命题P 与命题Q 的规律，请猜想与正数a ，b ，c ，d 相关的命题．中山市高二级2016—2017学年度第二学期期末统一考试高二数学试卷（文科）答案一、选择题： DCDAB AAABA CD 二、填空题：13．13； 15． 12； 15．42； 16．(,ln 28]-∞-. 三、解答题：17．解: (1) (13)(13)(3)(33)(9)i z i bi b b i +⋅=+⋅+=-++ ………………… 2分∵(13)i z +⋅为纯虚数，∴33090b b -=⎧⎨+≠⎩………………… 2分∴1b =，所以3z i =+ ………………… 5分(2)()()()()3i 2i 3i 7i 71i 2i 2i 2i 555+⋅-+-ω====-++⋅-, ………………… 8分∴ω==………………… 10分18.解：（1）由22430x ax a -+<得0)3)((<--a x a x当1=a 时，31<<x ，即p 为真时实数x 的取值范围是31<<x . …………2分由2(3)1x -<，得42<<x ，即q 为真时实数x 的取值范围是42<<x .………4分因为q p ∧为真，所以p 真且q 真，所以实数x 的取值范围是32<<x . …………6分(2) 由22430x ax a -+<得0)3)((<--a x a x ，所以，p 为真时实数x 的取值范围是a x a 3<<. …………8分因为 p ⌝是q ⌝的充分不必要条件，即q 是p 的充分不必要条件所以 2≤a 且a 34≤ …………10分所以实数a 的取值范围为：⎥⎦⎤⎢⎣⎡2,34. …………12分19. 解：（1）对于模型①：设2t x =，则21212y C x C C t C =+=+其中711721()()0.43()iii i i t t y y C t t ==--==-∑∑， ……………………… 1分21800.43692217.56C y C t =-=-⨯=- …………………… 3分所以20.43217.56y x =-， ………………… 4分当30x =时，估计产卵数为210.4330217.56169.44y =⨯-= …… 5分对于模型②：设ln z y =，则34ln y C x C =+其中713721()()0.32()iii ii z z x x C x x ==--==-∑∑，………………………………… 6分43 3.570.3226 4.75C z C x =-=-⨯=- ……………………… 8分所以0.32 4.75x y e -=， ………………………………… 9分当30x =时，估计产卵数为0.3230 4.75 4.852127.74y e e ⨯-===………… 10分（2）因为2212R R <，所以模型②的拟合效果更好 ………………………………… 12分20.解：（1）设椭圆的焦半距为c ，则|OF | = c ，|OA | = a ，|AF | =a c -．所以113e c a a c+=-，其中c e a =，又2223b a c ==-，联立解得2a =，1c =．所以椭圆C 的方程是22143x y +=． ………………………………………… 4分（2）由题意直线不能与x 轴垂直，否则将无法构成三角形． …………… 5分当直线l 与x 轴不垂直时，设其斜率为k ，那么l 的方程为1y kx =+．联立l 与椭圆C 的方程，消去y ，得22(43)880k x kx ++-=． Δ=22(8)32(43)k k ++，显然大于0．设点11(,)M x y ，22(,)N x y ．则122843k x x k +=-+，122843x x k =-+． ……… 7分所以12MN x =-=O 到l的距离d = 所以△OMN的面积12S d MN === ……… 10分令2433t k =+≥，那么S ==t = 3时取等．所以△OMN． ………………………………… 12分21.解：（1）由()ln k f x x x =+，知0x >，且()()210kf x x x x'=->，……1分因为曲线()y f x =在点()(),e f e 处的切线与直线2x =垂直，所以()0f e '=，所以210ke e -=，得k e =， ……3分所以()()2210e x e f x x x x x-'=-=>，令()0f x '<，得0x e <<，()f x 在()0,e 上单调递减；令()0f x '>，得x e >，()f x 在(),e +∞上单调递增，综上，()f x 的单调减区间为()0,e ,单调增区间为(),e +∞. ……5分（2）因为120x x >>，()()1212f x f x x x -<-恒成立，则有()()1122f x x f x x -<-，对120x x ∀>>恒成立， ……7分令()()()ln 0kg x f x x x x x x=-=+->，则()g x 在()0,+∞上单调递减，所以()2110kg x x x'=--≤在()0,+∞上恒成立， ……9分所以()2211024k x x x x ⎛⎫≥-+=--+> ⎪⎝⎭恒成立， ……10分令()21124h x x ⎛⎫=--+ ⎪⎝⎭，则()max 14k h x ≥=⎡⎤⎣⎦.所以k 的取值范围是1,4⎡⎫+∞⎪⎢⎣⎭. ……12分22. 解：（1）令a b =得：2233M ≤≤，故23M =； ……3分（2）先证明2223a b a b b a +≤++. ∵0a >，0b >，要证上式，只要证3(2)3(2)2(2)(2)a b a b a b a b b a +++≤++，即证222a b ab +≥ 即证2()0a b -≥，这显然成立. ∴2223a b a b b a +≤++. ……6分再证明2322a ba b b a≤+++. ∵0a >，0b >，要证上式，只要证3(2)3(2)2(2)(2)a a b b b a a b b a +++≥++，即证222a b ab +≥ 即证2()0a b -≥，这显然成立. ∴2322a ba b b a≤+++. ……9分（3）猜想结论：存在一个常数M ，使得不等式44444444a b c d a b c dM a b b c c d d a a b b c c d d a+++≤≤+++++++++++ 对任意正数a ，b ，c ，d 恒成立. ……12分。

湖北省孝感市七校教学联盟2016-2017学年高二下学期期末考试数学(理)试题-含解析

2016—2017学年度下学期孝感市七校教学联盟期末联合考试高二数学（理科）试卷本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分．第Ⅰ卷一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1. 设则“”是“”的A. 充分而不必要条件B. 必要而不充分条件C. 充要条件D. 既不充分也不必要条件【答案】B【解析】即;即..所以“”是“”的必要而不充分条件.2. 下列各式的运算结果为纯虚数的是A. B. C. D.【答案】C【解析】A.=i⋅2i=−2，是实数。

B.=−1+i，不是纯虚数。

C.=2i为纯虚数。

D.=i−1不是纯虚数。

故选：C.3. 已知命题；命题若,则．下列命题为真命题的是A. B. C. D.【答案】B【解析】命题成立。

故命题p为真命题；当a=1,b=−2时,成立，但a<b不成立，故命题q为假命题，...故命题p∧q，￢p∧q，￢p∧￢q均为假命题；命题p∧￢q为真命题，故选：B.4. 椭圆的离心率是A. B. C. D.【答案】B【解析】椭圆中.离心率，故选B.5. 已知直线的方向向量，平面的法向量，若，，则直线与平面的位置关系是A. 垂直B. 平行C. 相交但不垂直D. 直线在平面内或直线与平面平行【答案】D【解析】因为，即，所以直线在平面内或直线与平面平行，故选D．6. 已知双曲线（，）的一条渐近线方程为，且与椭圆有公共焦点．则的方程为A. B. C. D.【答案】B【解析】椭圆的焦点坐标(±3,0)，则双曲线的焦点坐标为(±3,0)，可得c=3，双曲线(a>0,b>0)的一条渐近线方程为，可得,即,可得,解得a=2,b=，所求的双曲线方程为：.7. 函数在上的最大值和最小值分别为A. B. C. D.【答案】A【解析】试题分析：对函数求导得，由于，所以在上是减函数，在上是增函数，而，所以在上的最大值和最小值分别是，故选A.考点：1、导数在函数研究中的应用；2、单调区间，极值.8. 若是正整数的值为A. B. C. D.【答案】D【解析】，故选D....9. 设函数的图象与轴相交于点，则曲线在点处的切线方程为A. B. C. D.【答案】C【解析】由，可令f()=0,即=1，解得=0可得P(0,0)，又f′()=−，∴f′(0)=−e0=−1.∴f()=1−在点P(0,0)处的切线方程为y−0=−1×(−0)，即y=−.故选：C.10. 已知，则的值为A. B. C. D.【答案】C.所以，故选C.11. 甲、乙、丙、丁四位同学一起去向老师询问成语竞赛的成绩，老师说，你们四人中有2位优秀，2位良好，我现在给甲看乙、丙的成绩，给乙看丙的成绩，给丁看甲的成绩，看后甲对大家说：我还是不知道我的成绩，根据以上信息，则A. 乙可以知道两人的成绩 B ．丁可能知道两人的成绩B. 乙、丁可以知道对方的成绩C. 乙、丁可以知道自己的成绩【答案】D【解析】四人所知只有自己看到，老师所说及最后甲说话，甲不知自己的成绩→乙丙必有一优一良,(若为两优,甲会知道自己的成绩;若是两良,甲也会知道自己的成绩) →乙看到了丙的成绩，知自己的成绩→丁看到甲、丁也为一优一良，丁知自己的成绩，故选：D.12. 已知函数的导函数满足，则对都有A. B. ...C. D.【答案】A【解析】构造函数F()=2f()，则F′()=2f()+2f′()=(2f()+f′())，当>0时,F′()>3>0,F()递增；当<0时,F′()<3<0,F()递减，所以F()=2f()在=0时取最小值，从而F()=2f()⩾F(0)=0，故选A.点睛：本题主要考查构造函数，常用的有：，构造f()；2f()+2f′()，构造2f()；，构造;，构造；，构造.等等.第Ⅱ卷二、填空题：本大题共4小题，每小题5分，共20分．13. 在数列中，()，猜想这个数列的通项公式是________．【答案】()【解析】试题分析：由已知，得，，，，．所以猜想该数列的通项公式为．考点：本题主要考查归纳推理的意义，递推数列。

2016-2017学年湖北省孝感市七校教学联盟高二(下)期末数学试卷(理科)(解析版)

2016-2017学年湖北省孝感市七校教学联盟高二（下）期末数学试卷（理科）一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．（5分）设x∈R，则“2﹣x≥0”是“|x﹣1|≤1”的（）A．充分而不必要条件B．必要而不充分条件C．充要条件D．既不充分也不必要条件2．（5分）下列各式的运算结果为纯虚数的是（）A．i（1+i）2B．i2（1﹣i）C．（1+i）2D．i（1+i）3．（5分）已知命题p：∃x∈R，x2﹣x+1≥0．命题q：若a2＜b2，则a＜b，下列命题为真命题的是（）A．p∧q B．p∧￢q C．￢p∧q D．￢p∧￢q 4．（5分）椭圆+＝1的离心率是（）A．B．C．D．5．（5分）已知直线l的方向向量，平面α的法向量，若＝（1，1，1），＝（﹣1，0，1），则直线l与平面α的位置关系是（）A．垂直B．平行C．相交但不垂直D．直线l在平面α内或直线l与平面α平行6．（5分）已知双曲线C：﹣＝1 （a＞0，b＞0）的一条渐近线方程为y＝x，且与椭圆+＝1有公共焦点，则C的方程为（）A．﹣＝1B．﹣＝1C．﹣＝1D．﹣＝17．（5分）函数y＝2x3﹣3x2﹣12x+5在区间[0，3]上最大值与最小值分别是（）A．5，﹣15B．5，﹣4C．﹣4，﹣15D．5，﹣168．（5分）若m是正整数的值为（）A．﹣1B．0C．1D．π9．（5分）设函数f（x）＝1﹣e x的图象与x轴相交于点P，则曲线在点P处的切线方程为（）A．ex+y＝0B．ex﹣y＝0C．x+y＝0D．y﹣x＝0 10．（5分）已知，则z的值为（）A．B．C．D．11．（5分）甲、乙、丙、丁四位同学一起去问老师询问成语竞赛的成绩．老师说：你们四人中有2位优秀，2位良好，我现在给甲看乙、丙的成绩，给乙看丙的成绩，给丁看甲的成绩．看后甲对大家说：我还是不知道我的成绩．根据以上信息，则（）A．乙可以知道四人的成绩B．丁可以知道四人的成绩C．乙、丁可以知道对方的成绩D．乙、丁可以知道自己的成绩12．（5分）已知函数f（x）的导函数f'（x）满足2f（x）+xf′（x）＞x2（x∈R），则对∀x∈R 都有（）A．x2f（x）≥0B．x2f（x）≤0C．x2[f（x）﹣1]≥0D．x2[f（x）﹣1]≤0二、填空题：本大题共4小题，每小题5分，共20分．13．（5分）在数列{a n}中，a1＝1，a n+1＝（n∈N*）猜想这个数列的通项公式为．14．（5分）函数y＝xlnx+1的单调减区间是．15．（5分）已知a∈R，设函数f（x）＝ax﹣lnx的图象在点（1，f（1））处的切线为l，则l 在y轴上的截距为．16．（5分）设动点P在棱长为1的正方体ABCD﹣A1B1C1D1的对角线BD1上，记＝λ．当∠APC为锐角时，λ的取值范围是．三、解答题：本大题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．17．（10分）（Ⅰ）求函数的导数；（Ⅱ）求．18．（12分）用反证法证明：如果，那么x2+2x﹣1≠0．19．（12分）如图，几何体是圆柱的一部分，它是由矩形ABCD（及其内部）以AB边所在直线为旋转轴旋转120°得到的，G是的中点．（Ⅰ）设P是上的一点，且AP⊥BE，求∠CBP的大小；（Ⅱ）当AB＝3，AD＝2，求二面角E﹣AG﹣C的大小．20．（12分）已知椭圆C的两个顶点分别为A（﹣2，0），B（2，0），焦点在x轴上，离心率为．（Ⅰ）求椭圆C的方程；（Ⅱ）点D为x轴上一点，过D作x轴的垂线交椭圆C于不同的两点M，N，过D作AM的垂线交BN于点E．求△BDE与△BDN的面积之比．21．（12分）圆柱型金属饮料罐的容积V一定时，它的高h与底面半径R具有怎样的关系时，才能使所用材料最省？22．（12分）已知函数f（x）＝alnx+（a∈R）在x＝2处的切线与直线4x+y＝0垂直．（Ⅰ）求函数f（x）的单调区间；（Ⅱ）若存在x∈（1，+∞），使f（x）（m∈Z）成立，求m的最小值．2016-2017学年湖北省孝感市七校教学联盟高二（下）期末数学试卷（理科）参考答案与试题解析一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．【解答】解：由2﹣x≥0得x≤2，由|x﹣1|≤1得﹣1≤x﹣1≤1，得0≤x≤2．则“2﹣x≥0”是“|x﹣1|≤1”的必要不充分条件，故选：B．2．【解答】解：A．i（1+i）2＝i•2i＝﹣2，是实数．B．i2（1﹣i）＝﹣1+i，不是纯虚数．C．（1+i）2＝2i为纯虚数．D．i（1+i）＝i﹣1不是纯虚数．故选：C．3．【解答】解：命题p：∃x＝0∈R，使x2﹣x+1≥0成立．故命题p为真命题；当a＝1，b＝﹣2时，a2＜b2成立，但a＜b不成立，故命题q为假命题，故命题p∧q，￢p∧q，￢p∧￢q均为假命题；命题p∧￢q为真命题，故选：B．4．【解答】解：椭圆+＝1，可得a＝3，b＝2，则c＝＝，所以椭圆的离心率为：＝．故选：B．5．【解答】解：∵•＝﹣1+1＝0，∴⊥，∴直线l在平面α内或直线l与平面α平行．故选：D．6．【解答】解：椭圆+＝1的焦点坐标（±3，0），则双曲线的焦点坐标为（±3，0），可得c＝3，双曲线C：﹣＝1 （a＞0，b＞0）的一条渐近线方程为y＝x，可得，即，可得＝，解得a＝2，b＝，所求的双曲线方程为：﹣＝1．故选：B．7．【解答】解：由题意y'＝6x2﹣6x﹣12令y'＞0，解得x＞2或x＜﹣1故函数y＝2x3﹣3x2﹣12x+5在（0，2）减，在（2，3）上增又y（0）＝5，y（2）＝﹣15，y（3）＝﹣4故函数y＝2x3﹣3x2﹣12x+5在区间[0，3]上最大值与最小值分别是5，﹣15故选：A．8．【解答】解：sin2mxdx＝（1﹣cos2mx）dx＝（x﹣sin2mx）＝π，故选：D．9．【解答】解：由1﹣e x＝0，解得x＝0，函数f（x）＝1﹣e x的图象与x轴相交于点P（0，0），函数f（x）＝1﹣e x的导数为f′（x）＝﹣e x，可得曲线在点P处的切线斜率为﹣e0＝﹣1，则曲线在点P处的切线方程为y＝﹣x，即有x+y＝0．故选：C．10．【解答】解：z1＝5+10i，z2＝3﹣4i，＝＝，则z＝．故选：C．11．【解答】解：四人所知只有自己看到，老师所说及最后甲说话，甲不知自己的成绩→乙丙必有一优一良，（若为两优，甲会知道自己的成绩；若是两良，甲也会知道自己的成绩）→乙看到了丙的成绩，知自己的成绩→丁看到甲、丁也为一优一良，丁知自己的成绩，给甲看乙丙成绩，甲不知道自已的成绩，说明乙丙一优一良，假定乙丙都是优，则甲是良，假定乙丙都是良，则甲是优，那么甲就知道自已的成绩了．给乙看丙成绩，乙没有说不知道自已的成绩，假定丙是优，则乙是良，乙就知道自己成绩．给丁看甲成绩，因为甲不知道自己成绩，乙丙是一优一良，则甲丁也是一优一良，丁看到甲成绩，假定甲是优，则丁是良，丁肯定知道自已的成绩了故选：D．12．【解答】解：构造函数F（x）＝x2f（x），则F'（x）＝2xf（x）+x2f'（x）＝x（2f（x）+xf'（x）），当x＞0时，F'（x）＞x3＞0，F（x）递增；当x＜0时，F'（x）＜x3＜0，F（x）递减，所以F（x）＝x2f（x）在x＝0时取最小值，从而F（x）＝x2f（x）≥F（0）＝0，故选：A．二、填空题：本大题共4小题，每小题5分，共20分．13．【解答】解：由a n+1＝得，，可知数列{}为公差为的等差数列，又＝1，所以＝，故（n∈N*）．故答案为：（n∈N*）．14．【解答】解：因为y＝f（x）＝xlnx+1，∴f'（x）＝lnx+1，∵x＞0∴当lnx+1＜0，即0＜x＜时，f'（x）＜0，f（x）递减．函数的单调减区间为：（0，）．故答案为：（0，）．15．【解答】解：函数f（x）＝ax﹣lnx，可得f′（x）＝a﹣，切线的斜率为：k＝f′（1）＝a﹣1，切点坐标（1，a），切线方程l为：y﹣a＝（a﹣1）（x﹣1），l在y轴上的截距为：a+（a﹣1）（﹣1）＝1．故答案为：1．16．【解答】解：由题设可知，建立如图所示的空间直角坐标系D﹣xyz，则有A（1，0，0），B（1，1，0），C（0，1，0），D（0，0，1）由＝（1，1，﹣1），得＝（λ，λ，﹣λ），所以＝（﹣λ，﹣λ，λ）+（1，0，﹣1）＝（1﹣λ，﹣λ，λ﹣1），＝（﹣λ，﹣λ，λ）+（0，1，﹣1）＝（﹣λ，1﹣λ，λ﹣1），所以∠APC为锐角等价于cos∠APC＞0，则等价于•＞0，即（1﹣λ）（﹣λ）+（﹣λ）（1﹣λ）+（λ﹣1）2＝（λ﹣1）（3λ﹣1）＞0，∵0≤λ＜1，∴，0≤λ＜因此，λ的取值范围是，故答案为．三、解答题：本大题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．17．【解答】解：（Ⅰ）；（Ⅱ）表示圆x2+y2＝a2与x轴所围成的上半圆的面积，因此．18．【解答】证明：假设x2+2x﹣1＝0，则x＝﹣1±，要证：，只需证：，只需证：上式显然成立，故有．而﹣1﹣，综上，﹣1+，﹣1﹣，都与已知相矛盾，因此假设不成立，也即原命题成立．19．【解答】（本小题满分12分）解：（Ⅰ）因为AP⊥BE，AB⊥BE，AB，AP⊂平面ABP，AB∩AP＝A，所以BE⊥平面ABP，…（2分）又BP⊂平面ABP，…（3分）所以BE⊥BP，又∠EBC＝120°，因此∠CBP＝30°…（4分）（Ⅱ）以B为坐标原点，分别以BE，BP，BA所在的直线为x，y，z轴，建立如图所示的空间直角坐标系．由题意得A（0，0，3）E（2，0，0），，，故，，，…（6分）设＝（x1，y1，z1）是平面AEG的一个法向量．由，得，取z1＝2，可得平面AEG的一个法向量＝（3，﹣，2）．…（8分）设＝（x2，y2，z2）是平面ACG的一个法向量．由，得，取z2＝﹣2，可得平面ACG的一个法向量＝（3，﹣，﹣2）．…（10分）所以cos＜＞＝＝．因此二面角E﹣AG﹣C的大小为60°．…（12分）20．【解答】解：（Ⅰ）∵焦点在x轴上，两个顶点分别为A（﹣2，0），B（2，0），∴a＝2，由，∴，∴b2＝a2﹣c2＝1，∴；（Ⅱ）设D（x0，0），M（x0，y0），N（x0，﹣y0），y0＞0，可得y02＝1﹣，直线AM的方程是，∵DE⊥AM，∴，直线DE的方程是，直线BN的方程是，直线BN与直线DE联立可得，，整理为：，即，即（x02﹣4）（x﹣x0）＝（x﹣2），解得x E＝，代入直线DE方程，求得y E＝﹣•＝﹣＝﹣y0，则＝又＝＝＝，则△BDE与△BDN的面积之比为4：5．21．【解答】（本小题满分12分）解：如图，饮料罐的表面积S＝2πRh+2πR2．…（2分）由V＝πR2h，得，则＝．（R＞0）…（4分）所以S＝＝3，当且仅当，即时，S取得最小值．…（10分）把代入，得，即h＝2R．…（11分）答：当饮料罐的高与底面的直径相等时，所用材料最省．…（12分）22．【解答】解：（Ⅰ），由已知，，解得：a＝1，∴，当x∈（0，1]时，f'（x）≤0，f（x）是减函数，当x∈[1，+∞）时，f'（x）≥0，f（x）是增函数，∴函数f（x）的单调递减区间是（0，1]，单调递增区间是[1，+∞）．（Ⅱ）解：∵x∈（1，+∞），∴等价于，即存在x∈（1，+∞），使成立，∴m＞g（x）min，设，则，设h（x）＝x﹣2﹣lnx（x＞1），则∴h（x）在（1，+∞）上单调递增，又h（3）＜0，h（4）＞0，∴h（x）在（1，+∞）上有唯一零点，设为x0，则x0﹣2＝lnx0，且x0∈（3，4），，又m＞x0+1，∴m的最小值是5．。

孝感市七校2016-2017学年高二下期末考试数学试题(理)含解析

2016—2017学年度下学期孝感市七校教学联盟期末联合考试高二数学（理科）试卷本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分．第Ⅰ卷一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1. 设则“”是“”的A. 充分而不必要条件B. 必要而不充分条件C. 充要条件D. 既不充分也不必要条件【答案】B【解析】即;即..所以“”是“”的必要而不充分条件.2. 下列各式的运算结果为纯虚数的是A. B. C. D.【答案】C【解析】A.=i⋅2i=−2，是实数。

B.=−1+i，不是纯虚数。

C.=2i为纯虚数。

D.=i−1不是纯虚数。

故选：C.3. 已知命题；命题若,则．下列命题为真命题的是A. B. C. D.【答案】B【解析】命题成立。

故命题p为真命题；当a=1,b=−2时,成立，但a<b不成立，故命题q为假命题，...故命题p∧q，￢p∧q，￢p∧￢q均为假命题；命题p∧￢q为真命题，故选：B.4. 椭圆的离心率是A. B. C. D.【答案】B【解析】椭圆中.离心率，故选B.5. 已知直线的方向向量，平面的法向量，若，，则直线与平面的位置关系是A. 垂直B. 平行C. 相交但不垂直D. 直线在平面内或直线与平面平行【答案】D【解析】因为，即，所以直线在平面内或直线与平面平行，故选D．6. 已知双曲线（，）的一条渐近线方程为，且与椭圆有公共焦点．则的方程为A. B. C. D.【答案】B【解析】椭圆的焦点坐标(±3,0)，则双曲线的焦点坐标为(±3,0)，可得c=3，双曲线(a>0,b>0)的一条渐近线方程为，可得,即,可得,解得a=2,b=，所求的双曲线方程为：.故选：B.7. 函数在上的最大值和最小值分别为A. B. C. D.【答案】A【解析】试题分析：对函数求导得，由于，所以在上是减函数，在上是增函数，而，所以在上的最大值和最小值分别是，故选A.考点：1、导数在函数研究中的应用；2、单调区间，极值.8. 若是正整数的值为A. B. C. D.【答案】D【解析】，故选D....9. 设函数的图象与轴相交于点，则曲线在点处的切线方程为A. B. C. D.【答案】C【解析】由，可令f(x)=0,即=1，解得x=0可得P(0,0)，又f′(x)=−，∴f′(0)=−e0=−1.∴f(x)=1−在点P(0,0)处的切线方程为y−0=−1×(x−0)，即y=−x.故选：C.10. 已知，则的值为A. B. C. D.【答案】C【解析】. 所以，故选C.11. 甲、乙、丙、丁四位同学一起去向老师询问成语竞赛的成绩，老师说，你们四人中有2位优秀，2位良好，我现在给甲看乙、丙的成绩，给乙看丙的成绩，给丁看甲的成绩，看后甲对大家说：我还是不知道我的成绩，根据以上信息，则A. 乙可以知道两人的成绩 B ．丁可能知道两人的成绩B. 乙、丁可以知道对方的成绩C. 乙、丁可以知道自己的成绩【答案】D【解析】四人所知只有自己看到，老师所说及最后甲说话，甲不知自己的成绩→乙丙必有一优一良,(若为两优,甲会知道自己的成绩;若是两良,甲也会知道自己的成绩)→乙看到了丙的成绩，知自己的成绩→丁看到甲、丁也为一优一良，丁知自己的成绩，故选：D.12. 已知函数的导函数满足，则对都有A. B. ...C. D.【答案】A【解析】构造函数F(x)=x2f(x)，则F′(x)=2xf(x)+x2f′(x)=x(2f(x)+xf′(x))，当x>0时,F′(x)>x3>0,F(x)递增；当x<0时,F′(x)<x3<0,F(x)递减，所以F(x)=x2f(x)在x=0时取最小值，从而F(x)=x2f(x)⩾F(0)=0，故选A.点睛：本题主要考查构造函数，常用的有：，构造xf(x)；2xf(x)+x2f′(x)，构造x2f(x)；，构造;，构造；，构造.等等.第Ⅱ卷二、填空题：本大题共4小题，每小题5分，共20分．13. 在数列中，()，猜想这个数列的通项公式是________．【答案】()【解析】试题分析：由已知，得，，，，．所以猜想该数列的通项公式为．考点：本题主要考查归纳推理的意义，递推数列。

湖北省孝感市七校教学联盟2016-2017学年高二下学期期末考试数学(理)试题-含解析

2016—2017学年度下学期孝感市七校教学联盟期末联合考试高二数学（理科）试卷本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分．第Ⅰ卷一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1. 设则“”是“”的A. 充分而不必要条件B. 必要而不充分条件C. 充要条件D. 既不充分也不必要条件【答案】B【解析】即;即..所以“”是“”的必要而不充分条件.2. 下列各式的运算结果为纯虚数的是A. B. C. D.【答案】C【解析】A.=i⋅2i=−2，是实数。

B.=−1+i，不是纯虚数。

C.=2i为纯虚数。

D.=i−1不是纯虚数。

故选：C.3. 已知命题；命题若,则．下列命题为真命题的是A. B. C. D.【答案】B【解析】命题成立。

故命题p为真命题；当a=1,b=−2时,成立，但a<b不成立，故命题q为假命题，...故命题p∧q，￢p∧q，￢p∧￢q均为假命题；命题p∧￢q为真命题，故选：B.4. 椭圆的离心率是A. B. C. D.【答案】B【解析】椭圆中.离心率，故选B.5. 已知直线的方向向量，平面的法向量，若，，则直线与平面的位置关系是A. 垂直B. 平行C. 相交但不垂直D. 直线在平面内或直线与平面平行【答案】D【解析】因为，即，所以直线在平面内或直线与平面平行，故选D．6. 已知双曲线（，）的一条渐近线方程为，且与椭圆有公共焦点．则的方程为A. B. C. D.【答案】B【解析】椭圆的焦点坐标(±3,0)，则双曲线的焦点坐标为(±3,0)，可得c=3，双曲线(a>0,b>0)的一条渐近线方程为，可得,即,可得,解得a=2,b=，所求的双曲线方程为：.7. 函数在上的最大值和最小值分别为A. B. C. D.【答案】A【解析】试题分析：对函数求导得，由于，所以在上是减函数，在上是增函数，而，所以在上的最大值和最小值分别是，故选A.考点：1、导数在函数研究中的应用；2、单调区间，极值.8. 若是正整数的值为A. B. C. D.【答案】D【解析】，故选D....9. 设函数的图象与轴相交于点，则曲线在点处的切线方程为A. B. C. D.【答案】C【解析】由，可令f()=0,即=1，解得=0可得P(0,0)，又f′()=−，∴f′(0)=−e0=−1.∴f()=1−在点P(0,0)处的切线方程为y−0=−1×(−0)，即y=−.故选：C.10. 已知，则的值为A. B. C. D.【答案】C. 所以，故选C.11. 甲、乙、丙、丁四位同学一起去向老师询问成语竞赛的成绩，老师说，你们四人中有2位优秀，2位良好，我现在给甲看乙、丙的成绩，给乙看丙的成绩，给丁看甲的成绩，看后甲对大家说：我还是不知道我的成绩，根据以上信息，则A. 乙可以知道两人的成绩 B ．丁可能知道两人的成绩B. 乙、丁可以知道对方的成绩C. 乙、丁可以知道自己的成绩【答案】D【解析】四人所知只有自己看到，老师所说及最后甲说话，甲不知自己的成绩→乙丙必有一优一良,(若为两优,甲会知道自己的成绩;若是两良,甲也会知道自己的成绩) →乙看到了丙的成绩，知自己的成绩→丁看到甲、丁也为一优一良，丁知自己的成绩，故选：D.12. 已知函数的导函数满足，则对都有A. B. ...C. D.【答案】A【解析】构造函数F()=2f()，则F′()=2f()+2f′()=(2f()+f′())，当>0时,F′()>3>0,F()递增；当<0时,F′()<3<0,F()递减，所以F()=2f()在=0时取最小值，从而F()=2f()⩾F(0)=0，故选A.点睛：本题主要考查构造函数，常用的有：，构造f()；2f()+2f′()，构造2f()；，构造;，构造；，构造.等等.第Ⅱ卷二、填空题：本大题共4小题，每小题5分，共20分．13. 在数列中，()，猜想这个数列的通项公式是________．【答案】()【解析】试题分析：由已知，得，，，，．所以猜想该数列的通项公式为．考点：本题主要考查归纳推理的意义，递推数列。