浅谈2005年高考数学试卷_全国卷_中的对称思想.kdh
2005年高考数学试卷 全国文科

2005年普通高等学校招生全国统一考试文科数学(全国卷Ⅱ)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
第Ⅰ卷1至2页。
第Ⅱ卷3到10页。
考试结束后,将本试卷和答题卡一并交回。
第Ⅰ卷注意事项:1.答第Ⅰ卷前,考生务必将自己的姓名、准考证号、考试科目涂写在答题卡上。
2.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号。
不能答在试题卷上。
3.本卷共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
参考公式:如果事件A 、B 互斥,那么 球是表面积公式)()()(B P A P B A P +=+ 24R S π=如果事件A 、B相互独立,那么 其中R 表示球的半径)()()(B P A P B A P ⋅=⋅ 球的体积公式如果事件A 在一次试验中发生的概率是P ,那么 334R V π= n 次独立重复试验中恰好发生k 次的概率 其中R 表示球的半径()(1)k K n k n n P k C P P -=-一、 选择题(1) 函数 |cos sin |)(x x x f +=的最小正周期是(A ) 4π (B) 2π (C) π (D)2π (2)正方体 ABCD-A 1B 1C 1D 1中P 、Q 、R 分别是AB 、AD 、B 1C 1的中点,那么,正方体的过P 、Q 、R 的截面图形是(A )三角形 (B)四边形 (C)五边形 (D)六边形(3)函数 )0(12≤-=x x y 反函数是 (A)1+=x y )1(-≥x (B)y = -1+x )1(-≥x(C)y =1+x )0(≥x (D)y =-1+x )0(≥x(4)已知函数wx y tan =在)2,2(ππ-内是减函数,则 (A)10≤<w (B)01<≤-w (C)1≥w (D)1-≤w(5)抛物线y x 42=上一点A 的纵坐标为4,则点A 与抛物线焦点的距离为(A) 2 (B) 3 (C) 4 (D) 5 (6)双曲线19422=-y x 的渐近线方程是 (A) x y 32±= (B) x y 94±= (C) x y 23±= (D)x y 49±= (7)如果数列||n a 是等差数列,则(A) 1345a a a a ++< (B)1345a a a a +=++(C)1345a a a a +>+ (D)1345a a a a = (8)10)2(y x -的展开式中46y x 项的系数是 (A)840 (B)-840 (C)210 (D) -210(9)已知点)0,3(),0,0(),1,3(C B A 设BAC ∠的平分线AE 与BC 相交于E,那么有λ=其中λ等于(A) 2 (B) 21 (C)-3 (D)31- (10)已知集合2{|47},{|60}M x x N x x x =-≤≤=-->则N M ⋂为(A){|4237}x x x -≤<-<≤或 (B){|4237}x x x -<≤-≤<或(C){|23}x x x ≤->或 (D){|23}x x x <-≥或(11)点P 在平面上作匀速直线运动,速度向量)3,4(-=v (即点P 的运动方向与v 相同,且每秒移动的距离|v |个单位).设开始时点P 的坐标为(-10,10),则5秒后点P 的坐标为(A)(-2,4) (B)(-30,25) (C)(10,-5) (D)(5,-10)(12)△ABC 的顶点B 在平面a 内,A 、C 在a 的同一侧,AB 、BC 与a 所成的角分别是30°和45°,若AB=3,BC=24 ,AC=5,则AC 与a 所成的角为(A)60° (B)45° (C)30° (D)15°第Ⅱ卷注意事项:1.用钢笔或圆珠笔直接答在试题卷上。
对2005年高考全国卷Ⅰ理科数学压轴题的再思考

对2005年高考全国卷Ⅰ理科数学压轴题的再思考发表时间:2009-07-22T15:42:12.357Z 来源:《中学课程辅导●教学研究》2009年第14期供稿作者:曹学锋[导读] 本文对一道高考数学题进行了再分析,旨在说明考试后的反思以及对典型考题的深层次思考和创造性见解的重要性。
对2005年高考全国卷Ⅰ理科数学压轴题的再思考曹学锋摘要:本文对一道高考数学题进行了再分析,旨在说明考试后的反思以及对典型考题的深层次思考和创造性见解的重要性。
关键词:数学;高考;再思考作者简介:曹学锋,任教于河南三门峡渑池高中数学组。
时间尽管过去了将近四年,关于这道题目的文章笔者也看了不少,大多数观点都局限于对命题组提供的两个标准答案(方法一和方法二)的讨论。
其实,通过笔者的深入研究,此题目的第二问有两个更为简捷的思路(方法三和方法四),特别是方法四,应该就是命题人站的高度。
平常大家都在说教学反思,其实,考试后的反思以及对典型考题的深层次思考和创造性见解也尤为重要,它可以重新定位数学教学活动中教师的角色,从而激发教师更积极主动地尝试新数学教育观下的教学实践。
Re-reflection on a Mathematics Item in 2005 NMMT Cao XuefengAbstract: This paper makes a re-analysis of mathematics items in NMMT, aiming at expounding the importance of reflection after exam and the importance of deep reflection and innovative ideas on typical mathematics items. Key words: mathematics; NMT; re-reflection。
2005年全国高考文科数学试题及答案(卷Ⅲ)

2005年普通高等学校招生全国统一考试文科数学(必修+选修Ⅰ)本试卷分第I 卷(选择题)和第II 卷(非选择题)两部分. 共150分. 考试时间120分钟.第I 卷参考公式: 如果事件A 、B 互斥,那么P (A+B )=P(A)+P(B) 如果事件A 、B 相互独立,那么P (A ·B )=P(A)·P(B)如果事件A 在一次试验中发生的概率是P ,那么 n 次独立重复试验中恰好发生k 次的概率P n (k)=C kn P k (1-P)n -k一、选择题:每小题5分,共60分. 1.已知α为第三象限角,则2α所在的象限是 ( )A .第一或第二象限B .第二或第三象限C .第一或第三象限D .第二或第四象限2.已知过点A(-2,m)和B(m ,4)的直线与直线2x+y-1=0平行,则m 的值为( )A .0B .-8C .2D .10 3.在8)1)(1(+-x x 的展开式中5x 的系数是( )A .-14B .14C .-28D .284.设三棱柱ABC-A 1B 1C 1的体积为V ,P 、Q 分别是侧棱AA 1、CC 1上的点,且PA=QC 1,则四棱锥B-APQC 的体积为 ( )A .16V B .14V C .13V D .12V 5.设713=x,则( )A .-2<x<-1B .-3<x<-2C .-1<x<0D .0<x<1 6.若ln 2ln 3ln 5,,235a b c ===,则( )A .a <b<cB .c<b<aC .c<a <bD .b<a <c球的表面积公式S=42R π其中R 表示球的半径, 球的体积公式V=334R π, 其中R 表示球的半径7.设02x π≤≤,sin cos x x =-,则 ( )A .0x π≤≤B .744x ππ≤≤C .544x ππ≤≤ D .322x ππ≤≤8.αααα2cos cos 2cos 12sin 22⋅+ =( )A .tan αB .tan 2αC .1D .129.已知双曲线1222=-y x 的焦点为F 1、F 2,点M 在双曲线上且120,MF MF ⋅=则点M 到 x 轴的距离为( )A .43 B .53C D 10.设椭圆的两个焦点分别为F 1、、F 2,过F 2作椭圆长轴的垂线交椭圆于点P ,若△F 1PF 2为等腰直角三角形,则椭圆的离心率是 ( )A B C .2 D 111.不共面的四个定点到平面α的距离都相等,这样的平面α共有 ( ) A .3个 B .4个 C .6个 D .7个12.计算机中常用十六进制是逢16进1的计数制,采用数字0~9和字母A ~F 共16个计数A .6EB .72C .5FD .B0第Ⅱ卷二.填空题:每小题4分,共(16分)13.经问卷调查,某班学生对摄影分别执“喜欢”、“不喜欢”和“一般”三种态度,其中执“一般”态度的比“不喜欢”态度的多12人,按分层抽样方法从全班选出部分学生座 谈摄影,如果选出的5位“喜欢”摄影的同学、1位“不喜欢”摄影的同学和3位执“一 般”态度的同学,那么全班学生中“喜欢”摄影的比全班人数的一半还多 人. 14.已知向量(,12),(4,5),(,10)OA k OB OC k ===-,且A 、B 、C 三点共线,则k= .15.曲线32x x y -=在点(1,1)处的切线方程为 .16.已知在△ABC 中,∠ACB=90°,BC=3,AC=4,P 是AB 上的点,则点P 到AC 、BC的距离乘积的最大值是 三.解答题:共74分. 17.(本小题满分12分)已知函数].2,0[,2sin sin 2)(2π∈+=x x x x f 求使()f x 为正值的x 的集合.18.(本小题满分12分)设甲、乙、丙三台机器是否需要照顾相互之间没有影响。
2005年普通高等学校招生全国统一考试数学及答案(江苏卷)

2005年普通高等学校招生全国统一考试数 学(江苏卷)第一卷(选择题 共60分)一、选择题:本大题共12小题,每小题5分,共60分. 在每小题给出的四个选项中,只有一项是符合题意要求的.(1)设集合{}12A =,,{}123B =,,,{}234C =,,,则()AB C =(A){}123,, (B){}124,, (C){}234,, (D){}1234,,, (2)函数123()x y x R -=+∈的反函数的解析表达式为(A)22log 3y x =- (B)23log 2x y -= (C)23log 2x y -= (D)22log 3y x=- (3)在各项都为正数的等比数列{}n a 中,首项13a =,前三项和为21,则345a a a ++=(A)33 (B)72 (C)84 (D)189 (4)在正三棱柱111ABC A B C -中,若2AB =,11AA =,则点A 到平面1A BC 的距离为(5)ABC ∆中,3A π=,3BC =,则ABC ∆的周长为(A))33B π++ (B))36B π++(C)6sin()33B π++ (D)6sin()36B π++ (6)抛物线24y x =上的一点M 到焦点的距离为1,则点M 的纵坐标是(A)1716 (B)1516 (C)78(D)0 (7)在一次歌手大奖赛上,七位评委为歌手打出的分数如下:94849499969497.,.,.,.,.,.,.,去掉一个最高分和一个最低分后,所剩数据的平均值和方差分别为(A)940484.,. (B)940016.,. (C)95004.,. (D)950016.,. (8)设αβγ,,为两两不重合的平面,l m n ,,为两两不重合的直线,给出下列四个命题:①若αγ⊥,βγ⊥,则//αβ;②若m α⊂,n α⊂,//m β,//n β,则//αβ;③若//αβ,l α⊂,则//l β;④若l αβ=,m βγ=,n γα=,//l γ,则//m n .其中真命题的个数是(A)1 (B)2 (C)3 (D)4(9)设12345k =,,,,,则5(2)x +的展开式中k x 的系数不可能是 (A)10 (B)40 (C)50 (D)80(10)若1sin()63πα-=,则2cos(2)3πα+= (A)97-(B)31- (C)31 (D)97(11)点(31)P -,在椭圆22221(0)yx a b a b+=>>的左准线上,过点P 且方向为(25)a =-,的光线经直线2-=y 反射后通过椭圆的左焦点,则这个椭圆的离心率为(A)33 (B)13 (C)22(D)12(12)四棱锥的8条棱代表8种不同的化工产品,有公共点的两条棱代表的化工产品放在同一仓库是危险的,没有公共顶点的两条棱所代表的化工产品放在同一仓库是安全的,现打算用编号为①、②、③、④的4个仓库存放这8种化工产品,那么安全存放的不同方法种数为 (A)96 (B)48 (C)24 (D)0二、填写题:本大题共6小题,每小题4分,共24分. 把答案填在答题卡相应位置. (13)命题“若a b >,则221a b >-”的否命题为 ▲ . (14)曲线31y x x =++在点(13),处的切线方程是 ▲ . (15)函数20.5log (43)y x x =-的定义域为 ▲ . (16)若[)30.6181a a k k =∈+,,,k Z ∈,则k = ▲ .(17)已知a b ,为常数,若2()43f x x x =++,2()1024f ax b x x +=++,则5a b -= ▲ . (18)在ABC ∆中,O 为中线AM 上一个动点,若2AM =,则()OA OB OC ⋅+的最小值是 ▲ . 三、解答题:本大题共5小题,共66分。
2005年全国1卷高考数学试卷(理科)q
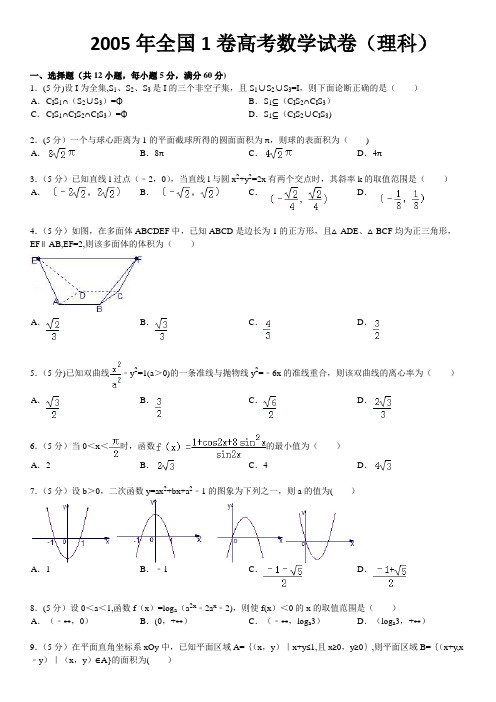
2005年全国1卷高考数学试卷(理科)一、选择题(共12小题,每小题5分,满分60分)1.(5分)设I为全集,S1、S2、S3是I的三个非空子集,且S1∪S2∪S3=I,则下面论断正确的是()A.C I S1∩(S2∪S3)=ΦB.S1⊆(C I S2∩C I S3)C.C I S1∩C I S2∩C I S3)=ΦD.S1⊆(C I S2∪C I S3)2.(5分)一个与球心距离为1的平面截球所得的圆面面积为π,则球的表面积为()A.B.8πC.D.4π3.(5分)已知直线l过点(﹣2,0),当直线l与圆x2+y2=2x有两个交点时,其斜率k的取值范围是()A.B.C.D.4.(5分)如图,在多面体ABCDEF中,已知ABCD是边长为1的正方形,且△ADE、△BCF均为正三角形,EF∥AB,EF=2,则该多面体的体积为()A.B.C.D.5.(5分)已知双曲线﹣y2=1(a>0)的一条准线与抛物线y2=﹣6x的准线重合,则该双曲线的离心率为()A.B.C.D.6.(5分)当0<x<时,函数的最小值为()A.2B.C.4D.7.(5分)设b>0,二次函数y=ax2+bx+a2﹣1的图象为下列之一,则a的值为()A.1B.﹣1 C.D.8.(5分)设0<a<1,函数f(x)=log a(a2x﹣2a x﹣2),则使f(x)<0的x的取值范围是()A.(﹣∞,0)B.(0,+∞)C.(﹣∞,log a3)D.(log a3,+∞)9.(5分)在平面直角坐标系xOy中,已知平面区域A={(x,y)|x+y≤1,且x≥0,y≥0},则平面区域B={(x+y,x ﹣y)|(x,y)∈A}的面积为()A.2B.1C.D.10.(5分)在△ABC中,已知tan=sinC,给出以下四个论断:①tanA•cotB=1,②1<sinA+sinB≤,③sin2A+cos2B=1,④cos2A+cos2B=sin2C,其中正确的是()A.①③B.②④C.①④D.②③11.(5分)过三棱柱任意两个顶点的直线共15条,其中异面直线有()A.18对B.24对C.30对D.36对12.(5分)复数=()A.﹣i B.i C.2﹣i D.﹣2+i二、填空题(共4小题,每小题4分,满分16分)13.(4分)若正整数m满足10m﹣1<2512<10m,则m=_________.(lg2≈0。
2005年高考全国卷1(文科数学)

2005年普通高等学校招生全国统一考试文科数学(全国卷Ⅰ)(适用:河北、河南、山西、安徽、海南)一、选择题 (本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求)1.2等于 A.i B.i -C.iD.i -2.设I 为全集,321S S S 、、是I 的三个非空子集,且123S S S I =,则下面论断正确的是A.123I C S S S =∅() B.122I I S C S C S ⊆() C.123(I I I C S C S C S =∅) D.122I I S C S C S ⊆() 3.一个与球心距离为1的平面截球所得的圆面面积为π,则球的表面积为 A.π28 B.π8 C.π24 D.π44.函数93)(23-++=x ax x x f ,已知)(x f 在3-=x 时取得极值,则a =A.2B.3C.4D.55.如图,在多面体ABCDEF 中,已知ABCD 是边长为1的正方形,且ADE ∆、 BCF ∆均为正三角形,EF ∥AB ,2EF =,则该多面体的体积为 A.32 B.33 C.34 D.236.已知双曲线2221x y a -=(0a >)的一条准线为23=x ,则该双曲线的离心率为 A.23 B.23 C.26 D.332 7.当20π<<x 时,函数x x x x f 2sin sin 82cos 1)(2++=的最小值为 A.2 B.32 C.4 D.34AB CD E F8.y =12x ≤≤)反函数是A.1y =11x -≤≤)B.1y =(01x ≤≤)C.1y =(11x -≤≤)D.1y =(01x ≤≤)9.设10<<a ,函数)22(log )(2--=x x a a a x f ,则使()0f x <的x 的取值范围是A.)0,(-∞B.),0(+∞C.)3log ,(a -∞D.),3(log +∞a10.在坐标平面上,不等式组131y x y x ≥-⎧⎪⎨≤-+⎪⎩所表示的平面区域的面积为 A.2 B.23 C.223 D.2 11.在ABC ∆中,已知C B A sin 2tan =+,给出以下四个论断: ①1cot tan =⋅B A ②2sin sin 0≤+<B A③1cos sin 22=+B A ④C B A 222sin cos cos =+其中正确的是A.①③B.②④C.①④D.②③12.点O 是ABC ∆所在平面内的一点,满足OA OB OB OC OC OA ⋅=⋅=⋅,则点O 是ABC ∆的A.三个内角的角平分线的交点B.三条边的垂直平分线的交点C.三条中线的交点D.三条高的交点二、本大题共4小题,每小题4分,共16分,把答案填在题中横线上.13.若正整数m 满足m m 102105121<<-,则m = .(lg 20.3010)≈ 14.81()x x-的展开式中,常数项为 .(用数字作答) 15.6名男生和4名女生中,选出3名代表,要求至少包含1名女生,则不同的选法有 种.16.在正方形1111ABCD A B C D -中,过对角线1BD 的一个平面交1AA 于E ,交1CC 于F ,则①四边形1BFD E 一定是平行四边形②四边形1BFD E 有可能是正方形③四边形1BFD E 在底面ABCD 内的投影一定是正方形④四边形1BFD E 有可能垂直于平面1BB D以上结论正确的为 .(写出所有正确结论的编号)三、解答题:本大题共6小题,共74分.解答应写出文字说明,证明过程或演算步骤.17.(本大题满分12分)设函数)(),0( )2sin()(x f y x x f =<<-+=ϕπϕ图像的一条对称轴是直线8π=x . (Ⅰ)求ϕ;(Ⅱ)求函数)(x f y =的单调增区间;(Ⅲ)画出函数)(x f y =在区间[0,]π上的图像.18.(本大题满分12分)已知四棱锥P ABCD -的底面为直角梯形,AB ∥DC ,90DAB ∠=,PA ⊥底面ABCD ,且112PA AD AB ===,M 是PB 的中点。
2005年高考全国卷(河北(共6页)
2005年高考(ɡāo kǎo)·全国卷Ⅰ(河北(hé běi)、河南、安徽、山西)理科数学(shùxué)试卷(shìjuàn)2005年普通高考全国(quán ɡuó)数学卷(一)考区(河北理科卷)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
第Ⅰ卷1至2页。
第Ⅱ卷3到10页。
考试结束后,将本试卷和答题卡一并交回。
第Ⅰ卷注意事项:1.答第Ⅰ卷前,考生务必将自己的姓名、准考证号、考试科目涂写在答题卡上。
2.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号。
不能答在试题卷上。
3.本卷共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
参考公式:如果事件A、B互斥,那么球是表面积公式如果事件A、相互独立,那么其中R表示球的半径球的体积公式如果事件A在一次试验中发生的概率是P,那么n次独立重复试验中恰好发生k次的概率其中R表示球的半径一.选择题(1)设为全集,是I的三个非空子集,且,则下面论断正确的是()(A)(B)(C)(D)(2)一个与球心距离为1的平面截球所得的圆面面积为,则球的表面积为()(A)(B)(C)(D)(3)已知直线过点,当直线l与圆有两个交点时,其斜率k的取值范围是()(A)(B)(C)(D)(4)如图,在多面体ABCDEF中,已知ABCD是边长为1的正方形,且均为正三角形(zhènɡ sān jiǎo xínɡ),EF∥AB,EF=2,则该多面体的体积(tǐjī)为()(A)(B)(C)(D)(5)已知双曲线的一条(yī tiáo)准线与抛物线的准线重合(chóngh é),则该双曲线的离心率为()(A ) (B )23 (C )(D )(6)当时,函数(h ánsh ù)的最小值为( ) (A )2(B )(C )4(D )(7)设,二次函数的图像为下列之一则的值为 (A )(B )(C )(D )(8)设,函数(h ánsh ù),则使的的取值范围(f ànw éi)是()(A )(B ) (C ) (D )(9)在坐标(zu òbi āo)平面上,不等式组所表示的平面(p íngmi àn)区域的面积为()(A ) (B )23 (C )(D )2 (10)在中,已知,给出以下(y ǐxi à)四个论断: ① ②③④其中正确的是 (A )①③(B )②④(C )①④(D )②③(11)过三棱柱任意两个顶点的直线共15条,其中异面直线有() (A )18对(B )24对(C )30对(D )36对(12)复数=( ) (A )(B )(C )(D )第Ⅱ卷注意事项:1.用钢笔(g āngb ǐ)或圆珠笔直接答在试题卷上。
N02--2005年普通高等学校招生全国统一考试数学及详细解析(山东卷.理)
2005年普通高等学校招生全国统一考试(山东卷)理科数学(必修+选修II )第I 卷(共60分)参考公式:如果事件A 、B 互斥,那么()()()P A B P A P B +=+如果事件A 、B 相互独立,那么()()()P A B P A P B ⋅=一.选择题:本大题共12小题,每题5分,共60分,在每小题给出的四个选项中,选择一个符合题目要求的选项.(1)2211(1)(1)i ii i -++=+-(A )i (B )i - (C )1 (D )1-(2)函数1(0)xy x x-=≠的反函数图像大致是(A ) (B ) (C ) (D )(3)已知函数sin()cos()1212y x x ππ=--,则下列判断正确的是(A )此函数的最小周期为2π,其图像的一个对称中心是(,0)12π(B )此函数的最小周期为π,其图像的一个对称中心是(,0)12π(C )此函数的最小周期为2π,其图像的一个对称中心是(,0)6π(D )此函数的最小周期为π,其图像的一个对称中心是(,0)6π(4)下列函数既是奇函数,又在区间[]1,1-上单调递减的是 (A )()sin f x x = (B )()1f x x =-+ (C )1()()2x x f x a a -=+ (D )2()ln 2x f x x-=+ (5)如果(3n x -的展开式中各项系数之和为128,则展开式中31x 的系数是 (A )7 (B )7- (C )21 (D )21-(6)函数21sin(),10(),0x x x f x e x π-⎧-<<⎪=⎨≥⎪⎩,若(1)()2,f f a +=则a 的所有可能值为(A )1 (B )-(C )1,- (D ) (7)已知向量,a b ,且2,56AB a b BC a b =+=-+,72CD a b =-,则一定共线的三点是(A )A 、B 、D (B )A 、B 、C (C )B 、C 、D (D )A 、C 、D(8)设地球的半径为R ,若甲地位于北纬45︒东经120︒,乙地位于南纬75︒东经120︒,则甲、乙两地的球面距离为(A(B )6R π(C )56R π(D )23R π (9)10张奖券中只有3张有奖,5个人购买,至少有1人中奖的概率是(A )310 (B )112 (C )12 (D )1112(10)设集合A 、B 是全集U 的两个子集,则A B ≠⊂是()U C A B U ⋃=的(A )充分不必要条件(B )必要不充分条件(C )冲要条件(D )既不充分也不必要条件 (11)01a <<,下列不等式一定成立的是(A )(1)(1)log (1)log (1)2a a a a +--++> (B )(1)(1)log (1)log (1)a a a a +--<+(C )(1)(1)log (1)log (1)a a a a +--++<(1)(1)log (1)log (1)a a a a +--++ (D )(1)(1)log (1)log (1)a a a a +---+>(1)(1)log (1)log (1)a a a a +---+(12)设直线:220l x y ++=关于原点对称的直线为l ',若l '与椭圆2214y x +=的交点为A 、B 、,点P 为椭圆上的动点,则使PAB ∆的面积为12的点P 的个数为(A )1 (B )2 (C )3 (D )4第II 卷(共90分)二.填空题:本大题共4小题,每小题4分,共16分.答案须填在题中横线上.(13)2222lim__________(1)n n nn C C n -→∞+=+. (14)设双曲线22221(0,0)x y a b a b-=>>的右焦点为F ,右准线l 与两条渐近线交于P 、Q两点,如果PQF ∆是直角三角形,则双曲线的离心率___________e =.(15)设x 、y 满足约束条件5,3212,03,0 4.x y x y x y +≤⎧⎪+≤⎪⎨≤≤⎪⎪≤≤⎩则使得目标函数65z x y =+的最大的点(,)x y 是____________(16)已知m n 、是不同的直线,αβ、是不重合的平面,给出下列命题:①若//,m αβα⊂,n β⊂则//m n ;②若,,//,m n m αβ⊂则//αβ③若,,//m n m n αβ⊥⊥,则//αβ④,m n 是两条异面直线,若//,//,//,//m m n n αβαβ,则//αβ上面的命题中,真命题的序号是______(写出所有真命题的序号)三.解答题:本大题共6小题,共74分.解答写出文字说明,证明过程或演算步骤. (17)(本小题满分12分)已知向量(cos ,sin )m θθ=和(2sin ,cos ),(,2)n θθθππ=-∈,且82m n +=求A1A BCD1B F1C 1D Ecos(28θπ+的值.(18)(本小题满分12分)袋中装有黑球和白球共7个,从中任取2个球都是白球的概率为1,7现有甲、乙两人从袋中轮流摸取1球,甲先取,乙后取,然后甲再取……取后不放回,直到两人中有一人取到白球时既终止,每个球在每一次被取出的机会是等可能的,用ξ表示取球终止所需要的取球次数.(I )求袋中原有白球的个数; (II )求随机变量ξ的概率分布; (III )求甲取到白球的概率. (19)(本小题满分12分)已知1x =是函数32()3(1)1f x mx m x nx =-+++的一个极值点,其中,,0m n R m ∈<,(I )求m 与n 的关系式; (II )求()f x 的单调区间;(III )当[]1,1x ∈-时,函数()y f x =的图象上任意一点的切线斜率恒大于3m ,求m 的取值范围.(20)(本小题满分12分)如图,已知长方体1111,ABCD A B C D -12,1,AB AA ==直线BD 与平面11AA B B 所成的角为30︒,AE 垂直BD 于E ,F 为11A B 的中点.(I )求异面直线AE 与BF 所成的角;(II )求平面BDF 与平面1AA B 所成的二面角; (III )求点A 到平面BDF 的距离. (21)(本小题满分12分)已知数列{}n a 的首项15,a =前n 项和为n S ,且*15()n n S S n n N +=++∈(I )证明数列{}1n a +是等比数列;(II )令212()n n f x a x a x a x =+++,求函数()f x 在点1x =处的导数(1)f '并比较2(1)f '与22313n n -的大小.(22)(本小题满分14分)已知动圆过定点,02p ⎛⎫⎪⎝⎭,且与直线2p x =-相切,其中0p >.(I )求动圆圆心C 的轨迹的方程;(II )设A 、B 是轨迹C 上异于原点O 的两个不同点,直线OA 和OB 的倾斜角分别为α和β,当,αβ变化且αβ+为定值(0)θθπ<<时,证明直线AB 恒过定点,并求出该定点的坐标.2005年普通高等学校招生全国统一考试(山东卷)(试题参考答案)理科数学(必修+选修II )一.选择题1. [答案] D[思路] 本题考查复数的概念和基本运算,()()221111iii i -++=+-111112222i i i ii i -+---++=+=--. 2. [答案] B[思路] 本题考查反函数的概念及函数的图象。
2005年普通高等学校招生全国统一考试数学及详细解析(全国卷Ⅰ.理)
2005年普通高等学校招生全国统一考试 理科数学(全国卷Ⅰ)河南河北山西安徽第Ⅰ卷参考公式:如果事件A 、B 互斥,那么 球的表面积公式)()()(B P A P B A P +=+ 2π4R S =如果事件A 、相互独立,那么 其中R 表示球的半径)()()(B P A P B A P ⋅=⋅ 球的体积公式 如果事件A 在一次试验中发生的概率是P ,那么3π34R V =n 次独立重复试验中恰好发生k 次的概率 其中R 表示球的半径kn k n P P k P --=)1(C )(k n 一.选择题 (1)复数=--i21i 23( )(A )i(B )i -(C )i 22-(D )i 22+-【解析】∵i i21i i)21(i21i 2i21i 23=--=-+=--,故选A .【点拨】对于复数运算应先观察其特点再计算,会简化运算.(2)设I 为全集,321S S S 、、是I 的三个非空子集,且I S S S =321 ,则下面论断正确的是( )(A )123I S S S =∅() (B )12I I S S ⊆((C)123I IIS S S =∅(D )12I IS S ⊆(【解析】∵2323()I II S S S S =所表示的部分是图中蓝色的部分,1I S 所表示的部分是图中除去1S 的部分,∴123123(I III I IS S S S S S ==∅),故选C .【点拨】利用韦恩图求解.(3)一个与球心距离为1的平面截球所得的圆面面积为π)(A )π28 (B )π8 (C )π24(D )π4【解析】∵截面圆面积为π,∴截面圆半径1=r ,∴球的半径为2221=+=r OO R ,∴球的表面积为π8,故选B. 【点拨】找相关的直角三角形.(4)已知直线l 过点)02(,-,当直线l 与圆x y x 222=+有两个交点时,其斜率k 的取值范围是( )(A )),(2222-(B )),(22-(C )),(4242- (D )),(8181-将x y x 222=+化为1)1(22=+-y x , ∴该圆的圆心为)0,1(,半径1=r ,设直线的方程为)2(+=x k y ,即02=+-k y kx ,设直线l 到圆心的距离为d ,则 ∵直线l 与圆x y x 222=+有两个交点,∴r d ≤, ∴11|2|2≤++=k k k d ,∴4242≤≤-k .故选C . 【点拨】利用圆心到直线的距离解直线与圆的位置关系.(5)如图,在多面体ABCDEF 中,已知ABCD 是边长为1的正方形,且BCF ADE ∆∆、均为正三角形,EF ∥AB ,EF =2,则该多面体的体积为( ) (A )32(B )33 (C )34(D )23【解析】过A 、B 两点分别作AM 、BN 垂直于EF ,垂足分别为M 、N ,连结DM 、CN ,可证得DM ⊥EF 、CN ⊥EF ,多面体ABCDEF 分为三部分,多面体的体积V 为+=-BNC AMD ABCDEF V VBNC F AMD E V V --+,∵21=NF ,1=BF ,∴23=BN ,作NH 垂直于点H ,则H 为BC的中点,则22=NH ,∴4221=⋅⋅=∆NH BC S BNC ,∴24231=⋅⋅=∆-NF S V BNC BNC F ,242==--BNC F AMD E V V ,42=⋅=∆-MN S V BNC BNC AMD ,∴32=ABCDEF V ,故选A .【点拨】将不规则的多面体分割或补全为规则的几何体进行计算.(6)已知双曲线)0( 1222>=-a y ax 的一条准线与抛物线x y 62-=的准线重合,则该双曲线的离心率为( )(A )23 (B )23 (C )26 (D )332 【解析】由)0( 1222>=-a y ax 得1=b ,∴221c a =+,抛物线x y 62-=的准线为23=x ,因为双曲线)0( 1222>=-a y ax 的一条准线与抛物线x y 62-=的准线重合,所以232=c a ,解得2=c ,所以3=a ,所以离心率为33232===a c e ,故选D . 【点拨】熟悉圆锥曲线各准线方程.(7)当2π0<<x 时,函数x x x x f 2sin sin 82cos 1)(2++=的最小值为( )(A )2 (B )32 (C )4 (D )34【解析】x xx x x x x x x x x x f cos sin 4sin cos cos sin 2sin 8cos 22sin sin 82cos 1)(222+=+=++= 4cos sin 4sin cos 2=⋅≥x x x x ,当且仅当x x x x cos sin 4sin cos =,即21tan =x 时,取“=”,∵2π0<<x ,∴存在x 使21tan =x ,这时4)(max =x f ,故选.【点拨】熟练运用三角函数公式进行化简运算.E FA BCDM N H(8)设0>b ,二次函数122-++=a bx ax y 的图像为下列之一则a(A )1(B )1-(C )251-- (D)251+- 【解析】∵0>b ,∴图像不能以轴为对称轴,∴一、二两个图不符;第四个图可知,0>a ,故其对称轴为02<-=abx ,所以也不符合;只有第三个图可以,由图象过原点,得012=-a ,开口向下,所以1-=a ,故选B .【点拨】熟悉二次函数图象的特点,分析对称轴、与轴的交点等形与数的关系.(9)设10<<a ,函数)22(log )(2--=x x a a a x f ,则使0)(<x f 的x 的取值范围是( )(A ))0,(-∞(B )),0(∞+(C ))3log ,(a -∞(D )),3(log ∞+a【解析】∵10<<a ,0)(<x f ,∴1222>--x x a a ,解得 3>x a 或1-<x a (舍去), ∴3log a a <,故选C . 【点拨】熟悉对数的性质. (10)在坐标平面上,不等式组⎩⎨⎧+-≤-≥1||31x y x y 所表示的平面区域的面积为( )(A )2(B )23(C )223 (D )2 【解析】原不等式化为⎩⎨⎧≥+-≤-≥)0(,131x x y x y 或⎩⎨⎧<+≤-≥)0(,131x x y x y ,所表示的平面区域如右图所示,)2,1(--A ,)21,21(-B , ∴23=S 【点拨】分类讨论,通过画出区域,计算面积. (11)在ABC ∆中,已知C BA sin 2tan=+,给出以下四个论断: ①1cot tan =⋅B A ②2sin sin 0≤+<B A ③1cos sin 22=+B A ④C B A 222sin cos cos =+其中正确的是( ) (A )①③ (B )②④(C )①④(D )②③【解析】∵2sin2cos2cot 2πtan 2tan C CC C B A ==-=+,2cos 2sin 2sin C C C =, ∴222sin =C ,∴︒=90C ,∵A B A 2tan cot tan =⋅,∴①不一定成立,∵=+=+A A B A cos sin sin sin )sin(2θ+A ,∴2sin sin 0≤+<B A ,∴②成立,∵A A A B A 22222sin 2sin sin cos sin =+=+,∴③不一定成立,∵C A A B A 22222sin 1sin cos cos cos ==+=+,∴④成立,故选B .【点拨】考查三角公式的灵活运用.(12)过三棱柱任意两个顶点的直线共15条,其中异面直线有( )(A )18对 (B )24对 (C )30对 (D )36对 【解析】解法一:(直接法)①与上底面的11B A 、11C A 、11C B 成异面直线的有15对;②与下底面的AB 、AC 、BC 成异面直线的有9对(除去与上底面的); ③与侧棱1AA 、1BB 、1CC 成异面直线的有6对(除去与上下底面的);④侧面对角线之间成异面直线的有6对; 所以异面直线总共有36对. 解法二:(间接法)①共一顶点的共面直线有60C 625=对; ②侧面互相平行的直线有6对; ③侧面的对角线有3对共面;所以异面直线总共有363660C 215=---对. 【点拨】解排列组合题的关键是分好类.第Ⅱ卷二.本大题共4小题,每小题4分,共16分,把答案填在题中横线上.(13)若正整数m 满足m m 102105121<<-,则m = 155 .)3010.02(lg ≈ 【解析】∵m m 102105121<<-,∴m m 10lg 2lg 10lg 5121<<-,即m m <<-2lg 5121,∴m m <<-112.1541,即 112.155112.154<<m ,∴155=m .【点拨】把指数形式化成对数形式.(14)9)12(xx -的展开式中,常数项为 672 .(用数字作答) 【解析】9)12(xx -的通项公式为23999992C )1()1()2(C rrr r r rrx xx ---⋅⋅⋅-=-⋅⋅,令0239=-r 得,6=r ,∴常数项为6722C )1(69696=⋅⋅-- 【点拨】熟悉二项式定理的展开式的通项公式.(15)ABC ∆的外接圆的圆心为O ,两条边上的高的交点为H ,)(m ++=,则实数=m .【解析】(特例法)设ABC ∆为一个直角三角形,则O 点斜边的中点,H 点为直角顶点,这时有OH ++=,∴1=m .【点拨】由特殊情况去检验一般情况.1A 1B 1C ABC(16)在正方体''''D C B A ABCD -中,过对角线'BD 的一个平面交'AA 于E ,交'CC 于F ,则①四边形E BFD '一定是平行四边形 ②四边形E BFD '有可能是正方形③四边形E BFD '在底面ABCD 内的投影一定是正方形 ④四边形E BFD '有可能垂直于平面D BB '以上结论正确的为 .(写出所有正确结论的编号) 【解析】①平面E BFD '与相对侧面相交,交线互相平行,∴四边形E BFD '一定是平行四边形;②四边形E BFD '若是正方形,则D E BE '⊥,又EB AD ⊥,∴⊥EB 平面A ADD ',产生矛盾;③四边形E BFD '在底面ABCD 内的投影是正方形ABCD ;④当E 、F 分别是'AA 、'CC 的中点时,AC EF //,又⊥AC 平面D BB ',∴四边形E BFD '有可能垂直于平面D BB '; 【点拨】边观察、边推导.三.解答题:本大题共6小题,共74分.解答应写出文字说明,证明过程或演算步骤. (17)(本大题满分12分)设函数)(),0π( )2sin()(x f y x x f =<<-+=ϕϕ图像的一条对称轴是直线8π=x . (Ⅰ)求ϕ;(Ⅱ)求函数)(x f y =的单调增区间;(Ⅲ)证明直线025=+-c y x 于函数)(x f y =的图像不相切.(18)(本大题满分12分)已知四棱锥P -ABCD 的底面为直角梯形,AB ∥DC ,⊥=∠PA DAB ,90底面ABCD ,且P A =AD =DC =21AB =1,M 是PB 的中点. (Ⅰ)证明:面P AD ⊥面PCD ; (Ⅱ)求AC 与PB 所成的角;(Ⅲ)求面AMC 与面BMC 所成二面角的大小. (19)(本大题满分12分)设等比数列{}n a 的公比为q ,前n 项和),2,1( 0 =>n S n . (Ⅰ)求q 的取值范围; (Ⅱ)设1223++-=n n n a a b ,记{}n b 的前n 项和为n T ,试比较n S 与n T 的大小.(20)(本大题满分12分)9粒种子分种在3个坑内,每坑3粒,每粒种子发芽的概率为5.0,若一个坑内至少有1粒种子发芽,则这个坑不需要补种,若一个坑内的种子都没发芽,则这个坑需要补种.假定每个坑至多补种一次,每补种1个坑需10元,用ξ表示补种费用,写出ξ的分布列并求ξ的数学期望.(精确到01.0)ABD PMABCDA 'B 'C 'D 'EF(21)(本大题满分14分)已知椭圆的中心为坐标原点O ,焦点在x 轴上,斜率为1且过椭圆右焦点F 的直线交椭圆于A 、B 两点,+与)1,3(-=a 共线. (Ⅰ)求椭圆的离心率;(Ⅱ)设M 为椭圆上任意一点,且),( R ∈+=μλμλ,证明22μλ+为定值.(22)(本大题满分12分)(Ⅰ)设函数)10( )1(log )1(log )(22<<--+=x x x x x x f ,求)(x f 的最小值; (Ⅱ)设正数n p p p p 2321,,,, 满足12321=++++n p p p p ,证明:np p p p p p p p n n -≥++++222323222121log log log log。
2005年高考理科数学全国卷Ⅱ试题含答案(黑龙江、吉林、广西、内蒙古、新疆等地区用)
2005年高考理科数学全国卷Ⅱ试题及答案(黑龙江吉林广西内蒙古新疆)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分1至2页第Ⅱ卷3到10页考试结束后,将本试卷和答题卡一并交回第Ⅰ卷注意事项:1.答第Ⅰ卷前,考生务必将自己的姓名、准考证号、考试科目涂写在答题卡上2.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑如需改动,用橡皮擦干净后,再选涂其它答案标号不能答在试题卷上3.本卷共12小题,每小题5分,共60分在每小题给出的四个选项中,只有一项是符合题目要求的 参考公式:如果事件A 、B 互斥,那么 球是表面积公式)()()(B P A P B A P +=+ 24R S π=如果事件A 、B相互独立,那么 其中R 表示球的半径)()()(B P A P B A P ⋅=⋅ 球的体积公式如果事件A 在一次试验中发生的概率是P ,那么334R V π=n 次独立重复试验中恰好发生k 次的概率 其中R 表示球的半径 ()(1)kKn kn n P k C P P −=−一、选择题(1)函数()sin cos f x x x =+的最小正周期是(A )4π (B )2π(C )π (D )2π (2)正方体1111ABCD A B C D −中,P 、Q 、R 分别是AB 、AD 、11B C 的中点.那么,正方体的过P 、Q 、R 的截面图形是(A )三角形(B )四边形(C )五边形(D )六边形(3)函数1(0)y x =≤的反函数是(A )1)y x =≥−(B )1)y x =≥−(C )0)y x =≥(D )0)y x =≥(4)已知函数tan y x ω=在(,)22ππ−内是减函数,则 (A )0<ω≤1(B )-1≤ω<0(C )ω≥1(D )ω≤-1 (5)设a 、b 、c 、d R ∈,若a bic di++为实数,则 (A )0bc ad +≠(B )0bc ad −≠ (C )0bc ad −=(D )0bc ad +=(6)已知双曲线22163x y −=的焦点为1F 、2F ,点M 在双曲线上且1MF x ⊥轴,则1F 到直线2F M 的距离为(A )5(B )6(C )65(D )56(7)锐角三角形的内角A 、B 满足1tan tan sin 2A B A−=,则有(A )sin 2cos 0A B −=(B )sin 2cos 0A B += (C )sin 2sin 0A B −=(D )sin 2sin 0A B +=(8)已知点A ,(0,0)B ,C .设BAC ∠的平分线AE 与BC 相交于E ,那么有BC CE λ=,其中λ等于 (A )2(B )12(C )-3(D )-13(9)已知集合{}23280M x x x =−−≤,{}260N x x x =−−>,则MN 为(A ){42x x −≤<−或}37x <≤(B ){42x x −<≤−或}37x ≤< (C ){2x x ≤−或}3x > (D ){2x x <−或}3x ≥(10)点P 在平面上作匀速直线运动,速度向量(4,3)v =−(即点P 的运动方向与v 相同,且每秒移动的距离为v 个单位).设开始时点P 的坐标为(-10,10),则5秒后点P 的坐标为(A )(-2,4)(B )(-30,25)(C )(10,-5)(D )(5,-10) (11)如果1a ,2a ,…,8a 为各项都大于零的等差数列,公差0d ≠,则(A )1a 8a >45a a (B )8a 1a <45a a (C )1a +8a >4a +5a (D )1a 8a =45a a (12)将半径都为1的4个钢球完全装入形状为正四面体的容器里,这个正四面体的高的最小值为(A)3(B )2+3(C )4+3(D)3第Ⅱ卷注意事项:1.用钢笔或圆珠笔直接答在试题卷上 2.答卷前将密封线内的项目填写清楚 3.本卷共10小题,共90分二、填空题:本大题共4小题,每小题4分,共16分,把答案填在题中横线上(13)圆心为(1,2)且与直线51270x y −−=相切的圆的方程为_____________. (14)设a 为第四象限的角,若sin 313sin 5a a =,则tan 2a =_____________. (15)在由数字0,1,2,3,4,5所组成的没有重复数字的四位数中,不能被5整除的数共有_____________个.(16)下面是关于三棱锥的四个命题:①底面是等边三角形,侧面与底面所成的二面角都相等的三棱锥是正三棱锥. ②底面是等边三角形,侧面都是等腰三角形的三棱锥是正三棱锥. ③底面是等边三角形,侧面的面积都相等的三棱锥是正三棱锥.④侧棱与底面所成的角相等,且侧面与底面所成的二面角都相等的三棱锥是正三棱锥. 其中,真命题的编号是_____________.(写出所有真命题的编号)三、解答题:本大题共6小题,共74分,解答应写出文字说明,证明过程或演算步骤 (17)(本小题满分12分)设函数11()2x x f x +−−=,求使()f x ≥的x 取值范围.(18) (本小题满分12分)已知{}n a 是各项均为正数的等差数列,1lg a 、2lg a 、4lg a 成等差数列.又21nn b a =,1,2,3,n =….(Ⅰ)证明{}n b 为等比数列;(Ⅱ)如果无穷等比数列{}n b 各项的和13S =,求数列{}n a 的首项1a 和公差d . (注:无穷数列各项的和即当n →∞时数列前项和的极限)(19)(本小题满分12分)甲、乙两队进行一场排球比赛.根据以往经验,单局比赛甲队胜乙队的概率为0.6,本场比赛采用五局三胜制,即先胜三局的队获胜,比赛结束.设各局比赛相互间没有影响.令ξ为本场比赛的局数.求ξ的概率分布和数学期望.(精确到0.0001)(20)(本小题满分12分)如图,四棱锥P-ABCD 中,底面ABCD 为矩形,PD 垂直于底面ABCD ,AD=PD ,E 、F 分别为CD 、PB 的中点. (Ⅰ)求证:EF 垂直于平面PAB ;(Ⅱ)设AB=2BC ,求AC 与平面AEF 所成的角的大小.(21)(本小题满分14分)P 、Q 、M 、N 四点都在椭圆1222=+y x 上,F 为椭圆在y 轴正半轴上的焦点.已知PF 与FQ 共线,MF 与FN 共线,且0=•MF PF .求四边形PMQN 的面积的最小值和最大值.(22)(本小题满分12分)已知0≥a ,函数xe ax x xf )2()(2−=.(Ⅰ)当x 为何值时,f(x)取得最小值?证明你的结论; (Ⅱ)设f(x)在[-1,1]上是单调函数,求a 的取值范围.2005年高考理科数学全国卷Ⅱ试题及答案(必修+选修Ⅱ)(黑龙江吉林广西内蒙古新疆)参考答案1-6: CDBBCC 7-12:ACACB C(2)分析:本题主要考查学生对截面图形的空间想像,以及用所学知识进行作图的能力,通过画图,可以得到这个截面与正方体的六个面都相交,所以截面为六边形,故选D.(12) 解析一:由题意,四个半径为1的小球的球心1234,,,O O O O ,恰好构成一个棱长为2的正四面体,并且各面与正四面体的容器P ABC −的各对应面的距离都为1如图一所示显然1HO =设,N T 分别为23,AB O O 的中点,在棱长为2的正四面体1234O O O O −中,1OT HT ==, ∴1O H =,且11sin 3TO H ∠=.作1O M PN ⊥,则11O M =, 由于11O PM TO H ∠=∠, ∴ 11111sin sin O M O MPO O PM TOH===∠∠∴ 11314PO PO O O HO =++=++=故选C解析二:由题意,四个半径为1的小球的球心1234,,,O O O O ,恰好构成一个棱长为2的正四面体,并且各面与正四面体的容器P ABC −的各对应面的距离都为1如图二所示,正四面体1234O O O O −与P ABC −有共同的外接球球心O 的相似正四面体,其相似比为:1263126143OH k OQ ==+,所以1126132632643()434312643OO OP k +===+所以32612626()3(1)43433PQ OP OQ =+=+++=+解析三:由题意,四个半径为1的小球的球心1234,,,O O O O ,恰好构成一个棱长为2的正四面体,并且各面与正四面体的容器P ABC −的各对应面的距离都为1 如图二所示,正四面体1234O O O O −与P ABC −有共同的外接球球心O 的相似正四面体,从而有113O P OO HQ OH==, 又1HQ =, 所以1O P=由于13O H =, 所以1113PQ OP OQ O H HQ O P =+=++=++=+13.22(1)(2)4x y −+−=;14.34−;15. 192;16. ①,④ (13)分析:本题就是考查点到直线的距离公式,所求圆的半径就是圆心(1,2)到直线5x -12y -7=0的距离:2r ==,再根据后面要学习的圆的标准方程,就容易得到圆的方程:222(1)(2)2x y −+−=(16)分析:②显然不对,比如三条侧棱中仅有一条不与底面边长相等的情况,侧面都是等腰三角形的三棱锥但不是正三棱锥. ③底面是等边三角形,侧面的面积都相等,说明顶点到底面三边的距离(斜高)相等,根据射影长的关系,可以得到顶点在底面的射影(垂足)到底面三边所在直线的距离也相等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第20卷 第1期 延边教育学院学报 Vol.20 No.1
2006年2月 Journal of Yanbian Institute of Education Feb. 2006
·48·
浅谈2005年高考数学试卷(全国卷)中的
对称思想
王雪晶 赵连生
(敦化市实验中学,吉林 敦化 133700)
摘要:近几年来,在高考命题中关于对称的数学命题每年均有体现,如何掌握好并巧妙运用对称的
思想方法解题,乃是数学学习应达到的目标。
关键词:数学;2005高考试卷;对称思想;运用
中图分类号:G633.6 文献标识码:B 文章编号:1673-4564(2006)01-0048-05
著名数学特级教师孙维刚曾积极倡导利用对称思想来解决数学问题,他认为,数学是非常美丽的,
它的美基于其高度的严谨和合理而达到的和谐,那是一种令人神怡的内在和谐。这种合理与和谐就是作
为数学科学的对称。在数学学习中,如果能熟练掌握对称的思想方法,在解决问题时将会易如反掌。现
列举几例说明2005年高考数学试题是怎样考查对称思想的。
一、利用图形对称解决问题
例1(选择题第2小题):正方体ABCD—A
1B1C1D1
中,P、Q、R
分别是AB、AD、B
1C1
的中点。那么,正方体的过P、Q、R的截面图
形是( )
A、三角形 B、四边形
C、五边形 D、六边形
解析:正方体ABCD—A
1B1C1D1中,A、C1
是关于体心对称的两
点,P、Q分别是下底面且从顶点A出发的两条棱的中点,R是上底面且从顶点C
1
出发的一条棱的中
点,由此找到上底面且从顶点C出发的另一条棱的中点H,连结RH,由PQ∥21BD∥21B1D1∥RH,
可知H为截面PQR上一点,再将截面延伸,因为截面PQR与平面B1BCC1有一个公共点R,由公理2
可知它们应存在一条交线,故应再找一点便可画出交线,由PQ与BC共面且不平等,便可知它们必存
在一交点E,E必为所求那点,连结ER,与BB
1交于F,由Rt△B1ER≌Rt△BFE,可知F为中点BB1
,
连结PF,由对称可知,DD1的中点G也截面上,故此截面为六边形。
∴选D。
例2(选择题第4小题):已知函数y=tanωx在(-
2π,2
π
)内是减函数,则( )
收稿日期:2005-12-18
D1C1B1A1H
P
Q
R
G
F
E
D
C
B
A
第1期 赵丽娟:抓住课改机遇 创办特色学校
·49·
A、0<ω≤1 B、-1≤ω<0 C、ω≥1 D、ω≤-1
解析:由正切函数y=tanx的图象及性质可知,它在(-2π,2π)内是增函数,若ω>0,y=tan
ωx的图象只会相应变得更“苗条”或“肥胖”,单调性则不会改变,所以根据f(x)与f(-x)关于y轴对
称这一特点,可知ω<0。又要求此函数在(-2π,2π)内至多具有一个周期的图象,∴T=ωπ≥π
∴︱ω︱≤1,即-1≤ω<0,∴选B。
例3(选择题第12小题):将半径为1的4个钢球完全装入形状为正四面体的容器里,这个正四面
体的高的最小值为( )
A、
3623+ B、3
62
2+
C、3624+ D、
3
6234+
解析:要想把4个大小相同的钢球完全装入一正四面体的V—ABC的容器里,由对称性可知,无
论从正四面体的哪一个面观察,每面均能看到3个球,且它们两两外切,连结4个小球的球心,可得到
一个小正四面体,顶点分别为O
1、O2、O3、O4
,且棱长为2,体心与大正四面体的体心重合,设其为
O,可求得小正四面体的高为362,点O到底面O2O3O4的距离则为66,∴O到底面ABC的距离
为1+66,又由正四面体的体心到底面的距离为高的41,∴大正四面体的高的最小值为4(1+66)=4
+362,∴选C。
评述:以上三题在不同程度上都运用了立体图形或函数图象的对称性来解决相关问题,能够恰当运
用其对称性质,可为解题带来极大的方便。
二、函数中的对称问题
例4(选择题第3小题):函数y=
132−x
(x≤0)的反函数是( )
延边教育学院学报 2006年
·50·
A、y=3)1(+x(x≥-1) B、y=-3)1(+x(x≥-1)
C、y=3)1(+x(x≥0) D、y=-3)1(+x(x≥0)
解析:观察函数y=
132−x
(x≤0)可知,其图象过点(-1,0),因此反函数图象必过点(0,
-1),排除A、C,又原函数的值域为[-1,+∞),∴反函数的定义域为[-1,+∞),即选B
评述:由互为反函数的函数y=f(x)和y=f
-1
(x)的图象关于直线y=x对称可知,若点(a,b)在函数
y=f(x)的图象上,则点(b,a)必在其反函数y=f
-1
(x)的图象上,反之亦然。
三、不同情况的对称分析
例5(解答题第19大题):甲、乙两队进行一场排球比赛,根据以往经验,单局比赛甲队胜乙队的
概率为0.6,本场比赛采用五局三胜制,即先胜三局的队获胜,比赛结束,设各局的比赛相互间没有影
响。令ζ为本场比赛的局数,求ζ的概率分布和数学期望(精确到0.001)。
解析:由题意可知,ζ的可能取值为3、4、5,当ζ=3时,说明只进行了三场比赛,胜方可能是
甲也可能是乙,若甲获胜,概率为0.6
3,对乙获胜作对称分析,概率为0.43
。
两事件为互斥事件 ∴P(ζ=3)=0.6
3+0.43
=0.28
ζ=4时,说明进行了四场比赛,胜方可能为甲也可能为乙。当甲方获胜时,前三场甲必输一场,
赢两场,而第四场必须赢,概率为23C×0.62×0.4×0.6;对乙获胜作对称分析,可知概率为23C×0.42×
0.6×0.4,两种情况为互斥的,∴概率为23C×0.62×0.4×0.6+23C×0.42×0.6×0.4=0.3744。
ζ=5时,说明进行了五场比赛,胜方可能为甲也可能为乙。当甲获胜时,前四场甲必须输两场,
赢两场,而第五场必须赢,概率为
24C×0.62×0.42×0.6;对乙获胜作对称分析,可知概率为2
4
C
×0.4
2
×0.62×0.4,两种情况为互斥的,∴概率为24C×0.62×0.42×0.6+24C×0.42×0.62×0.4=0.3456。
∴ζ的概率分布为:
ζ
3 4 5
P 0.28 0.3744 0.3456
∴Eζ=3×0.28+4×0.3744+5×0.3456=4.0656。
例6(解答题第21大题):P、Q、M、N四点都在椭圆1222=+yx上,F为椭圆在y轴正半轴
上的焦点,已知
PF与FQ共线,MF与FN共线,且PF·MF
=0,求四边形PMQN的面积的
第1期 金在律:谈幼儿生活行为和道德教育
·51·
最小值和最大值。
解析:由题设可知,直线PQ、MN在图中的位置是对称的,不妨设直线PQ的方程为:y=kx+1,
与椭圆方程
1222=+yx
联立,得012)2(1212222=−++⇒⎪⎩⎪⎨⎧=++=kxxkyxkxy
设P(x1,y1),Q(x2,y2),
则222122122122)1(224)(11kkxxxxkxxkPQ++=−+⋅+=−⋅+=
(1)k=0时,PQ⊥MN,直线PQ平行于x轴,直线MN垂直于x轴,
∴︱PQ︱=2,︱MN︱=22此时S=21︱PQ︱·︱MN︱=2
(2)K≠0时,直线MN的方程即为:11+−=xky,
由︱PQ︱=
2
2
2)1(22kk+
+
对称得到
︱MN︱=
2
2
2
2
12)11(22)1
(2
])1(1[22
k
kkk
++=−+
−+
,
∴S=21︱PQ︱·︱MN︱=
2
1
·222)1(22kk++·2212)11(22kk++=)12)(2()1(42222+++kkk
=2222112124kkkk++⋅++。
∵2212kk++>0,22112kk++>0,
O
y
x
N
Q
MP
F(1,0)
O
延边教育学院学报 2006年
·52·
∴2212kk++·22112kk++≤4921332 k112kk1k2 22222222=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡++=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡+++++kk (当且仅当
2212kk++=2
2
112kk+
+
即k=±1时取等号),
∴S≥916。
综合可知,916≤S≤2 ∴四边形PMQN的面积S的最大值为2,最小值为916。
评述:对不同情况作对称分析或对不同变量作对称替代在解题时很常见,如果能够巧妙运用对称,
定会使问题的解答简洁明了。
近几年来,在高考命题中关于对称的数学命题每年均有体现,如何掌握好并巧妙运用对称的思想方
法解题,乃是数学学习应达到的目标。
