12线性方程组的迭代法求解开题报告书
第四章线性方程组的迭代法范文

第四章 线性方程组的迭代法第一节 迭代法及其收敛性一、迭代法的一般格式在前面我们已经介绍了解线性方程组b Ax = (1)的一些直接方法,下面我们将简略介绍一下解方程组(1)的另一类方法——迭代法,所谓迭代法是这样一种方法,对任意给定初始近似()0x ,按某种规则逐次生成序列()()()() ,x x ,x ,x k 210使极限()*∞→=x x lim k k (2)为方程组(1)的解,即b Ax =*设把矩阵A 分解成矩阵N 和P 之差P N A -=其中N 为非奇异矩阵,于是,方程组(1)便可以表示成b Px Nx +=即f Bx b N Px N x +=+=--11 (3)其中b N f ;P N B 11--==,据此,我们便可以建立迭代公式 ()() 2101,,k fBx x k k =+=+ (4)我们称迭代公式(4)中的矩阵B 为迭代矩阵. 若序列(){}kx收敛()*∞→=x x lim k k显然有f Bx x +=**即,极限*x 便是所求方程组的解.定义1(1)对给定的方程组(3),用公式(4)逐步代入求近似解 的方法称为迭代法.(2) 如果()k k x lim ∞→存在 (记为*x ),则称迭代法收敛,此时*x 就是方程组的解,否则称此迭代法发散.为了讨论迭代公式(4)的收敛性,我们引进误差向量.()(),...,,k ,x x e k k 210=-=* (5)由(3)和(4)便得到误差向量所满足的方程()()k k Be e =+1 (6)递推下去,最后便得到()()()011e B e k k ++= (7)二、迭代法的收敛性若欲由(4)所确定的迭代法对任意给定的初始向量()0x 都收敛,则由(7)确定的误差向量()k e应对任何初始误差()0e 都收敛于0.定义2若()0=-∞→A A lim k k (8)则称矩阵序列(){}kA依范数‖·‖收敛于A .由范数的等价性可以推出,在某种范数意义下矩阵序列收敛,则在任何一种范数意义下该矩阵序列都收敛.因此,对矩阵序列(){}kA收敛到矩阵A ,记为()AA lim k k =∞→ (9)而不强调是在那种范数意义下收敛.从定义及矩阵的行(列)范数可以直接推出下面定理. 定理1 设矩阵序列()()()(),...,k a A n n k ijk 21==⨯及矩阵()nn ij a A ⨯=,则(){}kA 收敛于A 的充分必要条件为()ijk ij k a a lim =∞→, n ,...,j ,i 21=因此,矩阵序列的收 敛可归结为元素序列的收敛.此外,还可以推出下面定理.定理2 迭代法(4)对任何()0x都收敛的充分必要条件为=∞→k k B lim (10)定理3 矩阵序列{}kB 收敛于0的充分必要条件为()1<B ρ (11)证明:如果0=∞→k k B lim ,则在任一范数‖·‖意义下有=∞→kk B lim而由第六节定理4有()()[]kk k B B B ρρ=≥所以必有()1<B ρ反之,若()1<B ρ则存在足够小的正数ε,使()1<+ερB ,则第六节定理5可知,存在范数α⋅使,()1<+≤εραB B .于是[]()()kkkB B B εραα+≤≤因为()()0=+∞→kk B lim ερ所以=∞→αkk B lim 即0=∞→k k B lim定理 4:迭代法(4)对任意()0x 都收敛的充分必要条件为()1<B ρ三、迭代法的收敛速度考察误差向量()()()()0e B x x e k k k ⋅=-=*设B 有n 个线性无关的特征向量n ,...,,ηηη21,相应的特征值为n ,...,,λλλ21,由()∑==nj jj a e10η得()()()0eB e k k =∑==n j j kj B a 1η∑==nj j kj j a 1ηλ可以看出,当()1<B ρ愈小时,()∞→→k k j 0λ愈快,即()0→k e 愈快,故可用量()B ρ来刻划迭代法的收敛快慢.现在来确定迭代次数k ,使()[]s kB -≤10ρ (12)取对数得()B ln ln s k ρ-⋅≥10定义3 称()()B ln B R ρ-= (13) 为迭代法(4)的收敛速度.由此看出,()1<B ρ愈小,速度R(B)就愈大,(12)式成立所需的迭代次数也就愈少.由于谱半径的计算比较困难,因此,可用范数‖B ‖来作为()B ρ的一种估计. 定理5 如果迭代矩阵的某一种范数1<=q B γ,则对任意初始向量()0x,迭代公式(4)收敛,且有误差估计式γγ||||q q||x x ||)k ()k ()k (1x x 1-*--≤- (14)或γγ||||q q ||xx ||)()(k)k (01x x 1--≤-* (15)证明 利用定理4和不等式()γρB B ≤,可以立即证得收敛的充分条件,下面推导误差估计式.因为*x 方程组的精确解,则f Bx x +=**又()1<=≤q B B γρ,则由第六节定理7可知,I-B 可逆,且()q B ||B I ||-=-≤--11111γγ由于()()f Bx f Bx x x k k --+=-*-*1()()f B I B Bx k 11----= ()()()[]f x B I B I B k ---=--11()()()[]kk x x B I B --=--11两边取范数即得()γγγγγ||||qq||||B I B ||x x ||)k ()k ()k ()k ()k (111x x 1x x ---*--≤--≤-又由于()()()()()()()()011211x x B x x B x x k k k k k -=-=-----所以()()()()γγγ0111x x B x x k k k -≤---,即γγ||||q q ||xx ||)()(k)k (01x x 1--≤-*有了定理5的误差估计式,在实际计算时,对于预先给定的精度ε,若有()()εγ<-+k k x x 1则就认为()1+k x是方程组满足精度的近似解.此外,还可以用第二个估计式(15)来事先确定需要迭代的次数以保证()ε<k e第二节 雅可比迭代法与高斯—塞德尔迭代法一、雅可比迭代法设线性方程组b Ax = (1)的系数矩阵A 可逆且主对角元素nn a ,...,a ,a 2211均不为零,令 ()nn a ,...,a ,a diag D 2211=并将A 分解成()D D A A +-= (2)从而(1)可写成()b x A D Dx +-= 令11f x B x +=其中b D f ,A D I B 1111--=-=. (3) 以1B 为迭代矩阵的迭代法(公式)()()111f x B x k k +=+ (4)称为雅可比(Jacobi)迭代法(公式),用向量的分量来表示,(4)为⎩⎨⎧[],...,,k ,n ,...,i x a ba xnij j )k (j j i iii)k (i21021111==∑-=≠=+(5)其中()()()()()Tn x ,...x ,x x 002010=为初始向量. 由此看出,雅可比迭代法公式简单,每迭代一次只需计算一次矩阵和向量的乘法.在电算时需要两组存储单元,以存放()k x 及()1+k x.例1 用雅可比迭代法求解下列方程组⎪⎩⎪⎨⎧=+--=-+-=--2453821027210321321321.x x x .x x x .x x x解:将方程组按雅可比方法写成⎪⎪⎩⎪⎪⎨⎧++=++=++=840202083020107202010213312321.x .x .x .x .x .x .x .x .x取初始值()()()()()()TT,,,x ,x ,x x0000302010==按迭代公式()()()()()()()()()⎪⎪⎩⎪⎪⎨⎧++=++=++=+++840202083020107202010211331123211.x .x .x .x .x .x .x .x .x k k k k k k k k k进行迭代,其计算结果如表1所示表1二、高斯—塞德尔迭代法由雅可比迭代公式可知,在迭代的每一步计算过程中是用()k x 的全部分量来计算()1+k x的所有分量,显然在计算第i 个分量()1+k ix 时,已经计算出的最新分量()()1111+-+k i k x ,...,x 没有被利用,从直观上看,最新计算出的分量可能比旧的分量要好些.因此,对这些最新计算出来的第1+k 次近似()1+k x的分量()1+k jx 加以利用,就得到所谓解方程组的高斯—塞德(Gauss-Seidel )迭代法.把矩阵A 分解成U L D A --= (6)其中()nna ,...,a ,a diag D 2211=,U ,L --分别为A 的主对角元除外的下三角和上三角部分,于是,方程组(1)便可以写成 ()b Ux x L D +=-即22f x B x +=其中()()b L D f ,U L D B 1212---=-= (7)以2B 为迭代矩阵构成的迭代法(公式)()()221f x B x k k +=+ (8)称为高斯—塞德尔迭代法(公式),用 量表示的形式为⎩⎨⎧[],...,,k ,n ,,i x a x a b a xi j n i j )k (j ij )k (j ij i ii)k (i21021111111==∑∑--=-=+=++(9)由此看出,高斯—塞德尔迭代法的一个明显的优点是,在电算时,只需一组存储单元(计算出()1+k ix 后()k i x 不再使用,所以用()1+k ix 冲掉()k i x ,以便存放近似解.例2 用高斯——塞德尔迭代法求解例1.解:取初始值()()()()()()TT,,,x ,x ,x x 0000302010==,按迭代公式 ()()()()()()()()()⎪⎩⎪⎨⎧++=++=++=++++++840202083020107202010121113311123211.x .x .x .x .x .x .x .x .x k k k k k k k k k进行迭代,其计算结果如下表2表2从此例看出,高斯—塞德尔迭代法比雅可比迭代法收敛快(达到同样的精度所需迭代次数少),但这个结论,在一定条件下才是对的,甚至有这样的方程组,雅可比方法收敛,而高斯—塞德尔迭代法却是发散的. 三、迭代收敛的充分条件定理1 在下列任一条件下,雅可比迭代法(5)收敛. ①111<∑=≠=∞nij j ii ij ia a max B ;② 1111<∑=≠=nij i iiij ja a max B ;③ 111<∑=-≠=∞-nji i jjij jTa a max AD I定理2 设21B B ,分别为雅可比迭代矩阵与高斯—塞德尔迭代矩阵,则∞∞≤12B B (10)从而,当111<∑=≠=∞nij j iiij ia a max B时,高斯—塞德尔迭代法(8)收敛. 证明:由21B B ,的定义,它们可表示成()U L D B +=-11()()U D L D I U L D B 11112-----=-=用e 表示n 维向量()T,...,,e 111=,则有不等式 eB e B ∞≤11UD L D B 111--+=这里,记号|·|表示其中矩阵的元素都取绝对值,而不等式是对相应元素来考虑的,于是()()()Ie B L D I eL D B e U D ∞------≤-=111111容易验证()11==--nnL D L D所以,L D I 1--及L D I 1--可逆,且 ()()()1111111111-----------=++≤+++=-L D I LD ...L D I L D ...L D I LD I n n()I L D I ≥---11从而有()()((){}e I B L D I LD I eU D LD I e B ∞----------≤⋅-≤111111121{()()}eB eLD I I B I ∞--∞≤-⋅--=11111因此必有∞∞≤12B B因为已知11<∞B 所以12<∞B .即高斯—塞德尔迭代法收敛.若矩阵A 为对称,我们有定理3 若矩阵A 正定,则高斯—塞德尔迭代法收敛. 证明:把实正定对称矩阵A 分解为 TL L D A --=()TL U =,则D 为正定的,迭代矩阵()T L L D B 12--=设λ是2B 的任一特征值,x 为相应的特征向量,则()()x x L L D T λ=--1以L D -左乘上式两端,并由TL L D A --=有()Ax x L Tλλ=-1用向量x 的共轭转置左乘上式两端,得()Ax x x L xTTT--=-λλ1 (11)求上式左右两端的共轭转置,得Ax x x L x T T ----=⎪⎭⎫ ⎝⎛-λλ1以λ--1和λ-1分别乘以上二式然后相加,得()()Axx x L L x T T T -----⎪⎭⎫ ⎝⎛-+=+⎪⎭⎫ ⎝⎛--λλλλλλ211由TL L D A --=,得()()Axx x A D x T T -----⎪⎭⎫ ⎝⎛-+=-⎪⎭⎫ ⎝⎛--λλλλλλ211即()Ax x x L x TT---=-λλλ2211 (12)因为A 和D 都是正定的,且x 不是零向量,所以由(11)式得1≠λ,而由(12)式得012>-λ, 即1<λ,从而()12<B ρ,因而高斯—塞德尔迭代法收敛. 定义1 设()n n ij a A ⨯=为n 阶矩阵.① ①如果n,...,i ,a a nij i j ij ii 21=∑>≠= (13)即A 的每一行对角元素的绝对值都严格大于同行其他元素绝对值之和,则称A 为严格对角优势矩阵.② ②如果n,...,i ,a a nij i j ij ii 21=∑≥≠=且至少有一个不等式严格成立,则称A 为弱对角优势矩阵.例如⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-310131012是严格对角优势矩阵,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--310121011是弱对角优势矩阵.定义2 设()n n ij a A ⨯=是n 阶矩阵,如果经过行的互换及相应列的互换可化为⎥⎦⎤⎢⎣⎡2212110A A A ,即存在n 阶排列矩阵P,使⎥⎦⎤⎢⎣⎡=2212110A A A AP P T其中2211A ,A 为方阵,则称A 是可约的,否则称A 为不可约的.A 是可约矩阵,意味着b Ax =可经过若干次行列重排,化为两个低阶方程组,事实上, b Ax =可化为 ()b P x P AP P TTT=,记()()()()⎥⎦⎤⎢⎣⎡==⎥⎦⎤⎢⎣⎡==2121d d d b P ,y y y x P T T于是,求解b Ax =化为求解()()()()()⎪⎩⎪⎨⎧=+=+22221212111d y A d y A y A可以证明,如果A 为严格对角优势矩阵或为不可约弱对角优势矩阵,则A 是非奇异的.定理4 如果A 为严格对角优势矩阵或为不可约弱对角优势矩阵,则对任意()0x ,雅可比迭代法(4)与高斯—塞德尔迭代法(8)均为收敛的.证明:下面我们以A 为不可约弱对角优势矩阵为例,证明雅可比迭代法收敛,其他证明留给读者.要证明雅可比迭代法收敛,只要证()11<B ρ,1B 是迭代矩阵. 用反证法,设矩阵1B 有某个特征值μ,使得1≥μ,则()01=-B I det μ,由于A 不可约,且具有弱对角优势,所以1-D 存在,且()()D A D D A D I I B I -+=--=---μμμ111从而()0=-+D A D det μ另一方面,矩阵()D A D -+μ与矩阵A 的非零元素的位置是完全相同的,所以()D A D -+μ也是不可约的,又由于1≥μ,且A 弱对角优势,所以n,...,i ,a a a ni j i j ij ii ii 21=∑≥≥≠=μ并且至少有一个i 使不等号严格成立.因此,矩阵()D A D -+μ弱对角优势,故()D A D -+μ为不可约弱对角优势矩阵.从而()0≠-+D A D det μ 矛盾,故1B 的特征值不能大于等于1,定理得证.第三节 超松驰迭代法逐次超松驰迭代法(Successive Over Relaxation Me thod,简称SOR 方法)是高斯—塞德尔方法的一种加速方法,是解大型稀疏矩阵方程组的有效方法之一,它具有计算公式简单,程序设计容易,占用计算机内存较少等优点,但需要较好的加速因子(即最佳松驰因子).下面我们首先说说松驰一词的含意,再利用它来解释雅可比迭代法与高斯—塞德尔迭代法,最后给出逐次超松驰迭代法的推算公式和收敛性条件.设线性方程组b Ax = (1)其中()n n ij a A ⨯=可逆 ,且对角元素nn a ,...,a ,a 2211均不为0,如果()Tn x ,...x ,x x 21= 是(1)的近似解,一般说来n,...,i ,x a b r nj j ij i i 211=∑-== (2)不是0,这可理解为x “不合格”,把不合格的x 更换为新的近似解X ,希望新的残向量r ’“变小”,想实现这一点的简单方法是每一次只把x 在(2)中的一个式(例如第i 个)中的一个分量进行更换,使新的残向量的第i 个分量变成0.这样,我们就说第i 个方程被松弛了.一般都把第i 个式中第i 个元i x 换掉,这相当于求ξ使∑--∑-=+=-=ni j jij ii i j j ij i x a a x a b 1110ξ (3)因此,雅可比迭代法将()k x代换为()1+k x的过程,实际上是对1≤i ≤n 把()()∑-==nj k jij i k ix a b r 1(4)变为()()()∑--∑-=+=+-=ni j k jij k iii i j k jij i x a x a x a b 11110 (5)的过程(松驰的过程).由()k x代换为()1+k x还可看作是()()修正向量+=+k k x x 1 (6)而修正量与修正公式可写成为()()()n,...,i ,r a x x k i iik ik i2111=+=+ (7)倘若在修正量之前乘以一个因子ω,即以第i 个分量()()()n,...,i ,r a x x k i iik ik i2111=+=+∧ω (8)为向量作新的近似向量(第k+1次迭代向量)代替原来的()k x 就得到所谓带松驰因子ω的迭代法.注意到,用(8)中的()1+∧k ix 代替(4)中的()k i x ,一般并不能使()()()()∑--∑-=+=+∧-=+∧ni j k jij k i ii i j k jij i k ix a x a x a b r 11111 (9)为0,而为()()()k i k ir r ω-=+∧11 (10)在(8)中取1=ω, ()1+∧k ix 就是(7)中的()1+k x,恰好使新的残量()1+∧k ir 为0,这就使第i 个方程松驰了;如1>ω,则用()1+∧k i x 代换第i 个方程中的()k i x 将使残量由()k ir 变成与()k i r 有不同符号的新残量()1+∧k ir ,于是我们就说第i 个方程被松驰过头了(超松驰),或说()k i x 被修改过分了(超过了使残量正好为0的程度);如1<ω,则用()1+∧k ix 代换第i 个方程中的()k i x 时,新残量()1+∧k ir 与()k i r 同号,并且当0>ω时,它的绝对值小于()k i r 之绝对值,于是我们不妨认为第i 个方程还松驰得不够(低松驰)或称()k i x 被修改得不够,不管是超松驰还是低松驰(1>ω或1<ω),我们一概都称为超松驰,即1≠ω时,我们称⎩⎨⎧()n,...,,k ,n ,...,i x a b a xxn j )k (j ij i ii)k (i)k (i21021111==∑-+==+ω(11)为带松驰因子ω的同时迭代法(公式).带松驰因子ω的同时迭代法用处并不大,讲它的目的只是为了解释迭代,修改和松驰的含意,使我们能容易懂得什么是逐次超松驰法.下面介绍什么是逐次超松驰法.类似于高斯—塞德尔迭代法,在(11)式中用新的()1+k jx 代替旧的()k jx ,i ,...,j 121-= 可得⎩⎨⎧()n,...,,k ,n ,...,i x a x a b a xxn i j )k (j ij i j )k (j ij i ii)k (i)k (i2102111111==∑-∑-+==-=++ω(12)称为带松驰因子ω的逐个法或逐个超松驰迭代法(公式).显然,(12)式可改写成()()()()111+++-=k i~k ik ix x x ωω (13)其中()∑-∑-==-=++n i j )k (j ij i j )k (j ij i ii)k (i~x a x a b a x 11111为高斯—塞德尔迭代所得,所以逐个超松驰迭代法是高斯—塞德尔迭代法的一种加速方法.由(12)式()()∑-∑-+-==-=++nij )k (j ij i j )k (j ij i )k (iii )k (iii x a xa b xa xa 11111ωω用分解式U L D A --=,则上式为()()∑-∑-+-==-=++nij )k (j ij i j )k (j ij )k ()k (x a xa b DxDx11111ωω即ωωf x B x )k ()k (+=+1 (14) 其中[]U D )()L D (B ωωωω+--=-11b )L D (f 1--=ωωω (15)(14)为超松驰迭法(公式)的矩阵形式ωB 称为其迭代矩陈例:用逐次超松驰迭代法求解方程组⎪⎩⎪⎨⎧=+--=-+-=--2453821027210321321321.x x x .x x x .x x x解:取()()()()()()TT,,,x ,x ,x x 0000302010==,迭代公式 ()()(()()())()()(()()())()()(()()())⎪⎪⎪⎩⎪⎪⎪⎨⎧-++⋅+=+++⋅+=++-⋅+=++++++k k k k k k k k k k k k k k k x x x .x x x x x .x x x x x .x x 312113133211212321111524512103810121027101ωωω取0551.=ω计算结果为表3表3对ω取其他值,计算结果满足误差510-∞≤-*)k (x x的迭代次数如下:表4从此例看到,松驰因子选择得好,会使超松驰迭代法的收敛大大加速.使收敛最快的松驰因子称为最佳松驰因子.本例的最佳松驰因子为0551.=ω,一般地,最佳松驰因子*ω应满足()()ωωρρB min B =*最佳松驰因子理论是由Young(1950年)针对一类椭圆型微分方程数值解得到的代数方程组b Ax =(具有所谓性质A 和相容次序)所建立的理论,他给出了最佳松驰因子公式()J pt B 2112ρω-+=其中J B 是雅可比迭代矩阵.定理1 设n ,..,i ,a ii 210=≠,且超松驰迭代法(12)收敛,则松驰因子20<<ω (16)证明:设SOR 方法收敛,根据迭代法收敛的充要条件可知,()1<ωρB . 设ωB 的特征值为n ,...,λλλ21,则 ()(())nn B ...B det ωωρλλλ≤=21即()(())11<≤nnB B d e t ωωρ而()(())(())U D det LD det B det ωωωω+-⋅-=-11()nω-=1所以11<-ω该定理说明对于解一般线性方程组(1)()n ,...,,i ,a ii 210=≠,超松弛迭代法只有取松弛因子ω在()20,范围内才能收敛.反过来,对A 是正定矩阵有下面结果. 定理2 设A 是对称正定矩阵,且20<<ω,则超松弛迭代法(12)收敛. 证明:设λ是ωB 的任一特征值,在上述假定下,若能证明1<λ,那么定理得证. 事实上,设x 为λ对应特征向量,即 0≠=x ,x x B λω亦即()()()x L D x U D ωλωω-=+-1 考虑数量积 (()())(())x ,x L D x ,x U D ωλωω-=+-1则()()()()()x ,Lx x ,Dx x ,Ux x ,Dx x ,Dx ωωωλ-+-=显然()012>≡∑==σni i iix ax ,Dx记()βαi x ,Lx +=- 由于TA A =,所以T L U =()()βαi x ,Lx Lx ,x x ,Ux ________-=⎪⎭⎫ ⎝⎛-=-=-()()()ασ20+=--=<x ,x U L D x ,Ax所以()()ωβαωσωβωωσσλi i +++--=2 从而()()2222222βωαωσβωαωωσσλ+++--=当20<<ω时()2αωωσσ--()()()0222<-+=+-ωασωσαωσyy即1<λ.。
实验报告四线性方程组的求解_迭代

浙江大学城市学院实验报告课程名称 科学计算实验项目名称 线性方程组的求解-迭代法实验成绩 指导老师(签名 ) 日期 2012-4-6一. 实验目的和要求1. 掌握Jacobi 迭代方法.Gauss-Seidel 迭代方法.SOR 迭代方法的编程思想.能够分别用分量形式和矩阵形式编写相关程序。
2. 观察SOR 迭代法中松弛因子变化情况对收敛的影响。
3. 了解Hilbert 矩阵的病态性和作为线性方程组系数矩阵的收敛性。
二. 实验内容和原理编程题2-1要求写出Matlab 源程序(m 文件).并有适当的注释语句;分析应用题2-2.2-3.2-4要求将问题的分析过程、Matlab 源程序和运行结果和结果的解释、算法的分析写在实验报告上。
2-1 编程注释 设11121121222212,n n n n nn n a a a b a a a b A b a a a b ⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦对下述求解线性方程组的Matlab 程序添上注释语句.其中A 和b 分别为线性方程组的系数矩阵和右端向量;0x 为迭代初始向量(0)X;max N 为容许迭代最大次数.eps 为迭代终止条件的精度(容许误差).终止条件为前后两次迭代解的差的向量2-范数。
1) Jacobi 迭代:Jacobimethod(A,b,x0,Nmax,eps)2) Gauss-Seidel 迭代:GaussSeidelmethod(A,b,x0,Nmax,eps)3) 松弛迭代:SORmethod(A,b,x0,Nmax,eps,w)2-2 分析应用题利用2-1中的程序来分析用下列迭代法解线性方程组:123456410100014101050141012101410501014120010146x x x x x x --⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥---⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥----=⎢⎥⎢⎥⎢⎥---⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥----⎢⎥⎢⎥⎢⎥--⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦ 的收敛性.并求出使(1)()20.0001k k X X +-≤的近似解及相应的迭代次数.其中取迭代初始向量(0)X 为零向量。
实验报告四 线性方程组的求解-迭代

浙江大学城市学院实验报告课程名称科学计算实验项目名称线性方程组的求解-迭代法实验成绩指导老师(签名)日期2012-4-6一.实验目的和要求1.掌握Jacobi 迭代方法,Gauss-Seidel 迭代方法,SOR 迭代方法的编程思想,能够分别用分量形式和矩阵形式编写相关程序。
2.观察SOR 迭代法中松弛因子变化情况对收敛的影响。
3.了解Hilbert 矩阵的病态性和作为线性方程组系数矩阵的收敛性。
二.实验内容和原理编程题2-1要求写出Matlab 源程序(m 文件),并有适当的注释语句;分析应用题2-2,2-3,2-4要求将问题的分析过程、Matlab 源程序和运行结果和结果的解释、算法的分析写在实验报告上。
2-1编程注释设11121121222212,n n n n nn n a a a b a a a b A b a a a b ⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦ 对下述求解线性方程组的Matlab 程序添上注释语句,其中A 和b 分别为线性方程组的系数矩阵和右端向量;0x 为迭代初始向量(0)X;max N 为容许迭代最大次数,eps 为迭代终止条件的精度(容许误差),终止条件为前后两次迭代解的差的向量2-范数。
1)Jacobi 迭代:Jacobimethod(A,b,x0,Nmax,eps)2)Gauss-Seidel 迭代:GaussSeidelmethod(A,b,x0,Nmax,eps)3)松弛迭代:SORmethod(A,b,x0,Nmax,eps,w)2-2分析应用题利用2-1中的程序来分析用下列迭代法解线性方程组:123456410100014101050141012101410501014120010146x x x x x x --⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥---⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥----=⎢⎥⎢⎥⎢⎥---⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥----⎢⎥⎢⎥⎢⎥--⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦的收敛性,并求出使(1)()20.0001k k X X +-≤的近似解及相应的迭代次数,其中取迭代初始向量(0)X为零向量。
第3章 解线性方程组的迭代法
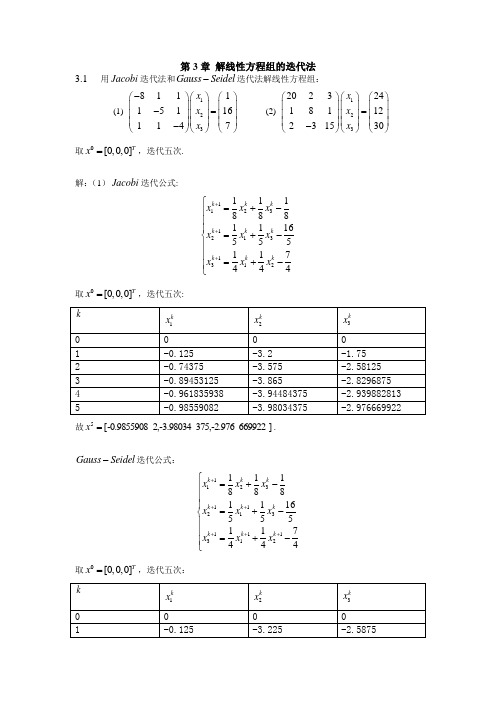
第3章 解线性方程组的迭代法3.1 用Jacobi 迭代法和Gauss Seidel -迭代法解线性方程组:(1)1238111151161147x x x -⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪-= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭⎝⎭(2)12320232418112231530x x x ⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭⎝⎭取0[0,0,0]Tx =,迭代五次.解:(1)Jacobi 迭代公式:⎪⎪⎪⎩⎪⎪⎪⎨⎧-+=-+=-+=+++4741415165151818181211331123211k k k k k k k k k x x x x x x x x x取0[0,0,0]Tx =,迭代五次:kk x 1k x 2 kx 30 01 -0.125 -3.2 -1.75 2 -0.74375 -3.575 -2.581253 -0.89453125 -3.865-2.8296875 4 -0.961835938 -3.94484375 -2.939882813 5 -0.98559082-3.98034375 -2.976669922故]669922375,-2.9762,-3.98034-0.9855908[5=x .Gauss Seidel -迭代公式:⎪⎪⎪⎩⎪⎪⎪⎨⎧-+=-+=-+=++++++4741415165151818181121113311123211k k k k k k k k k x x x x x x x x x 取0[0,0,0]Tx =,迭代五次:kk x 1 k x 2 kx 31 -0.125-3.225 -2.58752 -0.8515625 -3.8878125 -2.934843753 -0.977832031 -3.982535156 -2.9900917974 -0.996578369 -3.997334033 -2.998478101 5-0.999476517 -3.999590923 -2.99976686故]997668690923,-2.917,-3.9995-0.9994765[5=x(2)Jacobi 迭代公式:⎪⎪⎪⎩⎪⎪⎪⎨⎧++-=+--=+--=+++25115223818156203101211331123211k k k k k k k k k x x x x x x x x x 取0[0,0,0]Tx =,迭代五次:kk x 1 k x 2 kx 30 0 1 1.2 1.5 2 2 0.75 1.12.14 3 0.769 1.13875 2.124 0.768125 1.138875 2.125216667 5 0.767331.1383322922.125358333故]32.12535833138332292,0.76733,1.[5=x .Gauss Seidel -迭代公式:⎪⎪⎪⎩⎪⎪⎪⎨⎧++-=+--=+--=++++++25115223818156203101121113311123211k k k k k k k k k x x x x x x x x x 取0[0,0,0]Tx =,迭代五次:kk x 1 k x 2 kx 30 0 1 1.2 1.352.112 0.74851.14268752.12873753 0.766420625 1.138105234 2.12543163 4 0.767374732 1.138399205 2.12536321 50.767355598 1.138410149 2.12536795故]6795149,2.12538,1.1384100.76735559[5=x3.2 用Jacobi 迭代法解线性方程组123101091102702108x x x -⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪--= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭⎝⎭, 取初值向量0[0,0,0]Tx =,要求13||||10k k x x --∞-≤,并讨论方差的收敛性.解:Jacobi 迭代公式:⎪⎪⎪⎩⎪⎪⎪⎨⎧+=++=+=+++1081021071021011091012133112211k k k k k k k x x x x x x x取初值向量0[0,0,0]Tx =kk x 1 k x 2 kx 30 0 0 1 0.9 0.7 0.8 2 0.97 0.95 0.94 3 0.995 0.985 0.99 4 0.9985 0.9975 0.997 5 0.99975 0.99925 0.9995 6 0.9999250.999875 0.9998535610000625.0||-≤=-x x ,迭代6次后可以得到满足误差要求的解; ]99985.999875,0.0.999925,0[6=x ,Jacobi 迭代法收敛.3.3 社线性方程12311112211x x ⎪ ⎪ ⎪= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭讨论解该线性方程的Jacobi 迭代法和Gauss Seidel -迭代法的收敛性. 解:按Jacobi 迭代法展开:⎪⎪⎪⎭⎫ ⎝⎛---⎪⎪⎪⎭⎫ ⎝⎛----⎪⎪⎪⎭⎫ ⎝⎛=--=⎪⎪⎪⎭⎫ ⎝⎛-=010220022010111122111221U L D A(1) 对于Jacobi 迭代法,其迭代矩阵为:⎪⎪⎪⎭⎫⎝⎛-----=⎪⎪⎪⎭⎫ ⎝⎛-----⎪⎪⎪⎭⎫⎝⎛=+=--022101220022101220111)(11L U D B J J B 的特征矩阵为:3221122||λλλλλ=⎪⎪⎪⎭⎫⎝⎛-=-J B I 解得03,2,1=λ10)(<=J B ρ,故Jacobi 迭代法收敛.(2) 对Gauss Seidel -迭代法,其迭代矩阵为:⎪⎪⎪⎭⎫⎝⎛--=⎪⎪⎪⎭⎫ ⎝⎛--⎪⎪⎪⎭⎫⎝⎛------=-=--200320220010220122111)(11U L D B G G B 的特征矩阵为:2)2(20032022||-=⎪⎪⎪⎭⎫⎝⎛---=-λλλλλλG B I 解得:01=λ,23,2=λ12)(>=G B ρ,故Gauss Seidel -迭代法发散.3.4 设线性方程组1122332313a x b a x b ⎢⎥⎢⎥⎢⎥-=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦其中a 为参数,且0a ≠,试求a 的取值范围,使得解该线性方程组的Jacobi 迭代法收敛.解:按Jacobi 迭代法展开:⎪⎪⎪⎭⎫ ⎝⎛-⎪⎪⎪⎭⎫ ⎝⎛----⎪⎪⎪⎭⎫ ⎝⎛=--=⎪⎪⎪⎭⎫ ⎝⎛---=030120031020313212a a a U L D a a a AJacobi 迭代法,其迭代矩阵为:⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛---=⎪⎪⎪⎭⎫ ⎝⎛---⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛=+=-031302120313********)(1aaa a a a a aaU L D B J J B 的特征矩阵为:)14(313212||2a aaa a a aB I J +=⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛---=-λλλλλλ 解得01=λ,i a 142=λ,当1|14||14|)(<==ai a B J ρ,即14||>a 时,Jacobi 迭代法收敛.3.5 用Gauss Seidel -迭代法解线性方程组123142*********x x x --⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪-= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭, 是否收敛?若不收敛,则能否改写成线性方程组,使得Gauss Seidel -迭代法收敛.解:(1)按Gauss Seidel -迭代法展开:⎪⎪⎪⎭⎫⎝⎛--⎪⎪⎪⎭⎫ ⎝⎛---⎪⎪⎪⎭⎫ ⎝⎛-=--=⎪⎪⎪⎭⎫ ⎝⎛--=000240020040411420014241U L D A 对Gauss Seidel -迭代法,其迭代矩阵为⎪⎪⎪⎭⎫ ⎝⎛---=⎪⎪⎪⎭⎫ ⎝⎛-⎪⎪⎪⎭⎫ ⎝⎛--=⎪⎪⎪⎭⎫ ⎝⎛-⎪⎪⎪⎭⎫ ⎝⎛-=-=--480816024000024025.05.02014000000240420141)(11U L D B G G B 的特征矩阵为:)20(480816024||2-=⎪⎪⎪⎭⎫⎝⎛---=-λλλλλλG B I 120)(>=G B ρ,Gauss Seidel -迭代法发散.(2)将A 改写成严格对角占优矩阵,则Gauss Seidel -迭代法必收敛,比如:⎪⎪⎪⎭⎫ ⎝⎛=120014241C对Gauss Seidel -迭代法,其迭代矩阵为:⎪⎪⎪⎭⎫ ⎝⎛----=⎪⎪⎪⎭⎫ ⎝⎛--⎪⎪⎪⎭⎫ ⎝⎛--=⎪⎪⎪⎭⎫ ⎝⎛--⎪⎪⎪⎭⎫⎝⎛=-=--163208160240000240128014001000240120141)(11U L D B G G B 的特征矩阵为:316320816024||λλλλλ=⎪⎪⎪⎭⎫⎝⎛+--=-G B I 10)(<=G B ρ,Gauss Seidel -迭代法收敛.3.7 设迭代法f Bx x k k +=+1,,...)2,1,0(=k ,的迭代矩阵B 的谱半径()0B ρ=,试证明该迭代法最多迭代n 次便可得到方程组x Bx f =+的解*x ,即*n x x =.解:n 阶矩阵B 一定相似于它的若当标准型J ,即存在可逆矩阵P 使得1P BP J -=,因为()0B ρ=,故B 的特征值全为0,于是得:⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=000 J 由此可知0n J =.x Bx f =+显然有唯一解*x ,即**x Bx f =+,又1**()k k x x B x x +-=-,于是()*2(2)*(0)*()()n n n x x B x x B x x --=-==-又因为1110n n P BP J B P JP B P J P ---=⇒=⇒==所以()*0n xx -=,即*n x x =.3.8 给定线性方程组Ax b =,其中323,121A b ⎡⎤⎡⎤==⎢⎥⎢⎥-⎣⎦⎣⎦若用迭代法,...)1,0)((1=-+=+k b Ax x x k k k α,求解,问:(1) 实数取何值时该迭代法收敛;(2) 实数取何值时该迭代法收敛最快. 解:该迭代公式可改写为b x A I x k k αα-+=+)(1,其对应的迭代矩阵为:⎪⎪⎭⎫⎝⎛+++=+=ααααα21231A I B , B 的特征矩阵为:)]1()][41([)21()2()31(||αλαλαλαααλλ+-+-=⎪⎪⎭⎫ ⎝⎛+--+-+-=-B I , 解得αλ411+=,αλ+=12,41,0.4()max{|14|,|1|}1,0.4014,0,B ααραααααα--<-⎧⎪=++=+-<<⎨⎪+>⎩(1)1)(<B ρ,即⎩⎨⎧<+<+1|1|1|41|αα,解得021<<-α,该迭代法收敛.(2)在021<<-α上,当4.0-=α时,)(B ρ达到最小,该迭代法收敛最快.3.9 用SOR 迭代法解线性方程1233.21141 3.71 4.511 4.25x x x ⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭, 取初始向量0[0,0,0]Tx =, 1.25ω=,迭代三次,并讨论其收敛性. 解:SOR 迭代公式:⎪⎪⎪⎩⎪⎪⎪⎨⎧--+-=--+-=--+-=++++++)5(2.4)1()5.4(7.3)1()4(2.3)1()1(2)1(1)(3)1(3)(3)1(1)(2)1(2)(3)(2)(1)1(1k k k k k k k k k k k k x x x x x x x x x x x x ϖϖϖϖϖϖ 取初始向量0[0,0,0]Tx =, 1.25ω=,迭代三次,kk x 1k x 2 kx 31 1.56250.992398649 0.727708736 2 0.499958053 0.857418315 0.902186992 3 0.7501646640.747688781 0.816758774]58774781,0.81674,0.7476880.75016466[)3(=x因A 为对称正定矩阵,10)(<=A ρ,SOR 迭代法必收敛.3.11 用SOR 迭代法解线性方程组123410114140143x x x -⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪--= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪--⎝⎭⎝⎭⎝⎭其精确解*11[,1,]22Tx =-,分别取 1.03ω=,1ω=, 1.1ω=,要求当*5||||10kx x -∞-≤时迭代终止,并且对每一个ω值确定迭代次数. 解:用SOR 迭代公式:(1)()()112(1)()(1)()2213(1)()(1)332(1)[1]4(1)[4]4(1)[3]4k k k k k k k k k k x x x x x x x x x x ϖωϖωϖω+++++⎧=-++⎪⎪⎪=-+++⎨⎪⎪=-+-+⎪⎩(1) 取初值向量0[0,0,0]Tx =,当 1.03ω=时k错误!1kx2k x 3k x0 01 0.25751.09630625 -0.490201141 2 0.532073859 1.007893038 -0.498261509 3 0.501070241 1.000486458 -0.499926892 4 0.500093156 1.000028219 -0.499994927 5 0.500004472 1.000001611 -0.499999737 60.500000281 1.000000092 -0.4999999846*5||||0.00000028110x x -∞-=≤,迭代6次后得到满足精度要求的根:]999984092,-0.4991,1.0000000.50000028[6=x(2) 取初值向量0[0,0,0]Tx =,当1ω=时k错误!1kx2k x 3k x0 0 01 0.251.0625 -0.484375 2 0.515625 1.0078125 -0.498046875 3 0.501953125 1.000976563 -0.499755859 4 0.500244141 1.00012207 -0.499969482 5 0.500030518 1.000015259 -0.499996185 6 0.500003815 1.000001907 -0.499999523 70.500000477 1.000000238 -0.499999947*5||||0.00000047710x x -∞-=≤,迭代7次后得到满足精度要求的根:]99994238,-0.4997,1.0000000.50000047[7=x(3) 取初值向量0[0,0,0]Tx =,当 1.1ω=时k错误!1kx2k x 3k x0 010.275 1.175625 -0.5017031252 0.570796875 1.001438281 -0.499434163 0.49331584 0.998173634 -0.500558835 4 0.500166165 1.000074653 -0.499923587 5 0.500003913 1.000014624 -0.500003626 0.50000363 0.999998541 -0.5000000397 0.499999236 0.999999925 -0.5000000177*5||||0.00000076436110x x -∞-=≤,迭代7次后满足精度要求.3.12 考虑迭代法,...)1,0(1=+=+k f Bx x k k其中⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛-=021212102121210B ,⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--=21121f 证明:该迭代法收敛,取初始向量0[0,0,0]Tx =,计算4x . 证:B 的特征矩阵为3212121212121||λλλλλ=⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛-----=-B I 0)(=B ρ,该迭代法收敛.该迭代法的迭代公式为:⎪⎪⎪⎩⎪⎪⎪⎨⎧-+=++=--=+++21212112121212121211331123211k k k kk k k k k x x x x x x x x x 取初始向量0[0,0,0]Tx =,迭代四次:k错误!1kx2k x 3k x0 0 0 0 1 -0.5 1 -0.5 2 0.353553391 0.5 -0.353553391 3 0 1 0 40 1 0 故]0,1,0[)4( x。
数值分析线性方程组的迭代解法

数值分析课程实验报告实验名称 线性方程组的迭代解法Ax b =的系数矩阵对角线元素容许误差。
雅可比(Jacobi )迭代法解方程组的算法描述如下:任取初始向量(0)(0)1(xx =1+,并且 1,2,...,n ,计算 11(ni j ii j ib a a =≠-∑()k x ,结束;否则执行④,则不收敛,终止程序;否则转② 迭代法的算法描述)迭代法中,如果当新的分量求出后,马上用它来代替旧的分量,则可能会更快地接近方程组的准确解。
基于这种设想构造的迭代公式,n ,k = (2)算法可相应地从雅可比(Jacobi )迭代法改造得到(Gauss-Seidel)迭代得到的值进一()()()1((1k i ii k k i i x b a x x ωω==+-1,2,,n ,2,k =(3)为松弛因子(显然当1ω=塞德尔迭代公式) ()k ix 通常优于旧值(1)k ix -,在将两者加工成松弛值时,自然要求松弛因子1ω>,以尽量发挥新值的优势,这类迭代就称为逐次超松弛迭代法。
SOR 迭代的关键在于选取合适的松弛因子,松弛因子的取值对收敛速度影响很大,但如何选取最佳松弛因子的问题,至今仍未有效解决,在实际计算时,通常依据系数矩阵的特点,并结合以往的经验选取合适的松弛因子。
练习与思考题分析解答(0)(1,1,1,1)x =[ -0.999976, -0.999976, -0.999976, -0.999976]x =[ -0.99999, -0.999991, -0.999992, -0.999993]x =塞德尔迭代算法的收敛速度要比雅可比迭代算法的收敛速度快SOR 迭代实质上是高斯原理和基本方法相同。
如果选择合适的松弛因子,它能够加快收敛速度。
SOR 迭代算法更加普通,当选取一个合适的松弛因子后收敛速度明显加快。
迭代算法将前一步的结果[ -0.99999, -0.999991, -0.999992, -0.999993]x =[ -0.999992, -0.999993, -0.999994, -0.999995]x =[ -0.999993, -0.999994, -0.999995, -0.999995]x =[ -0.999992, -0.999993, -0.999994, -0.999995]x =[ -0.999999, -1.0, -1.0, -1.0]x =[ -0.999999, -1.0, -1.0, -1.0]x =因为为了保证迭代过程收敛,松弛因子1.3左右。
Jacobi迭代法求解线性方程组实验报告

仿真平台与工具应用实践Jacobi迭代法求解线性方程组实验报告院系:专业班级:姓名:学号:指导老师:一、实验目的熟悉Jacobi迭代法原理;学习使用Jacobi迭代法求解线性方程组;编程实现该方法;二、实验内容应用Jacobi迭代法解如下线性方程组:, 要求计算精度为三、实验过程(1)、算法理论迭代格式的引出是依据迭代法的基本思想: 构造一个向量系列, 使其收敛至某个极限, 则就是要求的方程组的准确解。
Jacobi迭代将方程组:在假设, 改写成如果引用系数矩阵, 及向量, , ,方程组(1)和(2)分别可写为: 及, 这样就得到了迭代格式用迭代解方程组时, 就可任意取初值带入迭代可知式, 然后求。
但是, 比较大的时候, 写方程组和是很麻烦的, 如果直接由, 能直接得到, 就是矩阵与向量的运算了, 那么如何得到, 呢?实际上, 如果引进非奇异对角矩阵将分解成:要求的解, 实质上就有而是非奇异的, 所以存在, 从而有我们在这里不妨令就得到迭代格式:(2)算法框图(3)、算法程序m 文件:function x=jacobi(A,b,P,delta,n)N=length(b); %返回矩阵b的最大长度for k=1:nfor j=1:Nx(j)=(b(j)-A(j,[1:j-1,j+1:N])*P([1:j-1,j+1:N]))/A(j,j);enderr=abs(norm(x'-P)); %求(x'-P)模的绝对值P=x';if(err<delta) %判断是否符合精度要求break;endendE=eye(N,N); %产生N行N列矩阵D=diag(diag(A));f=A*inv(D); %f是A乘D的逆矩阵B=E-f;Px=x';k,errBMATLAB代码:>> clear allA=[4, -1, 1;4, -8, 1;-2, 1, 5];b=[7, -21, 15]';P=[0,0,0]';x=jacobi(A,b,P,1e-7,20)(4)、算法实现用迭代法求解方程组:正常计算结果是2, 3, 4 , 下面是程序输出结果:P =2.00004.00003.0000k =17err =9.3859e-008B =0 -0.1250 -0.2000-1.0000 0 -0.20000.5000 0.1250 0x =2.00004.00003.0000四、实验体会五、MATLAB是非常实用的软件, 能够避免大量计算, 简化我们的工作, 带来便捷。
解线性方程组的迭代法

实验三 解线性方程组的迭代法(1) 实验目的1: 掌握Jacobi 迭代法,Gauss-Seidel 法和SOR 算法的基本思想和迭代步骤;2:编写上述算法的Matlab程序,通过上机计算理解迭代法求解线性方程组的特点,并能和消去法比较;运用所学的迭代法算法; 3: 理解终止步骤终止步骤∞+-)()1(k k x x < ε对迭代法敛散性的意义;了解初始解x (0)、松弛因子的选取对计算结果的影响。
其解。
(2)【实验要求】1、理解迭代法求解线性方程组,并能与消去法比较;2、分别对不同精度要求,如ε = 10−3 ,10−4 ,10−5由迭代次数体会该迭代法的收敛快慢;3、使用SOR 方法时,选取松弛因子ω =0.8,0.9,1,1.1,1.2 等,讨论对该算法收敛性的影响,并能找出你所选用的最佳松弛因子;4、给出各种算法的设计程序和计算结果。
5、上机计算时,终止步骤∞+-)()1(k k x x < ε 或k >(预给的迭代次数),对迭代法敛散性的影响;(3)【实验内容】1.编写Jacobi算法的Matlab程序,并选取不同的初始点求解问题14-2和16,分析该算法的收敛性;function [x, k, index]=Jacobi(A, b, ep, it_max)% 求解线性方程组的Jacobi 迭代法,其中% A --- 方程组的系数矩阵% b --- 方程组的右端项% ep --- 精度要求。
省缺为1e-5% it_max --- 最大迭代次数,省缺为100% x --- 方程组的解% k --- 迭代次数% index --- index=1表示迭代收敛到指定要求;% index=0表示迭代失败if nargin <4 it_max=100; endif nargin <3 ep=1e-5; endn=length(A); k=0;x=zeros(n,1); y=zeros(n,1); index=1;while 1for i=1:ny(i)=b(i);for j=1:nif j~=iy(i)=y(i)-A(i,j)*x(j);endendif abs(A(i,i))<1e-10 | k==it_maxindex=0; return;endy(i)=y(i)/A(i,i);endif norm(y-x,inf)<epbreak;endx=y; k=k+1;endA=[4 -1 0 -1 0 0-1 4 -1 0 -1 00 -1 4 0 0 -1-1 0 0 4 -1 00 -1 0 -1 4 -10 0 -1 0 -1 4];>> b=[2 1 2 2 1 2]';[x, k, index]=Jacobi(A, b, 1e-5, 100)不同初始点:2.编写GS算法的Matlab程序,并选取不同的初始点求解问题14-2和17,分析该算法的收敛性;3. 编写SOR算法的Matlab程序,并选取不同的初始点求解问题15, 选取松弛因子ω=0.8,0.9,1,1.1,1.2 等,讨论对该算法收敛性的影响,并能找出你所选用的最佳松弛因子4.对实验二所列线性方程组,试用Jacobi 迭代法,Gauss-Seidol 迭代法和SOR 方法进行求解,并与直接算法进行比较.。
解线性方程组的迭代法

|| x || 0 (非负性) ; (1)|| x || 0 ,当且仅当 x 0 时,
(2) || x ||| | || x || (齐次性); (3) || x y |||| x || || y || (三角不等式). 则称 || x || 为向量 x 的范数 (或模).
4.1.2 向量范数和向量序列的极限
常用的向量范数:设 x R n (1)向量的 - 范数 (最大范数): || x || max | xi |
1 i n
|| x ||1 (2)向量的 1 - 范数 (绝对值范数):
(3)向量的 2 - 范数:|| x ||2 ( x , x ) (
|| A ||2 3+2 2 , || A ||F 6
4.1.3 矩阵范数和矩阵序列的极限
(k ) ) R nn ,如果存 定义5 (矩阵序列的极限) 设有矩阵序列 Ak (aij
在 A (aij ) R nn,使
k (k ) lim aij aij ,
i, j 1, 2,
(4) || AB |||| A || || B || ; 则称 || A || 为矩阵 A 的范数.
4.1.3 矩阵范数和矩阵序列的极限
相容性: 设有矩阵范数 || ||s 和向量范数 || ||t ,如果对任何向量 x R n 及矩阵 A R nn ,有/2 || A ||F ( aij ) i , j 1 n
它是与向量 2-范数相容的矩阵范数,但不是从属范数.
4.1.3 矩阵范数和矩阵序列的极限
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
黄 冈 师 范 学 院
本科生毕业论文(设计)开题报告书
学 生姓 名 滑慧荐 专 业班 级 数学与应用 数学 指 导 教 师 王成 开 题
时 间
20 - -
课 题
名 称
线性方程组的迭代法求解
选题依据和意义
随着社会的发展,在科技、工程、医学、经济等各个领域中,很多问题常常归结为解
线性方程组,有些问题的数学模型虽不直接表现为求解线性方程组,但其数值解法却需将
该问题“离散化”或“线性化”为线性方程组。
本课题运用所学的数学专业知识研究,有助于我们进一步掌握大学数学方面的知识,
特别是迭代方法。通过课题的研究,我进一步掌握了迭代方法的思想,对于今后类似实际
问题的解法具有重要的意义。
研究内容(主要指标和预期目标)
主要指标
(1)介绍线性方程组的几种迭代解法。
(2)推导迭代的收敛公式。
(3)线性方程组的迭代解法在实际生活中的一些应用。
预期目标
(1)学会运用各种迭代方法解线性方程组。
(2)进一步学会迭代方法的数学思想。
研究条件(包括需要的仪器和材料)
仪器:电脑,PDF阅读器、WORD2003、公式编辑器等计算机应用软件.
材料:中国期刊网、万方数据库资料、图书馆书本资料.
文献资料
[1]钱志良,孔海涛.任意线性方程组的迭代求解法,常州信息职业技术学院学报.2008年,
第7卷(第6期:3页)
[2]李爱芹.线性方程组的迭代解法,科学技术与工程.2007年,第7卷(第14期:8页)
[3]孙霞林.一种线性方程组的迭代解法,武汉化工学院学报.2001年,第23卷(第2期:
3页)
[4]田学全,朱世建.有无穷解的线性方程组的迭代法,塔里木农垦大学学报.2004年,第
16卷(第2期:3页)
[5]杨德祥.在Excel中应用迭代法求解线性方程组—雅可比(Jacobi)和塞德尔(Seidel)
迭代法,工程地质计算机应用.2007年(1):33-34.
[6]杜衡吉,徐昆良. Jacobi和Gauss—Seidel迭代法求解线性方程组的分析及应用,曲靖
师范学院学报.2011,30(3)46-50.
[7]王育琳,贺迅宇,张尚先. Jacobi与Gauss—Seidel迭代法求解线性方程组收敛性比较
与研究,株洲师范高等专科学校学报.2004,9(3):23-25.
[8]何吉欢.大型线性方程组的变分迭代解法,工科数学.1999,15(2):119-123.
[9]郑亚敏.迭代法解线性方程组的收敛性比较,江西科学.2009,27(5):659-661.
[10]徐亚平,李让利.关于解线性方程组的迭代法,汉中师范学院学报(自然科学).1997,
15(1):5-9.
[11]王丽,孙明军,宋永忠.解非埃尔特线性方程组的外推迭代法的收敛性,南京师大学报
(自然科学版).2007,30(1):1-5.
[12]汪仲文.解线性方程组的迭代方法之比较,喀什师范学院学报.2008,29(6):21-25.
[13]韩艳丽.求解线性方程组的Jacobi和Gauss—Seidel迭代法的收敛定理,河南理工大学
学报.2009,20(3):31.
[14]陈丽红,周志刚,万立.求解线性方程组的一种迭代法的改进,武汉科技学院学
报.2010,23(2):33-35.
[15]常双领,张传林.球解线性方程组的一种迭代算法,暨南大学学报(自然科学版).2004,
25(3):256-259.
[16]曲双红,王雪莲.求解线性方程组迭代法的Excel实现,高校理科研究.2010年,第
21卷(第6期:5页)
[17] 高静.系数矩阵为L-矩阵的线性方程组的新迭代法,苏州市职业大学学报.2011年,
第22卷(第2期:4页)
[18] 张步林.线性代数方程组迭代解法的MATLAB实现,成都纺织高等专科学校学报.2008
年,第25卷(第4期:3页)
[19] 花威.线性方程组的迭代解法及其MALAB实现程序,长江工程职业技术学院学报.2009
年,第26卷(第4期:3页)
[20]杨廷鸿,但琦,汪益川,田艳芳.线性方程组迭代解法的另类矩阵形式,后勤工程学
院学报.2006年,第13卷(第3期:1页)
[21] 陈永林.一般限制线性方程组的迭代解法,应用数学学报.1996年,第19卷(第4期:
9页)
[22] 杨大衡.一类线性方程解的Jacobi和Seidel迭代的敛散性,天津职业技师师范学院学
报.1991年,第27卷(第2期:5页)
[23]张亚红.一种实用的线性方程组迭代预处理算法,淮阴工学院学报.2006年,第15卷(第
5期:3页)
[24]陈新,陈永林.用基于矩阵正常分裂的迭代法求解长方或奇异线性方程组,南京师大学
报(自然科学版).2006年,第29卷(第2期:5页)
研究方法和技术路线
研究方法:主要运用文献资料法、综合分析法、对比分析法等理论寻求解决问题的最
佳方案。
技术路线:①提出选题的依据。
②综合国内外学术界关于此问题的讨论,提出自己的见解。
③作归纳总结。
进展计划
本人自11—12学年第一学期以来,便着力于选择学位论文的选题,与指导教师商讨
论文开题和撰写论文的相关事宜,分别从图书馆、指导教师、相关网络资源上搜集、整理
学位论文所需资料,阅读并收集有关论文的材料,做了大量实践性的工作.
2011年10月8日—2012年12月16日 确定论文题目和资料的搜集.
2011年12月17日—2012年3月26日 完成文献综述和开题报告.
2012年3月27日—2012年4月18日 确定论文框架,完成初稿.
2012年4月19日—2012年5月10日 修改完善论文,完成定稿.
2012年5月11日—2012年5月20日 准备论文答辩.
指导教师意见
滑慧荐同学根据师范专业的特点,就本人感兴趣的数学问题,查阅了相关的参考资
料,并且多次征求指导老师的意见,选择了以《线性方程组的迭代法求解》为毕业论文研
究课题.该选题方向比较适合于本科生的毕业论文,工作量也比较适中.同意开题.
指导教师(签名) :
年 月 日
备注
