八年级几何证明常见模型

（1）手拉手模型

【例题1】在直线ABC 的同一侧作两个等边三角形△ABD 和△BCE ，

连接AE 与CD ，证明：（1） △ABE ≌△DBC （2） AE=DC

（3） AE 与DC 的夹角为60。

（4） △AGB ≌△DFB （5） △EGB ≌△CFB

（6） BH 平分∠AHC

（7） GF ∥AC

【变式练习】1、如果两个等边三角形△ABD 和△BCE ，连接AE 与CD ，证明：

（1） △ABE ≌△DBC

（2） AE=DC

（3） AE 与DC 的夹角为60。

（4） AE 与DC 的交点设为H,BH

平分∠AHC

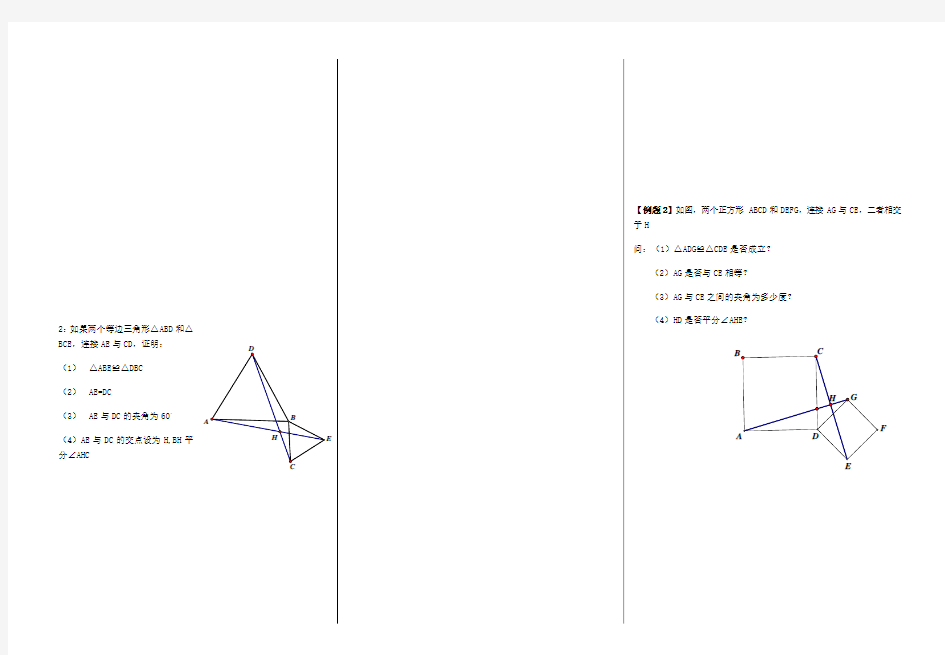
2：如果两个等边三角形△ABD和△BCE，连接AE与CD，证明：

（1）△ABE≌△DBC

（2）AE=DC

（3）AE与DC的夹角为60。

（4）AE与DC的交点设为H,BH平分∠AHC

【例题2】如图，两个正方形ABCD和DEFG，连接AG与CE，二者相交

于H

问：（1）△ADG≌△CDE是否成立？

（2）AG是否与CE相等？

（3）AG与CE之间的夹角为多少度？

（4）HD是否平分∠AHE？

【变式练习】1：如图两个等腰直角三角形ADC与EDG，连接AG,CE,

二者相交于H.

问（1）△ADG≌△CDE是否成立？

（2）AG是否与CE相等？

（3）AG与CE之间

的夹角为多少度？

AHE？

2：两个等腰三角形ABD与BCE，其中AB=BD,CB=EB,∠ABD=∠CBE=a

连接AE与CD.

问（1）△ABE≌△DBC是否成立？

（2）AE是否与CD相等？

（3）AE与CD之间的夹角为多少度？

（4）HB 是否平分∠AHC ？

【例题3】如图1，AB=AE ，AC=AD ，∠BAE=∠CAD=90°．（1）证明：EC=BD ；（2）证明：EC ⊥BD ；

（3）如图2，连接ED ，若N 点为DE 的中点，连接NA 并延长与BC 交于点M ，证明：AM ⊥BC ．

他条件不变，请问，（1）中的结论是否任然成立?若成立，

请证明；若不成立，请说明理由。

【变式练习】1，⊿ABC中，AG⊥BC于点G，以A为直角顶点，

分别以AB、AC为直角边，向⊿ABC作等腰Rt⊿ABE和等腰Rt

⊿ACF，过点E、F作射线GA的垂线，垂足分别为P、Q。（1）

试探究EP与FQ之间的数量关系，并证明你的结论；（2）

如图2，若连接EF交GA的延长线于H，由（1）中的结论你

能判断EH与FH的大小关系吗？并说明理由。（3）在（2）

的条件下，若BC=AG=24，请直接写出S⊿AEF=

（2）角平分线模型

【例题1】.如图1，OP是∠AOB的平分线，请你利用图形画

一对以OP为所在直线为对称轴的全等三角形，请你参考这个

全等三角形的方法，解答下列问题。

①、如图2，在△ABC中，∠ACB是直角，∠B=600，AD、CE

是∠BAC、∠BCA的角平分线，相交于点F，请你判断并写出

EF与DF之间的数量的关系。

②、如图3，在△ABC中，∠ACB不是直角，而（1）中的其

【变式练习】1、已知，，.

2、在四边形ABCD 中，BC>AB ，AD=CD ，BD 平分.

.求证：?=∠+∠180C A

3、已知四边形ABCD 中，

图4

【例题2】如图所示，在ABC ?中，AD 是BAC ∠的外角平分线，P

是AD 上异于点A 的任意一点，试比较PB PC +与AB AC +的大小，并说明理由．

21∠=∠43∠=∠BAC AP ∠平分求证：BAC

∠..,1800BAD AC CD BC D B ∠==∠+∠平分

求证：

【变式练习】1、在ABC ?中，AB AC >，AD 是BAC ∠的平分线．P 是AD 上任意一点．

求证：AB AC PB PC ->-．

2、如图，已知△ABC 中，AB ＝AC ，∠A ＝100°，∠B 的平分线交AC 于D ，

求证：AD ＋BD ＝BC

3、如图，已知△ABC 中，BC ＝AC ，∠C ＝90°，∠A 的平分线交BC 于D ，

求证：AC ＋CD ＝AB

4、如图1，AD∥BC，∠D＝90°，AE平分∠BAD，BE平分∠ABC，那

么AD、BC、AB三条线段有何数量关系？请你猜想并证明

(2) 如图2，将(1)中的∠D＝90°去掉，其余条件均不变，上述结论还成立

吗？请你推理并证明

（3）垂直模型

【例题1】如图1，在平面直角坐标系中，△ABC的顶点A(－3，0)、

B(0，3)，AD⊥BC于D交BC于D点，交y轴于点E(0，1)

(1) 求C点的坐标

(2) 如图2，过点C作CF⊥CB，且截取CF＝CB，连接BF，求△BCF的

面积

(3) 如图3，点P为y轴正半轴上一动点，点Q在第三象限内，QP⊥PC，

且QP＝PC，连接QO，过点Q作QR⊥x轴于R，求

的值

【变式练习】1、如图（1），已知△ABC中，∠BAC=90°，AB=AC，AE是过A的一

条直线，且B、C在A、E的异侧，BD⊥AE于D，CE⊥AE于E

（1）试说明：BD=DE+CE．

（2）若直线AE绕A点旋转到图（2）位置时（BD＜CE），其余条件不变，问BD与DE、

CE的关系如何？请直接写出结果；

（3）若直线AE绕A点旋转到图（3）位置时（BD＞CE），其余条件不变，问BD与DE、

CE的关系如何？请直接写出结果，不需说明理由．

2、已知：如图所示，Rt△ABC 中，AB=AC，，O为

BC中点，若M、N分别在线段AC、AB上移动，且在移动中保持AN=CM.

①、是判断△OMN的形状，并证明你的结论.

②、当M、N分别在线段AC、AB上移动时，四边形AMON 的面积如何变化？

思路：两种方法：

∠

BAC

（4）半角模型

条件：

思路：（1）、延长其中一个补角的线段

（延长

CD 到E ，使ED=BM ，连AE 或延长CB

到F ，使FB=DN ，连AF ）

结论：①MN=BM+DN ② ③AM 、AN 分别平分

∠BMN 和∠DNM

（2）、对称（翻折）

思路:分别将△ABM 和△ADN 以AM 和AN 为对称

轴翻折，但一定要证明

M 、P 、N 三点共线.（∠B+∠D =且AB=AD ）例1、在正方形ABCD 中，若M 、N 分别在边BC 、CD 上移动，且满足MN=BM +DN ，

求证：①.∠MAN=

②.

③.AM 、AN

分别平分∠BMN 和∠DNM.

1802

10=+=γθβα

且AB C CMN 2=

180

45AB

C CMN 2=

(完整版)初中几何基本图形归纳(基本图形常考图形)86168

初中几何常见基本图形

F E D C B A F E D C B A D C A 几何基本图形 1、如图，正三角形ABC 中，AE=CD ，AD 、BE 交于F ： ①△AEB ≌△ADC ②∠BFD=600 ③△AEF ∽△ABE 2、如图，正三角形ABC 中，F 是△ABC 中心，正三角形边长为a ： ①AF ：DF ：AD=2：1：3 ②内切圆半径DF= a 63 ③外接圆半径AF=a 3 3 3、如图Rt △ABC 中，∠C=900，∠B=300，AC=a ，D 是AC 上的点： ①内切圆半径为 a 2 1 3- ②外接圆半径为a 4、如图Rt △ABC 中，∠C=900，AB=AC=a ，D 是AC 上的点：为 a 2 5； ②当BD 是角平分线时，BD 长为a 224-。 ①当D 是AC 中点时，BD 长 C B A 300

D C A 45 A B C 5、如图，如图Rt △ABC 中，∠BAC=900，AB=AC=a ，E 、D 是BC 、AC 上的点，且∠AED=450： ①△ABE ∽ECD ②设BE=x ，则CD=a x ax 22-。 6、如图AB=AC ，∠A=360，则：BC= 2 1 5-AB 。 7、如图AB=AC ，D 是BC 上一点，AE=AD ，则： 2 1 ∠BAD=∠EDC 。 8、如图，D 、E 是△ABC 边BC 上两点，AC=CD ，BE=BA ，则当：①∠BAC=1000时，∠DAE=400；②当∠BAC=x 0时，∠DAE=2 180x -0 。 9、如图，△BCA 中，D 是三角形内一点， ①当点D 是外心时，∠BDC= 21 ∠A ；②当点D 是内心时，∠BDC=2 180A ∠+ 10、如图，∠ACB=900，DE 是AB 中垂线，则①AE=BE ，若AC=3，BC=4，设AE=x ，有 ()22234x x =+-； ②△BED ∽△BAC 。 11、如图，E 是正方形ABCD 对角线BD 上一点，AE 交BC 延长线于点F ，H 是FG 中点： ①△ADE ≌△CDE ； ②△EGC ∽ECF ； ③EC ⊥CH ； ④EC 是以BG 为直径的圆的切线。 12、如图，ABCD 、CGFE 是正方形：①△DCG ≌CBCE ； ②BE ⊥DG 。 13、如图，正方形ABCD 对角线交于O ，E 是OB 上一点，EF ∥BC ： ①△AOE ≌△BOF ； ②AE ⊥BF 。 14、如图，E 是正方形ABCD 对角线上一点，EF ⊥CD ，EG ⊥BC ： ①AE=FG ；②AE ⊥FG 。 15、如图，将矩形ABCD 顶点B 沿某直线翻折可与D 点重合： ①EF 是BD 中垂线； ②BE=DE ，若AB=3，AD=5，设DE=x ，则()2 2 253x x =-+。 16、将矩形ABCD 顶点A 沿BD 翻折，A 落在E 处，如图： ①BD 是AE 中垂线，AB=BE ；②△BEF ≌△DCF ；③BF=DF 。 A B C E A B C E D A B C D A B C D E A B C D E F G H A B C D E F G

初中几何基本图形归纳(基本图形+常考图形)

初中几何基本图形归纳(基本图形+常考图形) -CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN

初中几何常见基本图形

F E D C B A F E D B A D C A 几何基本图形 1、如图，正三角形ABC 中，AE=CD ，AD 、BE 交于F ： ①△AEB ≌△ADC ②∠BFD=600 ③△AEF ∽△ABE 2、如图，正三角形ABC 中，F 是△ABC 中心，正三角形边长为a ： ①AF ：DF ：AD=2：1：3 ②内切圆半径DF= a 63 ③外接圆半径AF=a 3 3 3、如图Rt △ABC 中，∠C=900，∠B=300，AC=a ，D 是AC 上的点： ①内切圆半径为 a 2 1 3- ②外接圆半径为a 4、如图Rt △ABC 中，∠C=900，AB=AC=a ，D 是AC 上的点： BD 长为 a 2 5 ； ②当BD 是角平分线时，BD 长为①当D 是AC 中点时， a 224-。 5、如图，如图Rt △ABC 中，∠BAC=900，AB=AC=a ，E 、D 是BC 、AC 上的点，且∠AED=450 ：①△ABE ∽ECD ②设BE=x ，则CD=a x ax 2 2-。 C B A 300

E D C B A 45 A B C 6、如图AB=AC ，∠A=360，则：BC= 2 1 5-AB 。 7、如图AB=AC ，D 是BC 上一点，AE=AD ，则：2 1 ∠BAD=∠EDC 。 8、如图，D 、E 是△ABC 边BC 上两点，AC=CD ，BE=BA ，则当：①∠ 时，∠ DAE=400； ②当∠ BAC=1000 BAC=x 0 时， ∠ DAE= 2 180x -0 。 9、如图，△BCA 中，D 是三角形内一点， ①当点D 是外心时，∠BDC= 21 ∠A ；②当点D 是内心时，∠BDC=2 180A ∠+ 10、如图，∠ACB=900，DE 是AB 中垂线，则①AE=BE ，若AC=3，BC=4，设AE=x ，有()222 34x x =+-； ②△BED ∽△BAC 。 11、如图，E 是正方形ABCD 对角线BD 上一点，AE 交BC 延长线于点F ，H 是FG 中点：①△ADE ≌△CDE ； ②△EGC ∽ECF ； ③EC ⊥CH ； ④EC 是以BG 为直径的圆的切线。 12、如图，ABCD 、CGFE 是正方形：①△DCG ≌CBCE ； ②BE ⊥DG 。 13、如图，正方形ABCD 对角线交于O ，E 是OB 上一点，EF ∥BC ： A B C E A B C E D A B C D A B C D E A B C D E F G H A B C D E F G

(完整word版)初二几何证明整理(经典题型)

如何做几何证明题【知识梳理】 1、几何证明是平面几何中的一个重要问题，它对培养学生逻辑思维能力有着很大作用。几何证明有两种基本类型：一是平面图形的数量关系；二是有关平面图形的位置关系。这两类问题常常可以相互转化，如证明平行关系可转化为证明角等或角互补的问题。 2、掌握分析、证明几何问题的常用方法：（1）综合法（由因导果），从已知条件出发，通过有关定义、定理、公理的应用，逐步向前推进，直到问题的解决；（2）分析法（执果索因）从命题的结论考虑，推敲使其成立需要具备的条件，然后再把所需的条件看成要证的结论继续推敲，如此逐步往上逆求，直到已知事实为止；（3）两头凑法：将分析与综合法合并使用，比较起来，分析法利于思考，综合法易于表达，因此，在实际思考问题时，可合并使用，灵活处理，以利于缩短题设与结论的距离，最后达到证明目的。 3、掌握构造基本图形的方法：复杂的图形都是由基本图形组成的，因此要善于将复杂图形分解成基本图形。在更多时候需要构造基本图形，在构造基本图形时往往需要添加辅助线，以达到集中条件、转化问题的目的。【例题精讲】【专题一】证明线段相等或角相等两条线段或两个角相等是平面几何证明中最基本也是最重要的一种相等关系。很多其它问题最后都可化归为此类问题来证。证明两条线段或两角相等最常用的方法是利用全等三角形的性质，其它如线段中垂线的性质、角平分线的性质、等腰三角形的判定与性质等也经常用到。【例1】已知：如图所示，?A B C 中，∠=?===C AC BC AD DB AE CF 90，，，。求证：DE ＝DF F E D C B A

【巩固】如图所示，已知?A B C 为等边三角形，延长BC 到D ，延长BA 到E ，并且使AE ＝BD ，连结CE 、DE 。求证：EC ＝ED 【例2】已知：如图所示，AB ＝CD ，AD ＝BC ，AE ＝CF 。求证：∠E ＝∠F 【专题二】证明直线平行或垂直在两条直线的位置关系中，平行与垂直是两种特殊的位置。证两直线平行，可用同位角、内错角或同旁内角的关系来证，也可通过边对应成比例、三角形中位线定理证明。证两条直线垂直，可转化为证一个角等于90°，或利用两个锐角互余，或等腰三角形“三线合一”来证。【例3】如图所示，设BP 、CQ 是?A B C 的内角平分线，AH 、AK 分别为A 到BP 、CQ 的垂线。求证：KH ∥BC A C E D F B A B D C E A B Q P H C K

八年级上数学几何证明练习题

C A B C D E P 图 ⑴八年级数学（上）几何证明练习题 1、已知：在⊿ABC 中，∠A=900 ，AB=AC ，在BC 上任取一点P ，作PQ ∥AB 交AC 于Q ，作PR ∥CA 交BA 于R ，D 是BC 的中点，求证：⊿RDQ 是等腰直角三角形。 B 2、已知：在⊿ABC 中，∠A=900 ，AB=AC ，D 是AC 的中点，AE ⊥BD ，AE 延长线交BC 于F ，求证：∠ADB=∠FDC 。 3、已知：在⊿ABC 中BD 、CE 是高，在BD 、CE 或其延长线上分别截取BM=AC 、CN=AB ，求证： MA ⊥NA 。 4、已知：如图(1)，在△ABC 中，BP 、CP 分别平分∠ABC 和∠ACB ，DE 过点P 交AB 于D ，交AC 于E ，且DE ∥BC ．求证：DE －DB=EC ．

5、在Rt △ABC 中，AB ＝AC ，∠BAC =90°，O 为BC 的中点。 (1)写出点O 到△ABC 的三个顶点A 、B 、C 的距离的大小关系(不要求证明)； (2)如果点M 、N 分别在线段AB 、AC 上移动，在移动中保持AN ＝BM ，请判断△OMN 的形状，并证明你的结论。 6、如图，△ABC 为等边三角形，延长BC 到D ，延长BA 到E ，AE=BD ，连结EC 、ED ，求证：CE=DE 7、如图，等腰三角形ABC 中，AB ＝AC ，∠A ＝90°，BD 平分∠ABC ，DE ⊥BC 且BC ＝10，求△DCE 的周长。 A B C O M N

几何证明习题答案 1. 连接AD,由△ABC为等腰直角三角形可得AD垂直AC,且AD=BD,∠DAQ=∠DBR=45度, 又由平行关系得,四边形RPQA为矩形,所以AQ=RP, △BRP也是等腰直角三角行,即BR=PR,所以AQ=BR 由边角边,△BRD全等于△AQD,所以∠BDR=∠ADQ,DR=DQ, ∠RDQ=∠RDA+∠ADQ=∠RDA+∠BDR=90度, 所以△RDQ是等腰RT△。 2. 作AG平分∠BAC交BD于G ∵∠BAC=90°∴∠CAG= ∠BAG=45° ∵∠BAC=90°AC=AB ∴∠C=∠ABC=45° ∴∠C=∠BAG ∵AE⊥BD ∴∠ABE+∠BAE=90° ∵∠CAF+∠BAE=90°∴∠CAF=∠ABE ∵AC=AB ∴△ACF ≌△BAG ∴CF=AG ∵∠C=∠DAG =45°CD=AD ∴△CDF ≌△ADG ∴∠CDF=∠ADB 3. 易证△ABM≌△NAC．∠NAM＝∠NAE＋∠BAM＝∠NAE＋ANE＝90° 4. 略 5.（1）因为直角三角形的斜边中点是三角形的外心，所以O到△ABC的三个顶点A、B、C距离相等；（2）△OMN是等腰直角三角形。证明：连接OA，如图， ∵AC=AB，∠BAC=90°，∴OA=OB，OA平分∠BAC，∠B=45°， ∴∠NAO=45°，∴∠NAO=∠B，在△NAO和△MBO 中， AN=BM ，∠NAO=∠B ，AO=BO ， ∴△NAO≌△MBO，∴ON=OM，∠AON=∠BOM， ∵AC=AB，O是BC的中点，∴AO⊥BC，即∠BOM+∠AOM=90°，∴∠AON+∠AOM=90°，即∠NOM=90°，∴△OMN是等腰直角三角形． 6. 延长CD到F，使DF=BC，连结EF ∵AE=BD ∴AE=CF ∵△ABC为正三角形∴BE=BF ∠B=60° ∴△EBF为等边三角形∴角F=60°EF=EB 在△EBC和△EFD中 EB=EF（已证）∠B=∠F（已证）BC=DF（已作） ∴△EBC≌△EFD（SAS）∴EC=ED 7. 周长为10.

初中几何基本图形归纳基本图形常考图形资料全

初中几何常见基本图形 AOC=BOD AOD=BOC OD OE ①BAD= C CAD= B ②AD2=BD·CD ③AB2=BD·BC ④AC2=CD·BC P=A+B+C A+B=C+D B=D P=90+A/2 P=A/2

P=90-A/2 AP平分BAC PB=PC

几何基本图形 1、如图，正三角形ABC 中，AE=CD ，AD 、BE 交于F ： ①△AEB ≌△ADC ②∠BFD=600 ③△AEF ∽△ABE 2、如图，正三角形ABC 中，F 是△ABC 中心，正三角形边长为a ： ①AF ：DF ：AD=2：1：3 ②内切圆半径DF= a 63 ③外接圆半径AF=a 3 3 3、如图Rt △ABC 中，∠C=900，∠B=300，AC=a ，D 是AC 上的点：

①内切圆半径为 a 2 1 3- ②外接圆半径为a 4、如图Rt △ABC 中，∠C=900，AB=AC=a ，D 是AC 上的点： ①当D 是AC 中点时，BD 长为 a 2 5 ； ②当BD 是角平分线时，BD 长为a 224-。 5、如图，如图Rt △ABC 中，∠BAC=900，AB=AC=a ，E 、D 是BC 、AC 上的点，且∠ AED=450：①△ABE ∽ECD ②设BE=x ，则CD=a x ax 2 2-。 6、如图AB=AC ，∠A=360，则：BC= 2 1 5-AB 。 7、如图AB=AC ，D 是BC 上一点，AE=AD ，则： 2 1 ∠BAD=∠EDC 。 8、如图，D 、E 是△ABC 边BC 上两点，AC=CD ，BE=BA ，则当：①∠BAC=1000时，∠DAE=400；②当∠BAC=x 0时，∠DAE= 2 180x -0 。 9、如图，△BCA 中，D 是三角形内一点， ①当点D 是外心时，∠BDC= 21 ∠A ；②当点D 是内心时，∠BDC=2 180A ∠+ 10、如图，∠ACB=900，DE 是AB 中垂线，则①AE=BE ，若AC=3，BC=4，设AE=x ，有()2 22 34x x =+-； ②△BED ∽△BAC 。 11、如图，E 是正方形ABCD 对角线BD 上一点，AE 交BC 延长线于点F ，H 是FG 中点：①△ADE ≌△CDE ； ②△EGC ∽ECF ； ③EC ⊥CH ； ④EC 是以BG 为直径的圆的切线。 12、如图，ABCD 、CGFE 是正方形：①△DCG ≌CBCE ； ②BE ⊥DG 。 13、如图，正方形ABCD 对角线交于O ，E 是OB 上一点，EF ∥BC ： ①△AOE ≌△BOF ； ②AE ⊥BF 。

八年级下册几何证明题

_D _C _B_C _A_B _A_B _E _A _B 四边形试题 1．已知：在矩形ABCD中，AE⊥BD于E，∠DAE=3∠BAE ，求：∠EAC的度数。 2．已知：直角梯形ABCD中，BC=CD=a且∠BCD=60?，E、F分别为梯形的腰AB、DC的中点，求：EF的长。 3、已知：在等腰梯形ABCD中，AB∥DC，AD=BC，E、F分别为AD、BC的中点，BD平分∠ABC交EF于G，EG=18，GF=10求：等腰梯形ABCD的周长。 4、已知：梯形ABCD中，AB∥CD，以AD，AC为邻边作平行四边形ACED，DC延长线交BE于F，求证：F是BE的中点。 5、已知：梯形ABCD中，AB∥CD，AC⊥CB，AC平分∠A，又∠B=60?，梯形的周长是20cm, 求：AB的长。

_ A _ B _B _ C _B _ F _ B _ C _ F _ B _A _ E 6、从平行四边形四边形ABCD 的各顶点作对角线的垂线AE 、BF 、CG 、DH ，垂足分别是E 、F 、G 、H ，求证：EF ∥GH 。 7、已知：梯形ABCD 的对角线的交点为E 若在平行边的一边BC 的延长线上取一点F ，使S ABC ?=S EBF ?，求证：DF ∥AC 。 8、在正方形ABCD 中，直线EF 平行于对角线AC ，与边AB 、BC 的交点为E 、F ，在DA 的延长线上取一点G ，使AG=AD ，若EG 与DF 的交点为H ，求证：AH 与正方形的边长相等。 9、若以直角三角形ABC 的边AB 为边，在三角形ABC 的外部作正方形ABDE ，AF 是BC 边的高，延长FA 使AG=BC ，求证：BG=CD 。 10、正方形ABCD ，E 、F 分别是AB 、AD 延长线上的一点，且AE=AF=AC ，EF 交BC 于G ，交AC 于K ，交CD 于H ，求证：EG=GC=CH=HF 。

青岛版初中数学八年级上册5.6几何证明举例

§5.6 几何证明举例（2）教学目标： 1. 学生能够证明等腰三角形的性质定理和判定定理。 2. 会运用等腰三角形的性质和判定进行有关的证明和计算。 3. 应用等腰三角形的性质和判定进一步认识等边三角形。 4. 培养学生分析问题和逻辑推理的能力。教学重、难点：重点：会证明等腰三角形的性质定理和判定定理。难点：等腰三角形的性质定理和判定定理的应用。教学准备：电子白板、直尺、圆规、直角三角板教学过程一、情境导入、复习回顾 1、等腰三角形的性质是什么，这个命题的逆命题是什么？二、交流展示(鼓励学生自己写出证明的过程，注意几何证明的三步) （1）“等腰三角形的两个底角相等”是真命题吗？怎样证明。证明：等腰三角形的两个底角相等。已知：如图，在△ABC中，AB=AC 求证：∠B=∠C 法1 证明：过点A作∠BAC的角平分线交BC于点D ∴∠BAD = ∠CAD (角平分线定义) 在△BAD与△CAD中 ∵AB = AC (已知) ∠BAD = ∠CAD (已证) AD = AD (公共边) ∴△BAD≌△CAD(SAS) ∴∠ B = ∠ C (全等三角形对应角相等) 法2 证明：作BC边上的中线 AD ∴ BD = CD (中线定义) 在△BAD与△CAD中 ∵AB = AC (已知) BD = CD （已证） AD = AD (公共边) ∴△BAD≌△CAD( SSS )

∴∠B = ∠ C (全等三角形对应角相等) （2）“等腰三角形的两个底角相等”的逆命题是真命题吗，怎样证明它的正确性？证明：有两个角相等的三角形是等腰三角形。已知：如图，在如图，在△ABC中，∠B=∠C 求证：AB=AC 证明：作AD⊥BC,垂足为D 则∠ADB=∠ADC=90°(垂直的定义)，在△ABD和△ACD中， ∵∠B=∠C (已知)， ∠ADB=∠ADC=90°(已证) AD=AD (公共边) ∴△ABD≌△ACD (AAS) ∴AB=AC(全等三角形的对应边相等) (3) 利用等腰三角形的性质定理和判定定理证明： (鼓励学生当老师讲给其他同学听) ①等边三角形的每个内角都是60° ②三个角都相等的三角形是等边三角形。三、精讲点拨： 1、等腰三角形的性质：性质1：性质2： 2、数学语言表达：性质1：性质2：在△ABC ∵ AB=AC ∵ AB=AC ∴∠B= ∠C ① AD平分∠BAC （等边对等角） ②AD⊥BC ③ BD=DC ( ①,② ,③均可作为一个条件，推出其他两项 ) （三线合一）四、典例精析例1 已知，D是△ABC内的一点，且DE=DC，BD平分∠ABC,CD平分∠ACB 求证：AB=AC

初中几何基本图形归纳(基本图形+常考图形)

初中几何常见基本图形 AOC=BOＤ AOD=BOC OD OE ①BAD=C CAＤ= Ｂ ②ＡD2=BD·CD ③AB2=ＢＤ·BＣ ④AC2=CＤ·BC P＝A＋B＋Ｃ A+Ｂ＝C+D B=D P=90+Ａ/2 Ｐ=A/2

Ｐ=90-A/2 ①AC平分BAD ②AB=CB ③BC∥AD AP平分BＡＣ PB＝PＣ ①AB=AC ②BD=CD ③AD BC

几何基本图形 1、如图,正三角形ＡBC 中，AE=CD ，AD 、B Ｅ交于F ： ①△ＡE Ｂ≌△A ＤC ②∠B ＦD ＝600 ③△ＡEF ∽△ＡＢE ２、如图,正三角形ABC 中，F 是△ABC 中心，正三角形边长为ａ: ①AF ：ＤF:AD ＝2:１：3 ②内切圆半径DF= a 63 ③外接圆半径AF ＝a 3 3 3、如图Rt △ABC 中，∠C ＝90０，∠B=３0０，AC=ａ，D 是AC 上的点： ①内切圆半径为 a 2 1 3 ②外接圆半径为a 4、如图Rt △ABC 中,∠C=９0０ ,ＡB=AC ＝a ,D 是AC 上的点：

F E D B A F E D C B A D C B A D C A 45 A B C a 2 5 ； ②当ＢD 是角平分线时,ＢD 长为a 224-。 ①当D 是AC 中点时,BD 长为 5、如图,如图R ｔ△ＡＢC 中,∠B ＡC=９00，A Ｂ=A Ｃ＝a ，Ｅ、Ｄ是BC 、ＡＣ上的点,且∠ ＡE Ｄ=4５0：①△ABE ∽ECD ②设BE=ｘ,则C Ｄ=a x ax 2 2-。 6、如图A Ｂ=AC,∠A ＝36０，则:BC ＝ 2 1 5-ＡB 。７、如图ＡＢ＝A Ｃ，D 是BC 上一点，AE=AD,则: 2 1 ∠BAD=∠ＥD Ｃ。 8、如图,D 、E 是△ABC 边BC 上两点,ＡC=CD,B Ｅ=ＢA,则当:①∠ＢA Ｃ＝1000时，∠ＤAE ＝400;②当∠BAC=x 0时,∠D ＡE=2 180x -０。 9、如图,△BC Ａ中，Ｄ是三角形内一点， ①当点D 是外心时，∠B ＤC= 21 ∠Ａ;②当点D 是内心时,∠BDC=2 180A ∠+ 1０、如图，∠AC Ｂ=９００，DE 是AB 中垂线，则①ＡE=B Ｅ,若ＡC=３,BC=４,设AE=ｘ，有()2 22 34x x =+-； ②△ＢED ∽△ＢAC 。１1、如图，Ｅ是正方形A ＢＣD 对角线ＢD 上一点,ＡE 交BC 延长线于点F ，Ｈ是FG 中点：①△ADE ≌△ＣＤE ； ②△ＥGC ∽EC Ｆ； ③EC ⊥C Ｈ； ④EC 是以ＢG 为直径的圆的切线。 12、如图，AB ＣD 、CGFE 是正方形:①△DCG ≌CBCE; ②ＢE ⊥DG 。 ? C B A 300 A B C E A B C E D A B C D A B C D E A B C D E F G H A B C D E F G

八年级下册几何证明题精选

八年级下册几何证明题精选 1、如图，矩形ABCD 中，AC 与BD 交于O 点，BE AC ⊥于BD CF E ⊥,于F ，求证：CF BE = 2、如图，在平行四边形ABCD 中，DN CL BL AN ,,,分别为D C B A ∠∠∠∠,,,的角平分线，试证明：四边形MNKL 是矩形 3、如图，矩形ABCD 的对角线相交于点O ，DE ∥CE AC ,∥CE DE DB ,,相交于E ，请判断四边形DOCE 的形状，并说明理由 4、如图，△ABC 中，B ACB ∠?=∠,90的平分线交高CD 于点E ，交AC 于F ， G AB FG ,⊥为垂足，请证明：四边形CEGF 是菱形 5、如图，平行四边形ABCD 的对角线相交于点O ，EF 经过点O ，分别与边AB ，DC 相交于点F E ,，点N M ,分别是线段OC OA , 的中点，求证：四B

边形ENFM是平行四边形 6、已知，如图，点M H F E, , ,分别是正方形ABCD的四条边上的点，并且DM CH BF AE= = =，求证：四边形EFHM是正方形 F B 7、如图，在梯形ABCD中，N M,分别为梯形两腰AB，CD的中点，ME∥AN交BC于点E，试证明：NE AM= 8、如图，在△ABC中，AC AB=，CE BD,分别为ACB ABC∠ ∠, 的平分线，求证：四边形EBCD是等腰梯形 9、如图，在直角梯形纸片ABCD中，AB∥DC，? = ∠90 A，CD〉AD，将纸片沿过点D的直线折叠，使点A落在边CD上的点E，折痕为DF，连结EF并展开纸片。（1）求证：四边形ADEF是正方形；（2）取线段AF的中点G，连结EG，结果CD BG=，试说明四边形GBCE是等腰梯形

八年级上册几何证明题专项练习

八年级上册几何证明题专项练习 1．如图，△ABC、△CDE均为等腰直角三角形，∠ACB=∠DCE=90°，点E在AB上．求证：△CDA≌△CEB． 2．如图，BD⊥AC于点D，CE⊥AB于点E，AD=AE．求证：BE=CD． 3．如图，已知点B，E，C，F在一条直线上，AB=DF，AC=DE，∠A=∠D．（1）求证：AC∥DE；（2）若BF=13，EC=5，求BC的长． 4．如图：点C是AE的中点，∠A=∠ECD，AB=CD，求证：∠B=∠D． 5．如图，点D是AB上一点，DF交AC于点E，DE=FE，FC∥AB 求证：AE=CE．

6．如图，BE⊥AC，CD⊥AB，垂足分别为E，D，BE=CD．求证：AB=AC． 7．如图，点A，B，C，D在同一条直线上，CE∥DF，EC=BD，AC=FD．求证：AE=FB． 8．如图，在△ABC中，AC=BC，∠C=90°，D是AB的中点，DE⊥DF，点E，F分别在AC，BC上，求证：DE=DF． 9．如图，点A、C、D、B四点共线，且AC=BD，∠A=∠B，∠ADE=∠BCF，求证：DE=CF． 10．如图，已知∠CAB=∠DBA，∠CBD=∠DAC．求证：BC=AD．

11．如图，点B、E、C、F在同一条直线上，AB=DE，AC=DF，BE=CF，求证：AB∥DE． 12．如图，AB∥CD，E是CD上一点，BE交AD于点F，EF=BF．求证：AF=DF． 13．已知△ABN和△ACM位置如图所示，AB=AC，AD=AE，∠1=∠2．（1）求证：BD=CE；（2）求证：∠M=∠N． 14．如图，∠ACB=90°，AC=BC，AD⊥CE，BE⊥CE，垂足分别为D，E．求证：△ACD≌△CBE． 15．如图，四边形ABCD中，E点在AD上，∠BAE=∠BCE=90°，且BC=CE，AB=DE．求证：△ABC≌△DEC．

初中几何基本图形归纳(基本图形+常考图形)

9 2 初中几何常见基本图形序号 1 基本图形 A C D B 基本结论 2 3 子母型 ① ② 2· C B 4 ③ 2· ④ 2· 5 C C A 6 D B D 7 D 8 90 + 2 A P B C D

16（）/2 ∥∥18 AD D E ∥ 20AD AE DE == AB AC BC 1090-2 11①平分 ② ③∥ “二推一” ⊕⊕→⊕ 12 13为中线 1:3:2 平分 14 A 12 B D C A ① “二推二” ② ③⊕⊕→⊕⊕ ④1= 15D E D、E为中点2 ∥ B C A D E、F为中点E F 17 B H D C E、F、G、H A为中点 G E B F C 四边形为平行四边形 A型A AE AD AE DE === BD CD AB AC BC 19 B C X型E D A ∥AD AE AD AE DE === BD CD AB AC BC B C 假A型 A E D B C

d B ④ O∠90° 25 AD P A PD == BC PC PB O 26 P A PD AD PC PB BC P 29 ∠∠ ∠∠180°假子母型A 21D2· B B C 221:1:2 A C C ①过圆心二推三 23 A O R E a/2 ②垂直于弦 ③平分弦平分弦所对的优弧 ⑤平分弦所对的劣弧 ⊕⊕→⊕⊕⊕ R22+(2)2 24A D C为直径 B 蝶型 D A P B C 规型 A B == O D C 27A型 A O B D P · PB PD BD == PC P A AC C A 28O D B AB BC AC == BD AB AD 2· C D A O 30 B C E ①过圆心“二推一” O②过切点 ③垂直于切线 A C B

八年级四边形几何证明提高题经典

八年级四边形几何证明提高题经典 Revised by BLUE on the afternoon of December 12,2020.

几何证明提高题 1、如图，在四边形ABCD 中，AB=AD ，CB=CD ，E 是CD 上一点，BE 交AC 于F ，连接DF ．（1）若AB ∥CD ，试证明四边形ABCD 是菱形；（2）在（2）的条件下，试确定E 点的位置，使得∠EFD=∠BCD ，并说明理由． 2、已知：如图平行四边形ABCD ，DE ⊥AC ，AM ⊥BD ，BN ⊥AC ，CF ⊥BD 求证：MN ∥EF 3、已知：如图菱形ABCD ，E 是BC 上一点，AE 、BD 交于 F ，若AE=AB ，∠DAE=2∠BAE 求证：BE=AF 4、已知：如图正方形ABCD ，P 、Q 分别是BC 、DC 上的点，若∠1=∠2 求证：PB+QD=PA 5、已知：如图正方形ABCD ，AC 、BD 交于点O ，E 、F 分别是BC 、OD 的中点求证：AF ⊥EF 6已知：如图，//AB CD ，AE ED =，BF FC =，//EM AF 交DC 于M ，求证：FM AE =。 7、已知：如图，⊿ABC 中，E 、F 分别是AB 、BC 中点，M 、N 是AC 上两点， EM 、FN 交于D ，若AM=MN=N C ，求证：四边形ABCD 是平行四边形。 8、已知：如图，12∠=∠，3AB AC =，BE AD ⊥，求证：AD DE =。 9、已知：如图，//AB CD ，090D ∠=， BE EC DC ==，求证：3AEC BAE ∠=∠。 10、已知：如图，AD BC ⊥，2B C ∠=∠，BE EC =，求证： 1 2 DE AB =。 11、已知：如图，AB DC =， AE DE =，BF FC =，FE 交BA 、CD 的延长线于G 、H ，求证：12∠=∠。 12、已知：如图，//AB CD ， 090ADC ∠=，BE EC =，求证： 2AED EDC ∠=∠。 13、已知:如图，正方形ABCD 中，E 是DC 上一点，DF ⊥AE 交BC 于F 求证：OE ⊥OF 14、如图，分别以△ABC 的三边为边长，在BC 的同侧作等边三角形 ABD ，等边三角形BCE ，等边三角形ACF ，连接DE ，EF 。求证：四边形ADEF 是平行四边形。 15、如图，点G 是正方形ABCD 对角线CA 的延长线上任意一点，以线段AG 为边作一个正方形AEFG ，线段EB 和GD 相交于点H ．（1）求证：EB=GD ；（2）判断EB 与GD 的位置关系，并说明理由；（3）若AB=2，AG=2，求EB 的长． O F E D C B A F D A

年八年级数学上册几何证明题有难度

年八年级数学上册几何证明题有难度 Last updated at 10:00 am on 25th December 2020

10.如图，已知AB>AD, ∠BAC=∠FAC,CD=BC.求证：∠ADC+∠B=1800. 11.如图，在△ABC 中，D,E 分别为AB,AC 边中点，连接CD、BE 并分别延长至F、G，使BE=EG,CD=DF,连接FA,GA.求证：AF=AG. 12.如图，△ABC 中，∠BAC=900，AB=AC，BD 是∠ABC 的平分线，BD 的延长线垂直于过C 点的直线于E，直线CE 交BA 的延长线于F．求证：BD=2CE． 13.如图,已知△ABC中，AD平分∠BAC，E、F 分别在 BD、AD 上．DE=CD，EF=AC．求证：EF∥AB. 14.如图，∠A+∠D=1800，BE 平分∠ABC，CE平分∠BCD，点 E在 AD上． (1)探讨线段AB、CD 和BC 之间的等量关系;(2)探讨线段BE 与CE 之间的位置关系． 15.已知AB=4，AC=2，D 是BC 中点，AD 是整数，求AD的长. 16.已知，E 是AB 中点，AF=BD，BD=5，AC=7，求DC的长. 17.如图,在△ABC 中，∠B，∠C相邻的外角的平分线交于点 D.求证：点 D 在∠A 的平分线上. 18.已知，在Rt△ABC 中，∠C=900，AC=BC，AD 为∠BAC 的平分线，DE⊥AB，垂足为C．求证：△DBE 的周长等于AB的长．

八年级几何证明题

几何证明题 1、已知：如图1所示，?ABC 中，∠=?===C AC BC AD DB AE CF 90，，，。求证：DE ＝DF 2、已知：如图2所示，AB ＝CD ，AD ＝BC ，AE ＝CF 。求证：∠E ＝∠F 3、如图3所示，设BP 、CQ 是?ABC 的内角平分线，AH 、AK 分别为A 到BP 、CQ 的垂线。求证：KH ∥BC

4、已知：如图4所示，AB ＝AC ，∠，，A AE BF BD DC =?==90。求证：FD ⊥ED 5、已知：如图6所示在?ABC 中，∠=?B 60，∠BAC 、∠BCA 的角平分线AD 、CE 相交于O 。求证：AC ＝AE ＋CD 6、已知：如图7所示，正方形ABCD 中，F 在DC 上，E 在BC 上，∠=?EAF 45。求证：EF ＝BE ＋DF

7、如图8所示，已知?ABC 为等边三角形，延长BC 到D ，延长BA 到E ，并且使AE ＝BD ，连结CE 、DE 。求证：EC ＝ED 8、例题：已知：如图9所示，∠=∠>12，AB AC 。求证：BD DC > 作业 1. 已知：如图11所示，?ABC 中，∠= C 90于E ，且有AC A D C E ==。求证：DE CD = 1 2 C 图11 A B D E

2. 已知：如图求证：BC ＝ 3. 已知：如图13所示，过?ABC 的顶点A ，在∠A 内任引一射线，过 B 、 C 作此射线的垂线BP 和CQ 。设M 为BC 的中点。求证：MP ＝MQ 4. ?ABC 中，∠=?⊥BAC AD BC 90，于D ，求证：()AD AB AC BC < ++4

八年级数学上册几何证明题有难度

八年级数学上册几何证明题（提高题） 1.如图，在平面上将△ABC 绕 B 点旋转到△A/BC/的位置时,AA/∥BC,∠ABC=700，则∠CBC/为度. 2.如图，△ABE 和△ADC 是△ABC 分别沿着AB、AC 边翻折1800形成的，若∠1:∠2:∠3=28:5:3，则∠a 的度数为 3.将直角三角形（∠ACB 为直角）沿线段CD 折叠使B 落在B/处，若∠ACB/=50°，则∠ACD 度数为______． 4.如图,已知BD 平分∠ABC,DE⊥AB 于E,S△ABC=36cm2,AB=18cm,BC=12cm,则DE 的长为 5.如图,∠DEF=360，AB=BC=CD=DE=EF，求∠A 的度数。 6.已知△ABC≌△A/B/C/，△ABC 的三边为3、m、n，△A/B/C/的三边为5、p、q，若△ABC的各边都是整数，则m+n+p+q 的最大值为__________ 7.长为L 的一根绳,恰好可围成两个全等三角形,则其中一个三角形的最长边x的取值范围为( ) 8.已知,如图,下列三角形中,AB=AC，则经过三角形的一个顶点的一条直线能够将这个三角形分成两个小等腰三角形的是（） A.①③④ B.①②③④ C.①②④ D.①③ 9.如图，ΔABC 和ΔBDE 是等边三角形，D 在AE 延长线上。求证：BD+DC=AD。 10.如图，已知AB>AD, ∠BAC=∠FAC,CD=BC.求证：∠ADC+∠B=1800. 11.如图，在△ABC 中，D,E 分别为AB,AC 边中点，连接CD、BE 并分别延长至F、G，使BE=EG,CD=DF,连接FA,GA.求证：AF=AG. 12.如图，△ABC 中，∠BAC=900，AB=AC，BD 是∠ABC 的平分线，BD 的延长线垂直于过C 点的直线于E，直线CE 交BA 的延长线于F．求证：BD=2CE． 13.如图,已知△ABC中，AD平分∠BAC，E、F 分别在 BD、AD 上．DE=CD，EF=AC．求证：EF∥AB. 14.如图，∠A+∠D=1800，BE 平分∠ABC，CE平分∠BCD，点 E在 AD上． (1)探讨线段AB、CD 和BC 之间的等量关系;(2)探讨线段BE 与CE 之间的位置关系． 15.已知AB=4，AC=2，D 是BC 中点，AD 是整数，求AD的长. 16.已知，E 是AB 中点，AF=BD，BD=5，AC=7，求DC的长. 17.如图,在△ABC 中，∠B，∠C相邻的外角的平分线交于点 D.求证：点 D 在∠A 的平分线上. 18.已知，在Rt△ABC 中，∠C=900，AC=BC，AD 为∠BAC 的平分线，DE⊥AB，垂足为C．求证：△DBE 的周长等于AB的长． 19.已知，如图,在△ABC 中,AD 是∠BAC的角平分线，E、F 分别是AB、AC上的点，且∠EDF+∠EAF=1800. 求证：DE=DF. 20.已知：如图，在△ABC 中，D 为BC 的中点，过D 点的直线GF 交AC 于F，交AC 的平行线BG 于点G，DE⊥GF，并交AB 于点E，连结EG．

初二奥数几何证明题

第一讲：如何做几何证明题【知识梳理】 1、几何证明是平面几何中的一个重要问题，它对培养学生逻辑思维能力有着很大作用。几何证明有两种基本类型：一是平面图形的数量关系；二是有关平面图形的位置关系。这两类问题常常可以相互转化，如证明平行关系可转化为证明角等或角互补的问题。 2、掌握分析、证明几何问题的常用方法：（1）综合法（由因导果），从已知条件出发，通过有关定义、定理、公理的应用，逐步向前推进，直到问题的解决；（2）分析法（执果索因）从命题的结论考虑，推敲使其成立需要具备的条件，然后再把所需的条件看成要证的结论继续推敲，如此逐步往上逆求，直到已知事实为止；（3）两头凑法：将分析与综合法合并使用，比较起来，分析法利于思考，综合法易于表达，因此，在实际思考问题时，可合并使用，灵活处理，以利于缩短题设与结论的距离，最后达到证明目的。 3、掌握构造基本图形的方法：复杂的图形都是由基本图形组成的，因此要善于将复杂图形分解成基本图形。在更多时候需要构造基本图形，在构造基本图形时往往需要添加辅助线，以达到集中条件、转化问题的目的。【例题精讲】【专题一】证明线段相等或角相等两条线段或两个角相等是平面几何证明中最基本也是最重要的一种相等关系。很多其它问题最后都可化归为此类问题来证。证明两条线段或两角相等最常用的方法是利用全等三角形的性质，其它如线段中垂线的性质、角平分线的性质、等腰三角形的判定与性质等也经常用到。【例1】已知：如图所示，「'ABC 中，.C=90，AC 二BC, AD 二DB，AE 二CF。求证：DE= DF

C F B

【巩固】如图所示，已知.ABC为等边三角形，延长BC到D,延长BA到E,并且使AE =BD 连结CE DE 求证：EC= ED 【专题二】证明直线平行或垂直在两条直线的位置关系中，平行与垂直是两种特殊的位置。证两【例2】已知：如图所示，A吐CD AD- BC AE= CF 求证：/ E=Z F D 直线平行，可用同位角、内错角或同旁内角的关系来证，也可通过边对应成比例、三角形中位线定理证明。证两条直线垂直，可转化为证一个角等于90°,或利用两个锐角互余，或等腰三角形“三线合一”来证。【例3】如图所示，设BP CQ是AABC的内角平分线，AH AK分别为A到BP CQ的垂线。求证：KH// BC A Q K H B C

八年级数学几何证明题技巧(含答案)

几何证明题的技巧 1. 几何证明是平面几何中的一个重要问题，它有两种基本类型：一是平面图形的数量关系；二是有关平面图形的位置关系。这两类问题常常可以相互转化，如证明平行关系可转化为证明角等或角互补的问题。 2. 掌握分析、证明几何问题的常用方法：（1）综合法（由因导果），从已知条件出发，通过有关定义、定理、公理的应用，逐步向前推进，直到问题解决；（2）分析法（执果索因）从命题的结论考虑，推敲使其成立需要具备的条件，然后再把所需的条件看成要证的结论继续推敲，如此逐步往上逆求，直到已知事实为止；（3）分析综合法：将分析与综合法合并使用，比较起来，分析法利于思考，综合法易于表达，因此，在实际思考问题时，可合并使用，灵活处理，以利于缩短题设与结论的距离，最后达到证明目的。 3. 掌握构造基本图形的方法：复杂的图形都是由基本图形组成的，因此要善于将复杂图形分解成基本图形。在更多时候需要构造基本图形，在构造基本图形时往往需要添加辅助线，以达到集中条件、转化问题的目的。 1、证明线段相等或角相等两条线段或两个角相等是平面几何证明中最基本也是最重要的一种相等关系。很多其它问题最后都可化归为此类问题来证。证明两条线段或两角相等最常用的方法是利用全等三角形的性质，其它如线段中垂线的性质、角平分线的性质、等腰三角形的判定与性质等也经常用到。例1. 已知：如图1所示，?ABC 中，∠=?===C AC BC AD DB AE CF 90，，，。求证：DE ＝DF C F B A E D 图1 分析：由?ABC 是等腰直角三角形可知，∠=∠=?A B 45，由D 是AB 中点，可考虑连结CD ，易得CD AD =， ∠=?DCF 45。从而不难发现??DCF DAE ? 证明：连结CD AC BC A B ACB AD DB CD BD AD DCB B A AE CF A DCB AD CD =∴∠=∠∠=?=∴==∠=∠=∠=∠=∠=90，，，， ∴?∴=??A D E CDF DE DF 说明：在直角三角形中，作斜边上的中线是常用的辅助线；在等腰三角形中，作顶角的平分线或底边上的中线或高是常用的辅助线。显然，在等腰直角三角形中，更应该连结CD ，因为CD 既是斜边上的中线，又是底边上的