线性时滞系统稳定性综述
基于Park积分不等式线性时滞广义系统稳定性分析

第32卷第2期 2 0 1 7年5月青岛大学学报(工程技术版)JOURNAL OF QINGDAO UNIVERSITY (E&T)Vol. 32 No. 2May 2 0 17文章编号:1006 - 9798(2017)02 - 0017 - 05; D O I: 10.13306/j.1006 - 9798.2017.02.004基于Park积分不等式线性时滞广义系统稳定性分析龚冠桦,赵南,刘臻臻,林崇(青岛大学复杂性科学研究所,山东青岛266071)摘要:针对时滞系统稳定性问题,本文主要对一类时滞广义系统的稳定性进行研究。
构造适当的Lyapunov-K ra so vskii泛函,并对其中所构造的泛函进行适当的处理,并应用P a rk双重积分不等式方法以及W irtin g e r型积分不等式方法进行处理,得到了新的判定时滞广义系统稳定性的充分条件。
同时,通过对M a tla b中的线性矩阵不等式工具箱的应用,来进行数值例子的求解以及验证,并通过本文得到的数据结果与以往相关文献中的数据进行比较分析。
分析结果表明,本文的结果能够获得更大的时滞上界,验证了本文方法可以获得更小的保守性,进一步说明了本文结果的有效性和优越性。
该结果对于深人研究时变时滞系统的稳定性及控制器设计都具有重要应用和意义。
关键词:时滞广义系统;稳定性;Lyapunov-K ra so vskii泛函方法;积分不等式中图分类号:T P13; N941. 1文献标识码:A广义系统是一种比正常系统更加广泛的动态系统,其研究和应用无论在理论上和实际中都拥有更为重要的 意义[1]。
时滞是广泛存在于自然界中的一种物理现象,它的影响和应用广泛地渗透于机械、物理、生物、医学、经 济、工程等领域;时滞系统就是在一处或几处的信号传递过程中有时间延迟的系统[21]。
现实存在的控制系统内 难免会有时滞现象的存在,这就成为导致控制系统的不稳定、使系统性能变差的重要因素,因此对时滞广义系统 稳定性分析具有极其重要的现实意义,而对于时滞系统的研究及发展已经成为一种必然的趋势。
线性系统的稳定性分析

将 0.2,n 86.6代入特征方程得
s3 34.6s2 7500s 7500K 0
由特征方程列劳斯表
s3
1
7500
s2 34.6
s1 346 7500 7500K
34.6
s0 7500K
7500K
要使系统稳定,必须满足
7500K 0
解不等式得
34.6 7500 7500K 0 34.6
3.线性定常系统稳定的充分必要条件:闭环 系统特征方程的所有根都具有负实部。这个 结论好像也不新鲜。有意义吗?
二、劳斯稳定判据
由以上讨论可知:判稳先求根。但是, 对高阶系统,在求根时将会遇到较大的困 难。人们希望寻求一种不需要求根而能判 别系统稳定性的间接方法,例如:直接用系 数就可以判断系统的稳定性。而劳斯判据 就是其中的一种。
号(正值)时,则系统是稳定的,否则系统是 不稳定的。且不稳定根的个数等于劳斯表中第 一列系数符号改变的次数。
注意:a0>0
例1:已知系统的特征方程如下,试用劳斯判据分析系统的稳定性。
s5 6s4 14s3 17s2 10s 2 0
解 列劳斯表 s5
1
14
10
s4
6
17
2
s3
6 14 117 67
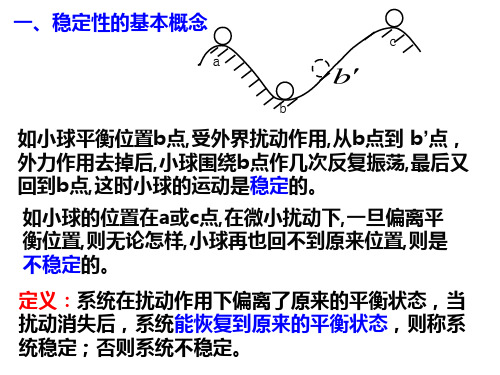
2.物理意义上的稳定概念
A'
Af
f A
图a 摆运动示意图 (稳定系统)
图b 不稳定系统
d c
f A
图c 小范围稳定系统
3.数学意义上的稳定概念
根据上述稳定性的定义,可以用 (t) 函数作 为扰动来讨论系统的稳定性。
设线性定常系统在初始条件为零时,输入一 个理想单位脉冲 , (这t) 相当于系统在零平衡状态 下,受到一个扰动信号的作用,如果当t趋于∞ 时,系统的输出响应c(t)收敛到原来的零平衡状 态,即
线性系统理论郑大钟5稳定性课件

随着研究的深入,线性系统稳定性的研究将面临更多挑战, 例如如何处理更复杂的系统模型、如何提高稳定性分析和控 制的实时性和鲁棒性等。
对实际应用的指导意义
1 2 3
设计准则
线性系统稳定性研究为实际系统的设计和改进提 供了重要的理论依据和技术指导,有助于提高系 统的稳定性和可靠性。
控制策略
基于线性系统稳定性研究的控制策略可以有效地 改善系统的性能,例如PID控制、状态反馈控制 等。
线性系统的分类与特点
分类
根据系统的动态行为,可以分为连续 系统和离散系统;根据系统的状态变 量,可以分为线性时不变系统和线性 时变系统。
特点
线性系统具有模块化、可加性和可替 代性等优点,这使得线性系统在工程 和科学领域中得到了广泛应用。
线性系统理论的应用领域
控制工程
线性系统理论是现代控制理论 的基础,广泛应用于航空航天 、化工、电力等领域的控制系
03
线性系统的稳定性分析
线性系统的稳定性判定
01
02
03
定义域判定
通过判断系统在定义域内 的行为,确定系统的稳定 性。
特征值判定
根据线性系统的特征值判 断系统的稳定性,如果所 有特征值都位于复平面的 左半部分,则系统稳定。
能量判定
对于能量有限的线性系统 ,如果系统的能量随时间 衰减,则系统稳定。
实际应用
在实际工程领域中,许多系统都可以近似为线性系统,因 此研究其稳定性对于保证系统的正常运作、预防和控制故 障具有关键作用。
学科交叉
线性系统稳定性研究涉及到数学、物理、工程等多个学科 领域,有助于促进不同学科之间的交流与融合。
未来研究的方向与挑战
研究方向
随着科技的发展和实际需求的不断变化,线性系统稳定性的 研究方向将更加多元化和复杂化,例如考虑非线性因素、时 变参数、不确定性等。
第四章 线性系统的稳定性

K H1 ( s ) = s( s + 1)( s + 10)
K取何值时系统为稳定系统。
+
F(s)
X(s) H1(s) Yf(s)
-
解 令加法器的输出为X(s), 则有
X ( s) = F ( s) − Y f ( s) Y f ( s ) = H1 ( s ) X ( s ) = H1 ( s )[ F ( s ) − Y f ( s )]
由式(4.8-20)和式(4.8-21)计算阵列的未知元素,得到阵列为 (4.8-20) (4.8-21)
1 an cn −1 = − an −1 an −1 k = 10 − 11 1 an cn −3 = − an −1 an −1
an − 2 1 1 10 =− an −3 11 11 k
1 11 K 10 − 11 K
N ( s) H ( s) = D( s)
D ( s ) = an s n + an −1s n −1 + L + a1s + a0
稳定系统的极点应位于s平面的左半平面, 因此D(s)根的 实部应为负值。 它对应以下两种情况: (1) 实数根, 其因式为 (s+a) a>0 (2) 共轭复根, 其因式为 (s+α+jβ)(s+α-jβ)=(s+α)2+β2 =s2+2αs+α2+β2=s2+bs+c 将D(s)分解后, 只有(s+a)、 (s2+bs+c)两种情况, 且a、 b、 c均为正值。 这两类因式相乘后, 得到的多项式系数必然为 正值, 并且系数为零值的可能性也受到了限制。 由此我们可 得到稳定系统与分母多项式 D(s)的系数关系:
线性控制系统的稳定性判据综述_佟婷婷

11 21 12 22
[
90
( 3 ) -1 2 1 -3
山
由 p12 p2 式 得 -1 0 p12 p22
西
p12 p22
电
子
技
术
2013 年
则
[
0
-1 1
[
p11 p21 7
][
- 3][ p 2
p11
21
]
+
中, 利用系统的闭环和开环特性对系统进行稳定性判据 。 此 类判据一般只被用在线性系统或近似线性系统之中 。 在现 系统的状态方程成了稳定判据的关键因素 。 由 代控制论中, 于这种稳定判据满足以多变量, 非线性, 时变为特征的现代 从而应用更为广泛。 然而, 控制系统对稳定性分析的要求, 虽然几种稳定判据被沿用多年, 但仍存在一些不能直观给出 判断、 需要经验和技巧的地方, 如劳斯判定在处理特殊情况 的时候, 需要采用无穷小的替代值; 李雅普诺夫第二法的李 雅普诺夫函数在一般情况下需要靠经验获得 。 参考文献 [ 1] 陈复扬. 自动 控制 原理[M] . 北京: 国防 工业 出版社, 2010. [ 2] 尹华杰. 自动控制多学科 视 角[ M] . 北京: 人 民 邮 电 出 2010. 版社, [ 3] 张爱民. 自动 控制 原理[M] . 北京: 清 华 大学 出版社, 2006.
[1 ]
。
然而, 李雅普诺夫函数不是容易找到的, 并且不是唯一 = Ax 中, 的。在线性定常系统 x 为了找到系统的李雅普诺夫
T 函数, 可取正定二次型函数 V = x Px。 根据李雅普诺夫方
程: A T P + AP = - Q.
· T
线性系统的稳定性

线性系统的稳定性
X
3
第
二.定义(BIBO)
页
一个系统,如果对任意的有界输入,其零状态响应也 是有界的,则称该系统有界输入有界输出(BIBO)稳 定的系统,简称稳定系统。
对所有的激励信号f(t) 其响应y(t)满足
f t M f
yt M y
则称该系统是稳定的。式中,
M
f
,
M
为有界正值。
y
稳定系统的充分必要条件是(绝对可积或可和条件):
X
6
第
四.由H(s)、 H(z) 的极点位置判断系统稳定性 页
例 7.2-2 如图7.2-4所示的离散系统,当K满足什么条件时, 系统是稳定的?
解:由左右加法器可得
X (z) (z 1 Kz2 ) X (z) F (z)
Y (z) (1 2z 1 3z 2 ) X (z) 则系统函数为
H(z)
0 0
0
因为A3(s)系数的罗斯阵列第一列元素全大于零,所以根据 R-H准则,H3(s)对应的系统为稳定系统。
线性系统的稳定性
X
17
第
页
六.离散系统的稳定性准则(朱里准则)
朱里提出了一种列表的方法来判断H(z)的极点是否全部 在单位圆内,这种方法称为朱里准则。朱里准则是根据H(z) 的分母A(z)的系数列成的表来判断H(z)的极点位置,该表又 称朱里排列。
罗斯和霍尔维兹提出了判断多项式为霍尔维兹多项式的准 则,称为罗斯-霍尔维兹准则(R-H准则)。罗斯-霍尔维兹准则包 括两部分,一部分是罗斯阵列,一部分是罗斯判据(罗斯准则)。
线性系统的稳定性
X
10
第
罗斯和霍尔维兹提出了判断多项式为霍尔维兹多项式的准则,页 称为罗斯-霍尔维兹准则 (R-H准则)。罗斯-霍尔维兹准则包括两 部分,一部分是罗斯阵列,一部分是罗斯判据(罗斯准则)。
线性系统的稳定性分析优秀课件

t
即输出增量收敛于原平衡点,则线性系统是(渐 近)稳定。
C(s) R(s)
ba00ssmnba11ssmn11
...bm1sbm ...an1san
B(s) D(s)
K
B(s)
k
a0 (spi) [s(j jj)][s(j jj)]
i1
j1
理想脉冲函数作用下 R(s)=1。
C(s)
K
R(s) s(s2s1)(s2)K
D (s ) s4 3 s 3 3 s2 2 s K 0
控制系统稳定的充分必要条件是:当a0>0时, 各 阶赫尔维茨行列式1、2、…、n均大于零。
1 2
a1 a3
a0 a2
0 n
a1
00
3
a5 a4 a3
0
n
0
一阶系统
0 0
a0>0时
a0>0时,
an1 0
an2 an
பைடு நூலகம்
D (s)a0sa10
1 a1 0
a1>0(全部系数数同号)
D (s)a0s2a1 s1 .a20
1 a1 0
2
a1 a0
a3 a2
a1a2a0a3
0
a1 a3 0 3 a0 a2 0 a22 0
0 a1 a3
a0>0时, a1>0, a2>0, a3>0(全部系数同号)
a1a2> a0 a3
四阶系统
D ( s ) a 0 s 4 a 1 s 3 .a 2 s 2 a 3 s a 4 0
(a)不稳定
临界稳定:若系统在扰动消失后,输出与原始的 平衡状态间存在恒定的偏差或输出维持等幅振荡, 则系统处于临界稳定状态。
3.5线性系统稳定性分析
列劳斯表如下: D(s) s4 3s3 3s2 2s K 0
s4
1
s3
3
3K 20
s2 7/3
K
s1 2 9K
7
s0 K
根据劳斯判据, 系统稳定必须满足:K 0,2 9K 0 7
因此, 使系统闭环稳定的K的取值范围为 0 K 14 9
在这种情况下,利用全为零行的上一行的系数,可 组成一个辅助方程,并用这个辅助方程导数的系数取 代全零行各项,最后用劳斯判据加以判断。由辅助方 程可以求出绝对值相等符号相异的特征根。
例题:一个控制系统的特征方程为
D(s) s6 2s5 8s4 12s3 20s2 16s 16 0
列劳斯表 S6 S5 S4 S3
1 1 0
2
a1 a0
a3 1 a2 2
5=3 10 7 0 3
2、劳斯稳定判据
(1)系统稳定的必要条件是特征方程的所有系数 ai>0均大于零。 ①不缺项。 ②系数同号。
它是系统稳定的必要条件,也就是说,只能用来 判断系统的不稳定而不能用来判别稳定。
(2)劳斯判据:线性系统稳定的充要条件是劳斯 表中第一列所有项系数均大于零,第一列系数变
根据特征方程系数判定系统稳定性
1、赫尔维茨稳定判据
D(s) 2s2 8s 12 0
(1)必要条件:ai>0( ①不缺项, ②系数同号)。若不满 足ai>0,则系统是不稳定的。若满足,则需进一步判断。
判定以下系统的稳定性
D(s) s3 8s 12 0
D(s) s5 6s 4 9s3 2s 2 8s 12 0 不稳定
s4
1
s3
3
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
线性时滞系统稳定性分析综述 摘要:时滞在工程领域广泛存在,对此综述了线性时滞系统的稳定性研究方法。从频域和时域两个角度详细介绍了各种方法的特点,着重讨论基于线性矩阵不等式(LMI)的分析方法,指出保守性是分析的重点。对现有结果的保守性进行比较和评述,并提出了改进的思路。 关键词:时滞系统;稳定性;保守性,线性矩阵不等式;时滞依赖
Survey on the stability analysis
of linear time—delay systems Abstract:As time-delays are extensively encounted in many fields of engineering,the stability analysis method of linear time-delay systems is outlined.The characters of frequency domain method and time domain method are illustrated in detail.The linear matrix inequality(LMI)-based stability analysis approach is mainly discussed.It is pointed out that the conservatism is important for the stability analysis.Comparison and discussion are given on some existing results.FinalIy,some improvement directions are discussed. Key words:Time-delay systems;Stability;Conservatism;Linear matrix inequality;Delay-dependent
l引言
从系统理论的观点看,任何实际系统的过去状态不可避免地要对当前的状态产生影响,即系统的演化趋势不仅依赖于系统当前的状态,也依赖于过去某一时刻或若干时刻的状态,这类系统称为时滞系统。时滞产生的原因有很多,如:系统变量的测量(复杂的在线分析仪)、长管道进料或皮带传输、缓慢的化学反应过程等都会产生时滞。时滞常见于电路、光学、神经网络、生物环境及医学、建筑结构、机械等领域,由于应用背景广泛,受到很多学者的关注。从理论分析的角度来看,在连续域中,时滞系统是一个无穷维的系统,特征方程是超越方程,有无穷多个特征根,而在离散域中,时滞系统的维数随时滞的增加按几何规律增长,这给系统的稳定性分
析和控制器设计带来了很大的困难。因此,对于时滞系统的控制问题,无论在理论还是在工程实践方面都具有极大的挑战性。 常见的时滞系统包括奇异时滞微分系统、脉冲时滞微分系统、Lurie时滞系统、中立型时滞系统和随机时滞系统等。其基本理论建立于20世纪五、六十年代,迄今为止,研究的成果相当丰富,本文作者限于水平及阅读范围,提到的只是极其有限的一部分结果。
2 时滞系统稳定性分析基本方
法 从工程实践的角度来看,时滞的存在往往导致系统的性能指标下降,甚至使系统失去稳定性。例如系统 ()0.5()xtxt (1) 是稳定的,但加入时滞项后,系统 ()0.5()1.3(1)xtxtxt (2)
变得不稳定.同时,时滞也可以用来控制动力系统的行为,例如时滞反馈控制已成为控制混沌的主要方法之一。 通常用泛函微分方程来描述时滞系统,以含单时滞的微分方程为例,即 ()(),,,nnxtAxBxthABR
()(),,0xtth
(3)
其中:h>0为时滞,初始条件由定义在[-h,0]的连续可微函数()•确定,系统t>0时的行为不仅依赖于0时刻的状态,而且与时间段[-h,0]内的运动有关,因此解空间是无穷维的。其特征方程是含有指数函数的超越方程,即 det(exp())0IAhB (4)
讨论特征根需要用到很多复变函数的知识.早在1942年,Pontryagin就提出了一种原则性方法—Pontryagin判据来解决这一问题,之后很多工作致力于对这一判据具体化,使之更加实用。 总之,时滞系统稳定性分析方法可分成3类。 2.1 无限维系统理论方法 这种方法是将时滞系统看成无穷维系统,用无穷维空间的适当算子来描述时滞系统的状态变化,一方面可对时滞系统进行一般建模;另一方面,也可表述系统的可观性和可控性等结构方面的概念。
2.2 代数系统理论方法 代数系统理论对于时滞系统的建模和分析都比较方便,但在控制器的设计方面目前尚处于初期阶段,还缺乏有效方法。
2.3 泛函微分方程理论方法 泛函微分方程理论考虑了系统的过去对系统变化率的影响。利用有限维空间以及泛函空间提供一套适当的数学结构以描述时滞系统的状态变化。 目前,研究时滞系统主要是应用泛函微分方程理论,研究范围涉及稳定性分析、控制器设计、H控制、无源与耗散控制、可靠控制、保成本控制、H滤波、Kalman滤波以及随机控制等。不管研究哪个分支,稳定性都是基础,对最终形成控制方案具有非常重要的理论和现实意义。时滞系统稳定性分析的目的是希望找到计算简单、切实有效并且保守性尽可能小的稳定性判据,研究方法主要分为两类:一类是以研究系统传递函数为主的频域方法;另一类是以研究系统状态方程为主的时域(状态空间)方法。
2.3.1 频域法 频域法是最早提出的稳定性分析方法,它基于超越特征方程根的分布或复Lyapunov矩阵函数方程的解来判别稳定性.类似于不包含时滞的线性系统,线性时滞系统稳定的充要条件是闭环特征方程的解均具有负实部.由于时滞系统闭环特征方程是一个具有无穷多解的超越方程,其稳定性分析比无时滞系统要复杂得多.但是利用频域法对系统进行分析具有直观易懂的特点,只要分析系统的特征根分布就可在一定程度上了解系统的稳定性和动态性能,并且计算量小、物理意义强,因此采用频域方法进行线性时滞系统稳定性分析,具有重要的理论意义和实际价值。 从频域角度出发,对系统进行稳定性分析的方法主要包括:图解法、解析法和复Lyapunov方法。 Nikiforuk于1965年提出一种简单的双轨迹法的图解方Mukherjee在此基础上探讨了控制环增益与系统前向通道中时滞之间的变化关系;最近,运用双轨迹法进行时滞系统稳定性分析的文献还有很多。 利用解析法进行相关研究的文献包括:文献利用超越特征方程根的分布得到了稳定的充分条件。Thowsen通过引入适当的变换,将特征方程化为非超越的形式。得到了Routh—Hurwitz型稳定性判据。Watanabe等通过有限谱配置分析时滞系统的稳定性。文献基于Pontryagin判据提出了适用于准多项式H(s,se)的Hermite-Biehler推广定理。Rekasius以时滞项的双线性变换为基础提出了一种伪时滞法,在此基础上olgac证明了这种双线性变换的引入有助于准多 项式H(s,se)的稳定性分析,并可用来方便地估计闭环特征式的虚轴零点。walton提出了一种不需要引入双线性变换而能够删除准多项式中指数项的直接法。Zhang给出基于Lyapunov方程的线性时滞系统稳定条件,并建立了该条件与用于鲁棒性分析的小增益定理之间的等价关系。国内学者胥布工、俞元洪、刘和涛、张作元等也在这一领域进行了相关研究。 复Lyapunov方法是Repin于20世纪80年代首次提出的,其思想是利用复Lyapunov方程的正定Hermitian矩阵解进行稳定性分析。该想法被Brierley等用来研究复Lyapunov方程正定Hermitian解的存在性,进而得到一个具有可公度时滞的线性系统稳定性的充要条件。Lee等将这一结果推广到中立型时滞系统。Agathoklis等进一步研究了具有不可公度滞后的线性系统,得到了稳定性的充分条件。 虽然频域法理论上容易得到系统稳定的充要条件,但在考虑控制器的设计时,由于涉及到系统特征方程的处理,计算非常复杂,特别是对于多变量高维系统、非线性微分系统或中立型系统.并且,频域法难于处理含有不确定项以及参数时变的时滞系统。
2.3.2 时域法 时域法是目前时滞系统稳定性分析和综合的主要方法,易于处理含有不确定项、时变参数和时变时滞的系统以及非线性时滞系统.时域法主要包括Lyapunov-Krasovskii泛函法、Lazumikhin函数法、Lyapunov函数结合Razumikhin型定理方法、时滞不等式方法。Lyapunov泛函法和Razumikhin函数法,分别由Krasovskii和Razumikhin于20世纪50年代末提出,是目前应用最广泛的两种方法.时滞不等式方法由Halanay建立于20世纪60年代,是非线性、脉冲、变时滞等复杂时滞系统稳定性分析的强有力工具。另外,通过估计方程的基本解矩阵也可得到稳定性条件,但该方法依赖于不等式技巧,得到的条件往往过于保守。下面重点介绍Lyapunov-Krasovskii泛函法和Razumikhin函数法。
2.3.2.1 Razumikhin函数法 使用Razumikhin函数法,避免了构造Lyapunov泛函的麻烦,被许多学
