材力习题解---自编Ch2-4
材料力学习题
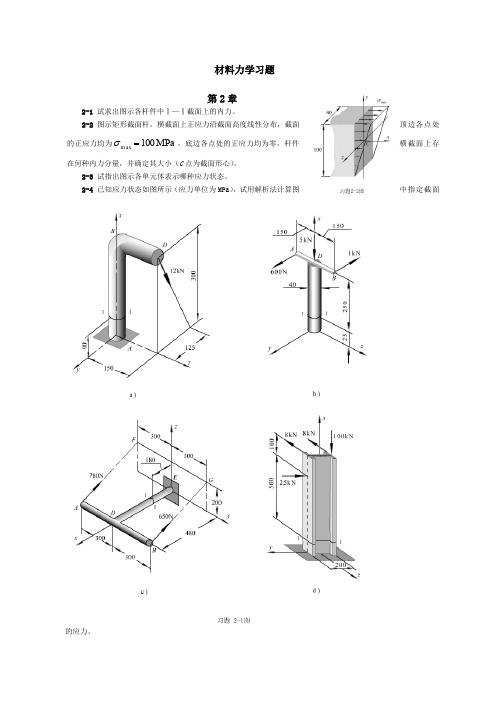
材料力学习题第2章2-1 试求出图示各杆件中Ⅰ—Ⅰ截面上的内力。
2-2图示矩形截面杆,横截面上正应力沿截面高度线性分布,截面顶边各点处的正应力均为MPa 100max =σ,底边各点处的正应力均为零。
杆件横截面上存在何种内力分量,并确定其大小(C 点为截面形心)。
2-3 试指出图示各单元体表示哪种应力状态。
2-4 已知应力状态如图所示(应力单位为MPa ),试用解析法计算图中指定截面的应力。
2-5 试作应力圆来确定习题2-4图中指定截面的应力。
2-6已知应力状态如图所示(应力单位为MPa ),试用解析法求:(1)主应力及主方向;(2)主切应力及主切平面;(3)最大切应力。
2-7 已知应力状态如习题2-6图所示,试作应力圆来确定:(1)主应力及主方向; (2)主切应力及主切平面;(3)最大切应力。
2-8已知构件内某点处的应力状态为两种应力状态的叠加结果,试求叠加后所得 应力状态的主应力、主切应力。
2-9图示双向拉应力状态,σσσ==y x。
试证明任一斜截面上的正应力均等 于σ,而切应力为零。
2-10 已知K 点处为二向应力状态,过K 点两个截面上的应力如图所示(应力单位为MPa )。
试分别用解析法与图解法确定该点的主应力。
2-11 一点处的应力状态在两种坐标系中的表示方法分别如图 a)和b)所示。
试确定未知的应力分量y y x xy '''σττ、、的大小与方向。
2-12 图示受力板件,试证明尖角A 处各截面的正应力与切应力均为零。
2-13 已知应力状态如图所示(单位为MPa ),试求其主应力及第一、第二、第三不变量321I I I 、、。
2-14 已知应力状态如图所示(单位为MPa ),试画三向应力圆,并求主应力、最大正应力与最大切应力。
第3章3-1 已知某点的位移分量u = A , v = Bx +Cy +Dz , w = Ex 2+Fy 2+Gz 2+Ixy +Jyz +Kzx 。
材力练习题.

一、计算题例1 求图1所示截面的形心C 的位置,及x I 、y I例2 试分别计算下图对形心轴x 、y 的的形心主惯性矩x I 、y I 和面积矩S 的最大值、截面模量X W 的最小值。
例3图3所示半径为R 的半圆形截面,形心C 与直径轴x 1的距离43c Ry π=,求半圆截面对于形心轴x c 的惯性矩I xc 。
图1图3例4将一根直径d =1mm 的直钢丝绕于直径D =1m 的卷筒上(图4),已知钢丝的弹性模量E =200GPa ,试求钢丝由于弹性弯曲而产生的最大弯曲正应力。
又材料的屈服极限σs =350MPa ,求不使钢丝产生塑性变形的卷筒轴径D 1应为多大。
例5 T 字形截面铸铁梁的荷载及截面尺寸如图5(a)示,C 为T 形截面的形心,惯矩I z=6013×104mm 4,试校核梁的抗剪强度和抗弯强度最大值。
例6矩形截面悬臂梁如图6示,试计算梁的最大切应力和最大正应力并比较大小。
例7图7所示悬臂梁由三块胶合在一起,截面尺寸为:b =100mm ,a =50mm 。
已知木材的[σ]=10MPa ,[τ]=1MPa ,胶合面的[τj ]=0.34Mpa 试求许可荷载[P ]。
例8一钢材试件,直径为25㎜,原标距为125㎜,做拉伸试验,当屈服点荷载为201.0KN ,达到最大荷载为250.3KN ,拉断后测的标距长为138㎜,求该钢筋的屈服点、抗拉强度及拉断后的伸长率。
图4图5图6图7二、选择题题1 请选择正确结论:图形对其对称轴的(a )。
(A)静矩为零,惯性矩不为零,惯性积为零(B)静矩不为零,惯性矩和惯性积均为零(C)静矩、惯性矩及惯性积均为零(D)静矩、惯性矩及惯性积均不为零题2 由惯性矩的平行移轴公式,I Z2的答案为(c )。
、(A) IZ2=IZ1+bh3/4(B) IZ2=IZ+bh3/4(C) IZ2=IZ+bh3(D) IZ2=IZ1+bh3题2图题3 图示矩形截面,Z轴过形心C,则该截面关于Z、Z1及Z2轴的惯性矩关系为(c ) (A) IZ>IZ1>IZ2 (B) IZ2>IZ>IZ1(C) IZ2>IZ1>IZ (D) IZ1>IZ>IZ2题3图题4在边长为2a的正方形中挖去一个边长为a的正方形,如图示,则该图形对Z轴的惯性矩IZ为( )(A) a4/4 (B) a4/3 (C) 4a4/5 (D) 5a4/4题4图题5 请选择图示截面对Z 轴惯性矩的正确答案( )。
材料力学习题(4)

解:
Q = F = 20 kN
M = Fa = 20kNm
A
σmax
B
τ
σ
C
τmax
A Q M B C
A
σmax
B
τ
σ
C
τmax
A点:
σmax
M 20×106 = = 6× = 60M Pa 2 W 50× 200
σ1 = 60M Pa
σ2 = σ3 = 0
主应力的方向为水平方向,铅垂方向及垂直于屏幕方向. 主应力的方向为水平方向,铅垂方向及垂直于屏幕方向.
解毕
σ
8 -6 解:
σx =σ y =σ
σ
σα
τ xy = 0
τα
α
σ σ
σα =
σ x +σ y
τα =
σα =
2 σ x −σ y
+
σ x −σ y
2
cos 2α −τ xy sin 2α
2
+
sin 2 +τ xy cos 2 α α
cos 2α −τ xy sin 2α = σ
σ +σ
σ −σ
ε x ε y γ xy
300 =
ε120
y
ε x +ε y
2
+
ε x −ε y
2
ε60
x
200 =
ε x +ε y
2
+
−
ε x −ε y
4
−
−
3γ xy 4
3γ xy 4
ε0
−100 =
ε x +ε y
2
ε x −ε y
材料力学1-4章部分作业
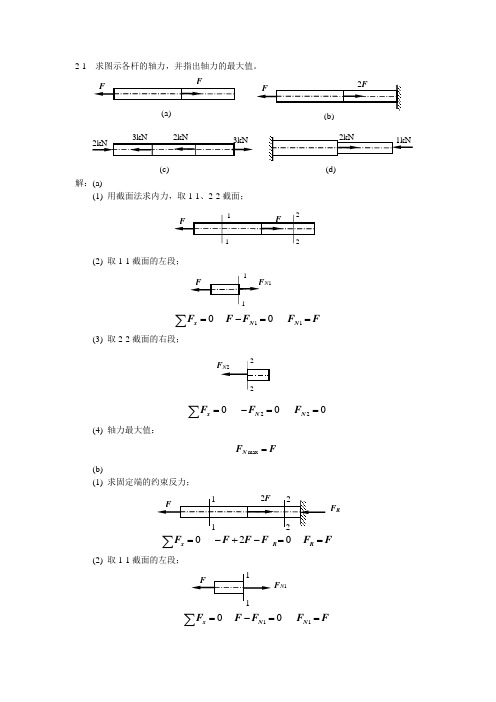
2-1 求图示各杆的轴力,并指出轴力的最大值。
解:(a)(1) 用截面法求内力,取1-1、2-2截面;(2) 取1-1截面的左段; 110 0 xN N FF F F F =-==∑(3) 取2-2截面的右段;220 0 0xN N FF F =-==∑(4) 轴力最大值:max N F F =(b)(1) 求固定端的约束反力;0 20 xR R FF F F F F =-+-==∑(2) 取1-1截面的左段;110 0 xN N FF F F F =-==∑(a)(c) (d)N 1F RF N 1220 0 xN R N R FF F F F F =--==-=-∑(4) 轴力最大值:max N F F =(c)(1) 用截面法求内力,取1-1、2-2、3-3截面;(2) 取1-1截面的左段;110 20 2 xN N FF F kN =+==-∑(3) 取2-2截面的左段;220 230 1 xN N FF F kN =-+==∑(4) 取3-3截面的右段;330 30 3 xN N FF F kN =-==∑(5) 轴力最大值:max 3 N F kN =(d)(1) 用截面法求内力,取1-1、2-2截面;FRF N 21 1F N 1N 2F N 3110 210 1 xN N FF F kN =--==∑(2) 取2-2截面的右段;220 10 1 xN N FF F kN =--==-∑(5) 轴力最大值:max 1 N F kN =各杆的轴力图。
(a)(b) (c) (d)FN 1F N 2FFFFF 1kN2-3 图示轴向受拉等截面杆,横截面面积A =500 mm 2,载荷F =50 kN 。
试求图示斜截面m -m 上的正应力与切应力,以及杆内的最大正应力与最大切应力。
解:2-11 图示桁架,杆1与杆2的横截面均为圆形,直径分别为d 1=30 mm 与d 2=20 mm ,两杆材料相同,许用应力[σ]=160 MPa 。
材力2,3章习题 文档

第二章2-1.求图示阶梯状直杆横截面1-1﹑2-2和3-3上的轴力,并作轴力图。
如横截面面积,,,求各横截面上的应力。
2-5.图示结构中,已知杆之横截面为的矩形,当杆横截面上的最大正应力为时,求此时的值。
2-6.直杆在两侧面受有沿轴线方向均匀分布的载荷(仅在段),其集度为;在端受集中力作用,。
已知杆横截面面积,,材料的弹性模量。
求:1、画出轴力图; 2、两截面的铅垂位移;3、过两点与轴线夹角斜截面上的应力。
2-8.图示一手动压力机,在工件上所加的最大压力为150kN。
已知立柱和螺杆所用材料的屈服点MPa,规定的安全系数n=1.5。
(1)试按强度要求选择立柱的直径D;(2)若螺杆的内径d=40mm试校核其强度。
3-1 夹剪如图所示。
销子C的直径d=5mm。
当加力P=0.2kN,剪直径与销子直径相同的铜丝时,求铜丝与销子横截面的平均剪应力。
已知a=30mm,b=150mm。
3-2 结构受力如图所示,若已知木材的许用切应力,试校核木接头剪切强度是否安全。
3-3 木梁由柱支撑如图所示,今测得柱中的轴向压力为,若已知木梁所能承受的许用挤压应力。
确定柱与木梁之间垫板的尺寸。
3-4 木构件和由两片层合板用胶粘接在一起,承受轴向载荷作用,如图所示。
已知和的空隙为;板宽;胶层的许用切应力。
确定层合板的长度。
3-5 水轮发电机组的卡环尺寸如图所示。
已知轴向荷载P=1450kN,卡环材料的许用剪应力=80MPa,许用挤压应力=150MPa。
试对卡环进行强度校核。
3-6 拉力P=80kN的螺栓连接如图所示。
已知b=80mm,t=10mm,d=22mm,螺栓的许用剪应力=130MPa,钢板的许用挤压应力=300MPa,许用拉应力 =170MPa。
试校核该接头的强度。
3-7 一托架如图所示。
已知外力P=35kN,铆钉的直径d=20mm,铆钉都受单剪。
求最危险的铆钉横截面上剪应力的数值及方向。
3-8 销钉式安全离合器如图所示,允许传递的外力偶矩m=30kN·cm,销钉材料的剪切强度极限=360MPa,轴的直径D=30mm,为保证m>30000N·cm时销钉被剪断,求销钉的直径d。
材料力学第二章习题选及其解答

2-1. 试求图示各杆1-1、2-2、3-3截面的轴力, 并作轴力图。
解: (a)(1)求约束反力kNR R X 500203040 0==-++-=∑(2)求截面1-1的轴力kNN NR X 500011==+-=∑(3)求截面2-2的轴力kNN NR X 10040 022==++-=∑(4)求截面3-3的轴力(a) (b)kNN NR X 2003040 033-==+++-=∑(5)画轴力图(b)(1)求截面1-1的轴力01=N(2)求截面2-2的轴力 PN4022==(3)求截面3-3的轴力PN P P NX 304 033==-+=∑(4)画轴力图2-2. 作用图示零件上的拉力P=38kN ,试问零件内最大拉应力发生于哪个横截面上?并求其值。
解:(1)1-1截面MPa A P 86.6720)2250(3103811=⨯-⨯==σ(2)2-2截面MPa A P 33.63152021038322=⨯⨯⨯==σ(3)3-3截面MPa A P 24.45215)2250(1038333=⨯⨯-⨯==σ(4)最大拉应力MPa 86.671max ==σσ2-3. 在图示结构中,若钢拉杆BC 的横截面直径为10mm ,试求拉杆内的应力。
设由BC 联接的两部分均为刚体。
3 3解:(1)以刚体CAE 为研究对象∑=⨯-⨯+⨯=035.15.4 0'P N N mC E A (2)以刚体BDE 为研究对象075.05.1 0=⨯-⨯=∑B E DN N m(3)联立求解kNN N N N N C EE C B 6 '=∴==(4)拉杆内的应力MPa A N B 4.7610410623=⨯⨯⨯==πσ 2-4. 图示结构中,1、2两杆的横截面直径分别为10mm 和20mm ,试求两杆内的应力。
设两根横梁皆为刚体。
解:(1)以整体为研究对象,易见A 处的水平约束反力为零; (2)以AB 为研究对象由平衡方程知0===A B B R Y X(3)以杆BD由平衡方程求得KNN N NY KNN N mC20010 01001101 021211==--===⨯-⨯=∑∑(4)杆内的应力为1MPa A N MPa A N 7.63204102012710410102322223111=⨯⨯⨯===⨯⨯⨯==πσπσ2-7. 某拉伸试验机的示意图如图所示。
8章题解材料力学课后习题题解
(b)
10 c
8.9 各单元体上的应力情况如图所示。试求主应力及最大 切应力(应力单位为MPa)。 20 解:z为主平面,对应的主应力为 x 30MPa;另外两个主应力按照 σx=-80MPa;σy=0;τxy=-20MPa 30 的平面应力状态计算得: 20
80
max
x y x y cos 2 xy sin 2 2 2 o sin 2 ; sin 2 90 可知ε’’方向: sin 2 90
可知ε’方向:
sin 2 45o cos 2
由题给条件,有:
30
o
30 270 10
o
6
F
4E 4 200 103 270 106 300 80MPa 3 0.3 3 F A 20 40 80 64 103 N 64kN
2 M T M e 16M e Wp Wp d3 Me
m
max 5.024kN m 16
d
2
A
8.5 已知一点处两个斜截面上的应力如图所示,试用解析法 求主应力及其方向,并画出主平面及主应力。(应力单位为 MPa) 10 解: 20
o sin 2 45o 90o cos 2 90
d
在纯剪时,单元体任意两垂直面上的正应力是等值反号的。 根据胡克定律: '
45
d
Me
o
"
Me
1 1 E E E 200 103 5 10 4 1 0.25 1 80 MPa E 200 103 3.75 10 4 60 MPa 1 0.25 1
材料力学习题的答案解析
第二章轴向拉伸与压缩2-1 试求图示直杆横截面1-1、2-2、3-3上的轴力,并画出轴力图。
F1=18kN (b)F3=25kN 3力。
解:2-2 图示中部对称开槽直杆,试求横截面1-1和2-2上的正应1 .轴力M1I2- , --------------------------------------------------------- 4kN* -------------- —------------------------------------- r .------------- *—1 2201 F2=3kNF4=10kN2 31518F N F14kN2.应力F N141031 1MPa175MPaA1 1204F N141032 2MPa350A2 22010 4由截面法可求得,杆各横截面上的轴力为2-3 图示桅杆起重机,起重杆 AB 的横截面是外径为 20mm 、 径为18 mm 的圆环,钢丝绳 BC 的横截面面积为 BC 横截面上的应力。
AB 和钢丝绳 o 10mm 2。
试求起重杆解:1 .轴力 取节点 F x 0 :B 为研究对象,受力如图所示, F NBC F NAB cos30 F cos 45 2-4 图示由铜和钢两种材料组成的等直杆,铜和钢的弹性模量分别为 E 1100 GPa 和 E 2210 GPa 。
若杆的总伸长为A l 0.126mm ,试求载荷F 和杆横截面上的应力。
2铜1钢/ /F140 . -400600解:1•横截面上的应力由题意有I 1Fh FI 2 l 2E 1AE 2A由此得到杆横截面上的应力为l h I 2 E 1 E 2 h E 1l 2E 20.126 600 400 100 103 210 103 MPa 15.9MPaF y 0 : 由此解得: 2 .应力 起重杆横截面上的应力为F NABABF NAB sin 30 F sin 45 F NAB 2.83kN , 2.83 103 A AB ____ 2。
材料力学作业题解_第1-4章
(a)(b)O SF M(c)1.2 试求图示结构m-m 和n-n 两截面上的内力,并指出AB 和BC 两杆的变形属于哪一类基本变形。
解:一、应用截面法,取n-n 截面以下部分为研究对象,受力图如(b ),由平衡条件A=0M∑,N 3320F ×−×=得 N 2kN F =BC 杆的变形属于拉伸变形。
二、应用截面法,取m-m 截面以右,n-n 截面以下部分为研究对象,受力图如(c ),由平衡条件O=0M∑,N 2310F M ×−×−=得 1 kN m M =⋅=0yF ∑,SN 30FF −+=得 S 1 kN F = AB 杆的变形属于弯曲变形。
1.3 在图示简易吊车的横梁上,F 力可以左右移动。
试求截面1-1和2-2上的内力及其最大值。
解:应用截面法,取1-1截面右侧部分为研究对象,受力图如(b ),由平衡条件A=0M∑,N1sin 0F l F x α⋅⋅−⋅= (1)得 N1sin F xF l α⋅=⋅因x 的变化范围为0x l ≤≤,所以当x l =时,N1F 达到最大值,即N1sin FF α=(a)(b)F (c)应用截面法,取图(a )所示1-1和2-2截面以右部分为研究对象,受力图如图(c ),由平衡条件=0x F ∑,N2N1cos 0FF α−⋅= (2) =0yF ∑,S2N1sin 0F F F α−+⋅= (3)O=0M∑,N12sin ()0F l x M α⋅⋅−−= (4)解以上各式,得N2cot /F x F l α=⋅⋅,S2(1/)F x l F =−,2()/M l x F x l =−⋅当x l =时,F N2达到最大值,即N2max cot F F α=⋅当0x =时,F S2达到最大值,即S2max F F =当/2x l =时,M 2达到最大值,即2max /4M F l =⋅1.4 拉伸试样上A ,B 两点间的距离l 称为标距。
材料力学习题选及其解答定稿版
材料力学习题选及其解答精编W O R D版IBM system office room 【A0816H-A0912AAAHH-GX8Q8-GNTHHJ8】5-1. 矩形截面悬臂梁如图所示,已知l =4m ,h/b=2/3,q=10kN/m ,[]=10MPa ,试确定此梁横截面的尺寸。
解:(由弯矩图知:(2)计算抗弯截面模量(3)强度计算5-2. 20a工字钢梁的支承和受力情况如图所示,若[]=160MPa ,试求许可载荷。
解:(1(2)查表得抗弯截面模量(3)强度计算取许可载荷5-3. 图示圆轴的外伸部分系空心轴。
试作轴弯矩图,并求轴内最大正应力。
qxMql 2x解:(1(2C截面:B 截面:(3)轴内的最大正应力值5-8. 压板的尺寸和载荷如图所示。
材料为45钢,s =380MPa ,取安全系数n=1.5。
试校核压板的强度。
(3)强度计算许用应力Mx强度校核压板强度足够。
5-12. ⊥形截面铸铁梁如图所示。
若铸铁的许用拉应力为[t ]=40MPa ,许用压应力为[c ]=160MPa ,截面对形心z c 的惯性矩I zc =10180cm4,h 1=96.4mm ,试求梁的许用载荷P 。
解:(1(2A 截面的最大压应力A 截面的最大拉应力C 截面的最大拉应力取许用载荷值5-15. 铸铁梁的载荷及截面尺寸如图所示。
许用拉应力[l ]=40MPa ,许用压应力[c ]=160MPa 。
试按正应力强度条件校核梁的强度。
若载荷不变,但将T 形截面倒置成为⊥形,是否合理何故x0.6解:(1)画梁的弯矩图截面(2形心位置和形心惯性矩(3)强度计算B 截面的最大压应力B 截面的最大拉应力C 截面的最大拉应力梁的强度足够。
(4)讨论:当梁的截面倒置时,梁内的最大拉应力发生在B 截面上。
梁的强度不够。
5-20. 试计算图示工字形截面梁内的最大正应力和最大剪应力。
解:(1A No16Mx QMx最大剪力和最大弯矩值是(2)查表得截面几何性质(3)计算应力最大剪应力最大正应力5-22. 起重机下的梁由两根工字钢组成,起重机自重Q=50kN,起重量P=10kN。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1 2—3解:求拉杆的轴力,由受力图可知 ∑MA=0, 3P-R(3+1.5)-NBC×1.5=0 ① ∑MD=0, 1.5 R′-0.75NBC=0 ② 联立① ② 求解
NBC=5.76P
σBC=ANBC=25.746dP=62101014.35.75.764 =76.4×103kN/cm2 =76.4MPa 2--4解:求螺栓的轴力,设工件的加紧力为G=2.5kN 由受力图可知 ∑MB=0, G l -N×l /3=0 N=3G=3×2.5=7.5kN ∴ 螺栓的应力 σ= N/A=4N/πd2
=62103.1714.35.74(4×7.5)/(3.14×17.3 2×10-6) =31.92×103 kPa=31.92MPa<[σ]=50MPa ∴螺栓是满足强度的
2--5解:求绳索的轴力 由受力图可知 cosα=22102525=0.93
∑MD=0, Ncosα×10-5G=0 建立强度条件 σ=N/A≤[σ]=40MPa N =G/2×0.93 ≤[σ]A G ≤ 40×103×5002×10-6 ×2×0.93 =37.2kN 2-6求杆AB的轴力 由受力图可知 ∑MC=0, Ncos45°×1-P×2=0 N=P×2÷cos45°=14.14kN 建立强度条件 σ=N/A≤[σ]=3MPa A≥N/[σ]=(P×2÷cos45°)÷(3×103)=a2
a ≥)103()45cos25(3=0.069m 杆AB的截面边长为70mm
2--12解:求各杆的轴力,由节点A可知 ∑X=0, NAD -Pcos45°=0
NAD = 22P (拉) 由节点D可知 ∑X=0, NDC cos45° - NAD =0
XD YD P = 7.5kN R A
B G D
NBC
XE YE
NBC R′
C E A
N R G
A
D N G
B C α
A NAC
P NAD
D NAD
NDC
NDB
XC YC C
P N
D
B 2
NDC =P (压) 根据结构的对称性 :
NDB = NAC = NAD =NCB= 22P (拉) 建立强度条件 σ=N/A≤[σ] 又 [σ] / [σt] =3 ∵ NDB/A≤[σt] ,
NDB= 22P ≤[σt] A ∴[P1] ≤2 [σt] A 而 ∵NDC/A≤[σC] ∴NDC=P≤[σC]A=3[σt] A ∴[P2] ≤ 3 [σt] A
此结构的最大许可载荷P为 [P1] ≤2 [σt] A 2--15 解:
Δl =∑ EA
Nl = 936101010905.161155.045
=-0.0167×10-3m=-16.7×10-3mm 2--16解:以AB梁为研究对象 ∑MA=0, Tsin45°(2+3)-4P=0
T=4×70/sin45°(2+3)=562 kN=N
钢丝绳的应力为 σ=N/A=562/(5×10-4)=1122×10 3 kPa ∵ Δl =EANl 其中 l =BC+AC=22+2232=6.434 m
∴ Δl =4610510200434.6256=5.096×10-3m AB梁在B点的位移为BB′ ∴BB′=Δl /cos45°=2 Δl =7.206×10-3m
6kN 45kN 60kN 9kN N (+) (-) 6kN
45kN
15kN T T A B
B′ △l
P 3
2--18解:以AB梁为研究对象 ∑MA=0, N×1-P×2=0 , N=2P 建立强度条件 σ=N/A≤[σ] , N≤[σ]A, P ≤[σ]A/2=160×103×500×10-6/2=40kN P
Δl =EANl =6610500102001402=0.8×16-3m δB=2 Δl =1.6×16-3m=1.6 mm 2--24解:以AB梁为研究对象 ∑MA=0, NCD×1+NEB×2-P×1.5=0 , NCD =200×1.5-2 NEB 变形协调条件 Δl CD = 2Δl EB
补充方程 铜铜AElNCDCD2 = 钢钢AElNEDEB
66105001012012CDN)=6610250102002
EBN
NCD =6N EB/5=200×1.5-2 NEB =300-2 NEB N EB=300/(2+6/5)=93.75kN , N CD =112.5kN
各竖杆的应力为 σCD=CDCDAN=6105005.112=225×103kPa=225MPa
σEB=EBEBAN=61025075.93 =375×103kPa=375MPa 钢杆的伸长 Δl EB =661025010200275.93=1.87×10-3m=1.87mm
2--27解:以AB梁为研究对象 ∑MA=0, N 2=2N 3 ⑴ ∑MA=0, N 1=N 3 ⑵
变形协调条件 (δ-Δl 3+Δl 1)/(Δl 1+Δl 2)=2/1 Δl 1+2Δl 2+Δl 3=δ
P A △l B
δB
N
B P=200kN A △lCD NCD △lEB NEB D
δ-△l3
N1 N2 N3 A B C
△l1 △l2 4
补充方程 EANNNlCD)2(321=δ , 10200)2(321NNN=0.8×10-3 ⑶
联立⑴、⑵、⑶式,得 N1=N3=5.33kN, N2=10.66 kN 2--28解:以阶梯杆为研究对象 ∑Y=0, N1-N2-P=0 变形协调条件 Δl = δ
补充方程 1111AElN+2222AElN=δ ① 空隙消失时, N2=0, ∴ N1=P , 1111AElN=δ
∴111AEPl=461040101001P =0.08×10-3 P=0.08×10-3 ×(100×10 6×40×10-4)=32Kn ② 当P=500kN时,有 N1-N2=500, ⑴
1111AE
lN
+2222AElN=δ,
4611040101001N+4621020102002
N=0.08×10-3 ⑵
联立⑴、⑵式 得 N2=-156kN, N1=344kN ∴σ1=11AN=41040344=86×10 3 kPa=86MPa
σ2=22AN=41020156=-78×10 3 kPa=-78MPa ③在第2问的基础上再升高20°C, 则 (P=0) 变形协调条件 Δl N +α lΔT =0
补充方程 1111AElN+2222AElN=-(α 1 l 1+α 2 l 2)ΔT 其中查表 α 1 =16.7×10-6, α 2 =12×10-6
4611040101001
N+4621020102002N=-(16.7×1+12×2)×10-6×20°=-0.814×10-3 ⑶
N1 N2 P 5 阶梯杆为研究对象 ∑Y=0, N′1=N′2 ⑷ 联立⑶、⑷式 得 N′1 =N′2 =-108.53 kN
∴σ″1= 111ANN=4104053.108344 =58.87×10 3 kPa=58.87MPa
σ″2=222ANN=4102053.108156 =-132.265×10 3 kPa=-132.265MPa 3--2解:剪切面为 AQ=πDδ, 而 [Q]=[P]=60kN 根据剪切条件 Q /AQ≤[τ] [Q]/τj x≤AQ=πDδ
D≥[Q]/πδτj x=3310200102060=0.00475m=4.8mm 3--3解:强度校核 销钉有两个受剪面,每个受剪面的剪力和面积分别为Q和AQ
Q= 2P=50kN
AQ=42d=π×30 2=706.86mm2 τ =Q /AQ=50/(706.86×10-6)=70.7MPa>[τ] ,强度不够. 选择直径 Q /AQ≤ [τ] AQ ≥ Q/[τ]=50/60×103
d≥][4Q=31060504 =0.0326 m=32.6mm 应改用 d≥32.6mm的销钉 3--4解:设每只螺栓所受剪力为Q ,由平衡条件
4Q×20D=M, Q=02DM
τ =QAQ=202dDM=921010802002=15.9MPa<[τ] 安全 3--5 解:设每个键所受的挤压力为P ,由平衡条件
2)4752(4P×10-3=m=4kN·m
P=310)4752(24 =20.2 kN
Q P/2 m n P m n Q P P/2
