3-1 力矩的瞬时效应 转动定律
合集下载
3-2力矩的功 定轴转动定律
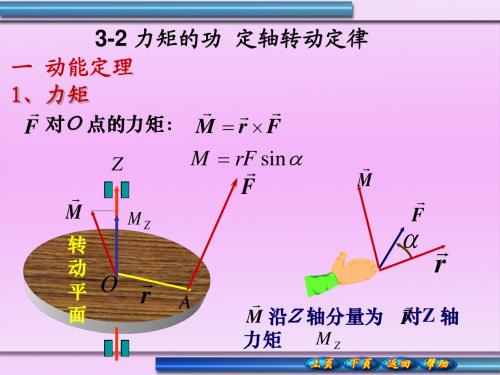
2、力矩的功
力矩的功:当刚体在外力矩作用下绕定轴转 动而发生角位移时,就称力矩对刚体做功。
d A F d r
力 F 对P 点作功:
0
F d s cos 2
0‘
F d s sin d s r d
r
d
dr
F
P
注:此处的力F在转动平面内,若为 空间力,可以将力分解为平面内和 垂直平面两个分量
2 1 2 d mRg I mR 3 2 dt
设圆盘经过时间t停止转动,则有
1 2 2 ( mRg )dt ( mR )d 0 2 3
t
0
由此求得
3 R t 0 4 g
2
1
Jd
1 1 2 J 2 J12 2 2
刚体绕定轴转动时,刚体所受外力矩所做的功等于 刚转动动能的增量,称为刚体定轴转动的动能定理。
例1、如图所示,一个质量为M,半径为R定滑轮上 面绕有细绳。绳的一端固定在滑轮边上,另一端挂一 质量为m的物体而下垂。忽略轴处摩擦,求物体m由 静止下落h高度时的速度和此刻滑轮的角速度。
与桌子的接触面上,力矩的计算要用积分法。在图中,把圆 盘分成许多环形质元. 每个质元的质量 dm m 2rdr
R 2
质量元dm 所受到的阻力矩是
2mr 2 dM rdmg g dr 2 R
圆盘受到的总阻力炬为
M
R
0
2mr 2 2 g 2 dr mRg R 3
根据定轴转动定律,阻力矩使圆盘减速,即获得负的角加速度.
F2R F1R 1 MR 2 2
a R
于是得到方程组:
F1 m1 g m1a F2 m2 g m2a
3-3,4力矩的功
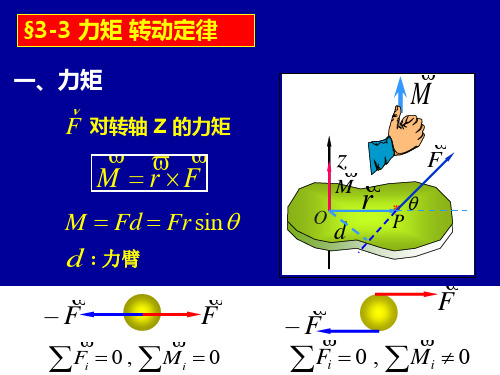
R,I
m
0 x x
例2 :
方法一:转动定律+ 方法一:转动定律+牛顿定律 方法二: 方法二:机械能守恒
2mgh − kh2 v= m+ I 2 R
F
R,I
T T’ m mg
0 x x
例3 : 求物体从弹簧原长时开始下落到h距离时的速度? 求物体从弹簧原长时开始下落到h距离时的速度?
m R,I
m
0 x x
v v v M = r ×F
注意 必须在转动平面内. 1)力 F 必须在转动平面内. 若力不在转动平面内, 2)若力不在转动平面内,分解成
ω
v
θ r
F
uu r uu r r u r M 若刚体受N个外力作用, 3)若刚体受N个外力作用, 合 = ∑Mi = ∑ri × Fi
uu v v r M = r × F// 平面
四、包括转动动能的机械能守恒
0 若刚体系统 ∑A外+ A非保守= ,或只有保守力 ∑ 做功, 常量。 (矩)做功,则系统的机械能守恒 E=常量。
A + A 保内 = E − E0 = ∆E 外 非
重力势能、 重力势能、 弹性势能、 弹性势能、 引力势能
E = EP + Ek平 + Ek转 E0 = EP0 + Ek 0平 + Ek 0转
π
1 A = mgL = −(∆Ep ) = −(Ep2 − Ep1 ) 2
三、刚体转动动能定理
v r 1 2 1 2 1. 类比 质点: 质点:A = ∫ F ⋅ dl = mv − mv0 2 2 r r 1 2 1 2 刚体: 刚体: = ∫ M ⋅ dθ = Iω − Iω0 A 2 2 2. 转动动能定理 合力矩
1-3力矩和力偶

第一章
1-3 力矩和力偶
学习目标
2
例题解析
知识要点
强化训练
1、了解力矩和力偶的概念 2、掌握力矩和力偶的计算方法
(一)力矩和力矩平衡条件 为了度量力使物体转动效应的大小而引进力矩的概念
1.力矩力矩等于从该点到力作用线上任一矢径与该力的矢量积,其转动效果由两个因素决定:
(1)力的大小与力臂的乘积;(2)力使物体绕点O的转动方向。力矩用M(F)表示。
1、力偶与力矩对物体的转动效果相同。() [分析]正确,了解力和力偶性质虽不同,但有相同效果 2、作用于刚体上的力,其作用线可在刚体上任意平行移动,其作用效果不变。() [分析]错误,熟悉力平移定理的正确定义,力平移时必须附加一个力偶 3、平面力偶系平衡充要件是:合力偶矩等于零。( ) [分析]正确,熟悉力偶系平衡条件选择 1、在平面中,力矩为零的条件是( ) A。力等于零B。力和力臂都不为零C。力与力臂乘积不为零D。力不过矩心 [分析]选A,明确力矩的两个因素
3n 4m
6n
6n
2m
=
=
3n
12n.m
4、平面力偶系平衡条件 平面力偶系平衡的充分必要条件是:力偶系中各力偶矩的代数和为零
5、力的平移定理 把作用在刚体上点A的力F平行移到一点B,但同时必需附加一个力偶,这个附加偶的矩 等原来的力F对新作用点B的矩 M=B
F
F
F
B
A
B
A
=
F
F
A
B
=
M
1.力矩的单位由力和力臂的单位决定,在国际单位制中用N·m [分析]本题要求熟悉力矩的单位 2.力矩平衡条件是:作用在物体上各力对转动中心的力矩的代数和等于零。 即合力矩等于零公式表示为Mo(F)=0 [分析]本题要求掌握力矩平衡条件的定义和表达式 3.物体受到大小相等,方向相反,作用线平行的二力所组成力系称为力偶 [分析]本题要求了解力偶的定义,并理解其含义 4.力对物体的作用,既能使物体移动,又能使物体转动 [分析]本题要求了解两种不同的力对物体的作用效果
1-3 力矩和力偶
学习目标
2
例题解析
知识要点
强化训练
1、了解力矩和力偶的概念 2、掌握力矩和力偶的计算方法
(一)力矩和力矩平衡条件 为了度量力使物体转动效应的大小而引进力矩的概念
1.力矩力矩等于从该点到力作用线上任一矢径与该力的矢量积,其转动效果由两个因素决定:
(1)力的大小与力臂的乘积;(2)力使物体绕点O的转动方向。力矩用M(F)表示。
1、力偶与力矩对物体的转动效果相同。() [分析]正确,了解力和力偶性质虽不同,但有相同效果 2、作用于刚体上的力,其作用线可在刚体上任意平行移动,其作用效果不变。() [分析]错误,熟悉力平移定理的正确定义,力平移时必须附加一个力偶 3、平面力偶系平衡充要件是:合力偶矩等于零。( ) [分析]正确,熟悉力偶系平衡条件选择 1、在平面中,力矩为零的条件是( ) A。力等于零B。力和力臂都不为零C。力与力臂乘积不为零D。力不过矩心 [分析]选A,明确力矩的两个因素
3n 4m
6n
6n
2m
=
=
3n
12n.m
4、平面力偶系平衡条件 平面力偶系平衡的充分必要条件是:力偶系中各力偶矩的代数和为零
5、力的平移定理 把作用在刚体上点A的力F平行移到一点B,但同时必需附加一个力偶,这个附加偶的矩 等原来的力F对新作用点B的矩 M=B
F
F
F
B
A
B
A
=
F
F
A
B
=
M
1.力矩的单位由力和力臂的单位决定,在国际单位制中用N·m [分析]本题要求熟悉力矩的单位 2.力矩平衡条件是:作用在物体上各力对转动中心的力矩的代数和等于零。 即合力矩等于零公式表示为Mo(F)=0 [分析]本题要求掌握力矩平衡条件的定义和表达式 3.物体受到大小相等,方向相反,作用线平行的二力所组成力系称为力偶 [分析]本题要求了解力偶的定义,并理解其含义 4.力对物体的作用,既能使物体移动,又能使物体转动 [分析]本题要求了解两种不同的力对物体的作用效果
第三章刚体的运动(大学物理)

F 解: a (3t 2 4t )i (12t 6) j m
v [(3t 2 4t )i (12t 6) j ]dt (t 3 2t 2 )i (6t 2 6t ) j
0
t
1 4 2 3 r [(t 2t )i (6t 6t ) j ]dt ( t t )i (2t 3 3t 2 ) j 0 4 3
A B A
B
C
C
A
B
C
*可用质心或任一点的运动来代表刚体的运动。
*平动是刚体的基本运动形式之一。
2.转动
*转动也是刚体的基本运动形 式之一,可分为定轴转动和 定点转动。
①定轴转动:运动中各质元均 做圆周运动,且各圆心都在同 一条固定的直线(转轴)上。
②定点转动:运动中刚体上只 有一点固定不动,整个刚体绕 过该定点的某一瞬时轴线转动。
m 1 2 y bdy ma ab 12
2
b 2 b 2
m 1 x adx mb2 ab 12
2
a
x
由垂直轴定理可得
1 J z J x J y m( a 2 b 2 ) 12
b
例题6 求质量为m、半径为R均匀圆盘的转动惯 量。轴与盘平面垂直并通过盘心。
R
解:取半径为r宽为dr的薄圆环; 圆盘的质量面密度为
M r F m
Or
·
0
M r F
M rF sin r0F
M
F
r0 r sin 称力臂 其中:
F
O
·
r
或: M 2.力偶矩
r F
例题2 物体在力场F (3t 2 4t )i (12t 6) j 中运动, 已知质量m=1kg,t=0时刻质点位于原点,且速度 为0。求:t=2s时该质点所受的对原点的力矩。
力对质点的瞬时效应——牛顿三定律

直向下的速率v 0 ,且在水中
B P ,则球在水中仅受
阻力Fr kv 的作用 m dv kv dt
v dv k
t
dt
v0 v
m0
v v0e( k / m )t
FB
Fr
v
y
P
v
v0
o
t
2.1.3 牛顿定律的应用举例
例2 光滑水平桌面
上放置一半径为R的固
• 惯性系 • 物体的运动速度远小于光速 • 只适用于宏观物体运动规律 • 仅适用于实物,不完全适用于场
2.1.3 牛顿定律的应用举例
一 解题步骤
隔离物体 受力分析 列方程 解方程
建立坐标 结果讨论
二 三类常见问题
已知力求运动状态 已知运动状态求力
rF
aa
r F
已知部分力、部分运动状态、求解部
dvx k dt
2.1.3 牛顿定律的应用举例
vx
m
kdvy k dt mg kvy m
t 0
v0x v0 cos v0 y v0 sin
yv0
Fr
A
P
v
代入初始条件解得: o
x
vx v0 cosekt/m
vy
(v0
sin
mg k
)ekt/ m
R
dv v2
R
dt
1
1
t
v v0 R
2.1.3 牛顿定律的应用举例
v Rv0 ( R v0t )
s
t
ds υ dt 0ds 0υ dt
2.定轴转动定理 (1)

1 J L1 = m L L2, 3 1 J O = mO R 2 2
mO
O’ •
2
mL
J L 2 = J O + mO d
1 1 2 J = m L L + mO R 2 + m O ( L + R ) 2 3 2
例:半经为 R ,质量为 m 的均匀圆环, 的均匀圆环, 求:对于沿直径转轴的转动惯量
df R
r O
dM = r ⋅ df = µσ 2πgr ⋅ dr
2
dM = 2πµσgr ⋅ dr
2
2 M = ∫ 2πµσgr dr = πµσgR 3 3 问题: 问题: 0
2
R
dr
若圆盘以ω 的初角速度转动, 圆盘转多少圈静止? 若圆盘以 0 的初角速度转动, 圆盘转多少圈静止?
一、刚体定轴转动的角动量 刚体上任一质元∆m i 在垂直 轴的平面内作圆周运动。 于 z 轴的平面内作圆周运动。 对 z 轴的角动量沿 z 轴 正向,大小为: 正向,大小为:
2
Jz =
∑ ∆m r
Lz = J zω
2
i i
——刚体对 z 轴的转动惯量 刚体对 轴的转动惯量
z
轴的角动量为: 刚体对 z 轴的角动量为:
ω
v ri O
即:刚体绕定轴转动时, 刚体绕定轴转动时, 对转轴的角动量,等于刚 对转轴的角动量,等于刚 体对转轴的转动惯量与 体对转轴的转动惯量与角 速度的乘积 的乘积。 速度的乘积。
J = ∫ R dm
2 0
M
M
o
dm
=R
2
∫
M
0
dm = MR
2
R
绕圆环质心轴的转动惯量: 绕圆环质心轴的转动惯量
第三章_刚体和流体的运动
dF pdA pLdy
h 100m
L 1000m
y
dA
dy
dF pdA pLdy 令大气压为 p0 ,则
p p0 g (h y)
h y
dF [ p0 g (h y)]Ldy
h
x O
1 F [ p0 g (h y )]Ldy p0 Lh gLh2 0 2
(x2,y2,z2)
系统的自由度是多少?
3-2 力矩 转动惯量 定轴转动定律
力矩 刚体绕 O z 轴旋转 , 力 F 作用在刚体上点 P , 且在转动 为由点O 到力的 平面内, r 作用点 P 的矢径. 一
M
F
*
M
O
z
Z F 对转轴 的力矩
r
d
P
M r F
0 5π rad s1, t = 30 s 时, 0. 解 (1) 设 t = 0 s 时, 0 0 .飞轮做匀减速运动 0 0 5π π 1 2 rad s rad s t 30 6
飞轮 30 s 内转过的角度
2 2 0 (5 π ) 2 75π rad 2 2 (π 6)
dJ r dm 2π r dr R 3 4 J 2π r dr π R 0
2 3
而
m π R
2
所以
2
1 2 J mR 2
例3 一质量为 m 、长为 l 的均匀细长棒,求 通过棒中心并与棒垂直的轴的转动惯量 . O
l 2
O
l 2
dr O´
O´
r
dr
l
解 设棒的线密度为 ,取一距离转轴 OO´ 为 处的质量元 dm dr dJ r 2dm r 2dr
刚体 定轴转动定律
1 12
mL2
mh 2
例:半径为R、质量均匀分布的细圆环及薄圆 盘,质量均为m,求对中垂轴的转动惯量。
r
R
(1)细圆环:
J r 2dm R2 dm mR 2
(2)薄圆盘:看作由许多宽为dr的细圆环组成
dm ds 2π rdr dJ r 2dm 2π r 3dr
J R 2πr 3dr 1 mR 2
(2) 3g sin 3g cos
2L
2L
d d d dt d dt
d d
d 3g cos d
2L
d
π 2
3g
cos
d
0
0 2L
L
mg
3g L
例:质量m的圆盘半径为R,绕中心旋转,与桌
面的摩擦系数为m。
求:圆盘从0到静止所需要的时间 t。
解: M f
J
J d dt
N
T2 m2 g m2a2
T1r T2r J
a1 a2 r
a1
a2
(m1 m2 )g
m1
m2
1 2
m
T1
2m1m2 g m1 m2
1 2
m1m3 g 1 2 m3
讨论 m3 0 :轻滑轮
3
T2
T1
T1 m3 T1 m3 g m1 a1
m1 g
a2
T2
T2
m2
m2 g
2m1m2
g
1 2
m2m
m1
T2
2mm2 1m122mg3 m1 m2
3
g
例:细杆质量为m,长为L,可绕水平光滑轴O
在竖直平面内转动,自水平静止释放。
求:(1)杆与铅直方向成 角时的;
3-2_力矩_刚体定轴转动的转动定律
M z xFy yFx
第3章 刚体力学基础
3–2 力矩 刚体定轴转动的转动定律
2
二
刚体定轴转动的转动定律
d M iz J dt J
绕定轴转动的刚体的角加速度与作用于刚体上 的合外力矩成正比,与刚体的转动惯量成反比.
第3章 刚体力学基础
3–2 力矩 刚体定轴转动的转动定律
3
3–2 力矩 刚体定轴转动的转动定律 一 力矩 定义:作用于质点的力对惯 性系中某参考点的力矩,等 于力的作用点对该点的位矢 与力的矢积,即
1
M r F
M 的方向垂直于r和F所决定的平 面,指向用右手法则确定。
M x yFz zFy
在直角坐标系中,表示式为
M y zFx xFz
第3章 刚体力学基础
k k J 即 J 2 1 k0 0 3 9J
2
2
3–2 力矩 刚体定轴转动的转动定律
12
(2)
d M J J dt
d k J dt
2
t=0时, 0 ,两边积分
1 0 3
0
d
2
第3章 刚体力学基础
3–2 力矩 刚体定轴转动的转动定律
8
例3.2 设质量为m,半径为R的细圆环和均匀圆盘分 别绕通过各自中心并与圆面垂直的轴转动,求圆环和 圆盘的转动惯量. 解 (1) 在环上任 取一质元,其质量 为dm,距离为R, 则该质元对转轴的 转动惯量为
dJ R dm
2
第3章 刚体力学基础
3–2 力矩 刚体定轴转动的转动定律
9
考虑到所有质元到转轴的距离均为R,所以细圆环对 中心轴的转动惯量为
第3章 刚体力学基础
3–2 力矩 刚体定轴转动的转动定律
2
二
刚体定轴转动的转动定律
d M iz J dt J
绕定轴转动的刚体的角加速度与作用于刚体上 的合外力矩成正比,与刚体的转动惯量成反比.
第3章 刚体力学基础
3–2 力矩 刚体定轴转动的转动定律
3
3–2 力矩 刚体定轴转动的转动定律 一 力矩 定义:作用于质点的力对惯 性系中某参考点的力矩,等 于力的作用点对该点的位矢 与力的矢积,即
1
M r F
M 的方向垂直于r和F所决定的平 面,指向用右手法则确定。
M x yFz zFy
在直角坐标系中,表示式为
M y zFx xFz
第3章 刚体力学基础
k k J 即 J 2 1 k0 0 3 9J
2
2
3–2 力矩 刚体定轴转动的转动定律
12
(2)
d M J J dt
d k J dt
2
t=0时, 0 ,两边积分
1 0 3
0
d
2
第3章 刚体力学基础
3–2 力矩 刚体定轴转动的转动定律
8
例3.2 设质量为m,半径为R的细圆环和均匀圆盘分 别绕通过各自中心并与圆面垂直的轴转动,求圆环和 圆盘的转动惯量. 解 (1) 在环上任 取一质元,其质量 为dm,距离为R, 则该质元对转轴的 转动惯量为
dJ R dm
2
第3章 刚体力学基础
3–2 力矩 刚体定轴转动的转动定律
9
考虑到所有质元到转轴的距离均为R,所以细圆环对 中心轴的转动惯量为
转动定理的积分形式力矩对时间和空间的累积效应
刚体绕定轴转动的动能 定理:合外力矩对绕定
0
轴转动的刚体所作的功
W=
1 2
J
2-
1 2
J
2 0
等于刚体的转动动能的 增量。
例题:如图所示,一质量为M、半径为R的圆盘,可绕一无摩擦的水平轴转动。圆盘上 绕有轻绳,一端悬挂质量为m的物体。问物体由静止下落高度h时,其速度的大小为多
少?设绳的质量忽略不计。
dW
Fvgdrv
F
drv
cos
2
Frd
sin
dW Md
W Md
说明:力矩作功的实质仍然是力作功。只是
对于刚体转动的情况,这个功不是用力的位移来 表示,而是用力矩的角位移来表示。
0
2、力矩的功率
(1)定义:
单位时间内力矩对刚体所作的功。
(2)公式
P dW =M d M
dt
dt
功率一定时,转速越大,力矩越小; 转速越小,力矩越大。
一、刚体定轴转动的角动量定理
v
定轴转动定理
v M
v dL
同牛顿第二定律
v F
dpv
dt
dt
类似,以微分形式反映了力或力矩对刚体质点或 质点系的瞬时作用规律。如果我们要考虑一段时 间内外力矩对刚体的作用效果,则可对转动定理
表式对时间积分可得积分形式——刚体定轴转 动的角动量定理
由
M
dL
dt
得
Mdt dL
(3)意义
表示力矩对刚体作功的快慢
3、刚体的转动动能
刚体以角速度ω作定轴转动,取一质元Δmi,距转轴 ri,则此质元的速度为vi=riω,
动能为ห้องสมุดไป่ตู้
