大学物理— 力矩 转动定律
合集下载
大学物理.第三章.刚体的转动
动 .试计算细杆转动到与竖直线成 角时的角加速度
和角速度 .
解 细杆受重力和
铰链对细杆的约束力
FN
作用 3g sin
2l
3g (1 cos )
l
§3-4 力矩的功 定轴转动的动能定理
一、力矩的功
z
O
d r
速度ω 绕端点转动，摩擦系数为μ 求M摩擦力。
ω
解: 质量线密度:
m L
dm
r dr
质量元:
r dm dr
所受摩擦力为:
dF gdm gdr
例3-5 现有一圆盘在平面内以角速度ω 转动，求 摩擦力产生的力矩（μ 、m、R）。
dr
ωr
解:
dm ds rdrd dF gdm grdrd dM1 rdF r2gdrd
I mi ri2 －质量不连续分布
i
r 2dm －质量连续分布
d －线分布λ＝m/ι 质量元: dm ds －面分布σ＝m/S
dV －体分布ρ＝m/V
二、决定转动惯量的三因素
1）刚体的质量； 2）刚体的质量分布； （如圆 环与圆盘的不同）；
3）刚体转轴的位置。 （如细棒绕中心、绕一端）
运动。 一、何谓刚体
在任何情况下形状和大小都不发生变化的
物体。即每个质元之间的距离无论运动或
受外力时都保持不变。
理想模型
ri j c mj
二、刚体运动的两种基本形式 mi
平动----刚体运动时，刚体内任一直线恒保 持平行的运动(即该直线方向保持不变)
刚体的平动过程
c a b
刚体的平动过程
能运用以上规律分析和解决包括 质点和刚体的简单系统的力学问题.
和角速度 .
解 细杆受重力和
铰链对细杆的约束力
FN
作用 3g sin
2l
3g (1 cos )
l
§3-4 力矩的功 定轴转动的动能定理
一、力矩的功
z
O
d r
速度ω 绕端点转动，摩擦系数为μ 求M摩擦力。
ω
解: 质量线密度:
m L
dm
r dr
质量元:
r dm dr
所受摩擦力为:
dF gdm gdr
例3-5 现有一圆盘在平面内以角速度ω 转动，求 摩擦力产生的力矩（μ 、m、R）。
dr
ωr
解:
dm ds rdrd dF gdm grdrd dM1 rdF r2gdrd
I mi ri2 －质量不连续分布
i
r 2dm －质量连续分布
d －线分布λ＝m/ι 质量元: dm ds －面分布σ＝m/S
dV －体分布ρ＝m/V
二、决定转动惯量的三因素
1）刚体的质量； 2）刚体的质量分布； （如圆 环与圆盘的不同）；
3）刚体转轴的位置。 （如细棒绕中心、绕一端）
运动。 一、何谓刚体
在任何情况下形状和大小都不发生变化的
物体。即每个质元之间的距离无论运动或
受外力时都保持不变。
理想模型
ri j c mj
二、刚体运动的两种基本形式 mi
平动----刚体运动时，刚体内任一直线恒保 持平行的运动(即该直线方向保持不变)
刚体的平动过程
c a b
刚体的平动过程
能运用以上规律分析和解决包括 质点和刚体的简单系统的力学问题.
大学物理公式大全
大学物理公式大全大学物理公式大全物理学是一门探索自然现象的科学，它研究宇宙的运动、力的作用、物质的组成和性质等。
在大学物理学学习中，我们会接触到众多的物理公式。
下面是一份大学物理公式大全，供大家参考。
1. 运动学公式：速度（v）= 位移（s）/ 时间（t）加速度（a）= （末速度（v）- 初速度（u））/ 时间（t）位移（s）= 初速度（u）* 时间（t） + 1/2 * 加速度（a）* 时间（t）^22. 牛顿第一定律（惯性定律）：一个物体在没有受到外力作用时，保持静止或匀速直线运动。
3. 牛顿第二定律（力与加速度的关系）：力（F）= 质量（m）* 加速度（a）4. 牛顿第三定律（作用与反作用定律）：两个物体之间的相互作用力，两个力的大小相等、方向相反。
5. 动能公式：动能（K）= 1/2 * 质量（m）* 速度^26. 动量公式：动量（p）= 质量（m）* 速度（v）7. 转动力矩（扭矩）公式：转动力矩（τ）= 力（F）* 力臂（r）8. 转动惯量公式：转动惯量（I）= 质量（m）* 半径（r）^29. 动量守恒定律：在一个封闭系统中，如果没有外力作用，系统的总动量保持不变。
10. 能量守恒定律：在一个封闭系统中，能量的总量保持不变。
11. 功公式：功（W）= 力（F）* 位移（s）12. 弹性势能公式：弹性势能（E）= 1/2 * 弹性系数（k）* 弹性变形^213. 引力公式：引力（F）= 万有引力常数（G）* （质量1（m1）* 质量2（m2））/ 距离^214. 等离子体温度公式：等离子体温度（T）= 等离子体内电子能量总量（Ee）/ 等离子体内电子数目（Ne）* Boltzmann常数（k）15. 麦克斯韦速度分布公式：概率密度（f）= （质量（m）/ (2 * π * Boltzmann常数（k） * 温度（T）））^(3/2) * e^(-（速度（v）^2）/ (2 * Boltzmann常数（k） * 温度（T）))16. 电场强度公式：电场强度（E）= 电力（F）/ 电荷量（q）17. 电能公式：电能（W）= 电流（I） * 电压（V） * 时间（t）18. 磁场强度公式：磁场强度（B）= 电流（I）* μ0 / (2 *π * r)19. 磁感应强度公式：磁感应强度（B）= 磁场强度（μ0） * 磁化强度（M）20. 麦克斯韦电磁场微分方程组：∇·E = ρ / ε0∇·B = 0∇×E = - ∂B / ∂t∇×B = μ0J + μ0ε0 ∂E / ∂t以上仅是大学物理中的一小部分公式，物理学的知识非常广泛且深入。
《大学物理》3.2转动定理
3.2 转动定理
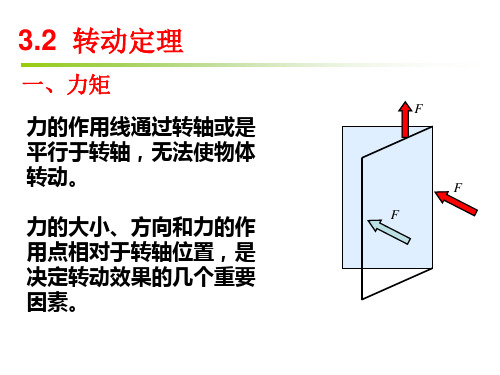
一、力矩
F
力的作用线通过转轴或是 平行于转轴，无法使物体 转动。 力的大小、方向和力的作 用点相对于转轴位置，是 决定转动效果的几个重要 因素。
F
F
1.定义：
力的大小与力臂乘积为力对转轴的力矩。用M表示
z
M
M F d Fr sin
F r P
M
z
F
1 2
1 其中滑轮转动惯量 J MR 2
2
a R
m m g a
2 1 1 2
m2 m1 g
M m1 m2 R 2
2 1
M m m 2
1 2
M m 2m g 2 T M m m 2
1 1 2
M m 2m g 2 T M m m 2
四、转动定理应用举例
例3-4如图所示，一不能伸长的轻绳跨过一轴承光滑的定 滑轮，滑轮视为圆盘，绳的两端分别悬有质量为m1和m2 的物体，且m1<m2,设滑轮的质量为M，半径为R，绳与 轮之间无相对滑动，求物体的加速度和绳中张力。
解：将三个物体隔离出来受力分析
其中 T 和 T 大小不能假定相等，但
m r 刚体内各质点相对于转轴的分布决定
M J
—— 绕定轴转动的刚体，其角加速度与它所 受合外力矩成正比，与刚体转动惯量成反比。 这一结论就是刚体定轴转动定理。
三、转动惯量
刚体的转动惯量等于刚体内各质点的质量与 其到转轴距离平方的乘积之和。
J m r J r dm
2
2
ij
j
F r f r m r
2 it i it i i i
一、力矩
F
力的作用线通过转轴或是 平行于转轴，无法使物体 转动。 力的大小、方向和力的作 用点相对于转轴位置，是 决定转动效果的几个重要 因素。
F
F
1.定义：
力的大小与力臂乘积为力对转轴的力矩。用M表示
z
M
M F d Fr sin
F r P
M
z
F
1 2
1 其中滑轮转动惯量 J MR 2
2
a R
m m g a
2 1 1 2
m2 m1 g
M m1 m2 R 2
2 1
M m m 2
1 2
M m 2m g 2 T M m m 2
1 1 2
M m 2m g 2 T M m m 2
四、转动定理应用举例
例3-4如图所示，一不能伸长的轻绳跨过一轴承光滑的定 滑轮，滑轮视为圆盘，绳的两端分别悬有质量为m1和m2 的物体，且m1<m2,设滑轮的质量为M，半径为R，绳与 轮之间无相对滑动，求物体的加速度和绳中张力。
解：将三个物体隔离出来受力分析
其中 T 和 T 大小不能假定相等，但
m r 刚体内各质点相对于转轴的分布决定
M J
—— 绕定轴转动的刚体，其角加速度与它所 受合外力矩成正比，与刚体转动惯量成反比。 这一结论就是刚体定轴转动定理。
三、转动惯量
刚体的转动惯量等于刚体内各质点的质量与 其到转轴距离平方的乘积之和。
J m r J r dm
2
2
ij
j
F r f r m r
2 it i it i i i
大学物理-力矩、转动定律、转动惯量
gh
yLdy
1 2
p0 Lh 2
1 6
gLh2
h
y
o
L
dA
x
dy
y
Q
dy
x
二、转动定律
质点的动力学问题 刚体的动力学问题
F ma
M
设刚体有n个质点组成，
先取任一质点i来研究
mi ri
外力：Fi 内力：Fi
由牛 顿第二定律得： Fi Fi miai
切线方向：Fit Fit miait
X
dV r2dZ (R2 Z 2 )dZ
其质量：dm dV (R2 Z 2 )dZ
其转动惯量：dJ 1 r 2dm 1 (R2 Z 2 )2 dZ
2
2
dJ 1 r 2dm 2
1 (R2 Z 2 )2 dZ
2
Z r dZ
O
R
Y
J dJ
X
R 1 (R2 Z 2 )2 dZ
比较
牛顿第二定律 F m a
转动定律
M J
三、转动惯量 J miri2 (4 9)
对质量连续分布的刚体 J r 2dm (4 11)
转动惯量的单位：kg m2
影响转动惯量得因素
注意：
（1）、刚体的质量（材料） （2）、刚体质量的分布
质点也有转动惯量
J mr2
（3）、转轴的位置
对质量不连续分布的刚体 J m 2
R 2
8 R5 2 mR2
m 4 R3
3
15
5
例3）求一质量为m的均匀实心球对其一条直径
为轴的转动惯量。
Z x
解：方法二 在球上取一体积元
dV
dV dxdydz
广石化大学物理3.1 3.2 刚体 力矩 刚体定轴转动的转动定律
(2) 为瞬时关系．
(3) 转动中 M J 与平动中F ma 地位相同．
动画
第三章 刚体力学基础
17
物理学
第五版
3-1(2) 力矩
转动定律
转动惯量
例2.20 如图2.37(a)所示，质量均为m的两物体A，B. A放在倾角 为α的光滑斜面上，通过定滑轮由不可伸长的轻绳与B相连.定滑轮是半 径为R的圆盘，其质量也为m.物体运动时，绳与滑轮无相对滑动.求绳中 张力 T1 和 T2 及物体的加速度a(轮轴光滑).
3-1(2) 力矩
aA aB R
转动定律
⑤
转动惯量
由于绳不可伸长，所以
又
J
1 mR 2 2
联立式①，②，③，④，⑤得
2+3sin mg 5
T1＝ T2＝
3+2sin mg 5 2(1-sin ) a A aB g 5
第三章
刚体力学基础
19
物理学
第五版
3-1(2) 力矩
l 2
刚体力学基础
12
第三章
物理学
第五版
3-1(2) 力矩
转动定律
转动惯量
例2 一质量为 m 、半径为 R 的均匀圆盘，求通 过盘中心 O 并与盘面垂直的轴的转动惯量. 解 设圆盘面密度为 在盘上取半径为 ，宽为 的圆环 dr
r
， R R O
圆环质量
dm 2 π r dr
2 3
r dr
圆环的转动惯量
d dt
分离变量，并考虑到t＝0时， 0 ，两边积分
1 0 3
0
d
k dt 2 0 J
t
大学物理上册、转动定律、转动能量
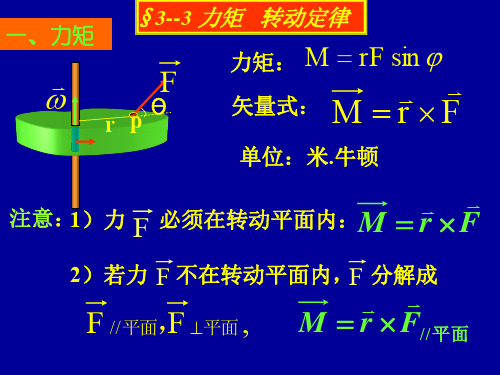
M 或 M I
I
说明：1）定律是瞬时对应关系；
2）M , J , 应是对同
一轴而言的
Z
如何求力对轴的矩呢？ 如图可将力分解为两个
MZ
F r
F F
力，只求那个垂直于轴
的力的力矩就可以了。
3）转动定律说明了I是物体转动惯性大小的量
度。因为： M一定时I I
mg
L
sin
2
mg
LБайду номын сангаас
0
2
2
0
2
A
1 2
mgL
(Ep )
Ep2
E p1
二、刚体的重力势能 Ep mgZC
mgL ZC－质心距0势能面的距离
mg(L L cos )
2
三、刚体转动动能定理
力矩的功定义式 dA Md dA Md Id I d d Id
J
1 2
m2 r 2…(3)
a = r…(4)
T=T’ …(5)
T= a=
m1m2g 2m1+m2
r
注意: =m1g
a等于常数且初速为零! h 1 at 2 2
=
2m1g 2m1+m2
=
m1gt2 2m1+m2
r 例2）质量分别为m1，m2的物体通过轻绳挂在质
量为m3半径为 的圆盘形滑轮上。求物体m1，m2
－力矩的功
θ 是刚体在力矩的作用下转过的角度
重力矩的功
设一细杆的质量为m，长为L，一端支以枢轴 而能自由旋转，设此杆自水平静止释放。求：
大学物理—力矩
2、 力矩对刚体做功： 刚体在外力矩作用下，发生角位移 mi : p 点质量 ri : p 点对 o 点位矢 (o p) 已知：
Fi : p 点所受外力 d : p点绕轴转过的角位移
Z
dsi : p 点元位移 : dsi 与 Fi 的夹角
O
d
dsi
Fi
i
i : ri 与 Fi 的夹角
( M
0
ri
i
)d
P
类比法
dsi rd i
i 900
5
§3-4
二、定轴转动的动能定理 1、 公式： 2、 证：
合外力（外力矩） 对刚体做功
定轴转动的动能定理
1 2 A 1 Jw2 Jw12 2 2
2
1
A dA Md
1
2
dw J d dt
M z r F2
M z 正方向的规定： 促进转动的力矩为正
1
§3-3
二、定轴转动定律
力矩 刚体定轴转动定律
dp F= dt
牛二
类比法
dv F =ma m dt
J
dw 转动定律 M z dLz dt dt （转动刚体的第二定律） 已知： mi : p 点质量 Z ri : p 点对 o 点位矢 (o p) 都在与轴 p 点所受合外力 F : i 垂直的平
§3-3
一、 力矩 1、力对定点的力矩：
F 对O点的力矩
力矩 刚体定轴转动定律
rF
Z
MO
F
P对O点的位矢
O
r
d
F1
P
F2
2、力对于转轴
oz 的力矩
大学物理力矩+转动定律+转动惯量-省公开课获奖课件市赛课比赛一等奖课件
26
例题
解 (1) 用隔离法分别 对各物体作受力分析，取 如图所示坐标系。
A
mA
FN
PmA AO
FT1
x
C
mC
mB B
FT1
FC
PC
FT2
FT2
O
mB
PB y
27
例题
FT1 mAa mB g FT2 mBa
RFT2 RFT1 J a R
FN
PmA AO
FT1
x
FT1
FC
32
例题
由角加速度旳定义
dω dω dθ ω dω
dt dθ dt dθ ωdω 3g sin θdθ
2l 代入初始条件积分得 ω
m,l FN θ mg
O
3g (1 cos θ) l
33
(mA mC 2)mB g mA mB mC 2
(2) B由静止出发作匀加速直线运动，下 落旳速率
v 2ay
2mB gy
mA mB mC / 2
30
例题
例2 一长为 l 、质量
为 m 匀质细杆竖直放置，
其下端与一固定铰链O相 接，并可绕其转动．因为 此竖直放置旳细杆处于非
m,l
θ mg
力矩为零，故 F 对转 轴旳力矩
M zk r F
z
F
k
O Fz r
F
M z rF sin
点击进入动画
2
讨论
(2) 合力矩等于各分力矩 旳矢量和 M M1 M2 M3
(3) 刚体内作用力和反作用力旳力 矩相互抵消。
M ij
rj
j
O
d ri
i Fji
例题
解 (1) 用隔离法分别 对各物体作受力分析，取 如图所示坐标系。
A
mA
FN
PmA AO
FT1
x
C
mC
mB B
FT1
FC
PC
FT2
FT2
O
mB
PB y
27
例题
FT1 mAa mB g FT2 mBa
RFT2 RFT1 J a R
FN
PmA AO
FT1
x
FT1
FC
32
例题
由角加速度旳定义
dω dω dθ ω dω
dt dθ dt dθ ωdω 3g sin θdθ
2l 代入初始条件积分得 ω
m,l FN θ mg
O
3g (1 cos θ) l
33
(mA mC 2)mB g mA mB mC 2
(2) B由静止出发作匀加速直线运动，下 落旳速率
v 2ay
2mB gy
mA mB mC / 2
30
例题
例2 一长为 l 、质量
为 m 匀质细杆竖直放置，
其下端与一固定铰链O相 接，并可绕其转动．因为 此竖直放置旳细杆处于非
m,l
θ mg
力矩为零，故 F 对转 轴旳力矩
M zk r F
z
F
k
O Fz r
F
M z rF sin
点击进入动画
2
讨论
(2) 合力矩等于各分力矩 旳矢量和 M M1 M2 M3
(3) 刚体内作用力和反作用力旳力 矩相互抵消。
M ij
rj
j
O
d ri
i Fji
刚体定轴转动定律
于 180°的夹角 θ 转向 F 时，拇指所指的方向就是力矩的方向。
可见，力矩的方向与转轴的方向平行，只有两个可能的方向，因此，可用 M 的正负表示力矩的方向。 一般可按力矩的作用来判断其正负：由转轴 Oz 正向俯视，若力矩的作用使刚体逆时针转动，则力矩为 正，否则为负。
刚体定轴转动定律 1.1 力矩
可加性
• 对同一转轴而言，刚体各部分转动惯量之 和等于整个刚体的转动惯量。
平行轴定理
• 设有两个彼此平行的转轴，一个通过刚体 的质心，另一个不通过质心。两平行轴之 间的距离为d，刚体的质量为m。
如果此刚体对通过质心转轴的转动惯量为 Jc ，则对另一 转轴的转动惯量 J 为 J Jc md 2
刚体定轴转动定律
刚体定轴转动定律Βιβλιοθήκη ， ，，，
例题讲解 2
如图所示，一轻绳跨过一轴承光滑的定滑轮。绳两边分别悬有质量为 m1 和 m2 的两个物体 A，B。已知 m1
小于 m2 ，滑轮可看作质量均匀分布的等厚圆盘，其质量为 m，半径为 r，设绳与滑轮间无相对滑动。求：① 物
体的加速度；② 滑轮的角加速度；③ 绳的张力。
i 1
n
用 M 表示，即 M (Δmiri2 ) β
i 1
n
n
式中的 (Δmiri2 ) 称为转动惯量，用 J 表示，即 J (Δmiri2 )
i 1
i 1
于是，式可写为 M Jβ
刚体定轴转动定律 1.2 转动定律
转动定律：刚体定轴转动时，刚体的角加速度与刚体所受的合外力矩成正比，与刚体的转动惯量 成反比。
r 2 dm
Ω
式中 r ——质元 dm 到转轴的距离（m）。 在国际单位制中，转动惯量的单位为 kg m2 。
可见，力矩的方向与转轴的方向平行，只有两个可能的方向，因此，可用 M 的正负表示力矩的方向。 一般可按力矩的作用来判断其正负：由转轴 Oz 正向俯视，若力矩的作用使刚体逆时针转动，则力矩为 正，否则为负。
刚体定轴转动定律 1.1 力矩
可加性
• 对同一转轴而言，刚体各部分转动惯量之 和等于整个刚体的转动惯量。
平行轴定理
• 设有两个彼此平行的转轴，一个通过刚体 的质心，另一个不通过质心。两平行轴之 间的距离为d，刚体的质量为m。
如果此刚体对通过质心转轴的转动惯量为 Jc ，则对另一 转轴的转动惯量 J 为 J Jc md 2
刚体定轴转动定律
刚体定轴转动定律Βιβλιοθήκη ， ，，，
例题讲解 2
如图所示，一轻绳跨过一轴承光滑的定滑轮。绳两边分别悬有质量为 m1 和 m2 的两个物体 A，B。已知 m1
小于 m2 ，滑轮可看作质量均匀分布的等厚圆盘，其质量为 m，半径为 r，设绳与滑轮间无相对滑动。求：① 物
体的加速度；② 滑轮的角加速度；③ 绳的张力。
i 1
n
用 M 表示，即 M (Δmiri2 ) β
i 1
n
n
式中的 (Δmiri2 ) 称为转动惯量，用 J 表示，即 J (Δmiri2 )
i 1
i 1
于是，式可写为 M Jβ
刚体定轴转动定律 1.2 转动定律
转动定律：刚体定轴转动时，刚体的角加速度与刚体所受的合外力矩成正比，与刚体的转动惯量 成反比。
r 2 dm
Ω
式中 r ——质元 dm 到转轴的距离（m）。 在国际单位制中，转动惯量的单位为 kg m2 。
3力矩转动定律(大学物理 - 刚体部分)
F
二、转动定律
刚体作定轴转动时，合外力矩等于 刚体的转动惯量与角加速度的乘积。 M Jβ
注意几点
1. 是矢量式 2. 具有瞬时性。 3. M、J、是对同一轴而言的。
§5.力矩、转动定律 / 二、转动定律
三. 解题方法及应用举例
M Jβ
1.确定研究对象。
2.受力分析（只考虑对转动有影响的力矩）。
M J
l 1 2 mg cos ml 2 3 3 g cos 2l
习题课 / 例3
m,l
mg
3 g cos 2l
60时
0时
3 g 4l 3 g 2l
m,l
mg
习题课 / 例3
3.列方程求解(平动物体列牛顿定律方程，转 动刚体列转动定律方程和角量与线量关系)。
§5.力矩、转动定律 / 三、解题方法及应用举例
例1：如图所示，两个同心圆盘结合在一 起可绕中心轴转动，大圆盘质量为 m1、 半径为 R，小圆盘质量为 m2、半径为 r， 两圆盘都用力 F 作用，求角加速度。
解：以 m1、 m2 为研 究对象，它们有共同 的角加速度，只有 F、 F 产生力矩。 FR Fr ( J1 J 2 )
第三节
力矩 转动定律
一、力矩
力与力臂的乘积。
O d
M
r
P r M dF r sin F M rF sin 根据矢量乘积法则： A B AB sin 用矢量方法表示力矩： M r F 单位：牛顿· 米， N ·m 方向：从r沿小于角右旋到F，大拇指指向。
§5.力矩、转动定律 / 一、力矩
m2 r
R
m1
大学物理(一)力矩、转动定律
大学物理（一）力矩、转动定律您的姓名： [填空题] *_________________________________1. 有两个力作用在一个有固定转轴的刚体上：（1）这两个力都平行于轴作用时，它们对轴的合力矩一定是零；（2）这两个力都垂直于轴作用时，它们对轴的合力矩可能是零；（3）当这两个力的合力为零时，它们对轴的合力矩一定是零；（4）当这两个对轴的合力矩是零时，它们的合力也一定是零。
对以上说法，下列判断正确的是[单选题] *只有（1）正确（1）、（2）正确，（3）、（4）错误(正确答案)（1）、（2）、（3）正确，（4）错误（1）、（2）、（3）、（4）都正确2. 关于力矩有以下几种说法：（1）对某个定轴转动刚体而言，内力矩不会改变刚体的角加速度；（2）一对作用力和反作用力对同一轴的力矩之和必为零；（3）质量相等，形状和大小不同的两个刚体，在相同力矩的作用下，他们的运动状态一定相同。
对以上说法，下述判断正确的是：[单选题] *只有（1）正确（1）、（2）是正确的(正确答案)（2）、（3）是正确的（1）、（2）、（3）都正确3. 下列关于刚体的表述中，不正确的是 [单选题] *刚体作定轴转动时，其上各点的角速度相同，但线速度不同刚体作定轴转动时的转动定律M=Jα，式中M、J、α均是对同一固定轴而言的，否则该式不成立刚体的转动动能等于刚体上所有各质元的动能之和对于给定的刚体而言，它的质量和形状是一定的，则其转动惯量也是唯一确定的(正确答案)4. 下列关于刚体定轴转动定律的表述中，正确的是 [单选题] *两个质量相等的刚体，在相同力矩的作用下，运动状态的变化情况一定相同作用在定轴转动刚体上的力越大，刚体转动的角速度就越大角速度的方向一定与外力矩的方向相同内力矩不会改变刚体的角加速度(正确答案)5. 一均匀木棒可绕于其一段的水平光滑轴自由转动，今使棒从水平位置由静止自由下落，忽略空气阻力的影响，在棒摆到竖直位置的过程中，下列说法正确的是[单选题] *角速度从小到大，角加速度不变角速度从小到大，角加速度从小到大角速度从小到大，角加速度从大变小(正确答案)角速度不变，角加速度为零。
《大学物理》第三章 刚体的定轴转动
P
t
=
1 2
ω J 2 自
t
=
ω J 2 自 2P
=
2×105× (30π)
2×736×103
2
=
1.21×103s
(2) ω进 = 1度 秒 = 0.0175rad/s
ω进 =
M
Jω自
M = Jω进ω自
M = 2×105×0.0175×30π= 3.3×105 N返回.m退出
3-14 在如图所示的回转仪中，转盘的 质量为 0.15kg , 绕其轴线的转动惯量为： 1.50×10-4 kg.m2 ,架子的质量为 0.03kg, 由转盘与架子组成的系统被支持在一个支柱 的尖端O，尖端O到转盘中心的距离为0.04 m , 当转盘以一定角速度ω 绕其轴旋转时， 它便在水平面内以1/6 rev/s的转速进动。
为25cm，轴的一端 A用一根链条挂起，如
果原来轴在水平位置，并使轮子以ω自=12 rad／s的角速度旋转，方向如图所示，求：
（1）该轮自转的角动量；
（2）作用于轴上的外力矩；
（3）系统的进动角速度， ω
并判断进动方向。
AO
B
R
l 返回 退出
解：
(1)
J
=
m
R
2
回
=
5×(0.25 )2
ω
= 0.313 kg.m2
a
=
m
1+
m m
1g 2+
J
r2
T1 =
m 1g (m 2+ J m 1+m 2 + J
r 2) r2
T2 =
m 1m 2g m 1+m 2 + J
大学物理-力矩-转动定律-转动惯量
F
p
18
2 – 5 刚体的定轴转动
第二章 动力学基础
解 (1) Fr J
Fr 98 0.2 39.2 rad/s2
J 0.5
mg T ma
(2) Tr J
a r
两者区别?
rO
F T
T
J
mgr mr 2
98 0.2 0.5 10 0.22
i
J r2dm
9
2 – 5 刚体的定轴转动
第二章 动力学基础
四. J 的计算
质量连续分布刚体的转动惯量
J mjrj2 r2dm dm ：质量元 j
对质量线分布的刚体： dm dl
：质量线密度
对质量面分布的刚体：
：质量面密度
对质量体分布的刚体：
在圆规迹切线方向
mk ak mk rk Fk fk
两边乘以rk，并对整个刚体求和
第二章 动力学基础
z
o
vk
mk
( mk rk2 ) Fk rk fk rk
k
k
k
5
2 – 5 刚体的定轴转动
第二章 动力学基础
( mk rk2 ) Fk rk fk rk
17
2 – 5 刚体的定轴转动
第二章 动力学基础
四、转动定律的应用举例
例1 一轻绳绕在半径 r =20 cm 的飞轮边缘， 在绳端施以F=98 N 的拉力，飞轮的转动惯量 J=0.5 kg·m2,飞轮与转轴间的摩擦不计 。
rO
求: (1) 飞轮的角加速度。
(2) 如以重量P =98 N的物体挂在 绳端,试计算飞轮的角加速度。
大学物理-第四章-力矩 转动定律 转动惯量
0
3
8
以上各例说明：
(1)刚体的转动惯量 与刚体的质量有关， 与刚体的质量分布有关， 与轴的位置有关。
(２)质量元的选取：
线分布 dm dx(或dl)
面分布 dm ds
体分布 dm dv
线分布
面分布
体分布
9
习题4-11： 质量为m1和m2 的两物体A、B 分别悬挂在图示的组合轮两端.设两轮的半 径分别为R 和r，两轮的转动惯量分别为J1 和J2 ，轮与轴承间、绳索与轮间的摩擦力 均略去不计，绳的质量也略去不计.试求两 物体的加度度和绳的张力.
解: 系统角动量守恒
J11 J22 (J1 J2 )
J11 J 22
(J1 J2 )
22
习题4-16：一质量为m′、半径为R 的均匀圆盘，通过 其中心且与盘面垂直的水平轴以角速度ω转动，若在 某时刻，一质量为m 的小碎块从盘边缘裂开，且恰好 沿垂直方向上抛，问它可能达到的高度是多少？ 破裂
Lz x mv y ymv x
15
2 刚体定轴转动的角动量
L mirivi ( miri2 )
i
i
z
L J
二 刚体定轴转动的角动量定理
dL d(J) M
dt dt
O ri
v i
mi
t2 Mdt
t1
L2 L1
dL
J2
J1
非刚体定轴转动的角动量定理
20
有许多现象都可以用角 动量守恒来说明. 它是自然 界的普遍适用的规律.
花样滑冰 跳水运动员跳水
飞轮
1
2
航天器调姿
大学物理课件考研备考期末复习 角动量 角动量守恒定律
解：对M：M ＝T1 R＝J
J＝ 1 MR2 2
对m : mg T1 ma a R
解 方 程 得 ：a
m
m M
2
g
v 2ah 4mgh 2m M
v 1 4mgh
R R 2m M
·R 绳 v0=0
m
th
2m g
r2 R2
dr
2 3
m gR
根据转动定律，得
M
2 3
m gR
4g
J
1 m R2
3R
2
角加速度为常量，且与ω0的方向相反，
表明圆盘作匀减速转动
0 t
当圆盘停止转动时，ω=0，则得
t 0 3R0 4g
一个质量为M、半径为R 的定滑轮 上面绕有细绳，绳的一端固定在滑轮边上， 另一端挂一质量为m 的物体而下垂。忽略 定轴O 轴处摩擦，求物体m由静止下落高度h时的 速度和此时滑轮的角速度。
Mdt
L2
L1
冲量矩
t2
M
dt
t1
质点的角动量定理：对同一参考点 O ，质点所 受的冲量矩等于质点角动量的增量.
3 质点的 角动量守恒定律 M 0, L 恒矢量
质点所受对参考点 O 的合力矩为零时，质点对该 参考点 O 的角动量为一恒矢量.
例
例1 一半径为 R 的光滑圆环置于竖直平面内.一质 量为 m 的小球穿在圆环上, 并可在圆环上滑动. 小球开始 时静止于圆环上的点 A (该点在通过环心 O 的水平面上), 然后从 A 点开始下滑.设小球与圆环间的摩擦略去不计.求 小球滑到点 B 时对环心 O 的角动量和角速度.
解 小虫与细杆的碰撞视为完全非弹性碰撞，碰撞 前后系统角动量守恒
(完整版)转动定律讲解
d力臂:转轴到力作用线的垂直距离
方向: r F 的方向 单位: N m
对于定轴转动；
z
M
r
Od
F
P*
规定转动正方向,力矩使刚体绕
正方向转动, M 取正,反之取负。
第四章 刚体的定轴转动
4 – 2 力矩 转动定律 转动惯量
大学物理学
讨论 1）与转轴平行的力对转轴不产生力矩;
2）与转 轴垂直但通过转轴的力对转轴不产生力矩； 3）若力 F 不在转动平面内，把力分解为平行和垂
直于转轴方 向的两个分 量 F Fz F
其中 Fz 对转轴的力
矩为零，故 F 对转轴的
力矩
M r F
M z rF sin
4）合 力矩 等于各分力矩的矢量和
M M1 M2 M3
第四章 刚体的定轴转动
z
k
Fz
F
O r
F
定轴转动：（规定转动 正方向）
M Mi
i
4 – 2 力矩 转动定律 转动惯量
力矩可以反映力的作用点的位置对物体运动的影响.
第四章 刚体的定轴转动
4 – 2 力矩 转动定律 转动惯量
大学物理学
一 力矩
刚体绕 O z 轴旋 转 , 力 F 作用在刚体上点 P ,
r 且在转动平面内, 为由点O 到力的作用点 P 的径
矢 .
F 对转轴 Z 的力矩 M rF
M
力矩是矢量
大小: M Frsin Fd
M i Fitri (mi )atri
at ri
Mi (mi )ri2
z
Fit
O
ri
mi
M Mi (mi )ri2 (mi )ri2
➢ 转动惯量
方向: r F 的方向 单位: N m
对于定轴转动；
z
M
r
Od
F
P*
规定转动正方向,力矩使刚体绕
正方向转动, M 取正,反之取负。
第四章 刚体的定轴转动
4 – 2 力矩 转动定律 转动惯量
大学物理学
讨论 1）与转轴平行的力对转轴不产生力矩;
2）与转 轴垂直但通过转轴的力对转轴不产生力矩； 3）若力 F 不在转动平面内，把力分解为平行和垂
直于转轴方 向的两个分 量 F Fz F
其中 Fz 对转轴的力
矩为零，故 F 对转轴的
力矩
M r F
M z rF sin
4）合 力矩 等于各分力矩的矢量和
M M1 M2 M3
第四章 刚体的定轴转动
z
k
Fz
F
O r
F
定轴转动：（规定转动 正方向）
M Mi
i
4 – 2 力矩 转动定律 转动惯量
力矩可以反映力的作用点的位置对物体运动的影响.
第四章 刚体的定轴转动
4 – 2 力矩 转动定律 转动惯量
大学物理学
一 力矩
刚体绕 O z 轴旋 转 , 力 F 作用在刚体上点 P ,
r 且在转动平面内, 为由点O 到力的作用点 P 的径
矢 .
F 对转轴 Z 的力矩 M rF
M
力矩是矢量
大小: M Frsin Fd
M i Fitri (mi )atri
at ri
Mi (mi )ri2
z
Fit
O
ri
mi
M Mi (mi )ri2 (mi )ri2
➢ 转动惯量
大学物理(上册) 4.2刚体定轴转动定律(20)
????????ddjdddtdjjk????2????2000???????ddjk20lnkj???????222lnkjn??????56例题423质量的两物体分别悬挂在质量的定滑轮两端如图示
4.2
刚体定轴转动定律 本节内容：刚体动力学；
1.力矩：使刚体产生角加速度的物理量；
2.转动定律：刚体定轴转动的动力学方程；
1 2 l l 1 2 2 J O J C md J C m ml m ml 2 12 2 3
2 2
解：分析 由刚体定轴转动定律可解。 （1）由题意知叶轮所受阻力矩方向与 其转动方向相反，其大小为：
M f k 2
(1)
由刚体定轴转动定律得：
d k J J dt
2
(2)
对上式分离变量并积分得：
0
k J
dt
0
0
t
2
d
2
(3)
得到所需时间为：
t
J k 0
M F (r sin ) F (d )
(1)
d : 力臂
注意： 1.若力 F 不在转动平面内，则可把力分解为平 行、垂直于转轴方向的两个分量：
其中 Fz 对转轴的力矩为零， 故 F 对转轴的力矩为: M rF r F
F Fz F
质元对
m dm dx dx l
m dJ o x dm x dx x dx l
2 2 2
oz轴转动惯量为：
细杆对 oz轴转动惯量为：
JO
（2）同理细杆对转轴 o z 的转动惯量： l 1 2 2 m J O x dx ml 0 l 3 讨论：1.结论：同一刚体对不同转轴，对应不同转动 惯量，故该量有关于刚体，还有关于转轴！ 2.由上述结果看出： 1 2 1 2 l 2 l 2 J O ml ml +m （ ） J O +m （ ） 3 12 2 2
4.2
刚体定轴转动定律 本节内容：刚体动力学；
1.力矩：使刚体产生角加速度的物理量；
2.转动定律：刚体定轴转动的动力学方程；
1 2 l l 1 2 2 J O J C md J C m ml m ml 2 12 2 3
2 2
解：分析 由刚体定轴转动定律可解。 （1）由题意知叶轮所受阻力矩方向与 其转动方向相反，其大小为：
M f k 2
(1)
由刚体定轴转动定律得：
d k J J dt
2
(2)
对上式分离变量并积分得：
0
k J
dt
0
0
t
2
d
2
(3)
得到所需时间为：
t
J k 0
M F (r sin ) F (d )
(1)
d : 力臂
注意： 1.若力 F 不在转动平面内，则可把力分解为平 行、垂直于转轴方向的两个分量：
其中 Fz 对转轴的力矩为零， 故 F 对转轴的力矩为: M rF r F
F Fz F
质元对
m dm dx dx l
m dJ o x dm x dx x dx l
2 2 2
oz轴转动惯量为：
细杆对 oz轴转动惯量为：
JO
（2）同理细杆对转轴 o z 的转动惯量： l 1 2 2 m J O x dx ml 0 l 3 讨论：1.结论：同一刚体对不同转轴，对应不同转动 惯量，故该量有关于刚体，还有关于转轴！ 2.由上述结果看出： 1 2 1 2 l 2 l 2 J O ml ml +m （ ） J O +m （ ） 3 12 2 2
大学物理 第四章 刚体的转动 4-2 力矩 转动定律 转动惯量
} ⇒ω
} ⇒θ
2、 M = Jα
F = ma
}⇒
17
m反映质点的平动惯性，J 反映刚体的转动惯性。 反映质点的平动惯性， 反映刚体的转动惯性。 反映质点的平动惯性
三 转动惯量
J 的计算方法 质量离散分布
J = ∑ ∆m r
j
2 j j
J = ∑ ∆m r = (∆m )r + (∆m2 )r + L+ (∆mN )r
质量为m，长为L的细棒绕其一端的 的细棒绕其一端的J 质量为 ，长为 的细棒绕其一端的
1 2 J c = mL 12
O1
O1’
L2 1 2 J = J c + m( ) = mL 2 3
d=L/2
O2 O2’
20
竿 子 长 些 还 是 短 些 较 安 全 ？
飞轮的质量为什么 大都分布于外轮缘？ 大都分布于外轮缘？
（3） ）
1 2 对M： T2 r − T1r = J α = M r α ： 2
4、运动学： 运动学：
rα = a
（4） ）
26
解以上四个联立方程式, 解以上四个联立方程式 可得
1 T2 ' ≠ T 、
原因： 原因：
' 1
' (1)若：T2 ' = T T2 ' r −T ' r = Jα v 1 1 FN v 1 T 1 ⇒ J = mr2 = 0 ⇒m = 0 2 m
21
例1（补充例题）：一个转动惯量为2.5 kg⋅m2 、 （补充例题） 一个转动惯量为 ⋅ 例题 直径为60cm 的飞轮，正以 的飞轮，正以130 rad⋅s−1 的角速度旋转。 直径为 ⋅ 的角速度旋转。 现用闸瓦将其制动, 现用闸瓦将其制动 如果闸瓦对飞轮的正压力为 500 N, 闸瓦与飞轮之间的摩擦系数为0.50。求： 闸瓦与飞轮之间的摩擦系数为 。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
例1：求质量为 m ,半径为 R 的均匀薄圆环的 转动惯量，轴与圆环平面垂直并且通过其圆心。
例2：求质量为 m ,半径为 R ，厚度为 l 的均 匀圆盘的转动惯量，轴与盘面垂直并通过圆心。
第二章 刚体的定轴转动
12
物理学
第五版
2.2 力矩 转动定律
例3：求质量为 m ,半径为 R 的均匀薄球壳的 转动惯量，转轴通过球心。
飞轮的质量为什么 大都分布于外轮缘？
第二章 刚体的定轴转动
竿 子 长 些 还 是 短 些 较 安 全 ？
16
物理学
第五版
2.2 力矩 转动定律
转动定律应用 说明
M J
1. 与 M 方向相同。 2.为瞬时关系。
3.转动中
M J
与平动中 F
ma
地位相同。
第二章 刚体的定轴转动
17
物理学
ji
O
M
d
ji
i ri
F ij
第二章 刚体的定轴转动
3
物理学
第五版
2.2 力矩 转动定律
例1：有一大型水坝高110 m、长1000m ,水深 100m，水面与大坝表面垂直，如图所示。求作用 在大坝上的力，以及这个力对通过大坝基点Q 且 与x 轴平行的力矩。
y
y
x
h
x
O Q O
L
4
第二章 刚体的定轴转动
第五版
2.2 力矩 转动定律
例6 一个飞轮的质量 m 60 kg ，半径 R 0 . 25 m ， 正在以 0 1000 r/min 的转速转动。现在要制动飞轮， 要求在 t 5 . 0 s 内使它均匀减速而最后停下来。求 闸瓦对轮子的压力 N 为多大？假定闸瓦与飞轮间 的滑动摩擦系数为 k 0 . 8 ，而飞轮的质量可以看 作全部均匀分布在轮的外周上。
物理学
第五版
2.2 力矩 转动定律
二 转动定律 (law of rotation)
1.单个质点与转轴刚性连接
F t ma t mr
z
M
Ft
M rF sin θ
M rF t mr
2
F
M mr
2
O r
m
Fn
第二章 刚体的定轴转动
5
物理学
第五版
z
k
F
rF sin
O
r
Fz
F
第二章 刚体的定轴转动
2
物理学
第五版
2.2 力矩 转动定律 2.合力矩等于各分力矩的矢量和
M M1 M 2 M3
3.刚体内作用力和反作用力的力矩互相抵消。
M ij
rj
j
F ji
M ij M
i
i
Mi 0
1
第二章 刚体的定轴转动
物理学
第五版
2.2 力矩 转动定律
讨论
1.若力 F 不在转动平面内，把力分解为平行和 垂直于转轴方向的两个分量 F F z F 其中 F z 对转轴的力 z 矩为零，故 F 对转轴
的力矩
M
M z k r F
第五版
2.2 力矩 转动定律
j
M
ej
( m j r j )α
2
z rj
Fej
m j
j
m jrj
2
J
r dm
2
F ij
转动定律 M J 刚体定轴转动的角加速度与它所受的合外力 矩成正比，与刚体的转动惯量成反比。
第二章 刚体的定轴转动
7
物理学
第二章 刚体的定轴转动
18
物理学
第五版
2.2 力矩 转动定律
例7 一个质量为 M ，半径为 R 的定滑轮（当 作均匀圆盘）上面绕有细绳。绳的一端固定在滑轮 边上，另一端挂一质量为 m 的物体而下垂。忽略轴 处摩擦，求物体由静止下落 h 高度时的速度和此时 滑轮的角速度。
第二章 刚体的定轴转动
19
物理学
物理学
第五版
2.2 力矩 转动定律 质量为 m 的刚体，如果 对其质心轴的转动惯量为 J ， 则对任一与该轴平行，相距 为 d 的转轴的转动惯量
C
四 平行轴定理 (parallel axis theorem)
d
C
m
O
J O J C md
2
第二章 刚体的定轴转动
15
物理学
第五版
2.2 力矩 转动定律
2
转动惯量的单位：kg· 2 m
J 的意义：转动惯性的量度。
第二章 刚体的定轴转动
9
物理学
第五版
2.2 力矩 转动定律
J 的计算方法
质量离散分布
J
j
m j r j m 1 r1 m 2 r2 m j r j
2 2 2
2
质量连续分布
J m jrj r dm
2.2 力矩 转动定律 质元受外力
M
ej
2.刚体
Fej
，内力
2 j
F ij
z
O
M ij m j r
rj
Fej
m j
外力矩
内力矩
F ij
j
M
ej
j
M
ij
j
m jrj
2
M ij M
ji
M ij 0
第二章 刚体的定轴转动
6
物理学
第五版
2.2 力矩 转动定律 转动定律 M J
讨论 1. M
J
2. 3.
M J J
d dt
M 0， ω =常量
第二章 刚体的定轴转动
8
物理学
第五版
2.2 力矩 转动定律
三 转动惯量 (moment of inertia)
J
j
m jrj , J
2
r dm ,
例4：求质量为 m ,半径为 R 的均匀实球体的 转动惯量，转轴通过球心。
第二章 刚体的定轴转动
13
物理学
第五版
2.2 力矩 转动定律
例5：求长度为 L ，质量为 m 的均匀细棒AB的 转动惯量： (1)对于通过棒的一端且与棒垂直的轴； (2)对于通过棒的中点与棒垂直的轴。
第二章 刚体的定轴转动
14
物理学
第五版
2.2 力矩 转动定律 用来描述力对刚体的转 动作用。
M Fr sin Fd
一 力矩 (torque)
z
M
F
d
F 对转轴z 的力矩 M rF
: 力臂
r
O
*
d
P
F
i
F
i
Fi 0 ,
Mi 0
F
F
Fi 0 ,
2 2 2
dm
：质量元
r dV
dV
V
：体积元
第二章 刚体的定轴转动
10
物理学
第五版
2.2 力矩 转动定律
说明
刚体的转动惯量与以下三个因素有关: 1.与刚体的体密度 有关。 2.与刚体的几何形状(及体密度 的分布)有关。 3.与转轴的位置有关。
第二章 刚体的定轴转动
11
物理学
第五版
2.2 力矩 转动定律
第五版
2.2 力矩 转动定律
例8 一根长 l ,质量为 m 的均匀直棒，其一端 有一固定的光滑水平轴，因而可以在竖直平面内转 动。最初棒静步在水平位置，求它由此下摆 角时 的角加速度和角速度，这时棒受轴的力的大小、方 向各如何？
第二章 刚体的定轴转动
20