第三章运输问题(补充习题答案)网络计划技术之重要概念——时间参数
第三章 运输问题 运筹学 课件

B1
B2
B3
B4
产量
6 4 2 1
5
3
4
3
4 7
1
5 3
4 6
A3 销量 2
7
3
4
6
3
5
4
8
3 13
x23检验数为 7-3+4-5=3
销地 产地 A1
A2
B1
B2
B3
B4
产量
6 4 2 1
5
3
4
3
4 7
1
5 3
4 6
A3 销量 2
7
3
4
6
3
5
4
8
3 13
x31检验数为 7-4+4-5=1
销地 产地 A1
销地 产地 A1
A2
B1
B2
B3
B4
产量
6
5 3
3 1
4
4
4
2 1
4 6
3
4 3
7
3
5
6
A3
销量 2
7
5
4
8
3 13
σ11=-3, σ12=-2,σ23=-4, σ31=-1,σ33=1, σ34=-1
销地 产地 A1
A2
B1
B2
B3
B4
产量
6
5 0
3 4
4
4
4
2 4
4 6
3
4 3
7
0
5
6
A3
销量 2
2、位势法 当运输问题变量的格数较多时,用闭 回路法计算检验数比较麻烦,而位势法比 较简便。 对于运输问题 minf=CX AX=b X≥0 设B为其一个可行基,则xij的检验数为 σ ij=CBB-1Pij-Cij
第13讲:第三章第三节:网络计划时间参数的计算(三)(2013年新版)

6.确定关键工作和关键线路在网络计划中,总时差最小的工作为关键工作。
当网络计划的计划工期等于计算工期时,总时差为零的工作就是关键工作。
找出关键工作之后,将这些关键工作首尾相连,便构成从起点节点到终点节点的通路,位于该通路上各项工作的持续时间总和最大,这条通路就是关键线路。
在关键线路上可能有虚工作存在。
【例题1】在某工程双代号网络计划中,工作N的最早开始时间和最迟开始时间分别为第20天和第25天,其持续时间为9天。
该工作有两项紧后工作,它们的最早开始时间分别为第32天和第34天,则工作N的总时差和自由时差分别为( )天。
A.3和0B.3和2C.5和0D.5和3答案:D解析:总时差=最迟开始时间-最早开始时间=25-20=5天自由时差={紧后工作最早开始时间-本工作最早完成时间} 的最小值= min{[32-(20+9)],[34-(20+9)]}=3天二时标注法:在上述计算过程中,是将每项工作的六个时间参数均标注在图中,故称为六时标注法。
为使网络计划的图面更加简洁,在双代号网络计划中,除各项工作的持续时间以外,通常只需标注两个最基本的时间参数——各项工作的最早开始时间和最迟开始时间即可,而工作的其他四个时间参数均可根据工作的最早开始时间、最迟开始时间及持续时间导出。
这种方法称为二时标注法。
【例题2】某工程双代号网络计划如下图所示,图中已标出每项工作的最早开始时间和最迟开始时间,该计划表明( )。
A.关键线路有2条B.工作1-3的总时差等于1C.工作4-7的自由时差等于2D.工作2-6的总时差与自由时差相等E.工作3-6的总时差与自由时差不等答案:A、B、D解析:A对,关键线路:1-2-3-5-6-7,1-2-4-6-7。
B对,总时差=最迟开始-最早开始;1-0=1C错,工作4-7最早完成时间为11+8=19;计划工期=计算工期=11+9=20;自由时差=计划工期-最早完成时间=20-19=1。
D对,工作2-6的总时差=7-5=2;自由时差=紧后工作最早开始-本工作最早完成=11-(5+4)=2,相等。
网络计划时间参数的计算(总时差、自由时差)

双代号按⼯作计算法 按节点计算法 双代号时标络计划 单代号 单代号搭接计划 总时差 等于该⼯作LFi-j—EFi-J,或LSi-j—ESi-J TFi-j=LFi-j-EFi-j =LTj-(ETi+Di-j) =LTj-ETi-Di-j以关键节点为完成节点的⼯作,其总时差和⾃由时差必然相等。
当两个关键节点间有多项⼯作,且⼯作间的⾮关键节点⽆其他内向箭线和外向箭线时,则两个关键节点间各项⼯作的总时差均相等。
在这些⼯作中,除以关键节点为完成节点的⼯作⾃由时差等于总时差外,其余⼯作的⾃由时差均为零。
(4)当两个关键节点间有多项⼯作,且⼯作间的⾮关键节点有外向箭线⽽⽆其他内向箭线时,则两个关键节点间各项⼯作的总时差不⼀定相等,因为有外向箭线的⼯作在计算总时差时,要考虑两个或两个以上的紧后⼯作的时间参数。
在这些⼯作中,除以关键节点为完成节点的⼯作⾃由时差等于总时差外,其余⼯作的⾃由时差均为零。
在计算⼯期等于计划⼯期的前提下,关键线路上⼯作的总时差和⾃由时差全部为零。
从终点节点开始,逆着箭线⽅向依次进⾏。
(1)以终点节点为完成节点的⼯作,其总时差应等于计划⼯期与本⼯作最早完成时间之差,即:TFi-n=Tp-EFi-n式中 TFi-n——以络计划终点节点n为完成节点的⼯作的总时差;EFi-n——以络计划终点节点n为完成节点的⼯作的最早完成时间。
(2)其他⼯作的总时差等于其紧后⼯作的总时差加本⼯作与该紧后⼯作之间的时间间隔所得之和的最⼩值,即:TFi-n=min{TFj-k+LAGi-j,j-k} 从终点节点开始,逆箭线⽅向按节点编号从⼤到⼩顺序依次进⾏。
(1)络计划终点节点n所代表的⼯作的总时差等于计划⼯期与计算⼯期之差。
当计划⼯期等于计算⼯期时,该⼯作的总时差为零。
(2)其他⼯作的总时差应等于本⼯作与其各紧后⼯作之间的时间间隔加该紧后⼯作的总时差所得之和的最⼩值。
TFn=Tp-TcTFi=min{LAGi,j+TFj}但在计算出总时差后,需要根据公式LFi=EFi+TFi判别该⼯作的最迟完成时间是否超出计划⼯期。
第三章 网络计划技术第四节 双代号时标网络计划综合练习与答案

第三章网络计划技术第四节双代号时标网络计划综合练习与答案一、单选题1、某工程双代号时标网络计划如下图所示,其中工作B的总时差和自由时差()。
A.均为1周B.分别为3周和1周C.均为3周D.分别为4周和3周【参考答案】:B【试题解析】:双代号时标网络中的工作总时差确定方法为:①以终点节点为完成节点的工作,其总时差应等于计划工期与本工作最早完成时间之差;②其他工作的总时差等于其紧后工作的总时差加本工作与该紧后工作之间的时间间隔所得之和的最小值。
据此计算,工作J的总时差为2周,工作H的总时差为0周,工作E与工作J的时间间隔为1周,工作E与工作H的时间间隔为2周,所以工作E的总时差为:min{0+2,2+1}=2(周),工作B的总时差为:1+2=3(周)。
B工作的自由时差为该工作箭线中波形线的水平投影长度,即为1周。
2、某工程双代号时标网络计划如下图所示,其中工作A的总时差为()天。
A.1B.2C.3D.4【参考答案】:A【试题解析】:其他工作的总时差等于其紧后工作的总时差加本工作与该紧后工作之间的时间间隔所得之和的最小值。
3、某工程双代号时标网络计划如下图所示,其中工作D的总时差和自由时差()。
A.均为2周B.分别为2周和3周C.均为3周D.分别为3周和2周【参考答案】:D【试题解析】:根据波形线的含义和TF i-j=min(LAG i-j,j—k+TF j—k),由于工作D箭线上有2周波形线,且紧后是实箭线,所以工作D与其紧后工作的时间间隔为2周,自由时差也是2周;又由于工作H的总时差和自由时差均为1周,所以TF i-j=2+1=3(周)。
4、不属于时标网络计划的坐标体系是()。
A.计算坐标体系B.工作日坐标体系C.日历坐标体系D.三维坐标体系【参考答案】:D【试题解析】:时标网络计划的坐标体系包括计算坐标体系、工作日坐标体系和日历坐标体系3种。
5、时标网络计划中,当某工作之后只紧接虚工作时,则该工作的自由时差为()。
网络计划时间参数的计算

网络计划时间参数的计算二、双代号网络计划时间参数的计算双代号网络计划的时间参数既可以按工作计算,也可以按节点计算.(一)按工作计算法所谓按工作计算法,就是以网络计划中的工作为对象,直接计算各项工作的时间参数。
这些时间参数包括:工作的最早开始时间和最早完成时间、工作的最迟开始时间和最迟完成时间、工作的总时差和自由时差。
此外,还应计算网络计划的计算工期。
为了简化计算,网络计划时间参数中的开始时间和完成时间都应以时间单位的终了时刻为标准。
如第3天开始即是指第3天终了(下班)时刻开始,实际上是第4天上班时刻才开始;第5天完成即是指第5天终了(下班)时刻完成。
下面是按工作计算法计算时间参数的过程。
1.计算工作的最早开始时间和最早完成时间工作最早开始时间和最早完成时间的计算应从网络计划的起点节点开始,顺着箭线方向依次进行。
其计算步骤如下:(1)以网络计划起点节点为开始节点的工作,当未规定其最早开始时间时,其最早开始时间为零。
(2)工作的最早完成时间可利用公式(3—3)进行计算:EFi-J=ESi-j+Di—j 公式(3—3)(3)其他工作的最早开始时间应等于其紧前工作最早完成时间的最大值。
(4)网络计划的计算工期应等于以网络计划终点节点为完成节点的工作的最早完成时间的最大值。
2.确定网络计划的计划工期网络计划的计划工期应按公式(3—1)或公式(3—2)确定。
①当已规定了要求工期时,计划工期Tp不应超过要求工期Tr,即:Tp≤Tr,(3—1)②当未规定要求工期时,可令计划工期Tp等于计算工期Tc,即:Tp=Tc (3—2)3.计算工作的最迟完成时间和最迟开始时间工作最迟完成时间和最迟开始时间的计算应从网络计划的终点节点开始,逆着箭线方向依次进行。
其计算步骤如下:(1)以网络计划终点节点为完成节点的工作,其最迟完成时间等于网络计划的计划工期Tp。
LFi—n=Tp (3-6)(2)工作的最迟开始时间可利用公式(3—7)进行计算:LSi-j=LFi-j-Di-j (3-7)(3)其他工作的最迟完成时间应等于其紧后工作最迟开始时间的最小值。
第11讲进度第三章第三节网络计划时间参数的计算(二)
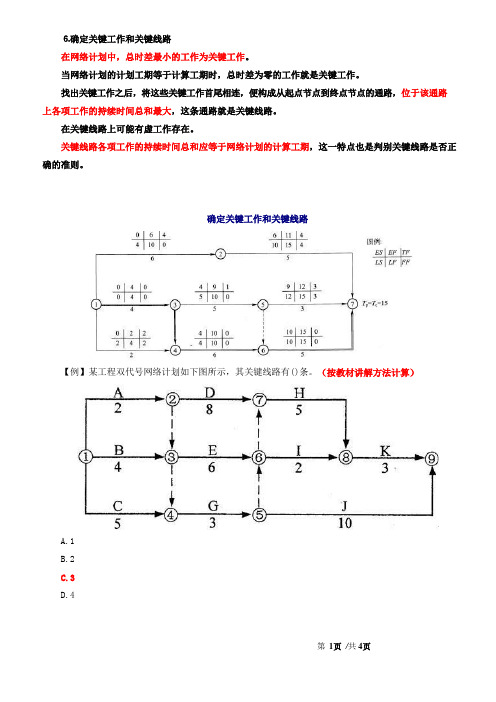
⒍确定关键工作和关键线路在网络计划中,总时差最小的工作为关键工作。
当网络计划的计划工期等于计算工期时,总时差为零的工作就是关键工作。
找出关键工作之后,将这些关键工作首尾相连,便构成从起点节点到终点节点的通路,位于该通路上各项工作的持续时间总和最大,这条通路就是关键线路。
在关键线路上可能有虚工作存在。
关键线路各项工作的持续时间总和应等于网络计划的计算工期,这一特点也是判别关键线路是否正确的准则。
确定关键工作和关键线路【例】某工程双代号网络计划如下图所示,其关键线路有()条。
(按教材讲解方法计算)A.1B.2C.3D.4【答案】C自行归纳的简单计算方法:适用于双代号网络计划、单代号网络计划、单代号搭接网络计划;双代号时标网络计划、二时标注法、节点计算法单独给出自行归纳的简单计算方法。
⒈计算最早时间,简单标注方式如下:双代号网络计划单代号网络计划⒉工期、自由时差⒊倒查关键线路,关键工作⒋总时差,有三种判定方式:⑴关键工作总时差为 0⑵以终点节点为完成节点的工作,总时差等于计划工期与本工作最早完成时间之差。
其他工作的总时差等于本工作与其各紧后工作之间的时间间隔加该紧后工作的总时差所得之和的最小值。
⑶从本工作,走最远的路,到终点节点,所富裕的机动时间。
⒌最迟时间【例】某工程双代号网络计划如下图所示,其中工作I 的最早开始时间是()。
A.7B.12C.14D.16【答案】D【例】某工程双代号网络计划如下图所示,关键线路有()条。
A.1B.2C.3D.4【答案】C【例】某工程双代号网络计划如下图所示,其中关键线路有()A.①→②→④→⑤→⑦B.①→②→③→④→⑤→⑥→⑦C.①→③→④→⑤→⑥→⑦D.①→③→④→⑤→⑦E.①→②→③→④→⑥→⑦【答案】BE【例】某工程双代号网络计划如下图所示,图中工作F 的最早完成时间和最迟完成时间分别是第() 周。
A.10 和 11B.9 和 11C.10 和 13D.9 和 13 【答案】A。
第三章网络计划技术
第三章网络计划技术本章考试大纲1.了解:网络计划费用优化和资源优化。
2.熟悉:双代号、单代号网络图的绘图规则和绘制方法;网络计划时间的参数的计算方法;工程费用与工期的关系;单代号搭接网络计划时间参数的计算方法。
3.掌握:网络计划时间参数;关键线路和关键工作的确定方法;双代号时标网络计划的绘制与应用;网络计划工期优化的方法;单代号搭接网络计划中的搭接关系。
本章知识框架体系1.给出网络图,指出图中错误(改错题)2.给出网络图,找出关键线路或关键工作(计算题)3.关于关键线路的判定方法(文字题)4.时标网络图中判定施工机械闲置问题(总时差应用问题)5.工期优化、费用优化的原则(文字题)一、普通双代号网络计划(一)基本组成(二)逻辑关系(三)绘制规则及绘制方法【例3-1】已知各工作之间的逻辑关系如表3—2所示,则可按下述步骤绘制其双代号网络图。
工作逻辑关系表表3-22.按前述原则(2)中的情况①绘制工作箭线C,如图3-13(b)所示。
3.按前述原则(1)绘制工作箭线D后,将工作箭线C和D的箭头节点合并,以保证网络图只有一个终点节点。
当确认给定的逻辑关系表达正确后,再进行节点编号。
表3-2给定逻辑关系所对应的双代号网络图如图3-13(c)所示。
图3-13 例3—1绘图过程【例3-2】已知各工作之间的逻辑关系如表3-3所示,则可按下述步骤绘制其双代号网络图。
工作逻辑关系表表3-32.按前述原则(2)中的情况③绘制工作箭线D,如图3-14(b)所示。
3.按前述原则(2)中的情况①绘制工作箭线E,如图3-l4(c)所示。
4.按前述原则(2)中的情况②绘制工作箭线G,当确认给定的逻辑关系表达正确后,再进行节点编号。
表3-3给定逻辑关系所对应的双代号网络图如图3-14(d)所示。
图3-14 例3-2绘图过程【例3-3】已知各工作之间的逻辑关系如表3-4所示.则可按下述步骤绘制其双代号网络图。
工作逻辑关系表表3-42.按前述原则(1)分别绘制工作箭线C和工作箭线E,如图3-15(b)所示。
《运筹学》第三章 运输问题
销量 3 6 5 6
A1 A2 A3
销量
B1 B1 B3 B4
2 1
6
5
3 3
3656
产量
7 4 9
精品课件
24
例:
B1 B2 B3 B4 产量
A1 (1) (2) 4 2 6 A2 3 (1) 2 (-1) 5 A3 (10) 6 (12) 3 9 销量 3 6 6 5
B1 B2 B3 B4 产量
(3) 在进行调运方案改进时,若沿闭合回路出现多个可作为 调出变量的数字格(即闭回路上的数字格最小值有多 个),此时,任选一个为调出变量,其余的填0,保证调 整后的调运方案中仍有m+n-1个数字格。
精品课件
23
例:
B1 B1 B3 B4 产量
A1 (0) (2) 5 2 7 A2 3 (2) (1) 1 4 A3 (9) 6 (12) 3 9
产 销 平 衡 表
单 位 运 价 表
精品课件
7
一般模 型表示 (ai=bj)
精品课件
8
三、模型的特点
1.变量数:mn个 2.约束方程数:m+n个
最大独立方程数:m+n-1 3.系数列向量结构:
0
Pij= 1 ——第i个分量
1 ——第m+j个分量 0
…… …
精品课件
9
······
······
x11 x12 ······ x1n x21 x22 ······ x2n ,············, xm1 xm2 ······ xmn
第3章 运输问题
精品课件
1
3.1 运输问题的典例和数学模型 3.2 运输问题的求解方法:表上作业 法 3.3 几类特殊的运输问题
第三章 网络计划技术第一节 基本概念综合练习与答案
第三章网络计划技术第一节基本概念综合练习与答案一、单选题1、在网络计划中,工作A是工作B的先行工作,则()。
A.工作B是工作A的后续工作,同时也是紧后工作B.工作B是工作A的后续工作,但不一定是紧后工作C.工作B是工作A平行工作D.工作B是工作A的紧后工作,同时也是后续工作【参考答案】:B【试题解析】:在网络计划中,如果工作A是工作B的先行工作,只能说明工作B是工作A的后续工作,但不一定是紧后工作。
2、在工程网络计划中,工作M和工作N之间由()决定的的先后顺序关系属于工艺关系。
A.劳动力调配需要B.原材料调配需要C.工艺过程D.组织安排需要【参考答案】:C【试题解析】:生产性工作之间由工艺过程决定的、非生产性工作之间由工作程序决定的先后顺序关系称为工艺关系;工作之间由于组织安排需要或资源(劳动力、原材料、施工机具等)调配需要而规定的先后顺序关系称为组织关系。
3、某工程双代号网络计划如下图所示,其中关键线路有()条。
A.1B.2C.3D.4【参考答案】:B【试题解析】:总持续时间最长的线路称为关键线路,本网络计划的关键线路为:①—②—⑥—⑦—⑨和①—②—③—④—⑤—⑦—⑨。
4、在某工程单代号网络计划中,下列说法不正确的是()。
A.关键线路只有一条B.在网络计划执行过程中,关键线路会发生转移C.关键工作的机动时间最小D.相邻关键工作之间的时间间隔为零【参考答案】:A【试题解析】:在关键线路法(CPM)中,线路上所有工作的持续时间总和称为该线路的总持续时间。
总持续时间最长的线路称为关键线路,关键线路的长度就是网络计划的总工期。
在网络计划中,关键线路可能不止一条。
5、双代号网络图中虚工作的特征是()。
A.不消耗时间,但消耗资源B.不消耗时间,也不消耗资源C.只消耗时间,不消耗资源D.既消耗时间,也消耗资源【参考答案】:B【试题解析】:在双代号网络图中,有时存在虚箭线,虚箭线不代表实际工作,称为虚工作。
虚工作既不消耗时间,也不消耗资源。
第三章-网络计划技术试题及答案
第三章网络计划技术试题及答案一、单项选择题1。
双代号网络计划中( B )表示前面工作的结束和后面工作的开始。
A 起始节点B 中间节点C终止节点 D虚拟节点2.网络图中游n条关键线路,那么这n条关键线路持续时间之和( A )。
A 相同B 不相同C有一条最长的 D以上都不对3.单代号网络计划的起点节点可( A )。
A 有一个虚拟B 有两个C有多个 D编号最大4.在时标网络计划中,“波折线”表示( C )。
A 工作持续时间B 虚工作C前后工作时间间隔 D总时差5.时标网络计划与一般网络计划相比,其优点是( D )。
A 能进行时间参数的计算B 能确定关键线路C能计算时差 D能增加网络的直观性6.( B )为零的工作肯定在关键线路上。
A 自由时差B 总时差C持续时间 D以上三者均7.在工程网络计划中,判别关键工作的条件是该工作( D )。
A 自由时差最小B 与其紧后工作之间的时间间隔为零C持续时间最长 D最早开始时间等于最迟开始时间8.当双代号网络计划的计算工期等于计划工期时,对关键工作的错误提法是( C )。
A 关键工作的自由时差为零B 相邻两项关键工作之间的时间间隔为零C关键工作的持续时间最长 D关键工作的最早开始时间与最迟开始时间相等9.网络计划工期优化的目的是为了缩短( B )。
A 计划工期B 计算工期C要求工期 D合同工期10。
某工程双代号网络计划的计划工期等于计算工期,且工作M的完成节点为关键节点,则该工作( B )A 为关键工作B 自由时差等于总时差C自由时差为零 D自由时差小于总时差二、填空题1。
双代号网络图的基本三要素为:_工作_、_节点_和_线路_.2。
在双代号网络图中,节点是表示_工作之间的逻辑关系__.3。
网络计划的优化有_工期优化、_费用优化_和_资源优化_三种.4. 在网络计划中工期一般有以下三种:_计算工期、要求工期和计划工期_。
5。
在双代号网络图中,虚工作既不消耗_资源_、也不消耗_时间__,只表示前后相邻工作间的逻辑关系.三、名词解释与简答1。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
下表是某一个产销平衡运输问题的产销平衡表和单位运价表,表中给出了各产地和各销地的
供应量和需求量,以及各产地至各销地的单位运价(单位:百元/吨)。
单位运价 销地
产地
B1 B2 B3 B4 产量(吨)
A1 5 13 5 12 70
A2 3 11 4 10 40
A3 9 6 12 7 90
销量(吨) 30 60 50 60 200 200
现要求:
1、给出最优调运方案。
2、若产地A2因故减少20吨的供应量,并且假设销地B2 需求量必须保证满足,而销地B1 、
B3 、B4 的需求量则相应地要受产地A2供应量减少的影响,其每缺少1吨损失分别为5,4,
3(单位:百元)。试写出此时该运输问题的产销平衡表和单位运价表(不必求解)。
3、在第1小题的基础上,因为科技的原因,产地A2在原来的基础上增加供应量20吨,如
果若产地A2因仓库容量限制,60吨货物必须全部运出去;产地A1 、A3因为保管货物需要
增加单位保管费分别为8和7(单位:百元/吨)。试写出此时该运输问题的产销平衡表和单
位运价表(不必求解)。
(参考答案)解:1、用最小元素法确定初始方案如下左表;并用位势法求检验数如下右表
产销平衡表 单位运价表 / 检验数
销地
产地
B1 B2 B3 B4 产量 B1 B2 B3 B4 U i
A1 40 30 70 5/1 13/2 (5) (12) 0
A2 30 10 40 (3) 11/1 (4) 10 /-1 -1
A3 60 30 90 9/10 (6) 12/12 (7) -5
销量 30 60 50 60 200 200 4 11 5 12 V j
因为δ24= -1 < 0 ,用闭回路法调整,过(2,4)作闭回路,θ=10,(r,s)=(2,3)
调整后的调运方案如下左表;用位势法求检验数如下右表。
产销平衡表 单位运价表 / 检验数
销地
产地
B1 B2 B3 B4 产量 B1 B2 B3 B4 U i
A1 50 20 70 5/0 13/2 (5) (12) 0
A2 30 10 40 (3) 11/2 4/1 (10) -2
A3 60 30 90 9/9 (6) 12/12 (7) -5
销量 30 60 50 60 200 200 5 11 5 12 V j
因为诸δij≥0,已经得到最优调运方案如上左表。
即A1 ——B3 50
——B4 20
A2 ——B1 30
——B4 10
A2 ——B2 60
最小总运费Z*=1250
(与书例子相比:总产量扩大10倍;单位运价同时增加2。
所以最优方案:调运量扩大10倍,总运费:85×10+20×10×2=1250)
2、(因为产地A2因故减少20吨的供应量,此时该运输问题是产销不平衡的运输问题:
需求量大于供应量)。增加虚设产地A4,产量20吨。因为已经假设销地B2 需求量必须保证
满足,所以产地A4到B2无运输路线,而销地B1 、B3 、B4 的需求量则相应地要受产地A2
供应量减少的影响,其每缺少1吨损失分别为5,4,3(单位:百元)。则可将其视为单位运
价。所以此时该运输问题的产销平衡表和单位运价表如下(不求解):
产销平衡表 单位运价表
销地
产地
B1 B2 B3 B4 产量 B1 B2 B3 B4
A1 70 5 13 5 10
A2 20 3 11 4 10
A3 90 9 6 12 7
A4 20 5 M 4 3
销量 30 60 50 60
200
200
3、(同上考虑:产地A2在原来的基础上增加供应量20吨,此时该运输问题是产销不平衡
的运输问题:供应量大于需求量)。增加虚设销地(仓库)B5,销量20吨。
如果若产地A2因仓库容量限制,20吨货物必须全部运出去,这意味着产地A2到B5无运输
路线。
产地A1 、A3因为保管货物需要增加单位保管费分别为8和7(单位:百元/吨),则可将其
视为单位运价。
所以此时该运输问题的产销平衡表和单位运价表如下(不求解):
产销平衡表 单位运价表
销地
产地
B1 B2 B3 B4 B5 产量 B1 B2 B3 B4 B5
A1 70 5 13 5 10 8
A2 60 3 11 4 10 M
A3 90 9 6 12 7 7
销量 30 60 50 60 20
220
220
A
工序时间(工时)——完成某道工序所需时间,用 t(i,j)表示——教材用D(i,j) 表示
B
事项的最早时间TE (i)——指从该事项开始的各道工序最早可能开始工作的时间。
(1)计算方向:始点→终点(从左至右)
(2)令TE(1)=0
(3)确定递推关系
例B1:
例B2:
C
事项的最迟时间TL(j)——指以该事项结束的所有工序最迟必须完成时间。
(1)计算方向:终点→始点(从右至左)
(2)TL(n)=完工期
(3)确定递推关系
例C1:
例C2:
ijk
TE(i)=5
a
6
b
7
TE(j)=?
1165),()()(jitiTjT
EE
i
1
i2i3jk
TE(i1)=5
TE(i2)=6
TE(i3)=4
a
3
b
4
c
5
d
6
TE(j)=?
10544635max ),()(max)(
jitiTjT
EE
ijk
TL(k)=15
a
6
b
7
TL(j)=?
8715),()()(kjtkTjT
LL
k
1
ik3j
k
2
TL(k1)=15
TL(k2)=19
TL(k3)=14
a
3
b
4
c
5
d
6
TL(j)=?
10314619515min ),()(min)(
kjtkTjT
LL
