机械工程控制基础复习
机械工程控制基础考试题完整版

机械控制工程基础一、填空题1. 线性控制系统最重要的特性是可以应用叠加原理,而非线性控制系统则不能。
2.反馈控制系统是根据输入量和反馈量的偏差进行调节的控制系统。
3。
根据自动控制系统是否设有反馈环节来分类,控制系统可分为__开环_控制系统、_闭环__控制系统。
4. 根据系统输入量变化的规律,控制系统可分为恒值控制系统、随动控制系统和程序控制系统.5. 如果在系统中只有离散信号而没有连续信号,则称此系统为离散(数字)控制系统,其输入、输出关系常用差分方程来描述。
6. 根据控制系统元件的特性,控制系统可分为__线性__ 控制系统、非线性_控制系统。
7。
线性控制系统其输出量与输入量间的关系可以用线性微分方程来描述.8。
对于一个自动控制系统的性能要求可以概括为三个方面:稳定性、快速性和准确性。
9。
在控制工程基础课程中描述系统的数学模型有微分方程、传递函数等。
10. 传递函数的定义是对于线性定常系统,在零初始条件下,系统输出量的拉氏变换与输入量的拉氏变换之比。
11. 传递函数的组成与输入、输出信号无关,仅仅决定于系统本身的结构和参数 ,并且只适于零初始条件下的线性定常系统。
12. 瞬态响应是系统受到外加作用激励后,从初始状态到最终稳定状态的响应过程.13。
脉冲信号可以用来反映系统的抗冲击能力。
14. 单位斜坡函数t的拉氏变换为 .15。
单位阶跃信号的拉氏变换是1/s 。
= .16.在单位斜坡输入信号作用下,0型系统的稳态误差ess17. I型系统在单位阶跃输入下,稳态误差为 0 ,在单位加速度输入下,稳态误差为∞。
18. 一阶系统的单位阶跃响应的表达是。
19.决定二阶系统动态性能的两个重要参数是阻尼系数ξ和无阻尼固有频率ωn。
20。
二阶系统的典型传递函数是。
21.二阶衰减振荡系统的阻尼比ξ的范围为.22。
二阶系统的阻尼比ξ为 0 时,响应曲线为等幅振荡。
23。
系统输出量的实际值与输出量的期望值之间的偏差称为误差。
机械工程控制基础考试题及答案

填空题每空1分,共20分1. 线性控制系统最重要的特性是可以应用___叠加__原理,而非线性控制系统则不能;2.反馈控制系统是根据输入量和__反馈量__的偏差进行调节的控制系统;3.在单位斜坡输入信号作用下,0型系统的稳态误差e ss =∞___; 4.当且仅当闭环控制系统特征方程的所有根的实部都是__负数__时,系统是稳定的;5.方框图中环节的基本连接方式有串联连接、并联连接和__反馈 _连接;6.线性定常系统的传递函数,是在_ 初始条件为零___时,系统输出信号的拉氏变换与输入信号的拉氏变换的比; 7.函数te -at的拉氏变换为2)(1a s +;8.线性定常系统在正弦信号输入时,稳态输出与输入的相位移随频率而变化的函数关系称为__相频特性__;9.积分环节的对数幅频特性曲线是一条直线,直线的斜率为__-20__dB /dec;10.二阶系统的阻尼比ξ为 _ 0_ 时,响应曲线为等幅振荡; 11.在单位斜坡输入信号作用下,Ⅱ型系统的稳态误差e ss =__0__; 12.0型系统对数幅频特性低频段渐近线的斜率为___0___dB/dec,高度为20lgKp;13.单位斜坡函数t 的拉氏变换为21s ;14. 根据系统输入量变化的规律,控制系统可分为__恒值__控制系统、___随动___ 控制系统和程序控制系统;15. 对于一个自动控制系统的性能要求可以概括为三个方面:稳定性、__快速性__和准确性;16. 系统的传递函数完全由系统的结构和参数决定,与__输入量、扰动量__的形式无关;17. 决定二阶系统动态性能的两个重要参数是阻尼系数ξ和_无阻尼自然振荡频率w n ;18. 设系统的频率特性Gj ω=R ω+jI ω,则幅频特性|Gj ω|=)()(22w I w R +;19. 分析稳态误差时,将系统分为0型系统、I 型系统、II 型系统…,这是按开环传递函数的__积分__环节数来分类的; 20. 线性系统稳定的充分必要条件是它的特征方程式的所有根均在复平面的___左___部分;21.ω从0变化到+∞时,惯性环节的频率特性极坐标图在____第四____象限,形状为___半___圆;22. 用频域法分析控制系统时,最常用的典型输入信号是_正弦函数_;23.二阶衰减振荡系统的阻尼比ξ的范围为10<<ξ; 24.Gs=1+Ts K的环节称为___惯性__环节;25.系统输出量的实际值与_输出量的希望值__之间的偏差称为误差;26.线性控制系统其输出量与输入量间的关系可以用___线性微分__方程来描述;27. 稳定性 、 快速性 和准确性是对自动控制系统性能的基本要求;28.二阶系统的典型传递函数是2222nn nw s w s w ++ξ;29.设系统的频率特性为)(jI )j (R )j (G ω+ω=ω,则)(R ω称为 实频特性 ;30. 根据控制系统元件的特性,控制系统可分为__线性__ 控制系统、 非线性_控制系统;31. 对于一个自动控制系统的性能要求可以概括为三个方面:稳定性、快速性和_准确性__;32.二阶振荡环节的谐振频率ωr 与阻尼系数ξ的关系为ωr =ωn122-ξ;33.根据自动控制系统是否设有反馈环节来分类,控制系统可分为__开环_控制系统、_闭环__控制系统;34.用频率法研究控制系统时,采用的图示法分为极坐标图示法和__对数坐标_图示法;35.二阶系统的阻尼系数ξ=时,为最佳阻尼系数;这时系统的平稳性与快速性都较理想;1. 传递函数的定义是对于线性定常系统,在初始条件为零的条件下,系统输出量的拉氏变换与输入量的拉氏变换之比;2. 瞬态响应是系统受到外加作用激励后,从初始状态到最终或稳定状态的响应过程;3. 判别系统稳定性的出发点是系统特征方程的根必须为负实根或负实部的复数根,即系统的特征根必须全部在复平面的左半平面是系统稳定的充要条件;4. I 型系统G s Ks s ()()=+2在单位阶跃输入下,稳态误差为 0 ,在单位加速度输入下,稳态误差为 ∞ ;5. 频率响应是系统对正弦输入稳态响应,频率特性包括幅频和相频两种特性;6. 如果系统受扰动后偏离了原工作状态,扰动消失后,系统能自动恢复到原来的工作状态,这样的系统是渐进稳定的系统;7. 传递函数的组成与输入、输出信号无关,仅仅决定于系统本身的结构和参数,并且只适于零初始条件下的线性定常系统;8. 系统的稳态误差与输入信号的形式及系统的结构和参数或系统的开环传递函数有关;9. 如果在系统中只有离散信号而没有连续信号,则称此系统为离散数字控制系统,其输入、输出关系常用差分方程来描述; 10. 反馈控制系统开环对数幅频特性三频段的划分是以ωc 截止频率附近的区段为中频段,该段着重反映系统阶跃响应的稳定性和快速性;而低频段主要表明系统的稳态性能;11. 对于一个自动控制系统的性能要求可以概括为三个方面:稳定性、快速 性和精确或准确性; 单项选择题:1.当系统的输入和输出已知时,求系统结构与参数的问题,称为 A.最优控制 B.系统辩识 C.系统校正 D.自适应控制2.反馈控制系统是指系统中有A.反馈回路B.惯性环节C.积分环节 调节器3. =1s a+,a 为常数;A. Le -atB. Le atC. Le-t -aD. Le-t+at 2e 2t= A. 123()s - B. 1a s a ()+C.223()s + D. 23s5.若Fs=421s +,则Lim f t t →0()= A. 4 B. 2 C. 0 D. ∞ 6.已知ft=e at,a 为实数,则L f t dt t()0⎰=A. as a- B. 1a s a ()+ C.1s s a ()- D. 1a s a ()-t=3202t t ≥<⎧⎨⎩,则Lft=A. 3sB. 12s e s -C. 32s e s -D. 32se s 8.某系统的微分方程为52000 () ()()()x t x t x t x t i +⋅=,它是A.线性系统B.线性定常系统C.非线性系统D.非线性时变系统 9.某环节的传递函数为Gs=e-2s,它是A.比例环节B.延时环节C.惯性环节D.微分环节 10.图示系统的传递函数为A. 11RCs + B. RCs RCs +1C. RCs+1D. RCs RCs+1 11.二阶系统的传递函数为Gs=341002s s ++,其无阻尼固有频率ωn 是A. 10B. 5C.D. 25 12.一阶系统K Ts 1+的单位脉冲响应曲线在t=0处的斜率为 A. K T B. KT C. -K T2D. K T 213.某系统的传递函数Gs=KT s +1,则其单位阶跃响应函数为A. 1T e Kt T -/B. K Te t T -/ C. K1-e -t/TD. 1-e-Kt/T14.图示系统称为 型系统;A. 0B. ⅠC. ⅡD. Ⅲ15.延时环节Gs=e-τs的相频特性∠Gjω等于A. τωB. –τωC.90°D.180°16.对数幅频特性的渐近线如图所示,它对应的传递函数Gs为A. 1+TsB. 11+TsD. 1+Ts2C. 1Ts17.图示对应的环节为A. TsB. 11+TsC. 1+TsD. 1Ts18.设系统的特征方程为Ds=s3+14s2+40s+40τ=0,则此系统稳定的τ值范围为A. τ>0B. 0<τ<14C. τ>14D. τ<019.典型二阶振荡环节的峰值时间与 有关;A.增益B.误差带C.增益和阻尼比D.阻尼比和无阻尼固有频率20.若系统的Bode 图在ω=5处出现转折如图所示,这说明系统中有环节; A. 5s+1 B. 5s+12C. +1D.10212(.)s +21.某系统的传递函数为Gs=()()()()s s s s +-+-72413,其零、极点是 A.零点s=-,s=3;极点s=-7,s=2 B.零点s=7,s=-2;极点s=,s=3C.零点s=-7,s=2;极点s=-1,s=3D.零点s=-7,s=2;极点s=-,s=3 22.一系统的开环传递函数为32235()()()s s s s +++,则系统的开环增益和型次依次为A. 0.4,ⅠB. ,ⅡC. 3,ⅠD. 3,Ⅱ23.已知系统的传递函数Gs=K Te sts 1+-,其幅频特性|Gj ω|应为A. K T e 1+-ωτB. KT e 1+-ωτωC.K T e 2221+-ωτω D.K T 122+ω24.二阶系统的阻尼比ζ,等于A.系统的粘性阻尼系数B.临界阻尼系数与系统粘性阻尼系数之比C.系统粘性阻尼系数与临界阻尼系数之比D.系统粘性阻尼系数的倒数25.设ωc 为幅值穿越交界频率,φωc 为开环频率特性幅值为1时的相位角,则相位裕度为A. 180°-φωcB. φωcC. 180°+φωcD. 90°+φωc 26.单位反馈控制系统的开环传递函数为Gs=45s s ()+,则系统在rt=2t 输入作用下,其稳态误差为A. 104B. 54C. 45D. 0 27.二阶系统的传递函数为Gs=1222s s n n++ζωω,在0<ζ<22时,其无阻尼固有频率ωn 与谐振频率ωr 的关系为A. ωn <ωrB. ωn =ωrC. ωn >ωrD. 两者无关28.串联相位滞后校正通常用于A.提高系统的快速性B.提高系统的稳态精度C.减少系统的阻尼D.减少系统的固有频率29.下列串联校正装置的传递函数中,能在频率ωc =4处提供最大相位超前角的是A. 411s s ++B. s s ++141C. 01106251..s s ++ D. 06251011..s s ++30.从某系统的Bode 图上,已知其剪切频率ωc ≈40,则下列串联校正装置的传递函数中能在基本保持原系统稳定性及频带宽的前提下,通过适当调整增益使稳态误差减至最小的是A. 000410041..s s ++B. 04141.s s ++C. 41101s s ++ D. 41041s s ++. 单项选择题每小题1分,共30分二、填空题每小题2分,共10分1.系统的稳态误差与系统开环传递函数的增益、_______和_______有关;2.一个单位反馈系统的前向传递函数为K s s s3254++,则该闭环系统的特征方程为_______开环增益为_______;3.二阶系统在阶跃信号作用下,其调整时间t s 与阻尼比、_______和_______有关;4.极坐标图Nyquist 图与对数坐标图Bode 图之间对应关系为:极坐标图上的单位圆对应于Bode 图上的_______;极坐标图上的负实轴对应于Bode 图上的_______;5.系统传递函数只与_______有关,与______无关; 填空题每小题2分,共10分1.型次 输入信号+5s 2+4s+K=0,K 43.误差带 无阻尼固有频率分贝线 -180°线5.本身参数和结构 输入1. 线性系统和非线性系统的根本区别在于CA .线性系统有外加输入,非线性系统无外加输入;B .线性系统无外加输入,非线性系统有外加输入;C .线性系统满足迭加原理,非线性系统不满足迭加原理;D .线性系统不满足迭加原理,非线性系统满足迭加原理;2.令线性定常系统传递函数的分母多项式为零,则可得到系统的 BA .代数方程B .特征方程C .差分方程D .状态方程3. 时域分析法研究自动控制系统时最常用的典型输入信号是DA .脉冲函数B .斜坡函数C .抛物线函数D .阶跃函数 4.设控制系统的开环传递函数为Gs=)2s )(1s (s 10++,该系统为BA .0型系统B .I 型系统C .II 型系统D .III 型系统5.二阶振荡环节的相频特性)(ωθ,当∞→ω时,其相位移)(∞θ为 BA .-270°B .-180°C .-90°D .0°6. 根据输入量变化的规律分类,控制系统可分为 AA.恒值控制系统、随动控制系统和程序控制系统B.反馈控制系统、前馈控制系统前馈—反馈复合控制系统C.最优控制系统和模糊控制系统D.连续控制系统和离散控制系统7.采用负反馈连接时,如前向通道的传递函数为Gs,反馈通道的传递函数为Hs,则其等效传递函数为 CA .)s (G 1)s (G + B .)s (H )s (G 11+C .)s (H )s (G 1)s (G +D .)s (H )s (G 1)s (G -8. 一阶系统Gs=1+Ts K 的时间常数T 越大,则系统的输出响应达到稳态值的时间AA .越长B .越短C .不变D .不定9.拉氏变换将时间函数变换成DA .正弦函数B .单位阶跃函数C .单位脉冲函数D .复变函数10.线性定常系统的传递函数,是在零初始条件下DA .系统输出信号与输入信号之比B .系统输入信号与输出信号之比C .系统输入信号的拉氏变换与输出信号的拉氏变换之比D .系统输出信号的拉氏变换与输入信号的拉氏变换之比 11.若某系统的传递函数为Gs=1Ts K+,则其频率特性的实部R ω是A A .22T 1Kω+ B .-22T1Kω+C .T1K ω+D .-T1K ω+12. 微分环节的频率特性相位移θω= AA. 90°B. -90°C. 0°D. -180°13. 积分环节的频率特性相位移θω= BA. 90°B. -90°C. 0°D. -180°14.传递函数反映了系统的动态性能,它与下列哪项因素有关 CA.输入信号B.初始条件C.系统的结构参数D.输入信号和初始条件15. 系统特征方程式的所有根均在根平面的左半部分是系统稳定的 CA.充分条件B.必要条件C.充分必要条件D.以上都不是16. 有一线性系统,其输入分别为u 1t 和u 2t 时,输出分别为y 1t 和y 2t;当输入为a 1u 1t+a 2u 2t 时a 1,a 2为常数,输出应为 BA. a 1y 1t+y 2tB. a 1y 1t+a 2y 2tC. a 1y 1t-a 2y 2tD. y 1t+a 2y 2t17. I 型系统开环对数幅频渐近特性的低频段斜率为 BA. -40dB/decB. -20dB/decC. 0dB/decD. +20dB/dec 18. 设系统的传递函数为Gs=255252++s s ,则系统的阻尼比为CA.25B. 5C. 21D. 119.正弦函数sintω的拉氏变换是BA.ω+s 1B.22s ω+ωC.22s s ω+ D.22s 1ω+20.二阶系统当0<ζ<1时,如果增加ζ,则输出响应的最大超调量%σ将 BA.增加B.减小C.不变D.不定 21.主导极点的特点是DA.距离实轴很远B.距离实轴很近C.距离虚轴很远D.距离虚轴很近 22.余弦函数costω的拉氏变换是CA.ω+s 1B.22s ω+ωC.22s s ω+ D.22s 1ω+23.设积分环节的传递函数为Gs=s1,则其频率特性幅值M ω=CA.ωKB.2K ω C.ω1 D.21ω24. 比例环节的频率特性相位移θω= C° ° ° °25. 奈奎斯特稳定性判据是利用系统的 C 来判据闭环系统稳定性的一个判别准则;A.开环幅值频率特性B.开环相角频率特性C.开环幅相频率特性D.闭环幅相频率特性 26. 系统的传递函数CA.与输入信号有关B.与输出信号有关C.完全由系统的结构和参数决定D.既由系统的结构和参数决定,也与输入信号有关 27. 一阶系统的阶跃响应,DA.当时间常数T 较大时有振荡B.当时间常数T 较小时有振荡C.有振荡D.无振荡28. 二阶振荡环节的对数频率特性相位移θω在 D 之间;°和90° °和-90° °和180° °和-180° 29. 某二阶系统阻尼比为,则系统阶跃响应为 CA. 发散振荡B. 单调衰减C. 衰减振荡D. 等幅振荡 二.设有一个系统如图1所示,k 1=1000N/m, k 2=2000N/m, D=10N/m/s,当系统受到输入信号t t x i sin 5)(= 的作用时,试求系统的稳态输出)(t x o ;15分 解:()()()1015.001.021211+=++=s sk k Ds k k Ds k s X s X i o 然后通过频率特性求出 ()() 14.89sin 025.0+=t t x o三.一个未知传递函数的被控系统,构成单位反馈闭环;经过测试,得知闭环系统的单位阶跃响应如图2所示;10分问:1 系统的开环低频增益K 是多少 5分2 如果用主导极点的概念用低阶系统近似该系统,试写出其近似闭环传递函数;5分 解:100718K K =+,07K =2 ()()8025.07+=s s X s X i o四.已知开环最小相位系统的对数幅频特性如图3所示;10分 1. 写出开环传递函数Gs 的表达式;5分 2. 概略绘制系统的Nyquist 图;5分 1.)100s )(01.0s (s 100)1100s )(101.0s (s K)s (G ++=++=2.五.已知系统结构如图4所示, 试求:15分 1. 绘制系统的信号流图;5分 2. 求传递函数)()(s X s X i o 及)()(s N s X o ;10分六.系统如图5所示,)(1)(t t r =为单位阶跃函数,试求:10分 1. 系统的阻尼比ξ和无阻尼自然频率ωn ;5分2. 动态性能指标:超调量M p 和调节时间%)5(=∆s t ;5分1.)2s (s )2S (S 4n 2nξω+ω=+ 2.%5.16%100eM 21p =⨯=ξ-ξπ-七.如图6所示系统,试确定使系统稳定且在单位斜坡输入下e ss ≤225.时,K的数值;10分由劳斯判据:第一列系数大于零,则系统稳定得54K 0<< 又有:K9e ss =≤可得:K ≥4 ∴ 4≤K <54八.已知单位反馈系统的闭环传递函数32)(+=Φs s ,试求系统的相位裕量γ;10分解:系统的开环传递函数为1s 2)s (W 1)s (W )s (G +=-=112|)j (G |2cc =+ω=ω,解得3c =ω三、设系统的闭环传递函数为Gcs=ωξωωnn ns s 2222++,试求最大超调量σ%=%、峰值时间tp=秒时的闭环传递函数的参数ξ和ωn 的值;解:∵%100%21⨯=--ξξπσe=%∴ξ= ∵t p =πωξn 12-=∴ωn =πξt p 13140210622-=-=...s四、设一系统的闭环传递函数为G c s=ωξωωnn nss 2222++,试求最大超调量σ%=5%、调整时间t s =2秒△=时的闭环传递函数的参数ξ和ωn的值;解:∵%100%21⨯=--ξξπσe =5%∴ξ= ∵t s =ξωn 3=2∴ωn = rad/s五、设单位负反馈系统的开环传递函数为 )6(25)(+=s s s G k 求1系统的阻尼比ζ和无阻尼自然频率ωn ;2系统的峰值时间t p 、超调量σ%、 调整时间t S △=;解:系统闭环传递函数2562525)6(25)6(251)6(25)(2++=++=+++=s s s s s s s s s G B 与标准形式对比,可知 62=n w ξ ,252=n w故 5=n w , 6.0=ξ 又 46.015122=-⨯=-=ξnd w w六、某系统如下图所示,试求其无阻尼自然频率ωn ,阻尼比ζ,超调量σ%,峰值时间p t ,调整时间s t △=;解: 对于上图所示系统,首先应求出其传递函数,化成标准形式,然后可用公式求出各项特征量及瞬态响应指标;与标准形式对比,可知 08.02=n w ξ ,04.02=n w 七、已知单位负反馈系统的开环传递函数如下: 求:1 试确定系统的型次v 和开环增益K ; 2试求输入为t t r 31)(+=时,系统的稳态误差; 解:1将传递函数化成标准形式 可见,v =1,这是一个I 型系统 开环增益K =50;2讨论输入信号,t t r 31)(+=,即A =1,B =3 根据表3—4,误差06.006.00503111=+=+∞+=++=V p ss K B K A e 八、 已知单位负反馈系统的开环传递函数如下: 求:1 试确定系统的型次v 和开环增益K ; 2试求输入为2425)(t t t r ++=时,系统的稳态误差; 解:1将传递函数化成标准形式可见,v =2,这是一个II 型系统 开环增益K =100; 2讨论输入信号,2425)(t t t r ++=,即A =5,B =2, C=4根据表3—4,误差04.004.00010042151=++=+∞+∞+=+++=a V p ssK C K B K A e 九、 已知单位负反馈系统的开环传递函数如下: 求:1 试确定系统的型次v 和开环增益K ; 2试求输入为2252)(t t t r ++=时,系统的稳态误差; 解:1该传递函数已经为标准形式 可见,v =0,这是一个0型系统 开环增益K =20;2讨论输入信号,2252)(t t t r ++=,即A =2,B =5,C=2 根据表3—4,误差∞=∞+∞+=+++=+++=212020520121Ka C K B K A e V p ss十、设系统特征方程为s 4+2s 3+3s 2+4s+5=0试用劳斯-赫尔维茨稳定判据判别该系统的稳定性;解:用劳斯-赫尔维茨稳定判据判别,a 4=1,a 3=2,a 2=3,a 1=4,a 0=5均大于零,且有所以,此系统是不稳定的; 十一、设系统特征方程为试用劳斯-赫尔维茨稳定判据判别该系统的稳定性;解:用劳斯-赫尔维茨稳定判据判别,a 4=1,a 3=6,a 2=12,a 1=10,a 0=3均大于零,且有 所以,此系统是稳定的; 十二、设系统特征方程为试用劳斯-赫尔维茨稳定判据判别该系统的稳定性;解:用劳斯-赫尔维茨稳定判据判别,a 4=1,a 3=5,a 2=2,a 1=4,a 0=3均大于零, 且有所以,此系统是不稳定的; 十三、设系统特征方程为试用劳斯-赫尔维茨稳定判据判别该系统的稳定性;解:1用劳斯-赫尔维茨稳定判据判别,a 3=2,a 2=4,a 1=6,a 0=1均大于零,且有所以,此系统是稳定的;十四、设系统开环传递函数如下,试绘制系统的对数幅频特性曲线;解:该系统开环增益K =30;有一个积分环节,即v =1;低频渐近线通过1,20lg30这点,斜率为-20dB/dec ;有一个惯性环节,对应转折频率为5002.011==w ,斜率增加-20dB/dec;系统对数幅频特性曲线如下所示;20lg30十五、设系统开环传递函数如下,试绘制系统的对数幅频特性曲线;解:该系统开环增益K =100;有一个积分环节,即v =1;低频渐近线通过1,20lg100这点,即通过1,40这点斜率为-20dB/dec ; 有两个惯性环节,对应转折频率为101.011==w ,10001.012==w ,斜率分别增加-20dB/dec系统对数幅频特性曲线如下所示;十六、设系统开环传递函数如下,试绘制系统的对数幅频特性曲线;解:该系统开环增益K =1;无积分、微分环节,即v =0,低频渐近线通过1,20lg1这点,即通过1,0这点斜率为0dB/dec ;有一个一阶微分环节,对应转折频率为101.011==w ,斜率增加20dB/dec;系统对数幅频特性曲线如下所示;dec十七、如下图所示,将方框图化简,并求出其传递函数;解:十八、如下图所示,将方框图化简,并求出其传递函数; 解:十九、如下图所示,将方框图化简,并求出其传递函数;L /dB20 dB / dec 10rad/s一一H 1G 1 G 2H 2 RSCS一 一H 1/G 2 G 1 G 2H 2RS CS一 H 1/G 2 G 1 RS CS G 2 1+ G 2H 2 一H 1/G 2RSCS G 1G 2 1+ G 2H 2 RSCSG 1G 2 1+ G 2H 2+G 1H 1解:三、简答题共16分1.4分已知系统的传递函数为2432s s ++,求系统的脉冲响应表达式;2.4分已知单位反馈系统的开环传递函数为K s s ()71+,试问该系统为几型系统系统的单位阶跃响应稳态值为多少3.4分已知二阶欠阻尼系统的单位阶跃响应如下,如果将阻尼比ζ增大但不超过1,请用文字和图形定性说明其单位阶跃响应的变化;4.4分已知各系统的零点o 、极点x 分布分别如图所示,请问各个系统是否有非主导极点,若有请在图上标出; 四、计算题本大题共6小题,共44分一 一 G 1G 3H 1 RSCSG 2H 1一 H 1 G 3 RSCSG 1G 2 1+ G 2H 1RSCSG 1G 2G 31+ G 2H 1+ G 1G 2H 1一一G 1G 3RSCSG 2H 11.7分用极坐标表示系统14212s s ++的频率特性要求在ω→∞、ω=0、ω=ωn 等点准确表示,其余定性画出;2.7分求如下系统Rs 对Cs 的传递函数,并在图上标出反馈通道、顺馈通道;3.6分已知系统的调节器为问是否可以称其为PID 调节器,请说明理由;4.8分求如图所示机械网络的传递函数,其中X 为输入位移,Y 为输出位移;5.10分已知单位反馈闭环系统的开环传递函数为40110011s s s (.)(.)++,请绘出频率特性对数坐标图Bode 图,并据图评价系统的稳定性、动态性能和静态性能要说明理由;6.6分请写出超前校正装置的传递函数,如果将它用于串联校正,可以改善系统什么性能 三、简答题共16分1.24311132s s s s ++=++-+ gt=e -t -e -3t ,t ≥0 2.Ⅰ型;稳态值等于13.上升时间变大;超调量减少;调节时间减小大体上;4.无非主导极点;非主导极点;非主导极点四、计算题共44分1.ω→∞点ω=0点ωn=点曲线大体对2.C sR s G G GG Gf() ()() =++13.6分G0s=T3+T4+T3T4s+1/sG 0s 由比例部分T 3+T 4、微分部分T 3T 4s 及积分部分1/s 相加而成 4.8分B ( )xy Ky --=0 Gs=Ts Ts +1,T=B/k 5.开环传递函数在复半平面无极点,据图相位裕度为正,幅值裕度分贝数为正,根据乃奎斯特判据,系统稳定;系统为Ⅰ型,具有良好的静态性能;相位裕度约为60度,具有良好的动态性能;s=K Ts Tsαα++≥111,可增加相位裕度,调整频带宽度;设系统的特征方程为DS =S 5+3S 4+4S 3+12S 2-5S-15 试用Routh 表判别系统的稳定性,并说明该系统具有正实部特征根的个数; 解:根据特征方程的系数,列Routh 表如下:S 5 1 4-5 0S 4 3 12 -15 0 S 3由第二行各元素得辅助方程2p=4,p=2FS= 3S 4+12S 2-15=0 取FS 对S 的导数,则得新方程12S3+24S=0得如下的Routh表S5 1 4 -5 0S4 3 12 -15 0S312 24 0 0S2 6 -15 0S154 0S0-15 符号改变一次,系统不稳定该系统具有正实部特征根个数为1;。
机械工程控制基础-----填空简答题知识点

1、反馈:输出信号被测量环节引回到输入端参与控制的作用。
2、开环控制系统与闭环控制系统的根本区别:有无反馈。
3、线性及非线性系统的定义及根本区别:当系统的数学模型能用线性微分方程描述时,该系统的称为线性系统。
非线性系统:一个系统,如果其输出不与其输入成正比,则它是非线性的。
根本区别:线性系统遵从叠加原理,而非线性系统不然。
4、传递函数的定义及特点:零初始条件下,系统输出量的拉斯变换与输入量的拉斯变换的比值。
用G〔s〕表示。
特点:1〕、传递函数是否有量纲取决于输入与输出的性质,同性质无量纲。
2〕、传递函数分母中S的阶数必n不小于分子中的S的阶数m,既n=>m ,因为系统具有惯性。
3〕、假设输入已给定,则系统的输出完全取决于其传递函数。
4〕、物理量性质不同的系统,环节和元件可以具有相同类型的传递函数。
5〕、传递函数的分母与分子分别反映系统本身与外界无关的固有特性和系统同外界的关系。
5、开环函数的定义:前向通道传递函数G〔s〕与反馈回路传递函数H(s)之积。
6、时间响应的定义和组成:系统在激励信号作用下,输出随时间的变化关系。
按振动来源分为:零状态响应和零输入响应。
按振动性质:自由响应和强迫响应。
7、瞬态性能指标以及反映系统什么特性:性能指标:上升时间tr、峰值时间tp、最大超调量Mp、调整时间ts、振荡次数N。
这些性能指标主要反映系统对输入的响应的快速性。
8、稳态误差的定义及计算公式:系统进入稳态后的误差。
稳态误差反映稳态响应偏离系统希望值的程度。
衡量控制精度的程度。
稳态误差不仅取决于系统自身结构参数,而且与输入信号有关。
系统误差:输入信号与反馈信号之差。
9、减少输入引起稳态误差的措施:增大干扰作用点之前的回路的放大倍数K1,以及增加这一段回路中积分环节的数目。
10、频率响应的概念:线性定常系统对谐波输入的稳态响应称为频率响应。
11、频率特性的组成:幅频特性和相频特性。
12、稳定性的概念:系统在扰动作用下,输出偏离原平衡状态,待扰动消除后,系统能回到原平衡状态〔无静差系统〕或到达新的平衡状态〔有静差系统〕。
2022年大连理工大学期末考试《机械工程控制基础》复习参考题

2、用极坐标图表示频率特性的优缺点是什么?
答:
(1)极坐标图表示频率特性的优点:
在一幅图上同时给出了系统在整个频率域的实频特性、虚频特性、幅频特性和相频特性。它比较简洁直观地表明了系统的频率特性。
(2)缺点:
不能明显地表示出系统传递函数中各个环节在系统中的作用,绘制较麻烦。
对数幅频特性曲线与横坐标轴相交处的频率称为幅值穿越频率。
15、函数框图
把元件或环节的传递函数写在框图单元内,并用表明信号传递方向的箭头将这些框图单元连接起来,主要用来说明环节特性、信号流向及变量关系,便于分析系统。
16、时变系统
描述系统微分方程的系数随时间变化的系统,称为时变系统。
17、时间响应
控制系统在典型输入信号的作用下,输出量随时间变化的函数关系称为系统的时间响应。
23、采样系统或离散系统
如果在系统中,计算机参与工作时,环节之间所传递的信息除了有连续信号外,还有离散信号,这样的系统称为采样系统或离散系统。
24、自动控制:在没有人直接参与的情况下,利用控制器使生产过程或被控制对象的某一物理量自动地按照预定的规律运行。
25、系统:由相互联系、相互作用的若干部分构成且具有一定运动规律的一个有机整体。
3、用波德图表示频率特性的优点是什么?
答:
(1)可将串联环节幅值的乘、除,化为幅值的加、减。因而简化了计算与作图过程。
(2)可用近似方法作图。先分段用直线作出对数幅频特性的渐近线,再用修正曲线对渐近线进行修正,就可得到较准确的对数幅频特性图。这给作图带来了很大方便。
(3)可分别作出各个环节的波德图,然后用叠加方法得出系统的波德图,并由此可以看出各个环节对系统总特性的影响。
机械工程控制基础知识总结
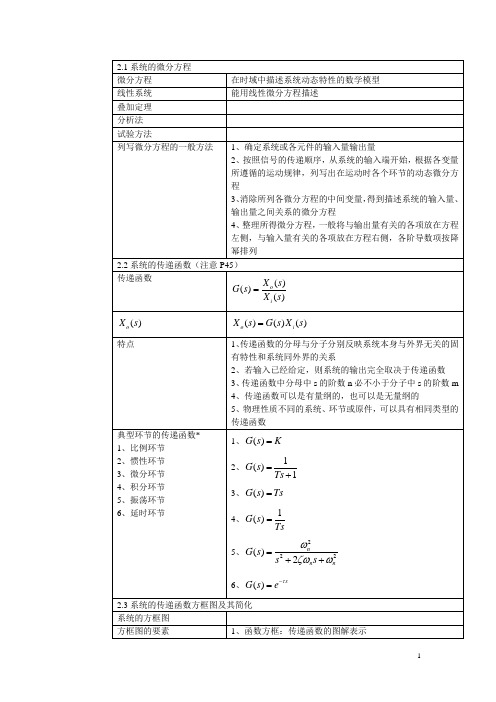
()o x ∞时所需的时间4nξω≈当增加系统的型别时,系统的准确性将提高。
当系统采用增加开环传递函数中积分环节的数0]或滞后0]的特性。
正负:正值:逆时针方向;负值:顺时针方向幅频特性()A ω和相频特性()ϕω的总称|()|G j e ω=是将()G s90对数幅频特性曲线:在整个频率范围内是一的直线。
当90的水平线。
ω=时,90对数幅频特性曲线:在整个频率范围内是一直线当90的水平线。
、将系统的传递函数准形式的环节的传递函数(即惯性、一阶微0,00a ;、三阶系统(3)n =稳定的充要条件:0,00a ,120a a 。
、在Routh 表中任意一行的第一个元为零,后各元均不为零或部分不为零:用一个很小的正ε来代替第一列等于零的元,然后计算表的其余各元;、当Routh 表的任意一行中的所有元均为零:用该行的上一行的元构成一个辅助多项式,并用180开始向上。
j-(1,0)180开始向下。
+∞时,在开环对数幅频特性曲线为正值的频率范围内,开环对数180线正穿越与负穿越次数之时,闭环系统稳定;否则不稳定。
g ω,则闭环系统稳定;g ω,则闭环系统不稳定;g ω=,则闭环系统临界稳定;为剪切频率0)时,相频特性180线的相位差值γ。
(ϕω+对于稳定系统,γ必在Bode 180线以上。
:对于稳定系统,自:第三象限。
180线以下。
:对于稳定系统,自:第二象限。
0)时,开环幅频的倒数。
()|H j K ω记0;:对于稳定系统,1。
右侧通过。
:对于稳定系统,K 必在0分贝线以0;:对于稳定系统,1。
左侧通过。
线以上;分贝线以下。
8086汇编指令速查手册一、数据传输指令它们在存贮器和寄存器、寄存器和输入输出端口之间传送数据.1. 通用数据传送指令.MOV 传送字或字节.MOVSX 先符号扩展,再传送.MOVZX 先零扩展,再传送.PUSH 把字压入堆栈.POP 把字弹出堆栈.PUSHA 把AX,CX,DX,BX,SP,BP,SI,DI依次压入堆栈.POPA 把DI,SI,BP,SP,BX,DX,CX,AX依次弹出堆栈.PUSHAD 把EAX,ECX,EDX,EBX,ESP,EBP,ESI,EDI依次压入堆栈.POPAD 把EDI,ESI,EBP,ESP,EBX,EDX,ECX,EAX依次弹出堆栈.BSWAP 交换32位寄存器里字节的顺序XCHG 交换字或字节.( 至少有一个操作数为寄存器,段寄存器不可作为操作数)CMPXCHG 比较并交换操作数.( 第二个操作数必须为累加器AL/AX/EAX )XADD 先交换再累加.( 结果在第一个操作数里 )XLAT 字节查表转换.── BX 指向一张 256 字节的表的起点, AL 为表的索引值(0-255,即0-FFH); 返回 AL 为查表结果. ( [BX+AL]->AL )2. 输入输出端口传送指令.IN I/O端口输入. ( 语法: IN 累加器, {端口号│DX} )OUT I/O端口输出. ( 语法: OUT {端口号│DX},累加器 ) 输入输出端口由立即方式指定时, 其范围是 0-255; 由寄存器 DX 指定时,其范围是 0-65535.3. 目的地址传送指令.LEA 装入有效地址.例: LEA DX,string ;把偏移地址存到DX.LDS 传送目标指针,把指针内容装入DS.例: LDS SI,string ;把段地址:偏移地址存到DS:SI.LES 传送目标指针,把指针内容装入ES.例: LES DI,string ;把段地址:偏移地址存到ES:DI.LFS 传送目标指针,把指针内容装入FS.例: LFS DI,string ;把段地址:偏移地址存到FS:DI.LGS 传送目标指针,把指针内容装入GS.例: LGS DI,string ;把段地址:偏移地址存到GS:DI.LSS 传送目标指针,把指针内容装入SS.例: LSS DI,string ;把段地址:偏移地址存到SS:DI.4. 标志传送指令.LAHF 标志寄存器传送,把标志装入AH.SAHF 标志寄存器传送,把AH内容装入标志寄存器.PUSHF 标志入栈.POPF 标志出栈.PUSHD 32位标志入栈.POPD 32位标志出栈.二、算术运算指令ADD 加法.ADC 带进位加法.INC 加 1.AAA 加法的ASCII码调整.DAA 加法的十进制调整.SUB 减法.SBB 带借位减法.DEC 减 1.NEC 求反(以 0 减之).CMP 比较.(两操作数作减法,仅修改标志位,不回送结果).AAS 减法的ASCII码调整.DAS 减法的十进制调整.MUL 无符号乘法.IMUL 整数乘法.以上两条,结果回送AH和AL(字节运算),或DX和AX(字运算), AAM 乘法的ASCII码调整.DIV 无符号除法.IDIV 整数除法.以上两条,结果回送:商回送AL,余数回送AH, (字节运算);或商回送AX,余数回送DX, (字运算).AAD 除法的ASCII码调整.CBW 字节转换为字. (把AL中字节的符号扩展到AH中去)CWD 字转换为双字. (把AX中的字的符号扩展到DX中去)CWDE 字转换为双字. (把AX中的字符号扩展到EAX中去)CDQ 双字扩展. (把EAX中的字的符号扩展到EDX中去) 三、逻辑运算指令AND 与运算.OR 或运算.XOR 异或运算.NOT 取反.TEST 测试.(两操作数作与运算,仅修改标志位,不回送结果). SHL 逻辑左移.SAL 算术左移.(=SHL)SHR 逻辑右移.SAR 算术右移.(=SHR)ROL 循环左移.ROR 循环右移.RCL 通过进位的循环左移.RCR 通过进位的循环右移.以上八种移位指令,其移位次数可达255次.移位一次时, 可直接用操作码. 如 SHL AX,1.移位>1次时, 则由寄存器CL给出移位次数.如 MOV CL,04SHL AX,CL四、串指令DS:SI 源串段寄存器 :源串变址.ES:DI 目标串段寄存器:目标串变址.CX 重复次数计数器.AL/AX 扫描值.D标志 0表示重复操作中SI和DI应自动增量; 1表示应自动减量.Z标志用来控制扫描或比较操作的结束.MOVS 串传送.( MOVSB 传送字符. MOVSW 传送字. MOVSD 传送双字. )CMPS 串比较.( CMPSB 比较字符. CMPSW 比较字. )SCAS 串扫描.把AL或AX的内容与目标串作比较,比较结果反映在标志位.LODS 装入串.把源串中的元素(字或字节)逐一装入AL或AX中.( LODSB 传送字符. LODSW 传送字. LODSD 传送双字. )STOS 保存串.是LODS的逆过程.REP 当CX/ECX<>0时重复.REPE/REPZ 当ZF=1或比较结果相等,且CX/ECX<>0时重复.REPNE/REPNZ 当ZF=0或比较结果不相等,且CX/ECX<>0时重复. REPC 当CF=1且CX/ECX<>0时重复.REPNC 当CF=0且CX/ECX<>0时重复.五、程序转移指令1>无条件转移指令 (长转移)JMP 无条件转移指令CALL 过程调用RET/RETF过程返回.2>条件转移指令 (短转移,-128到+127的距离内)( 当且仅当(SF XOR OF)=1时,OP1<OP2 )JA/JNBE 不小于或不等于时转移.JAE/JNB 大于或等于转移.JB/JNAE 小于转移.JBE/JNA 小于或等于转移.以上四条,测试无符号整数运算的结果(标志C和Z).JG/JNLE 大于转移.JGE/JNL 大于或等于转移.JL/JNGE 小于转移.JLE/JNG 小于或等于转移.以上四条,测试带符号整数运算的结果(标志S,O和Z).JE/JZ 等于转移.JNE/JNZ 不等于时转移.JC 有进位时转移.JNC 无进位时转移.JNO 不溢出时转移.JNP/JPO 奇偶性为奇数时转移.JNS 符号位为 "0" 时转移.JO 溢出转移.JP/JPE 奇偶性为偶数时转移.JS 符号位为 "1" 时转移.3>循环控制指令(短转移)LOOP CX不为零时循环.LOOPE/LOOPZ CX不为零且标志Z=1时循环.LOOPNE/LOOPNZ CX不为零且标志Z=0时循环.JCXZ CX为零时转移.JECXZ ECX为零时转移.4>中断指令INT 中断指令INTO 溢出中断IRET 中断返回5>处理器控制指令HLT 处理器暂停, 直到出现中断或复位信号才继续.WAIT 当芯片引线TEST为高电平时使CPU进入等待状态. ESC 转换到外处理器.LOCK 封锁总线.NOP 空操作.STC 置进位标志位.CLC 清进位标志位.CMC 进位标志取反.STD 置方向标志位.CLD 清方向标志位.STI 置中断允许位.CLI 清中断允许位.六、伪指令DW 定义字(2字节).PROC 定义过程.ENDP 过程结束.SEGMENT 定义段.ASSUME 建立段寄存器寻址. ENDS 段结束.END 程序结束.。
3机械控制工程基础复习题及参考答案

一、单项选择题:1. 某二阶系统阻尼比为0,则系统阶跃响应为A. 发散振荡B. 单调衰减C. 衰减振荡D. 等幅振荡2. 一阶系统G(s)=1+Ts K的时间常数T 越小,则系统的输出响应达到稳态值的时间A .越长B .越短C .不变D .不定3. 传递函数反映了系统的动态性能,它与下列哪项因素有关?A.输入信号B.初始条件C.系统的结构参数D.输入信号和初始条件4.惯性环节的相频特性)(ωθ,当∞→ω时,其相位移)(∞θ为A .-270°B .-180°C .-90°D .0° 5.设积分环节的传递函数为G(s)=s1,则其频率特性幅值M(ω)= A.ωKB. 2K ωC. ω1D. 21ω6. 有一线性系统,其输入分别为u 1(t)和u 2(t)时,输出分别为y 1(t)和y 2(t)。
当输入为a 1u 1(t)+a 2u 2(t)时(a 1,a 2为常数),输出应为A. a 1y 1(t)+y 2(t)B. a 1y 1(t)+a 2y 2(t)C. a 1y 1(t)-a 2y 2(t)D. y 1(t)+a 2y 2(t)7.拉氏变换将时间函数变换成A .正弦函数B .单位阶跃函数C .单位脉冲函数D .复变函数8.二阶系统当0<ζ<1时,如果减小ζ,则输出响应的最大超调量%σ将A.增加B.减小C.不变D.不定9.线性定常系统的传递函数,是在零初始条件下A .系统输出信号与输入信号之比B .系统输入信号与输出信号之比C .系统输入信号的拉氏变换与输出信号的拉氏变换之比D .系统输出信号的拉氏变换与输入信号的拉氏变换之比10.余弦函数cos t ω的拉氏变换是A.ω+s 1B.22s ω+ω C.22s s ω+ D. 22s 1ω+ 11. 微分环节的频率特性相位移θ(ω)=A. 90°B. -90°C. 0°D. -180°12. II 型系统开环对数幅频渐近特性的低频段斜率为A. -40(dB/dec)B. -20(dB/dec)C. 0(dB/dec)D. +20(dB/dec)13.令线性定常系统传递函数的分母多项式为零,则可得到系统的A .代数方程B .特征方程C .差分方程D .状态方程14. 主导极点的特点是A.距离实轴很远B.距离实轴很近C.距离虚轴很远D.距离虚轴很近15.采用负反馈连接时,如前向通道的传递函数为G(s),反馈通道的传递函数为H(s),则其等效传递函数为A .)s (G 1)s (G + B .)s (H )s (G 11+C .)s (H )s (G 1)s (G + D .)s (H )s (G 1)s (G -二、填空题:1.线性定常系统在正弦信号输入时,稳态输出与输入的相位移随频率而变化的函数关系称为__ __。
机械工程控制基础__复习提纲-淮阴工学院
第 1页,总1页 机械工程控制基础 复习提纲一、问答题。
1.自动控制系统的工作的首要条件是什么? 2.对自动控制系统的基本要求是什么?试举例来说明。
3.自动控制系统主要是由哪几大部分组成的?各组成部分都有些什么功能? 4.闭环控制系统是怎样实现控制作用的?试举例来说明。
5.什么是传递函数?用传递函数作为数学模型来描述系统有些什么特点? 6.什么是闭环系统的开环传递函数和闭环传递函数? 7.自动控制系统在阶跃信号作用下的瞬态响应的基本特征取决于系统闭环零点还是闭环极点的分布? 8.一阶系统的动态性能指标如何计算?闭环极点距离s 平面原点的远近对响应速度影响有何不同? 9. 二阶系统阻尼比取值不同,则系统阶跃响应分别是什么形式?10. 控制系统闭环稳定条件是什么?掌握劳斯判据应用。
11. 系统稳态误差如何计算?12. 控制系统通常是由哪些典型环节构成的?13. 什么是控制系统的频率特性?14. 控制系统的频率特性都有哪些表示方法?二、由方框图求系统的传递函数。
教材54页图2-46 难度三、第三章习题3.7 、3.9劳斯判据判别系统的稳定性。
若如下图的系统, 能够使系统稳定的K 的取值是多少?四、二阶系统分析和性能指标计算。
掌握控制系统的参数阻尼比ξ,固有频率ωn ,计算系统在单位阶跃函数输入()t r =1时的动态性能指标s t ,00σ。
第三章习题3.12 、3.13、3.15五 画出奈奎斯特图,并用奈奎斯特稳定判据判断系统是否稳定。
第四章例题4.7、4.8 、4.10、六 、绘制系统开环的近似对数幅频特性曲线,并求取系统的相角裕度,判别系统的稳定性。
第四章习题4.9-(3)、(4)和4.10-(2)、(3)1.现有电阻1R 和2R ,电感L 和电容C ,连结成四臂交流电桥,试画出能满足电桥平衡的正确接桥方法,并写出该电桥的平衡条件。
(设激励为i u ,输出为o u )。
答:正确的接桥方法如图所示:(3’)电桥的平衡条件是:121L R R jwL jwC C =⋅=。
机械控制工程复习与考试题(含答案)
机械控制⼯程复习与考试题(含答案)机械控制⼯程复习⼀、填空题1.线性控制系统最重要的特性是可以应⽤叠加原理,⽽⾮线性控制系统则不能。
2.反馈控制系统是根据输⼊量和反馈量的偏差进⾏调节的控制系统。
3.根据⾃动控制系统是否设有反馈环节来分类,控制系统可分为__开环_控制系统、_闭环__控制系统。
4.根据系统输⼊量变化的规律,控制系统可分为恒值控制系统、随动控制系统和程序控制系统。
5.如果在系统中只有离散信号⽽没有连续信号,则称此系统为离散(数字)控制系统,其输⼊、输出关系常⽤差分⽅程来描述。
6.根据控制系统元件的特性,控制系统可分为__线性__控制系统、⾮线性_控制系统。
7.线性控制系统其输出量与输⼊量间的关系可以⽤线性微分⽅程来描述。
8.对于⼀个⾃动控制系统的性能要求可以概括为三个⽅⾯:稳定性、快速性和准确性。
9.在控制⼯程基础课程中描述系统的数学模型有微分⽅程、传递函数等。
10.传递函数的定义是对于线性定常系统,在零初始条件下,系统输出量的拉⽒变换与输⼊量的拉⽒变换之⽐。
11.传递函数的组成与输⼊、输出信号⽆关,仅仅决定于系统本⾝的结构和参数,并且只适于零初始条件下的线性定常系统。
12.瞬态响应是系统受到外加作⽤激励后,从初始状态到最终稳定状态的响应过程。
13.脉冲信号可以⽤来反映系统的抗冲击能⼒。
14.单位斜坡函数t的拉⽒变换为1/s215.单位阶跃信号的拉⽒变换是1/s。
16.在单位斜坡输⼊信号作⽤下,0型系统的稳态误差ess=19.决定⼆阶系统动态性能的两个重要参数是阻尼系数ξ和⽆阻尼固有频率ωn。
22.⼆阶系统的阻尼⽐ξ为0时,响应曲线为等幅振荡。
23.系统输出量的实际值与输出量的期望值之间的偏差称为误差。
24.系统的稳态误差与输⼊信号的形式及系统的结构和参数或系统的开环传递函数有关。
25.分析稳态误差时,将系统分为0型系统、I型系统、II型系统…,这是按开环传递函数的积分环节数来分类的。
《机械工程控制基础》课后答案
目录第一章自动控制系统的基本原理第一节控制系统的工作原理和基本要求第二节控制系统的基本类型第三节典型控制信号第四节控制理论的内容和方法第二章控制系统的数学模型第一节机械系统的数学模型第二节液压系统的数学模型第三节电气系统的数学模型第四节线性控制系统的卷积关系式第三章拉氏变换第一节傅氏变换第二节拉普拉斯变换第三节拉普拉斯变换的基本定理第四节拉普拉斯逆变换第四章传递函数第一节传递函数的概念与性质第二节线性控制系统的典型环节第三节系统框图及其运算第四节多变量系统的传递函数第五章时间响应分析第一节概述第二节单位脉冲输入的时间响应第三节单位阶跃输入的时间响应第四节高阶系统时间响应第六章频率响应分析第一节谐和输入系统的定态响应第二节频率特性极坐标图第三节频率特性的对数坐标图第四节由频率特性的实验曲线求系统传递函数第七章控制系统的稳定性第一节稳定性概念第二节劳斯判据第三节乃奎斯特判据第四节对数坐标图的稳定性判据第八章控制系统的偏差第一节控制系统的偏差概念第二节输入引起的定态偏差第三节输入引起的动态偏差第九章控制系统的设计和校正第一节综述第二节希望对数幅频特性曲线的绘制第三节校正方法与校正环节第四节控制系统的增益调整第五节控制系统的串联校正第六节控制系统的局部反馈校正第七节控制系统的顺馈校正第一章自动控制系统的基本原理定义:在没有人的直接参与下,利用控制器使控制对象的某一物理量准确地按照预期的规律运行。
第一节控制系统的工作原理和基本要求一、控制系统举例与结构方框图例1.一个人工控制的恒温箱,希望的炉水温度为100C°,利用表示函数功能的方块、信号线,画出结构方块图。
图1人通过眼睛观察温度计来获得炉内实际温度,通过大脑分析、比较,利用手和锹上煤炭助燃。
比较图2例2.图示为液面高度控制系统原理图。
试画出控制系统方块图和相应的人工操纵的液面控制系统方块图。
解:浮子作为液面高度的反馈物,自动控制器通过比较实际的液面高度与希望的液面高度,调解气动阀门的开合度,对误差进行修正,可保持液面高度稳定。
机械工程控制基础复习参考资料2240讲解
2009、4机械工程控制基础复习参考资料(2240)1.单位脉冲响应函数为t t h 189)(=,则系统的传递函数为 【 A 】 A .2189sB .s189C .2189sD .s1892.关于叠加原理,下列叙述正确的是 【 B 】 A .适合于非线性定常系统 B .适合于线性定常系统C .适合于所有系统D .适合于非线性系统3.对于一阶系统s e s s G 812.31)(-+=,则该系统可看成下述环节由串联而成 【 A 】A .惯性环节、延时环节B .比例环节、惯性环节、延时环节C .惯性环节、超前环节D .比例环节、惯性环节、超前环节4.若二阶阻尼系统的无阻尼固有频率为n ω,则有阻尼固有频率d ω为 【 C 】A .等于n ωB .大于n ωC .小于n ωD .与n ω无关5.下列叙述正确的是 【 C 】 A .时域响应只能分析系统的瞬态特性B .频率响应只能分析系统的稳态特性C .时域响应和频率响应都能揭示系统的动态特性D .频率响应无量纲6.关于线性系统的正确描述是 【 C 】 A .都可以用传递函数表示 B .只能用传递函数表示C .可以用不同模型描述D .都是稳定的7.已知环节的波德图如下图,则该环节为 【 B 】A .比例环节B .微分环节C .积分环节D .惯性环节8.对于二阶系统而言,阻尼比越大,系统的 【 B 】A .相对稳定性越差B .相对稳定性越好C .稳态误差越小D .稳态误差越大9.属于系统时域的数学模型是 【 C 】A .频率特性B .传递函数C .微分方程D .频响函数10.一线性系统的特征方程为)()(5)(3)(223t x t t x t x t x⋅=++ 则该系统是 【 C 】 A .线性定常系统B .线性系统C .非线性系统D .非线性时变系统11.典型环节的传递函数为:)1/(1)(s s G +=,该环节为: 【 A 】 A .惯性环节B .积分环节C .微分环节D .比例环节12.系统的微分方程为F t x t x t x4)(3)(2)(=++ ,系统的极点为 【 A 】 A .21j s ±-= B .j s ±=2C .01=s j s ±=223D .全不是13.关于线性系统响应时间的描述正确的是: 【 C 】 A .时间响应为系统输出的稳态值B .由单位阶跃响应和单位脉冲响应组成C .由强迫响应和自由响应组成D .与系统初始状态无关 14.已知系统传递函数44)(2++=s s s G ,则阻尼比为: 【 A 】 A .0.25B .0.5C .1D .215.二阶振荡系统的阻尼比为7.00<<ζ,则关于无阻尼固有频率n ω,有阻尼固有频率d ω,振荡频率r ω的关系 【 C 】 A .r d n ωωω<< B .d r n ωωω<< C .n d r ωωω<< D .r n d ωωω<< 16.单位反馈系统的传递函数)9)(4)(2(1)(--++=s s s s s G ,则系统 【 B 】A .稳定B .不稳定C .临界稳定D .无法判断17.单位反馈闭环系统的误差为零时,则输出 【 C 】 A .为0B .停止改变C .等于希望值D .无法判断18.一阶微分环节G(s)=1+Ts ,当频率ω=1时,则相频特性∠G(jω)为 【 A 】 A. 45° B. -45° C. 90° D. -90°19.对于稳定系统,幅值裕量Kg 为 【 A 】A .大于0dBB .小于0 dBC .小于等于0 dBD .等于120.系统传递函数 【 B 】A .与外界无关B .反应了系统、输入、输出的关系C .完全反应系统的动态特性D .与系统初始状态有关21.线性系统稳定与否取决于 【 A 】A .系统的结构和参数B .系统的输入C .系统的干扰D .系统的初始状态22.减小一阶系统的时间常数,则系统 【 C 】A .系统准确定变差B .系统响应变慢C .系统响应快D .稳定性变差23.欠阻尼二阶系统而言,瞬态响应的超调量表征了系统的 【 D 】A .系统的可靠性B .系统的准确性C .系统响应快速性D .系统相对稳定性24.二阶系统的指标中,与阻尼比有关的是 【 B 】A .固有频率B .超调量C .上升时间D .调整时间25.对最小相位系统,系统如果稳定,则相位裕量和幅值裕量 【 A 】A .二者都大于零B .二者都小于零C .相位裕量大于零,幅值裕量小于零D .相位裕量小于零,幅值裕量大于零 26.系统的单位脉冲响应函数为te t w 2.03)(-=,则系统的传递函数为 【 C 】A .32.0+s B .2.06.0+sC .2.03+sD .36.0+s 27.典型环节的传递函数为:11)(+=Ts s G ,该环节为: 【 D 】 A .积分环节B .比例环节C .微分环节D .惯性环节28.对于一阶系统523)(+=s s G ,则时间常数和增益为 【 C 】A .2 3B .2 1.5C .0.4 0.6D .2.5 1.529.系统正常工作的必要条件是 【 B 】 A .系统具有快速响应特点 B .系统必须是稳定的C .系统必须准确反应输出D .系统必须是线性的30.在零初始条件下,系统传递函数是 【 C 】 A .输入与输出的拉氏变换之比 B .输出与偏差的拉氏变换之比C .输出与输入的拉氏变换之比D .输入与偏差的拉氏变换之比31.对于一阶系统44)(2++=s s s G ,允许误差为2%,则系统调整时间为 【 B 】 A .8B .2C .7D .3.532.下列哪个系统是最小相位系统 【 B 】 A .s01.011-B .s01.011+C .101.01-sD .)1.01(1s s -33.系统稳定的充要条件是 【 B 】 A .传递函数的零点具有负实部B .传递函数的极点具有负实部C .传递函数的零点和极点具有负实部D .传递函数的零点和极点具有正实部34.在乃奎斯特图上,当相位裕量和幅值裕量大于零时,系统是 【 C 】A .临界稳定B .不稳定C .稳定的D .无法判断35.机械工程控制论是研究该领域中系统的动力学问题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
机械工程控制基础复习 第一章 绪论 1.控制理论在工程技术领域中体现为工程控制论,在机械工程领域则体现为机械工程控制论。 2.工程控制论实质上是研究工程技术中广义系统的动力学问题。具体地说,它研究的是工程技术中的广义系统在一定的外界条件(即输入或激励,包括外加控制与外加干扰)作用下,从系统的一定的初始状态出发,所经历的由其内部的固有特性(即由系统的结构与参数所决定的特性)所决定的整个动态历程;研究这一系统及其输入、输出三者之间的动态关系。 3.
y(t)称为系统的输出,显然,y(t)(它就是微分方程的解)是由系统的初始状态、系统的固有特性、系统与输入之间的关系以及输入所决定的。 4.工程控制论(包括机械工程控制论)的内容大致可归纳为如下五个方面: ⑴当系统已定、输入(或激励)已知时,求出系统的输出(或响应),并通过输出来研究系统本身的有关问题,此即系统分析问题; ⑵当系统已定,确定输入,且所确定的输入应使得输出尽可能符合给定的最佳要求,此即最优控制问题; ⑶当输入已知时,确定系统,且所确定的系统应使得输出尽可能符合给定的最佳要求,此即最优设计问题; ⑷当输出已知时,确定系统,以识别输入或输入中的有关信息,此即滤波与预测问题; ⑸当输入与输出均已知时,求出系统的结构与参数,即建立系统的数学模型,此即系统识别或系统辨识问题。 5.反馈:系统的输出不断地、直接或间接地、全部或部分地返回,并作用于系统。负反馈:输出(被控量)偏离设定值(目标值)时,反馈作用使输出偏离程度减小,并力图达到设定值。反馈的作用:消除偏离 正反馈: 输出偏离初始值(或稳定值)时,反馈作用使输出偏离程度加剧。反馈的作用:加剧偏离。 6.开环控制:只有输入量对输出量产生控制作用,输出量不参与对系统的控制。特点是 结构简单、维护容易、成本低、不存在稳定性问题;输入控制输出;输出不参与控制; 系统没有抗干扰能力。适用范围:输入量已知、控制精度要求不高、扰动作用不大。 开环系统比闭环系统稳定性好!控制论的中心思想(或曰方法论)就是“反馈控制”。 7.对控制系统的基本要求:稳定性、快速性和准确性。 8.控制理论发展的简单回顾 ①经典控制理论肇源于1788年J.Watt的蒸汽机离心调速器(一个自动调节系统)所带来的离心调速问题。②1948年,N.Wiener出版了著名的《控制论》,形成了完整的经典控制理论。③钱学森创立了“工程控制论”这门学科,并于1954年出版了《工程控制论》这一名著。 第二章 系统的数学模型 1.微分方程是在时域中描述系统(或元件)动态特性的数学模型。线性系统可以运用叠加原理,当有几个输入量同时作用于系统时,可以逐个输入,求出对应的输出,然后把各个输出进行叠加,即为系统的总输出。非线性系统不能应用叠加原理。建立系统数学模型有两种方法:分析法和实验法。 2.列写微分方程的一般方法:输出量放在方程左侧,输入量放在方程右侧。(列写微分方程
my( t ) + cy( t ) + ky( t ) = f( t )...
y( 0 ) = y0 y( 0 ) = y0
..
不考) 3. Laplace变换(简称拉氏变换):若一个时间函数 f(t),称为原函数,经过下式计算转换为象函数F (s): 称F(s)为f(t)的Laplace变换(简称拉氏变换)。其中算子s=σ+ jω为复数。 几个常用函数的拉氏变换: (1)阶跃函数: ⑵指数函数: ⑶正弦函数: ⑷余弦函数: ⑸t的幂函数: ⑹单位脉冲函数: 拉氏变换的主要运算定理 ⑴微分定理: ⑵积分定理: ⑶延迟定理: ⑷初值定理: ⑸终值定理: ⑹留数定理: 4.系统的传递函数:线性定常系统在零初始条件下,输出量的Laplace变换与输入量的Laplace变换之比。P36 5.典型环节的传递函数 ⑴比例环节 ⑵惯性环节 ⑶微分环节 ⑷导前环节(一阶微分环节) ⑸积分环节 ⑹振荡环节 ⑺延迟环节 5.系统传递函数方框图及其化简 ⑴串联环节的等效变换规则 ⑵并联环节的等效变换规则 ⑶方框图的反馈连接及其等效规则 ⑷分支点移动规则:前移,串入G(s);后移,串入1/G(s)。 ⑸相加点移动规则:后移,串入G(s);前移,串入1/G(s)。 ⑹分支点之间、相加点之间相互移动规则:同类之间可以相互移动,不改变原有的数学关系。不同类之间不能相互移动。
6.对一个闭环系统,当输入的取法不同时,前向通道的传递函数不同,反馈回路的传递函数 不同,系统的传递函数也不同,但系统传递函数的分母不变,因为这一分母反映了系统本身的固有特性,这特性与外界无关。 7.相似原理 一般称能用形式相同的数学模型来描述的物理系统(环节)为相似系统(环节),称在微分方程或传递函数中占相同位置的物理量为相似量。 第三章 系统的时间响应分析 1.时间响应及其组成
n与si同系统的初态和输入无关,而取决于系统的结构和参数的固有特性。
2.系统的时间响应按振动性质分为自由响应与强迫响应;按振动来源分为零输入响应与零状态响应;按稳定性质分为瞬态响应与稳态响应。 3.在此还要强调:特征根实部Re[si]的正负决定自由响应的收敛性. Re s i是大于还是小于零,决定系统稳定还是不稳定; Re s i绝对值大小,决定系统的快速性; Re[si]<0,自由响应收敛,绝对值越大收敛越快; Re[si]>0,自由响应发散,绝对值越大发散越快。 特征根实部Im[si]的大小决定自由响应的振荡频率,影响系统响应的准确性。 4.一阶系统
单位脉冲响应和单位阶跃函数的关系? 对比一阶系统的单位脉冲响应和单位阶跃响应可知,二者存在导数关系,即单位脉冲函数是单位阶跃函数(在t=0处)的导数,单位脉冲响应也是单位阶跃响应的导数。这一关系可
tBeAeAtynitsinitsiii1211)(
零 状 态 响应 零 输 入 响应
tkFtkFtytytynnnncos11cos11cos)0(sin)0()(22.自 由 响应 强 迫 响应 以推广,即若输入是某函数的积分,则响应也为某函数的响应的积分。但若为不定积分,则需确定积分常数。 5.二阶系统
6.二阶系统响应的性能指标 ⑴上升时间 ⑵峰值时间 ⑶最大超调量 ⑶调整时间 ⑸振荡次数 7.若高阶系统中离虚轴最近的极点, 其实部小于其它极点实部的1/5, 并且附近不存在零点,可以认为系统的响应主要由这一极点决定,称为主导极点。系统的响应特性主要由主导极点决定 8.系统误差分析与计算
提高系统的准确度,增加系统的抗干扰能力,必须增大干扰作用点前的回路放大倍数K1,以及增加这一段回路中积分环节的数目。 第四章 系统的频率特性分析 1.频率特性概述 ⑴频率响应:线性定常系统对谐波输入的稳态响应。 ⑵频率特性 ⑶频率特性的求法 2,。频率特性的极坐标图 ⑴Nyquist图 频率特性的极坐标图又称Nyquist图,也称幅相频率特性图。 常见的Nyquist图 ⑵频率特性的对数坐标图
3.绘制系统Bode图的步骤 ⑴将G(s)转化为若干个标准形式的环节的传递函数的乘积形式; ⑵求G(jω); ⑶确定各环节转角频率; ⑷作出各环节的对数幅频特性的渐近线; ⑸根据误差曲线进行修整; ⑹各环节的对数幅频特性曲线叠加(不包括系统总的增益K); ⑺将叠加后的曲线整体垂直移动20lgK; ⑻作出各环节的对数相频特性曲线,然后叠加; ⑼如有延时环节,对数幅频特性不变,对数相频特性则加上-τω。 绘制系统Bode图的顺序频率法 ⑴将G(s)转化为若干个标准形式的环节的传递函数的乘积形式。 ⑵求G(jω) 。 ⑶确定各环节转角频率,并将转角频率由低到高依次标注在横轴上。 ⑷绘制的对数幅频特性的低频渐近线,若系统为0型系统,低频段为一水平线,高度为20lgK;若是Ⅰ型或Ⅱ型以上系统,低频段在ω =1处的幅值为20lgK,斜率为-20vdB/dec。 ⑸按转角频率由低到高的顺序,在低频渐近线的基础上,每遇到一个转角频率,根据环节的性质改变渐近线斜率,绘制渐近线。斜率改变的原则是:遇到惯性环节的转角频率,斜 率改变-20dB/dec,一阶微分环节+ 20dB/dec ,振荡环节-40dB/dec ,二阶微分环节+40dB/dec,如此,最后一段的渐近线斜率应为-20(n-m)dB/dec 。 ⑹如有必要对曲线进行适当修正 4.最小相位传递函数:在右半s平面内既无极点也无零点的传递函数。非最小相位传递函数:在右半s平面内有极点也或有零点的传递函数。在具有相同幅值特性的系统中,最小相位传递函数(系统)的相角范围,在所有这类系统中是最小的。任何非最小相位传递函数的相角范围,都大于最小相位传递函数的相角范围。 第五章 系统的稳定性 1.系统能在实际中应用的必要条件是系统要稳定。(稳定性是系统能正常工作的首要条件) 系统稳定与否取决于系统内部条件,而与输入无关;系统发生不稳定必有适当的反馈作用; 控制理论中讨论的稳定性是输入为零而初始状态不为零的稳定性。稳定性是指自由响应的收敛性。 2.系统稳定的充要条件为:当系统所有的特征根si(i=1,2,…,n)均具有负实部(位于[s]平面的左半平面),自由响应收敛,系统稳定;若有任一sk具有正实部(位于[s]平面的右半平面),自由响应发散,系统不稳定。 3.Routh稳定判据
4.Nyquist稳定判据
