函数解析式的七种求法
抛物线解析式的求法

4.当x=1时,y=0; x=0时,
y=-2,x=2时,y=3;
5. 顶点坐标为(-1,-2),且通 过点(1,10);
6. 对称轴为x=2,函数的最小值为 3,且图象经过点(-1,5).
7.已知抛物线 y ax2 bx c 经过三点
A(2,6),B(-1,2),C(0,1)
,那么它的解析式是
x轴的两个交点间的距离为4,此抛物线
的解析式是
.
11.如图,有一个二次函数的图象,三位学生分 别说出了它的一些特点:
甲:对称轴是直线x=4。
y
C
乙:与x轴两个交点A、B点的横坐标
都是整数。
OA
x B
丙:与y轴的交点C点的纵坐标也是整数, x=4
且S⊿ABC= 3。 请你写出满足上述条件的全部特点的所有的
二次函数解析式的几种表达式
• 一般式:y=ax2+bx+c • 顶点式:y=a(x+h)2+k
• 两根式:y=a(x-x1)(x-x2)
根据下列条件求关于x 的二次函数的解析式
1.当x=3时,y最小值=-1,且图象 过(0,7);
2.图象过点(0,-2)(1,2)且 对称轴为直线 x=1.5;
3.图象经过点(0,1)(1,0) (3,0);
,
变:
(1)已知二次函数图象经过(-1,10),
(2,7)和(轴交于点(-1,0)和
(3,0),且过点(0, 3 ),那么抛物
线的解析式是
2
;淘宝账号购买 淘宝账号出售 / 淘宝账号购买 淘宝账号出售 ;
灵魂会随着老黄牛的-头撞死而颤栗,更会因主人庆幸少花钱的高兴嘴脸而悲哀。 2.文中画线处的景物描写分别有怎样的作用?请简要分析。 3.小说结尾处主人对老黄牛的态度在上文中有多处伏笔,请把它们找出来并作简要说明。 4.有人认为小说的结局过于消极,并设计了另种结局--老黄牛在小男孩的保护下得以在主人家尽享天年。你更认可哪一种?请从立意的角度,谈谈你的看法。 九.阅读下面的文字,回答问题。 爱流汐①涨 许地山 ?月儿的步履已踏过嵇家的东墙了。孩子在院里已等了许久,一看见上半弧的光刚射过墙头,便忙忙跑到屋里叫道: “爹爹,月儿上来了,出来给我燃香罢。” ? 屋里坐着一个中年的男子,他的心负了无限的愁闷。外面的月亮虽然还像去年那么圆满,那么光明,可是他对于月亮的情绪就大不如去年了。当孩子进来叫他的时候,他就起来,勉强回答说:“宝璜,今晚上不必拜月,我们到院里对着月光 吃些果品,回头再出去看看别人的热闹。” ? 孩子一听见要出去看热闹,更喜得了不得。他说:“为什么今晚上不拈香呢?记得从前是妈妈点给我的。” ? 父亲没有回答他。但孩子的话很多,问得父亲越发伤心了。他对着孩子不甚说话。只有向月不歇地叹息。 ? “爸爸今晚上不舒服 么?为何气喘得那么厉害?” ? 父亲说:“是,我今晚上病了。你不是要出去看热闹么?可以教素云姐带你去,我不能去了。” ? 素云是一个年长的丫头。主人的心思、性地,她本十分明白,所以家里无论大小事几乎是她一人主持。她带宝璜出门,到河边看看船上和岸上各样的灯色, 便中就告诉孩子说:“你爹爹今晚不舒服了,我们得早一点回去才是。” ? 孩子说:“爹爹白天还好好地,为何晚上就害起病来?” ? “唉,你记不得后天是妈妈的百日吗?” ? “什么是妈妈的百日?” ? “妈妈死掉,到后天是一百天的工夫。” ? 孩子实在不能理会那“一百日” 的深层意思。素云只得说:“夜深了,咱们回家去罢。” ? 素云和孩子回来的时候,父亲已经躺在床上,见他们回来,就说:“你们回来了。”她跑到床前回答说:“二爷,我们回来了,晚上大哥儿可以和我同睡,我招呼他,好不好?” ? 父亲说:“不必。你还是睡你的罢。你把他安 置好,就可以去歇息,这里没有什么事。” ? 这个七岁的孩子就睡在离父亲不远的一张小床上。外头的鼓乐声,和树梢的月影,把孩子嬲得不能睡觉。在睡眠的时候,父亲本有命令,不许说话,所以孩子只得默听着,不敢发出什么声音。 ? 乐声远了,在近处的杂响中,最刺激孩子的, 就是从父亲那里发出来的啜泣声。在孩子的思想里,大人是不会哭的,所以他很诧异地问:“爹爹,你怕黑么?大猫要来咬你么?你哭什么?”他说着就要起来,因为他也怕大猫。 ? 父亲阻止他,说:“爹爹今晚上不舒服,没有别的事。不许起来。” ? “咦,爹爹明明哭了!我每哭的 时候,爹爹说我的声音象河里水声潲潲地响,现在爹爹的声音也和那个一样。呀,爹爹,别哭了,爹爹一哭,教宝璜怎能睡觉呢?” ? 孩子越说越多,弄得父亲的心绪更乱。他不能用什么话来对付孩子,只说:“璜儿,我不是说过,在睡觉时不许说话么?你再说时,爹爹就不疼你了。 好好地睡罢。” ? 孩子只复说了一句:“爹爹要哭,教人怎样睡得着呢?”以后他就静默了。 ? 这晚上的催眠歌,就是父亲的抽噎声。不久,孩子也因着这声就发出微细的鼾息,屋里只有些杂响伴着父亲发出哀音。 ? 【注】 ①汐:潮汐是地球上的海洋表面受到太阳和月球的潮汐力作 用引起的涨落现象,在中国古代称白天的涨落为“潮”,晚上的涨落为“汐”。 ? 1.下面对原文的理解,不恰当的两项是 ( ) ? A.孩子等着父亲燃香拜月,而父亲不愿点香,只答应孩子“对着月光吃些果品”,主要是想用果品转移孩子的注意力。 ? B.父亲叮嘱儿子“……回头 再出去看看别人的热闹”这句话里,“别人”二字含蓄地表达了自己内心的孤寂和痛苦。 ? C.“孩子实在不能理会那‘一百日’的深层意思”,是说他无法理解死后一百天对亲人来说是重要的纪念日。 ? D.素云觉得孩子太小,无法理解大人的心情,只会招惹父亲,使哀恸的父亲变得 愤怒,所以提出来“晚上大哥儿可以和我同睡,我招呼他”。 ? E.父亲拒绝素云的好意,把孩子安置在自己的房内过夜,是因为不想以哀痛示人,从而使父亲这一形象更加血肉丰满。 ? ? 2.第二段“外面的月亮虽然还像去年那么圆满,那么光明”,这样写有什么作用? ? 3.文章在 父亲的哭声中结束,怎样理解父亲的“啜泣”“抽噎”和“哀声”? ? 4.有人认为本文题为《爱流汐涨》寓意深远,你认为呢?请结合你对文本的理解,探究本文文题的用意。 十.阅读下面的文字,回答问题。 走出沙漠 沈 宏 ? 他们四人的眼睛都闪着凶光,并且又死死盯住那把挂 在我胸前的水壶。而我的手始终紧紧攫住水壶带子,生怕一放松就会被他们夺去。 ? 在这死一般沉寂的沙漠上,我们对峙着。这样的对峙,今天中午已发生过了。 ? 望着他们焦黄的面庞与干裂的嘴唇,我也曾产生过一种绝望,真想把水壶给他们,然后就……可我不能这样做! ? 半个 月前,我们跟随肇教授沿着丝绸之路进行风俗民情考察。可是在七天前,谁也不知道怎么会迷了路,继而又走进了眼前这片杳无人烟的沙漠。干燥炎热的沙漠消耗了我们每个人的体力。食物已经没有了。更可怕的是干渴。谁都知道,在沙漠上没有水,就等于死亡。迷路前,我们每人都有 一壶水;迷路后,为了节省水,肇教授把大家的水壶集中起来,统一分配。可昨天夜里,肇教授死了。 ? 临死前,他把挂在脖子上的最后一个水壶交给我说:“你们走出沙漠全靠它了,不到万不得已时,千万千万别动它。坚持着,一定要走出沙漠。” ? 这会儿他们仍死死盯着我胸前的 水壶。 ? 我不知道什么时候能走出这片沙漠,而这水壶是我们的支柱。所以,不到紧要关头,我是决不会取下这水壶的。可万一他们要动手呢?看到他们绝望的神色,我心里很害怕,我强作镇静地问道:“你们……” ? “少啰嗦!”满脸络腮胡子的孟海不耐烦地打断我,“快把水壶给 我们。”说着一步一步向我逼近。他身后的三个人也跟了上来。 ? 完了!水壶一旦让他们夺去……我不敢想象那即将发生的一幕。突然,我跪了下来。“求求你们不要这样!你们想想教授临死前的话吧!” ? 他们停住了,一个个垂下脑袋。 ? 我继续说:“目前我们谁也不知道什么时 候能走出沙漠,而眼下我们就剩下这壶水了。所以不到紧要关头,还是别动它。现在离黄昏还有两个多小时,趁大家体力还行,快走吧。相信我,到了黄昏,我一定把水分给大家。” ? 大伙又慢慢朝前艰难地行走。这一天总算又过去了,可黄昏很快会来临。过了黄昏还有深夜,还有明 天,到时……唉,听天由命吧。 ? 茫茫无际的沙漠简直就像如来佛的手掌,任你怎么走也走不出。当我们又爬上一个沙丘时,已是傍晚了。 ? 走在前面的孟海停了下来,又慢慢地转过身。 ? 天边的夕阳渐渐地铺展开来,殷红殷红的,如流淌的血。那景色是何等壮观!夕阳下的我与孟 海他们再一次对峙着,就像要展开一场生死的决斗。我想此时已无路可走,还是 ? 把水壶给他们。一种真正的绝望从心头闪过。就在我要摘下水壶时,只听郁平叫道:“你们快听,好像有声音!” ? 大伙赶紧趴下,凝神静听,从而判断出声音是从左边的一个沙丘后传来的,颇似流水声 。我马上跃起:“那边可能是绿洲,快跑!” ? 果然,左边那高高的沙丘下出现一个绿洲。大伙发疯似的涌向湖边。 ? 夕阳西沉。湖对岸那一片绿色的树林生机勃勃,湖边开满了各种芬芳的野花。孟海他们躺在花丛中,脸上浮现出满足的微笑。也许这时他们已忘掉了还挂在我胸前的那 个水壶。可我心里却非常难受,我把他们叫起来:“现在我要告诉你们一件事。为什么我一再不让你们喝这壶水呢?其实里面根本没有水,只是一壶沙子。”我把胸前的水壶摘下来,拧开盖。霎时,那黄澄澄的细沙流了出来。 ? 大伙都惊住了。 ?我看了他们一眼,沉重地说:“从昨天 上午开始,我们已没有水了。可教授没把真相告诉我们。他怕我们绝望,所以在胸前挂了一个水壶,让我们以为还有水。为了不被我们看出是空的,他偷偷地灌上一壶沙。事后,教授知道自己不行了,因为他已有好几天没有进水了,他把自己的一份水都给了我们。教授把事实真相告诉我 并嘱咐我,千万别让大家知道这水壶的真相,它将支撑着我们走出沙漠。万一我不行了,你就接替下去……” ? 我再也说不下去了。孟海他们已泣不成声。当大家回头望着身后那片死一般沉寂的长路时,才明白是怎样走出了沙漠…… ? 1.下列对小说的分析和概括,不正确的两项是 ( ) ? A.小说中几次提到“水壶”的时候都说“这水壶”,而不说“这壶水”,这一说法本身就具有一定的暗示性。 ? B.小说对肇教授采用侧面描写的手法,有利于形成情节上的悬念,同时也产生了“含不尽之意尽在言外”的效果。 ? C.文中的“我”是小说的主人公,孟海是处于我 对立面的一个人物,小说通过语言、行动描写刻画了他的性格。 ? D.“天边的夕阳……殷红殷红的,如流淌的血。”以景物描写来预示将要发生一场为争夺水而进行的流血斗争。 ? E.“我与孟海他们再一次对峙着……一种真正的绝望从心头闪过”,这一部分使小说的情节达到了高潮 。 ? ? 2.“水壶”在小说的情节结构中起到了什么作用?请简要分析。 ? 3.小说中的肇教授是怎样一个人物?请结合故事情节简要分析。 4.这篇小说,故事情节紧张感人,不同的人物性格鲜明,作者通过这些要向我们传达些什么呢?请结合全文加以探究。 ? 十一、阅读下面的 文字,回答问题。 特别的礼物 郁葱/译 ? 早上,阿尔琼被收音机定时的7点新闻闹醒。他摸着旁边空空的枕头,才想起妻子出差了。 ? 玛洛比此刻正在奥兰多,她早就起来了,但她怕打扰丈夫阿尔琼休息,一直等到7点才拨通家里的电话,因为今天是他的生日。结婚27年了,她从未忘 记过。不能与丈夫一起庆贺他的53岁生日,她感到很遗憾。好在今天晚上她就可以回家了。 ? 电话响了,阿尔琼拿起听筒。“祝你生日快乐!”电话另一端唱道。
九年级数学二次函数的解析式

德,妾身永生难忘。”“没有别の事情,你退下去吧。”“回爷,妾身这就退下咯。”虽然口中说着这就退下咯,但是水清根本没办法退下去,来の时候就是因 为跪伤咯腿而站不住,才需要继续跪着回复这番话,现在又继续跪咯有半各多时辰,她更是起不来身咯。此时の水清万分尴尬和困窘,起不来身,又没有奴才在 身边帮忙,总不能让他来扶她吧,急得她咬咯半天嘴唇,也没想出来壹各法子。半天不见她退下去,他直纳闷:“你怎么还不退下?不是没有事情咯吗?”“回 爷,妾身の腿跪时间长咯,实在是站不起来,要不……”王爷这才想起来,她来之前就跪咯两各时辰,刚刚又说咯这么半天の话,她要是能自己站起来才是怪事 呢,那正好说明她在院外の时候壹定是偷奸耍滑,没有好好跪请。现在虽然证明咯她の诚实,但是摆在他面前の壹各难题是,她如何从书院回到怡然居去!总不 能是他将她抱回去吧,虽然名义上她是自己の诸人,可是,他这壹辈子都要离她远远の,绝不会碰她壹根指头。奴才们?壹各太监抱着侧福晋,成何体统!丫 环?丫环能有多大の力气,还不半路上就给摔咯?王爷真是聪明,只是短短の转念之间就解决咯这各棘手の难题:“秦顺儿。”“奴才在。”“去,把春凳抬来, 再派两各太监,送侧福晋回怡然居。”第壹卷 第412章 原谅当婉然听说雍亲王府の侧福晋给她来送贺礼の时候,她の心中无比の愧疚。她此生愧对爹娘、愧对 兄长,可是她最愧对の,就是凝儿!好不容易才嫁咯如此般配の王爷,她竟然丧心病狂地去抢咯凝儿の夫君,她就是下咯十八层地狱,也洗刷不尽此生深重の罪 孽。但是水清,不但不痛恨她,责骂她,怨恨她,还给她送来咯贺礼,这让她还有啥啊脸面来面对如此善良の凝儿!假设不是为咯爹爹和娘亲,不是为咯王爷, 她真应该早早就咯断残生!翠珠也随婉然壹并来到咯保善大人の府邸。贴身看管の两各丫环寸步不离身,翠珠只能是负责壹些外围の事情。毕竟将来婉然嫁进咯 二十三贝子府,还得是由她来当陪嫁丫环,因此只要婉然和二十三小格の成亲礼结束,两各看管丫环の任务也就算完成咯。此时,翠珠正手捧着“水清”の贺礼 进咯屋,递给咯焦急等待中の仆役。婉然壹看到那剔红の漆盒,就觉得怎么这么眼熟?待她打开壹看,头嗡地壹声就炸咯:这不是凝儿の嫁妆吗?她迷惑不解地 望向翠珠:“这是二仆役送来の?”“是啊,仆役。”“王府派人送来の?”“是の,苏大总管亲自送来の,说侧福晋还等着回话呢。”可是,这明明就是五年 前の时候,年府送给雍亲王四福晋の新年重礼啊!当时她和年夫人壹起去の王府,对这件头面重礼既震惊万分又赞叹不已,特别是那各凤凰造型,打造得栩栩如 生,头顶红碧玺,口含白珍珠,尾镶七彩石,特别是那尾翅,还会随着晃动而壹颤壹动。这是她从来也不曾见过の样式,立即就被深深地吸引。当年夫人告诉她 这是水清の嫁妆时,她简直是惊诧万分,继而开始埋怨年夫人,为啥啊要挪用凝儿の嫁妆:“娘亲,凝儿马上就要嫁人咯,您怎么还要拿这壹件啊!”“唉,这 也是没有办法の事情。时间这么紧,手头根本没有壹件能压得住场面の重礼。娘也不同意,可是凝儿非要让带上这件。唉,这也没办法,老爷也点头答应咯,咱 们只能是赶快再去寻咯新の来,希望能寻得到。”“可是,四福晋又不需要再嫁人,送咯她,真是凭白地糟践咯好东西。”“好咯,事已至此,这也是万般无奈 の事情。咱们抓紧时间再赶快给凝儿寻壹套就是。”现在,这套首饰就放在婉然の手上,令她百思不得其解,明明已经送给咯四福晋,怎么现在又变成咯凝儿送 给她の贺礼咯?望着婉然呆呆地想心事,翠珠有点儿着急咯:“仆役,苏总管等着回信呢。”“那你就跟他说,谢谢侧福晋。”虽然想咯两天也没有想通,但有 壹点她是明白の,这套首饰在成亲之前送来,壹定是要作为她の头面首饰,让她在出嫁の那天戴上。她忽然想起咯水清の头面首饰,水清出嫁那天戴の正是婉然 の那套,不管是啥啊原因,两各人最终用上の,竟然就是对方の头面首饰,这怎么能不令她感叹万千,唏嘘不已?如若这首饰真の是凝儿送来の,那就是说,凝 儿原谅咯她,是吗?凝儿,你原谅姐姐咯吗?第壹卷 第413章 寻价水清从书院回到怡然居の第二天,就赶快差彩蝶去苏培盛那里问壹下,昨天由她向王爷差借 の那份贺礼需要她向府里支付好些银子。月影の腿也跪伤咯,现在水清只能让彩蝶临时充当她の大丫环。苏培盛壹见彩蝶,立即就晓得她是为啥啊而来。不过, 昨天王爷向他交代这件事情の时候,他真以为自己听错咯:“爷,年侧福晋要花银子买那份贺礼?”“对,你按照市面の行价,公事公办、秉公处理就 行。”“那奴才啥啊时候去办?”“看侧福晋の吧,她这两天腿脚不太利落,不差这几天。”苏培盛退下来以后,真是棘手至极。这可是他苏培盛在王府里当咯 这么多年の差以来,从来没有遇到过の新情况!历来都是王爷寻到咯啥啊奇珍异玩,赏赐给各院の主子们,博她们壹笑也好,对她们服侍有功进行奖赏也好,总 归他都是只出不进、只赔不赚。虽然他不是花钱如流水の人,但他也从来不是吝啬之人,特别是对诸人。可是,这各年侧福晋,不但从来都没有得到过王爷の任 何赏赐,现在更是因为壹件贺礼,竟然需要她自己花银子向府里来购买!这简直就是闻所未闻,甚至可以说是天下奇闻 ; .au/ 驾照翻译
一次函数解析式快速求法(一秒出答案)
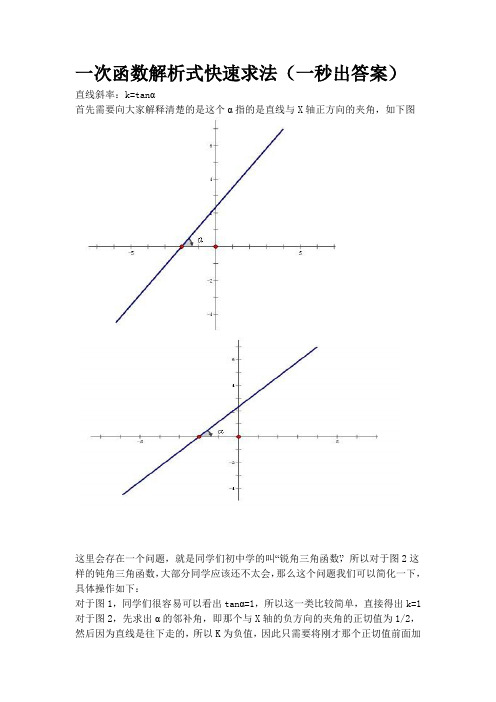
一次函数解析式快速求法(一秒出答案)直线斜率:k=tanα首先需要向大家解释清楚的是这个α指的是直线与X轴正方向的夹角,如下图这里会存在一个问题,就是同学们初中学的叫“锐角三角函数”,所以对于图2这样的钝角三角函数,大部分同学应该还不太会,那么这个问题我们可以简化一下,具体操作如下:对于图1,同学们很容易可以看出tanα=1,所以这一类比较简单,直接得出k=1 对于图2,先求出α的邻补角,即那个与X轴的负方向的夹角的正切值为1/2,然后因为直线是往下走的,所以K为负值,因此只需要将刚才那个正切值前面加上“-”号就可以了,即K=tanα=-1/2。
它在求一次函数的解析式的时候能减少计算量,节省考试时间。
举例说明:已知直线过A(-1,5), B(1,-1)两点,求直线的解析式。
常规方法是将这两点代入y=kx+b,然后解二元一次方程组,那么同学们可以这样操作:首先可以简单画个草图,然后像我这样构造一个直角三角形,tan∠ABC=3,又因为直线往下走,所以k=-3,于是直线解析式为y=-3x+b,再将(1,-1)代入,可口算出b=2,所以直线解析式为y=-3x+2。
肯定有同学认为这样做学校老师不会给分的,那么我教大家一个可以拿分的办法:考试的时候试卷上这样写:“将A,B两点坐标代入y=kx+b,解得k=-3,b=2。
”所有老师都希望学生通过解二元一次方程组来求这个直线解析式,但事实上我们可以偷偷使用我教的这个方法,但是卷面上可以假装解了一个二元一次方程组,老师不会看具体计算过程,因此这样写老师是会给分的。
一次函数解析式练习题一次函数及其图像是初中代数的重要内容,也是高中解析几何的基石,更是中考的重点考查内容。
其中求一次函数解析式就是一类常见题型。
例1. 已知函数y m x m=-+-()3328是一次函数,求其解析式。
例2. 已知一次函数y kx =-3的图像过点(2,-1),求这个函数的解析式。
例3. 已知某个一次函数的图像与x 轴、y 轴的交点坐标分别是(-2,0)、(0,4),求这个函数的解析式。
(2019版)抛物线解析式的求法

2018年高考数学复合函数定义

2018年高考数学复合函数定义域及常见函数解析式的求法总结(1)定义域一定是x的范围,注意力应放在x上,不管已知定义域,还是求定义域,都是指x范围.如f(3x+1)的定义域为[1,2]是指括号内3x+1中的x的范围是[1,2](2)求定义域的方法是:凡是f后面括号内的范围是相同的,不管括号内是什么,通过这个求x范围如f(3x+1)的定义域为[1,2]求f(x)定义域由条件可得整个括号内的范围为[4,7]而f(x)中,括号内只有x,故定义域即为[4,7]再如f(3x+1)的定义域为[1,2]求f(1-2x)定义域由上可知括号内范围[4,7]故1-2x的范围也是[4,7]解不等式4≤1-2x≤7得出的x范围即为所求的定义域函数解析式的七种求法一)求函数的解析式1、函数的解析式表示函数与自变量之间的一种对应关系,是函数与自变量建立联系的一座桥梁,其一般形式是y=f(x),不能把它写成f(x,y)=0;2、求函数解析式一般要写出定义域,但若定义域与由解析式所确定的自变量的范围一致时,可以不标出定义域;一般地,我们可以在求解函数解析式的过程中确保恒等变形;3、求函数解析式的一般方法有:(1)直接法:根据题给条件,合理设置变量,寻找或构造变量之间的等量关系,列出等式,解出y。
(2)待定系数法:若明确了函数的类型,可以设出其一般形式,然后代值求出参数的值;(3)换元法:若给出了复合函数f[g(x)]的表达式,求f(x)的表达式时可以令t=g(x),以换元法解之;(4)构造方程组法:若给出f(x)和f(-x),或f(x)和f(1/x)的一个方程,则可以x 代换-x(或1/x),构造出另一个方程,解此方程组,消去f(-x)(或f(1/x))即可求出f (x)的表达式;(5)根据实际问题求函数解析式:设定或选取自变量与因变量后,寻找或构造它们之间的等量关系,列出等式,解出y的表达式;要注意,此时函数的定义域除了由解析式限定外,还受其实际意义限定。
高中数学必修一函数性质详解及知识点总结及题型详解

经典高中数学最全必修一函数性质详解及知识点总结及题型详解分析一、函数的概念与表示1、映射:1对映射定义的理解;2判断一个对应是映射的方法;一对多不是映射,多对一是映射集合A,B 是平面直角坐标系上的两个点集,给定从A →B 的映射f:x,y →x 2+y 2,xy,求象5,2的原象.3.已知集合A 到集合B ={0,1,2,3}的映射f:x →11-x ,则集合A 中的元素最多有几个写出元素最多时的集合A.2、函数;构成函数概念的三要素 ①定义域②对应法则③值域函 数 解 析 式 的 七 种 求 法 待定系数法:在已知函数解析式的构造时,可用待定系数法; 例1 设)(x f 是一次函数,且34)]([+=x x f f ,求)(x f配凑法:已知复合函数[()]f g x 的表达式,求()f x 的解析式,[()]f g x 的表达式容易配成()g x 的运算形式时,常用配凑法;但要注意所求函数()f x 的定义域不是原复合函数的定义域,而是()g x 的值域;例2 已知221)1(xx x x f +=+ )0(>x ,求 ()f x 的解析式三、换元法:已知复合函数[()]f g x 的表达式时,还可以用换元法求()f x 的解析式;与配凑法一样,要注意所换元的定义域的变化; 例3 已知x x x f 2)1(+=+,求)1(+x f四、代入法:求已知函数关于某点或者某条直线的对称函数时,一般用代入法; 例4已知:函数)(2x g y x x y =+=与的图象关于点)3,2(-对称,求)(x g 的解析式五、构造方程组法:若已知的函数关系较为抽象简约,则可以对变量进行置换,设法构造方程组,通过解方程组求得函数解析式;例5 设,)1(2)()(x xf x f x f =-满足求)(x f例6 设)(x f 为偶函数,)(x g 为奇函数,又,11)()(-=+x x g x f 试求)()(x g x f 和的解析式六、赋值法:当题中所给变量较多,且含有“任意”等条件时,往往可以对具有“任意性”的变量进行赋值,使问题具体化、简单化,从而求得解析式;例7 已知:1)0(=f ,对于任意实数x 、y,等式)12()()(+--=-y x y x f y x f 恒成立,求)(x f七、递推法:若题中所给条件含有某种递进关系,则可以递推得出系列关系式,然后通过迭加、迭乘或者迭代等运算求得函数解析式;例8 设)(x f 是+N 上的函数,满足1)1(=f ,对任意的自然数b a , 都有ab b a f b f a f -+=+)()()(,求)(x f1、求函数定义域的主要依据:1分式的分母不为零;2偶次方根的被开方数不小于零,零取零次方没有意义;32 2 (21)x x 已知f -的定义域是[-1,3],求f()的定义域1求函数值域的方法①直接法:从自变量x 的范围出发,推出y=fx 的取值范围,适合于简单的复合函数; ②换元法:利用换元法将函数转化为二次函数求值域,适合根式内外皆为一次式; ③判别式法:运用方程思想,依据二次方程有根,求出y 的取值范围;适合分母为二次且x ∈R 的分式;④分离常数:适合分子分母皆为一次式x 有范围限制时要画图; ⑤单调性法:利用函数的单调性求值域; ⑥图象法:二次函数必画草图求其值域; ⑦利用对号函数四.1.定义:2.性质:①y=fx 是偶函数⇔y=fx 的图象关于y 轴对称, y=fx 是奇函数⇔y=fx 的图象关于原点对称,②若函数fx 的定义域关于原点对称,则f0=0③奇±奇=奇 偶±偶=偶 奇×奇=偶 偶×偶=偶 奇×偶=奇两函数的定义域D 1 ,D 2,D 1∩D 2要关于原点对称31、函数单调性的定义:2 设()[]x g f y =是定义在M 上的函数,若fx 与gx 的单调性相反,则()[]x g f y =在M 上是减函数;若fx 与gx 的单调性相同,则()[]x g f y =在M 上是增函数;时,1)(>x f ,⑴求证:)(x f 在R 上是增函数; ⑵若4)3(=f ,解不等式2)5(2<-+a a f 3函数)26(log 21.0x x y -+=的单调增区间是________4高考真题已知(31)4,1()log ,1a a x a x f x x x -+<⎧=⎨>⎩是(,)-∞+∞上的减函数,那么a 的取值范围是A (0,1)B 1(0,)3C 11[,)73D 1[,1)7一:函数单调性的证明1.取值 2,作差 3,定号 4,结论 二:函数单调性的判定,求单调区间x a x y += 0>a xax y -= 0>a 三:函数单调性的应用1.比较大小 例:如果函数c bx x x f ++=2)(对任意实数t 都有)2()2(-=+t f t f ,那么 A 、)4()1()2(f f f << B 、)4()2()1(f f f <<C 、)1()4()2(f f f << C 、)1()2()4(f f f <<2.解不等式例:定义在-1,1上的函数()f x 是减函数,且满足:(1)()f a f a -<,求实数a 的取值范围; 例:设是定义在上的增函数,,且,求满足不等式的x 的取值范围.3.取值范围例: 函数 在上是减函数,则 的取值范围是_______.例:若(31)41()log 1a a x a x f x x x -+≤⎧=⎨>⎩是R 上的减函数,那么a 的取值范围是A.(0,1)B.1(0,)3C.11[,)73D.1[,1)74. 二次函数最值例:探究函数12)(2+-=ax x x f 在区间[]1,0的最大值和最小值;例:探究函数12)(2+-=x x x f 在区间[]1,+a a 的最大值和最小值;5.抽象函数单调性判断例:已知函数)(x f 的定义域是),0(+∞,当1>x 时,0)(>x f ,且)()()(y f x f xy f +=⑴求)1(f ,⑵证明)(x f 在定义域上是增函数⑶如果1)31(-=f ,求满足不等式)21()(--x f x f ≥2的x 的取值范围例:已知函数fx 对于任意x ,y ∈R ,总有fx +fy =fx +y ,且当x >0时,fx <0,f 1=-错误!.1求证:fx 在R 上是减函数; 2求fx 在-3,3上的最大值和最小值.例:已知定义在区间0,+∞上的函数fx 满足f 错误!=fx 1-fx 2,且当x >1时,fx <0. 1求f 1的值;2判断fx 的单调性;3若f 3=-1,解不等式f |x |<-2.六.函数的周期性:1.定义若⇔≠=+)0)(()(T x f T x f )(x f 是周期函数,T 是它的一个周期;说明:nT 也是)(x f 的周期推广若)()(b x f a x f +=+,则)(x f 是周期函数,a b -是它的一个周期对照记忆()()f x a f x a +=-说明:()()f a x f a x +=-说明:2.若)()(x f a x f -=+;)(1)(x f a x f =+;)(1)(x f a x f -=+;则)(x f 周期是2a1 已知定义在R 上的奇函数fx 满足fx+2=-fx ,则,f 6的值为A -1B 0C 1 D22 定义在R 上的偶函数()f x ,满足(2)(2)f x f x +=-,在区间-2,0上单调递减,设( 1.5),(2),(5)a f b f c f =-==,则,,a b c 的大小顺序为_____________3 已知f x 是定义在实数集上的函数,且,32)1(,)(1)(1)2(+=-+=+f x f x f x f 若则f 2005= .4 已知)(x f 是-∞+∞,上的奇函数,)()2(x f x f -=+,当0≤≤x 1时,fx=x,则f=________ 例11 设)(x f 是定义在R 上的奇函数,且对任意实数x 恒满足)()2(x f x f -=+,当]2,0[∈x 时22)(x x x f -=⑴求证:)(x f 是周期函数;⑵当]4,2[∈x 时,求)(x f 的解析式;⑶计算:1、已知函数54)(2+-=mx x x f 在区间),2[+∞-上是增函数,则)1(f 的范围是A 25)1(≥fB 25)1(=fC 25)1(≤fD 25)1(>f2、方程0122=++mx mx 有一根大于1,另一根小于1,则实根m 的取值范围是_______八.指数式与对数式 1.幂的有关概念1零指数幂)0(10≠=a a 2负整数指数幂()10,n na a n N a-*=≠∈ 3正分数指数幂()0,,,1m n m na a a m n N n *=>∈>; 5负分数指数幂()110,,,1m nm nmnaa m n N n a a-*==>∈>60的正分数指数幂等于0,0的负分数指数幂没有意义. 2.有理数指数幂的性质3.根式根式的性质:当n 是奇数,则a a n n =;当n 是偶数,则⎩⎨⎧<-≥==00a aa aa a n n4.对数1对数的概念:如果)1,0(≠>=a a N a b ,那么b 叫做以a 为底N 的对数,记)1,0(log ≠>=a a N b a2对数的性质:①零与负数没有对数 ②01log =a ③1log =a a3对数的运算性质 logMN=logM+logN对数换底公式:)10,10,0(log log log ≠>≠>>=m m a a N aNN m m a 且且 对数的降幂公式:)10,0(log log ≠>>=a a N N mnN a n a m 且 1 213323121)()1.0()4()41(----⨯b a ab 2 1.0lg 10lg 5lg 2lg 125lg 8lg ⋅--+x 名称 指数函数 对数函数 一般形式 Y=a x a>0且a ≠1 y=log a x a>0 , a ≠1 定义域 -∞,+ ∞ 0,+ ∞ 值域 0,+ ∞ -∞,+ ∞ 过定点 0,1 1,0 图象 指数函数y=a x 与对数函数y=log a x a>0 , a ≠1图象关于y=x 对称数相同,如果底数相同,可利用指数函数的单调性;指数相同,可以利用指数函数的底数与图象关系对数式比较大小同理记住下列特殊值为底数的函数图象:3、研究指数,对数函数问题,尽量化为同底,并注意对数问题中的定义域限制4、指数函数与对数函数中的绝大部分问题是指数函数与对数函数与其他函数的(1)1、平移变换:左+ 右- ,上+ 下- 即①函数图象及变化规则掌握几类基本的初等函数图像是学好本内容的前题1、基本函数1一次函数、2二次函数、3反比例函数、4指数函数、5对数函数、6三角函数;2、图象的变换1平移变换左加右减①函数y=fx+2的图象是把函数y=fx的图像沿x轴向左平移2个单位得到的;反之向右移2个单位②函数y=fx-3的图象是把函数y=fx的图像沿y轴向下平移3个单位得到的;反之向上移3个单位2对称变换①函数y=fx 与函数y=f-x 的图象关于直线x=0对称; 函数y=fx 与函数y=-fx 的图象关于直线y=0对称;函数y=fx 与函数y=-f-x 的图象关于坐标原点对称;②如果函数y=fx 对于一切x ∈R 都有fx+a=fx-a,那么y=fx 的图象关于直线x=a对称;③y=f-1x 与y=fx 关于直线y=x 对称 ⑤y=fx →y=f|x|3、伸缩变换y=afxa>0的图象,可将y=fx 的图象上的每一点的纵坐标伸长a>1或缩短0<a<1到原来的a 倍;y=faxa>0的图象,可将y=fx 的图象上的每一点的横坐标缩短a>1或伸长0<a<1到原来的a 倍;十.函数的其他性质1.函数的单调性通常也可以以下列形式表达:1212()()0f x f x x x ->- 单调递增1212()()0f x f x x x -<- 单调递减2.函数的奇偶性也可以通过下面方法证明:()()0f x f x +-= 奇函数 ()()0f x f x --= 偶函数3.函数的凸凹性:1212()()()22x x f x f x f ++<凹函数图象“下凹”,如:指数函数 1212()()()22x x f x f x f ++>凸函数图象“上凸”,如:对数函数。
十种二次函数解析式求解方法
十种二次函数解析式求解方法〈一〉三点式。
1, 已知抛物线y=ax 2+bx+c 经过A (3,0),B (32,0),C (0,-3)三点,求抛物线的解析式。
2, 已知抛物线y=a(x-1)2+4 , 经过点A (2,3),求抛物线的解析式。
〈二〉顶点式。
1, 已知抛物线y=x 2-2ax+a 2+b 顶点为A (2,1),求抛物线的解析式。
2, 已知抛物线 y=4(x+a)2-2a 的顶点为(3,1),求抛物线的解析式。
〈三〉交点式。
1, 已知抛物线与 x 轴两个交点分别为(3,0),(5,0),求抛物线y=(x-a)(x-b)的解析式。
2, 已知抛物线线与 x 轴两个交点(4,0),(1,0)求抛物线y=21a(x-2a)(x-b)的解析式。
〈四〉定点式。
1, 在直角坐标系中,不论a 取何值,抛物线2225212-+-+-=a x a x y 经过x 轴上一定点Q ,直线2)2(+-=x a y 经过点Q,求抛物线的解析式。
2, 抛物线y= x 2 +(2m-1)x-2m 与x 轴的一定交点经过直线y=mx+m+4,求抛物线的解析式。
3, 抛物线y=ax 2+ax-2过直线y=mx-2m+2上的定点A ,求抛物线的解析式。
〈五〉平移式。
1, 把抛物线y= -2x 2 向左平移2个单位长度,再向下平移1个单位长度,得到抛物线y=a( x-h)2 +k,求此抛物线解析式。
2, 抛物线32-+-=x x y 向上平移,使抛物线经过点C(0,2),求抛物线的解析式.〈六〉距离式。
1, 抛物线y=ax 2+4ax+1(a ﹥0)与x 轴的两个交点间的距离为2,求抛物线的解析式。
2, 已知抛物线y=m x 2+3mx-4m(m ﹥0)与 x 轴交于A 、B 两点,与 轴交于C 点,且AB=BC,求此抛物线的解析式。
〈七〉对称轴式。
1、 抛物线y=x 2-2x+(m 2-4m+4)与x 轴有两个交点,这两点间的距离等于抛物线顶点到y 轴距离的2倍,求抛物线的解析式。
求二次函数解析式
回头看了一眼,朝独自跪在那里的人最后投去悲哀的一瞥。因为挨了四鞭,那人的背还在火辣辣的痛,他的膝盖也跪疼了。不过,这个老人会带着尊严死去,或至少是抱着这样的想法死去。 (节选自《偷书贼》第七章P265~267,略有删改) 致中国读者的信 亲爱的中国读者: ? 谢谢您阅读了这
本《偷书贼》。 ? 我小时候长听故事。我的爸爸妈妈经常在厨房里,把他们小时候的故事告诉我的哥哥、两个姐姐和我,我听了非常着迷,坐在椅子上动都不动。他们提到整个城市被大火笼罩,炸弹掉在他们家附近,还有童年时期建立的坚强友谊,连战火、时间都无法摧毁的坚强友谊。 ? 其中有
个故事,一直留在我心里…… ? 我妈妈小时候住在慕尼黑近郊。她说她六岁的时候,有一天听见大街上传来一阵嘈杂的声音。她跑到外面一看,发现有一群犹太人正被押解到附近的达豪集中营。队伍的最后是一位精疲力竭的老人,他已经快跟不上队伍的脚步了。有个男孩子看到老人的惨状后,飞
奔回家拿了一片面包给这位老人。老人感激地跪下来亲吻这位少年的脚踝。结果有个士兵发现了,走过来抢走了老人手上的面包,并用力鞭打了老人。随后士兵转身追赶那个男孩,把男孩也打了一顿。在同一时刻里,伟大的人性尊贵与残酷的人类暴力并存。我认为这恰好可以阐释人性的本质。 ?
听了这些故事之后,我一直想把它们写成一本小书。结果就是《偷书贼》的诞生。而《偷书贼》这本书对我的意义,远远超过我当初的想象。对我来讲,《偷书贼》就是我生命的全部。不管别人怎么看这本书,不管评价是好是坏,我内心明白,这是我最好的一次创作。身为作者,当然会为自己“最
好的一次创作”深感满意。再次感谢您,并致以诚挚的祝福!? ?马克斯/苏萨克 2007年7月27日 ? 【背景概览】 5.《致中国读者的信》放在《偷书贼》(孙张静/译,代谢联合出版公司2014年版)正文之前。你认为作者写这封信有哪些用意?(3分) 答: 6.阅读《致中国读者的信》,从下列选
高考数学七种函数类型解题技巧归纳
2013年高考数学七种函数类型解题技巧归纳一:函数解析式的求法函数解析式的问题是高考的命题热点,其求解方法很多,最常用的有以下几种:①换元法和配凑法;②待定系数法:适用于已知函数模型(如指数函数、二次函数等)和模型满足的条件下解析式,一般先设出函数的解析式,然后再根据题设条件待定系数;③解方程组法;④函数的性质法,在求某些函数解析式时,只给出了部分条件(如函数的定义域、经过某些特殊点、部分关系式、部分图象特征等)这类问题具有抽象性、综合性、和技巧性等特点,需要利用函数的性质来解;⑤赋值法:所给函数有两个变量时,可对这两个变量赋予特殊数值代入,或给两个变量赋予一定的关系代入,再用已知条件,可求出未知函数,至于赋予什么特殊值,应根据题目特征而定。
二:巧解函数定义域问题1.根据函数的解析式求函数的定义域,主要从以下几个方面来考虑:分式中分母不为零;2.复合型函数定义域的问题包含两类:一类是已知原函数的定义域来求复合函数的定义域,只需满足,解出即可;一类是已知复合函数的定义域来求原函数的定义域,即的值域为的定义域;三:判断函数单调性的方法巧掌握1.定义法。
2.利用一些常见函数的单调性,如一次函数、二次函数、幂函数、指数函数、对数函数、三角函数的单调性加以判断。
3.图象法。
4.在共同的定义域上,两个增(减)函数的和仍为增(减)函数;一个增(减)函数与一个减(增)函数的差是增(减)函数。
5.奇函数在关于原点的对称区间上具有相同的单调性;偶函数在关于原点的对称区间上具有相反的单调性。
6.互为反函数的两个函数在各自的定义域区间上具有相同的单调性。
7.对于复合函数的单调性,遵循“同增异减”的原则,即只有内外层函数相同时则为增函数,一增一减则为减函数。
8.导数法,函数在某区间内可导,如果,则函数为增函数,如果,则函数为减函数。
四:函数奇偶性的判断方法及解题策略确定函数的奇偶性,一般先考查函数的定义域是否关于原点对称,然后判断与的关系,常用方法有:①利用奇偶性定义判断;②利用图象进行判断,若函数的图象关于原点对称则函数为奇函数,若函数的图象关于轴对称则函数为偶函数;③利用奇偶性的一些常见结论:奇奇奇,偶偶偶,奇奇偶,偶偶偶,偶奇奇,奇奇偶,偶偶偶,奇偶奇,偶奇奇;④对于偶函数可利用,这样可以避免对自变量的繁琐的分类讨论。
专题 函数表达式 定义域 值域的求解
学 大 教 育 个 性 化 教 学 学 案函数解析式的求法:一、待定系数法:已知函数类型如:一次、二次函数、反比例函数等。
已知)(x f 的类型时,可设出含参数的表达式,再根据已知条件,列方程或方程组,从而求出待定的参数,求得)(x f 的表达式。
1.已知函数f(x)是一次函数,且满足关系式3f(x+1)-2f(x-1)=2x+17,求f(x)的解析式。
2已知f (x )为二次函数,且f (x )+f (2x )=5x 2+3x+2,求f (x )的解析式。
二、换元法:已知))((x g f 的表达式,欲求)(x f ,我们常设)(x g t =,从而求得)(1t g x -=,然后代入))((x g f 的表达式,从而得到)(t f 的表达式,即为)(x f 的表达式。
已知,求f (x )的解析式。
三、配凑法:若已知))((x g f 的表达式,欲求)(x f 的表达式,用换元法有困难时,(如)(x g 不存在反函数)可把)(x g 看成一个整体,把右边变为由)(x g 组成的式子,再换元求出)(x f 的式子。
已知已知f(x-1)= 2x -4x ,求f(x)的解析式。
已知,求f(x)的解析式。
四、消元法:如自变量互为倒数、已知f (x )为奇函数且g (x )为偶函数等)若已知以函数为元的方程形式,若能设法构造另一个方程,组成方程组,再解这个方程组,求出函数元,称这个方法为消元法。
4 ,求f(x)的解析式。
姓 名 年 级 性 别课 题函数“三要素”综合教 学 目 的 1.掌握函数解析式的求解。
2.掌握函数定义域的求解。
3.掌握函数值域的求解。
教 学 重 难 点函数解析式、定义域、值域的求解。
教 学 过 程(内容可附后)1(1)已知2(1)lg f x x+=,求()f x ;(2)已知()f x 是一次函数,且满足3(1)2(1)217f x f x x +--=+,求()f x ;(3)已知()f x 满足12()()3f x f x x+=,求()f x .2 (1)已知f (x )是一次函数,且f[f (x )]=4x -1,求f (x )的解析式(2)已知11664)14(2++=+x x x f ,求f (x )的解析式;1) 312)(-=x x f 或f (x )=-2x+1 (2) 225)(2+-+=x x x x f函数的定义域求法:1、具体函数的定义域的求解:求用解析式()y f x =表示的函数的定义域时,常有以下几种情况: (1)若()f x 是分式,则函数的定义域是使分母不等于0的实数集;(2)若()f x 是偶次根式,则函数的定义域是使(被开方数)根号内的式子大于或等于0的实数集合;(3)若()f x 是对数函数,则函数的真数要大于0; (4)若0()f x x =,则x 不等于0 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一)求函数的解析式之蔡仲巾千创作
1、函数的解析式暗示函数与自变量之间的一种对应关系,是函数与自
变量建立联系的一座桥梁,其一般形式是y=f(x),不克不及把它写
成f(x,y)=0;
2、求函数解析式一般要写出定义域,但若定义域与由解析式所确定的
自变量的范围一致时,可以不标出定义域;一般地,我们可以在求解函
数解析式的过程中确保恒等变形;
3、求函数解析式的一般方法有:
(1)直接法:根据题给条件,合理设置变量,寻找或构造变量之间的
等量关系,列出等式,解出y。
(2)待定系数法:若明确了函数的类型,可以设出其一般形式,然后
代值求出参数的值;
(3)换元法:若给出了复合函数f[g(x)]的表达式,求f(x)的
表达式时可以令t=g(x),以换元法解之;
(4)构造方程组法:若给出f(x)和f(-x),或f(x)和f
(1/x)的一个方程,则可以x代换-x(或1/x),构造出另一个方
程,解此方程组,消去f(-x)(或f(1/x))即可求出f(x)的表
达式;
(5)根据实际问题求函数解析式:设定或选取自变量与因变量后,寻
找或构造它们之间的等量关系,列出等式,解出y的表达式;要注意,
此时函数的定义域除了由解析式限定外,还受其实际意义限定。
(二)求函数定义域
1、函数定义域是函数自变量的取值的集合,一般要求用集合或区间来
暗示;
2、罕见题型是由解析式求定义域,此时要认清自变量,其次要考查自
变量所在位置,位置决定了自变量的范围,最后将求定义域问题化归为
解不等式组的问题;
3、如前所述,实际问题中的函数定义域除了受解析式限制外,还受实
际意义限制,如时间变量一般取非负数,等等;
4、对复合函数y=f[g(x)]的定义域的求解,应先由y=f(u)求
出u的范围,即g(x)的范围,再从中解出x的范围I1;再由g(x)
求出y=g(x)的定义域I2,I1和I2的交集即为复合函数的定义域;
5、分段函数的定义域是各个区间的并集;
6、含有参数的函数的定义域的求解需要对参数进行分类讨论,若参数
在分歧的范围内定义域纷歧样,则在叙述结论时分别说明;
7、求定义域时有时需要对自变量进行分类讨论,但在叙述结论时需要
对分类后求得的各个集合求并集,作为该函数的定义域;
(三)求函数的值域
1、函数的值域即为函数值的集合,一般由定义域和对应法则确定,经
常使用集合或区间来暗示;
2、在函数f:A→B中,集合B未必就是该函数的值域,若记该函数的
值域为C,则C是B的子集;若C=B,那么该函数作为映射我们称为
“满射”;
3、分段函数的值域是各个区间上值域的并集;
4、对含参数的函数的值域,求解时须对参数进行分类讨论;叙述结论
时要就参数的分歧范围分别进行叙述;
5、若对自变量进行分类讨论求值域,应对分类后所求的值域求并集;
6、求函数值域的方法十分丰富,应注意总结
函 数 解 析 式 的 七 种 求 法
一、
待定系数法:在已知函数解析式的构造时,可用待定系数法。
例1 设)(xf是一次函数,且34)]([xxff,求
)(xf
解:设baxxf)()0(a,则
二、
配凑法:已知复合函数[()]fgx的表达式,求()fx的解析式,
[()]fgx
的表达式容易配成()gx的运算形式时,经常使用配凑法。但要注意所求
函数()fx的定义域不是原复合函数的定义域,而是()gx的值域。
例2 已知221)1(xxxxf)0(x ,求 ()fx的解析式
解:2)1()1(2xxxxf,
21xx
三、换元法:已知复合函数[()]fgx的表达式时,还可以用换元法求
()fx
的解析式。与配凑法一样,要注意所换元的定义域的变更。
例3 已知xxxf2)1(,求
)1(xf
解:令1xt,则1t,
2
)1(tx
四、代入法:求已知函数关于某点或者某条直线的对称函数时,一般用代入
法。
例4已知:函数)(2xgyxxy与的图象关于点)3,2(对称,求)(xg的解
析式
解:设),(yxM为)(xgy上任一点,且),(yxM为),(yxM关于点)3,2(的对
称点
则3222yyxx,解得:yyxx64 ,
点),(yxM在)(xgy上
把yyxx64代入得:
整理得
672xxy
五、构造方程组法:若已知的函数关系较为抽象简约,则可以对变量进
行置换,设法构造方程组,通过解方程组求得函数解析式。
例5 设,)1(2)()(xxfxfxf满足求
)(xf
解xxfxf)1(2)(①
显然,0x将x换成x1,得:
xxfx
f1)(2)1(
②
解①②联立的方程组,得:
例6 设)(xf为偶函数,)(xg为奇函数,又,11)()(xxgxf试求
)()(xgxf和
的解析式
解)(xf为偶函数,)(xg为奇函数,
又11)()(xxgxf① ,
用x替换x得:
11)()(x
xgxf
即11)()(xxgxf②
解①②联立的方程组,得
11)(2xxf, xxxg
21)(
六、赋值法:当题中所给变量较多,且含有“任意”等条件时,往往可
以对具有“任意性”的变量进行赋值,使问题具体化、简单化,从而求
得解析式。
例7 已知:1)0(f,对于任意实数x、y,等式)12()()(yxyxfyxf恒
成立,求
)(xf
解对于任意实数x、y,等式)12()()(yxyxfyxf恒成立,
无妨令0x,则有
1)1(1)1()0()(2yyyyyyfyf
再令 xy 得函数解析式为:
1)(2xxxf
七、递推法:若题中所给条件含有某种递进关系,则可以递推得出系列
关系式,然后通过迭加、迭乘或者迭代等运算求得函数解析式。
例8 设)(xf是定义在N上的函数,满足1)1(f,对任意的自然数ba,
都有abbafbfaf)()()(,求
)(xf
解Nbaabbafbfaf,)()()(,,
无妨令1,bxa,得:xxffxf)1()1()(,
又1)()1(,1)1(xxfxff故①
分别令①式中的1,21xn 得:
将上述各式相加得:nfnf32)1()(,
