七年级数学思维探究(24)认识三角形(含答案)
苏科版2020-2021学年七年级数学下册7.4认识三角形考点同步训练(含答案)

苏科版2020-2021 学年七年级数学下册7.4 认识三角形考点同步训练考点一.三角形:1.如图,图中直角三角形共有()A.1 个B.2 个C.3 个D.4 个2.某同学在纸上画了四个点,如果把这四个点彼此连接,连成一个图形,则这个图形中会有个三角形出现.3.如图,直角三角形的个数为.4.过A、B、C、D、E 五个点中任意三点画三角形;(1)其中以AB 为一边可以画出个三角形;(2)其中以C 为顶点可以画出个三角形.考点二.三角形的角平分线、中线和高:5.用三角板作△ABC 的边BC 上的高,下列三角板的摆放位置正确的是()A.B.C.D.6.以下是四位同学在钝角三角形△ABC 中画AC 边上的高,其中正确的是()A.B.C.D.7.在数学课上,同学们在练习画边AC 上的高时,出现下列四种图形,其中正确的是()A.B.C.D.8.如图,△ABC 中,∠BAC 是钝角,AD⊥BC、EB⊥BC、FC⊥BC,则下列说法正确的是()A.AD 是△ABC 的高B.EB 是△ABC 的高C.FC 是△ABC 的高D.AE、AF 是△ABC 的高9.如图,已知P 为直线l 外一点,点A、B、C、D 在直线l 上,且PA>PB>PC>PD,下列说法正确的是()A.线段PD 的长是点P 到直线l 的距离B.线段PC 可能是△PAB 的高C.线段PD 可能是△PBC 的高D.线段PB 可能是△PAC 的高10.如果一个三角形的三条高的交点恰是三角形的一个顶点,那么这个三角形是()A.锐角三角形B.钝角三角形C.直角三角形D.等边三角形11.如图,在四边形ABCD 中,AB∥CD,3AB=4AD=6CD,E 为AB 的中点.萧钟同学用无刻度的直尺先连接CE 交BD 于点F,再连接AF.则线段AF 是△ABD 的()A.中线B.高线C.角平分线D.中线、高线、角平分线(三线合一)12.如图,D、E 分别是△ABC 的边AC、BC 的中点,则下列说法不正确的是()A.DE 是△ABC 的中线B.BD 是△ABC 的中线C.AD=DC,BE=EC D.DE 是△BCD 的中线13.如图,AD⊥BC 于D,BE⊥AC 于E,CF⊥AB 于F,GA⊥AC 于A,在△ABC 中,AB边上的高为()A.AD B.GA C.BE D.CF14.如图,在△ABC 中,∠ACB=60°,∠BAC=75°,AD⊥BC 于D,BE⊥AC 于E,AD 与BE 交于H,则∠CHD=.15.在△ABC 中,AC=5cm,AD 是△ABC 中线,若△ABD 周长与△ADC 的周长相差2cm,则BA=cm.16.如图,在△ABC 中(AB>BC),AB=2AC,AC 边上中线BD 把△ABC 的周长分成30和20 两部分,求AB 和BC 的长.17.如图,△ABC 的周长是21cm,AB=AC,中线BD 分△ABC 为两个三角形,且△ABD的周长比△BCD 的周长大6cm,求AB,BC.18.已知:∠MON=40°,OE 平分∠MON,点A、B、C 分别是射线OM、OE、ON 上的动点(A、B、C 不与点O 重合),连接AC 交射线OE 于点D.设∠OAC=x°.(1)如图1,若AB∥ON,则①∠ABO 的度数是;②当∠BAD=∠ABD 时,x=;当∠BAD=∠BDA 时,x=.(2)如图2,若AB⊥OM,则是否存在这样的x 的值,使得△ADB 中有两个相等的角?若存在,求出x 的值;若不存在,说明理由.考点三.三角形的面积:19.如图,AD 是△ABC 的中线,DE 是△ADC 的高线,AB=3,AC=5,DE=2,那么点D 到AB 的距离是()A. B. C. D.2 20.如图,在△ABC 中,已知点E、F 分别是AD、CE 边上的中点,且S△BEF=4cm2,则S△ABC 的值为()A.1cm2 B.2cm2 C.8cm2 D.16cm221.已知AD 是△ABC 的中线,BE 是△ABD 的中线,若△ABC 的面积为18,则△ABE 的面积为(A.5 )B.4.5C.4 D.922.如图,D,E,F 分别是边BC,AD,AC 上的中点,若S 四边形的面积为3,则△ABC的面积是()A.5 B.6 C.7 D.8 23.如图,长方形ABCD 中,AB=4cm,BC=3cm,点E 是CD 的中点,动点P 从A 点出发,以每秒1cm 的速度沿A→B→C→E 运动,最终到达点E.若点P 运动的时间为x 秒,那么当x =时,△APE 的面积等于5.24.把一张三角形的纸折叠成如图后,面积减少,已知阴影部分的面积是50 平方厘米,则这张三角形纸的面积是平方分米.考点四.三角形的稳定性:25.如图,工人师傅砌门时,常用木条EF 固定长方形门框ABCD,使其不变形,这样做的根据是()A.两点之间的线段最短B.三角形具有稳定性C.长方形是轴对称图形D.长方形的四个角都是直角26.下列图形中不具有稳定性是()A.B.C.D.27.用八根木条钉成如图所示的八边形木架,要使它不变形,至少要钉上木条的根数是()A.3 根B.4 根C.5 根D.6 根考点五.三角形的重心:28.三角形的重心是()A.三角形三条边上中线的交点B.三角形三条边上高线的交点C.三角形三条边垂直平分线的交点D.三角形三条内角平分线的交点29.在Rt△ABC 中,AD 是斜边BC 边上的中线,G 是△ABC 重心,如果BC=6,那么线段AG 的长为.考点六.三角形三边关系:30.下列长度的三条线段能组成三角形的是()A.3,4,8 B.5,6,11 C.5,6,10 D.1,2,3 31.如图,为估计池塘岸边A、B 两点的距离,小方在池塘的一侧选取一点O,测得OA=15 米,OB=10 米,A、B 间的距离不可能是()A.5 米B.10 米C.15 米D.20 米32.已知关于x 的不等式组至少有两个整数解,且存在以3,a,7 为边的三角形,则a 的整数解有()A.4 个B.5 个C.6 个D.7 个33.若a、b、c 为△ABC 的三边长,且满足|a﹣4|+=0,则c 的值可以为()A.5 B.6 C.7 D.834.已知三角形两边的长分别是4 和10,则此三角形第三边的长可能是()A.5 B.6 C.12 D.1635.△ABC 中,AB=10,BC=2x,AC=3x,则x 的取值范围.36.在△ABC 中,若AB=4,BC=2,且AC 的长为偶数,则AC=.37.若a、b、c 为三角形的三边,且a、b 满足+(b﹣2)2=0,第三边c 为奇数,则c=.38.三角形的两边长分别是3 和4,第三边长是方程x2﹣13x+40=0 的根,则该三角形的周长为.39.如图:已知AD 为△ABC 的中线,且∠1=∠2,∠3=∠4,求证:BE+CF>EF.40.在△ABC 中,AB=5,AC=3,AD 是BC 边上的中线,则AD 的取值范围是.参考答案1.解:如图,图中直角三角形有Rt△ABD、Rt△BDC、Rt△ABC,共有3 个,故选:C.2.解:∵①当四个点共线时,不能作出三角形;②当三个点共线,第四个点不在这条直线上时,能够画出3 个三角形;③若4 个点能构成凹四边形,则能画出4 个三角形;④当任意的三个点不共线时,则能够画出8 个三角形.∴0 或3 或4 或8.3.解:如图,直角三角形有:△ADC、△BCD、△CDE、△BDE、△ACE、△ACB,一共6 个,故答案为:6.4.解:(1)如图,以AB 为一边的三角形有△ABC、△ABD、△ABE 共3 个;(2)如图,以点C 为顶点的三角形有△ABC、△BEC、△BCD、△ACE、△ACD、△ CDE 共6 个.故答案为:(1)3,(2)6.5.解:B,C,D 都不是△ABC 的边BC 上的高,故选:A.6.解:A、高BD 交AC 的延长线于点D 处,符合题意;B、没有经过顶点B,不符合题意;C、做的是BC 边上的高线AD,不符合题意;D、没有经过顶点B,不符合题意.故选:A.7.解:AC 边上的高应该是过B 作垂线段AC,符合这个条件的是C;A,B,D 都不过B 点,故错误;故选:C.8.解:△ABC 中,画BC 边上的高,是线段AD.故选:A.9.解:A.线段PD 的长不一定是点P 到直线l 的距离,故本选项错误;B.线段PC 不可能是△PAB 的高,故本选项错误;C.线段PD 可能是△PBC 的高,故本选项正确;D.线段PB 不可能是△PAC 的高,故本选项错误;故选:C.10.解:一个三角形的三条高的交点恰是三角形的一个顶点,这个三角形是直角三角形.故选:C.11.解:∵3AB=6CD,E 为AB 的中点,∴CD=AB,BE=AB,∴CD=BE,又∵AB∥CD,∴∠EBF=∠CDF,又∵∠EFB=∠CFD,∴△BEF≌△DCF(AAS),∴BF=DF,∴线段AF 是△ABD 的中线,故选:A.12.解:∵D、E 分别是△ABC 的边AC、BC 的中点,∴DE 是△ABC 的中位线,不是中线;BD 是△ABC 的中线;AD=DC,BE=EC;DE 是△BCD 的中线;故选:A.13.解:∵AB 边上的高是指过顶点C 向AB 所在直线作的垂线段,∴在AD⊥BC 于D,BE⊥AC 于E,CF⊥AB 于F,GA⊥AC 于A 中,只有CF 符合上述条件.故选:D.14.解:延长CH 交AB 于点H,在△ABC 中,三边的高交于一点,所以CF⊥AB,∵∠BAC=75°,且CF⊥AB,∴∠ACF=15°,∵∠ACB=60°,∴∠BCF=45°在△CDH 中,三内角之和为180°,∴∠CHD=45°,故答案为∠CHD=45°.15.解:如图,∵AD 是△ABC 中线,∴BD=CD,∴△ABD 周长﹣△ADC 的周长=(BA+BD+AD)﹣(AC+AD+CD)=BA﹣AC,∵△ABD 周长与△ADC 的周长相差2cm,∴|BA﹣5|=2,∴解得BA=7 或3.故答案为:3 或7.16.解:设AC=x,则AB=2x,∵BD 是中线,∴AD=DC=x,由题意得,2x+x=30,解得,x=12,则AC=12,AB=24,∴BC=20﹣×12=14.答:AB=24,BC=14.17.解:∵BD 是中线,∴AD=CD=AC,∵△ABD 的周长比△BCD 的周长大6cm,∴(AB+AD+BD)﹣(BD+CD+BC)=AB﹣BC=6cm①,∵△ABC 的周长是21cm,AB=AC,∴2AB+BC=21cm②,联立①②得:AB=9cm,BC=3cm.18.解:(1)①∵∠MON=40°,OE 平分∠MON,∴∠AOB=∠BON=20°,∵AB∥ON,∴∠ABO=20°,②∵∠BAD=∠ABD,∴∠BAD=20°,∵∠AOB+∠ABO+∠OAB=180°,∴∠OAC=120°,∵∠BAD=∠BDA,∠ABO=20°,∴∠BAD=80°,∵∠AOB+∠ABO+∠OAB=180°,∴∠OAC=60°;故答案为:①20°;②120,60;(2)①当点D 在线段OB 上时,∵OE 是∠MON 的角平分线,∴∠AOB=∠MON=20°,∵AB⊥OM,∴∠AOB+∠ABO=90°,∴∠ABO=70°,若∠BAD=∠ABD=70°,则x=20若∠BAD=∠BDA=(180°﹣70°)=55°,则x=35若∠ADB=∠ABD=70°,则∠BAD=180°﹣2×70°=40°,∴x=50②当点D 在射线BE 上时,因为∠ABE=110°,且三角形的内角和为180°,所以只有∠BAD=∠BDA,此时x=125.综上可知,存在这样的x 的值,使得△ADB 中有两个相等的角,且x=20、35、50、125.19.解:∵AC=5,DE=2,∴△ADC 的面积为=5,∵AD 是△ABC 的中线,∴△ABD 的面积为5,∴点D 到AB 的距离是.故选:A.20.解:∵由于E、F 分别为AD、CE 的中点,∴△ABE、△DBE、△DCE、△AEC 的面积相等,∴S△BEC=2S△BEF=8(cm2),∴S△ABC=2S△BEC=16(cm2).故选:D.21.解:∵AD 是△ABC 的中线,∴S△ABD=S△ABC=×18=9,∵BE 是△ABD 的中线,∴S△ABE=S△ABD=×9=4.5.故选:B.22.解:∵D 为BC 的中点,∴S△ABD=S△ACD=S△ABC,∵E,F 分别是边AD,AC 上的中点,∴S△BDE=S△ABD,S△ADF=S△ADC,S△DEF=S△ADF,∴S△BDE=S△ABC,S△DEF=S△ADC=S△ABC,S△BDE+S△DEF=S△ADC+ S△ABC=S△ABC,∴S△ABC=S 阴影部分=×3=8.故选:D.23.解:①如图1,当P 在AB 上时,∵△APE 的面积等于5,∴x•3=5,x=;②当P 在BC 上时,∵△APE 的面积等于5,∴S 长方形ABCD﹣S△CPE﹣S△ADE﹣S△ABP=5,∴3×4﹣(3+4﹣x)×2﹣×2×3﹣×4×(x﹣4)=5,x=5;③当P 在CE 上时,∴ (4+3+2﹣x)×3=5,x=<3+4,此时不符合;故答案为:或5.24.解:∵折叠后面积减少,∴阴影部分的面积占三角形纸的面积的(1﹣﹣)=,∴三角形纸的面积=50÷ =200 平方厘米=2 平方分米.故答案为:2.25.解:加上EF 后,原图形中具有△AEF 了,故这种做法根据的是三角形的稳定性.故选:B.26.解:根据三角形具有稳定性,只要图形分割成了三角形,则具有稳定性.显然B 选项中有四边形,不具有稳定性.故选:B.27.解:过八边形的一个顶点作对角线,可以做5 条,把八边形分成6 个三角形,因为三角形具有稳定性.故选:C.28.解:三角形的重心是三条中线的交点,故选:A.29.解:∵AD 是斜边BC 边上的中线,∴AD=BC=×6=3,∵G 是△ABC 重心,∴=2,∴AG=AD=×3=2.故答案为2.30.解:3+4<8,则3,4,8 不能组成三角形,A 不符合题意;5+6=11,则5,6,11 不能组成三角形,B 不合题意;5+6>10,则5,6,10 能组成三角形,C 符合题意;1+2=3,则1,2,3 不能组成三角形,D 不合题意,故选:C.31.解:连接AB,根据三角形的三边关系定理得:15﹣10<AB<15+10,即:5<AB<25,∴A、B 间的距离在 5 和25 之间,∴A、B 间的距离不可能是5 米;故选:A.32.解:解不等式①,可得x<a,解不等式②,可得x≥4,∵不等式组至少有两个整数解,∴a>5,又∵存在以3,a,7 为边的三角形,∴4<a<10,∴a 的取值范围是5<a<10,∴a 的整数解有4 个,故选:A.33.解:∵|a﹣4|+ =0,∴a﹣4=0,a=4;b﹣2=0,b=2;则4﹣2<c<4+2,2<c<6,5 符合条件;故选:A.34.解:设第三边的长为x,∵三角形两边的长分别是4 和10,∴10﹣4<x<10+4,即6<x<14.故选:C.35.解:根据题意得:3x﹣2x<10<3x+2x,解得:2<x<10.故答案为:2<x<10.36.解:因为4﹣2<AC<4+2,所以2<AC<6,因为AC 长是偶数,所以AC 为4,故答案为:4.37.解:∵a、b 满足+(b﹣2)2=0,∴a=9,b=2,∵a、b、c 为三角形的三边,∴7<c<11,∵第三边c 为奇数,∴c=9,故答案为9.38.解:x2﹣13x+40=0,(x﹣5)(x﹣8)=0,所以x1=5,x2=8,而三角形的两边长分别是3 和4,所以三角形第三边的长为5,所以三角形的周长为3+4+5=12.故答案为12.39.证明:延长ED 到H,使DE=DH,连接CH,FH,∵AD 是△ABC 的中线,∴BD=DC,∵DE、DF 分别为∠ADB 和∠ADC 的平分线,∴∠1=∠2=∠ADB,∠3=∠4=∠ADC,∴∠1+∠4=∠2+∠3=∠ADB+ ∠ADC=×180°=90°,∵∠1=∠5,∴∠5+∠4=90°,即∠EDF=∠FDH=90°,在△EFD 和△HFD 中,,∴△EFD≌△HFD(SAS),∴EF=FH,在△BDE 和△CDH 中,,∴△BDE≌△CDH(SAS),∴BE=CH,在△CFH 中,由三角形三边关系定理得:CF+CH>FH,∵CH=BE,FH=EF,∴BE+CF>EF.40.解:如图,延长AD 到E,使DE=AD,∵AD 是BC 边上的中线,∴BD=CD,在△ABD 和△ECD 中,,∴△ABD≌△ECD(SAS),∴CE=AB,∵AB=5,AC=3,∴5﹣3<AE<5+3,即2<AE<8,1<AD<4.故答案为:1<AD<4.。
新版精编2019年七年级下册数学单元测试题《三角形的初步认识》完整题(含答案)

2019年七年级下册数学单元测试题第一单元 三角形的初步认识一、选择题1.如图,CD 是△ABC 的中线,DE 是△ACD 的中线,BF 是△ADE 的中线,若△AEF 的面积是 1cm 2,则△ABC 的面积是( )A . 4cm 2B .5 cm 2C . 6 cm 2D .8 cm 2答案:D2.如图,AD ,BE 都是△ABC 的高,则与∠CBE 一定相等的角是( )A .∠ABEB .∠BADC .∠DACD .以上都不是答案:C3.如图,直线123,,l l l 表示三条相互交叉的公路,现要建造一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有( )A .一处B .两处C .三处D .四处答案:D4.如图所示,由∠ABC=∠DCB ,∠ACB=∠DBC ,直接能判定全等的三角形是 ( )A .△AB0≌△DODB .△ABC ≌△DCB C .△ABD ≌△DCA D .△OAD ≌△0BC答案:B5.如图所示,在Rt △ABC 中,∠BAC=90°,AD 是高,则图中互余的角有( )A . 2对B .3对C .4对D .5对答案:C6.将矩形ABCD 沿AE 折叠.得到如图所示的图形,已知∠CED ′=60°.那么∠AED 的大小是( )A .50°B .55°C .60°D .75°答案:C7.以下列各组线段的长为边,能构成三角形的是( )A .4 cm ,5 cm ,6 cmB .2 cm ,3 cm ,5 cmC .4 cm ,4 cm 。
9 cmD .12 cm ,5 cm ,6 cm答案:A8.一个三角形的两边长分别是3和6,第三边长为奇数,那么第三边长是( )A 5或7B .7或9C .3或5D .9答案:A二、填空题9.在△ABC 和△DEF 中,AB=4,,∠A=35°,∠B =70°, DE=4 ,∠D = ,∠E=70°,根据 判定△ABC ≌△DEF.解析:35°, ASA10.如图,AB =AC ,要使ACD ABE ∆∆≌,应添加的条件是____________ (添加一个条件即可)解析:B C ∠=∠(答案不唯一)11.在ABC △中,BC 边不动,点A 竖直向上运动,A ∠越来越小,BC ∠∠,越来越大.若A ∠减少α度,B ∠增加β度,C ∠增加γ度,则αβγ,,三者之间的等量关系是 .解析:αβγ=+12.已知BD 是ΔABC 的一条中线, 如果ΔABD 和ΔBCD 的周长分别是21,12,则BC AB -的长是 .解析:913.在下列条件中:①∠A+∠B=∠C ;②∠A ∶∠B ∶∠C=1∶2∶3;③∠A=900-∠B ;④∠A=∠B=12∠C 中,能确定△ABC 是直角三角形的条件有 个. 解析:414.如图所示:(1)若△ABD ≌△ACE ,AB=AC ,则对应边还有 ,对应角有 .(2)若△BOE ≌△COD ,则0E 的对应边是 ,∠EB0的对应角是 ;(3)若△BEC ≌△CDB ,则相等的边有 .解析: (3)BE=CD ,CE=BD ,BC=CB (1)AD 与AE ,BD 与CE ;∠A 与∠A ,∠ABD 与∠ACE ,∠ADB 与∠AEC ;(2)OD ,∠DCO ;15.如图所示,已知点D ,E ,F 分别是BC ,AC ,DC 的中点,△EFC 的面积为6 cm 2,则△ABC 的面积为 .解析:48cm 216.已知△ABC 三边为a,b ,c ,且a ,b 满足21(3)0a b -+-=,c 为整数,则c 的取值为 .解析:3三、解答题17.如图,DB 是△ABC 的高,AE 是∠BAC 的角平分线,∠BAE=26°,求∠BFE 的度数.解析:64°18.如图所示,已知∠α,线段a,b,求作一个三角形,使其两边长分别为a,a+b,两边的夹角等于∠α.解析:略19.如图所示,已知线段a,b和∠α,用直尺和圆规作△ABC,使∠B=∠α,AB=a,BC=b.解析:略20.如图所示,已知∠E=∠F=90°,∠B=∠C,AE=AF,则以下结论有哪些是成立的?并挑选一个将理由补充完整.①∠1=∠2;②BE=CF;③CD=FN;④△AEM≌△AFN.成立的有:.我选,理由如下:解析:①②④,以下略21.如图所示,已知AD=AE,∠l=∠2.请说明OB=OC成立的理由.解析:略22.如图所示,以Rt△ABC的两直角边AB,BC为边向外作正△ABE和正△BCF,连结EF,EC,请说明EF=EC.解析:略23.如图所示,四边形ABCD 中,AB=CD,BC=AD,请你添一条辅助线,把它分成两个全等的三角形.你有几种添法?分别说明理由.解析:连结AC或连结BD,都是根据SSS说明三角形全等24.请你在如图所示的方格纸中,画一个与左上角已有图形全等的图形.解析:略25.如图所示,把△ACB沿着AB翻转,点C与点D重合,请用符号表示图中所有的全等三角形.解析:△ACE≌△ADE,△BCE≌△BDE,△ACB≌△ADB26.如图所示为由6个面积为1的小正方形组成的矩形,点A,B,C,D,E,F,G是小正方形的顶点,以这7个点中的任意三个点为顶点,可组成多少个面积为1的三角形?请写出所有满足条件的三角形.解析:共l4个三角形,具体表示略27.A,B是平面上的两个固定点,它们之间的距离为5 cm,请你在平面上找一点C(1)要使点C到A,B两点的距离之和等于5 cm ,则C点在什么位置?(2)要使点C到A,B两点的距离之和大于5 cm ,则点C在什么位置?(3)能使点C到A,B两点的距离之和小于5 cm吗?为什么?解析:(1)点C在线段AB上;(2)点C在线段AB外;(3)不能,因为两点之间线段最短(为5 cm)28.如图所示,已知△ABC.画出AC边上的中线BM和∠BAC的平分线AD.解析:略29.已知△ABC中,以点A为顶点的外角为120°,∠B=30°,求∠C的度数.解析:∠C=90°30.如图所示,在Rt △ABC中,∠ACB为直角,∠CAD的平分线交BC的延长线于点E,若∠B=35°,求∠BAE和∠E的度数.解析:∠E=27.5°,∠BAF=117.5°。
七年级数学三角形全等之动点问题(建等式)(北师版)(专题)(含答案)

三角形全等之动点问题(建等式)(北师版)(专题)一、单选题(共8道,每道10分)1.已知:如图,等边△ABC的边长为8,点D是BC上一点,且BD=6.动点P从点C出发,以每秒2个单位的速度沿CA—AB—BC向终点C运动,连接AD,AP,BP.设点P运动的时间为t秒.解答下列问题:(1)当4≤t≤8时,线段AP的长可用含t的式子表示为( )A.2tB.-2t+16C.2t-8D.-2t+8答案:C解题思路:点P速度已知,可判断此题为动点问题,按照动点问题的解决方法解决:1.研究基本图形,标注:2.研究动点运动状态,包括起点、终点、状态转折点、速度、时间范围,如图:3.表达线段长,建等式.由题意,点P在运动过程中有2个状态转折点,需分成3种情况:①点P在CA上,对应的时间范围:0≤t≤4;②点P在AB上,对应的时间范围:4<t≤8;③点P在BC上,对应的时间范围:8<t≤12.由题意,当4≤t≤8时,点P在线段AB上运动,如图:点P已走路程为CA+AP=2t,因此AP=2t-CA=2t-8.故选C.试题难度:三颗星知识点:动点问题2.(上接第1题)(2)当点P在AC上运动时,若某一时刻△ABP≌△BAD,则t的值为( )A.1B.2C.3D.4答案:A解题思路:当点P在CA上时,即0≤t≤4,在等边△ABC中,AB=BA=8,∠BAP=∠ABD=60°,要使△ABP≌△BAD,则需AP=BD,即8-2t=6,解得t=1.故选A.试题难度:三颗星知识点:动点问题3.已知:如图,在长方形ABCD中,AB=4,AD=6.点E是BC上一点,CE=2,连接DE.动点P从点D出发,以每秒2个单位的速度沿DA-AB-BC向终点C运动,设点P的运动时间为t 秒.解答下列问题:(1)请你根据题意画出对应的运动状态分析图,并指出当P在DA,BC上运动时,对应的t 的取值范围分别为( )A.0≤t≤5;5<t≤8B.0≤t≤3;5≤t≤8C.0≤t≤3;3<t≤8D.0≤t≤3;3<t≤5答案:B解题思路:点P速度已知,可判断此题为动点问题,按照动点问题的解决方法解决:1.研究基本图形,标注:2.研究动点运动状态,包括起点、终点、状态转折点、速度、时间范围,如图:3.表达线段长,建等式.由题意,点P在运动过程中有2个状态转折点,需分成3种情况:①点P在DA上,对应的时间范围:0≤t≤3;②点P在AB上,对应的时间范围:3<t≤5;③点P在BC上,对应的时间范围:5<t≤8.故选B.试题难度:三颗星知识点:动点问题4.(上接第3题)(2)当P在BC上运动时,线段BP的长可用含t的式子表示为( )A.2t-10B.2tC.-2t+10D.-2t+16答案:A解题思路:当P在BC上运动时,如图:点P已走路程为DA+AB+BP=2t,则BP=2t-DA-AB=2t-10.故选A.试题难度:三颗星知识点:动点问题5.(上接第3,4题)(3)连接AP,BP.若△ABP和△DEC全等,则此时t的值为( )秒A.2B.1或7C.1或6D.2或6答案:D解题思路:根据点P的运动状态分三种情况分析:①当点P在DA上运动时,0≤t≤3;∵AB=CD且∠A=∠C=90°,∴点A和点C,点P和点E是对应点,∴△ABP≌△CDE,∴AP=CE,即6-2t=2,解得:t=2;②当点P在AB上运动时,3<t≤5,不符合题意,舍去;③当点P在BC上运动时,5<t≤8,∵AB=CD且∠B=∠C=90°,∴点B和点C,点P和点E是对应点,∴△BAP≌△CDE,∴BP=CE,即2t-10=2,解得:t=6.综上,当t=2或6时,△ABP和△DEC全等.故选D.试题难度:三颗星知识点:动点问题6.已知:如图,在△ABC中,AB=AC=18,BC=12,点D为AB的中点.点P在线段BC上以每秒3个单位的速度由B点向C点运动,同时点Q在线段CA上由C点向A点以每秒a个单位的速度匀速运动,连接DP,QP.设点P的运动时间为t秒,解答下列问题:(1)根据点P的运动,对应的t的取值范围为( )A.0≤t≤4B.0≤t≤6C.0≤t≤12D.0≤t≤18答案:A解题思路:点P速度已知,可判断此题为动点问题,按照动点问题的解决方法解决:①研究基本图形,标注:②研究动点运动状态,包括起点、终点、状态转折点、速度、时间范围,如图:③表达线段长,建等式.由点P的运动状态可知,对应的t的取值范围为0≤t≤4.故选A.试题难度:三颗星知识点:动点问题7.(上接第6题)(2)根据点P的运动,线段BP,PC的长可用含t的式子分别表示为( )A.at;3tB.3t;atC.12-3t;3tD.3t;12-3t答案:D解题思路:由题意,线段BP为点P已走路程,∴BP=3t,PC为点P未走路程,∴PC=12-3t.故选D.试题难度:三颗星知识点:动点问题8.(上接第6,7题)(3)若某一时刻△BPD与△CQP全等,则t的值与相应的CQ的长为( )A.t=2,CQ=9B.t=1,CQ=3或t=2,CQ=9C.t=1,CQ=3或t=2,CQ=6D.t=1,CQ=3答案:B解题思路:由题意,△BPD与△CQP全等,对应关系不明确,首先分析其对应情况,∵∠B=∠C,∴B和C是对应点,因此应分为两种情况:①△BPD≌△CQP,此时即解得②△BPD≌△CPQ,此时即解得综上:当t=1,CQ=3或t=2,CQ=9时,△BPD与△CQP全等.故选B.试题难度:三颗星知识点:动点问题。
七年级下册数学三角形测试题(含答案)(有代表性测试题)

D
A
B
第 20 题图
四、拓广探索
22.已知,如图,在△ ABC 中,AD,AE 分别是 △ ABC 的高和角平分线,
若∠B=30°,∠C=50°.
A
(1)求∠DAE 的度数。
(2)试写出 ∠DAE 与∠C-∠B 有何关系?(不必证明)
B
ED C
第 26 题图
-3-
第七章三角形
23.如图,已知 D 为△ABC 边 BC 延长线上一点,DF⊥AB 于 F 交 AC 于 E,∠A=35°,∠D=42°,求∠ACD 的度数.
所以∠ACD=180°-∠CED-∠D=180°-55°-42=83°.
28.解:设∠DAE=x,则∠BAC=40°+x. 因为∠B=∠C,所以 2∠2=180°-∠BAC,
∠C=90°- 1 ∠BAC=90°- 1 (40°+x). 同理∠AED=90°- 1 ∠DAE=90°- 1 x.
2
2
2
2
(∠C 除外)相等的角的个数是(
)
第 5 题图
A、3 个 B、4 个 C、5 个 D、6 个
6.如图,将一副三角板叠放在一起,使直角的顶点重合于 O, 则∠AOC+∠DOB=( )
A、900
B、1200
C、1600
D、1800
第 6 题图
7.以长为 13cm、10cm、5cm、7cm 的四条线段中的三条线段为边,可以画出三角形的个数是( )(A)1 个 (B)2 个 (C)3 个 (D)4 个 8.给出下列命题:①三条线段组成的图形叫三角形 ②三角形相邻两边组成的角叫三角形的内角 ③三 角形的角平分线是射线 ④三角形的高所在的直线交于一点,这一点不在三角形内就在三角形外 ⑤任何
北师大版七年级下册数学第四章 三角形含答案(综合题)
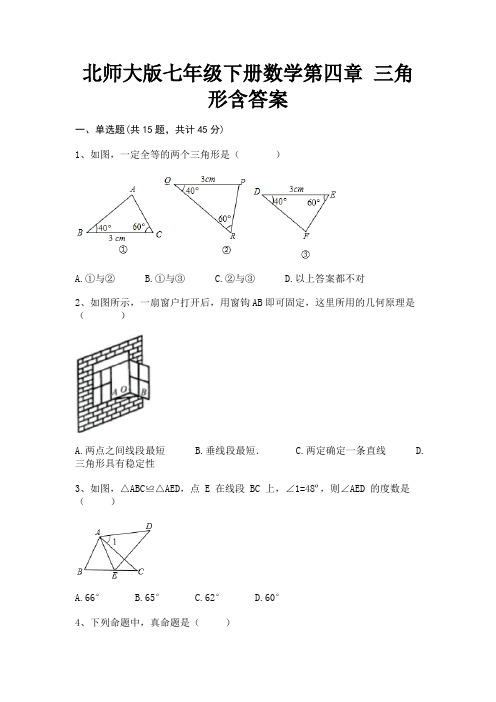
北师大版七年级下册数学第四章三角形含答案一、单选题(共15题,共计45分)1、如图,一定全等的两个三角形是()A.①与②B.①与③C.②与③D.以上答案都不对2、如图所示,一扇窗户打开后,用窗钩AB即可固定,这里所用的几何原理是()A.两点之间线段最短B.垂线段最短.C.两定确定一条直线D.三角形具有稳定性3、如图,△ABC≌△AED,点 E 在线段 BC 上,∠1=48º,则∠AED 的度数是()A.66°B.65°C.62°D.60°4、下列命题中,真命题是()A.周长相等的锐角三角形都全等B.周长相等的直角三角形都全等C.周长相等的钝角三角形都全等D.周长相等的等腰直角三角形都全等5、如图,△ABC和△CDE均为等腰直角三角形,点B,C,D在一条直线上,点M是AE的中点,下列结论:①tan∠AEC=;②四边形CGMH是矩形;③△EGM≌△MHA;④S△ABC +S△CDE≥S△ACE;⑤图中的相似三角形有10对.正确结论是()A.①②③④B.①②③⑤C.①③④D.①③⑤6、下列条件中,不能判定△ABC是直角三角形的是()A.∠A:∠B:∠C=3:4:5B.∠A ∠B= ∠CC.∠B=50°,∠C=40°D.a=5,b=12,c=137、以下列各组线段长为边,能组成三角形的是( )A.1cm,2cm,3cmB.2cm,3cm,8cmC.5cm,12cm,6cm D.4cm,6cm,9cm8、如图,在等边中,,点在上,且,点是上一动点,连结,将线段绕点逆时针旋转得到线段.要使点恰好落在上,则的长是()A. B. C. D.9、若△ABC∽△A'B'C',∠A=30°,∠C=110°,则∠B'的度数为()A.30°B.50°C.40°D.70°10、如图,中,于D,下列条件中:① ;②;③ ;④ ;⑤,⑥ ,一定能确定为直角三角形的条件的个数是()A.1B.2C.3D.411、如图,,,,,则A.27°B.54°C.30°D.55°12、如图,在△ABC中,∠C=40 ° ,按图中虚线将∠C剪去后,∠1+∠2等于().A.140°B.210°C.220°D.320°13、已知m是整数,以4m+5、2m-1、20-m这三个数作为同一个三角形三边的长,则满足条件的三角形个数有()A.0个B.1个C.2个D.无数个14、如图,矩形ABCD中,AB=3,AD=9,点E在边AD上,AE=1,过E、D两点的圆的圆心O在边AD的上方,直线BO交AD于点F,作DG⊥BO,垂足为G.当△ABF与△DFG全等时,⊙O的半径为()A. B. C. D.15、如图所示,在中,,于,,则线段的长是()A.3B.4C.8D.1二、填空题(共10题,共计30分)16、下列关于两个三角形全等的说法:①面积相等的两个三角形全等;②三条边对应相等的两个三角形全等;③有两角和其中一个角的对边对应相等的两个三角形全等;④有两边和一个角对应相等的两个三角形全等;⑤腰相等的两个等腰三角形一定全等.其中说法正确的是________.(填写序号)17、如图,△ABC中,∠ACB=90°,沿CD折叠△CBD,使点B恰好落在AC边上的点E处.若∠A=22°,则∠ADE=________°.18、如图,AB=AC,AD=AE,∠BAC=∠DAE,点D在线段BE上.若,∠2=30°,∠3=55°则∠1=________.19、已知等腰三角形的周长为20,腰长为x,则x的取值范围是________ .20、如图,中有6个条形方格图,图上由实线围成的图形是全等形的有哪几对________21、如图,△ABD与△AEC都是等边三角形,AB≠AC.下列结论中,正确的是________.①BE=CD;②∠BOD=60º;③△BOD∽△COE.22、已知,如图,AC=AE,∠1=∠2,AB=AD,若∠D=25°,则∠B的度数为________.23、若等腰三角形的两边长为3cm和7cm,则该等腰三角形的周长为________ cm.24、如图,在△ABC中,已知D,E,F分别为边BC,AD,CE的中点,且,则阴影部分的面积为________ cm2.25、三角形的一边是5,另一边是1,第三边如果是整数,则第三边是________.三、解答题(共5题,共计25分)26、如图,AB∥CD,AB=CD,CE=BF.请写出DF与AE的数量关系,并证明你的结论.27、如图,△ABC中,∠ACB=90°,AC=6,BC=8。
【同步练习】北师大版2019年 七年级数学下册 探索三角形全等的条件 同步练习(含答案)

北师大版七年级数学下册探索三角形全等的条件同步练习一、选择题1.如图,在△ABC和△DEF中,已有条件AB=DE,还需要添加两个条件才能使△ABC≌△DEF.不能添加的一组条件是()A.∠B=∠E,BC=EFB.∠A=∠D,BC=EFC.∠A=∠D,∠B=∠ED.BC=EF,AC=DF2.如图,已知∠1=∠2,要得到△ABD≌△ACD,还需从下列条件中补选一个,则错误的选法是()A.AB=AC B.DB=DC C.∠ADB=∠ADC D.∠B=∠C3.如图,在△ABC和△DEC中,已知AB=DE,还需添加两个条件才能使△ABC≌△DEC,不能添加的一组条件是()A.BC=EC,∠B=∠EB.BC=EC,AC=DCC.BC=DC,∠A=∠DD.∠B=∠E,∠A=∠D4.如图,AE=AF,AB=AC,EC与BF交于点O,∠A=60°,∠B=25°,则∠EOB的度数为()A.60°B.70°C.75°D.85°5.如图,已知AE=CF,∠AFD=∠CEB,那么添加下列一个条件后,仍无法判定△ADF≌△CBE的是()A.∠A=∠CB.AD=CBC.BE=DFD.AD∥BC6.已知△AB1C1,△A2B2C2的周长相等,现有两个判断:1①若A1B1=A2B2,A1C1=A2C2,则△A1B1C1≌△A2B2C2;②若∠A1=∠A2,∠B1=∠B2,则△A1B1C1≌△A2B2C2,对于上述的两个判断,下列说法正确的是()A.①正确,②错误B.①错误,②正确C.①,②都错误D.①,②都正确7.如图.从下列四个条件:①BC=B′C,②AC=A′C,③∠A′CA=∠B′CB,④AB=A′B′中,任取三个为条件,余下的一个为结论,则最多可以构成正确的结论的个数是()A.1个 B.2个 C.3个D.4个8.如下图,已知△ABE≌△ACD,∠1=∠2,∠B=∠C,不正确的等式是()A.AB=ACB.∠BAE=∠CADC.BE=DCD.AD=DE9.如图所示的4×4正方形网格中,∠1+∠2+∠3+∠4+∠5+∠6+∠7=()A.330°B.315°C.310°D.320°10.如图,已知在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点在同一条直线上,连接BD,BE.以下四个结论:①BD=CE;②∠ACE+∠DBC=45°;③BD⊥CE;④∠BAE+∠DAC=180°.其中结论正确的个数是()A.1B.2C.3D.4二、填空题11.如图示,点B在AE上,∠CBE=∠DBE,要使ΔABC≌ΔABD, 还需添加一个条件是__________.(填上你认为适当的一个条件即可)12.如图,已知∠1=∠2,AC=AD,请增加一个条件,使△ABC≌△AED,你添加的条件是.13.如图,在△ABC中,AB=AC,AD⊥BC于D点,E、F分别为DB、DC的中点,则图中共有全等三角形对.14..要测量河两岸相对的两点A,B的距离,先在AB的垂线BF上取两点C,D,使CD=BC,再定出BF的垂线DE,使A,C,E在一条直线上(如图所示),可以说明△EDC≌△ABC,得ED=AB,因此测得ED的长就是AB的长,判定△EDC≌△ABC最恰当的理由是15.如图,在△ABC中,AB=AC,BE、CF是中线,则由可得△AFC≌△AEB.16.如图,AD、A′D′分别是锐角△ABC和△A′B′C′中BC与B′C′边上的高.(只需填写一个你认为适当的条件)17.如图EB交AC于M,交FC于D,AB交FC于N,∠E=∠F=90°,∠B=∠C,AE=AF.给出下列结论:①∠1=∠2;②BE=CF;③△ACN≌△ABM;④CD=DN.其中正确的结论有(填序号).18.在平面直角坐标系中,点A(2,0),B(0,4),作△BOC,使△BOC与△ABO全等,则点C坐标为 .三、解答题19.如图,在△AEC中,点D是EC上的一点,且AE=AD,AB=AC,∠1=∠2.求证:BD=EC.20.如图,在△ABC,AB=AC,BD⊥AC于D,CE⊥AB于E,BD、CE相交于F.求证:AF平分∠BAC.21.如图,AB=AE,∠1=∠2,∠C=∠D.求证:△ABC≌△AED.22.如图,已知在四边形ABCD中,E是AC上一点,∠1=∠2,∠3=∠4.求证:∠5=∠6.23.如图,已知∠B+∠CDE=180°,AC=CE.求证:AB=DE.24.已知:在△ABC中,∠BAC=90°,AB=AC,AE是过点A的一条直线,且BD⊥AE于D,CE⊥AE于E.(1)当直线AE处于如图①的位置时,有BD=DE+CE,请说明理由;(2)当直线AE处于如图②的位置时,则BD、DE、CE的关系如何?请说明理由;(3)归纳(1)、(2),请用简洁的语言表达BD、DE、CE之间的关系.25.如图,△ABC中,∠BAC=90度,AB=AC,BD是∠ABC的平分线,BD的延长线垂直于过C点的直线于E,直线CE交BA的延长线于F.求证:BD=2CE.答案1.B.2.B3.C4.B5.B6.D7.B8.D9.B10.D11.答案为:BC=BD;12.答案为:AE=AB.13.答案为414.答案为:ASA15.答案为:SAS.16.添加∠C=∠C´,可以利用AAS判定其全等;还可添加AC=A′C′,∠CAD=∠C′A′D′等.17.答案为:①②③.18.答案为:(-2,0),(-2,4),(2,4);19.证明:∵∠1=∠2,∴∠1+∠DAC=∠2+∠DAC,即∠DAB=∠EAC,在△EAC和△DAB中,,∴△EAC≌△DAB(SAS),∴BD=EC.20.证明:∵BD⊥AC,CE⊥AB∴∠ADB=∠AEC=90∵∠BAD=∠CAE,AB=AC∴△ABD≌△ACE (AAS)∴AE=AD∵AF=AF∴△ADF≌△AEF (HL)∴∠BAF=∠CAF21.证明:∵∠1=∠2,∴∠1+∠EAC=∠2+∠EAC,即∠BAC=∠EAD,∵在△ABC和△AED中,,∴△ABC≌△AED(AAS).22.证明:∵,∴△ADC≌△ABC(ASA).∴DC=BC.又∵,∴△CED≌△CEB(SAS).∴∠5=∠6.23.证明:如图,过E点作EH∥AB交BD的延长线于H,故∠A=∠CEH,在△ABC与△EHC中,∴△ABC≌△EHC(ASA),∴AB=HE,∵∠B+∠CDE=180°,∠HDE+∠CDE=180°∴∠HDE=∠B=∠H,∴DE=HE.∵AB=HE,∴AB=DE.24.解:(1)在△ABC中,∠BAC=90°,∴∠BAD=90°-∠EAC。
最新版精编2019年七年级下册数学单元测试题《三角形的初步认识》完整题(含答案)
2019年七年级下册数学单元测试题第一单元三角形的初步认识一、选择题1.如图,△ABC三个内角的平分线AD、BF、CE交于点O,则∠1+∠2等于()A.100°B.90°C. 95°D.不能确定答案:B2.若AD是△ABC的中线,则下列结论中,错误的是()A.AD平分∠BAC B.BD =DC C.AD平分BC D.BC =2DC答案:A3.在△ABC中,∠A=30°,∠B=50°,则∠C的外角=()A.60°B.80°C.100°D.120°答案:B4.如图,在ΔABC中,BC边上的垂直平分线交AC于点D, 已知AB=3,AC=7,BC=8,则ΔABD 的周长为()A.10 B.11 C. 12 D. 15答案:A5.下列图形中,能说明∠1>∠2的是()答案:D6.如图所示,△ABC中,AB=AC,BE=CE,则由“SSS”可直接判定()A.△ABD≌△ACD B.△ABE≌△ACE C.△BED≌△CED D.以上答案都不对答案:B7.如图,△ABD≌△CDB,∠ABD=40°,∠C=110°,则∠CBD等于()A.20°B.30°C.40°D.50°答案:B8.下列说法中正确的个数有()①全等i角形对应角所对的边是对应边,对应边所夹的角是对应角②全等三角形对应边所对的角是对应角,对应边所夹的角是对应角③全等三角形中的公共边是对应边,公共角是对应角,对顶角是对应角④两个全等三角形中,相等的边是对应边,相等的角是对应角A.1个 B 2个C.3个D.4个答案:D9.如图所示,△ABC≌△BAD.A与B,C与D是对应顶点,若AB=4cm,BD=4.5 cm,AD=1.5 cm,则BC的长为()A 4.5 cm B.4 cm C.1.5 cm D.不能确定答案:C10.如图所示,在4×4的正方形网格中,∠l,∠2,∠3的大小关系是()A.∠l>∠2>∠3 B.∠1=∠2>∠3C.∠l<∠2=∠3 D.∠l=∠2=∠3答案:B11.如图所示,AD⊥BC于D,那么以AD为高的三角形有()A. 3个B.4个C. 5个D.6个答案:D12.以下列各组线段的长为边,能构成三角形的是()A.4 cm,5 cm,6 cm B.2 cm,3 cm,5 cmC.4 cm,4 cm。
2019-2020初中数学七年级下册《三角形的初步认识》专项测试(含答案) (39)
浙教版初中数学试卷2019-2020年七年级数学下册《三角形的初步认识》精选试卷学校:__________ 题号一二三总分得分评卷人得分一、选择题1.(2分)如图,从下列四个条件:①BC=B′C,②AC=A′C,③∠A′CA =∠B′CB,④AB=A′B′中,任取三个为条件,余下的一个为结论,则最多可以构成正确结论的个数是()A. 1 B.2 C.3 D.42.(2分)在Rt △ABC中,∠BAC=90度,AD是高,则图中互余的角有()A.一对B.二对C.三对D.四对3.(2分)已知AD是△ABC的角平分线,则下列结论正确的个数有()①BD=CD,②BC=2CD AD平分BC,④∠BAC=2∠DACA.一个B.二个C.三个D.四个4.(2分)下列说法正确的是()A.周长相等的两个三角形全等B.面积相等的两个三角形全等C.三个角对应相等的两个三角形全等D.三条边对应相等的两个三角形全等5.(2分)已知△ABC中,(1)如图1,若P点是∠ABC和∠ACB的角平分线的交点,则∠P=90°+12∠A;(2)如图2,若P点是∠ABC和外角∠ACE的角平分线的交点,则∠P=90°-∠A;(3)如图3,若P点是外角∠CBF和外角∠BCE的角平分线的交点,则∠P=90°-1 2∠A.AB CD图1 图2 图3上述说法正确的有( )A .0个B .1个C .2个D .3个6.(2分)一块试验田的形状是三角形(设其为ABC △),管理员从BC 边上的一点D 出发,沿DC CA AB BD →→→的方向走了一圈回到D 处,则管理员从出发到回到原处在途中身体( )A .转过90oB .转过180oC .转过270oD .转过360o7.(2分)如图,123,,∠∠∠的大小关系为( ) A .213>>∠∠∠ B .132>>∠∠∠ C .321>>∠∠∠ D .123>>∠∠∠8.(2分)如图,已知BE=CF ,且∠B=∠DEF, ∠A=∠D ,那么△ABC 和△DEF 是( )A .一定全等B .一定不全等C . 无法判定D .不一定全等9.(2分)用9根火柴棒(等长)拼成一个三角形,火柴棒不允许剩余重叠和折断,则能摆出不同的三角形的个数是( )A .1 个B .2 个C .3 个D .4个10.(2分)如图所示,已知AB=A ′B ′,∠A=∠A ′,若△ABC ≌△A ′B ′C ′,还需要( )A .∠B=∠B ′ B .∠C=∠C ′ C .AC=A ′C ′D .以上均可11.(2分)在△ABC 和△A ′B ′C ′中,①AB=A ′B ′;②BC=B ′C ′;③AC=A ′C ′;④∠A=∠A ′;⑤∠B=∠8′;⑥∠C=∠C ′,则下列条件中不能使△ABC ≌△A ′B ′C ′的是( )A .②④⑤B .①②③C .①③⑤D .①②⑤12.(2分)下列长度的三条线段,能够组成三角形的是 ( )A .2.5,2.5,5B . l ,6,6C .2,8,4D .10,7,213.(2分)有下列关于两个三角形全等的说法:①三个角对应相等的两个三角形全等;②三条边对应相等的两个三角形全等;③两角与一边对应相等的两个三角形全等;④两边和一角对应相等的两个三角形全等.其中正确的个数是()A.1 B.2 C.3 D.414.(2分)如图所示,∠A=32°,∠B=45°,∠C=38°,则∠DFE的度数为()A.120°B. ll5°C.110°D.105°评卷人得分二、填空题15.(2分)如图,△ABC≌△CDA,A与C对应,D与B对应,则∠1与是对应角.16.(2分)如图△ABC中,D、E分别在BC上,∠BAE=∠AEB,∠CAD=∠CDA.若∠BAC=x度,则∠DAE的度数是.17.(2分)如图,将一副三角板折叠放在一起,使直角的顶点重合于点O,则AOC DOB∠+∠=.18.(2分)已知:△ABC中,∠A=100°,∠B-∠C=60°,则∠C=__________.19.(2分)如图:请写出图中有个三角形,分别是.20.(2分)如图,在ΔABC中,D是边BC上一点,AD平分∠BAC,在AB上截取AE=AC,连结DE,已知DE=2cm,BD=3cm,线段BC= .21.(2分)判断正误,对的打“√”,错的打“×”.(1)经过线段中点的直线是线段的中垂线. ( )(2)以AB为直径可以作一个圆. ( )(3)已知两条边和一个角可以作唯一的三角形. ( )(4)已知两角一边可以作唯一的三角形. ( )22.(2分)判断正误,在括号内打“√”或“×”.(1)三角形的一条角平分线把三角形分成面积相等的两部分. ( )(2)若一个三角形的两条高在这个三角形外部,则这个三角形是钝角三角形. ( )(3)直角三角形的三条高的交点恰为直角顶点. ( )(4)三角形的中线可能在三角形的外部. ( )评卷人得分三、解答题23.(7分)如图,已知BE=CF ,AB=CD ,∠B=∠C ,则AF=DE 吗?请说明理由.24.(7分)如图,在ABC △中,7050A B CD ∠=∠=o o ,,平分ACB ∠.求∠ADC 的度数.25.(7分)如图,一块三角形模具的阴影部分已破损.(1)只要从残留的模具片中度量出哪些边、角,就可以不带残留的模具片到店铺加工一块与原来的模具ABC 的形状和大小完全相同的模具A B C '''?请简要说明理由.(2)作出模具A B C '''△的图形.(要求:尺规作图,保留作图痕迹,不写作法和证明)26.(7分)已知线段a ,c ,∠α(如图),利用尺规作△ABC ,使AB=c ,BC=a ,∠ABC=∠α.B C AD B A27.(7分)如图所示,画出△ABC的角平分线BD,AB边上的高CE,BC边上的中线AF.28.(7分)如图所示,在矩形ABCD中,F是BC边上一点,AF的延长线交DC的延长线于G,DE⊥AG于E,且DE=DC,∠l=∠2,根据上述条件,请在图中找出一对全等三角形,并证明你的结论.29.(7分)如图所示,在Rt △ABC中,∠ACB为直角,∠CAD的平分线交BC的延长线于点E,若∠B=35°,求∠BAE和∠E的度数.30.(7分)在△ABC 中,已知∠A+∠B=70°,∠C=2∠A ,求∠A ,∠B ,∠C 的度数.【参考答案】***试卷处理标记,请不要删除一、选择题1.B2.D3.A4.D5.C6.D7.D8.A9.C10.D11.C12.B13.B14.B二、填空题15.∠316.90°-x 217.180°18.10°19.3,ΔABD 、ΔAB C 、ΔA CD20.5cm21.(1)× (2)√ (3)× (4)×22.(1)× (2)√ (3)√ (4)×三、解答题23.利用SAS 说明△ABF ≌△DCE24.80°25.(1)只要度量残留的三角形模具片的B C ∠∠,的度数和边BC 的长, 因为两角及其夹边对应相等的两个三角形全等;(2)略26.略.27.略28.略29.∠E=27.5°,∠BAF=117.5°30.∠A=55°,∠B=15°,∠C=110°。
鲁教版(五四制)数学七年级上册第一章《三角形》3.1认识三角形同步练习(含答案)
初中数学鲁教版七年级上册第一章《三角形》3.1认识三角形学校:___________姓名:___________班级:___________得分:___________一、选择题(本大题共10小题,共30分)1.给出下列长度的三条线段,能组成三角形的是( )A.3cm ,4cm ,5cmB.8cm ,7cm ,15cmC.13cm ,12cm ,25 cmD.5cm ,5cm ,11cm2.若一个三角形的两边长分别为3cm 、6cm ,则它的第三边的长可能是( )A.2cmB.3cmC.6cmD.9cm 3.下列长度的三条线段能组成三角形的是( )A.2,2,6B.3,4,8C.4,6,10D.5,6,104.在△ABC 中,AB=1,BC=,下列选项中,可以作为AC 长度的是( )A.2B.4C.5D.65.如果三角形的两边长分别为5和7,第三边长为偶数,那么这个三角形的周长可以是( )A.15B.16C.19D.266.若三角形的两边a 、b 的长分别为3和5,则其第三边c 的取值范围是( )A.2<c <5B.3<c <8C.2<c <8D.2≤c ≤87.如图,一个三角形只剩下一个角,这个三角形为( )A.锐角三角形B.钝角三角形C.直角三角形D.都有可能 8.下列说法中,正确的个数有( )①三角形具有稳定性;②如果两个角相等,那么这两个角是对顶角;③三角形的角平分线是射线;④直线外一点到这条直线的垂线段叫做这点到直线的距离;⑤任何一个三角形都有三条高、三条中线、三条角平分线;⑥三角形的三条角平分线交于一点,且这点在三角形内; A.2B.3C.4D.59.下列四个图形中,线段BE 是△ABC 的高的图形是( )A. B. C. D.10.已知三角形的三边长分别为2、x 、3,则x 可能是( )A.1B.4C.5D.6二、填空题(本大题共5小题,共15分)11.若三角形的三边长分别为3,x ,5,请写出x 可能的整数值______。
精选2019年七年级下册数学单元测试题《三角形的初步认识》测试题(含答案)
2019年七年级下册数学单元测试题第一单元 三角形的初步认识一、选择题1.若△ABC ≌△DEF ,AB=DE ,∠A=35°,∠B=75°,则F 的度数是( )A . 35°B . 70°C .75°D .70°或75° 答案:B2.如图,在△ABC 中,∠ABC 与∠ACB 的角平分线交于点0,且∠BOC=α,则∠A 的度数是 ( )A .180°-αB .2α-180°C .180°-2αD .12α答案:B3.如图,△ABE 和△ADC 是△ABC 分别沿着AB ,AC 边翻折180°形成的,若∠1∶∠2∶∠3=28∶5∶3,则∠α的度数为( )A .80°B .100°C .60°D .45° 解析:A4.下列说法正确的是( )A .周长相等的两个三角形全等B .面积相等的两个三角形全等C .三个角对应相等的两个三角形全等D .三条边对应相等的两个三角形全等 答案:D5.如图,123,,∠∠∠的大小关系为( ) A .213>>∠∠∠ B .132>>∠∠∠ C .321>>∠∠∠ D .123>>∠∠∠ 答案:D6.如图所示,由∠ABC=∠DCB ,∠ACB=∠DBC ,直接能判定全等的三角形是 ( )A .△AB0≌△DODB .△ABC ≌△DCB C .△ABD ≌△DCA D .△OAD ≌△0BC答案:B7.如图所示,已知AD=CB,∠AD0=∠CB0,那么可用“SAS”全等识别法说明的是() A.△AD0≌△CB0 B.△AOB≌△COD C.△ABC≌△CDA D.△ADB≌△CBD答案:D8.任意一个三角形被一条中线分成两个三角形,则这两个三角形:①形状相同,②面积相同,③全等.上述说法正确的有()A.0个B.1个C.2个D.3个答案:B9.如图所示,∠A=32°,∠B=45°,∠C=38°,则∠DFE的度数为()A.120°B. ll5°C.110°D.105°答案:B10.关于三角形的高的位置,下列判断中正确的是()A.必在三角形内B.必在三角形外C.不在三角形内,就在三角形外D.以上都不对答案:D11.如果三角形的两边长分别为7和2,且它的周长为偶数,那么,第三边的长为() A.5 B.6 C.7 D.8答案:C二、填空题12.如图,在△ABC中,AD是高,E是AB上一点,AD与CE相交于点P,已知∠APE=50°,∠AEP=80°,则∠B= .解析:40°13.如图,已知任意三角形的内角和为180°,试利用多边形中过某一点的对角线条数,寻求多边形内角和的公式.根据上图所示,①一个四边形可以分成2个三角形,于是四边形的内角和为度;②一个五边形可以分成3个三角形,于是五边形的内角和为度;……,③按此规律,n边形可以分成个三角形,于是n边形的内角和为度.解答题解析: 360,540,(n-2),180(n-2)14.如图所示,∠1=∠2,∠ABC=∠DCB,AC,BD相交于O,请将下列说明AB=DC的理由的过程补充完整.解:∵∠ABC=∠DCB,∠l=∠2(已知),∴∠ABC一∠l=∠DCB一∠2,即∠DBC= .在△ABC和△DCB中,= ( ),= ( ),= ( ),∴≌ ( ),∴AB=DC( ).解析:∠ACB,∠ACB,∠DBC,已证,∠ABC,∠DCB,已知,BC,CB,公共边,△ABC,△DCB,AAS,全等三角形对应边相等15.仔细观察下图:(1)图中的△ABC与△A′B′C′全等吗? .(2)由图中的信息,你可以得到的重要结论是:.解析:(1)不全等;(2)有两边及其中一边的对角对应相等的两个三角形不一定全等16.△ABC与△DEF全等,AB=DE,若∠A=50°,∠B=60°,则∠D= .解析:50°或60°E B D CA 17.如图所示.(1)AD 是△ABC 的角平分线,则∠BAC=2 =2 ;(2)AE 是△ABC 的中线,则 = 2BE=2 .解析:(1)∠BAD ,∠CAD ;(2)BC ,CE18.如图所示,∠1= .解析:120°19.(1)自行车用脚架撑放比较稳定的原因是 .(2)若AABC 的三边长都为整数,周长为11,有一边长为4,且任何两边都不相等,则这个三角形的最大边长为 .解析:(1)三角形的稳定性;(2)5三、解答题20.如图,CD 是△ABC 的AB 边上的高,CB 是△ADC 的中线,已知AD=10,CD=6,请求出△ABC 的面积.解析:15. 21.如图,AD 平分∠BAC ,交BC 于点D ,∠ADB=105°,∠ACB=65°,CE 是AB 边上的高,求∠BAC ,∠BCE 的度数.A B C D解析:∠BAC=80°,∠BCE=55°.22.如图,AD平分∠BAC,AB=AC,则BD=CD,试说明理由.解析:△ABD≌△ACD(SAS),则BD=CD.23.画一个三角形,使两个内角分别为45°和60°,它们的夹边为2.5cm.解析:略24.如图所示,已知线段a,b和∠α,用直尺和圆规作△ABC,使∠B=∠α,AB=a,BC=b.解析:略25.如图所示,四边形ABCD 中,AB=CD,BC=AD,请你添一条辅助线,把它分成两个全等的三角形.你有几种添法?分别说明理由.解析:连结AC或连结BD,都是根据SSS说明三角形全等26.如图所示,△ABC与△DFE全等,AC与DE是对应边.(1)找出图中相等的线段和相等的角;(2)若BE=14 cm,FC=4 cm,求出EC的长.解析:(1)BF=CE,AC=DE,AB=DF,BC=EF,∠A=∠D,∠B=∠EFD,∠ACB=∠E;(2)5 cm27.三角形的三条中线、三条高、三条角平分线都分别交于一点,其中交点可能不在三角形内部的是哪种线段?请通过画图说明.解析:高线的交点可以在三角形的外部、内部及其顶点上28.如图所示,CD是△ABC的高,∠BAE=25°,∠BCD=35°.求∠AEC的度数.解析:80°29.如图所示,在△ABC中,∠A=∠ACB,CD是∠ACB的平分线,CE⊥AB于E.(1)试说明∠CDB=3∠DCB;(2)若∠DCE=48°,求∠ACB的度数.解析:(1)略;(2)28°30.如图所示,一张三个内角都相等的三角形纸片ABC,∠CBP=20°(图①).现将纸片沿射线BP折叠成图②的形状,BP交AC于点E,BC′交AC于点D.求图②中∠ADC′,∠AEC′的度数.解析:∠ADC′=80°,∠AEC′=20°。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
24.认识三角形 解读课标从房屋的顶梁到自行车的三脚架,从起重机的三角形吊臂再到爱因妥芬(心电图的发明者)三角形,生活中处处可看到三角形,三角形是最简单、最基本的几何图形,它不仅是研究其他图形的基础,在解决实际问题中也有着广泛的应用.认识三角形,就是认识三角形的概念及基本要素——边与角,与边与角相关的知识有:三角形三边关系定理、三角形内角和定理及推论,它们在线段、角度的计算,图形的计数等方面有广泛的应用. 代数化及分类讨论法是解与三角形基本要素相关问题的重要方法.代数化即用方程、不等式解边与角的计算及简单推理题,分类讨论即按边或角对三角形进行分类. 问题解决例1 在ABC △中,高BD 和CE 所在直线想交于O 点,若ABC △不是直角三角形,且60A ∠=︒,则BOC ∠=_________度.试一试 因三角形的高不一定在三角形内部,这样ABC △形状应分两种情况讨论. 例2 如图,将纸片ABC △沿着DE 折叠压平,则( ).A .12A ∠=∠+∠B .()122A ∠=∠1+∠C .()113A ∠=∠+∠2D .()1124A ∠=∠+∠试一试 在折叠动态变化中,不变关系是B C AED ADE ∠+∠=∠+∠,这是解本例的关键.例3 (1)如图①,AD BC ⊥于D ,AE 平分BAC ∠,试探寻DAE ∠与C ∠、B ∠的关系.(2)如图②,若将点A 在AE 上移动到F ,FD BC ⊥于D ,其他条件不变,那么EFD ∠与C ∠、D ∠是否还有(1)中的关系?说明理由. (3)请你提出一个类似的问题.试一试 对于(2),通过作辅助线,将问题转化为(1).例4 如图①,已知A 为x 轴负半轴上一点,B 为x 轴正半轴上一点,()0,2C -,()3,2D --. (1)求BCD △的面积;(2)如图②,若AC BC ⊥,作CBA ∠的平分线交CO 于P ,交CA 于Q ,判断CPQ ∠与CQP ∠的大小关系,并证明你的结论;(3)如图③,若ADC DAC ∠=∠,点B 在x 轴正半轴上运动,ACB ∠的平分线CE 交DA 的延长线于21DAB ED ABCE 图①DABCF 图②点E ,在B 点的运动过程中,EABC∠∠的值是否变化?若不变,求出其值;若变化,请说明理由.试一试 对于(3),ABC ∠能否用E ∠的式子表示?由数到形,分解出基本图形是解题的关键. 例5 在三角形纸片内有2008个点,连同三角形纸片的3个顶点,共有2011个点,在这些点中,没有三点在一条直线上.问:以这2011个点为顶点能把三角形纸片分割成多少个没有重叠部分的小三角形?解法一 我们不妨先退一步,考察三角形内有一个点、两个点、三个点…的简单情形,有下表所示的3个小三角形,以后每增加一个点,这个点必落在已连好的某一个小三角形内,它与该三角形的三个顶点可得到三个小三角形,从而增加了两个小三角形,于是可以推出,当三角形内有2008个点时,连接可得到小三角形的个数为:()32200814017+⨯-=(个).解法二 整体核算法.设连线后把原三角形分割成n 个小三角形,则它们的内角和为180n ︒⋅,又因为原三角形内每一个点为小三角形顶点时,能为小三角形提供360︒的内角,2008个点共提供内角2008360⨯︒,于是得方程1803602008180n =⨯+,解得4017n =,即这2008个点能将原三角形纸片分割成4017个小三角形. 角平分线角平分线是联系角与角之间关系的纽带,当角平分线与三角形相遇可生成内涵上有关联性、解法上有共通性的组图.例6 (1)如图①,已知ABC △中的两内角平分线交于P 点,两外角平分线交于M 点,一内角平分线与一外角平分线交于N 点.试分别探究BPC ∠、M ∠、N ∠与A ∠关系;(2)如图②,在凹四边形ABCD 中,已知ABD ∠与ACD ∠的平分线交于点E ,求证:2ADE ∠+∠∠=.分析与解 (1)1902BPC A ∠=︒+∠,1902M A ∠=︒-∠,12N A ∠=∠.(2)凹四边形ABCD 形似“规形”,易证BDC A B C ∠=∠+∠+∠.图①图②图③NPABC图①x y yxD A BCE 图②图②可分解为两个“规形”,BE ∵、CE 分别平分ABD ∠、ACD ∠,∴可设ABE DBE x ∠=∠=,ACE DCE y ∠=∠=. 由(1)得E A x y ∠=∠++,① D E x y ∠=∠++,②②-①得D E E A ∠-∠=∠-∠,2A DE ∠+∠∠=∴.数学冲浪 知识技能广场1.一副三角板叠在一起如图放置,最小锐角的顶点D 恰好放在等腰直角三角板的斜边AB 上,BC 与DE 交于点M .若100ADF ∠=︒,则BM D ∠=_________度.2.一副三角板,如图所示叠放在一起,则图中1∠的度数为_______.3.如图,ABC △中,80A ∠=︒,剪去A ∠后,得到四边形BCED ,则12∠+∠=_______.4.如图,在ABC △中,A α∠=,ABC ∠的平分线与ACD ∠的平分线交于点1A ,得1A ∠;1A BC ∠的平分线与1ACD ∠的平分线相交于点2A ,得2A ∠;…,2008A BC ∠的平分线与2008A CD ∠的平分线相交于点2009A ,得2009A ∠,则2009A ∠=________.5.如图,ABC △中,A ∠、B ∠、C ∠的外角分别记为α、β、γ.若::3:4:5αβγ=,则::A B C ∠∠∠=( ).A .3:2:1B .1:2:3C .3:4:5D .5:4:3MABCEF 1ECBA DABA 1A 26.如图,BP 是ABC △中ABC ∠的平分线,CP 是ACB ∠的邻补角的平分线.若20ABP ∠=︒,50ACP ∠=︒,则A P ∠+∠=( ).A .70︒B .80︒C .90︒D .100︒7.在等腰ABC △中,AB AC =,一边上的中线BD 将这个三角形的周长分为15和12两部分,则这个等腰三角形的底边长为( ).A .7B .11C .7或11D .7或108.如图,ABC △中,ABD DBE EBC ∠=∠=∠,ACD DCE ECB ∠=∠=∠,若145BEC ∠=︒,则B D C ∠等于( ).A .100︒B .105︒C .110︒D .115︒9.如图,已知射线OM 与射线ON 互相垂直,B 、A 分别为OM 、ON 上一动点,ABM ∠、BAN ∠的平分线交于C .问:B 、A 在OM 、ON 上运动过程中,C ∠的度数是否改变?若不改变,求出其值;若改变,说明理由.10.如图①,已知ABC △中,ABC ACB ∠=∠,D 为BC 边上一点,E 为直线AC 上一点,且ADE AED ∠=∠.(1)求证:2BAD CDE ∠=∠,(2)如图②,若D 在BC 的反向延长线上,其他条件不变,(1)中的结论是否仍成立?证明你的结论.CBA γαβMPABCECBA D OMNA C思维方法天地11.在ABC △中,50A ∠=︒,高BE 、CF 交于O ,且O 不与B 、C 重合,则BOC ∠的度数为_______. 12.如图,已知C ∠=45︒,452B α∠=︒+,453BAC α∠=︒+,AE 平分BAD ∠,则CAE ∠=_______.13.如图,BP 平分ABC ∠交CD 于F ,DP 平分ADC ∠交AB 于E ,AB 与CD 相交于G ,如果42A ∠=︒,38C ∠=︒,那么P ∠的度数为________.14.如图,已知ABC △中,A ACB ∠=∠,CP 平分ACB ∠,BD 、CD 分别为ABC △的两外角的平分线,给出下列结论:①CP CD ⊥;②1902D A ∠=︒-∠;③P D A C ∥.其中正确结论的个数是( ).A .0B .1C .2D .315.如图,31ABC ∠=︒,又BAC ∠的平分线AE 与FCB ∠的平分线CE 相交于E 点,则AEC ∠为( ). A .14.5︒ B .15.5︒ C .16.5︒ D .20︒图①A BCE 图②EC BADDABCEDGPABCEF DPAB C EFDABCEF16.如图,ABC △中,90BAC ∠=︒,AD BC ⊥,ABC ∠的平分线BE 交AD 于点F ,AG 平分DAC ∠.给出下列结论:①BAD C ∠=∠;②A E F A F E ∠=∠;③E B C C ∠=∠;④A G E F ∠⊥.其中正确的结论是( ).A .②③④B .①③④C .①②④D .①②③17.平面内的四条线段AB 、BC 、CD 、DA 首尾顺次连接,已知24ABC ∠=︒,42ADC ∠=︒. (1)如图①,若BAD ∠与BCD ∠的平分线交于点M ,求AMC ∠的值;(2)如图②,点E 在BA 的延长线上,DAE ∠的平分线和BCD ∠的平分线交于点N ,求ANC ∠的值.18.如图,在BCD △中,BE 平分DBC ∠交CD 于F ,延长BC 至G ,CE 平分DCG ∠,且EC 、DB的延长线交于A 点,若30A ∠=︒,75DFE ∠=︒. (1)求证:DFE A D E ∠=∠+∠+∠; (2)求E ∠的度数;(3)若在图中作CBE ∠与GCE ∠的平分线交于1E ,作1C B E ∠与1GCE ∠的平分线交于2E ,作2CB E ∠与2GCE ∠的平分线交于3E ,依此类推,n CBE ∠与n GCE ∠的平分线交于1n E +,请用含有n 的式子表示1n E +∠的度数.应用探究乐园19.把一副学生用三角板(30︒、60︒、90︒和45︒、45︒、90︒)如图①放置在平面直角坐标系中,点A 在y 轴正半轴上,直角边AC 与y 轴重合,斜边AD 与y 轴重合,直角边AE 交x 轴于F ,斜边AB 交x 轴于G ,O 是AC 中点,8AC =.(1)把图①中的Rt AED △绕A 点顺时针旋转α度得图②,此时AGH △的面积是10,AHF △的面积是8,分别求F 、H 、B 三点的坐标;(2)如图③,设AHF ∠的平分线和AGH ∠的平分线交于点M ,EFH ∠的平分线和FOC ∠的平分线交于点N ,当AED △绕A 点转动时,N M ∠+∠的值是否会改变,若改变,请说明理由,若不改变,请求出其值.GABCEFCBAD图①DNABCE图②DGABC F20.问题提出 以n 边形的他个顶点和它内部的m 个点,共()m n +个点作为顶点,可把原n 边形分割成多少个互不重叠的小三角形?问题探究 为了解决上面的问题,我们将采取一般问题特殊化的策略,先从简单和具体的情形入手:探究一:以ABC △的三个顶点和它内部的1个点P ,共4个点为顶点,可把ABC △分割成多少个互不重叠的小三角形?如图①,显然,此时可把ABC △分割成3个互不重叠的小三角形.探究二:以ABC △的三个顶点和它内部的2个点P ,Q ,共5个点为顶点,可把ABC △分割成多少个互不重叠的小三角形?在探究一的基础上,我们可看作在图①ABC △的内部,再添加1个点Q ,那么点Q 的位置会有两种情况:一种情况,点Q 在图①分割成的某个小三角形内部,不妨假设点Q 在PAC △内部,如图②; 另一种情况,点Q 在图①分割成的小三角形的某条公共边上,不妨假设点Q 在PA 上,如图③. 显然,不管哪种情况,都可把ABC △分割成5个互不重叠的小三角形. 探究三:以ABC △的三个顶点和它内部的3个点P ,Q ,R 共6个点为顶点,可把ABC △分割成______个互不重叠的小三角形,并在图④中画出一种分割示意图.探究四:以ABC △的三个顶点和它内部的m 个点,共()3m +个顶点,可把ABC △分割成______个互不重叠的小三角形.探究拓展:以四边形的4个顶点和它内部的m 个点,共()4m +个顶点,可把四边形分割成_____个互不重叠的小三角形,问题解决 以n 边形的挖个顶点和它内部的m 个点,共()m n +个顶点,可把ABC △分割成____个互不重叠的小三角形.实际应用 以八边形的8个顶点和它内部的2012个点,共2020个顶点,可把八边形分割成多少个互不重叠的小三角形?(要求列式计算)图①图②图③图①图②图③ABC图④24.认识三角形 问题解决例l 当ABC △为锐角三角形时,120BOC ∠=︒;当ABC △为钝角三角形时,60BOC ∠=︒.例2 B 180B C AED ADE A ∠+∠=∠+∠=︒-∠,又12360B C A E D A D E ∠+∠+∠+∠+∠+∠=︒,得()218012360A ︒-∠+∠+∠=︒,化简得()1122A ∠=∠+∠.例3 (1)()12DAE C B ∠=∠-∠;(2)过A 作AG BC ⊥于G ,则()12EFD EAG C B ∠=∠=∠-∠;(3)略例4 (1)3BCD S =△(2)可证明CPQ CQP ∠=∠.(3)CD AB ∥,可证明1122ABCE ABC ABC ∠∠==∠∠为定值.数学冲浪1.85 2.75︒ 3.260︒ 4.20092α5.A 6.C 7.C 8.C9.190452C AOB ∠=︒-∠=︒,为一定值.10.(1)证明略;(2)(1)中的结论仍然成立 11.50︒或130︒ 12.126︒13.40︒ 如图,由对顶三角形性质得122122A P A C ∠+∠=∠+∠⎧⎨∠+∠=∠+∠⎩,解得40P ∠=︒.14. D 15. B 16.C17.(1)可证明()1332AMC ABC ADC ∠=∠+∠=︒.(2)可证明()11801232ANC B D ∠=︒+∠+∠=︒.18.(1)略;(2)2D E ∠=∠,代入(1)得15E ∠=︒;(3)122113022n n n E D +++∠=∠=⋅︒.19.(1)()5,0F -,()1,0H -,()8,4B -. (2)22.52M α∠=︒+,752N α∠=︒-,97.5M N ∠+∠=︒,故M N ∠+∠的值不会改变.20.探究三:7分割示意图:(答案不唯一). 探究四:()321m +-或21m + 探究拓展:()421m +-或22m +21PGFEDCBA问题解决:()21n m +-或22m n +-实际应用:把8n =,2012m =代入上述代数式,得2222012824024824030m n +-=⨯+-=+-=.CBA。
