Bezier曲线的绘制和拼接实验报告
129512786937031250实验四 实现Bezier曲线的生成算法
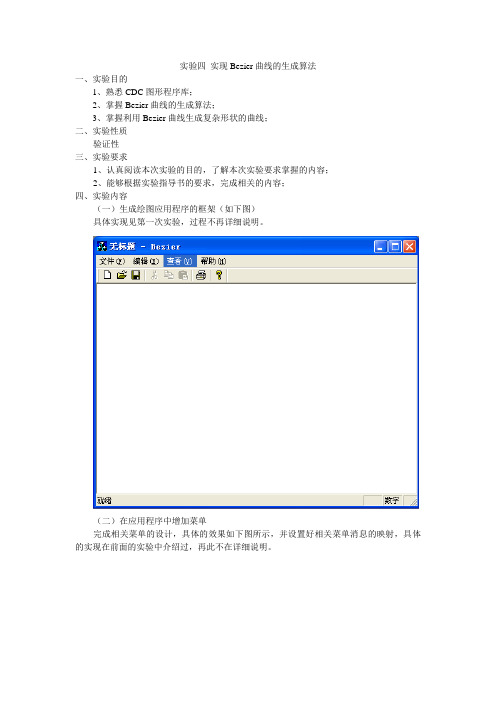
实验四实现Bezier曲线的生成算法一、实验目的1、熟悉CDC图形程序库;2、掌握Bezier曲线的生成算法;3、掌握利用Bezier曲线生成复杂形状的曲线;二、实验性质验证性三、实验要求1、认真阅读本次实验的目的,了解本次实验要求掌握的内容;2、能够根据实验指导书的要求,完成相关的内容;四、实验内容(一)生成绘图应用程序的框架(如下图)具体实现见第一次实验,过程不再详细说明。
(二)在应用程序中增加菜单完成相关菜单的设计,具体的效果如下图所示,并设置好相关菜单消息的映射,具体的实现在前面的实验中介绍过,再此不在详细说明。
(三)在绘图函数中添加代码通过以上步骤,得到了与菜单对应的消息映射,就可以在函数中添加代码绘制图形了。
1、利用Bezier曲线的生成算法实现二次Bezier曲线的生成(算法的详细原理见教材)。
void CBezierV iew::OnBezier2(){// TODO: Add your command handler code hereCDC*pDC=GetDC();//得到绘图类指针RedrawWindow();//重绘窗口CPen bluepen(PS_SOLID,2,RGB(0,0,255));//创建画实线、线宽为2的蓝色画笔CPen *old=pDC->SelectObject(&bluepen);float x0=100,y0=100,x1=200,y1=50,x2=150,y2=250;float i,x,y,dt,t,n=30.0;dt=1/n;for(i=0;i<=n;i++){t=i*dt;x=x0*(1-t)*(1-t)+x1*2*t*(1-t)+x2*t*t;y=y0*(1-t)*(1-t)+y1*2*t*(1-t)+y2*t*t;if(i==0)pDC->MoveTo(x,y);pDC->LineTo(x,y);pDC->MoveTo(x0,y0);pDC->LineTo(x1,y1);pDC->LineTo(x2,y2);pDC->SelectObject(old);ReleaseDC(pDC);}由以上代码绘出的图形如下:2、利用Bezier曲线的生成算法实现二次Bezier曲线的生成(算法的详细原理见教材)。
实验三 自由曲线的生成

实验三 Bezier曲线生成一、实验目的1. 理解并会自己编程实现二维Bezier曲线的画图二、实验内容和要求1.选择自己熟悉的任何编程语言, 建议使用VB,VC或JAVA。
2.创建良好的用户界面,包括菜单,参数输入区域和图形显示区域。
3.实现二维2、3、4阶Bezier曲线的描画。
4.将生成算法以菜单或按钮形式集成到用户界面上。
5.坐标参数可以用鼠标或键盘输入。
三.实验报告1.用户界面的设计思想和框图。
2.各种实现算法的算法思想。
3.算法验证例子。
4.上交源程序。
四.Bezier曲线生成程序设计的步骤如下:1.创建工程名称为“Test”单文档应用程序框架(1)启动VC,选择“文件”|“新建”菜单命令,并在弹出的新建对话框中单击“工程”标签。
(2)选择MFC AppWizard(exe),在“工程名称”编辑框中输入“Test”作为工程名称,单击“确定”按钮,出现Step 1对话框。
(3)选择“单个文档”选项,单击“下一个”按钮,出现Step 2对话框。
(4)接受默认选项,单击“下一个”按钮,在出现的Step 3~Step 5对话框中,接受默认选项,单击“下一个”按钮。
(5)在Step 6对话框中单击“完成”按钮,即完成“Test”应用程序的所有选项,随后出现工程信息对话框(记录以上步骤各选项选择情况),如图1-2所示,单击“确定”按钮,完成应用程序框架的创建。
图1-2 信息程序基本2.编辑菜单资源设计如图1-1所示的菜单项。
在工作区的ResourceView标签中,单击Menu项左边“+”,然后双击其子项IDR_MAINFRAME,并根据表1-1中的定义编辑菜单资源。
此时VC已自动建好程序框架,如图1-2所示。
表1-1菜单资源表3.添加消息处理函数利用ClassWizard(建立类向导)为应用程序添加与菜单项相关的消息处理函数,ClassName栏中选择CTestView,根据表1-2建立如下的消息映射函数,ClassWizard会自动完成有关的函数声明。
实验5 交互绘制Bezier曲线

实验5 交互绘制Bezier曲线一、实验步骤1.打开Test工程试验框架。
2.窗口极大化显示方法:将Test.cpp文件的InitInstance()中的语句:m_pMainWnd->ShowWindow(SW_SHOW);改为:m_pMainWnd->ShowWindow(SW_MAXIMIZE);3.修改CTestView类(1)添加成员变量:方法:在工作区中选择ClassView类窗口,右击CTestView类,选择“Add Member Variable…”,定义如下的成员变量:protected:bool m_flag;// 鼠标绘图标志CPoint *pt;//顶点int CtrlPNum;//控制点个数(2)在“TestView.h”文件头添加如下预处理命令:#define N_MAX_POINT 10//控制多边形的最大顶点数(3)添加成员函数方法:在工作区中选择ClassView类窗口,右击CTestView类,选择“Add Member F unction…”,定义如下的成员函数:public:void DrawCtrPolygon();//绘制控制多边形void DrawBezier();//绘制Bezier函数long DeCasteliau(double,long *p);//德卡斯特里奥函数(4)按照教程130页编辑DeCasteliau(double,long *p)函数(5)按照教程131页编辑DrawBezier()函数(6)按照教程131页编辑DrawBezier()函数(7)按照教程131页编辑DrawCtrPolygon()函数4.按照教材38页添加WM_LBUTTONDOWN消息映射函数,并按照教程132页编辑5.添加WM_RBUTTONDOWN消息映射函数6.按照教材39页添加WM_MOUSEMOVE消息映射函数注意:(1)需要在“TestView.cpp”文件头加入下列命令:#include "MainFrm.h"//包含CMainFrame头文件,用于状态栏显示鼠标坐标位置(2)将文件“MainFrm.h”里的成员数据m_wndStatusBar属性修改为public(3)修改文件“MainFrm.cpp”中的indicators数组7.完善“绘图”子菜单消息处理函数,代码如下:void CTestView::OnDrawpic(){// TODO: Add your command handler code hereMessageBox("左键绘制控制多边形,右键绘制曲线","提示",MB_OK);pt=new CPoint [N_MAX_POINT];m_flag=TRUE;//可以使用鼠标绘制控制点CtrlPNum=0;//控制点初始个数为0}。
绘制一个“Bezier”曲线

计算机图形学作业3姓名学号班级作业内容绘制一个“Bezier”曲线效果截图关键程序(<40行) #include<gl/glut.h>void Initial(void){glClearColor(0,0,0,0);glLineWidth(1);GLfloat ControlP[4][3]={{-66,-88,0},{-44,55,0},{22,-33,0},{77,66,0}};glMap1f(GL_MAP1_VERTEX_3,0,1,3,4,*ControlP);glEnable(GL_MAP1_VERTEX_3);}void Display(void){glClear(GL_COLOR_BUFFER_BIT);glColor3f(1,0,0);glMapGrid1f(100,0,1);glEvalMesh1(GL_LINE,0,100);glFlush();}void Reshape(GLint newWidth,GLint newHeight){glViewport(0,0,newWidth,newHeight);glMatrixMode(GL_PROJECTION);glLoadIdentity();gluOrtho2D(-100,100,-100,100);}void main(){glutInitDisplayMode(GLUT_SINGLE|GLUT_RGB); //使用双缓存及RGB模型glutInitWindowSize(666, 488); //指定窗口的尺寸glutInitWindowPosition(288, 155); //指定窗口在屏幕上的位置glutCreateWindow("朱");Initial();glutDisplayFunc(Display);glutReshapeFunc(Reshape);glutMainLoop();}小结这一次的用OpenGL绘制贝塞尔曲线实验比上一次花了更长的时间,原来以为对OpenGL应该算是有了一些了解,这次实验过后发现,没搞明白的尚且有许多,更不用提还有许多根本不知道的应用方法。
Bezier曲线的拼接及其连续性.

1 ) i i,n(
P 1 )P 1 ) P 1 ) 0B 0 ,n( 1B 1 ,n( nB n ,n(
Bezier曲线通过特征多边形的起点和终点。
P n
(2)一阶导数
n! i1 ni ni1 i Bi,n (t) (i t (1 t) (n i)( 1 t ) t ) i!(n i)! n(n 1)! t i1 (1 t)(n1)(i1) (i 1)!((n 1) (i 1))! n(n 1)! t i (1 t)(n1)i i!((n 1) i)! n(Bi1,n1 (t) Bi,n1 (t))
Bezier曲线的拼接及其连续性
组员:栗周亚(主讲)樊凯 葛序理 牛辰光
顾超锋
尹顺源
Bezier曲线
由于几何外形设计的要求越来越高,传统的曲
线曲面表示方法, 已不能满足用户的需求。 1962年,法国雷诺汽车公司的P.E.Bézier 构造了一种以逼近为基础的参数曲线和曲 面的设计方法。Bézier方法将函数逼近同 几何表示结合起来,使得设计师在计算机 上就象使用作图工具一样得心应手。
Q (t ) n Pi ( Bi 1,n 1 (t ) Bi ,n 1 (t ))
i 0
n
n((P1 P0 ) B0,n 1 (t ) ( P2 P1 ) B1,n 1 (t ) ( Pn Pn 1 ) Bn 1,n 1 (t )) n ( Pi Pi 1 ) Bi 1,n 1 (t )
(5)几何不变性
曲线的形状仅与特征多边形各顶点 的相对位置有关,而与坐标系的选 择无关。
三次Bezier曲线的插值
插值要求得到的曲线精确的通过采样点,四个控制点决定 一条Bezier曲线,插值M个点(M>4)设计到曲线拼接连续性 的问题,要求达到切线连续。
三次贝塞尔曲线

三次贝塞尔曲线计算机图形学延安大学计算机学院实验报告专用纸一.实验目的熟悉三次贝塞尔曲线的生成算法,并能在TC环境下生成图形,并能熟悉四次贝塞尔曲线的生成,比较两者的异同。
二.实验内容三.实验环境Window某P;TC2.0;四.实验步骤①算法思想P0、P1、P2、P3四个点在平面或在三維空間中定義了三次方贝塞尔曲線。
曲線起始计算机图形学於P0走向P1,並從P2的方向來到P3。
一般不會經過P1或P2;這兩個點只是在那裡提供方向資訊。
P0和P1之間的間距,決定了曲線在轉而趨進P3之前,走向P2方向的。
曲线的参数形式为︰②具体代码#include"graphic.h"#include"math.h"main(){int某0=50,y0=300,某1=250,y1=150,某2=452,y2=150,某3=550,y3=300;int某,j,y,n=15;floati,dt,t;charmg[80];intgdriver=DETECT,gmode;regiterbgidriver(EGAVGA_driver);initgraph(&gdriver,&gmode,"c:\\TC");etbkcolor(2);etcolor(YELLOW);dt=1/(float)n;/某3_Bezier绘制曲线图某/for(i=0;i<=n;i++){t=i某dt;某=某0某(1-t)某(1-t)某(1-t)+某1某3某t某(1-t)某(1-t)+某2某3某t某t某(1-t)+某3某t某t某t;y=y0某(1-t)某(1-t)某(1-t)+y1某3某t某(1-t)某(1-t)+y2某3某t某t某(1-t)+y3某t某t某t;if(i==0)moveto(某,y);lineto(某,y);}line(某0,y0,某1,y1);line(某1,y1,某2,y2);line(某2,y2,某3,y3);printf(mg,"%%d%%d,%d%","P",0,"(",某0,y0,")");outte某t某y(某0,y0,mg);printf(mg,"%%d%%d,%d%","P",1,"(",某1,y1,")");outte某t某y(某1,y1,mg);printf(mg,"%%d%%d,%d%","P",2,"(",某2,y2,")");outte某t某y(某2,y2,mg);printf(mg,"%%d%%d,%d%","P",3,"(",某3,y3,")");outte某t某y(某3,y3,mg);getch();/某等待按一键结束某/计算机图形学cloegraph();/某关闭图形系统,回到文本模式某/}③实验结果。
三次Bezier曲线的生成与拼接

科 技 视 界
科技·探索·争鸣
3 微信公众平台在高校图书馆移动信息服务中的具体 应用 建设 .这样就极 大程度上提 高了平 台内容 的实用性和针对性 .满足广
大师生对信息的多样化需求
3.1 借阅 、预约 、查询服务
4.2.2 创新服务模式 .提供个 性化服务
用微信 公众平 台开 展信息服 务 .对推 动图书馆创新 服务 、增 强图书馆 时进行调整 .以实 现微信公众平 台在 图书馆移动信息服务 中功能 的最
活力有着 不言而喻的重大作用 但是微信公众平 台在 图书馆信息服务 大化和服务的最优化。●
的具体 应用 中也出现 了一 些问题 .如 微信公众平 台推广范 围不够普
的平 台。
族大学图书馆购买了微信打印机 .读者关注 图书馆微 信公 众平台后就
3.4 实 时互 动 交 流 服 务
可以 自助打印 自己的个性 LOGO照片。打印机投人使用后就立即吸引
微 信即时性和互 动性强 .读者可通 过语音 、文字 、图片、视频等形 了众多学生前来体 验 。纷纷关 注了图书馆微信公 众平台 .一周 时间内
类 等其他 职业资格考试的服务平台 .读者注册登 录后 即可随时随地利 行宣传推广。
用 手机 获取在线学习服务。 由此可见 。微信本身并 不是一个类似数据
前期 的宣传度微信公众平 台的运营十分重要 .如果宣传不到位 。即
库 一样 的学习资源载体 .而是一个可 以快速整合 网络学习资源的强大 使开通了微 信服务 ,也会 严重影 响微信公众平 台的运 营效果 。西藏民
式 与负责微信 公众平台运营的工作人员进行交 流互 动 .拉近 了读者 和 微信平台关 工作人 员的距离。微信的机制基本上是点对 点的 ,能够防止无
CG_实验5_Bezier曲线

实验5 Bezier曲线1.实验目的:了解曲线的生成原理,掌握几种常见的曲线生成算法,利用VC+OpenGL实现Bezier曲线生成算法。
2.实验内容:(1)结合示范代码了解曲线生成原理与算法实现,尤其是Bezier曲线;(2)调试、编译、修改示范程序。
(3)尝试实现B样条曲线算法。
3.实验原理:Bezier曲线是通过一组多边形折线的顶点来定义的。
如果折线的顶点固定不变,则由其定义的Bezier曲线是唯一的。
在折线的各顶点中,只有第一点和最后一点在曲线上且作为曲线的起始处和终止处,其他的点用于控制曲线的形状及阶次。
曲线的形状趋向于多边形折线的形状,要修改曲线,只要修改折线的各顶点就可以了。
因此,多边形折线又称Bezier曲线的控制多边形,其顶点称为控制点。
三次多项式,有四个控制点,其数学表示如下:4.实验代码:#include <glut.h>#include <stdio.h>#include <stdlib.h>#include <vector>using namespace std;struct Point { int x, y; }; Point pt[4], bz[11];vector<Point> vpt;bool bDraw;int nInput;void CalcBZPoints(){float a0,a1,a2,a3,b0,b1,b2,b3;a0=pt[0].x;a1=-3*pt[0].x+3*pt[1].x;a2=3*pt[0].x-6*pt[1].x+3*pt[2].x;a3=-pt[0].x+3*pt[1].x-3*pt[2].x+pt[3].x;b0=pt[0].y;b1=-3*pt[0].y+3*pt[1].y;b2=3*pt[0].y-6*pt[1].y+3*pt[2].y;b3=-pt[0].y+3*pt[1].y-3*pt[2].y+pt[3].y;float t = 0;float dt = 0.01;for(int i = 0; t<1.1; t+=0.1, i++){bz[i].x = a0+a1*t+a2*t*t+a3*t*t*t;bz[i].y = b0+b1*t+b2*t*t+b3*t*t*t;}}void ControlPoint(vector<Point> vpt){ int i;glPointSize(2);for(i=0; i<vpt.size(); i++){glBegin (GL_POINTS);glColor3f (1.0f, 0.0f, 0.0f); glVertex2i (vpt[i].x,vpt[i].y);glEnd ();}}void PolylineGL(Point *pt, int num){glBegin (GL_LINE_STRIP);for(int i=0;i<num;i++){glColor3f (1.0f, 1.0f, 1.0f);glVertex2i (pt[i].x,pt[i].y);}glEnd ();}void myDisplay(){glClear(GL_COLOR_BUFFER_BIT);glColor3f (1.0f, 1.0f, 1.0f);if (vpt.size() > 0) {ControlPoint(vpt);}if(bDraw){PolylineGL(pt, 4);CalcBZPoints();PolylineGL(bz, 11);}glFlush();}void Init(){ glClearColor(0.0, 0.0, 0.0, 0.0);glShadeModel(GL_SMOOTH);printf("Please Click left button of mouse to input control point of Bezier Curve!\n");}void Reshape(int w, int h){glViewport(0, 0, (GLsizei) w, (GLsizei) h);glMatrixMode(GL_PROJECTION);glLoadIdentity();gluOrtho2D(0.0, (GLdouble) w, 0.0, (GLdouble) h);}void mouse(int button, int state, int x, int y){switch (button){case GLUT_LEFT_BUTTON:if (state == GLUT_DOWN){if (nInput == 0){pt[0].x = x;pt[0].y = 480 - y;nInput = 1;vpt.clear();vpt.push_back(pt[0]);bDraw = false;glutPostRedisplay();//}else if (nInput == 1){pt[1].x = x;pt[1].y = 480 - y;vpt.push_back(pt[1]);nInput = 2;glutPostRedisplay();//}else if (nInput == 2){pt[2].x = x;pt[2].y = 480 - y;vpt.push_back(pt[2]);nInput = 3;glutPostRedisplay();//}else if (nInput == 3){pt[3].x = x;pt[3].y = 480 - y;bDraw = true;vpt.push_back(pt[3]);nInput = 0;glutPostRedisplay();//}}break;default:break;}}int main(int argc, char *argv[]){glutInit(&argc, argv);glutInitDisplayMode(GLUT_RGB | GLUT_SINGLE);glutInitWindowPosition(100, 100);glutInitWindowSize(640, 480);glutCreateWindow("Hello World!");Init();glutDisplayFunc(myDisplay);glutReshapeFunc(Reshape);glutMouseFunc(mouse);glutMainLoop();return 0;}。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Bezier曲线的绘制实验报告 一、程序实现环境 1操作系统:Windows XP 、Windows7 2.编程语言:C++ 3.程序实现环境:Visual C++ 6.0 二、算法思想
三、使用说明 程序界面如下图:
用户可以在编辑框中输入4个控制点的坐标,也可以通过在绘图区内直接通过鼠标的单击指定4个控制点的位置,输入4个控制端点后,单击“画Bezier曲线”按钮即可绘制Bezier曲线。 四、实验结果
五、程序代码(关键代码) void CMFC_BezierCurve2Dlg::OnLButtonDown(UINT nFlags, CPoint point) { if(pointOrd==1) //原点(490,270) { m_p1_x = point.x - 490; m_p1_y = 270 - point.y; } if(pointOrd==2) { CDC *pDC=GetDC(); pDC->MoveTo(490+m_p1_x, 270-m_p1_y); pDC->LineTo(point.x, point.y);
m_p2_x = point.x - 490; m_p2_y = 270 - point.y; } if(pointOrd==3) { CDC *pDC=GetDC(); pDC->MoveTo(490+m_p2_x, 270-m_p2_y); pDC->LineTo(point.x, point.y);
m_p3_x = point.x - 490; m_p3_y = 270 - point.y; } if(pointOrd==4) { CDC *pDC=GetDC(); pDC->MoveTo(490+m_p3_x, 270-m_p3_y); pDC->LineTo(point.x, point.y);
m_p4_x = point.x - 490; m_p4_y = 270 - point.y; } pointOrd++; UpdateData(FALSE);
CDialog::OnLButtonDown(nFlags, point); }
voidGetCnk (int n, int *c) { inti,k; for(k=0; k<=n; k++) { c[k]=1; for(i=n; i>=k+1; i--) c[k]=c[k]*i; for(i=n-k; i>=2; i--) c[k]=c[k]/i; } }
void CMFC_BezierCurve2Dlg::GetPointPos(intControlN, double t, int *c) { int k, n=ControlN-1; double Bernstein; Pt.x=0.0; Pt.y=0.0; for(k=0; k{ Bernstein=c[k]*pow(t,k)*pow(1-t,n-k); Pt.x += ControlP[0][k].x * Bernstein; Pt.y += ControlP[0][k].y * Bernstein; } }
void CMFC_BezierCurve2Dlg::OnButtonDrawBeziercurve() { UpdateData(); pointOrd=1; CDC *pDC=GetDC(); ControlP[0][0].x=m_p1_x;ControlP[0][0].y=m_p1_y; ControlP[0][1].x=m_p2_x;ControlP[0][1].y=m_p2_y; ControlP[0][2].x=m_p3_x;ControlP[0][2].y=m_p3_y; ControlP[0][3].x=m_p4_x;ControlP[0][3].y=m_p4_y;
pDC->MoveTo(490+m_p1_x, 270-m_p1_y); pDC->LineTo(490+m_p2_x, 270-m_p2_y); pDC->LineTo(490+m_p3_x, 270-m_p3_y); pDC->LineTo(490+m_p4_x, 270-m_p4_y); int *C, i; intControlN=4, m=500; C=new int[ControlN]; GetCnk (ControlN-1, C); for(i=0; i<=m; i++) { GetPointPos(ControlN, (double)i/(double)m, C); pDC->SetPixel(490+Pt.x, 270-Pt.y, 255); } } 两段Bezier曲线的拼接实验报告 一、程序实现环境 1操作系统:Windows XP 、Windows7 2.编程语言:C++ 3.程序实现环境:Visual C++ 6.0 二、算法思想
三、使用说明 程序界面如下图:
用户可以在编辑框中输入4个控制点的坐标,也可以通过在绘图区内直接通过鼠标的单击指定4个控制点的位置,输入4个控制端点后,单击“画Bezier曲线”按钮即可绘制Bezier曲线。 分别绘制完两段Bezier曲线后,单击拼接即可实现两段曲线的拼接。 四、实验结果 五、程序代码(关键代码) void CMFC_BezierCurve2Dlg::OnLButtonDown(UINT nFlags, CPoint point) { if(pointOrd==1) //原点(490,270) { m_p1_x = point.x - 490; m_p1_y = 270 - point.y; } if(pointOrd==2) { CDC *pDC=GetDC(); pDC->MoveTo(490+m_p1_x, 270-m_p1_y); pDC->LineTo(point.x, point.y);
m_p2_x = point.x - 490; m_p2_y = 270 - point.y; } if(pointOrd==3) { CDC *pDC=GetDC(); pDC->MoveTo(490+m_p2_x, 270-m_p2_y); pDC->LineTo(point.x, point.y); m_p3_x = point.x - 490; m_p3_y = 270 - point.y; } if(pointOrd==4) { CDC *pDC=GetDC(); pDC->MoveTo(490+m_p3_x, 270-m_p3_y); pDC->LineTo(point.x, point.y);
m_p4_x = point.x - 490; m_p4_y = 270 - point.y; }
pointOrd++; UpdateData(FALSE);
CDialog::OnLButtonDown(nFlags, point); }
voidGetCnk (int n, int *c) { inti,k; for(k=0; k<=n; k++) { c[k]=1; for(i=n; i>=k+1; i--) c[k]=c[k]*i; for(i=n-k; i>=2; i--) c[k]=c[k]/i; } }
void CMFC_BezierCurve2Dlg::GetPointPos(intControlN, double t, int *c) { int k, n=ControlN-1; double Bernstein; Pt.x=0.0; Pt.y=0.0; for(k=0; k{ Bernstein=c[k]*pow(t,k)*pow(1-t,n-k); Pt.x += ControlP[pointGroup][k].x * Bernstein; Pt.y += ControlP[pointGroup][k].y * Bernstein; } }
void CMFC_BezierCurve2Dlg::BezierCurve() { CDC *pDC=GetDC(); pDC->MoveTo(490 + ControlP[pointGroup][0].x, 270 - ControlP[pointGroup][0].y); pDC->LineTo(490 + ControlP[pointGroup][1].x, 270 - ControlP[pointGroup][1].y); pDC->LineTo(490 + ControlP[pointGroup][2].x, 270 - ControlP[pointGroup][2].y); pDC->LineTo(490 + ControlP[pointGroup][3].x, 270 - ControlP[pointGroup][3].y);
int *C, i; intControlN=4, m=500; C=new int[ControlN]; GetCnk (ControlN-1, C); for(i=0; i<=m; i++) { GetPointPos(ControlN, (double)i/(double)m, C); pDC->SetPixel(490+Pt.x, 270-Pt.y, 255); } }
void CMFC_BezierCurve2Dlg::OnButtonDrawBeziercurve() { UpdateData(); pointOrd=1;
ControlP[pointGroup][0].x=m_p1_x; ControlP[pointGroup][0].y=m_p1_y; ControlP[pointGroup][1].x=m_p2_x; ControlP[pointGroup][1].y=m_p2_y; ControlP[pointGroup][2].x=m_p3_x; ControlP[pointGroup][2].y=m_p3_y; ControlP[pointGroup][3].x=m_p4_x; ControlP[pointGroup][3].y=m_p4_y;
BezierCurve(); pointGroup++; }
void CMFC_BezierCurve2Dlg::OnButtonMatch() { pointGroup--;
double dx, dy; double k1, k2, s, s1, s2; int i; CPoint temp;
