安徽省2017瑶海二模
2017年安徽合肥高三模拟考试(二模)

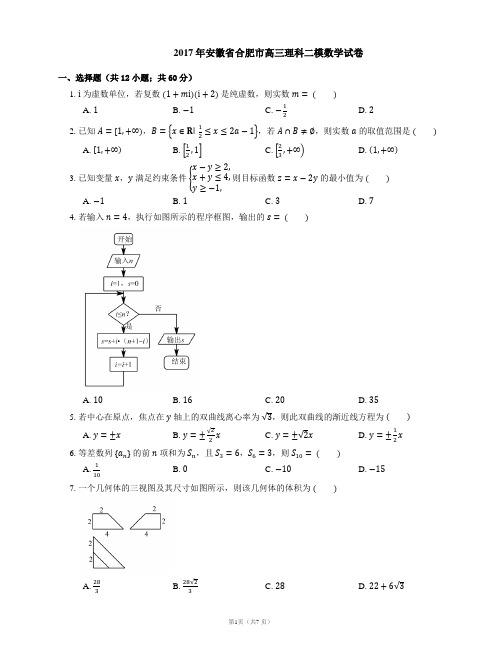
2017年安徽合肥高三模拟考试(二模)文科数学一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.设集合{4,3,2,1,0,1}M =----,2{|30}N x R x x =∈+<,则M N = ( ) A .{3,2,1,0}--- B .{2,1,0}-- C .{3,2,1}--- D .{2,1}--2.设i 为虚数单位,复数z 满足11ii z+=-,则复数z =( ) A .2i B .2i - C .i D .i - 3.角A 是ABC ∆的一个内角,若命题:3p A π<,命题3:sin 2q A <,则p 是q 的( ) A .充分不必要条件 B .必要不充分条件 C .充分必要条件 D . 既不充分也不必要条件4.我们知道,“心有灵犀”一般是对人的心理活动非常融洽的一种描述,它也可以用数学来定义:甲、乙两人都在{1,2,3,4,5,6}中说一个数,甲说的数记为a ,乙说的数记为b ,若||1a b -≤,则称甲、乙两人“心有灵犀”,由此可以得到甲、乙两人“心有灵犀”的概率是( ) A .19 B .29 C. 13 D .495.执行如图所示的程序框图,则输出的S 的值为( )A .16B .32 C. 64 D .10246.在等比数列{}n a 中,23427a a a =,727a =,则首项1a =( ) A .3± B .1± C. 3 D .17.某空间几何体的三视图如图所示,则该几何体的体积是( )A . 32B .322 C.323 D .32238.已知双曲线C :22221(0,0)x y a b a b -=>>的左、右焦点与虚轴的一个端点构成一个角为120 的三角形,则双曲线C 的离心率为( )A .52 B .62C. 3 D .5 9.若函数3xy ae x =+在R 上有小于零的极值点,则实数a 的取值范围是( ) A .(3,)-+∞ B .(,3)-∞- C. 1(,)3-+∞ D .1(,)3-∞- 10.函数2sin ln(1)y x x x =++在[,]ππ-上的图象大致为( )A .B .C. D .11.设函数sin (0)y x ωω=>的最小正周期是T ,将其图象向左平移14T 后,得到的图象如图所示,则函数sin (0)y x ωω=>的单增区间是( )A .7777[,]()624624k k k Z ππππ-+∈ B .7777[,]()324324k k k Z ππππ-+∈ C. 7777[,]()312312k k k Z ππππ-+∈ D .77721[,]()624624k k k Z ππππ++∈ 12.已知实数,x y 满足条件2222x x y x y ≤⎧⎪+≥⎨⎪-≥⎩,则2y x y x ++的取值范围是( )A .[0,1]B .1[,1]3 C. 12[,]23 D .1[,1]2二、填空题(每题5分,满分20分,将答案填在答题纸上)13.若抛物线28y x =的准线和圆2260x y x m +++=相切,则实数m 的值是 .14.已知向量||3a = ,||2b = ,且()0a a b -= ,则a b - 的模等于 .15.设,A B 是球O 的球面上两点,且90AOB ∠=,若点C 为该球面上的动点,三棱锥O ABC -的体积的最大值为292ππ立方米,则球O 的表面积是 平方米. 16.已知数列{}n a 是各项均不为零的等差数列,n S 为其前n 项和,且2*21()n n S a n N -=∈,若不等式112231111log n n n a a a a a a πλ++++≤ 对任意*n N ∈恒成立,则实数λ的最大值是 .三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17. 在ABC ∆中,角,,A B C 的对边分别是,,a b c ,其外接圆的半径是1,且满足222(sin sin )(2)sin A C a b B -=-.(1)求角C 的大小;(2)求ABC ∆的面积的最大值.18. 在矩形ABCD 中,将ABC ∆沿其对角线AC 折起来得到1AB C ∆,且顶点1B 在平面ACD 上的射影O 恰好落在边AD 上(如图所示).(1)证明:1AB ⊥平面1B CD ;(2)若1AB =,3BC =,求三棱锥1B ABC -的体积.19. 为响应阳光体育运动的号召,某县中学生足球活动正如火如荼地展开,该县为了解本县中学生的足球运动状况,根据性别采取分层抽样的方法从全县24000名中学生(其中男生14000人,女生10000人)中抽取120名,统计他们平均每天足球运动的时间,如下表:(平均每天足球运动的时间单位为小时,该县中学生平均每天足球运动的时间范围是[0,3]).(1)请根据样本估算该校男生平均每天足球运动的时间(结果精确到0.1);(2)若称平均每天足球运动的时间不少于2小时的学生为“足球健将”,低于2小时的学生为“非足球健将”.①请根据上述表格中的统计数据填写下面22⨯列联表,并通过计算判断,能否有90%的把握认为是否为“足球健将”与性别有关?②若在足球运动时间不足1小时的男生中抽取2名代表了解情况,求这2名代表都是足球运动时间不足半小时的概率.参考公式:22()()()()()n ad bc k a b c d a c b d -=++++,其中n a b c d =+++.参考数据:20()P K k ≥0.05 0.40 0.25 0.15 0.10 0.05 0.025 0.0100k3.841 0.708 1.323 2.072 2.706 3.841 5.0246.63520. 已知椭圆E :22221(0)x y a b a b +=>>的离心率是22,12,F F 是椭圆的左、右焦点,点A 为椭圆的右顶点,点B 为椭圆的上顶点,且1212ABF S ∆+=.(1)求椭圆E 的方程;(2)若直线l 过右焦点2F 且交椭圆E 于,P Q 两点,点M 是直线2x =上的任意一点,直线2,,MP MF MQ 的斜率分别为123,,k k k ,问是否存在常数λ,使得132k k k λ+=成立?若存在,求出λ的值;若不存在,请说明理由. 21. 设函数32()23(1)6f x x a x ax =-++,a R ∈. (1)讨论()f x 的导函数'()f x 在[1,3]-上的零点个数;(2)若对于任意的[3,0]a ∈-,任意的12,[0,2]x x ∈,不等式212|()()|m am f x f x -≥-恒成立,求实数m 的取值范围.请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分.22.选修4-4:坐标系与参数方程在平面直角坐标系中,以坐标原点O 为极点,x 轴非负半轴为极轴,并在两坐标系中取相同的长度单位,若直线l 的极坐标方程是sin()224πρθ+=,且点P 是曲线C :3cos sin x y θθ⎧=⎪⎨=⎪⎩(θ为参数)上的一个动点. (1)将直线l 的方程化为直角坐标方程; (2)求点P 到直线l 的距离的最大值与最小值. 23.选修4-5:不等式选讲 已知()|1||2|f x x x =-++.(1)若不等式2()f x a >对任意实数x 恒成立,求实数a 的取值的集合T ; (2)设,m n T ∈,证明:3|||3|m n mn +<+.试卷答案一、选择题题号 1 2 3 4 5 6 7 8 9 1011 12答案D C A D C D B B B AA C1、D 解析:{}03<<-∈=x R x N ,所以=N M {}1,2-- 2、C.解析:由题意可知,i iiz =-+=11 3、A 解析:由题意知命题q :03A π<<或ππ<<A 32,所以p 是q 的充分不必要条件. 4、D 解析:若,1=a 则2,1=b ;若,6=a 则6,5=b ;若2,3,4,5a =,则b 都有3种取值.所以,甲、乙两人“心有灵犀”的事件数是.163422=⨯+⨯基本事件总数是3666=⨯. 因此他们“心有灵犀”的概率是.943616= 5、C 解析: 1110=⨯==S n ,;2211=⨯==S n ,; 8422=⨯==S n ,;64883=⨯==S n ,.6、D 解析:4732343123327,3,9,13a a a a a a q a a q =∴===∴=== 又. 7、B 解析:几何体为直三棱柱..232442421=⨯⨯⨯=V 8、B 解析:根据双曲线的对称性知:.26,32,360tan 22=∴=∴==e a c b c 9、B 解析:a e ae y xx 3,03-==+=',则03>-a ,且,13<-a所以.3-<a 10、A 解析:显然y 是偶函数.当x π=时,0>y ,排除B,D.12)cos (sin 2+++='x x x x x y .∴当02x π⎛⎫∈ ⎪⎝⎭,时,0>'y ,y 在⎥⎦⎤ ⎝⎛2,0π单调递增,排除C.11、A. 解析:由已知图象知,sin (0)y x ωω=>的最小正周期是,671272ππ=⨯所以,672πωπ=解得.712=ωx y 712sin =.由2271222ππππ+≤≤-k x k 得到,单增区间是 )(24767,24767Z k k k ∈⎥⎦⎤⎢⎣⎡+-ππππ 或:因为,2ωπ=T 所以将sin (0)y x ωω=>的图象向左平移T 41后,所对应的解析式为)2(sin ωπω+=x y .由图象知,,23)2127(πωππω=+所以.712=ωx y 712sin =. 由2271222ππππ+≤≤-k x k 得到,单增区间是)(24767,24767Z k k k ∈⎥⎦⎤⎢⎣⎡+-ππππ 12、C 解析:方法1:设k x=y ,画出可行域如右下图所示,易求出 ]1,0[∈k ,]2,34[∈x ,∴]1,0[,21121212∈+-=++=++=++k k k k xy x yx y x y ∴]32,21[2∈++x y x y 方法2:设m xy x y =++2.∵]2,34[∈x ,∴1m ≠∴由x mm y m x y x y --=⇒=++1122令k mm =--112,由kx y =,易求出]1,0[∈k ∴32m 2111120≤≤⇒≤--≤m m ,∴]32,21[2∈++x y x y注:教师在评讲此题时,可拓展此题为:“求322++++x y x y 的取值范围”.二、填空题:(本大题共4小题,每小题5分,共20分.) 13、8 14、1 15、36 16、2113、.8解析:0622=+++m x y x 的圆心为)0,3(-,半径为m -9,抛物线x y 82=的准线是直线,2-=x 所以m -=+-932,得.8=m14、.1解析:因为⇒=-⋅0)(b a a b a a ⋅=2,所以22222)(b b a a b a b a +⋅-=-=-,14322=+-=+-=b a ∴.1=-b a15、.36【解析】如图所示,当点C 位于垂直于面AOB 的直径端点时,三棱锥O ABC -的体积最大,设球O 的半径为R ,此时.9,296121312232πππ===⨯⨯==--R R R R V V ABO C ABC O 则球O 的表面积为.3642==R S π16、21【解析】.12)12(2))(12(22121-=⇒=-⇒=+--n a a a n a a a n n n n n n .12)12112171515131311(2111113221+=+--+⋅⋅⋅+-+-+-=+⋅⋅⋅+++n n n n a a a a a a n n λ8113221log 111n a a a a a a n n ≤+⋅⋅⋅+++对任意*∈N n 恒成立,也就是121log 81+≥n λ对任意*∈N n 恒成立,所以.21,31)121(log max 81≤=+≥λλn 三、解答题(本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤) 17、(本小题满分12分) 解析:(Ⅰ)将22sin ,22sin ,22sin cR c C b R b B a R a A ======代入已知等式得到,,2)2()44(222bb ac a ⋅-=- 即2222b ab c a -=-,ab c b a 2222=-+. 由余弦定理得,=C cos ,22222222==-+ab ab ab c b a .45 =C(Ⅱ)ab c b a 2222=-+就是ab b a 2)45sin 2(222=-+ ,即222222-≥=-+ab ab b a , 所以,22+≤ab 当且仅当b a =时等号成立.所以,21245sin 21+≤=∆ ab S ABC 故ABC ∆面积的最大值是.212+ 18、(本小题满分12分)解析:(Ⅰ)⊥O B 1 平面ABCD ,CD ⊂平面ABCD , ∴1B O CD ⊥. 又 CD AD ⊥,AD ⋂1B O =O , ∴CD ⊥平面1AB D . 而1AB ⊂平面1AB D ,∴.1CD AB ⊥ 又 11AB B C ⊥,且1B C ⋂CD =C ,1AB ∴⊥平面1B CD .(Ⅱ)由于1AB ⊥平面1B CD ,1B D ⊂平面1B CD ,所以11AB B D ⊥.在1Rt AB D ∆中,22112B D AD AB =-=.由111B O AD AB B D ⋅=⋅得,111AB B D B O AD ⋅=.36=所以11111621333236B ABC ABC V S B O -∆=⋅=⨯⨯⨯⨯=19、(本小题满分12分)解析:(Ⅰ)由分层抽样得:男生抽取的人数为14000120=7014000+10000⨯人,女生抽取人数为1207050-=人,故x =5,y =2. ………………2分则该校男生平均每天足球运动的时间为,6.170575.21025.22275.12825.1375.0225.0≈⨯+⨯+⨯+⨯+⨯+⨯故该校男生平均每天足球运动的时间约为6.1小时; (Ⅱ)①由表格可知:足球健将 非足球健将总 计 男 生 15 55 70 女 生 5 45 50 总 计20100120故2K的观测值706.2743.23596705010020)5554515(12022>≈=⨯⨯⨯⨯-⨯=k 因此有90%的把握认为是否为“足球健将”与性别有关.②记不足半小时的两人为a 、b ,足球运动时间在[0.51),内的三人为1,2,3,则总的基本事件个数是(ab ),(a1),(a2),(a3),(b1),(b2),(b3),(12),(13),(23),其中2名代表足球运动时间都不足半小时的是(ab ),∴.101=P 20、(本小题满分12分)解析:(Ⅰ)),0(),0,(),0,(1b B a A c F -,则b c a S ABF )(212121+=+=∆, ,12)(+=+b c a 即.12)(22+=-+c a c a ……2分又c a a c e 2,22===,代入上式中得到, .1,122)2(22=+=-+c c c c c 于是.1,2==b a故椭圆E 的方程为.1222=+y x(Ⅱ)由(Ⅰ)知2F 的坐标为)0,1(2F .设),(11y x P ,),(22y x Q ,),2(t M . (1)当直线l 的斜率不为零时,设l 的方程为1+=my x .联立⎪⎩⎪⎨⎧=++=12122y x m y x 消去x 得,012)2(22=-++my y m .∴22221+-=+m m y y ,.21221+-=m y y ∴22221131--+--=+x t y x t y k k 112211--+--=my ty my t y )1)(1()1)(()1)((211221----+--=my my my t y my t y 1)(2))(1(2212122121++-+++-=y y m y y m t y y mt y my 122222)1(222222222++++-+++++-=m m m m t m mt m m m t m t t m 2224422=++=.又∵t tk =-=122,∴2312k k k =+ . (2)当直线l 的斜率为零时,显然有:231222222k t tt k k ==-++=+∴2312k k k =+仍成立.综上知,存在2=λ,使得231k k k λ=+成立. 21. (本小题满分12分)解析:(1)2()66(1)66(1)()f x x a x a x x a '=-++=--,当31>-<a a 或时,)(x f '在[]3,1-上有1个零点; 当1a =时,)(x f '在[]3,1-上有1个零点;当31≤≤-a 且1a ≠时,)(x f '在[]3,1-上有2个零点. (Ⅱ)对于任意的[]12,0,2x x ∈,不等式212()()m am f x f x -≥-恒成立,等价于212max()()m am f x f x -≥-易得,()f x 在[]0,1上单调递减,在[]1,2上单调递增,(0)0,(2)4f f ==,12max ()()(2)(1)53f x f x f f a ∴-=-=-.则问题转化为对于任意的[]3,0a ∈-,253m am a -≥-恒成立,即对于任意的[]3,0a ∈-,2(3)50m a m --+≤恒成立.令[]2()(3)5,3,0g a ma m a =--+∈-,只需(3)0(0)0g g -≤⎧⎨≤⎩55372≥⇒⎪⎩⎪⎨⎧≥-≤≥⇒m m m m 或故实数m 的取值范围是[).,5∞+ 22. (本小题满分10分) 解析:(Ⅰ)由 22)4sin(=+πθρ22)cos 22sin 22=+⇒θθρ(. 将θρθρsin ,cos ==y x 代入,即可得到直线l 的直角坐标方程是04=-+y x .(Ⅱ) P 到直线l 的距离2|4sin cos 3|-+=θθd 2)3sin(24πθ+-=.∴2min =d ,23max =d .23. (本小题满分10分)解析:(Ⅰ)由绝对值不等式的性质知,.3)2()1(21=+--≥++-x x x x …2分 因为2()f x a >恒成立,所以23a <,即33a -<<,所以().3,3-=T (Ⅱ)2222)3()(3)3()3(+-+=+-+mn n m mn n m).3)(3(96363222222---=---++=n m mn n m n mn m因为,,T n m ∈所以,3,322<<n m 故,0)3)(3(22<---n m 所以,)3()3(22+<+mn n m 即.33+<+mn n m。
【安徽省安庆】2017学年高考二模数学年(理科)试题答案

(Ⅰ)将直线 l 的方程化为直角坐标方程; (Ⅱ)求点 P 到直线 l 的距离的最大值与最小值.
【选修 4-5:不等式选讲】
23.已知 f ( x) | x- 1| +| x 2 | . (1)若不等式 f ( x ) a 2 对任意实数 x 恒成立,求实数 a 的取值的集合 T ;
(Ⅱ)设 m、 n T ,证明: 3|m n| |mn 3|.
请考生在第 22、 23 题中任选一题作答【选修 4-4:坐标系与参数方程】
22.在平面直角坐标系中,以原点为极点, x 轴的非负半轴为极轴,并在两坐标系中取相同的长度单位,若
直线 l 的极坐标方程是 sin( π) 2 2 ,且点 P 是曲线 C : x 3cos ( 为参数)上的一个动点.
4
y sin
三、解答题(共 5 小题,满分 60 分)
17 .已知数列 { an } 中, a1 2 , a2 4 ,设 Sn 为数列 { an } 的前 n 项和,对于任意的 n 1 , n N * ,
-2-/ 4
Sn 1 Sn - 1 2( Sn 1) .
(1)求数列 { an} 的通项公式;
(2)设 bn
2.设 i 是虚数单位,复数 a i 为纯虚数,则实数 a 的值为(
)
1i
A. 1
B.1
C. 2
D. 2
3.设命题 p : x 0 (0,
) , x0 1 3 ;命题 q : x (2, ) , x 2 2x ,则下列命题为真的是(
)
x0
A . p (¬ q )
B. (¬ p) q
C. p q
D. (¬ p) q
P , M 与直线 m 交于点 Q,求证:以线段 PQ 为直
【安徽省安庆】2017学年高考二模数学年(理科)试题

三、解答题(共5小题,满分60分)17.解:(1)对于任意的1n >,*n ∈N ,1121n n n S S S +-+=+(),2121n n n S S S +++=+(), 相减可得:212n n n a a a +++=.(*)又2n =时,3122(1)S S S +=+,即1231222(1)a a a a a ++=++,12a =,24a =,解得36a =. ∴1n =时(*)也满足.∴数列{}n a 是等差数列,公差为2, ∴22(1)2n a n n =+-=.(2)2242n n a n nn n nb ===, ∴{}n b 的前n 项和23123 (4444)n n nT =+++,221121 (144444)n n n n T n +-++=+, 可得21111(1)1144 (1444413144)4n n n n n n n T ++-+---+==, 18.证明:(Ⅰ)取AD 中点O ,以O 为原点,OA 为x 轴, 过O 作AB 的平行线为y 轴,OE 为z 轴,建立空间直角坐标系, 则(1,1,0)B,E ,(1,0,0)A ,(1,2,0)C -,F ,1(BE =-,-,(AF =-,(2,2,0)AC =-, 1430BE AF =-+=,220BE AC =-=,∴BE AF ⊥,BE AC ⊥, 又AFAC A =,∴BE ACF ⊥平面.解:(Ⅱ)(2,1,0)BC =-,(BF =-,设平面BCF 的法向量(,,)n x y z =,则2030n BC x y n BF x y ⎧=-+=⎪⎨=-++=⎪⎩,取1x =,得(1,2,n =,平面ABC 的法向量π(0,0,1)=, 设二面角A BC F --的平面角为,则||cos 1m n m n===+∴二面角A BC F --的余弦值为4.19.解:(Ⅰ)由题意5x =, 1.072y =,21()10i i x x =-=∑,∴121()()0.064()niii nii x x yy b x x ==--==-∑∑,0.752a y bx =-=,∴从3月到6月,y 关于x 的回归方程为0.060.75y x =+,12x =时,147y =..即可预测第12月份该市新建住宅销售均价为1.47万元/平方米;(Ⅱ)x 的取值为1,2,3,31241(1)55P x c ===,334312327(3)55c P x c ⨯===,27(2)1(1)(3)55P x P x P x ==-=-==, x 的分布列为20.解:(Ⅰ)由题意可得:直线l 的斜率存在,设方程为:2y kx =+, 设11(,)A x y ,22(,)B x y ,动点(,)C x y ,由222p y kx x py =⎧⎪⎨=+⎪⎩,可得2220x pkx p =--.可得212x x p =-. OA :1112y x y x x x p==;OB :2x x =;由122x xx p x y =⎧=⎪⎨⎪⎩可得1222x p y x p ==, 即点C 的轨迹方程为2py =-. (Ⅱ)证明:设直线m 的方程为:y kx m =+,由22x py y kx m⎧=⎨=+⎩可得2220x pkx pm =--可得2248p k pm =+,因为直线m 与抛物线相切, ∴0=,可得220pk m +=,可得(,)P pk m -,又由2y kx m py =+⎧⎪⎨=⎪⎩,可得2(,)22p m p Q k +--,(,)2p FP FQ pk m =--2(,)22p m pk +--2(2)022p p p m pm =-+++=,可得FP FQ ⊥,∴以线段PQ 为直径的圆过点F .21.(1)解:∵2()e xax x a f x ++=,∴1(1)(1)()e x a x x a f x ---+'=①0a >,11a a -<,1(,1)a x a-∈时,()0f x '>,故函数的单调增区间为1(,1)a a -; ②0a <,11a a->,1(,1)(,)a x a -∈-∞+∞时,()0f x '>,故函数的单调增区间为(,1)x ∈-∞和1(,)a a -+∞;(2)0a =,()ex xf x =,122x x x <<<,证明:121121()()()()f x f x f x f x x x x x -->--,只要证明11()()()f x f x g x x x -=-在1(,2)x 上单调递减. 111211()e e e ()()x x xx x x x x g x x x ---+'=-,设1111()()e e e x x x x x x h x x x -=--+, ∴1()(2)()0e xx x x h x --'=<,∴()h x 在1(,2)x 上是减函数, ∴()0h x <,∴()0g x '<, ∴11()()()f x f x g x x x -=-在1(,2)x 上单调递减.∵122x x x <<<,22.解:(Ⅰ)∵直线l 的极坐标方程是sin()4+=, ∴ππ(sin coscos sin )2244+=, ∴sin cos 4+=,由sin y =,cos x =,得10x y +=-. ∴直线l 的直角坐标方程为10x y +=-.(Ⅱ)∵点P 是曲线C :sinx y ⎧=⎪⎨=⎪⎩(为参数)上的一个动点,∴,sin )P ,点P 到直线l 的距离d ===,23.(Ⅰ)解:∵||()1||2123f x x x x x =++≥=----,不等式2()f x a >对任意实数x 恒成立,∴23a >,∴a <,∴{|a Ta <=;(Ⅱ)证明:由(Ⅰ)可得23m <,23n <,∴22(3)(3)0m n --<, ∴223()(3)m n mn +<+,安徽省安庆市2017年高考数学(理科)二模试卷解析一、选择题1.【考点】补集及其运算.【分析】化简集合A,求出∁UA.【解答】解:集合U={1,2,3,4},集合A={x∈N|x2﹣5x+4<0}={x∈N|1<x<4}={2,3},所以∁UA={1,4}.故选:B.2.【考点】复数代数形式的乘除运算.【分析】由复数代数形式的乘除运算化简,由整理出实部和虚部,由纯虚数的定义列出方程组,求出a 的值.【解答】解:由题意得,===,因为复数为纯虚数,所以,解得a=﹣1,故选A.3.【考点】复合命题的真假.【分析】先判断命题p、q的真假,再利用复合命题真假的判定方法即可得出.【解答】解:命题p:∃x0∈(0,+∞),x0+>3,是真命题,例如取x0=4;命题q:∀x∈(2,+∞),x2>2x,是假命题,取x=4时,x2=2x.则下列命题为真的是p∧(¬q).故选:A.4.【考点】等比数列的通项公式.【分析】利用等比数列的通项公式和等差中项,列出方程组,由此能求出{an}的公比.【解答】解:∵等比数列{an}中,a3﹣3a2=2,且5a4为12a3和2a5的等差中项,∴,解得a1=﹣1,q=2.∴{an}的公比等于2.故选:C.5.【考点】由三视图求面积、体积.【分析】由三视图可知:该几何体为一个横放的直三棱柱,高为4,底面是一个直角边长分别为2,4的直角三角形,其中下面的一个侧面为边长为4的正方形,对角线相交于点O1.则球心O满足OO1⊥侧面ABB1A1.设OO1=x,则x2+=(2﹣x)2+,解得x.可得该多面体外接球的半径r.【解答】解:由三视图可知:该几何体为一个横放的直三棱柱,高为4,底面是一个直角边长分别为2,4的直角三角形,其中下面的一个侧面为边长为4的正方形,对角线相交于点O1.则球心O满足OO1⊥侧面ABB1A1.设OO1=x,则x2+=(2﹣x)2+,解得x=1.∴该多面体外接球的半径r==3.表面积为4π×32=36π.故选:C.6.【考点】双曲线的简单性质.【分析】根据中位线定理,求得C点坐标,由•=0,利用向量数量积的坐标运算,利用双曲线的性质,即可求得双曲线的离心率.【解答】解:由题意可知:设椭圆的方程为:,(a>0,b>0),由AB为双曲线的通径,则A(c,),B(c,﹣),F1(﹣c,0),由OC为△F1F2B中位线,则丨OC丨=,则C(0,﹣),则=(﹣c,﹣),=(﹣2c,),由AC⊥BF1,则•=0,则2c2﹣=0整理得:3b4=4a2c2,由b2=c2﹣a2,3c4﹣10a2c2+3a4=0,椭圆的离心率e=,则3e4﹣10e2+3=0,解得:e2=3或e2=,由e>1,则e=,故选B.7.【考点】程序框图.【分析】分析程序中各变量、各语句的作用,再根据流程图所示的顺序,可知:该程序的作用是利用循环计算并输出变量y的值,模拟程序的运行,用表格对程序运行过程中各变量的值进行分析,不难得到输出结果.【解答】解:程序在运行过程中各变量的值如下表示:x y|y﹣x|是否小于或等于2 是否继续循环循环前20/第一圈20 8|8﹣20|=12>2 是第二圈8 2|2﹣8|=6>2 是第三圈2﹣1|﹣1﹣2|=3>2 是第四圈﹣1﹣|﹣﹣(﹣1)|=<2 否故输出y的值为﹣.故选:D.8.【考点】简单线性规划.【分析】画出约束条件表示的可行域,通过表达式的几何意义,求出表达式的最小值.【解答】解:x,y满足|x|≤y≤1,表示的可行域如图:x2+y2+2x=(x+1)2+y2﹣1它的几何意义是可行域内的点到(﹣1,0)的距离的平方减去1.显然D(﹣1,0)到直线x+y=0的距离最小,最小值为:=,所求表达式的最小值为:,故选:D.9.【考点】函数y=Asin (ωx +φ)的图象变换.【分析】由周期求出ω,由最值以及特殊点求A 、B ,由五点法作图求出φ的值,可得f (x )的解析式;利用函数y=Asin (ωx +φ)的图象变换规律,正弦函数的图象的对称性,求得m 的最小值. 【解答】解:根据函数f (x )=Asin (ωx +φ)+B (A >0,ω>0,|φ|<)的部分图象,可得y 轴右侧第一条对称轴为x==,故=﹣,∴ω=2.∵x=时函数取得最小值,故有2•+φ=,∴φ=.再根据B ﹣A=﹣3,且Asin (2•+)+B=+B=0,∴A=2,B=﹣1,即f (x )=2sin (2x+)﹣1.将函数f (x )的图象向左平移m (m >0)个单位后,得到y=g (x )=2sin (2x+2m+)﹣1的图象,根据得到的函数g (x )图象关于点(,﹣1)对称,可得2•+2m+=kπ,k ∈Z ,∴m=﹣,则m 的最小值是,故选:A .10.【考点】函数奇偶性的性质.【分析】根据对数函数的单调性,我们易判断出log220∈(4,5),结合已知中f (x+1)=f (x ﹣1)且x ∈(﹣1,0)时,f (x )=2x ﹣1,利用函数的周期性与奇偶性,即可得到f (log220)的值. 【解答】解:∵f (x+1)=f (x ﹣1) ∴函数f (x )为周期为2的周期函数 又∵log232>log220>log216 ∴4<log220<5∴f (log220)=f (log220﹣4)=f (log2)=﹣f (﹣log2) 又∵x ∈(﹣1,0)时,f (x )=2x ﹣1 ∴f (﹣log2)=﹣,故f(log220)=.故选:D.11.【考点】几何概型.【分析】求出使得≥2的区域的面积,以面积为测度,即可求出概率.【解答】解:由题意,取A(1,0),B(0,1),设P(x,y),则(x﹣1,y)•(﹣1,1)≥2,∴x﹣y+1≤0,相应的面积为﹣=,∴所求概率为,故选A.12.【考点】函数的值.【分析】由题意函数f(x)的图象关于点(2,0)对称,函数f(x)与y=的图象恰有个交点,且这个交点关于(2,0)对称,由此能求出x1+x2+…+xn的值.【解答】解:∵函数f(x)=,∴函数f(x)的图象关于点(2,0)对称,结合图象知:x1、x2、…xn满足==…==,∴函数f(x)与y=的图象恰有个交点,且这个交点关于(2,0)对称,除去点(2,0),故有x1+x2+…+xn=x1+x2+x3+x4=8.故选:C.二、填空题(共4小题,每小题5分,满分20分)13.【考点】二项式系数的性质.【分析】利用通项公式即可得出.【解答】解:通项公式Tr+1==(﹣a)r x6﹣2r,令6﹣2r=0,解得r=3.∴(﹣a)3=20,解得a=﹣1.故答案为:﹣1.14.【考点】异面直线及其所成的角.【分析】画出立体图形,根据中点找平行线,把所求的异面直线角转化为一个三角形的内角来计算.【解答】解:如图,连接CF,取BF的中点M,连接CM,EM,则ME∥AF,故∠CEM即为所求的异面直线角.设这个正四面体的棱长为2,在△ABD中,AF==CE=CF,EM=,CM=.∴cos∠CEM==.故答案为.15.【考点】椭圆的简单性质.【分析】利用直线的斜率公式,求得kPA•kPB==﹣,由A在椭圆上,则=﹣,即可求得=,求得a=2b,利用三角形的面积相等,即•丨PQ丨•丨OM丨=•丨PQ丨•d,即可求得d的值.【解答】解:根据题意可得P(0,b)、Q(0,﹣b),设A(x,y),B(﹣x,﹣y),由直线PA、PB的斜率之积为﹣,则kPA•kPB=•==﹣,由A在椭圆上可得+=1,则=﹣∴=,即a=2b,△PMQ的面积S=•丨PQ丨•丨OM丨=×2b×a=2b2,设P到直线MQ的距离d,则S=•丨PQ丨•d=וd=•d=2b2,解得:d=,∴P到直线QM的距离,故答案为:.16.【考点】正弦定理.【分析】利用正弦定理把题设中关于边的等式转换成角的正弦,进而利用两角和公式化简整理求得cosC,进而求得C.根据余弦定理求得a和b的不等式关系,进而利用三角形面积公式表示出三角形的面积,利用a和b的不等式关系求得三角形面积的最大值,进而得解.【解答】解:∵acosB+bcosA=2cosC,且c=1,∴由题意及正弦定理可得:sinAcosB+sinBcosA=2sinCcosC,即sinC=2sinCcosC,∵sinC≠0,∴cosC=,可解得:sinC=,可得:cosC==,∴ab=a2+b2﹣1≥2ab﹣1,即ab≤1,等号当a=b时成立,∴可得:S△ABC=absinC≤.又∵h是边AB上的高,S△ABC=ch=h≤.∴解得:h≤,则h的最大值为.故答案为:.三、解答题(共5小题,满分60分)17.【考点】数列的求和;数列递推式.【分析】(1)利用数列递推关系、等差数列的通项公式即可得出.(2)利用“错位相减法”与等比数列的求和公式即可得出.18.【考点】二面角的平面角及求法;直线与平面垂直的判定.【分析】(Ⅰ)取AD中点O,以O为原点,OA为x轴,过O作AB的平行线为y轴,OE为z轴,建立空间直角坐标系,利用向量法能证明BE⊥平面ACF.(Ⅱ)求出平面BCF的法向量和平面ABC的法向量,利用向量法能求出二面角A﹣BC﹣F的余弦值.19.【考点】线性回归方程;频率分布折线图、密度曲线.【分析】(Ⅰ)求出回归系数,可得回归方程,即可预测第12月份该市新建住宅销售均价;(Ⅱ)X的取值为1,2,3,求出相应的概率,即可求X的分布列和数学期望.20.【考点】直线与抛物线的位置关系;抛物线的简单性质.【分析】(Ⅰ)判断直线l的斜率存在,设方程为:y=kx+,设A(x1,y1),B(x2,y2),动点C(x,y)联立直线与抛物线的方程组,利用韦达定理可得x1x2═﹣p2.求出OA;OB方程;然后求解轨迹方程.(Ⅱ)设直线m的方程为:y=kx+m,由,得△=4p2k2+8pm,利用直线m与抛物线相切,得P(pk,﹣m),求出Q(),通过=0,说明以线段PQ为直径的圆过点F.21.【考点】利用导数研究函数的单调性;利用导数求闭区间上函数的最值.【分析】(1)若a≠0,求导数,分类讨论,即可求函数f(x)的单调递增区间;(2)a=0,f(x)=,x1<x<x2<2,证明:>,只要证明g(x)=在(x1,2)上单调递减.22.【考点】参数方程化成普通方程;简单曲线的极坐标方程.【分析】(Ⅰ)直线l的极坐标方程转化为ρsinθ+ρcosθ=4,由ρsinθ=y,ρcosθ=x,能求出直线l的直角坐标方程.(Ⅱ)由题意P(),从而点P到直线l的距离d==,由此能求出点P到直线l的距离的最大值与最小值.23.【考点】绝对值三角不等式;绝对值不等式的解法.【分析】(1)利用绝对值三角不等式求得f(x)的最小值为3,可得3>a2,由此求得实数a的取值的集合T;(2)由(1)可得m2<3,n2<3,再整理,即可证明结论.。
2017年安徽省合肥市高三理科二模数学试卷
2017年安徽省合肥市高三理科二模数学试卷一、选择题(共12小题;共60分)1. 为虚数单位,若复数是纯虚数,则实数A. B. C. D.2. 已知,,若,则实数的取值范围是A. B. C. D.3. 已知变量,满足约束条件则目标函数的最小值为A. B. C. D.4. 若输入,执行如图所示的程序框图,输出的A. B. C. D.5. 若中心在原点,焦点在轴上的双曲线离心率为,则此双曲线的渐近线方程为A. B. C. D.6. 等差数列的前项和为,且,,则A. B. C. D.7. 一个几何体的三视图及其尺寸如图所示,则该几何体的体积为A. B. C. D.8. 对函数,如果存在使得,则称与为函数图象的一组奇对称点.若(为自然数的底数)存在奇对称点,则实数的取值范围是A. B. C. D.9. 若平面截三棱锥所得截面为平行四边形,则该三棱锥与平面平行的棱有A. 条B. 条C. 条D. 条或条10. 已知件产品中有件次品,现逐一检测,直至能确定所有次品为止,记检测的次数为,则A. B. C. D.11. 锐角中,内角,,的对边分别为,,,且满足,若,则的取值范围是A. B. C. D.12. 已知函数(为自然对数的底数)有两个极值点,则实数的取值范围是A. B. C. D.二、填空题(共4小题;共20分)13. 等比数列满足,且,则 ______.14. 已知,,.(1)求与的夹角 ______;(2)求 ______ ; ______.15. 在的展开式中,常数项为______.16. 已知关于的方程在上有实根.则实根的最大值是______.三、解答题(共7小题;共91分)17. 已知,,函数.(1)求函数图象的对称轴方程;(2)若方程在上的解为,,求的值.18. 某校计划面向高一年级名学生开设校本选修课程,为确保工作的顺利实施,先按性别进行分层抽样,抽取了名学生对社会科学类,自然科学类这两大类校本选修课程进行选课意向调查,其中男生有人.在这名学生中选择社会科学类的男生、女生均为人.附:,其中.(1)分别计算抽取的样本中男生及女生选择社会科学类的频率,并以统计的频率作为概率,估计实际选课中选择社会科学类学生数;(2)根据抽取的 名学生的调查结果,完成下列列联表.并判断能否在犯错误的概率不超过的前提下认为科类的选择与性别有关?选择自然科学类选择社会科学类合计男生女生合计19. 如图 ,矩形 中, , ,点 为 中点,沿 将 折起至 ,如图 所示,点 在面 的射影 落在 上.(1)求证: ; (2)求二面角 的余弦值.20. 如图,抛物线 与圆 相交于 , 两点,且点 的横坐标为.过劣弧 上动点 作圆 的切线交抛物线 于 , 两点,分别以 , 为切点作抛物线 的切线 , , 与 相交于点 .(1)求 的值; (2)求动点 的轨迹方程.21. 已知 .(1)求 的单调区间;(2)设 , , 为函数 的两个零点,求证: .22. 在直角坐标系 中,以坐标原点为极点, 轴的非负半轴为极轴建立极坐标系,圆 的极坐标方程为 .(1)求出圆 的直角坐标方程;(2)已知圆 与 轴相交于 , 两点,直线 关于点 对称的直线为.若直线 上存在点 使得 ,求实数 的最大值.23. 已知函数 .(1)求函数 的定义域;(2)若当 时,不等式 恒成立,求实数 的取值范围.答案第一部分1. D2. A3. B4. C5. B6. D7. A8. B9. C 10. B11. A 12. A第二部分13.14. (1);(2);15.16.第三部分17. (1)令,得,即的对称轴方程为.(2)由条件知,且,易知与关于对称,则,所以18. (1)由条件知,抽取的男生为人,女生为人;男生选择社会科学类的频率为,女生选择社会科学类的频率为;由题意,男生总数为人,女生总数为人,所以,估计选择社会科学的人数为人.(2)根据统计数据,可得列联表如下:选择自然科学类选择社会科学类合计男生女生合计计算观测值,所以,在犯错误的概率不超过的前提下认为科类的选择与性别有关.19. (1)由条件,点在平面的射影落在上,所以平面平面,易知,所以平面,而平面,所以.(2)以为坐标原点,以过点且平行于的直线为轴,过点且平行于的直线为轴,直线为轴,建立如图所示直角坐标系.,,,,设平面的法向量为,则即令,可得,设平面的法向量为,则即令,可得,所以,考虑到二面角为钝二面角,则二面角的余弦值为.20. (1)由点的横坐标为,可得点的坐标为,代入,解得.(2)设,,,.切线,代入得,由解得,所以方程为,同理方程为,联立解得因为方程为,其中,满足,,联立方程得,则代入可知满足代入得,考虑到,知.所以动点的轨迹方程为,.21. (1)因为,所以,当时,所以,即的单调递增区间为,无减区间;当时,所以,由,得,时,,时,,所以时,易知的单调递增区间为,单调递减区间为.(2)由()知的单调递增区间为,单调递减区间为.不妨设,由条件知即构造函数,与图象两交点的横坐标为,,由可得,而,所以,知在区间上单调递减,在区间上单调递增.可知,欲证,只需证,即证,考虑到在上递增,只需证,由知,只需证,令,则即单增,又,结合知,即成立,即成立.22. (1)由得,即,即圆的标准方程为.(2)关于点的对称直线的方程为,而为圆的直径,故直线上存在点使得的充要条件是直线与圆有公共点,故,于是,实数的最大值为.23. (1)要使原函数有意义,则,即,得,当时,解得,函数的定义域为;当时,解得,函数的定义域为.(2),记,因为,所以需且只需即解得,又,所以,且.。
安徽省百所重点高中2017届高三第二次模拟考试试题

安徽省百所重点高中2017届高三第二次模拟考试试题一、选择题(共12小题;共60分)1. 已知集合,,则集合的子集的个数为A. B. C. D.2. 已知复数的共轭复数(为虚数单位),则复数的虚部为A. B. C. D.3. 已知正方形的中心为,且其边长为,则A. B. C. D.4. “”是“”的A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件5. 已知实数,满足不等式,记,则的最小值为A. B. C. D.6. 若展开式中的常数项是,则A. B. C. D.7. 执行如图所示的程序框图,若输出的值为,则判断框中可以填A. B. C. D.8. 已知某几何体的三视图如图所示,则该几何体的表面积是A. B. C. D.9. 已知等差数列为递减数列,数列满足,,,则A. B. C. D.10. 将函数的图象向左平移个单位长度,再向下平移个单位长度,得到函数的图象,则下列关于函数的说法错误的是A. 函数的最小正周期为B. 函数是奇函数C. 函数的图象与直线,,围成的图形的面积为D. 函数的单调递增区间为()11. 已知为坐标原点,是椭圆:的左焦点,,分别为的左、右顶点,为上一点,且轴,过点的直线与线段交于点,与轴交于点,若直线经过的中点,则椭圆的离心率为A. B. C. D.12. 已知在中,角,,所对的边分别为,,,且,的外接圆半径为周长的取值范围为A. B. C. D.二、填空题(共4小题;共20分)13. 已知,的取值为:从散点图可知与呈线性相关关系,且回归直线方程为,则当时,的取值为.14. 已知双曲线的离心率为,且它的一个焦点到一条渐近线的距离为,则双曲线的标准方程是.15. 已知三棱锥的体积为,是等腰直角三角形,其斜边,且三棱锥的外接球的球心恰好是的中点,则球的体积为.16. 设函数,若存在唯一的整数,使得成立,则的取值范围为.三、解答题(共7小题;共91分)17. 已知在数列中,,,且.(1)证明:数列为等比数列,并求数列的通项公式;(2)令,求数列的前项和.18. 交通运输部和公安部联合下发了《关于印发机动车驾驶培训教学与考试大纲的通知》,发布了新一版的《机动车驾驶培训教学与考试大纲》.某市交警大队为了解该市报考驾校的市民对驾考新规的“支持”或“反对”态度,随机从各驾校中抽取了男性、女性学员共名进行调查,调查结果如下:支持反对合计男性女性合计参考公式:,其中.参考数据:(1)根据以上数据,是否有的把握认为“支持驾考新规”与“性别”有关?(2)现从参与调查的女性学员中按分层抽样的方法抽取人,从抽取的这人中再随机抽取人赠送价值元的车饰小礼品,记这人中持“支持”态度的人数为,求的分布列与数学期望.19. 如图所示的几何体由平面截棱长为的正方体得到,其中,为原正方体的顶点,,为原正方体侧棱的中点,正方形为原正方体的底面,为棱上的动点.(1)求证:平面平面;(2)设,当为何值时,平面与平面所成的角为?20. 如图,设直线与抛物线(,为常数)交于不同的两点,,且当时,弦的长为.(1)求抛物线的标准方程;(2)过点的直线交抛物线于另一点,且直线过点,求证:直线过定点.21. 已知函数.(1)讨论函数的单调性及最值;(2)当时,设函数的两个极值点为,,若,恰为函数的零点,求的最小值.22. 已知椭圆的参数方程为为参数,直线的参数方程为为参数.(1)当时,求交所得的弦长;(2)若椭圆上的点到直线的距离的最小值为,求的值.23. 已知,,函数的最小值为.(1)求的值;(2)求证:.答案第一部分1. D 【解析】由题意知,则,故的子集的个数为.2. C 【解析】,故,其虚部为.3. D 【解析】4. B 【解析】由可得,当,时,,无意义;反之,由可得,故.因此“”是“”的必要不充分条件.5. C【解析】表示的平面区域为如图所示的四边形内部及其边界,由图可知当直线经过点时,取得最小值,所以.6. B 【解析】,的展开式的通项为,令,则,所以其展开式中的常数项为,依题意知,,结合选项得.7. D 【解析】第一次循环,得,,;第二次循环,得,,;第三次循环,得,,;第四次循环,得,,;第五次循环,得,观察可知,要想输出,则.8. D 【解析】由三视图可知该几何体是一个半圆柱和一个三棱柱的组合体,故其表面积为.9. A 【解析】设等差数列的公差为,因为,所以当时,为常数,因为,所以,则数列为等比数列,设的公比为,则,由,得,所以,由,得,即解得(舍去)或即,因为,所以,.10. D【解析】,将其图象向左平移个单位长度得到的图象,再向下平移个单位长度得到的图象,易知A,B正确;对于C,所求图形面积,C正确;令(),解得(),故的单调递增区间为(),D错误.11. A 【解析】由题意设直线的方程为(),分别令与得,,设的中点为,由,得,即,整理得,所以椭圆的离心率.12. C 【解析】由,得,由正弦定理得,即,又,所以,所以,由得,所以,所以.又的外接圆半径为,所以.通解:由得,,故,所以.优解:由余弦定理,得(当且仅当时取等号),即,所以.第二部分13.【解析】由表格可知,,所以这组数据的样本点的中心是,根据样本点的中心在回归直线上,得,得,所以这组数据对应的回归直线方程是,将代入,得.14. 或【解析】易知双曲线的焦点到渐近线的距离为,故,又,所以,解得,所以该双曲线的标准方程是或.15.【解析】设球的半径为,球心到平面的距离为,则由是的中点得,点到平面的距离等于,所以,解得,记的中点为,则平面.在中,,即,所以球的体积.16.【解析】将,转化为,设,则,令,则,因而在上单调递增,则仅有一解.在上,单调递减,在上,单调递增,故的最小值为,而恒过点,当过时,,当过时,,数形结合可知,若存在唯一的整数,使得成立,则,从而.第三部分17. (1)由,得,因此数列是公比为,首项为的等比数列.所以当时,,当时,也符合,故.(2)由()知,所以,得所以.18. (1)由列联表可得所以没有的把握认为“支持驾考新规”与“性别”有关.(2)依题意可知,所抽取的名女性学员中,持“支持”态度的有人,持“反对”态度的有人.易知的所有可能取值为,,,,,,从而的分布列为.19. (1)由已知可知,,且,如图,连接,则四边形是平行四边形,所以.因为底面为正方形,所以.因为底面,所以.又,所以平面,所以平面.因为平面,所以平面平面.(2)以为原点建立如图所示的空间直角坐标系,则,,,,,,设是平面的法向量,故令,可得为平面的一个法向量,而平面的一个法向量为.于是,解得,又,所以.20. (1)设,,当时,直线,即,联立得即.所以,,于是得,又,所以,即抛物线的标准方程为.(2)设点,,,易得直线,,的斜率均存在,则直线的斜率是,从而直线的方程是,即.同理可知的方程是,的方程是.又易知点在直线上,从而有,即,点在直线上,从而有,即,化简得.代入的方程得.所以直线过定点.21. (1),.当时,由,解得,即当时,,单调递增;由,解得,即当时,,单调递减.故,无最小值.当时,,即在上单调递增,无最值.当时,,故,即在上单调递增,无最值.所以当时,的单调递增区间为,单调递减区间为,的最大值为,无最小值;当时,的单调递增区间为,无单调递减区间,无最值.(2),则,所以的两根,即方程的两根.因为,所以,,.又,为的零点,所以,,两式相减得,得,而,所以令,由得,因为,所以两边同时除以,得,因为,故,解得或,所以.设,所以,则在上是减函数,所以,即的最小值为.22. (1)易知椭圆的普通方程为,令,则直线的参数方程可化为代入椭圆的方程,整理得,两根分别为,,故弦长为.(2)直线的普通方程为,椭圆上的动点到直线的距离,其中,当时,的最小值为,不符合题意;当时,;当时,.所以或.23. (1)因为,当且仅当时,等号成立,又,,所以,所以的最小值为,所以.(2)由()知,,所以,当且仅当且,即,时取等号.所以,所以,即.。
2017年高三-安徽-合肥-二模-理数

2 21 1 第5题合肥市2017年高三第二次教学质量检测数学试题(理科)一、选择题(共10小题,每小题5分,满分50分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.复数2z i =+(其中为i 虚数单位),则z 的模是( )2.双曲线22154x y -=的焦点坐标为( ) A. (3,0)和(3,0)- B. (2,0)和(2,0)- C. (0,3)和(0,3)- D. (0,2)和(0,2)-3.已知命题:p 所有的素数都是奇数,则命题p ⌝是( )A. 所有的素数都不是奇数B. 有些的素数是奇数C.存在一个素数不是奇数D. 存在一个素数是奇数4.在ABC ∆中,4,30,AB ABC D =∠=︒是边BC 上的一点,且AD AB AD AC =,则AD AB的值等于( )A.0B.4C.8D.-45.若正四棱锥的正视图如右图所示,则该正四棱锥的体积为( )A.3B.3C.3D.36.执行如图所示程序框图,则输出的结果为( ) A.-1 B.1 C.-2 D.27已知集合{(,)||2||3|1}A x y x y =-+-≤,集合()2222{,|y 0,4B x y x Dx Ey F D E F =++++≤+->若集合A 、B 恒满足“A ⊂B ”,则集合B 中的点所形成的几何 图形面积的最小值是( ) B.π C. 12π8.在ABC ∆中,a b c 、、分别是角A 、B 、C 的对边, 若,1,3A b ABC π==∆的面积为2,则a 的值为( ) A.1 B.29.中小学校车安全引起社会的关注,为了彻底消除校车安全隐患,某市购进了50台完全相同的校车,准备发放给10所学校,每所学校至少2台,则不同的发放方案的种数有( )(提示:m n C 表示组合数)A. 941CB. 938CC. 940CD. 939C10.定义域为R 的偶函数()f x 满足对x R ∀∈,有(2)()(1)f x f x f +=-,且当[2,3]x ∈时2()21218f x x x =-+-,若函数()log (1)a y f x x =-+在0+∞(,)上至少有三个零点,则a 的取值范围为( )A. B.(0,2 C 。
中考历史知识点汇编十二近现代的经济和社会生活
2017年中考历史知识点汇编(十二)近现代的经济和社会生活第I卷(选择题)1.19世纪初,大部分的妇女都缠足,到了民国这一陋习逐渐消失,促动缠足陋习开始改变的重要历史事件是()A. 辛亥革命B. 新文化运动C. 新中国成立D. 改革开放【来源】[首发]2017届广东省深圳市罗湖区九年级下学期第二次调研(二模)历史试题(带解析)【答案】A2.下列现象和近代前期的社会生活有关,其中有一项的叙述有当时的史实不符合,它是()A. 张某在阅读《申报》时获知日本强占台湾的消息,他悲愤万分B. 戊戌变法期间,李某在商务印书馆担任编辑C. 《辛丑条约》签订后,王某一家被迫从世代居住的东交民巷搬出D. 刘某乘坐火车,沿着中国自己设计建造的第一条铁路干线到北京参加科举考试【来源】2017河南省中考历史模拟试卷(郑州名师出题)【答案】D3.下表反映了中国民族资本主义企业1894——1913年的发展状况,对其理解正确的是()A. 《马关条约》签订,促进中国民族资本主义快速发展B. 民族资产阶级力量壮大,开始登上历史舞台C. 民族工业比重日益增加,成为经济主导D. 一战期间,帝国主义放松侵略,民族资本主义发展较快【来源】2017届安徽省合肥市瑶海区第二次模拟考试历史学科试题(带解析)【答案】B4.著名作家冰心曾谈到:“我启蒙的第一本书,就是商务印书馆出版的《国文教科书》……我的第一本小说集《超人》和第一本诗集《繁星》都是在商务印书馆出版的。
”《天演论》,1905年由商务印书馆首次出版铅印本,至1921年,重印20次。
这些说明商务印书馆()① 是中国近代重要的文化出版机构② 开启了中国教育近代化之路③ 传播了西方先进思想文化④推动中国文化事业的发展A. ①②③B. ①②④C. ①③④D. ②③④【来源】[中学联盟]河南省郑州轻工业学院附属学校2017届九年级中考模拟历史试题【答案】C5.观察下图,影响清朝晚期税收变化的原因包括()①洋务运动的有力推动②戊戌变法的客观影响③民族工业的初步发展④一战期间的难得机遇A. ①③④B. ②③④C. ①②③D. ①②④【来源】[中学联盟]河南省郑州轻工业学院附属学校2017届九年级中考模拟历史试题【答案】C6.报纸是政策、新闻、广告宣传的重要媒介,下列哪一份是中国创办的最早的报纸?()A. B. C. D.【来源】山东省兰陵县2017年中考历史模拟试题【答案】D7.下列是小明同学制作的“社会生活变化”知识表,表中的★处应当填写()A. 交通、通讯的发展B. 社会习俗的变化C. 文化生活新气象D. 科学、思想和文化【来源】[中学联盟]江苏省灌南县私立新知双语学校2017届九年级模拟检测历史试题【答案】C8.在外国人办的报刊中,由中国人主执笔政的,《申报》是第一家。
安徽省2017届高三模拟考试含答案
安徽省2017届高三模拟考试含答案数学(文)试题第Ⅰ卷(共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 已知集合{N |24}A x x =∈-<<,1{|24}2x B x =≤≤,则A B =( ) A .{|12}x x -≤≤ B .{1,0,1,2}- C .{1,2} D .{0,1,2}2.已知i 为虚数单位,若复数11ti z i-=+在复平面内对应的点在第四象限,则t 的取值范围为( ) A .[1,1]- B .(1,1)- C .(,1)-∞-D .(1,)+∞ 3.下列函数中,与函数3y x =的单调性和奇偶性一致的函数是( )A.y =.tan y x = C.1y x x=+ D .e e x x y -=- 4.已知双曲线1C :22143x y -=与双曲线2C :22143x y -=-,给出下列说法,其中错误的是( ) A.它们的焦距相等 B .它们的焦点在同一个圆上C.它们的渐近线方程相同 D .它们的离心率相等5.某学校上午安排上四节课,每节课时间为40分钟,第一节课上课时间为8:00~8:40,课间休息10分钟.某学生因故迟到,若他在9:10~10:00之间到达教室,则他听第二节课的时间不少于10分钟的概率为( )A .15B .310C .25D .456.若倾斜角为α的直线l 与曲线4y x =相切于点()1,1,则2cos sin 2αα-的值为( )A .12-B .1C .35-D .717- 7.在等比数列{}n a 中,“4a ,12a 是方程2310x x ++=的两根”是“81a =±”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件8.执行如图所示的程序框图,则输出的S 值为( )A.1009 B .-1009 C.-1007 D .10089.已知一几何体的三视图如图所示,则该几何体的体积为( )A .163π+B .112π+C .1123π+D .143π+ 10.已知函数()sin()f x A x ωϕ=+(0,0,||)A ωϕπ>><的部分图象如图所示,则函数()cos()g x A x ϕω=+图象的一个对称中心可能为( )A .5(,0)2-B .1(,0)6 C.1(,0)2- D .11(,0)6- 11.《几何原本》卷2的几何代数法(以几何方法研究代数问题)成了后世西方数学家处理问题的重要依据,通过这一原理,很多的代数的公理或定理都能够通过图形实现证明,也称之为无字证明.现有如图所示图形,点F 在半圆O 上,点C 在直径AB 上,且OF AB ⊥,设AC a =,BC b =,则该图形可以完成的无字证明为( )A.2a b +≥(0,0)a b >> B .222a b ab +≥(0,0)a b >>C.2ab a b ≤+(0,0)a b >> D .2a b +≤(0,0)a b >> 12.已知球O 是正三棱锥(底面为正三角形,顶点在底面的射影为底面中心)A BCD -的外接球,3BC =,AB =E 在线段BD 上,且3BD BE =,过点E 作圆O 的截面,则所得截面圆面积的取值范围是( )A .[],4ππB .[]2,4ππC .[]3,4ππD .(]0,4π第Ⅱ卷(共90分)二、填空题(每题5分,满分20分,将答案填在答题纸上)13. 已知(1,)a λ= ,(2,1)b = ,若向量2a b + 与(8,6)c = 共线,则a = .14.已知实数x ,y 满足不等式组20,250,20,x y x y y --≤⎧⎪+-≥⎨⎪-≤⎩目标函数422log log z y x =-,则z 的最大值为 .15.在ABC ∆中,角A ,B ,C 的对边分别为a ,b ,c ,cos c B -是cos b B 与cos a A的等差中项且8a =,ABC ∆的面积为b c +的值为 .16.已知抛物线C :24y x =的焦点是F ,直线1l :1y x =-交抛物线于A ,B 两点,分别从A ,B 两点向直线2l :2x =-作垂线,垂足是D ,C ,则四边形ABCD 的周长为 .三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.已知函数()212f x x mx =+(0m >),数列{}n a 的前n 项和为n S ,点(),n n S 在()f x 图象上,且()f x 的最小值为18-. (1)求数列{}n a 的通项公式;(2)数列{}n b 满足12(21)(21)nn n a n a a b +=--,记数列{}n b 的前n 项和为n T ,求证:1n T <. 18.如图,点C 在以AB 为直径的圆O 上,PA 垂直与圆O 所在平面,G 为AOC ∆的垂心.(1)求证:平面OPG ⊥平面PAC ;(2)若22PA AB AC ===,点Q 在线段PA 上,且2PQ QA =,求三棱锥P QGC -的体积.19.2017高考特别强调了要增加对数学文化的考查,为此某校高三年级特命制了一套与数学文化有关的专题训练卷(文、理科试卷满分均为100分),并对整个高三年级的学生进行了测试.现从这些学生中随机抽取了50名学生的成绩,按照成绩为[)50,60,[)60,70,…,[]90,100分成了5组,制成了如图所示的频率分布直方图(假定每名学生的成绩均不低于50分).(1)求频率分布直方图中的x 的值,并估计所抽取的50名学生成绩的平均数、中位数(同一组中的数据用该组区间的中点值代表);(2)若高三年级共有2000名学生,试估计高三学生中这次测试成绩不低于70分的人数;(3)若在样本中,利用分层抽样的方法从成绩不低于70分的三组学生中抽取6人,再从这6人中随机抽取3人参加这次考试的考后分析会,试求[)[]80,90,90,100两组中至少有1人被抽到的概率.20.已知椭圆C :22221(0)x y a b a b+=>>的长轴长为,且椭圆C 与圆M :221(1)2x y -+=的公共(1)求椭圆C 的方程.(2)经过原点作直线l (不与坐标轴重合)交椭圆于A ,B 两点,AD x ⊥轴于点D ,点E 在椭圆C 上,且()()0AB EB DB AD -⋅+=uu u r uu r uu u r uuu r ,求证:B ,D ,E 三点共线.. 21.已知函数()2ln f x m x x =-,()23e 3x g x x -=(R m ∈,e 为自然对数的底数). (1)试讨论函数()f x 的极值情况;(2)证明:当1m >且0x >时,总有()()30g x f x '+>.请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分.22.已知直线l的参数方程为4,x y ⎧=+⎪⎪⎨⎪=⎪⎩(t为参数),以坐标原点为极点,x 轴的非负半轴为极轴建立极坐标系,圆C 的极坐标方程为4cos ρθ=,直线l 与圆C 交于A ,B 两点.(1)求圆C 的直角坐标方程及弦AB 的长;(2)动点P 在圆C 上(不与A ,B 重合),试求ABP ∆的面积的最大值.23.已知函数()|21||1|f x x x =-++.(1)求函数()f x 的值域M ;(2)若a M ∈,试比较|1||1|a a -++,32a ,722a -的大小.试 卷 答 案一、选择题1-5:D B D D A 6-10:D A B C C 11 D 、12: B二、填空题13.1 15..18+三、解答题17.(1)解:()()22122m f x x m =+-, 故()f x 的最小值为2128m -=-. 又0m >,所以12m =,即21122n S n n =+. 所以当2n ≥时,1n n n a S S n -=-=;当1n =时,11a =也适合上式,所以数列{}n a 的通项公式为n a n =.(2)证明:由(1)知12(21)(21)nn n n b +==--1112121n n +---, 所以11111113372121n n n T +=-+-++--- 11121n +=--, 所以1n T <.18.(1)证明:如图,延长OG 交AC 于点M .因为G 为AOC ∆的重心,所以M 为AC 的中点.因为O 为AB 的中点,所以//OM BC .因为AB 是圆O 的直径,所以BC AC ⊥,所以OM AC ⊥.因为PA ⊥平面ABC ,OM ⊂平面ABC ,所以PA OM ⊥.又PA ⊂平面PAC ,AC ⊂平面PAC ,PA AC A = ,所以OM ⊥平面PAC ,即OG ⊥平面PAC .又OG ⊂平面OPG ,所以平面OPG ⊥平面PAC .(2)解:由(1)知OM ⊥平面PAC ,所以GM 就是点G 到平面PAC 的距离.由已知可得,1OA OC AC ===,所以AOC V 为正三角形,所以2OM =.又点G 为AOC V 的重心,所以136GM OM ==.故点G 到平面PQC所以13P QGC G PQC PQC V V S --==V 1233PAC GM S GM ⋅=⨯⋅V 212192=⨯⨯⨯=19.解:(1)由频率分布直方图可得第4组的频率为10.10.30.3---0.10.2-=,故0.02x =.故可估计所抽取的50名学生成绩的平均数为(550.01650.03⨯+⨯750.03850.02+⨯+⨯+)950.011074⨯⨯=(分).由于前两组的频率之和为0.10.30.4+=,前三组的频率之和为0.10.30.30.7++=,故中位数在第3组中. 设中位数为t 分,则有()700.030.1t -⨯=,所以1733t =, 即所求的中位数为1733分. (2)由(1)可知,50名学生中成绩不低于70分的频率为0.30.20.10.6++=,由以上样本的频率,可以估计高三年级2000名学生中成绩不低于70分的人数为20000.61200⨯=.(3)由(1)可知,后三组中的人数分别为15,10,5,故这三组中所抽取的人数分别为3,2,1.记成绩在[)70,80这组的3名学生分别为a ,b ,c ,成绩在[)80,90这组的2名学生分别为d ,e ,成绩在[]90,100这组的1名学生为f ,则从中任抽取3人的所有可能结果为(),,a b c ,(),,a b d ,(),,a b e ,(),,a b f ,(),,a c d ,(),,a c e ,(),,a c f ,(),,a d e ,(),,a d f ,(),,a e f ,(),,b c d ,(),,b c e ,(),,b c f ,(),,b d e ,(),,b d f ,(),,b e f ,(),,c d e ,(),,c d f ,(),,c e f ,(),,d e f 共20种.其中[)[]80,90,90,100两组中没有人被抽到的可能结果为(),,a b c ,只有1种, 故[)[]80,90,90,100两组中至少有1人被抽到的概率为11912020P =-=. 20.(1)解:由题意得2a =a =由椭圆C 与圆M :()22112x y -+=其长度等于圆M 的直径,可得椭圆C经过点1,⎛ ⎝⎭, 所以211212b+=,解得1b =. 所以椭圆C 的方程为2212x y +=. (2)证明:设()11,A x y ,()22,E x y ,则()11,B x y --,()1,0D x .因为点A ,E 都在椭圆C 上,所以2211222222,22,x y x y ⎧+=⎪⎨+=⎪⎩ 所以()()1212x x x x -++()()121220y y y y -+=, 即()121212122y y x x x x y y -+=--+. 又()()AB EB DB AD -⋅+uu u r uu r uu u r uuu r 0AE AB =⋅=uu u r uu u r , 所以1AB AE k k ⋅=-, 即1121121y y y x x x -⋅=--, 所以()11211212y x x x y y +⋅=+ 所以()1211122y y y x x x +=+ 又1211212BE BD y y y k k x x x +-=-=+121212120y y y y x x x x ++-=++, 所以BE BD k k =,所以B ,D ,E 三点共线.21.(1)解:()f x 的定义域为()0,+∞,()21m f x x '=-=2x m x--. ①当0m ≤时,()0f x '<,故()f x 在()0,+∞内单调递减,()f x 无极值;②当0m >时,令()0f x '>,得02x m <<;令()0f x '<,得2x m >.故()f x 在2x m =处取得极大值,且极大值为()()22ln 22f m m m m =-,()f x 无极小值.(2)证法一:当0x >时,()()30g x f x '+>⇔23e 3630x m x x-+->⇔23e 3630x x mx -+->. 设函数()23e 3x u x x =-63mx +-,则()()3e 22x u x x m '=-+.记()e 22x v x x m =-+, 则()e 2xv x '=-. 当x 变化时,()v x ',()v x 的变化情况如下表:由上表可知()()ln 2v x v ≥,而()ln2ln 2e 2ln 22v m =-+=22ln 22m -+=()2ln 21m -+,由1m >,知ln 21m >-,所以()ln 20v >,所以()0v x >,即()0u x '>.所以()u x 在()0,+∞内为单调递增函数.所以当0x >时,()()00u x u >=.即当1m >且0x >时,23e 3x x -630mx +->.所以当1m >且0x >时,总有()()30g x f x '+>.证法二:当0x >时,()()30g x f x '+>⇔23e 3630x m x x-+->⇔23e 3630x x mx -+->. 因为1m >且0x >,故只需证()22211x e x x x >-+=-.当01x <<时,()21x e x >1>-成立;当1x ≥时,()221xx e x e x >-⇔>-1,即证2x e x >-1.令()2x x e x ϕ=-+1,则由()212x x e ϕ'=-1=0,得2ln 2x =. 在()1,2ln 2内,()0x ϕ'<;在()2ln 2,+∞内,()0x ϕ'>,所以()()2ln 222ln 210x ϕϕ≥=-+>.故当1x ≥时,()21x e x >-成立.综上得原不等式成立.22.解:(1)由4cos ρθ=得24cos ρρθ=,所以2240x y x +-=,所以圆C 的直角坐标方程为22(2)4x y -+=.将直线l 的参数方程代入圆:C 22(2)4x y -+=,并整理得20t +=, 解得10t =,2t =-.所以直线l 被圆C截得的弦长为12||t t -=(2)直线l 的普通方程为40x y --=.圆C 的参数方程为22cos ,2sin ,x y θθ=+⎧⎨=⎩(θ为参数), 可设圆C 上的动点(22cos ,2sin )P θθ+,则点P 到直线l的距离d=|2cos()4πθ=+. 当cos()14πθ+=-时,d 取最大值,且d的最大值为2所以12ABP S ∆≤⨯(22=+ 即ABP ∆的面积的最大值为223. 解:(1)3,1,1()2,1,213,.2x x f x x x x x ⎧⎪-<-⎪⎪=--≤≤⎨⎪⎪>⎪⎩ 根据函数()f x 的单调性可知, 当12x =时,min 13()()22f x f ==. 所以函数()f x 的值域3[,)2M =+∞.(2)因为a M ∈,所以32a ≥,所以3012a <≤. 因为|1||1|1a a a -++=-123a a ++=≥, 所以3|1||1|2a a a-++> 因为37222a a ⎛⎫--= ⎪⎝⎭24732a a a -+=()()1432a a a -- 又由32a ≥,知10a ->,430a ->, 所以(1)(43)02a a a-->, 所以37222a a >-, 所以|1||1|a a -++>37222a a >-.。
2017年高三-安徽-合肥-二模-理数
A. (0,
3 )
B.
(0,
2 )
C 。 (0,
5).
D.
3
2
5
6 (0, )
6
第二卷(满分 100 分) 二、填空题(本大题共 5 小题,每小题 5 分,共 25 分。把答案填在答题卡的相应的位置)
11. 已知集合 A { a1,a2, a3, a4 ,a5, a6 , a7} , A B { a1, a2 , a3, a4,a5 , a6, a7 , ,a100} , 则所
③函数 y f ( x) 可以是奇函数;
④函数 y f ( x) 如果是偶函数,则值域是 [ 1,0) 或(0,1] ;
⑤函数 y f ( x) 值域是 ( 1,1) ,则一定是奇函数。
其中正确的命题的序号是 _______(填上所有正确的序号) 三、解答题(本大题共 6 小题,共 75 分。解答应写出文字说明、证明过程或演算步骤。解
若A
, b 1, ABC 的面积为 3 ,则 a 的值为( )
3
2
A. 1
B.
2
C.
3
D.
3
2
2
2
11 第5题
开始
i 1, S 1, A 2
i
i1
S
SA
1
A
1
A
i 20 12 ? 是
输出 S
结束
否 第6 题
9. 中小学校车安全引起社会的关注,为了彻底消除校车安全隐患,某市购进了
50 台完全相
同的校车, 准备发放给 10 所学校, 每所学校至少 2 台,则不同的发放方案的种数有 ( )(提
4. 在 ABC 中, AB 4, ABC 30 , D 是边 BC 上的一点,且 AD AB AD AC,则
2017年安徽省宣城市高考数学二模试卷(理科)(解析版)
2017年安徽省宣城市高考数学二模试卷(理科)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)设(1+i)(x+yi)=2,其中i为虚数单位,x,y是实数,则|2x+yi|=()A.1B.C.D.2.(5分)已知集合A={x|x2﹣2x﹣3<0},集合B={x|2x﹣1≥1},则A∩B=()A.[﹣1,3)B.[0,3)C.[1,3)D.(1,3)3.(5分)一支田径队共有运动员98人,其中女运动员42人,用分层抽样的方法抽取一个样本,每名运动员被抽到的概率都是,则男运动员应抽取()A.18人B.16人C.14人D.12人4.(5分)已知m,n是两条不同的直线,α,β是两个不同的平面,给出下列四个命题,错误的命题是()A.若m∥α,m∥β,α∩β=n,则m∥nB.若α⊥β,m⊥α,n⊥β,则m⊥nC.若α⊥β,α⊥γ,β∩γ=m,则m⊥αD.若α∥β,m∥α,则m∥β5.(5分)某程序框图如图所示,该程序运行后输出的S的值是()A.1007B.3025C.2017D.30246.(5分)中国古代数学著作《算法统宗》中有这样一个问题:“三百七十八里关,初行健步不为难,次日脚痛减一半,六朝才得到其关,要见次日行里数,请公仔细算相还.”其意思为:有一个人走378里路,第一天健步行走,从第二天起脚痛每天走的路程为前一天的一半,走了6天后到达目的地,请问第二天走了()A.24里B.48里C.96里D.192里7.(5分)二项式(x﹣)6的展开式中常数项为()A.﹣15B.15C.﹣20D.208.(5分)已知双曲线两渐近线的夹角θ满足,焦点到渐近线的距离d=1,则该双曲线的焦距为()A.B.或C.或D.以上都不是9.(5分)设数列{a n}为等差数列,S n为其前n项和,若S1≤13,S4≥10,S5≤15,则a4的最大值为()A.3B.4C.﹣7D.﹣510.(5分)如图,网格纸上小正方形的边长为1,粗线画出的是某三棱锥的三视图,则该三棱锥的外接球的表面积是()A.25πB.πC.29πD.π11.(5分)已知集合M={(x,y)|y=f(x)},若对于任意(x1,y1)∈M,存在(x2,y2)∈M,使得x1x2+y1y2=0成立,则称集合M是“好集合”.给出下列4个集合:①②M={(x,y)|y=e x﹣2}③M={(x,y)|y=cos x}④M={(x,y)|y=lnx}其中所有“好集合”的序号是()A.①②④B.②③C.③④D.①③④12.(5分)若函数f(x)=e x(sin x+a cos x)在(,)上单调递增,则实数a的取值范围是()A.(﹣∞,1]B.(﹣∞,1)C.[1,+∞)D.(1,+∞)二、填空题(每题5分,满分20分,将答案填在答题纸上)13.(5分)|sin x|dx等于.14.(5分)已知向量,满足,,,则=.15.(5分)在△ABC中,,,若最大边长为63,则最小边长为.16.(5分)已知P是圆x2+y2=4上一点,且不在坐标轴上,A(2,0),B(0,2),直线P A 与y轴交于点M,直线PB与x轴交于点N,则|AN|+2|BM|的最小值为.三、解答题(本大题共5小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.(12分)已知向量,,函数,函数f(x)在y轴上的截距为,与y轴最近的最高点的坐标是.(Ⅰ)求函数f(x)的解析式;(Ⅱ)将函数f(x)的图象向左平移φ(φ>0)个单位,再将图象上各点的纵坐标不变,横坐标伸长到原来的2倍,得到函数y=sin x的图象,求φ的最小值.18.(12分)如图1,在直角梯形ABCD中,∠ADC=90°,CD∥AB,AB=4,AD=CD=2,M为线段AB的中点.将△ADC沿AC折起,使平面ADC⊥平面ABC,得到几何体D ﹣ABC,如图2所示.(Ⅰ)求证:BC⊥平面ACD;(Ⅱ)求二面角A﹣CD﹣M的余弦值.19.(12分)某校在高二年级开展了体育分项教学活动,将体育课分为大球(包括篮球、排球、足球)、小球(包括乒乓球、羽毛球)、田径、体操四大项(以下简称四大项,并且按照这个顺序).为体现公平,学校规定时间让学生在电脑上选课,据初步统计,在全年级980名同学中,有意申报四大项的人数之比为3:2:1:1,而实际上由于受多方面条件影响,最终确定的四大项人数必须控制在2:1:3:1,选课不成功的同学由电脑自动调剂到田径类.(Ⅰ)随机抽取一名同学,求该同学选课成功(未被调剂)的概率;(Ⅱ)某小组有五名同学,有意申报四大项的人数分别为2、1、1、1,记最终确定到田径类的人数为X,求X的分布列及数学期望EX.20.(12分)已知f(x)=e x﹣ax2,g(x)是f(x)的导函数.(Ⅰ)求g(x)的极值;(Ⅱ)若f(x)≥x+1在x≥0时恒成立,求实数a的取值范围.21.(12分)如图,已知椭圆E:的离心率为,A、B为椭圆的左右顶点,焦点到短轴端点的距离为2,P、Q为椭圆E上异于A、B的两点,且直线BQ 的斜率等于直线AP斜率的2倍.(Ⅰ)求证:直线BP与直线BQ的斜率乘积为定值;(Ⅱ)求三角形APQ的面积S的最大值.请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分.[选修4-4:坐标系与参数方程]22.(10分)已知极点与直角坐标系的原点重合,极轴与x轴的正半轴重合,圆C的极坐标方程是ρ=a sinθ,直线l的参数方程是(t为参数)(1)若a=2,直线l与x轴的交点是M,N是圆C上一动点,求|MN|的最大值;(2)直线l被圆C截得的弦长等于圆C的半径的倍,求a的值.[选修4-5:不等式选讲]23.已知f(x)=|ax﹣1|,不等式f(x)≤3的解集是{x|﹣1≤x≤2}.(Ⅰ)求a的值;(II)若<|k|存在实数解,求实数k的取值范围.2017年安徽省宣城市高考数学二模试卷(理科)参考答案与试题解析一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.(5分)设(1+i)(x+yi)=2,其中i为虚数单位,x,y是实数,则|2x+yi|=()A.1B.C.D.【解答】解:由(1+i)(x+yi)=2,得:x﹣y+(x+y)i=2,则,解得x=1,y=﹣1.∴|2x+yi|=|2﹣i|==.故选:D.2.(5分)已知集合A={x|x2﹣2x﹣3<0},集合B={x|2x﹣1≥1},则A∩B=()A.[﹣1,3)B.[0,3)C.[1,3)D.(1,3)【解答】解:由A中不等式变形得:(x﹣3)(x+1)<0,解得:﹣1<x<3,即A=(﹣1,3),由B中不等式变形得:2x﹣1≥1=20,即x﹣1≥0,解得:x≥1,即B=[1,+∞),则A∩B=[1,3),故选:C.3.(5分)一支田径队共有运动员98人,其中女运动员42人,用分层抽样的方法抽取一个样本,每名运动员被抽到的概率都是,则男运动员应抽取()A.18人B.16人C.14人D.12人【解答】解:∵有运动员98人,其中女运动员42人,∴男运动员56人,∴每名运动员被抽到的概率都是,∴男运动员应抽取56×=16,故选:B.4.(5分)已知m,n是两条不同的直线,α,β是两个不同的平面,给出下列四个命题,错误的命题是()A.若m∥α,m∥β,α∩β=n,则m∥nB.若α⊥β,m⊥α,n⊥β,则m⊥nC.若α⊥β,α⊥γ,β∩γ=m,则m⊥αD.若α∥β,m∥α,则m∥β【解答】解:对于A,因为若m∥α,m∥β,α∩β=n,根据线面平行的性质与判定,可得m∥n,正确;对于B,由m⊥α,n⊥β且α⊥β,则m与n一定不平行,否则有α∥β,与已知α⊥β矛盾,通过平移使得m与n相交,且设m与n确定的平面为γ,则γ与α和β的交线所成的角即为α与β所成的角,因为α⊥β,所以m与n所成的角为90°,故命题正确.对于C,因为γ,β垂直于同一个平面α,故γ,β的交线一定垂直于α,正确.对于D,若α∥β,m∥α,则m∥β或m⊂β,不正确,故选:D.5.(5分)某程序框图如图所示,该程序运行后输出的S的值是()A.1007B.3025C.2017D.3024【解答】解:模拟程序框图的运行过程,得出该程序运行后输出的算式:S=a1+a2+a3+a4+…+a2014+a2015+a2016+a2017=(0+1)+(﹣2+1)+(0+1)+(4+1)+…+(0+1)+(2015+1)+(0+1)+(﹣2016+1)+(0+1)=6+…+6+1=6×+1=3025;所以该程序运行后输出的S值是3025.故选:B.6.(5分)中国古代数学著作《算法统宗》中有这样一个问题:“三百七十八里关,初行健步不为难,次日脚痛减一半,六朝才得到其关,要见次日行里数,请公仔细算相还.”其意思为:有一个人走378里路,第一天健步行走,从第二天起脚痛每天走的路程为前一天的一半,走了6天后到达目的地,请问第二天走了()A.24里B.48里C.96里D.192里【解答】解:由题意可知此人每天走的步数构成为公比的等比数列,由题意和等比数列的求和公式可得=378,解得a1=192,∴第此人二天走192×=96步故选:C.7.(5分)二项式(x﹣)6的展开式中常数项为()A.﹣15B.15C.﹣20D.20【解答】解:二项式(x﹣)6的展开式的通项公式为T r+1=•(﹣1)r•,令6﹣=0,求得r=4,故展开式中常数项为=15,故选:B.8.(5分)已知双曲线两渐近线的夹角θ满足,焦点到渐近线的距离d=1,则该双曲线的焦距为()A.B.或C.或D.以上都不是【解答】解:∵双曲线两渐近线的夹角θ满足,∴=2或,设焦点为(c,0),渐近线方程为y=x,则d==b=1,又b2=c2﹣a2=1,解得c=或.则有焦距为或2.故选:C.9.(5分)设数列{a n}为等差数列,S n为其前n项和,若S1≤13,S4≥10,S5≤15,则a4的最大值为()A.3B.4C.﹣7D.﹣5【解答】解:∵S4≥10,S5≤15,∴a1+a2+a3+a4≥10,a1+a2+a3+a4+a5≤15,∴a5≤5,a3≤3,即:a1+4d≤5,a1+2d≤3,两式相加得:2(a1+3d)≤8,∴a4≤4,故选:B.10.(5分)如图,网格纸上小正方形的边长为1,粗线画出的是某三棱锥的三视图,则该三棱锥的外接球的表面积是()A.25πB.πC.29πD.π【解答】解:由已知中的三视图可得:该几何体是一个以俯视图为底面的三棱锥,其外接球相当于以俯视图为底面的三棱柱的外接球,底面三角形的外接圆半径r=×=,球心到底面的距离d=,故球半径R满足,R2=r2+d2=,故球的表面积S=4πR2=π,故选:D.11.(5分)已知集合M={(x,y)|y=f(x)},若对于任意(x1,y1)∈M,存在(x2,y2)∈M,使得x1x2+y1y2=0成立,则称集合M是“好集合”.给出下列4个集合:①②M={(x,y)|y=e x﹣2}③M={(x,y)|y=cos x}④M={(x,y)|y=lnx}其中所有“好集合”的序号是()A.①②④B.②③C.③④D.①③④【解答】解:对于①y=是以x,y轴为渐近线的双曲线,渐近线的夹角为90°,在同一支上,任意(x1,y1)∈M,不存在(x2,y2)∈M,满足好集合的定义;对任意(x1,y1)∈M,在另一支上也不存在(x2,y2)∈M,使得x1x2+y1y2=0成立,所以不满足好集合的定义,不是好集合.对于②M={(x,y)|y=e x﹣2},如图(2)在曲线上两点构成的直角始存在,例如取M(0,﹣1),N(ln2,0),满足好集合的定义,所以正确.对于③M={(x,y)|y=cos x},如图(3)对于任意(x1,y1)∈M,存在(x2,y2)∈M,使得x1x2+y1y2=0成立,例如(0,1)、(,0),∠yox=90°,满足好集合的定义,旋转90°,都能在图象上找到满足题意的点,所以集合M是好集合;对于④M={(x,y)|y=lnx},如图(4)取点(1,0),曲线上不存在另外的点,使得两点与原点的连线互相垂直,所以不是好集合.故选:B.12.(5分)若函数f(x)=e x(sin x+a cos x)在(,)上单调递增,则实数a的取值范围是()A.(﹣∞,1]B.(﹣∞,1)C.[1,+∞)D.(1,+∞)【解答】解:∵f(x)=e x(sin x+a cos x)在(,)上单调递增,∴f′(x)=e x[(1﹣a)sin x+(1+a)cos x]≥0在(,)上恒成立,∵e x>0在(,)上恒成立,∴(1﹣a)sin x+(1+a)cos x≥0在(,)上恒成立,∴a(sin x﹣cos x)≤sin x+cos x在(,)上恒成立∴a≤,设g(x)=,∴g′(x)=<0在(,)上恒成立,∴g(x)在(,)上单调递减,∴g(x)>g()=1,∴a≤1,故选:A.二、填空题(每题5分,满分20分,将答案填在答题纸上)13.(5分)|sin x|dx等于4.【解答】解:∫02π|sin x|dx=2∫0πsin xdx=2(﹣cos x)|0π=2(1+1)=4.故答案为:414.(5分)已知向量,满足,,,则=2.【解答】解:∵,,,∴|+|2=||2+||2+2•,∴2•=1+4﹣5=0,∴|2﹣|2=4||2+||2﹣4•=4+4=8,∴|2﹣|=2故答案为:15.(5分)在△ABC中,,,若最大边长为63,则最小边长为25.【解答】解:若A为钝角,∵sin A=<,>cos B=>,∴150<A<180°,30°<B<60°,∴A+B>180°,矛盾,故A为锐角,∵sin A=<,>cos B=>,∴0<A<30°<B<60°,且cos A=,sin B=∴C为钝角,∴c最大,最大为63,a最小,∴sin C=sin(A+B)=sin A cos B+cos A sin B=×+×=,由正弦定理可得=,∴a=×=25,故最小为a=25,故答案为:2516.(5分)已知P是圆x2+y2=4上一点,且不在坐标轴上,A(2,0),B(0,2),直线P A 与y轴交于点M,直线PB与x轴交于点N,则|AN|+2|BM|的最小值为8.【解答】解:设P(x0,y0),直线P A的方程为y=x+2,令y=0得M(,0).直线PB的方程为y=(x﹣2),令x=0得N(0,).∴|AN|•|BM|=(2﹣)(2﹣)=4+4×=8,∴|AN|+2|BM|≥2=8,故|AN|+2|BM|的最小值为8.故答案为8.三、解答题(本大题共5小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17.(12分)已知向量,,函数,函数f(x)在y轴上的截距为,与y轴最近的最高点的坐标是.(Ⅰ)求函数f(x)的解析式;(Ⅱ)将函数f(x)的图象向左平移φ(φ>0)个单位,再将图象上各点的纵坐标不变,横坐标伸长到原来的2倍,得到函数y=sin x的图象,求φ的最小值.【解答】解:(Ⅰ),由,得,此时,,由,得b=1或b=﹣1,当b=1时,,经检验为最高点;当b=﹣1时,,经检验不是最高点,故舍去.故函数的解析式为.(Ⅱ)函数f(x)的图象向左平移φ个单位后得到函数的图象;横坐标伸长到原来的2倍后,得到函数的图象,∴(k∈Z),(k∈Z),因为φ>0,所以φ的最小值为.18.(12分)如图1,在直角梯形ABCD中,∠ADC=90°,CD∥AB,AB=4,AD=CD=2,M为线段AB的中点.将△ADC沿AC折起,使平面ADC⊥平面ABC,得到几何体D ﹣ABC,如图2所示.(Ⅰ)求证:BC⊥平面ACD;(Ⅱ)求二面角A﹣CD﹣M的余弦值.【解答】解:(Ⅰ)在图1中,可得,从而AC2+BC2=AB2,故AC⊥BC取AC中点O连接DO,则DO⊥AC,又面ADC⊥面ABC,面ADC∩面ABC=AC,DO⊂面ACD,从而OD⊥平面ABC,(4分)∴OD⊥BC又AC⊥BC,AC∩OD=O,∴BC⊥平面ACD(6分)另解:在图1中,可得,从而AC2+BC2=AB2,故AC⊥BC∵面ADC⊥面ABC,面ADE∩面ABC=AC,BC⊂面ABC,从而BC⊥平面ACD(Ⅱ)建立空间直角坐标系O﹣xyz如图所示,则,,,(8分)设为面CDM的法向量,则即,解得令x=﹣1,可得又为面ACD的一个法向量∴∴二面角A﹣CD﹣M的余弦值为.(12分)19.(12分)某校在高二年级开展了体育分项教学活动,将体育课分为大球(包括篮球、排球、足球)、小球(包括乒乓球、羽毛球)、田径、体操四大项(以下简称四大项,并且按照这个顺序).为体现公平,学校规定时间让学生在电脑上选课,据初步统计,在全年级980名同学中,有意申报四大项的人数之比为3:2:1:1,而实际上由于受多方面条件影响,最终确定的四大项人数必须控制在2:1:3:1,选课不成功的同学由电脑自动调剂到田径类.(Ⅰ)随机抽取一名同学,求该同学选课成功(未被调剂)的概率;(Ⅱ)某小组有五名同学,有意申报四大项的人数分别为2、1、1、1,记最终确定到田径类的人数为X,求X的分布列及数学期望EX.【解答】解:(Ⅰ)随机抽取一名同学,该同学选课成功(未被调剂)的概率:.(Ⅱ)X的所有可能取值为1,2,3,4.,,,.∴X的分布列为:.20.(12分)已知f(x)=e x﹣ax2,g(x)是f(x)的导函数.(Ⅰ)求g(x)的极值;(Ⅱ)若f(x)≥x+1在x≥0时恒成立,求实数a的取值范围.【解答】解:(Ⅰ)f(x)=e x﹣ax2,g(x)=f'(x)=e x﹣2ax,g'(x)=e x﹣2a,当a≤0时,g'(x)>0恒成立,g(x)无极值;当a>0时,g'(x)=0,即x=ln(2a),由g'(x)>0,得x>ln(2a);由g'(x)<0,得x<ln(2a),所以当x=ln(2a)时,有极小值2a﹣2aln(2a).(Ⅱ)令h(x)=e x﹣ax2﹣x﹣1,则h'(x)=e x﹣1﹣2ax,注意到h(0)=h'(0)=0,令k(x)=e x﹣1﹣x,则k'(x)=e x﹣1,且k'(x)>0,得x>0;k'(x)<0,得x<0,∴k(x)≥k(0)=0,即e x≥1+x恒成立,故h'(x)≥x﹣2ax=(1﹣2a)x,当时,1﹣2a≥0,h'(x)≥0,于是当x≥0时,h(x)≥h(0)=0,即f(x)≥x+1成立.当时,由e x>1+x(x≠0)可得e﹣x>1﹣x(x≠0).h'(x)<e x﹣1+2a(e﹣x﹣1)=e﹣x(e x﹣1)(e x﹣2a),故当x∈(0,ln(2a))时,h'(x)<0,于是当x∈(0,ln(2a))时,h(x)<h(0)=0,f(x)≥x+1不成立.综上,a的取值范围为.21.(12分)如图,已知椭圆E:的离心率为,A、B为椭圆的左右顶点,焦点到短轴端点的距离为2,P、Q为椭圆E上异于A、B的两点,且直线BQ的斜率等于直线AP斜率的2倍.(Ⅰ)求证:直线BP与直线BQ的斜率乘积为定值;(Ⅱ)求三角形APQ的面积S的最大值.【解答】解:(Ⅰ)证明:由椭圆的离心率e==,则a=c,由焦点到短轴端点的距离为2,即a=2,则c=,b2=a2﹣c2=2,∴椭圆的标准方程为:;设P点坐标(x,y),y2=(4﹣x2)则A(﹣2,0),B(2,0),则k AP=,k BP=,则k AP•k BP==﹣由k BQ=2k AP,故k BP•k BQ=﹣1.∴直线BP与直线BQ的斜率乘积为﹣1为定值;(Ⅱ)当直线PQ的斜率存在时,设l PQ:y=kx+b与x轴的交点为M,,整理得:(2k2+1)x2+4kbx+2b2﹣4=0,设P(x1,y1),Q(x2,y2),则,,由,得y1y2+x1x2﹣2(x1+x2)+4=0,得,4k2+8kb+3b2=0,得b=﹣2k或.y=kx﹣2k或,所以过定点(2,0)或,点(2,0)为右端点,舍去,,=,=,令(0<t<1),,0<t+t2<1,,当直线l PQ的斜率k不存在时,P(x1,y1),Q(x1,﹣y1),,即,解得,,,∴S△APQ的最大值为.请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分.[选修4-4:坐标系与参数方程]22.(10分)已知极点与直角坐标系的原点重合,极轴与x轴的正半轴重合,圆C的极坐标方程是ρ=a sinθ,直线l的参数方程是(t为参数)(1)若a=2,直线l与x轴的交点是M,N是圆C上一动点,求|MN|的最大值;(2)直线l被圆C截得的弦长等于圆C的半径的倍,求a的值.【解答】解:(1)当a=2时,圆C的直角坐标方程为x2+y2=2y,即x2+(y﹣1)2=1.∴圆C的圆心坐标为C(0,1),半径r=1.令y==0得t=0,把t=0代入x=﹣得x=2.∴M(2,0).∴|MC|==.∴|MN|的最大值为|MC|+r=.(2)由ρ=a sinθ得ρ2=aρsinθ,∴圆C的直角坐标方程是x2+y2=ay,即x2+(y﹣)2=.∴圆C的圆心为C(0,),半径为||,直线l的普通方程为4x+3y﹣8=0.∵直线l被圆C截得的弦长等于圆C的半径的倍,∴圆心C到直线l的距离为圆C半径的一半.∴=||,解得a=32或a=.[选修4-5:不等式选讲]23.已知f(x)=|ax﹣1|,不等式f(x)≤3的解集是{x|﹣1≤x≤2}.(Ⅰ)求a的值;(II)若<|k|存在实数解,求实数k的取值范围.【解答】解:(Ⅰ)由|ax﹣1|≤3,得﹣3≤ax﹣1≤3,解得:﹣2≤ax≤4,a>0时,﹣≤x≤,而f(x)≤3的解集是{x|﹣1≤x≤2},故,解得:a=2;a<0时,≤x≤﹣,不等式f(x)≤3的解集是{x|﹣1≤x≤2},故,以a=2;(Ⅱ)=,故要使<|k|存在实数解,只需|k|>,解得k>或k<﹣,∴实数k取值范围是(﹣∞,﹣)∪(,+∞).。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2017年九年级质量调研检测瑶海区(二)历史试卷(开卷)学校:___________姓名:___________班级:___________考号:___________
一、单项选择题(本大题共10 小题, 每小题2 分,共20 分,请把正确答案写在题前的括号内)1.天干地支与十二生肖,是我国古代历法研究的成果。2017年是“鸡年”,用天干地支表示又叫( )A.乙未年 B.丙申年 C.丁酉年 D.戊戌年2.史实是真实并存在的客观事实,下列属于史实的( )A.女娲补天 B.大禹治水 C.武王伐纣 D.哪吒闹海3.中华诗词,以其独特的魅力,传颂千年。《三字经》中“嬴秦氏,始兼并……追至隋,一土宇……元灭金,绝宋世。太祖兴,国大明”反映出我国由分裂走向统一的朝代有( )A .汉朝 B .元朝 C. 唐朝 D.宋朝4.“驾驶汽车的车夫是有能而无权的,汽车的主人是无能而有权的,这个有权的主人便应该靠有能的专家去代他驾驶汽车。民国的大事,也是一样的道理。国民是主人,就是有权的人,政府是专家,就是有能的人。”这实质上反映了孙中山主张( )A .主权在民 B .权能分开 C. 天赋人权 D.自由平等5.下表反映了中国民族资本主义企业1894——1913年的发展状况,对其理解正确的是( )
时间企业总数资本总额(万元)
1894年约50家(资本1万元以上)3519
1913年约550家(资本10万元以上)120288A.《马关条约》签订,促进中国民族资本主义快速发展B.民族资产阶级力量壮大,开始登上历史舞台C.民族工业比重日益增加,成为经济主导D.一战期间,帝国主义放松侵略,民族资本主义发展较快6.某校九年级学生在一次重走长征路的研究性学习活动中使用了以下简图,其中a、b、c、d四个地点对应的城市分别是( )A.瑞金——遵义——会宁——吴起镇B.井冈山——遵义——吴起镇——会宁 C.井冈山——泸定桥——会宁——吴起镇D.瑞金——赤水河——泸定桥——吴起镇7.1868年4月,日本以天皇的名义公布了“五条誓文”,下列誓文的内容对日本社会最有影响的是( )A.广兴会议,决万机于公议 B.上下一心,以盛行经纶C.破旧有之陋习,基于天地之公道 D.求知识于世界,大振皇基8.英国史学家W·包登提到:“十八世纪后叶的英国,国内的需求是那样多,英国人控制的海外市场又是那样广大,以至如果没有新的生产方法,工厂主的任何努力都不能满足商业的需求。”与材料所述现象相关的是( )A.资产阶级革命 B.启蒙运动 C.工业革命 D.三角贸易9.近代自然科学的奠基人是( )A.孟德斯鸠 B.牛顿 C.达尔文 D.爱因斯坦
10.中国漫画家华君武1947年创作的漫画《黄鼠狼给鸡拜年的结果》,隐喻马歇尔计划,由此我们可以得出的正确认识是( )A.漫画具有很强的主观性,没有史料价值B.漫画属于图片史料,客观反映了马歇尔计划的影响C.该漫画是美苏冷战在文艺领域的反映D.漫画虽然是艺术作品,但还有一定的史料价值
二、组合列举(本大题共3小题,每空1分,共10分)11.一座城市的历史,就是一个民族的历史,请写出与下列提示相对应的城市名称。(1)六朝古都金陵城,近代中国由此开始 。(2)物华天宝人杰昌,军旗升起英雄城 。(3)南湖圣地有游船,开天辟地共产党 。12.历史上有很多个“第一”都对社会发展产生了深远影响,根据提示相对应的“第一”。(1)我国历史上第一个以华夏族为主的多民族的大一统国家是____________。(2)一百多年来中国人民反对帝国主义侵略第一次取得完全胜利的战争是 。(3)世界上第一辆使用汽油内燃机的汽车是由德国人______ _____设计制造的。13.船,在日常生活中是一种交通工具。在历史发展的长河中,船可能承载更多的历史。(1) 1873年,北洋大臣 在上海创办轮船招商局。(2) 1917年10月24日晚,“ ”巡洋舰向俄国资产阶级临时政府所在地冬宫,发起了最后攻击的炮声,宣告了十月社会主义革命的胜利。(3) 1522年,葡萄牙的麦哲伦船队的“维多利亚”号历尽艰辛,完成了人类首次 。(4) 美国著名工程师 制造的第一艘以蒸汽机为动力的轮船,于1803年在法国的塞纳河试航成功。
三、辨析改错(本大题共4小题,共8分)14.社会主义核心价值观中强调民主、平等、和谐、法制。辨别下列史实的正误,在“答题卷”该题前的括号内正确的打“√”;错误的打“×”,并加以改正。【 】(1)雅典民主政治是西方民主政治的源头,在伯里克利时期地主阶级的民主政治发展到顶峰。错误:_________ 改正:___________。【 】(2)美国资产阶级革命中颁发的《人权宣言》被称为“人类历史上第一个人权宣言”。错误:__________ 改正:________________。【 】(3)1972年尼克松访华,在上海签署的《中美联合公报》,中美两国结束了二十多年的对抗,两国关系开始走向正常化。错误:__________ 改正:________________。【 】(4)1942年1月1日,美英中苏等26国在华盛顿签署《联合国宣言》,标志着国际反法西斯联盟成立。错误:__________ 改正:________________。
四、材料解析(本大题共2小题,每小题10分,共20分。)15.重大事件深刻影响历史进程。阅读下列材料,回答问题。材料一:《申报》刊云:“新众院昨以全体名义电外使谓山东问题近日消息不佳,务坚持勿退让。”刘参议员也表示:“所述日本要求于合约内专列一条将青岛问题由德国交由日本自由处理,此事在我国坚持到底断难承认。如果加入此条,我国当然不能签字”——江铁《从看巴黎和会期间中国政府解决山东问题的态度》(1) 材料一所述的事件发生在哪一年?(2分)由此引发的我国历史上一次爱国运动有何历史意义(2分) 材料二: (2)结合所学知识指出材料二中所述会议召开的历史背景?(4 分) (3)材料二中会议的召开有何重要历史意义?(2分) 16.历史的长河中有前进也有倒退,在不断的徘徊前进中,恰当的政策调整是推动历史进步的重要因素。【历史的前进】材料一:隋唐时期重新建立起大一统的帝国并且使之更为完善,接下来100年间的和平与繁荣使唐时国力超过了汉朝,同时制度和文化也取得了突破性进展,而这一进展反过来又推动了国家的全民发展。——费正清《中国:传统与变迁》(1) 依据材料一和所学知识,指出“突破性进展”在制度革新上的表现有哪些?(2分) 【历史的探索】材料二:1921年列宁说:“目前已经很清楚。我们用冲击的办法,即用简捷、迅速、直接的办法实行社会主义生产和分配的原则尝试已经失败了。……政治形势向我们表明,在许多经济问题上,必须退到国家资本主义上去,从冲击转到围攻的办法上去。”——周尚文《苏联兴亡史》(2)依据材料二并结合所学知识,说明“从冲击转到围攻的办法上去”的转变指什么?这样的转变带来了什么影响(4 分)
【历史的借鉴】材料二:他迅速制定了一系列有效的法规和政策。诸如,通过紧急银行法来整顿银行秩序;……签署农业调整法,以帮助恢复农产品价格;通过全国工业复兴法为经济恢复注入资金。新政期间,美国还建立起养老和失业等方面的社会保障体系,整个美国就像经历了一场由总统推动的社会革命。在美国人的记忆中,这是政府第一次如此广泛、如此深刻地影响了他们的生活。——《大国崛起》解说词(3)材料中“他”是谁?如何理解材料中所述的“这是政府第一次如此广泛、如此深刻地影响了他们的生活”(4分)
五.活动与探究(本大题共12分)17.材料:中国近代化进程(1840——1919年)。 依据材料,提取有效信息,自行拟定一个具体的论题,并就所拟定论题进行简要阐述。(要求明确写出所拟论题,简述须有史实依据) 2017 年九年级质量调研检测 (二)历史参考答案(开卷)一、单项选择(本大题共10 小题, 每小题2 分,共20 分,请把正确答案写在题前的括号内)
题号12345678910答案CCBABADCBD二、 组合列举 (本大题共3 小题;每空1 分,共10 分)11. (1) 南京 (2)南昌 (3) 嘉兴12. (1) 秦朝 (2) 抗日战争 (3) 卡尔·本茨13. (1)李鸿章 (2)阿芙尔乐号 (3)环球航行 (4)富尔顿三、辨析改错 (本大题共4 小题;每小题2 分,共8 分)14. (1)错误;“地主阶级”改为“奴隶主阶级”; (2)错误;“《人权宣言》”改为 “《独立宣言》”;(3)正确; (4)错误;“《联合国宣言》”改为“《联合国家宣言》”。四、 材料解析 (本大题共2 小题, 每小题10 分,共20 分)15. (l)1919年(2 分); 标志着中国新民主主义革命的开始。(2分)(2) 历史背景:粉碎“四人帮”以后,人民要求纠正“文化大革命”中的错误;当时中共中央的主要领导人仍然坚持“左”的指导思想,这引起全国上下的不满;1978年,思想理论界展开了一场真理标准问题的讨论,为十一届三中全会的召开做了思想准备。(4 分)(3) 意义:我国进入社会主义现代化建设新时期,走上改革开放,建设中国特色社会主义的正确道路。 (2 分)16. (l)制度:科举制、三省六部制。(2分)(2)转变:从战时共产主义政策转为新经济政策。(2 分)影响:调动了人民生产积极性,使苏俄经济摆脱困境;巩固工农联盟和苏维埃政权;人民群众的物质文化生活也有了初步好转。(每点1分,任答其中2点即可得2分)(3)罗斯福新政(2 分);罗斯福新政开创了资产阶级政府大规模干预经济生活的先河。(2分)五、活动探究题 (共12 分)17.论题选择的角度:领域:经济——政治——思想;内容:从民族国家独立诉求到个人主义启蒙;民族国家独立、富强的诉求贯穿始终;结
