作已知线段的垂直平分线
1.3线段的垂直平分线

回顾 思考 线段的垂直平分线
我们曾经利用折纸的方法得到:
线段垂直平分线上的点到这条线段两个端点距离相等.
你能证明这一结论吗?
已知:如图,直线MN⊥AB,垂足为C, 且AC=CB.
P是MN上任意一点.
求证:PA=PB.
M P
分析:要证明PA=PB,
1.3线段的垂直平分线
第1课时
驶向胜利 的彼岸
• 1. 掌握线段垂直平分线的性质定理和判 定定理的证明方法.
• 2.会用尺规作已知线段的垂直平分线.
• 3、会用线段垂直平分线的性质定理和 判定定理进行计算或证明。
1.什么是线段垂直平分线?
垂直 并且 平分 一条线段的直线称为这条 线段的垂直平分线,简称 中垂线 .
这条线段的垂直平分线上.
P
∵PA=PB(已知),
∴点P在AB的垂直平分线上(到一条
线段两个端点距离相等的点,在这条
线段的垂直平分线上).
A
B
老师提示:这个结论是经常用来
证明点在直线上(或直线经过某一点) 的根据之一.
从这个结果出发,你还能联想到什么?
你能根据上述定
M
理和逆定理,说出
线段的垂直平分线
A
AE
B D
E BD C
2.已知:如图,AD是ABC的高,E为AD上一点,且 BE=CE,则ABC为 等腰 三角形.
巩固练习 2
挑战自我
3.如图,已知点D在AB的垂直平分线上,如
果AC=5cm,BC=4cm,则△BDC的周长为
_9__cm__。
C
P
Байду номын сангаас
M
19.3.5作已知线段的垂直平分线 学案

19.3.5《作已知线段的垂直平分线》学案学习目标1.掌握作已知线段的垂直平分线的方法及一般步骤,并熟练掌握基本作图语言。
2.通过动手操作、合作探究,培养学生的作图、语言表达、逻辑思维和推理能力。
3.激情投入,全力以赴,让学生认识到尺规作图与实际生活的紧密联系,激发学生的学习兴趣。
重点:掌握作已知线段的垂直平分线的作法。
难点:尺规作图的理论依据。
课堂研讨一、复习导学1.线段的垂直平分线的性质是: 。
2.如图19.3.9,对已知线段AB 的垂直平分线上的任意两点C 、D ,总有CA =CB , DA =DB.由此,你能发现作垂直平分线的方法吗?二、研讨过程问题1:作已知线段的垂直平分线如图19.3.10,已知线段AB ,试按下列步骤用直尺和圆规准确地作出线段AB 的垂直平分线. 作法: 第一步: . 第二步: . 则直线CD 就是所要作的线段AB 的垂直平分线. 我们可以证明这样作出来的直线是符合要求的,即证明直线CD 垂直平分线段AB . 如图19.3.11,连结CA 、CB 、DA 、DB , ∵ AC =BC , AD =BD ,CD =CD , ∴ △ ≌△ (S .S .S .), ∴ ∠ACD =∠BCD (全等三角形的对应角相等), ∴ CD 垂直平分线段AB (等腰三角形“三线合一”). 由于直线CD 与线段AB 的交点就是AB 的中点,因此我们可以用这种方法作出线段AB 的中点,从而也可以作出任一个三角形的三条中线.图19.3.9图19.3.10图19.3.11三、练习1.四等分已知线段AB.2.如图,作△ABC边BC的垂直平分线.(第2题)完成下列作图,并写出作法.1.如图,已知线段AB和CD,求作一条线段,使它等于AB-2CD.(第1题)(第2题)2.如图,已知∠A和∠B,求作一个角,使它等于∠A-2∠B.3.如图,已知线段a和b,求作一个等腰三角形,使它的腰长等于a,底边长等于b.(第3题)(第4题)4.如图,已知线段a和b,求作一个直角三角形,使它的两条直角边分别等于线段a和b.5.已知等腰三角形ABC,AB=AC,∠A≠90°,在AC所在的直线上求作一点P,使PA=PB.四、小结与作业课本第86页习题19.3第6题。
用尺规作图(作线段的垂直平分线)

2.画一个直角三角形,使其斜边和直 角边分别等于已知的两条线段.
(第 4 题)
E F B D C
2,书本上的练习
作业
课堂作业:书本P37 上的7,9,11题 (画在书本上) 家庭作业(方便居民的生 活,计划在三个住宅小区A、B、 C之间修建一个购物中心,试问, 该购物中心应建于何处,才能 使得它到三个小区的距离相等。
A
·
B
C
问题探讨
以C为圆心,任一线段的长为半径 画弧,交l于A、B两点,则C是线段 AB的中点.因此,过C画直线l的垂 线转化为画线段AB的垂直平分线.
图 24.4.9
作法:(1)以点C为圆心,任一线段的 长为半径画弧,交直线l于点A、B; (2)以点A为圆心,以CB长为半径在 直线一侧画弧; (3)以点D为圆心,以同样的长为半径 在直线的同一侧画弧,两弧交于点D; (4)经过点C、D作直线CD. 则直线CD即为所求.
你能做出下面五角星的一条对称轴吗?
A
A’
生活中的数学
A
在某高速公路L的同侧,有两个工厂A、B,为了便 于两厂的工人看病,市政府计划在公路边上修建一所医 院,使得两个工厂的工人都没意见,问医院的院址应选 在何处?你的方案是什么?
B
L
高 速 公 路
1,已知,如图,AD是△ABC的角平分线, DE,DF,分别是△ABD和△ACD的高。 求证:AD垂直平分EF A
思考:
有时我们感觉两个平面图形是轴对称图形,如何验 证呢?不折叠图形,你能准确的作出轴对称图形的对称 轴吗?
如果两个图形成轴对称,其对称轴是任何 一对对应点所连线段的垂直平分线.因此,我们 只要找到一对对应点,作出连接它们的线段的 垂直平分线,就可以得到这两个图形的对称轴。
用尺规作图(作线段的垂直平分线)

我们已熟悉尺规的四个基本作图:画 线段,画角.画角平分线、画线段的 垂线,那么利用尺规还能解决什么作 图问题呢?
画线段的垂直平分线;
如图,已知线段AB,画出它的垂直平 分线.
作法:(1)以点图A为2 4 .圆4 .7心,以大于AB一 半的长为半径画弧; (2)以点B为圆心,以同样的长为半径 画弧,两弧的交点记为C、D; (3)经过点C、D作直线CD. 直线CD即为所求.
·
B
C
问题探讨
在V型公路(∠AOB)内部,有两个村 庄C、D。你能选择一个纺织厂的厂址P,使P 到V型公路的距离相等,且使C、D两村的工 人上下班的路程一样吗?
A
O
C. D.
B
1,已知,如图,AD是△ABC的角平分线,
DE,DF,分别是△ABD和△ACD的高。
求证:AD垂直平分EF
A
E F
B
D
C
你能做出下面五角星的一条对称轴吗?
A
A’
生活中的数学
A
在某高速公路L的同侧,有两个工厂A、B,为了便
于两厂的工人看病,市政府计划在公路边上修建一所医 院,使得两个工厂的工人都没意见,问医院的院址应选 在何处?你的方案是什么?
B
L
高速公路
生活中的数学
A
某区政府为了方便居民的生 活,计划在三个住宅小区A、B、 C之间修建一个购物中心,试问, 该购物中心应建于何处,才能 使得它到三个小区的距离相等。
思考:
有时我们感觉两个平面图形是轴对称图形,如何验 证呢?不折叠图形,你能准确的作出轴对称图形的对称 轴吗?
如果两个图形成轴对称,其对称轴是任何 一对对应点所连线段的垂直平分线.因此,我们 只要找到一对对应点,作出连接它们的线段的 垂直平分线,就可以得到这两个图形的对称轴。
尺规作图(画线段的垂直平分线)PPT教学课件

长为半径画弧,两弧相交于D点; 2
❖ (4)过C、D两点作直线CD。 ❖ 所以,直线CD就是所求作的。
练习 ❖ 1、如图,过点P画∠O两边的
垂线.
(第 1 题)
❖ 2、如图,画△ABC边 BC上的高.
(第 2 题)
挑战自我 ❖如图,已知线段a,h, ❖求作:△ABC,使AB=AC,
❖已知线段AB,画出它的垂直平分线.
说出你的 作图思路
议一议;能否说出这 种画法的依据,小组 讨论交流一下。
试一试你的能力
1、如图,点C在直线上,试过 点C画出直线的垂线。
2、如图,如果点C不在直线上,试和同学 讨论,应采取怎样的步骤,过点C画出直 线的垂线?
作法:
❖ (1)任取一点M,使点M和点C在的两侧; ❖ (2)以C点为圆心,以CM长为半径画弧,
且BC=a,高为h
h
a
动手实践
❖ AB、AC分别是菱形 ABCD的一条边和对角线, 请你用尺规把这个菱形补 充完整。
C
A
B
生活离不开数学
❖ A、B是两个村庄,要从灌 溉总渠引两条水渠便于灌溉, 请你选择最佳方案。
B A
灌溉总渠
❖教学反思 ❖ 本节课你掌握了哪些知识? ❖ 还有哪些疑惑?
华师大版九年级上24.3《命题与定理》
❖(1)定义、命题、公理、定理的概 念。
❖(2)命题的真假。 ❖(3)命题的形式与命题的题设和结
论。
(4) 说明一个命题是假命题,只需举一 反例
❖
小考卷3
细心!
判断下列命题的真假:
1、相等的两角是对顶角。 (假)
2、若XY=0,则X=0。
线段垂直平分线的作法
D
E
AK
B
.
F
课堂练习
练习4 如图,过点P 画∠AOB 两边的垂线,并和 同桌交流你的作图过程.
A
P
O
B
.
【跟踪训练】
1.下图中的五角星有几条对称轴?作出
n
这些对称轴.
A
B
作法:(1)找出五角星的一对
对应点A和B,连接AB.
Байду номын сангаас(2)作出线段AB的垂直平分线n.
则n就是这个五角星的一条对称轴.
用同样的方法,可以找出五条对称轴,所以五角星有五 条对称轴.
.
课堂小结
本节课你有什么收获?
.
布置作业 P65、66 习题13.1第6、9题.
.
只要我们找到一对对应 点,作出连接它们的线段的 垂直平分线,就可以得到这 两个图形的对称轴了.
.
尺规作图
如何用尺规作图的方法经过直线外一点作已知直线 的垂线?
(1)为什么任意取一点K ,使点K与点C 在直线两旁?
(2)为什么要以大于 1 D E 的长为半径作弧? 2
(3)为什么直线CF 就是所求作的垂线? C
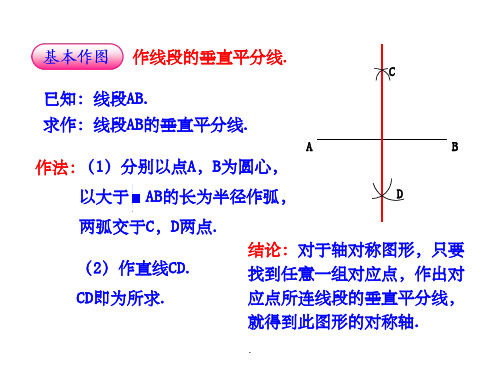
作线段的垂直平分线.
C
已知:线段AB.
求作:线段AB的垂直平分线.
A
B
作法:(1)分别以点A,B为圆心,
以大于 1 AB的长为半径作弧,
D
2
两弧交于C,D两点.
(2)作直线CD.
结论:对于轴对称图形,只要 找到任意一组对应点,作出对
CD即为所求.
应点所连线段的垂直平分线, 就得到此图形的对称轴.
.
问题思考:既然轴对称图形的对称轴是任何 一对对称点所连线段的垂直平分线,那么轴对称 图形的对称轴如何来作呢?
19.3_用尺规作图(作线段的垂直平分线)
图 24.4.9
以C为圆心,任一线段的长为半径 画弧,交l于A、B两点,则C是线段 AB的中点.因此,过C画直线l的垂 线转化为画线段AB的垂直平分线.
作法:(1)以点C为圆心,任一线段的 长为半径画弧,交直线l于点A、B; (2)以点A为圆心,以CB长为半径在 直线一侧画弧; (3)以点D为圆心,以同样的长为半径 在直线的同一侧画弧,两弧交于点D; (4)经过点C、D作直线CD. 则直线CD即为所求.
E F B D C
2,书本上的练习
作业
课堂作业:书本P37 上的7,9,11题 (画在书本上) 家庭作业(周末):精析精练
生活中的数学
某区政府为了方便居民的生 活,计划在三个住宅小区A、B、 C之间修建一个购物中心,试问, 该购物中心应建于何处,才能 使得它到三个小区的距离相等。
A
·
B
C
问题探讨
你能做出下面五角星的一条对称轴吗?
A
A’
生活中的数学
A
在某高速公路L的同侧,有两个工厂A、B,为了便 于两厂的工人看病,市政府计划在公路边上修建一所医 院,使得两个工厂的工人都没意见,问医院的院址应选 在何处?你的方案是什么?
B
L
高 速 公 路
1,已知,如图,AD是△ABC的角平分线, DE,DF,分别是△ABD和△ACD的高。 求证:AD垂直平分EF A
2.如图,如果点C不在直线l上,试和 同学讨论,应采取怎样的步骤,过点 C画出直线l的垂线?
图 24.4.10
作法:(1)以点C为圆心,以适当长为 半径画弧,交直线l于点A、B; (2)以点A为圆心,以CB长为半径在 直线另一侧画弧. (3)以点B为圆心,以CB长为半径在直 线另一侧画弧,交前一条弧于点D. (4)经过点C、D作直线CD. 则直线CD即为所求.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
作已知线段的垂直平分线教学设计
课 题
13.4.4作已知线段的垂直平分线
教学目标
1、会画线段的垂直平分线
2、探究三角形的三边垂直平分线的交点位置
重点难点
重点:线段的垂直平分线的画法
难点:线段的垂直平分线的画法依据
教学设想 自主探究 动手实践
教 学 过 程 一:自学质疑: 导入:回忆轴对称和轴对称图形,引出线段的垂直平分线的定义 1、.自学目标: 会画线段的垂直平分线 探究三角形的三边垂直平分线的交点位置 2、自学提示: 用3-5分钟时间认真阅读教材P90 -91页,对重点及疑难问题做出标记,并完
成下列问题
(1)画线段垂直平分线关键是找什么?如何找出的?
(2)尺规作线段垂直平分线的依据是什么?
3、尝试练习:
(1)如图,点A,B关于某直线成轴对称,你能只用圆规和直尺作出这条直线吗?
●
A ● B
(2)、你能把线段AB四等分吗?
(3)、分别画一个锐角三角形、直角三角形、钝角三角形,再分别作出三边的垂直平
分线
观察:
你有什么发现?(三条垂直平分线的交点位置;这点到三个顶点的距离之间的关
系。)
二:合作释疑:
各小组学生探讨上述问题,对疑难问题做出标记
三:展示评价:
小组中等水平学生展示作图内容,优等生进行点评,老师进行总结,说明注意问题
注意:这个作图方法就是线段垂直平分线的尺规作图,可以用来确定线段的中点
四:挑战自我
如图,已知线段a,h,
求作:△ABC,使AB=AC,且BC=a,且BC边上高为h
a
h
五:拓展提升,请你出题
结合本节知识出一题考考同桌
六:巩固深化(题目)
有一如图的地块,在∠AOB内有点M、N,小强想确定点P,使点P到角两边的距离
相等且到M、N的距离相等。(不写作法,但要保留作图痕迹)
a) 如图,∠AOB与点E、F,请利用尺规作图找一点P,使点P到∠AOB两边
距离相等,且到点E、F点的距离也相等。
教 学 过 程 五、课堂小结:
本节课你学到了哪些内容?
注意:满足条件(到角两边距离相等地,到两点距离相等)的点在(角的平分线、线
段的垂直平分线)图形上,作图时要先搞准要求,再一步步进行,不要看少了条件。
板书设计及作业布置 板书:
12.1.3线段垂直平分线的作法
一:线段的垂直平分线的画法及作图过程
作业布置:
教材习题13.4 第3题,第5题
教学反思 线段的垂直平分线的作法比较简单,但日常生活中十分有用,特别是与角平分线作图相结合,是生活中与测试中考查的热点,学生除了会作图外,更要理解其现实意义,
本节课学生通过作线段AB的垂直平分线,作线段的四等分点,巩固深化了训练,基本
掌握了本节内容,但尺规作图还要加强的点训练。
B O
A
M
N
