二次函数
二次函数的性质

二次函数的性质二次函数是高中数学中一个重要的概念,它是一种形如y=ax²+bx+c的函数,其中a、b、c是实数且a≠0。
在本文中,我将详细介绍二次函数的性质,包括定义、图像、顶点、对称轴、零点、判别式以及二次函数的分类。
一、二次函数的定义二次函数是一种多项式函数,它的最高次项是二次项,即x的平方项。
一般地,我们可以表示为y=ax²+bx+c,其中a、b、c为实数,且a≠0。
常见的二次函数包括抛物线、开口方向为上或下的曲线。
二、二次函数的图像二次函数的图像通常是一个U形或者倒U形的曲线,也即抛物线。
抛物线开口的方向取决于二次函数的系数a的正负。
1. 当a>0时,抛物线开口向上,图像在坐标系的正半轴上方;2. 当a<0时,抛物线开口向下,图像在坐标系的负半轴上方。
三、二次函数的顶点二次函数的顶点是抛物线的最低点(开口向上)或最高点(开口向下)。
顶点的横坐标可以通过用-b/2a求得,纵坐标可以通过将横坐标代入函数得出。
四、二次函数的对称轴二次函数的对称轴是指通过顶点并垂直于x轴的一条直线。
对称轴的方程为x=-b/2a。
五、二次函数的零点二次函数的零点是指使函数取值为零的x的值。
可以通过求解二次方程ax²+bx+c=0来得到零点。
根据一元二次方程的求根公式,可得x=(-b±√(b²-4ac))/(2a)。
当判别式b²-4ac>0时,方程有两个不相等的实根;当b²-4ac=0时,方程有两个相等的实根;当b²-4ac<0时,方程没有实根。
六、二次函数的判别式二次函数的判别式D=b²-4ac可以用来判断二次函数的图像和零点的性质。
1. 当D>0时,方程有两个不相等的实根,图像与x轴有两个交点;2. 当D=0时,方程有两个相等的实根,图像与x轴有一个交点;3. 当D<0时,方程没有实根,图像与x轴无交点。
《二次函数》知识点总结(修改版)
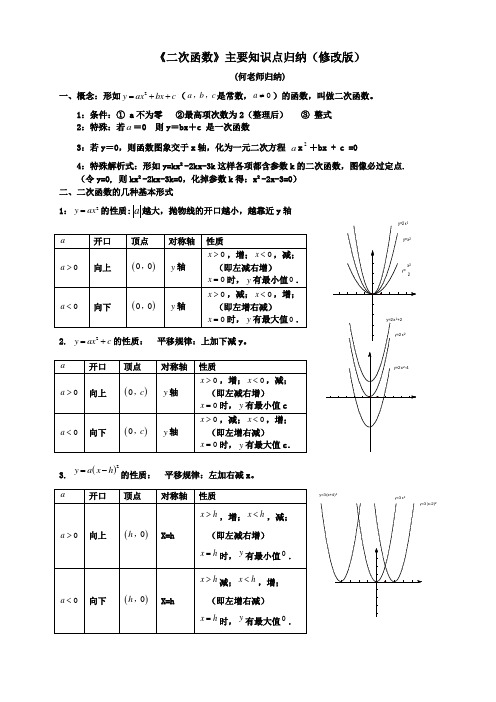
《二次函数》主要知识点归纳(修改版)(何老师归纳)一、概念:形如2y ax bx c=++(a b c,,是常数,0a≠)的函数,叫做二次函数。
1:条件:① a不为零②最高项次数为2(整理后)③整式2:特殊:若a=0 则y=bx+c 是一次函数3:若y=0,则函数图象交于x轴,化为一元二次方程a x2+bx + c =04:特殊解析式:形如y=kx²-2kx-3k这样各项都含参数k的二次函数,图像必过定点.(令y=0, 则kx²-2kx-3k=0,化掉参数k得:x²-2x-3=0)二、二次函数的几种基本形式1:2y ax=的性质:a越大,抛物线的开口越小,越靠近y轴2. 2y ax c=+的性质:平移规律:上加下减y。
3.()2y a x h=-的性质:平移规律:左加右减x。
y=3(x+4)2(x-2)2y=3x24.()2y a x h k=-+(顶点式)的性质:平移规律:左加右减x 。
上加下减y,5.2y ax bx c =++(一般式)的性质: 先将一般式2y ax bx c =++通过配方法化成22424b ac b y a x a a -⎛⎫=++ ⎪⎝⎭,再对比顶点式,()2y a x h k =-+可得2424b ac b h k a a -=-=,.故两者性质相同。
三、二次函数2y ax bx c =++(或()2y a x h k =-+)图象及性质再归纳: 1:开口方向.①:当0>a 时,开口向上;当0<a 时,开口向下; ②:a 相等,几条抛物线的开口大小、形状相同. ③:a 越大,抛物线的开口越小,越靠近y 轴 2:对称轴,直线abx 2-=(或直线x =h ) 3:顶点坐标:),(ab ac a b 4422-- 或(h,k )4:增减性 ①:若0>a ,当x<a b 2-时,y 减;当x>a b2-时,y 增,简记:左减右增; ②:若0<a ,当x<a b 2-时,y 增;当x>ab2-时,y 减,简记:左增右减;5:最值 ⑴:若定义域是全体实数,则在顶点处取得最大值(或最小值),即:当a b x 2-=时,ab ac y 442-=最值,(或当x =h 时,最值是y =k )2-32⑵: 若定义域是21x x x ≤≤, 则:①:若a b 2-在21x x x ≤≤内,则当x=a b 2-时,ab ac y 442-=最值;②:若ab2-不在21x x x ≤≤内,则需要考虑函数在21x x x ≤≤范围内的增减性, A: 若y 为增,则当2x x =时,c bx ax y ++=222最大,当1x x =时,c bx ax y ++=121最小; B: 若y 为减,则当1x x =时,c bx ax y ++=121最大,当2x x =时,c bx ax y ++=222最小。
二次函数知识再归纳

二次函数知识再归纳一. 二次函数的性质1.抛物线开口向上(即a >0):抛物线上的点到对称轴的距离越远,y 值越大,到对称轴的距离越近,y 值越小.即:抛物线上的三点A(1x ,1y ),B(2x ,2y ),顶点C(0x ,0y ),若|1x -0x |>|2x -0x |, 则1y >2y ;若|1x -0x |<|2x -0x |,则1y <2y ;2.抛物线开口向下(即a <0):抛物线上的点到对称轴的距离越远,y 值越小,到对称轴的距离越近,y 值越大.即:抛物线上的三点A(1x ,1y ),B(2x ,2y ),顶点C(0x ,0y ),若|1x -0x |>|2x -0x |, 则1y <2y ;若|1x -0x |<|2x -0x |,则1y >2y ;3.无论开口向上还是向下,抛物线上的点到对称轴的距离相等,则y 值相等;反之,抛物线上的点y 值相同,那么它们到对称轴的距离相等(即横坐标相加除以2就是对称轴);4.已知抛物线上的三点A(1x ,1y ),B(2x ,2y ),C(0x ,0y ),且C 为顶点,若1y >2y ≥0y ,则a >0;若1y <2y ≤0y ,则a <0.二.平移1.图象(或图象上的)点的平移法则:左减右加,上加下减;2.表达式的平移法则:左加右减,上加下减;例如:将y=-2x ²+x-2先向左平移1个单位,再向下平移2个单位,得到:y=-2(x+1)²+(x+1)-2-2=y=-2x ²-3x-5;(1)平移不改变二次项系数“a ”①左右平移:不改变函数值(即y 值),若图象与x 轴有两个交点,那么两交点之间的距离不变;若与x 轴交于点A(1x ,1y ),点B(2x ,2y ),则:|AB|=|21x -x |=221)x x (-=21221x x 4-)x x (+②上下平移:不改变自变量(即x)的值,对称轴不变(即a ,b 都不变);三.轴对称(即翻折)1.关于x 轴对称(1)一般式:y=ax ²+bx+c(a ≠0)变为y=-ax ²-bx-c 顶点式:y=a(x-h)²+k(a ≠0)变为y=-a(x-h)²-k2.关于y 轴对称(1)一般式:y=ax ²+bx+c(a ≠0)变为y=ax ²-bx+c顶点式:y=a(x-h)²+k(a ≠0)变为y=a(x+h)²+k3.关于x=m 对称 【特别提示:两抛物线的交点在直线x=m 上】(1)y=ax ²+bx+c(a ≠0)思路:如图:A(1x ,1y ),B(2x ,2y ),C(0,c),作出这三点关于直线x=m 的对称点A ´、B ´、C ´,利用中点坐标公式求出三点的坐标分别为A ´(2m-1x ,0),B ´(2m-2x ,0),C ´(2m ,c),再代入新抛物线的表达式中求即可.(2)顶点式:y=a(x-h)²+k(a ≠0)如图,作出顶点P(h ,k)关于直线x=m 的对称点P ´,利用中点坐标公式求得P ´(2m-h ,k),然后代入新抛物线的表达式中求得:y=a(x-2m+h)²+k4.关于y=n 对称 【特别提示:若两抛物线有交点,则交点在直线y=n 上】(1)y=ax ²+bx+c(a ≠0)思路:如图:A(1x ,1y ),B(2x ,2y ),C(0,c),作出这三点关于直线y=n 的对称点A ´、B ´、C ´,利用中点坐标公式求出三点的坐标分别为A ´(1x ,2n-1y ),B ´(2x ,2n-2y ),C ´(0,2n-c),然后代入新抛物线的表达式中求即可.(2)顶点式:y=a(x-h)²+k(a ≠0)如图,作出顶点P(h ,k)关于直线y=n 的对称点P ´,利用中点坐标公式求得P ´(h ,2n-k),然后代入新抛物线的表达式中求得:y=-a(x-h)²+2n-k四.成中心对称(即绕着某一点旋转180°) 【注:旋转180°,二次项系数“a ”变为了“-a ”】1.关于原点对称(即绕着原点旋转180°)一般式:y=ax ²+bx+c(a ≠0)变为y=-ax ²+bx-c顶点式:y=a(x-h)²+k(a ≠0)变为y=-a(x+h)²-k2.关于任意一点成中心对称(即绕任意一点旋转180°)(1)y=ax ²+bx+c(a ≠0)思路:如图:A(1x ,1y ),B(2x ,2y ),C(0,c),作出这三点关于点P(m ,n)的对称点A ´、B ´、C ´,利用中点坐标公式求出三点的坐标分别为A ´(2m-1x ,2n-1y ),B ´(2m-2x ,2n-2y ),C ´(2m ,2n-c),然后代入新抛物线的表达式中求即可.(2)顶点式:y=a(x-h)²+k(a ≠0)如图,作出顶点Q(h ,k)关于点P(m ,n)的对称点Q ´,利用中点坐标公式求得Q ´(2m-h ,2n-k),然后代入新抛物线的表达式中求得:y=-a(x-2m+h)²+2n-k五.动点问题1.求PA+PC 最小思路:作A 点关于P 点所在直线l 的对称点B ,连接BC 与l 相交的点即所求点P.变式:求△PAC 周长的最小值 (提示:求出PA+PC 的最小值,再加上AC)2.求|PA-PC|最大值思路:若点A 、C 在P 点所在直线l 的同侧,直接连接AC 并延长与l 相交的点即P 点;若点A 、C 在P 点所在直线l 的异侧,任选一定点(如点A)作关于l 的对称点(B),转化到l 同侧,再连接BC 并延长与l 相交的点即P 点.3.等腰三角形例如:已知:y=x ²-2x-3,与x 轴的交点A(-1,0),C(3,0),B(0,-3),P 为对称轴上一点.求△PBC 为等腰三角形时,P 点的坐标.解析:设点P(1,m),∵B(0,-3),C(3,0),∴PB=22)3m ()01(++-=10m 6m 2++, PC=22)0m ()31(-+-=4m 2+,BC=22)03()30(--+-=32,然后分①PB=BC ;②PC=BC ;③PB=PC 三种情况讨论.4.等边三角形(例如:如图,y=x ²-2x-3,则顶点P(1,-4),在抛物线上是否存在M 、N 两点,使得△PMN 为等边三角形.解析:存在. 设M(t ,t ²-2t-3),则MQ=1-t ,PQ=t ²-2t-3-(-4)=t ²-2t+1,∴PQ=3MQ , 即t ²-2t+1=3(1-t),解出t ,就可求出M 点的坐标,进而求出N 点的坐标(当然M 点也可能在右侧,N 点在左侧)5.直角三角形(1)动点在对称轴或其它直线上思路:设出动点的坐标,并求出其它两个已知点的坐标,利用两点间的距离公式,表示出三边,再分直角顶点讨论.例如:如图,y=x ²-2x-3与x 轴交于A ,B 两点,与y 轴交于点C ,对称轴为l ,问l 上是否存在点P 使得△PBC 为直角三角形?解析:存在. 设点P(1,m),∵B(3,0),C(0,-3),∴PB ²=(1-3)²+(m-0)²=m ²+4, PC ²=(1-0)²+(m+3)²=m ²+6m+10,BC ²=(3-0)²+(0+3)²=18,然后分:①∠PBC=90°,即PB ²+BC ²=PC ²;②∠PCB=90°,即PC ²+BC ²=PB ²;③∠BPC=90°,即PB ²+PC ²=BC ²三种情况讨论.(2)动点在抛物线上若直角顶点的坐标已知,利用1k .k 21-=求;若直角顶点为动点,过直角顶点构造“三垂直型的K 字型”,利用△相似求.例如:如图,y=x ²-2x-3与x 轴交于A ,B 两点,与y 轴交于点C ,问在抛物线上是否存在点P 使得△PBC 为直角三角形?解析:存在. 若∠1P CB=90°,由题意可得直线BC 的表达式为:y=x-3,∴可设BP 1的表达式为y=-x+m ,将B(3,0)代入求得m=3,∴BP 1的表达式为:y=-x+3.将y=-x+3与y=x ²-2x-3联立即可求出点P 1的坐标.若∠2P CB=90°,方法同上,先求出P 2C 的表达式为y=-x-3,然后与y=x ²-2x-3联立即可求出点P 2的坐标.若∠C 3P B=90°,过点P 3作y 轴的垂线,垂足为N ,再过B 点作BM ⊥NP 3交NP 3的延长线于点M ,BM=|p y |=-x ²+2x+3,P 3M=3-x ,P 3N=x ,CN=-3-(x ²-2x-3)=-x ²+2x ,而△CNP 3∽△P 3MB , ∴BM N P M P CN 33=,即3x 2x x x 3x 2x -22++-=-+,解得x=2131+或x=213-1,然后代入表达式即可求出y 值.【同时也求出了满足题意的另一个点P 4的坐标】6.等腰直角三角形(1)动点在对称轴或其它直线上思路:设出动点的坐标,并求出其它两个已知点的坐标,利用两点间的距离公式,表示出三边,再分直角顶点讨论,同时让两条直角边相等.例如:如图,y=x ²-2x-3与x 轴交于A ,B 两点,与y 轴交于点C ,对称轴为l ,问l 上是否存在点P 使得△PBC 为等腰直角三角形?解析:存在. 设点P(1,m),∵B(3,0),C(0,-3),∴PB²=(1-3)²+(m-0)²=m²+4,PC²=(1-0)²+(m+3)²=m²+6m+10,BC²=(3-0)²+(0+3)²=18,然后分:①∠PBC=90°,即PB²+BC²=PC²,且PB²=BC²;②∠PCB=90°,即PC²+BC²=PB²,且PC²=BC²;③∠BPC=90°,即PB²+PC²=BC²,且PB²=PC²三种情况讨论.(2)动点在抛物线上思路:先在图中找出满足题意的点,分别过各自的直角顶点构造“三垂直型的K字型”,利用△全等求.例如:y=x²-2x-3的图象上是否存在一点P使△PBC为等腰直角三角形?解析:不存在.①∠BCP1时,由△CMP1≌△BOC可求得P1(3,-6),将x=3代入得9-6-3=0,∴P1不在抛物线上,舍去;②∠CBP2时,由△CNB≌△BQP2可求得P2(3,3),将x=3代入得9-6-3=0,∴P2也不在抛物线上,舍去;③∠CP3B=90°时,此时P3(0,0)也不满足题意.∴不存在满足题意的点P.【提示:若让在平面内找点P,那么以上三个点都满足题意】7.三角形相似【注意:“∽”只有一种情况;“相似”需分类讨论】思路:一般能够确定一组对应角相等,不确定的角,找出其中一个,然后分情况(一般有两种)讨论.例如:二次函数的图象经过点A(1,0)、B(3,0)两点.设该二次函数的顶点为D,与y轴交于点C,它的对称轴与x轴交于点E,连接AD、DE和DB,当△AOC与△DEB相似时,求这个二次函数的表达式.解:∵A(1,0)、B(3,0),所以设y=a(x-1)(x-3)即y=ax²-4ax+3a,当x=0时,y=3a,当x=2时,y=-a,∴C(0,3a),D(2,-a) ∴OC=|3a|,∵A(1,0)、E(2,0),∴OA=1,EB=1,DE=|-a|=|a|,在△AOC 与△DEB 中,∵∠AOC=∠DEB=90°, ∴当DEEB OC AO =时,△AOC ∽△BED ,∴||1|3|1a a =时,此方程无解, ∴当EB DE OC AO =时,△AOC ∽△DEB ,∴1|||3|1a a =时,解得33=a 或33-=a 综上所得:所求二次函数的表达式为:3334332+-=x x y 或3334332-+-=x x y 8.平行四边形(1)一般的平行四边形【先在图中画出满足题的平行四边形是正确解题的关键】注意:“□ABCD ”与“以点A 、B 、C 、D 为顶点的四边形是平行四边”的区别,前者字母顺序确定,后者字母顺序不确定.思路:①以已知边为边利用“平移”的方法求;②以已知边为对角线利用中点坐标公式求.例如:已知:y=x ²-2x-3,A ,B ,C 三点如图所示,问在x 轴上是否存在点Q ,抛物线上是否存在点P ,使得以点B,C,P ,Q 为顶点的四边形为平行四边?解析:存在. 连接BC.i) 以BC 为边(P 1、P 2、P 3)设Q(m ,0),由图可知,当C 点向右平移3个单位,再向上平移3个单位后到达B 点, 此时Q 1平移到了P 1,Q 3平移到了P 3,得到P 1、P 3的纵坐标均为3,代入表达式即可求出P 1、P 3两个点的坐标;当B 点向左平移3个单位,再向下平移3个单位后到达C 点,此时Q 2平移到了P 2,得到P 2的纵坐标均为-3,代入表达式即可求出P 2的坐标.ii)以BC 为对角线(P 4)求出BC 的中点坐标M(23-23,),由中点坐标公式可得到P 4的纵坐标为-3,此时和P 2重合.(2)特殊的平行四边形①菱形思路:先确定它为平行四边形,再让邻边相等或对角线垂直.②矩形思路:先确定它为平行四边形,再保证有一个内角为90°(用勾股定理逆定理:a ²+b ²=c ²)或对角线相等.例如:抛物线C:y=x ²+bx(b <0)与x 轴的一个交点为A ,顶点为P ,将其绕着原点旋转180°后得到抛物线C ´,点A 的对应点为点A ´,顶点为P ´,若以点A 、A ´、P 、P ´为顶点的四边形是矩形,求抛物线的表达式.解析:由题意可得P(4b -2b 2, ),OA=OA ´,OP=OP ´,∴四边形APP ´A ´是平行四边形,∴只需OP=OP ´即OA=OP ,∵OP=AP ,∴△OPA 为等边三角形,∴PE=3AE ,即4b 2=3(-2b ),解得b=-23或b=0(舍去),∴C ´的表达式为:y=x ²-23x.③正方形思路:先确定它为平行四边,再让一组邻边垂直且相等或对角线垂直且相等.例如:已知:y=x ²-2x-3,A ,B ,C 三点如图所示,问在平面内是否存在点P 、Q ,使得以点A,C,P ,Q 为顶点且以AC 为边的四边形是正方形?解析:存在. 连接AC.当四边形ACQ 1P 1是正方形时,△AOC ≌△P 1NO ,得P 1(2,1),又由平移得Q 1(3,-2); 当四边形ACQ 2P 2是正方形时,△AOC ≌△P 2MA ,得P 2(-4,-1),又由平移得Q 2(-3,-4).9.线段、面积的最值(1)求线段最大例如:已知:y=x ²-2x-3,A ,B ,C 三点如图所示,P 为线段BC 上一点,过P 点作PQ ⊥x 轴交抛物线于点Q ,求PQ 的最大值及点Q 的坐标.解析:由题意可求得BC 的表达式为:y=x-3,可设点P(m ,m-3))(0<m <3),∴Q(m ,m ²-2m-3),∴PQ=m-3-m ²+2m+3=-(m-23)²+49,∵-1<0,∴当m=23时,PQ 最大,最大值为49,然后将m=2代入m ²-2m-3求得y=-415,∴Q(23,-415),PQ 的最大值为49. (2)求面积最大例如:已知:y=-x ²+2x+3,A ,B ,C 三点如图所示,在BC 上方的抛物线上是否存在一点P 使得四边形ABPC 面积最大?若存在,求出最大面积及点P 的坐标;若不存在,请说明理由.解析:存在.连接PB ,PC ,BC ,过点P 作PQ ⊥x 轴交BC 于点Q ,设P(m ,-m ²+2m+3)(0<m <3),由题意可求得BC 的表达式为:y=-x+3,∴Q(m ,-m+3),PBC ABC ABPC S S S △△四边形+==21AB.OC+21OB.PQ=21×4×3+21×3(-m ²+2m+3+m-3) =-23(m-23)²+875,∴当m=23时,四边形ABPC 的面积最大,最大面积为875, 将m=23代入-m ²+2m+3得y=415,∴P(23,415),四边形ABPC 的面积最大值为875.10.面积相等(1)公共边已知(公共边为底)思路:过(除公共边外的)另一定点作公共边的平行线与抛物线相交的点即所求点. 例如:已知:y=-x ²+2x+3,A ,B ,C 三点如图所示,在抛物线上找一点M.(2)公共边未知(公共边为底)思路:先忽略掉公共底,连接剩下的两个点,然后过公共底的已知点作连成的线段的平行线,与抛物线相交,交点即所求点.例如:已知:y=x ²-2x-3,B(1,0),D(2,-3),在抛物线上找一点P ,使得PCD PBD S S △△=. 解析:连接BC ,过点D 作DP ∥BC 交抛物线于点P.∵BC 的表达式为:y=3x-3,∴可设PD 的表达式为:y=3x+m ,将D(2,-3)代入得:m=-9,∴PD 的表达式为:y=3x-9,将其和y=x ²-2x-3联立即可求出点P 的坐标.(3)高相等(或相同)思路:截取相等的底例如:已知:y=-x ²+6x-5与x 轴交于A ,B 两点,与y 轴交于点C ,顶点为P ,过点C 作l ∥x 轴,l 上是否存在点Q ,使PAC PBQ S S △△=.解析:存在. CAE PAE PAC S S S △△△+=,QMB PMB PBQ S S S △△△+=,而△PAE 和△PMB 高相同,△CAE 和△QMB 高相等,∴只需底BM=AE 即可.∵A(1,0),B(5,0),C(0,-5),P(3,4),∴PC 的表达式为:y=3x-5,∴E(35,0),∴AE=32, ∴BM=32,∴M 1(313,0),M 2(317,0),∴PM 1的表达式为:y=-3x+13,将其和y=-x ²+6x-5联立即可求出点Q 1的坐标;PM 2的表达式为:y=-23x+217,将其和y=-x ²+6x-5联立即可求出点Q 2的坐标;(4)不同底,也不等高思路:用21×底×高(或21×水平宽×铅垂高)表示出面积,使其和已知三角形(或四边形)的面积相等.例如:已知:y=-x ²+2x+3,A 、B 、C 三点如图所示,M 为顶点,连接BC ,BM ,CM ,在x 轴下方的抛物线上是否存在一点P ,使BCM ABP S S △△=解析:利用21×水平宽×铅垂高求出BCM S △=21OB.MN=21×3×2=3,ABP S △=21AB.|P y | =21×4×|-x ²+2x+3|=2(x ²-2x-3)=2x ²-4x-6,∴3=2x ²-4x-6,解出x 即可求出点P 的坐标.(即图中的P 1,P 2)(5)面积的倍、分关系例如:已知:y=x ²-2x-3,A ,B ,C 三点如图所示,D(4,5),抛物线上是否存在一点P ,使 2ABP S △=ACBD S 四边形.解析:存在. ∵2ABP S △=ACBD S 四边形,∴2×21AB|P y |=21AB.D y +21AB.OC ∴4|P y |=21×4×5+21×4×3,即|x ²-2x-3|=4,求出x 即可求出满足题意的点P 的坐标. 11.角相等这类题目比较灵活,常见的解题方法有:①利用“△的相似”求解;②利用“三角函数值相等”求解;③利用“△全等”求解;④“作平行线”求解等.(1)作平行线、作对称(△全等)例如:已知:y=x ²-2x-3,A ,B ,C 三点如图所示,在抛物线上是否存在点P ,使∠ABP=∠CAB ?解析:存在. 若P 点在x 轴上方的抛物线上,过点B 作BP 1∥AC 交抛物线于点P 1,由两直线平行,内错角相等得∠ABP 1=∠CAB ;若P 点在x 轴下方的抛物线上,作C 点关于对称轴的对称点P 2,过P 2作P 2M ⊥x 轴于点M ,则△P 2BM ≌△CAO ,∴∠ABP 2=∠CAB.例如:已知:y=-x ²+2x+3,A 、B 、C 三点如图所示,D(2,3),问抛物线上是否存在一点P 使∠CBD=∠CBP ?解析:存在.由题意可得CD ⊥y 轴,OB=OC ,∴∠OBC=∠OCB=45°,∴∠DCB=45°,CD=2,在y 轴上截取CG=CD=2,∴G(0,1),△DCB ≌△GCB(SAS),∴∠CBD=∠CBP ,延长BG 交抛物线于一点,这点就是所求的点P.求出BG 的表达式为:y=-31x+1,将其与y=-x ²+2x+3联立即可求出点P 的坐标.(2)利用“三角函数值相等”(或“△的相似”)求例如:已知:y=x ²-4x+3,与x 轴交于点A ,B 与y 轴交于点C ,顶点为D ,对称轴为l ,在l 上是否存在一点M 使∠ABC=∠AMD ?解析:存在.过点A 作AE ⊥BC 于点E ,利用ABC S △=21AB.OC=21BC.AE ,得AE=BC OC AB .=2332⨯=2,∴ CE=22AE AC -=22,∴tan ∠ACB=CE AE =21222=,设M(2,m),AN=1, ∴tan ∠AMD=MN AN =|m |1=21,∴m=±2,∴M(2,2)或(2,-2).。
二次函数的定义及特点

二次函数的定义及特点二次函数是形如f(x) = ax² + bx + c的数学函数,其中a、b、c都是实数且a ≠ 0。
特点一:二次函数的图像是抛物线。
抛物线可以是开口向上的,也可以是开口向下的,这取决于二次项系数a的正负。
特点二:二次函数的对称轴垂直于x轴,具有形如x=-b/(2a)的垂直线对称轴方程。
特点三:二次函数的顶点是抛物线的最高或最低点,具有形如(-b/(2a),f(-b/(2a)))的坐标。
特点四:二次函数的自变量x在整个实数范围内都有定义,即定义域为全体实数R。
特点五:二次函数的值域的范围是根据二次项系数a的正负而定。
若a>0,则值域为[f(-b/(2a)),+∞),即抛物线开口向上的情况;若a<0,则值域为(-∞,f(-b/(2a))],即抛物线开口向下的情况。
特点六:根据二次函数的图像,可以分析二次函数的零点和极值。
零点是函数图像与x轴的交点,是方程ax² + bx + c = 0的根;极值则是函数图像的最高或最低点,是顶点坐标的纵坐标值。
特点七:二次函数的导数是一次函数,导数函数f'(x) = 2ax + b,而且对于开口向上的二次函数,导数恒大于0;对于开口向下的二次函数,导数恒小于0。
特点八:二次函数的最大值或最小值是在其顶点处取得的,与一次函数不同,二次函数的最大值或最小值唯一存在。
特点九:二次函数与x轴的交点个数根据二次方程ax² + bx + c = 0的判别式来确定。
若判别式Δ = b² - 4ac > 0,则有两个不同实根,即抛物线与x轴有两个交点;若Δ = 0,则有一个重根,即抛物线与x 轴有一个交点;若Δ < 0,则无实根,即抛物线与x轴无交点。
特点十:二次函数的图像可以通过平移图像、伸缩图像、翻转图像等操作来得到其他二次函数的图像。
根据平移、伸缩和翻转的参数不同,可以得到不同形状和位置的抛物线图像。
二次函数特性

二次函数特性二次函数是数学中的重要概念,具有许多特性和性质。
本文将详细探讨二次函数的性质,包括顶点、对称轴、开口方向、零点、图像、以及常见的应用。
1. 顶点和对称轴二次函数的一般形式为y = ax^2 + bx + c,其中a、b、c为常数,且a不等于0。
顶点是二次函数的最高点或者最低点,对称轴则是通过顶点的一条直线。
顶点的横坐标可以通过 x = -b/(2a) 公式计算得出。
此时,纵坐标即为函数的最大值或最小值。
对称轴则是与纵坐标轴平行的直线,其方程为 x = -b/(2a)。
2. 开口方向二次函数的开口方向与a的正负有关。
当a大于0时,二次函数开口向上;当a小于0时,二次函数开口向下。
开口向上的函数具有最小值,开口向下的函数则具有最大值。
开口方向确定了函数的整体趋势,对于不同的应用场景,我们可以根据开口方向进行分析和推断。
3. 零点和因式分解二次函数的零点是函数与x轴交点的横坐标值。
求二次函数的零点可以通过将函数设置为0,得到一个二次方程进行求解。
一般来说,二次函数有两个不同的零点,也有可能有一个重解。
对于给定的二次函数,可以使用因式分解的方法来求得其零点。
将二次函数进行因式分解,得到的两个一次因子即为零点所对应的因子。
4. 图像二次函数的图像通常为一条平滑曲线,称为抛物线。
抛物线的形状和位置取决于a、b、c的值。
当a大于0时,抛物线开口向上,顶点在图像的最低点。
当a小于0时,抛物线开口向下,顶点在图像的最高点。
图像的对称轴通过顶点,并且与纵坐标轴平行。
从图像中可以读取二次函数的特征信息,如顶点、开口方向等。
5. 应用二次函数在实际生活中有着广泛的应用。
例如,抛物线的运动轨迹可以用二次函数来描述。
在物理学中,自由落体、抛体运动等都可以通过二次函数来建模。
经济学中,成本、利润等与产量的关系也可以用二次函数来刻画。
在工程学领域,二次函数可以用来描述材料的弯曲性能、光的反射特性等。
总结:二次函数是数学中一个重要的概念,具有许多特性和性质。
二次函数知识点

中考数学二次函数知识点二次函数概念:1.二次函数的概念:一般地,形如2y a x b x c =++(a b c ,,是常数,0a ≠)那么y 叫做x 的二次函数.这里需要强调:和一元二次方程类似,二次项系数0a ≠,而b c ,可以为零.二次函数的定义域是全体实数.二次函数2y a x b x c =++的结构特征:⑴ 等号左边是函数,右边是关于自变量x 的二次式,x 的最高次数是2,0a ≠. ⑵ a b c ,,是常数,a 是二次项系数,b 是一次项系数,c 是常数项.2.二次函数2ax y =的性质(1)抛物线2ax y =的顶点是坐标原点(0,0),对称轴是y 轴. (2)函数2ax y =的图像与a 的符号关系.①当0>a 时⇔抛物线开口向上⇔顶点(0,0)为其最低点;②当0<a 时⇔抛物线开口向下⇔顶点(0,0)为其最高点.(3)顶点是坐标原点,对称轴是y 轴的抛物线的解析式形式为2ax y =)(0≠a . 3.二次函数 cbx ax y ++=2的图像是对称轴平行于(包括重合)y 轴的抛物线. 4.二次函数c bx ax y ++=2用配方法可化成:()k h x a y+-=2的形式,其中abac k a b h 4422-=-=,. 5.二次函数由特殊到一般,可分为以下几种形式:①2ax y =;②k ax y +=2;③()2h x a y-=;④()kh x a y +-=2;⑤c bx ax y ++=2. 6.抛物线的三要素:开口方向、对称轴、顶点.①a 的符号决定抛物线的开口方向:当0>a 时,开口向上;当0<a 时,开口向下;a 相等,抛物线的开口大小、形状相同.②平行于y 轴(或重合)的直线记作h x =.特别地,y 轴记作直线0=x .7.顶点决定抛物线的位置.几个不同的二次函数,如果二次项系数a 相同,那么抛物线的开口方向、开口大小完全相同,只是顶点的位置不同.8.求抛物线的顶点、对称轴的方法(1)公式法:a b ac a b x a c bx ax y 442222-+⎪⎭⎫⎝⎛+=++=,∴顶点是),(ab ac a b 4422--,对称轴是直线a bx 2-=. (2)配方法:运用配方的方法,将抛物线的解析式化为()kh x a y +-=2的形式,得到顶点为(h ,k ),对称轴是直线h x =.(3)运用抛物线的对称性:由于抛物线是以对称轴为轴的轴对称图形,所以对称轴的连线的垂直平分线是抛物线的对称轴,对称轴与抛物线的交点是顶点.用配方法求得的顶点,再用公式法或对称性进行验证,才能做到万无一失.9.抛物线cbx ax y ++=2中,c b a ,,的作用 (1)a 决定开口方向及开口大小,a 的值越大,开口越小,反之a 的值越小,开口越大。
二次函数知识整理
二次函数知识整理一、二次函数的概念1、二次函数的基本概念一般地,我们把形如y=ax²+bx+c(a,b,c均为常数,a≠0)的函数叫做二次函数,称y=ax²+bx+c(a,b,c均为常数,a≠0)为二次函数的一般式,称a为二次项系数,b为一次项系数,c为常数项。
,y轴二、二次函数的基本形式1、一般式:y=ax²+bx+c(a,b,c均为常数,a≠0)2、两根式:二次函数y=ax²+bx+c可转化为两根式y=a(x-x₁)(x₁-x₂),若与x轴无交点,则不能这样表示。
3、顶点式:y=a(x-m)²+k(a,m,k是常数,a≠0)三、二次函数图像的性质1、二次函数的基本形式:y=ax²(a≠0)2、y=ax²(a≠0)的基本性质由y=ax²(a≠0)向上(当c>0)或向下(c<0)平移|c|个单位得。
4、y=a(x-m) ²的基本性质5、y=a(x-m) ²+k的基本性质由y=ax²(a≠0)先向右(当m>0)或向左(当m<0)平移|m|个单位,再向上(当k >0)或向下(k<0)平移|k|个单位得到。
四、二次函数图像的平移1、对于抛物线y=ax²+bx+c(a≠0)的平移通常先将一般式转化为顶点式y=a(x-m) ²+k,再遵循左加右减,上加下减的原则。
化为顶点式有两种方法:配方法,顶点坐标公式法。
在用顶点坐标公式法求出顶点坐标后,在写顶点式时,要减去顶点的横坐标,加上顶点的纵坐标。
2、y=ax²+bx+c沿y轴平移:向上(下)平移m(m>0)个单位,y=ax²+bx+c变成y=ax²+bx+c+m(或y=ax²+bx+c-m)3、当然,对于抛物线的一般式平移时,也可以不把它化为顶点式y=ax²+bx+c向左(右)平移m(m>0)个单位,变成y=a(x+m)²+b(x+m)+c (或y=a(x-m)²+b (x-m)+c)五、抛物线y=ax²+bx+c,中,a、b、c的作用1、a决定开口方向及开口大小,这与y=ax²中的a完全一样2、b和a共同决定抛物线对称轴的位置,由于抛物线y=ax²+bx+c的对称轴是直线x=-b/2a,故:b=0时,对称轴为y轴;b/a>0(即a、b同号)时,对称轴在y轴左侧;b/a<0(即a,b 异号) 时,对称轴在y轴右侧。
二次函数所有公式
二次函数所有公式
二次函数是高中数学中常见的函数,它可以用来描述椭圆、抛物线和双曲线。
它的形式为:y=ax²+bx+c(a≠0),其中a、b、c是常数。
二次函数有很多应用,比如在物理学中,可以
用来描述物体运动的轨迹,在经济学中,可以用来描述价格和需求的关系,在统计学中,可以用来描述数据的变化趋势等。
除了上述的一般形式,二次函数还有一些其他形式,如标准型:y=ax²+c;一般开根号型:y=a(x-h)²+k;反比例型:
y=k/x²;双曲线型:y=a/x²+bx+c;及抛物线型:y=ax²+bx+c (a>0)等。
二次函数也有一些关键特征,比如轴对称性、有界性和凹凸性。
轴对称性指的是二次函数图像在直线上对称,有界性指的是二次函数图像在横纵坐标轴两端都有确定的范围,凹凸性指的是二次函数图像的凹凸性,比如抛物线是凹的,双曲线则是凸的。
另外,二次函数还有一些其他的特征,比如二次函数的图像的最大值和最小值、二次函数的图像的极值点、二次函数的图像的单调性、二次函数的图像的对称性等。
总之,二次函数是一种非常有用的函数,它可以用来描述椭圆、抛物线和双曲线等几何图形,还可以用来描述物体运动的轨迹、价格和需求的关系、数据的变化趋势等。
它具有轴对
称性、有界性和凹凸性等关键特征,可以让我们更好地理解几何图形以及其他的数学问题。
二次函数所有表达式
二次函数所有表达式
二次函数是一种常见的数学函数,它的一般表达式为
y=ax^2+bx+c,其中a、b、c都是常数。
除了一般表达式,二次函数还可以用其他形式来表示。
1. 顶点式:y=a(x-h)^2+k,其中(h,k)为顶点坐标。
2. 截距式:y=a(x-p)(x-q),其中p、q分别为x轴上的两个点的坐标。
3. 标准式:(x-h)^2/4p+(y-k)^2/4q=1,其中(h,k)为椭圆的中心坐标,2p为椭圆在x轴上的轴长,2q为椭圆在y轴上的轴长。
4. 参数式:x=acosθ,y=bsinθ,其中(a,b)为椭圆的长短半轴长度,θ为椭圆上某一点与x轴正方向的夹角。
了解不同的二次函数表达式,可以更方便地进行函数的转化、计算和图像绘制。
- 1 -。
二次函数的三种表示方法
二次函数的三种表示方法
二次函数是一类在几何学、建筑学、计算机图形学和机械设计等领域研究中非常重要的函数。
由X和Y两个变量组成,用来描述四边形以上形状的函数,其可以用以下三种形式表示:
(1)通用表达式: y = ax2 + bx + c。
这是二次函数最基本的形式,各系数a、b、c可以有正有负,当a>0时,二次函数是一条上凸的曲线;当a<0时,是一条下凹的曲线。
(2)标准形式:y = a(x-h)2 + k。
它的系数a和复数h、k也可以有正有负,标准形式中,函数的顶点位于(h,k),曲线对称轴为点(h,k)中的 x 轴。
(3)终语:y = a(x + p)(x + q)。
这是二次函数的另一种形式,它表示由两个一次项和乘积组成。
各参数a、p、q也可以有正有负,两个根为:x1= -p and x2= -q。
以上就是二次函数的三种表示方法,它们在几何学、建筑学、计算机图形学等许多学科都有着广泛的应用。
充分利用它们可以很好的求解一些复杂的函数表达式,进而做出有效的工程计算。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
∴点C、D关于二次函数对称轴对称.
∵由二次函数解析式可得其对称轴为x=1,点C的坐标为(0,3),
∴点D的坐标为(2,3).
六、一元二次不等式:
一元二次不等式其实就是在一元二次方程的基础上进行的。其所有的都是围绕一元二次方程与X轴的交点问题进行。下面我们以y=ax2+bx+c(a>0)为例进行探讨。
在解答题甚至填空题时往往不会很直白的告诉你三个点的坐标,而是与我们已经学过的一次函数或者反比例函数联立使用,告诉我们二次函数与一次函数或者反比例函数相交,或者顶点坐标在其上面。例如二次函数与一次函数y=kx+b相交,则交点既在二次函数上也在一次函数上。因此在没有给定交点时,我们可以设点坐标为(x,kx+b)后,再带入求解。
解:∵二次函数的图象过点(-3,0),(1,0),
∴可设二次函数为y=a(x+3) (x-1) (a≠0),
展开,得y=ax2+2ax-3a,
顶点的纵坐标为 ,
由于二次函数图象的顶点到x轴的距离2,
∴|-4a|=2,即a= .
所以,二次函数的表达式为y= ,或y=-
三、二次函数与一次函数或者反比例函数的联立计算。
列表描述如下:
一元二次不等式 的解集:
设相应的一元二次方程 的两根为 , ,则不等式的解的各种情况如下表:
二次函数
( )的图象
一元二次方程
有两相异实根
有两相等实根
无实根
任意解
无解
无解
例:解关于x的不等式
解:原不等式可以化为:
若 即 则 或
若 即 则
若 即 则 或
练习:
1、抛物线y=ax2+bx+c的图象如图,则下列结论:①abc>0;②a+b+c=2;③a> ;
③:△<0,此时方程与坐标轴无交点,即对于任意的X均可以使y>0。
我们可以给出一个求一元二次不等式时的常见步骤,仍然以y=ax2+bx+c>0(a ),为例:
(1)、令y=ax2+bx+c=0,进而求出方程与坐标轴的交点(x1,0)和(x2,0)。
(2)、判断a的值确定函数的开口方向。
(3)、大致画出函数图像,判断取值范围。X轴上半部分,y值大于0;X轴下半部分y值小于0。
y>0,即ax2+bx+c>0。
①:△=b2-4ac>0,则说明方程y=ax2+bx+c与x轴有两个交点(x1,0)(x2,0)且x1<x2。再由图像可知ax2+bx+c>0的解就是x<x1或x>x2
②:△=0,此时方程与x轴仅有一个交点(x0,0),故对此要使ax2+bx+c>0,则x x0,即可。
二次函数解题方法归纳
一、对于给定的一个二次函数y=ax2+bx+c,我们首先要观察判断以下三点:
(1)a值,a的正负决定了开口方向,|a|的大小决定了二次函数开口大小。即a>0,开口向上,a<0开口向下。|a|越大,二次函数越扁平。
(2)顶点坐标。顶点坐标给了我们两个信息,一是对称轴x= ,对称轴可以用来判断y随x的变化而变化趋势。二是在X取全体实数的情况下,函数的最值。
(3)该二次函数图象上有一点D(x,y)(其中x>0,y>0),使S△ABD=S△ABC,求点D的坐标.
解:(1)将(3,0)代入二次函数解析式,得
-32+2×3+m=0.解得,m=3.
(2)二次函数解析式为y=-x2+2x+3,令y=0,得
-x2+2x+3=0 解得x=3或x=-1. ∴点B的坐标为(-1,0).
令y=ax2+bx+c(a>0),
在解答这类问题中,还是一点看对称轴,x= 与X的取值范围的关系:
①x= ,则对称轴在 的左侧,此时y随x的增大而增大,因此当x=a时,函数取最小值,而当x=b时,函数取最大值。
② ,即当 时,函数取得最小值,而对于最大值,则分别取x=a,和x=b带入计算,哪个对应的函数值较大,哪个就是最大值。
(1)求这个二次函数的解析式;
(2)设该二次函数图象的对称轴与x轴交于点C,连结BA.BC,求△ABC的面积.
7、已知不等式 的解是 求不等式 的解.
同时还要关注点的坐标求法。例如,直线x=5上的点横坐标均为5,这个要灵活应用,真的是要练才行。像此类题目多数是二次函数与一次函数联立,或者二次函数上有一动点的问题。
例:如图所示,二次函数y=-x2+2x+m的图象与x轴的一个交点为A(3,0),另一个交点为B,且与y轴交于点C.
(1)求m的值;(2)求点B的坐标;
4、已知抛物线 ( >0)的对称轴为直线 ,且经过点 ,试比较 和 的大小: _ (填“>”,“<”或“=”)
5、已知抛物线 与x轴没有交点.
(1)求c的取值范围;
(2)试确定直线y=cx+l经过的象限,并说明理由.
6、如图,已知二次函数y=- x2+bx+c的图象经过A(2,0)、B(0,—6)两点.
由于当1≤x≤16时,G随x的增大而增大,故当x=4时,即第4年可收回投资.
五、二次函数习题中面积求解。
在二次函数解题中涉及到面积求解时,所求面积肯定不是我们所知道的特殊图形面积。因此我们需要将所求面积分割,通常是沿坐标轴方向分割要么垂直做直线,要么竖直做垂线,或者延长图中直线与坐标轴相交。总之,目的只要一个,要把图形中的底和高Байду номын сангаас做成垂直坐标轴的,以便于计算。
③ 时,即对称轴在 的右侧,此时y随x的增大而减小,因此当x=a时取得最大值,当x=b时取得最小值。
例3:某企业投资100万元引进一条产品加工生产线,若不计维修、保养费用,预计投产后每年可创利33万.该生产线投产后,从第1年到第x年的维修、保养费用累计为y(万元),且y=ax2+bx,若第1年的维修、保养费用为2万元,第2年为4万元.
因为题目中往往不会很直白的给定三点坐标,而是仅给出一些特殊点的坐标,比如二次函数与横坐标的交点,此时我们可以设二次函数方程为截距式。因为这样设方程之后将点带入,即可化为仅含有一个字母的函数表达式。此后再利用题目给定的信息,便于计算。
例:已知二次函数的图象过点(-3,0),(1,0),且顶点到x轴的距离等于2,求此二次函数的表达式.
④b<1.其中正确的结论是______
第一题 第二题
2、如图,已知正方形ABCD的边长为4 ,E是BC边上的一个动点,AE⊥EF, EF交DC于F, 设BE= ,FC= ,则当点E从点B运动到点C时, 关于 的函数表达式__________
3、已知抛物线y=ax2+bx+c(a≠0)与x轴的两个交点的坐标是(5,0),(-2,0),则方程ax2+bx+c=0(a≠0)的解是_____
(1)求y的解析式;
(2)投产后,这个企业在第几年就能收回投资?
解:(1)由题意,x=1时,y=2;x=2时,y=2+4=6,分别代入y=ax2+bx,得a+b=2,
4a+2b=6,解得,a=1,b=1,所以y=x2+x.
(2)设G=33x-100-x2-x,则G=-x2+32x-100=-(x-16)2+156.
(3)函数与坐标的交点。函数与y轴的交点坐标即为(0,C)。函数与X轴的坐标为(X1,0)和(X2,0),可以通过ax2+bx+c=0计算得来。其中对称轴x= = 。
二、二次函数的表达式
(1)三点式,即已知任意的三个坐标点时可以设二次函数表达式为y=ax2+bx+c,进而带入求解。设方程时有个技巧要注意当已知二次函数与y轴交点时,比如该点为(0,5)可以直接设方程为y=ax2+bx+5,然后再带入其他两个点即可,简化我们的工作量。
例2已知某二次函数的最大值为2,图像的顶点在直线y=x+1上,并且图象经过点(3,-1),求二次函数的解析式.
分析:在解本例时,要充分利用题目中所给出的条件——最大值、顶点位置,从而可以将二次函数设成顶点式,再由函数图象过定点来求解出系数a.
解:∵二次函数的最大值为2,而最大值一定是其顶点的纵坐标,
(2)顶点式,当已知坐标轴顶点时,可设方程为y=a(x+ )2+k。之后再有一个点即可求出二次函数表达式。其实有时候题目中也会给出已知两点坐标和对称轴类的题型,在这种题型下我们依然可以设为顶点式或者也可以用一般式。其实顶点式就一般式的变形。
(3)截距式,即当已知二次函数与横坐标(X1,0)和(X2,0)时,可设方程为y=a(x-x1)(x-x2)。此后再已知一点即可求出函数表达式。
∴顶点的纵坐标为2.
又顶点在直线y=x+1上,
所以,2=x+1,∴x=1.
∴顶点坐标是(1,2).
设该二次函数的解析式为 ,
∵二次函数的图像经过点(3,-1),
∴ ,解得a=-2.
∴二次函数的解析式为 ,即y=-2x2+8x-7.
四、关于二次函数求最值。
在x取全体实数时,函数的最值就是顶点纵坐标。但是,更多的情况下,X是有一定的取值范围的,尤其是在实际问题中求取最值是最常见的。下面就二次函数给定取值范围的情况下判断最值点,如下:
